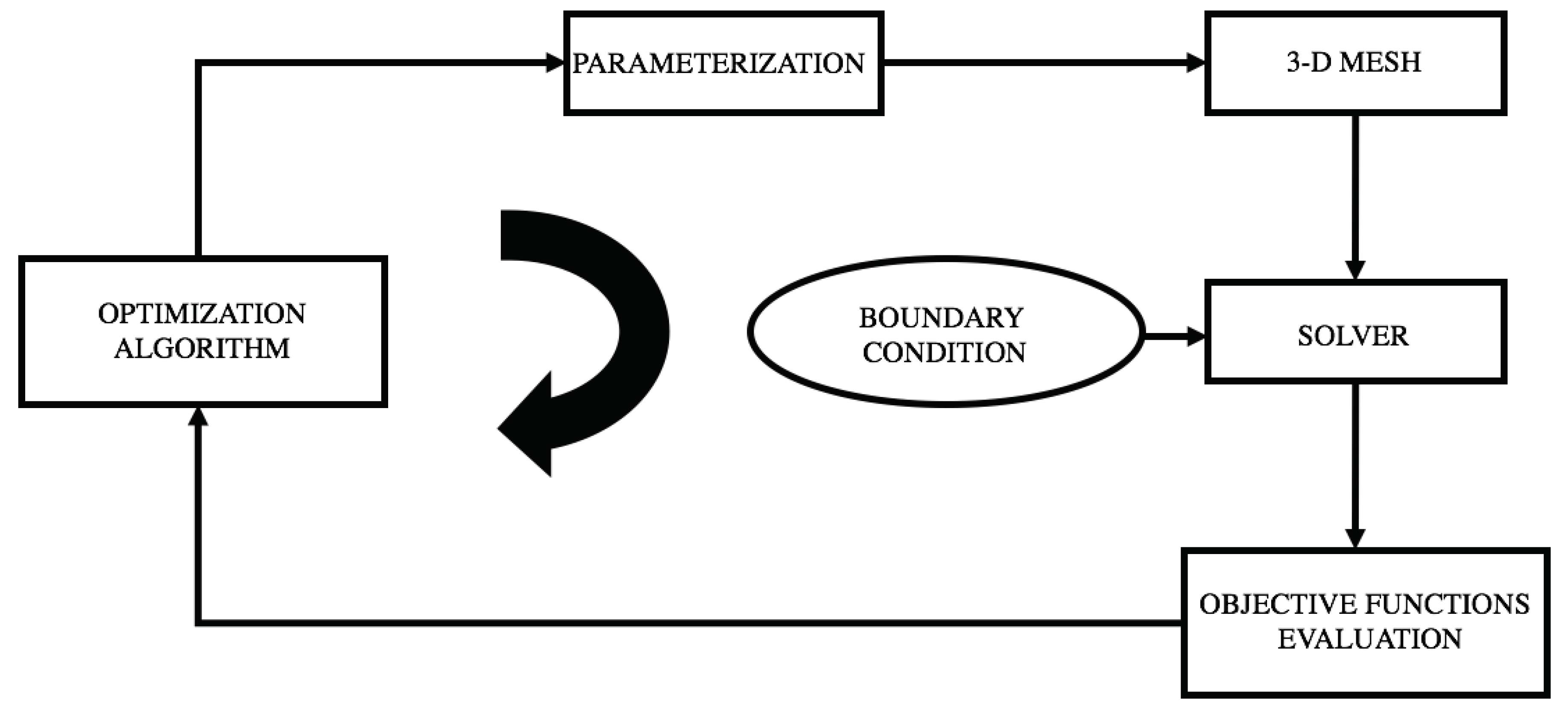
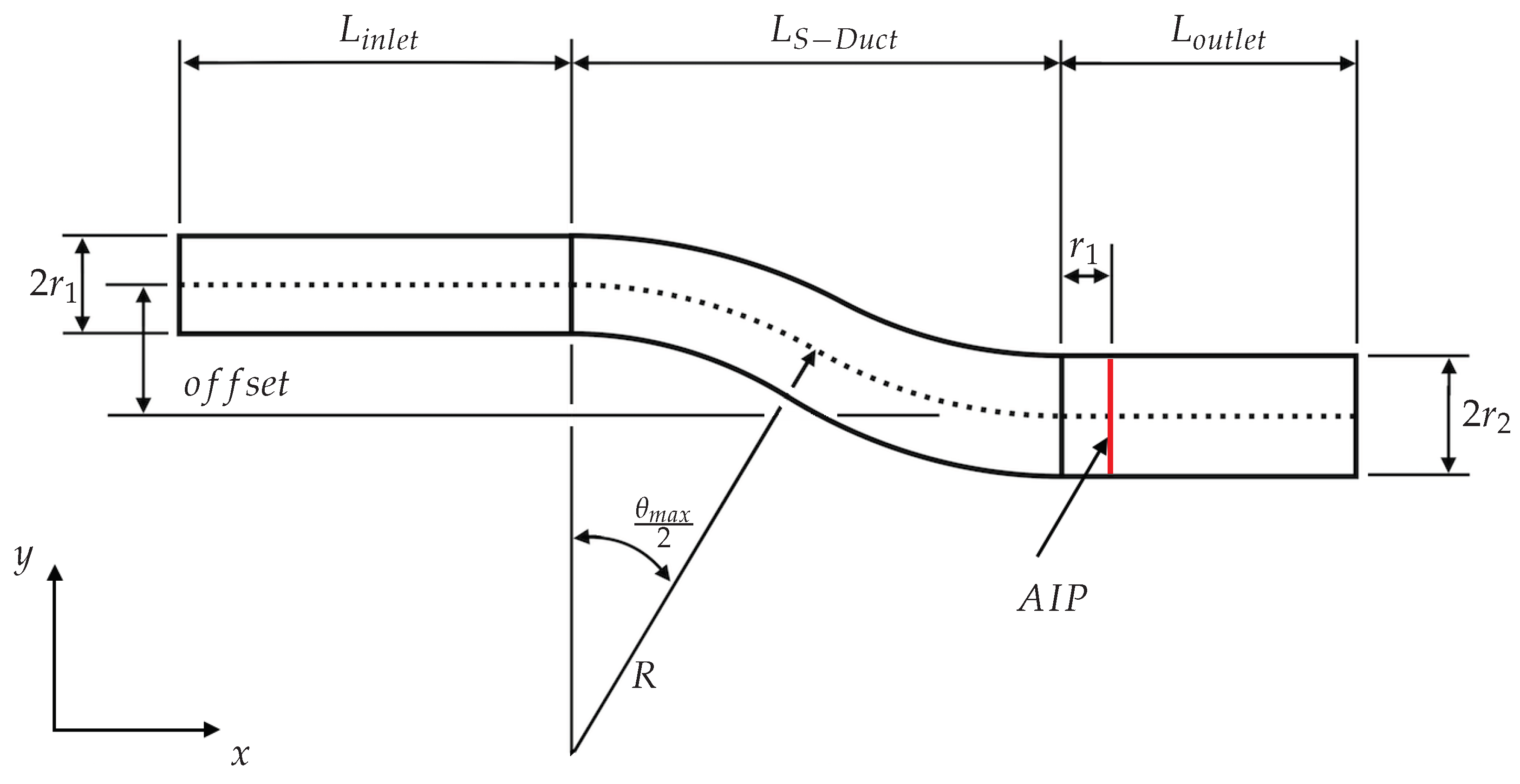
4.2. Results From the Optimization Process
The final results of our optimization are outlined in
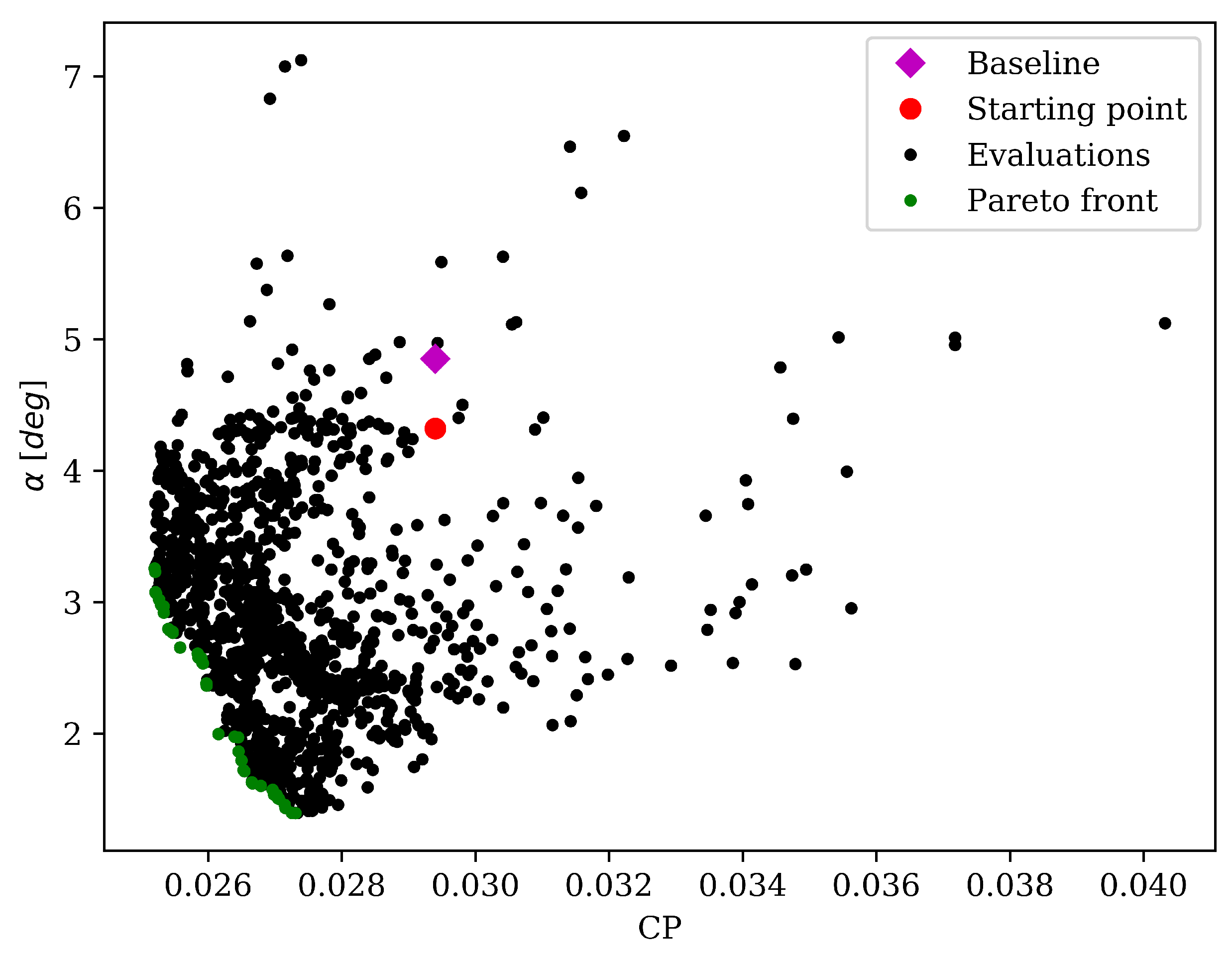
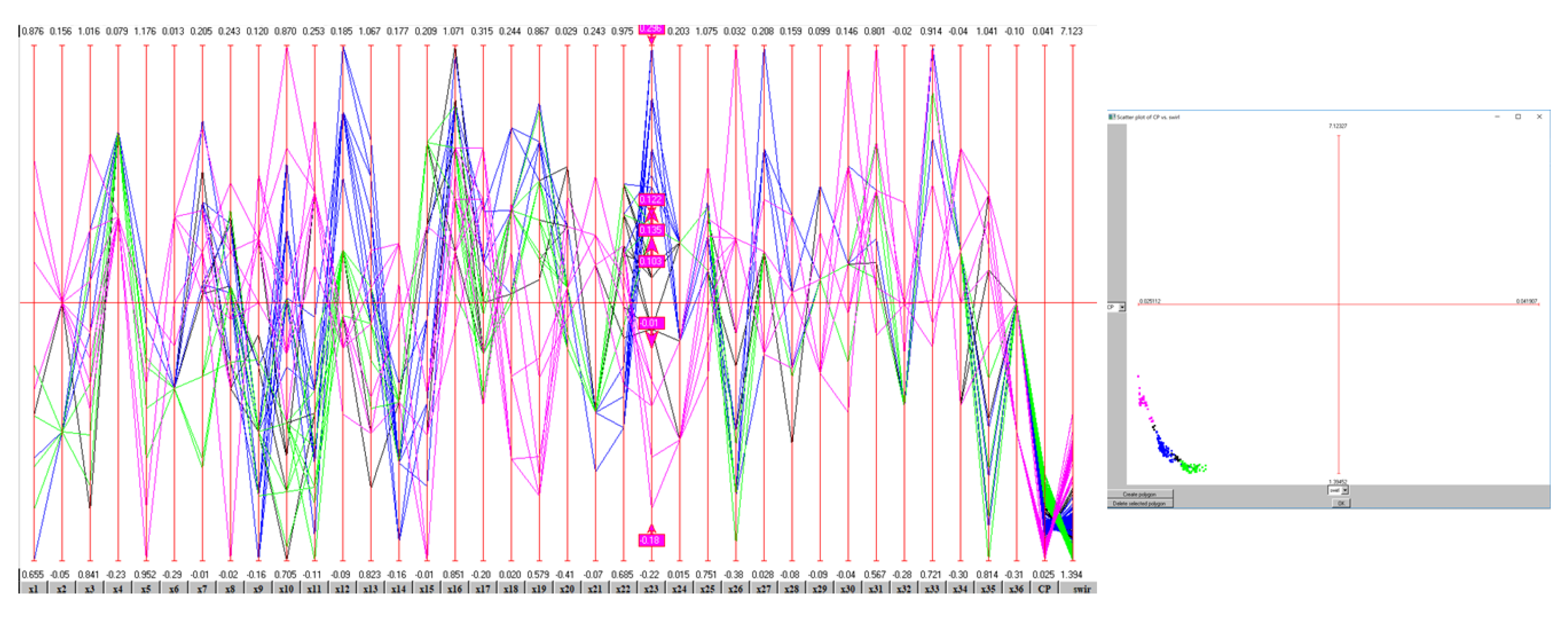
Figure 8. The baseline objective functions are indicated with a violet diamond. As already said, this is not the optimization starting point which instead is represented by a red dot. This point represents the value of the objective function of the geometry obtained employing our new parameterization. We performed a total of 1300 evaluations which produced the Pareto front highlighted by the green dots. This result however shows some discontinuity in the Pareto front which means that not all the design space has been explored and more evaluations are needed.
Despite this, our optimization already shows remarkable results as enlighten in
Table 7 in which there are collected the objective functions value for the two extreme point and some trade-off solutions on the Pareto front. The solution with minimal total pressure losses is named
and shows a reduction of about
compared to the baseline geometry. The solution with minimal swirl is named
and shows a reduction of about
compared to the baseline geometry. The trade-off solutions are named
,
and
and they are the point on the border of the main discontinuity in the Pareto front.
and
have similar
but different swirl angle;
and
instead has similar swirl angle and different
.
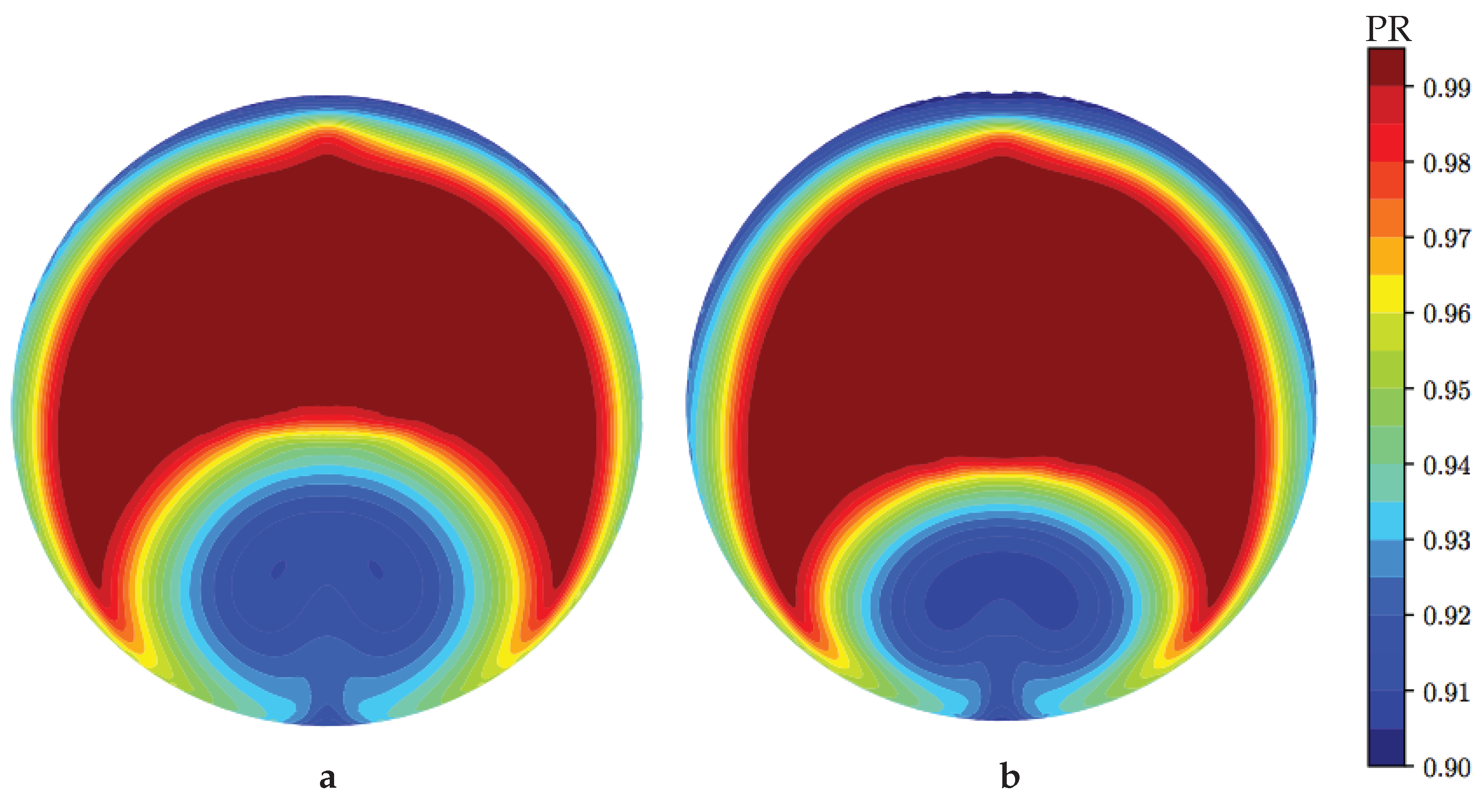
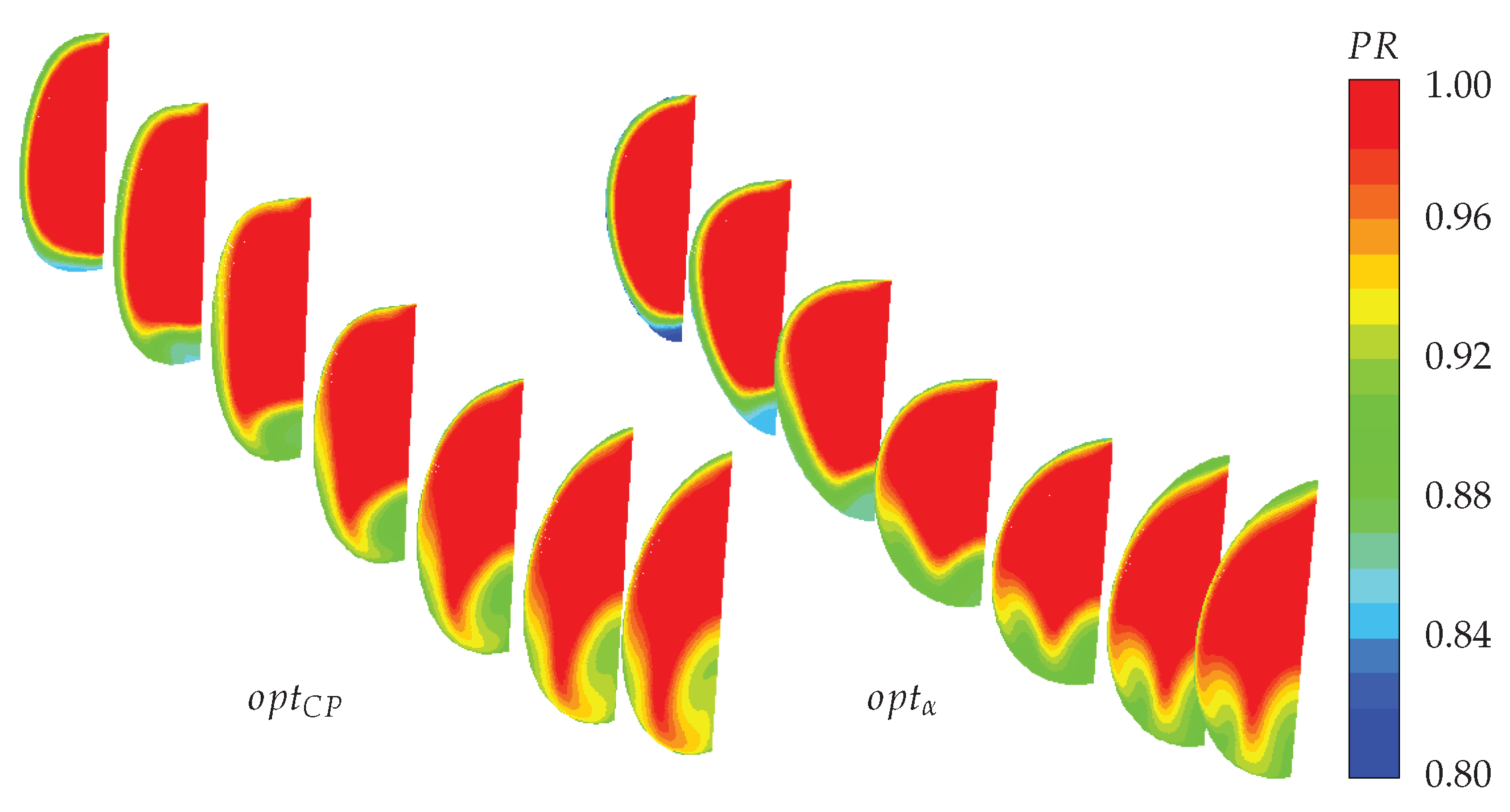
Analyzing the AIP distribution of total pressure we can see how in
(
Figure 9a) the low total pressure area near the lower duct portion has almost the same dimensions as the baseline, while the mean total pressure value has increased. However, a second and smaller low total pressure area appeared: its dimension is still small and its extension is confined near the external surface. Furthermore, we can see a general reduction in pressure losses near the external duct surface. If we consider now
(
Figure 9b) we can see how this second area increase in dimension to the point of equaling the main area. The latter has considerably diminished its dimensions compared to the baseline; however, the presence of this second low total pressure area frustrates any improvements.
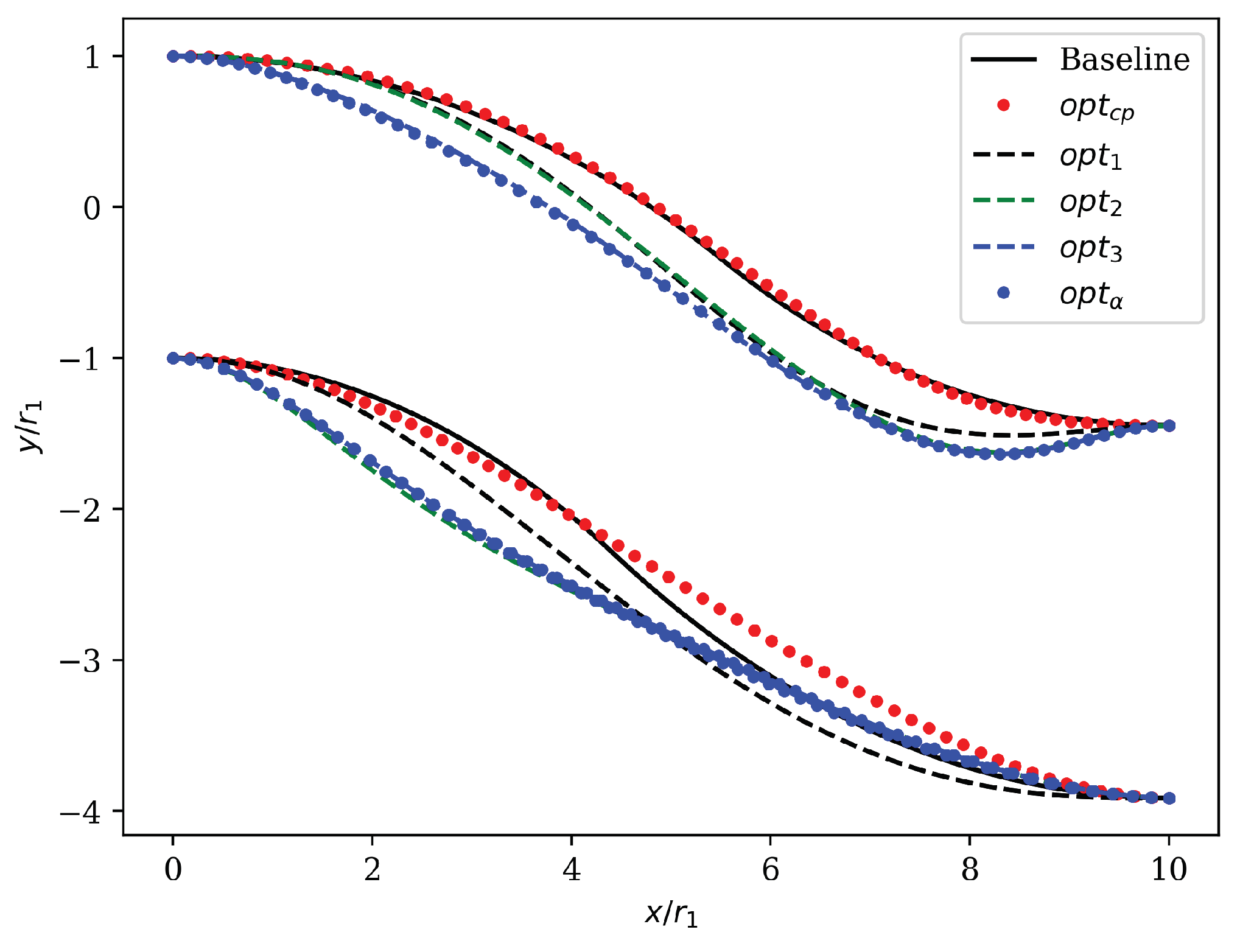
To understand this behavior we have to compare the geometry of the optimized ducts. In
Figure 10 there are a series of cross-section perpendicular to
x-direction from
and
showing total pressure contours. The appearance of the second low total pressure region we discuss earlier occurs in the second half part of the duct and its presence is relative to the particular shape that the duct assumes in the first half part: here
approaches a rectangular shape while
approaches a triangular shape. From
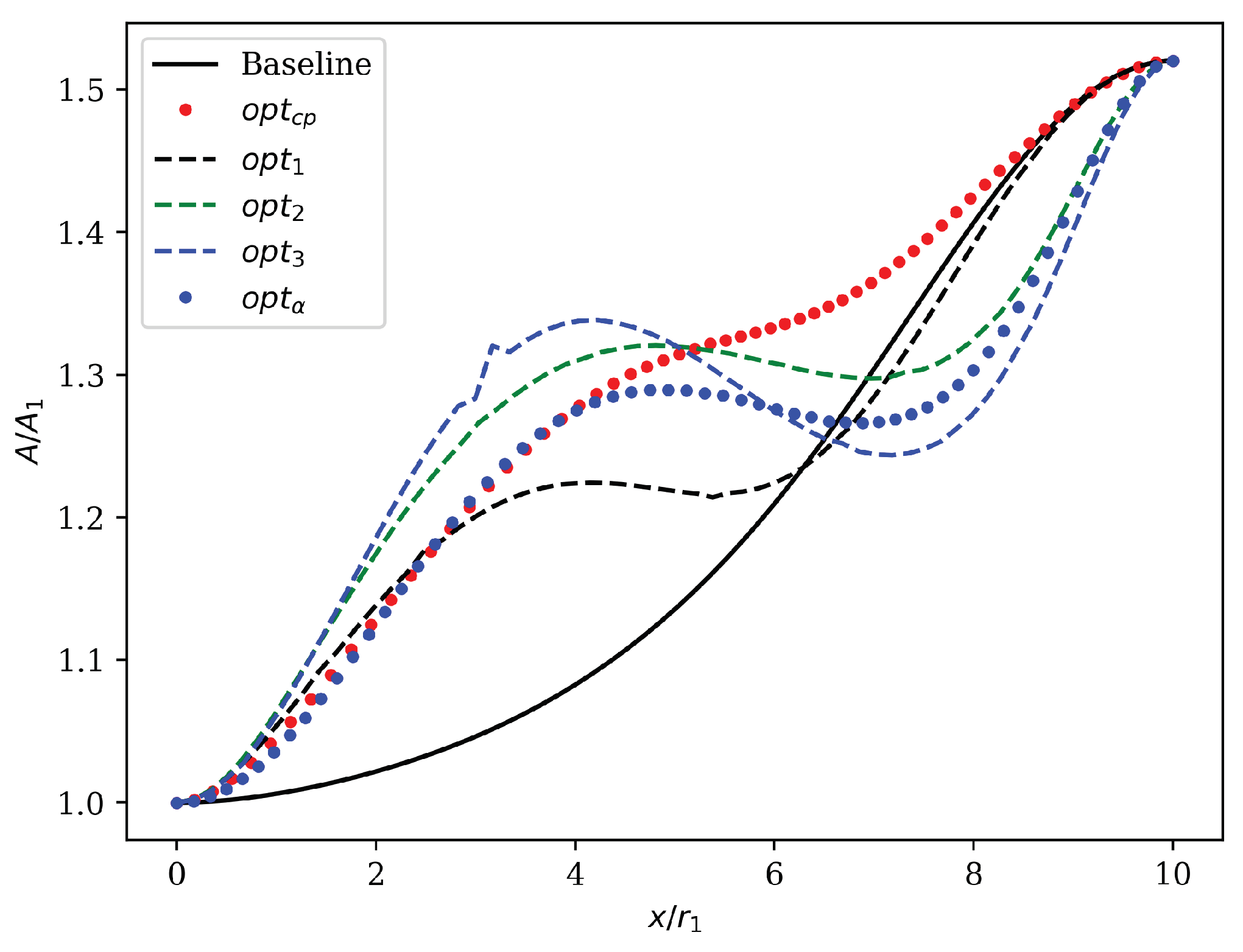
Figure 11 we can see that in the first half part of the duct both
and
has the same cross-section area; however, its distribution is completely different. In
the area distribution is almost symmetrical with respect to
-plane instead in
, since the triangular shape, the area distribution is mainly concentrated in the upper half part of the duct. To satisfy the constraint of circular cross-section at the outlet, each duct undergoes a deformation in their second half part. In correspondence of this enlargement occurs a second boundary-layer separation (
Figure 12) which leads to the creation of the secondary lower total pressure region. This behavior is much more evident in
since the transformation from triangular to circular shape in the lower part of the duct is much deeper and sudden.
In [
22] a similar optimization was performed on a S-Duct with rectangular cross-section. The best solutions in terms of
reduction show values smaller than
. Even if our best
is several times greater than this result, it is interesting to note how our optimization lead to find a best solution in terms of
reduction characterized by a rectangular cross-section.
Figure 13 illustrates the axial velocity distribution on the symmetry plane: here we can observe a significant shrinking of the separation bubble for all the optimal solutions compared to the baseline. Also in this case
and
show two different behavior: while in the first case the separation region is restricted just after the first duct bent, in the second case we can see a long separation area which runs for all the S-Duct length. Despite this, it remains very narrow and adjacent to the wall. Same behavior is shown by
and
, while
is much similar to
.
The size of the separation bubble is quantified from the distribution of the
x-component of the wall shear stress on the duct wall. The length of the recirculation region is calculated as the axial length for which we detected a negative shear stress, as outlined in
Figure 14. The baseline geometry shows a wide recirculation area located in the second half part of the duct. In
and
, instead, we can observe a reduction on the axial velocity in the lower part of the duct:
shows only a small and very weak recirculation region in the first half part of the duct while
shows no recirculation at all. High flow distortions are responsible for the low total pressure area in a S-Duct. However, even if
does not show any recirculation area it is not the best solution in terms of pressure losses reduction. This is due to its cross-section shape that, like
has, is triangular which means the presence of a second low total pressure region.
For
,
and
, instead, the recirculation area is clearly evident and it occurs in the initial/central part of the duct upstream of where it occurs in the baseline. Furthermore
and
show a secondary and weaker recirculation region towards the end of the S-Duct. Despite this, the separation region remains always very narrow and close to the duct lower wall. This behavior comes from two different geometric factors. The first is the ducts profile on the symmetry plane: the lower curve starts with a strong and fast downward bent followed by a constant slope section that ends at the outlet fitting (
Figure 15). This are the reason of the early separation in comparison with the baseline. The second is the cross-section area distribution: unlike the baseline and
, all the other ducts present a first fast increase in the cross-section area followed by a local minimum and a second fast increase (
Figure 11) characterized by a similar slope as the first part. This means that at about three quarter of these ducts there is a gauge as highlighted also by the upper line in the symmetry plane section (
Figure 15). This gauge forces the flow to increase its velocity and, in particular, to decrease its static pressure through it.
To better understand this last statement we have to consider
Figure 16 in which are represented the static pressure profile in different cross-section of
and
. As already experimentally observed in Wellborn et al. [
3,
8],
shows an inversion in the pressure gradient direction about halfway along the length of the duct. This explain why in this geometry (together with the baseline and
) the separation region is pushed towards the upper wall continuing to increase its size. In
instead, static pressure is almost constant in the first half part of the duct and a weaker pressure gradient with respect to
appears only in the second half part. Same behavior is shown by
and
. This explains both the long narrow separation region and the second separation region in
and
.
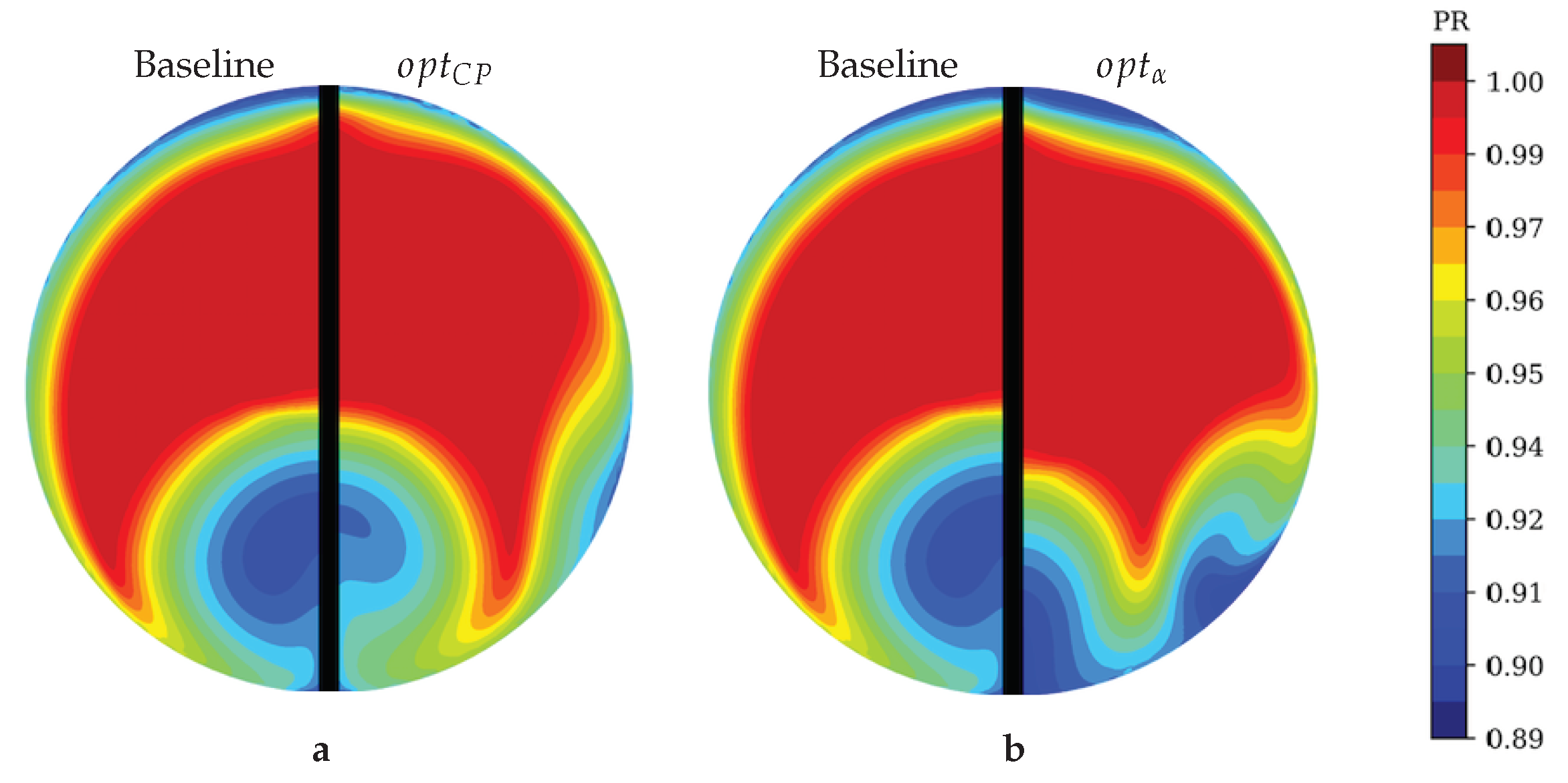
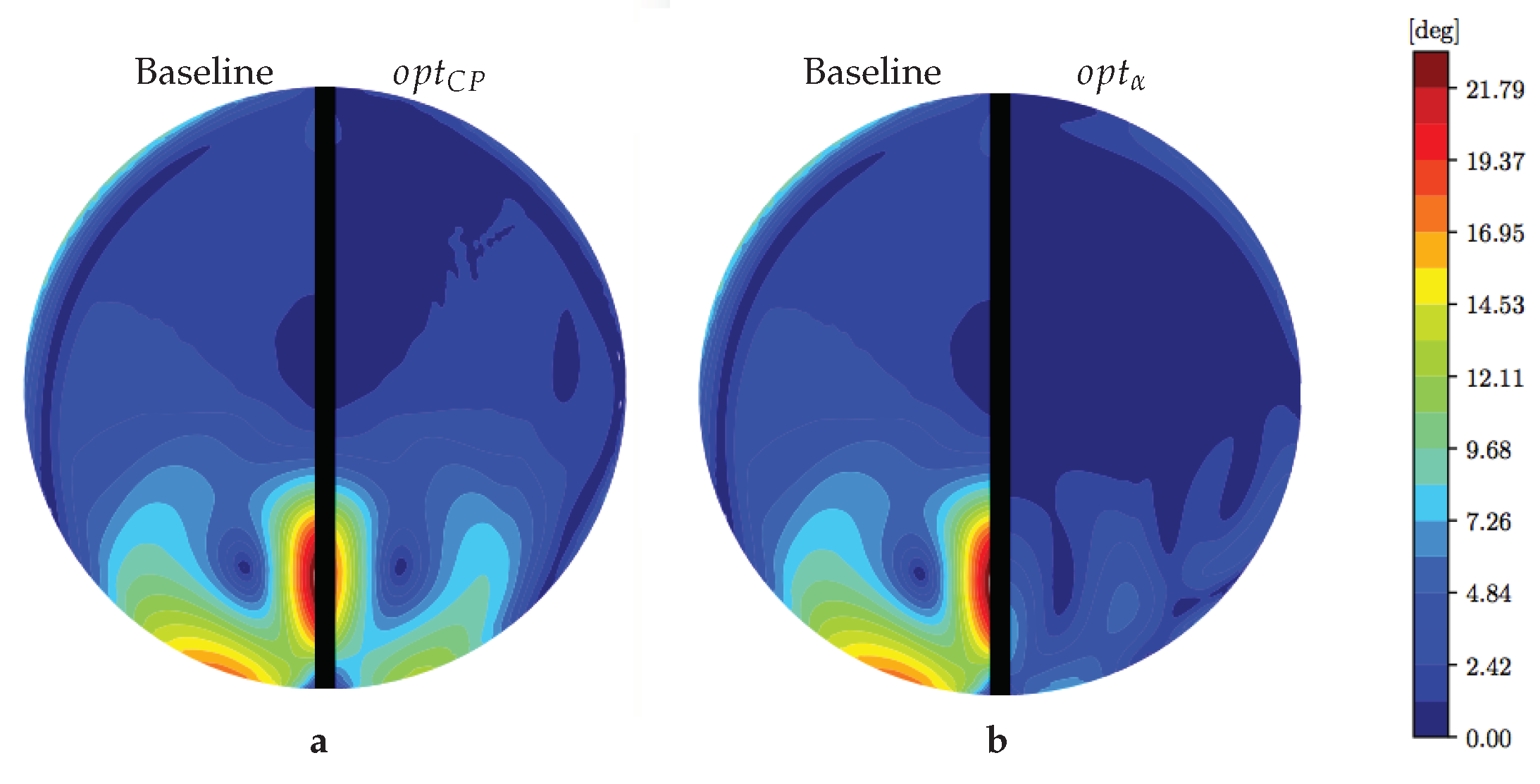
The swirl reduction is the main achievement of this numerical simulation. In fact, in
we obtained an impressive reduction of mean swirl angle of about
at the AIP. Here the swirl angle has a maximum value of
, almost one third with respect to the baseline (
). If we consider the contour plot at the AIP (
Figure 17) we can see how
differs from zero only in the lower part of the duct. Furthermore
, even if it represents the worst solution in terms of swirl angle reduction, shows a substantial improvement of about
. Remembering the definition of swirl angle (Equation (
16)), to explain this achievement we have to analyze the axial and tangential velocity distribution: all depends on the ratio of these two quantities at the AIP. In
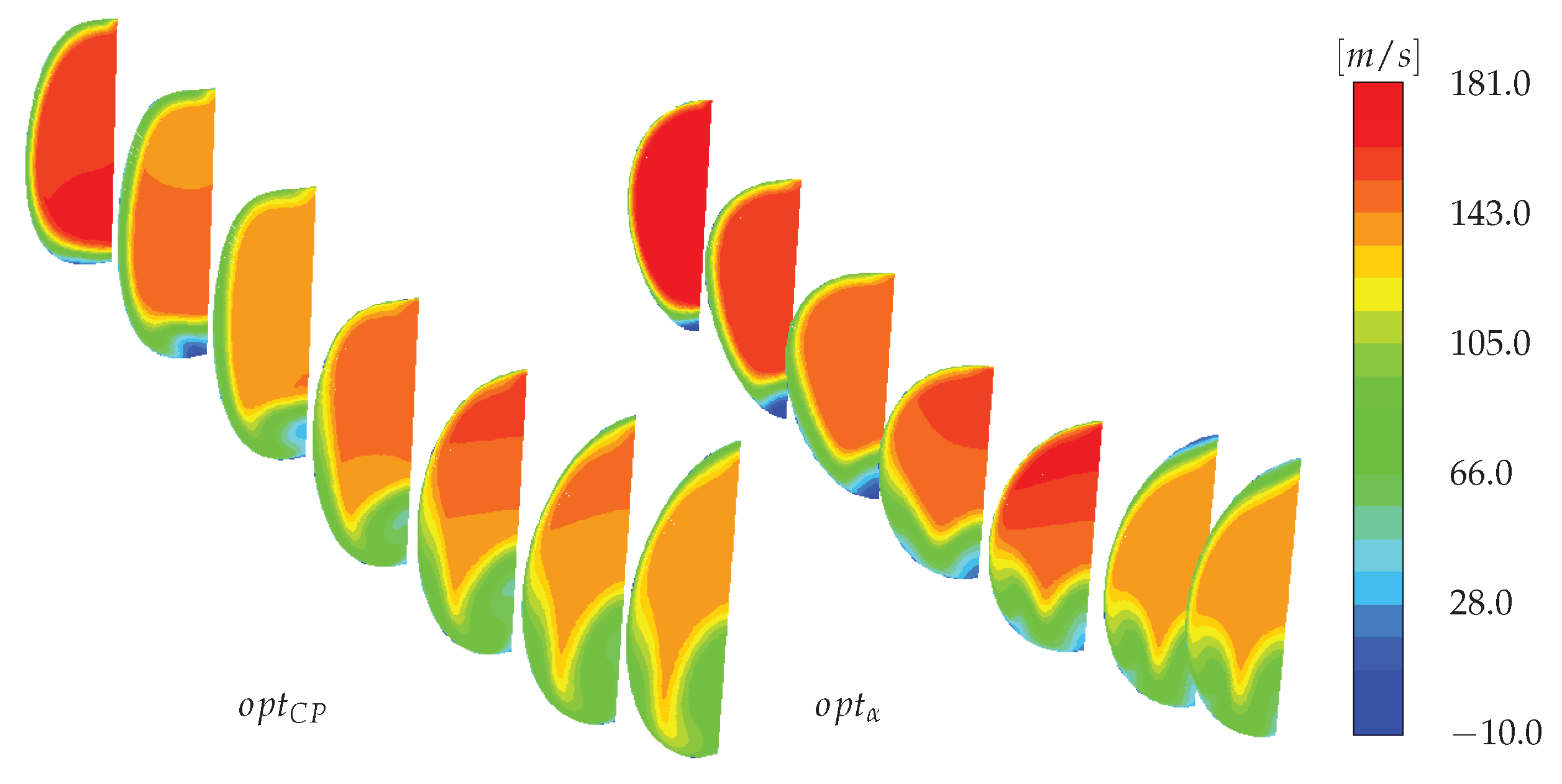
Figure 13 it is represented the axial velocity profile in different cross-section of
and
. At the AIP we can observe a similar velocity distribution with the exception of presence of the second low total pressure area in the first half part of
. For that reason swirl angle is strongly linked to tangential velocity distribution.
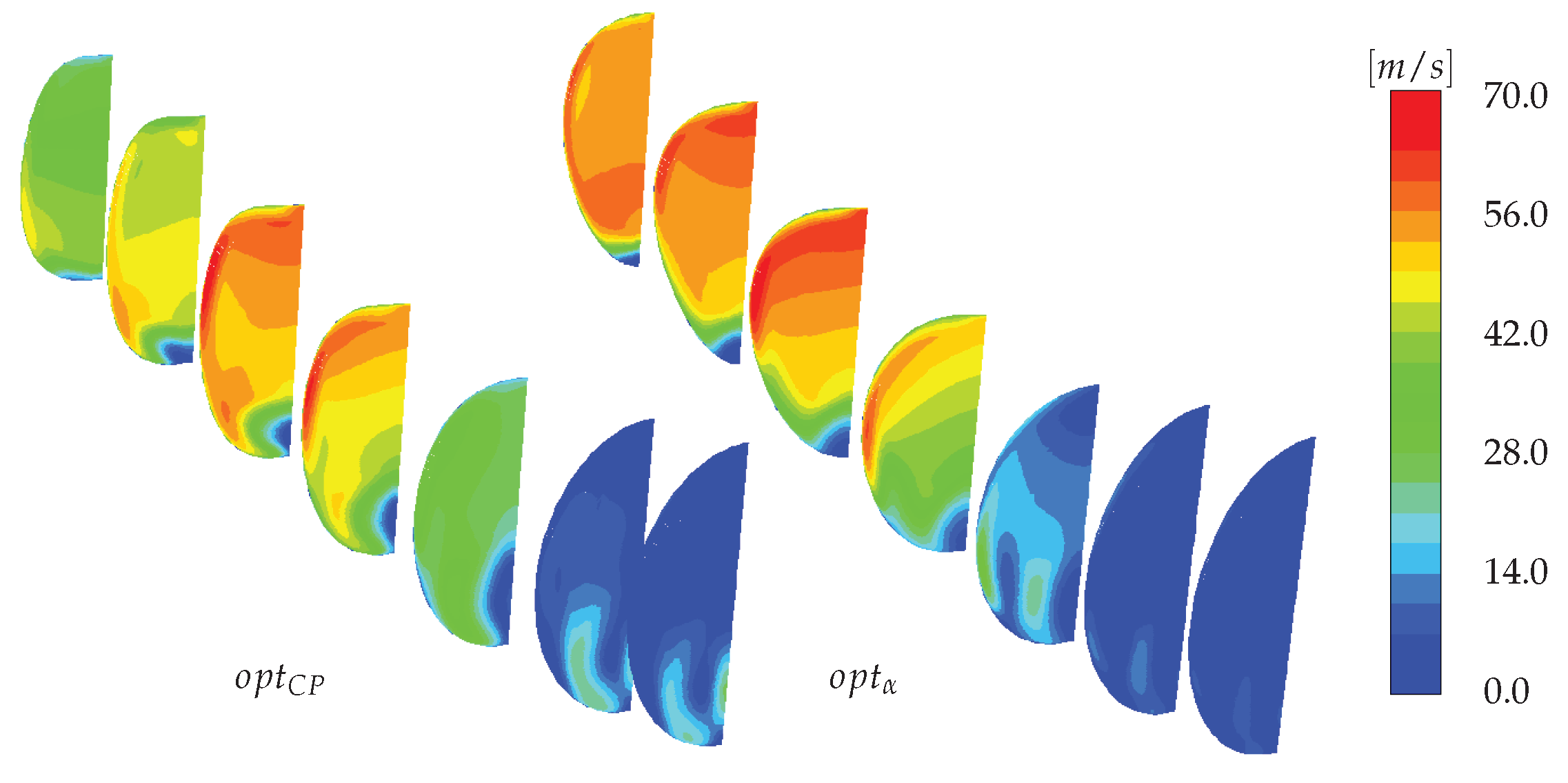
In
Figure 18 it is represented the absolute value of tangential velocity profile in different cross-section of
and
. At the AIP the tangential velocity is close to zero in the upper part of both ducts. The lower part instead, is characterized by higher values due to the separation region. Here we can in fact distinguish two regions of high tangential velocity just in correspondence to the two separation regions, one on the symmetry plane and one near the external wall. The extreme low tangential velocity value in
is, also in this case, linked to the particular triangular shape of this duct. As already said, the strong area increases in the ending and lower part of the duct due to the transition from triangular to circular cross-section implement the diffusing duct characteristic leading to an increase in static pressure and a strong reduction in tangential velocity.