Temporal Limits of Visual Motion Processing: Psychophysics and Neurophysiology
Abstract
:1. Introduction
2. Methods
2.1. Electrophysiological Preparation and Recordings
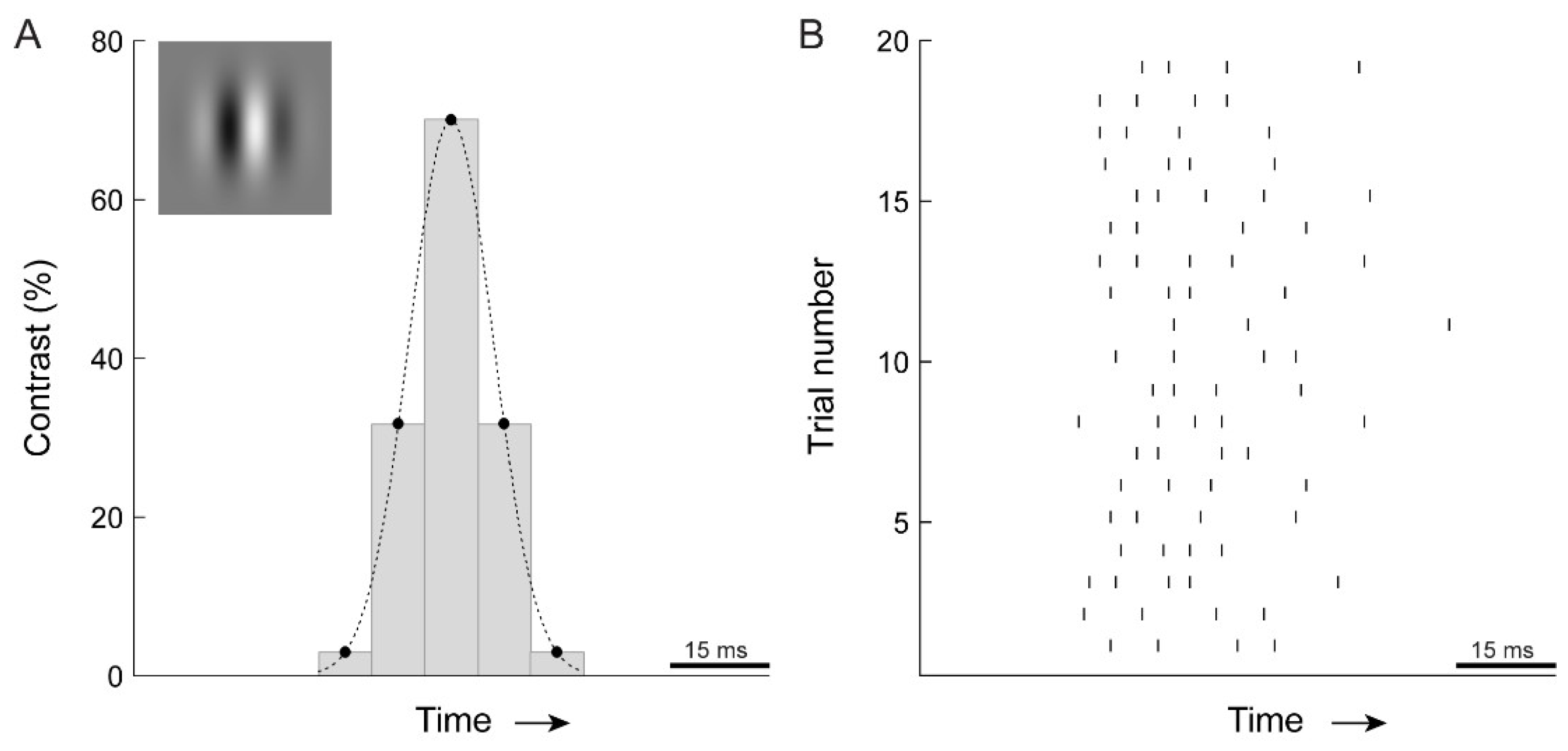
2.2. Visual Stimulation
2.3. Psychophysics
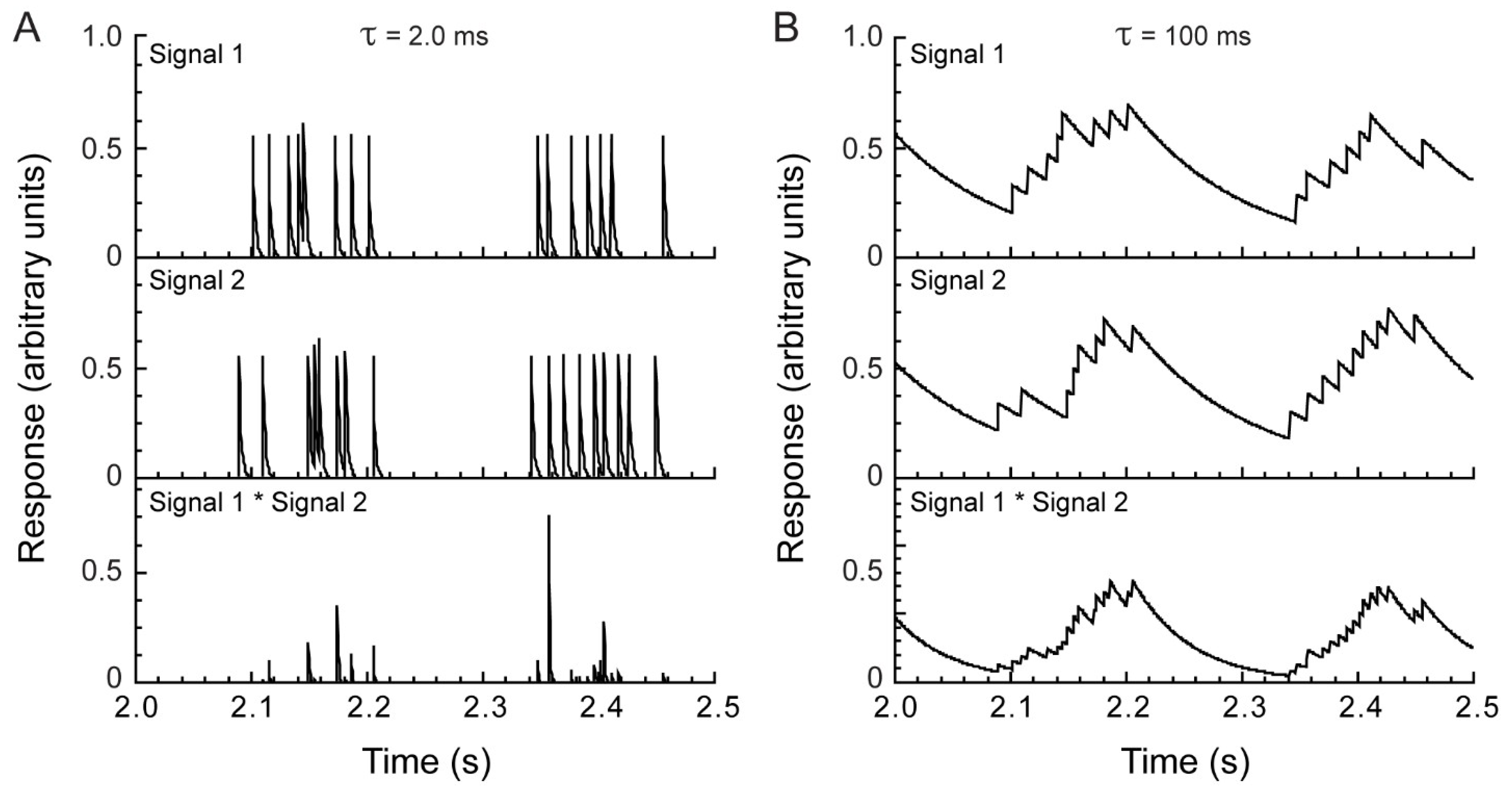
2.4. Model Analysis
3. Results
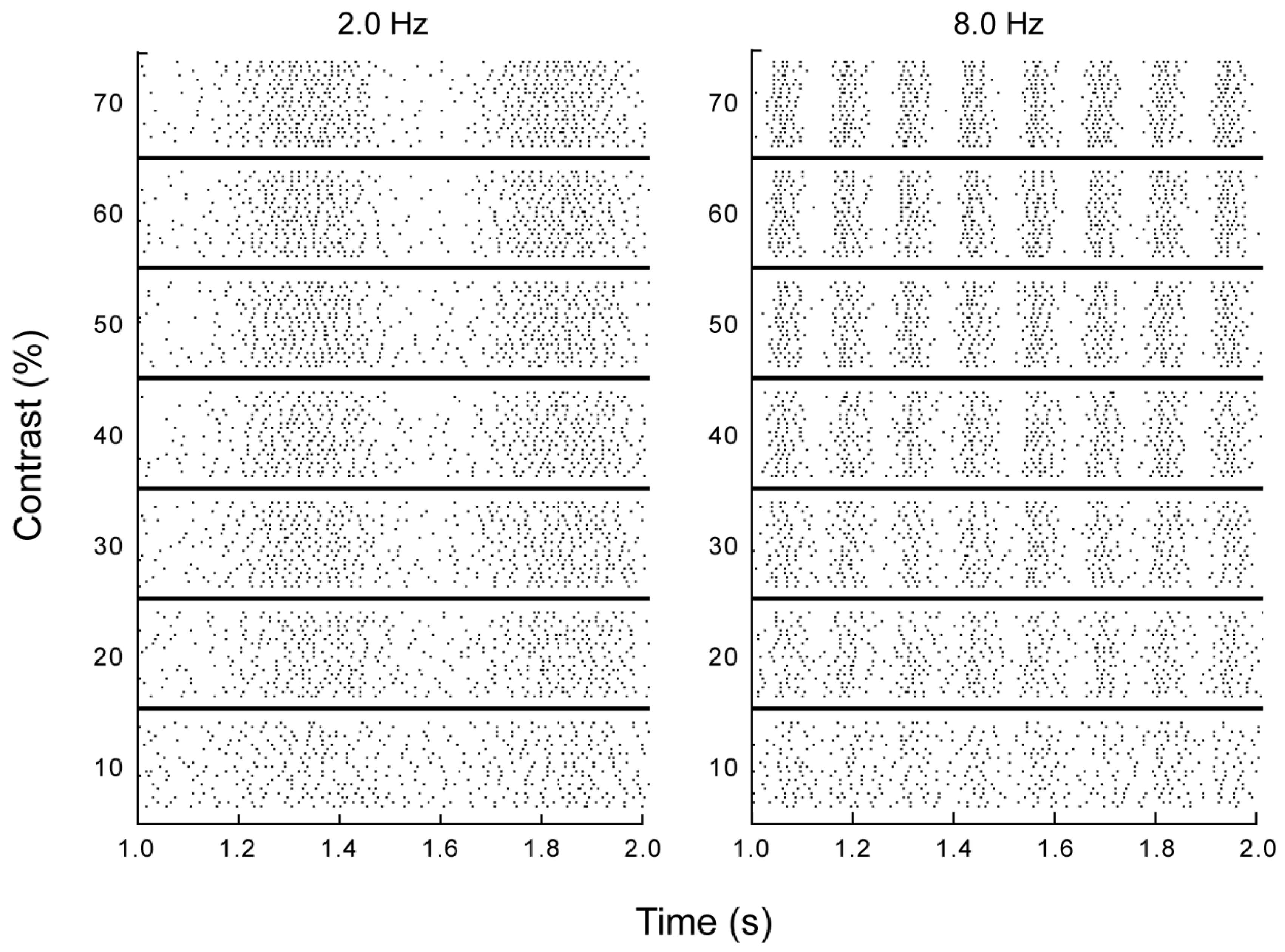
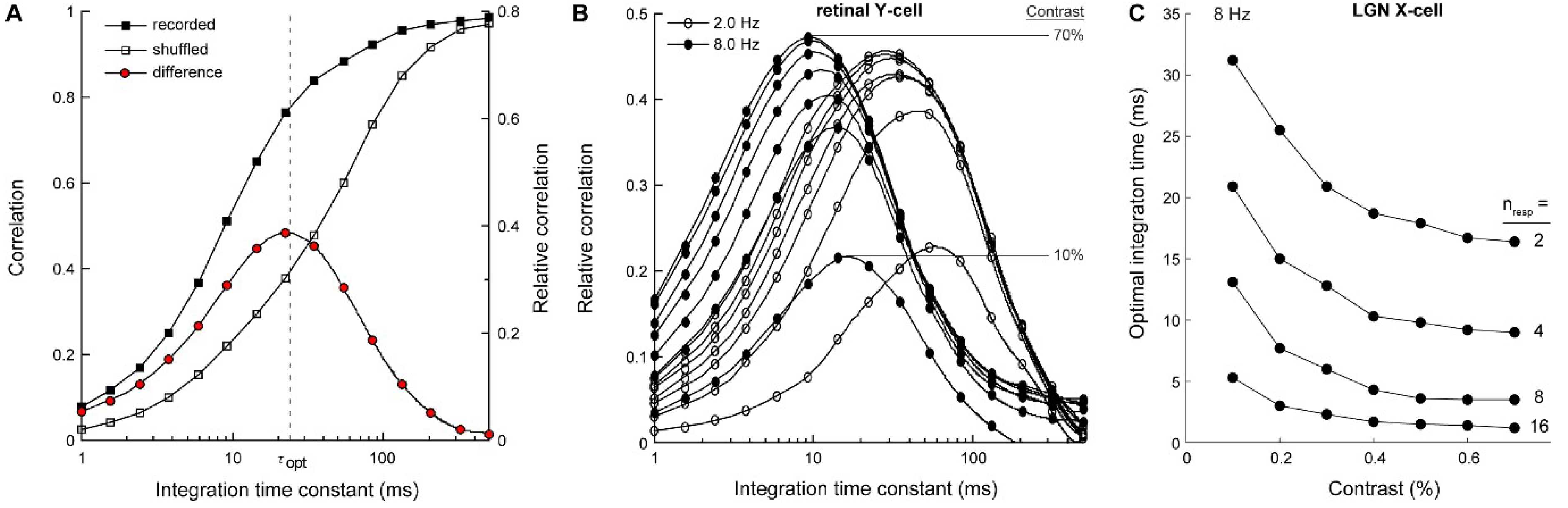
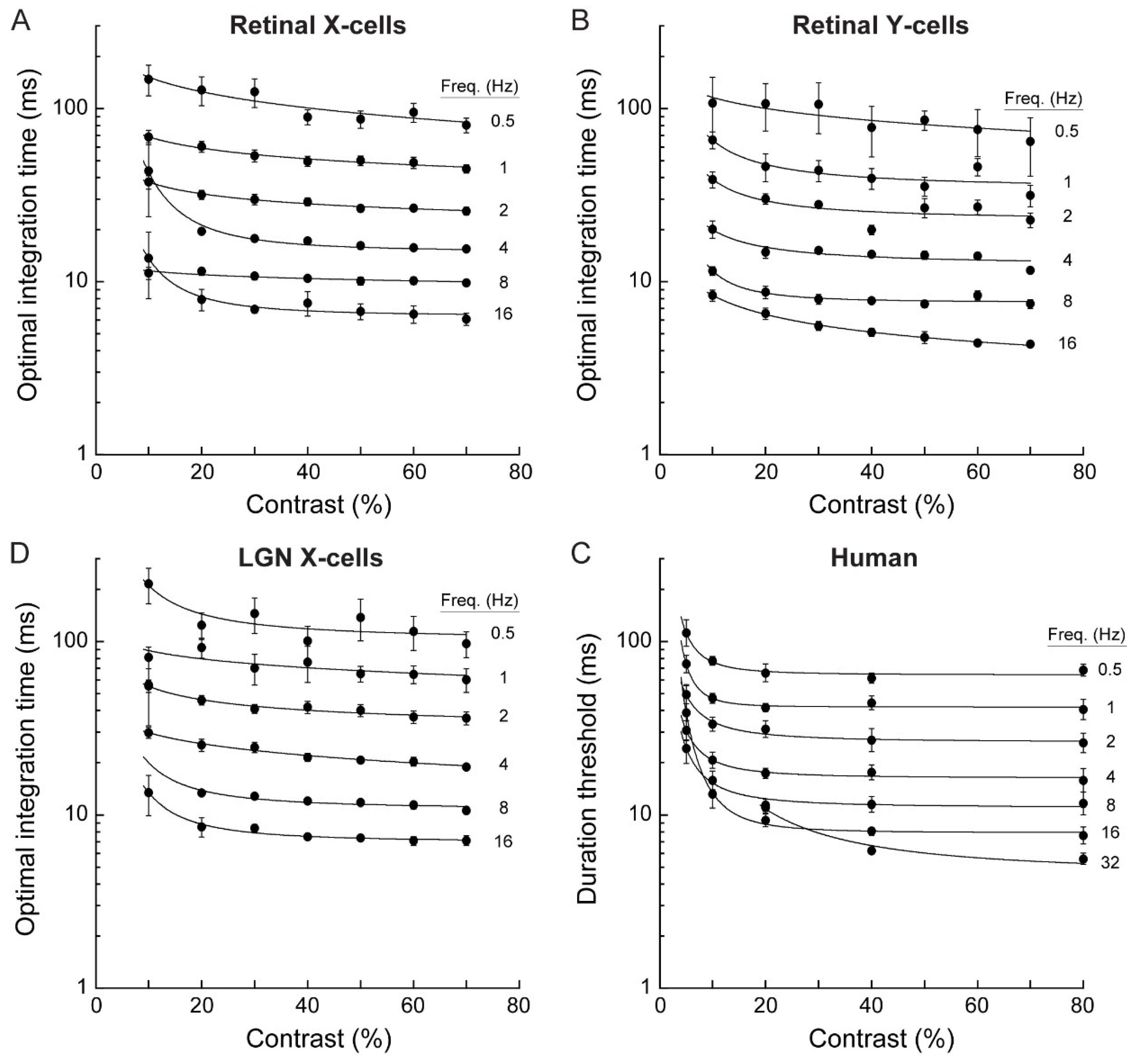
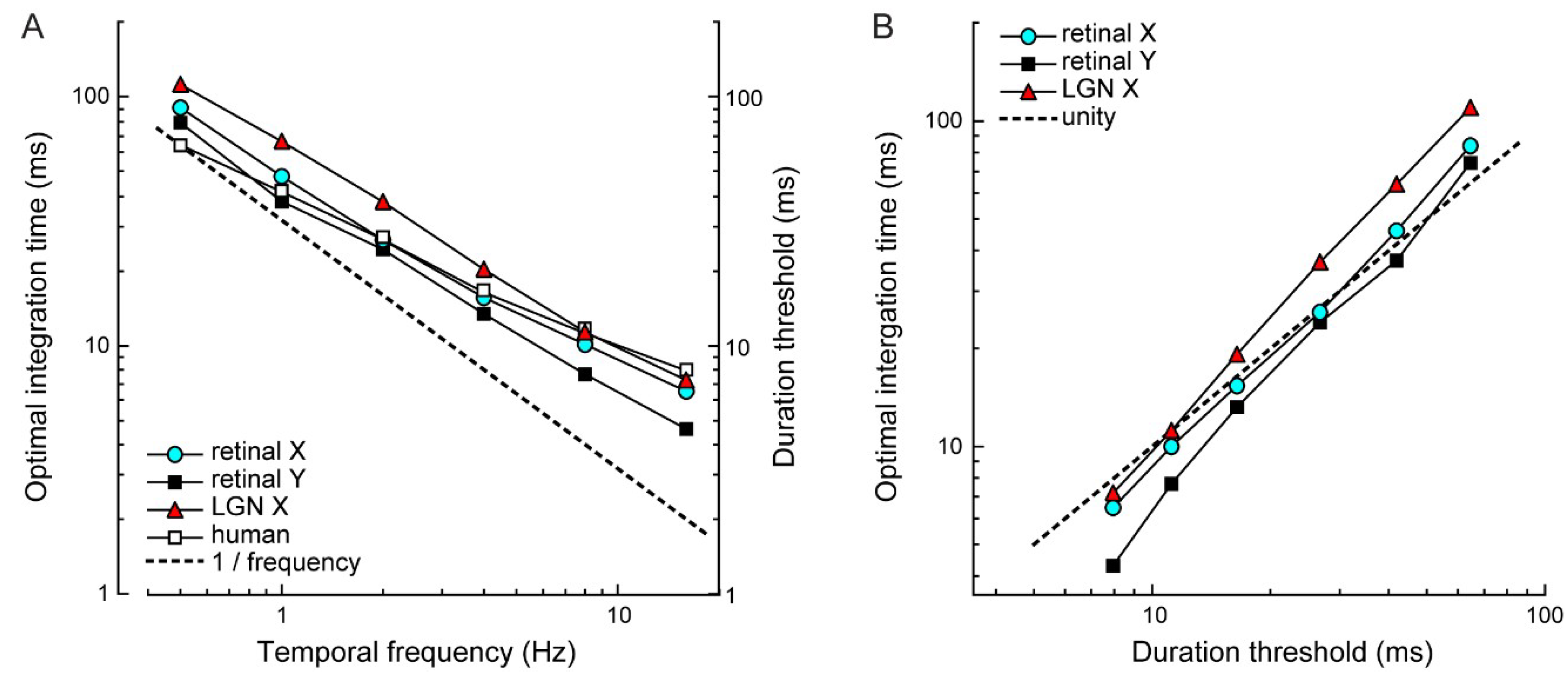
3.1. Electrophysiology and Modeling
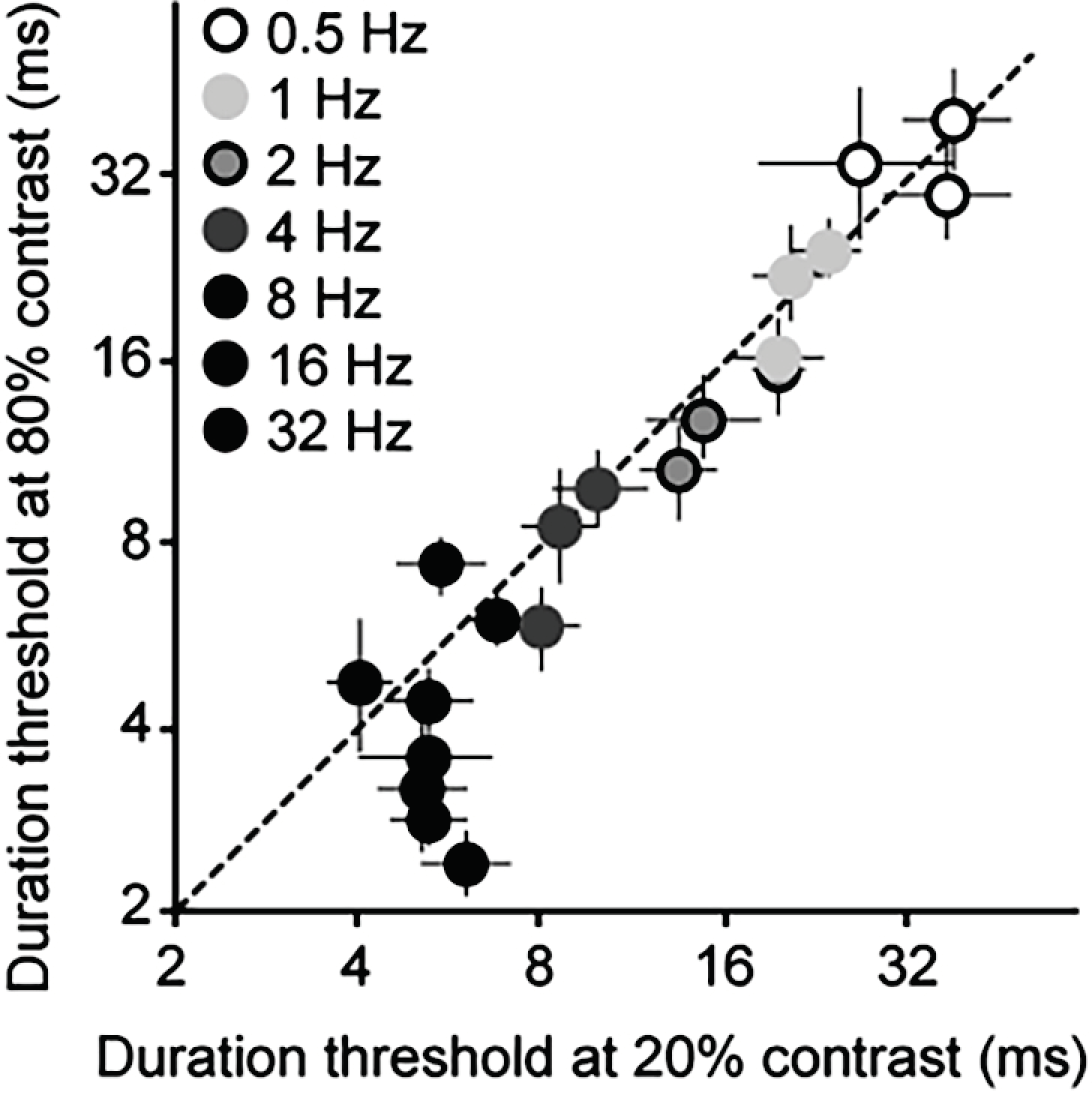
3.2. Psychophysics
4. Discussion
4.1. Comparison to Other Reports of Motion Acuity
4.2. Comparing Electrophysiology to Psychophysics
4.3. Significance of the Optimal Integration Time
4.4. Use of Single Cells to Assess Correlation Detection
4.5. Species Differences
4.6. Psychophysical Assumptions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Exner, S. Experimentelle Untersuchung der einfachsten psychischen Processe: III. Abhandlung, Der persönlichen Gleithung zweiter Teil. Pflügers Archiv für die gesamte Physiologie der Menschen und der Thiere 1875, 11, 403–432. [Google Scholar] [CrossRef]
- Sweet, A.L. Temporal discrimination by the human eye. Am. J. Psychol. 1953, 66, 185–198. [Google Scholar] [CrossRef] [PubMed]
- Wehrhahn, C.; Rapf, D. ON- and OFF-pathways form separate neural substrates for motion perception: Psychophysical evidence. J. Neurosci. 1992, 12, 2247–2250. [Google Scholar] [CrossRef]
- Westheimer, G.; McKee, S.P. Perception of temporal order in adjacent visual stimuli. Vis. Res. 1977, 17, 887–892. [Google Scholar] [CrossRef]
- Born, R.T.; Bradley, D.C. Structure and function of visual area MT. Annu. Rev. Neurosci. 2005, 28, 157–189. [Google Scholar] [CrossRef]
- Schmolesky, M.T.; Wang, Y.; Hanes, D.P.; Thompson, K.G.; Leutgeb, S.; Schall, J.D.; Leventhal, A.G. Signal timing across the macaque visual system. Child Abuse Negl. 1998, 22, 481–491. [Google Scholar] [CrossRef]
- Fairbank, B.A., Jr. Moving and nonmoving visual stimuli: A reaction time study. Percept. Mot. Skills 1969, 29, 79–82. [Google Scholar] [CrossRef] [PubMed]
- Buracas, G.T.; Zador, A.M.; DeWeese, M.R.; Albright, T.D. Efficient discrimination of temporal patterns by motion-sensitive neurons in primate visual cortex. Neuron 1998, 20, 959–969. [Google Scholar] [CrossRef]
- Elstrott, J.; Feller, M.B. Vision and the establishment of direction-selectivity: A tale of two circuits. Curr. Opin. Neurobiol. 2009, 19, 293–297. [Google Scholar] [CrossRef]
- Lochmann, T.; Blanche, T.J.; Butts, D.A. Construction of direction selectivity through local energy computations in primary visual cortex. PLoS ONE 2013, 8, e58666. [Google Scholar] [CrossRef] [PubMed]
- Peterson, M.R.; Li, B.; Freeman, R.D. The derivation of direction selectivity in the striate cortex. J. Neurosci. 2004, 24, 3583–3591. [Google Scholar] [CrossRef] [PubMed]
- Stanley, G.B.; Jin, J.; Wang, Y.; Desbordes, G.; Wang, Q.; Black, M.J.; Alonso, Jo. Visual orientation and directional selectivity through thalamic synchrony. J. Neurosci. 2012, 32, 9073–9088. [Google Scholar] [CrossRef] [PubMed]
- Chichilnisky, E.J.; Kalmar, R.S. Temporal resolution of ensemble visual motion signals in primate retina. J. Neurosci. 2003, 23, 6681–6689. [Google Scholar] [CrossRef] [PubMed]
- Frechette, E.S.; Sher, A.; Grivich, M.I.; Petrusca, D.; Litke, A.M.; Chichilnisky, E.J. Fidelity of the ensemble code for visual motion in primate retina. J. Neurophysiol. 2005, 94, 119–135. [Google Scholar] [CrossRef] [PubMed]
- Borghuis, B.G. Spike Timing Precision in the Visual Front-End; Utrecht University Library: Utrecht, The Netherlands, 2003; pp. 97–121. [Google Scholar]
- Butts, D.A.; Weng, C.; Jin, J.; Yeh, C.; Lesica, N.A.; Alonso, J.; Stanley, G.B. Temporal precision in the neural code and the timescales of natural vision. Nature 2007, 449, 92–95. [Google Scholar] [CrossRef] [PubMed]
- Angueyra, J.M.; Rieke, F. Origin and effect of phototransduction noise in primate cone photoreceptors. Nat. Neurosci. 2013, 16, 1692–1700. [Google Scholar] [CrossRef] [PubMed]
- Mainen, Z.F.; Sejnowski, T.J. Reliability of spike timing in neocortical neurons. Science 1995, 268, 1503–1506. [Google Scholar] [CrossRef] [PubMed]
- Reid, R.C.; Victor, J.D.; Shapley, R.M. The use of m-sequences in the analysis of visual neurons: Linear receptive field properties. Vis. Neurosci. 1997, 14, 1015–1027. [Google Scholar] [CrossRef] [PubMed]
- Reinagel, P. Information theory in the brain. Curr. Biol. 2000, 10, R542–R544. [Google Scholar] [CrossRef]
- Uzzell, V.J.; Chichilnisky, E.J. Precision of spike trains in primate retinal ganglion cells. J. Neurophysiol. 2004, 92, 780–789. [Google Scholar] [CrossRef]
- Hass, C.A.; Angueyra, J.M.; Lindbloom-Brown, Z.; Rieke, F.; Horwitz, G.D. Chromatic detection from cone photoreceptors to V1 neurons to behavior in rhesus monkeys. J. Vis. 2015, 15, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beaman, C.B.; Eagleman, S.L.; Dragoi, V. Sensory coding accuracy and perceptual performance are improved during the desynchronized cortical state. Nat. Commun. 2017, 8, 1308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reinoso-Suarez, F. Topographischer Hirnatlas der Katze, transl. ed.; E. Merck AG: Darmstad, Germany, 1961; p. 74. [Google Scholar]
- Eysel, U.T.; Burandt, U. Fluorescent tube light evokes flicker responses in visual neurons. Vis. Res. 1984, 24, 943–948. [Google Scholar] [CrossRef]
- Hochstein, S.; Shapley, R.M. Quantitative analysis of retinal ganglion cell classifications. J. Physiol. 1976, 262, 237–264. [Google Scholar] [CrossRef] [PubMed]
- Foster, K.H.; Gaska, J.P.; Nagler, M.; Pollen, D.A. Spatial and temporal frequency selectivity of neurones in visual cortical areas V1 and V2 of the macaque monkey. J. Physiol. 1985, 365, 331–363. [Google Scholar] [CrossRef] [PubMed]
- Perrone, J.A.; Thiele, A. Speed skills: Measuring the visual speed analyzing properties of primate MT neurons. Nat. Neurosci. 2001, 4, 526–532. [Google Scholar] [CrossRef] [PubMed]
- Brainard, D.H. The Psychophysics Toolbox. Spat. Vis. 1997, 10, 433–436. [Google Scholar] [CrossRef]
- Pelli, D.G. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spat. Vis. 1997, 10, 437–442. [Google Scholar] [CrossRef]
- Tyler, C.W. Colour bit-stealing to enhance the luminance resolution of digital displays on a single pixel basis. Spat. Vis. 1997, 10, 369–377. [Google Scholar] [CrossRef]
- Tadin, D.; Lappin, J.S.; Gilroy, L.A.; Blake, R. Perceptual consequences of center-surround antagonism in visual motion processing. Nature 2003, 424, 312–315. [Google Scholar] [CrossRef]
- Murray, S.O.; Schallmo, M.P.; Kolodny, T.; Millin, R.; Kale, A.; Thomas, P.; Rammsayer, T.H.; Troche, S.J.; Bernier, R.A.; Tadin, D. Sex Differences in Visual Motion Processing. Curr. Biol. 2018, 28, 2794–2799.e3. [Google Scholar] [CrossRef] [PubMed]
- Tadin, D.; Lappin, J.S.; Blake, R. Fine temporal properties of center-surround interactions in motion revealed by reverse correlation. J. Neurosci. 2006, 26, 2614–2622. [Google Scholar] [CrossRef] [PubMed]
- Watson, A.B.; Pelli, D.G. QUEST: A Bayesian adaptive psychometric method. Percept. Psychophys. 1983, 33, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Glasser, D.M.; Tadin, D. Increasing stimulus size impairs first- but not second-order motion perception. J. Vis. 2011, 11. [Google Scholar] [CrossRef] [PubMed]
- van Rossum, M.C. A novel spike distance. Neural Comput. 2001, 13, 751–763. [Google Scholar] [CrossRef] [PubMed]
- Dow, B.M.; Snyder, A.Z.; Vautin, R.G.; Bauer, R. Magnification factor and receptive field size in foveal striate cortex of the monkey. Exp. Brain Res. 1981, 44, 213–228. [Google Scholar] [CrossRef] [PubMed]
- Tadin, D. Suppressive mechanisms in visual motion processing: From perception to intelligence. Vis. Res. 2015, 115 Pt A, 58–70. [Google Scholar] [CrossRef]
- Watson, A.B.; Turano, K. The optimal motion stimulus. Vis. Res. 1995, 35, 325–336. [Google Scholar] [CrossRef] [Green Version]
- Burr, D.C. Temporal summation of moving images by the human visual system. Proc. R. Soc. Lond. B Biol. Sci. 1981, 211, 321–339. [Google Scholar]
- Burr, D.C.; Corsale, B. Dependency of reaction times to motion onset on luminance and chromatic contrast. Vis. Res. 2001, 41, 1039–1048. [Google Scholar] [CrossRef] [Green Version]
- Edwards, M.; Badcock, D.R.; Nishida, S. Contrast sensitivity of the motion system. Vis. Res. 1996, 36, 2411–2421. [Google Scholar] [CrossRef]
- Nakayama, K.; Silverman, G.H. Detection and discrimination of sinusoidal grating displacements. J. Opt. Soc. Am. A 1985, 2, 267–274. [Google Scholar] [CrossRef]
- van de Grind, W.A.; Koenderink, J.J.; van Doorn, A.J. Influence of contrast on foveal and peripheral detection of coherent motion in moving random-dot patterns. J. Opt. Soc. Am. A 1987, 4, 1643–1652. [Google Scholar] [CrossRef] [PubMed]
- Burr, D.C.; Ross, J. Contrast sensitivity at high velocities. Vis. Res. 1982, 22, 479–484. [Google Scholar] [CrossRef] [Green Version]
- Tadin, D.; Lappin, J.S.; Blake, R.; Glasser, D.M. High temporal precision for perceiving event offsets. Vis. Res. 2010, 50, 1966–1971. [Google Scholar] [CrossRef] [Green Version]
- Zanker, J.M.; Harris, J.P. On temporal hyperacuity in the human visual system. Vis. Res. 2002, 42, 2499–2508. [Google Scholar] [CrossRef]
- Kelly, D.H. Adaptation effects on spatio-temporal sine-wave thresholds. Vis. Res. 1972, 12, 89–101. [Google Scholar] [CrossRef]
- Teller, D.Y. Linking propositions. Vis. Res. 1984, 24, 1233–1246. [Google Scholar] [CrossRef]
- Dan, Y.; Atick, J.J.; Reid, R.C. Efficient coding of natural scenes in the lateral geniculate nucleus: Experimental test of a computational theory. J. Neurosci. 1996, 16, 3351–3362. [Google Scholar] [CrossRef] [PubMed]
- Keat, J.; Reinagel, P.; Reid, R.C.; Meister, M. Predicting every spike: A model for the responses of visual neurons. Neuron 2001, 30, 803–817. [Google Scholar] [CrossRef]
- Reich, D.S.; Victor, J.D.; Knight, B.W.; Ozaki, T.; Kaplan, E. Response variability and timing precision of neuronal spike trains in vivo. J. Neurophysiol. 1997, 77, 2836–2841. [Google Scholar] [CrossRef] [PubMed]
- Chichilnisky, E.J.; Kalmar, R.S. Functional asymmetries in ON and OFF ganglion cells of primate retina. J. Neurosci. 2002, 22, 2737–2747. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borghuis, B.G.; Tadin, D.; Lankheet, M.J.M.; Lappin, J.S.; van de Grind, W.A. Temporal Limits of Visual Motion Processing: Psychophysics and Neurophysiology. Vision 2019, 3, 5. https://doi.org/10.3390/vision3010005
Borghuis BG, Tadin D, Lankheet MJM, Lappin JS, van de Grind WA. Temporal Limits of Visual Motion Processing: Psychophysics and Neurophysiology. Vision. 2019; 3(1):5. https://doi.org/10.3390/vision3010005
Chicago/Turabian StyleBorghuis, Bart G., Duje Tadin, Martin J.M. Lankheet, Joseph S. Lappin, and Wim A. van de Grind. 2019. "Temporal Limits of Visual Motion Processing: Psychophysics and Neurophysiology" Vision 3, no. 1: 5. https://doi.org/10.3390/vision3010005
APA StyleBorghuis, B. G., Tadin, D., Lankheet, M. J. M., Lappin, J. S., & van de Grind, W. A. (2019). Temporal Limits of Visual Motion Processing: Psychophysics and Neurophysiology. Vision, 3(1), 5. https://doi.org/10.3390/vision3010005



