Influence of Playing Standard on Upper- and Lower-Body Strength, Power, and Velocity Characteristics of Elite Rugby League Players
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Design
2.3. Procedures
2.3.1. Physical Measurements
2.3.2. Strength Testing
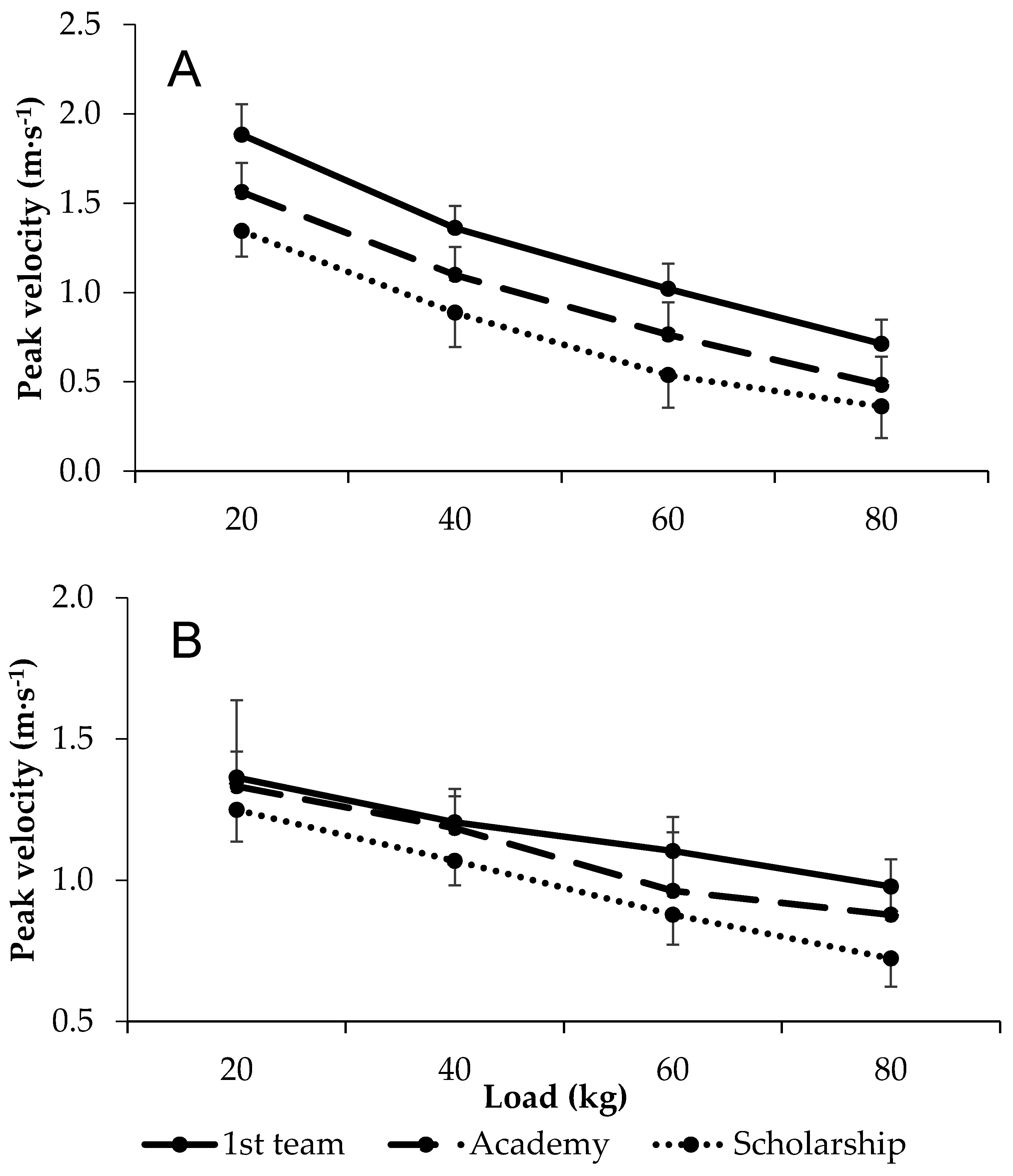
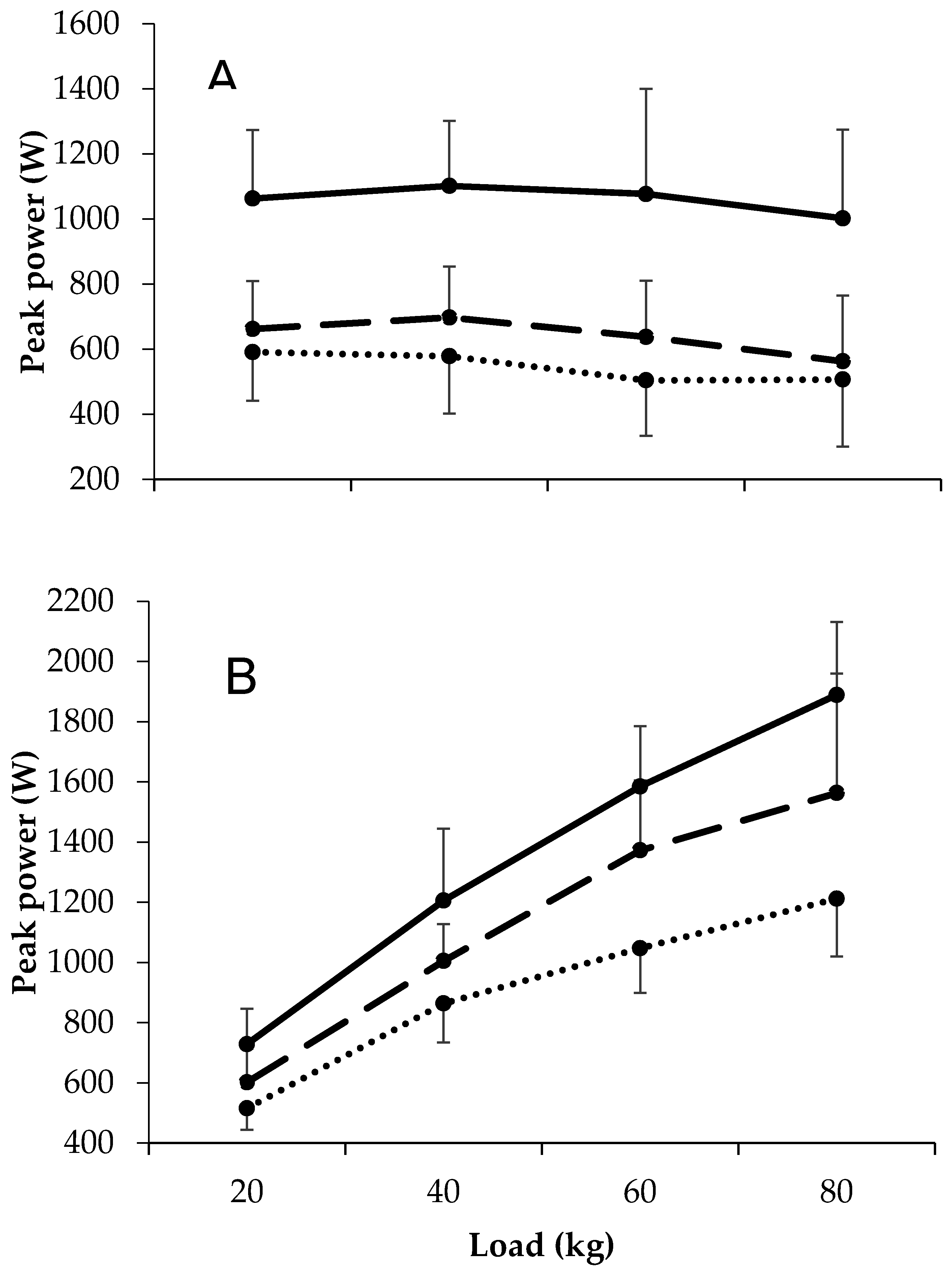
2.3.3. Assessment of Peak Velocity and Power
2.4. Statistical Analyses
3. Results
3.1. Physical Characteristics
3.2. Peak Velocity
3.3. Peak Power
3.4. Partial Correlations
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dobbin, N.; Moss, S.L.; Highton, J.; Twist, C. The discriminant validity of standardised testing battery and its ability to differentiate anthropometric and physical characteristics between youth, academy and senior professional rugby league players. Int. J. Sports Physiol. Perform. 2019, 1–21. [Google Scholar] [CrossRef]
- Speranza, M.J.A.; Gabbett, T.J.; Johnston, R.D.; Sheppard, J.M. Effect of strength and power training on tackling ability in semiprofessional rugby league players. J. Strength Cond. Res. 2016, 30, 336–343. [Google Scholar] [CrossRef] [PubMed]
- Baker, D. Comparison of upper-body strength and power between professional and college-aged rugby league players. J. Strength Cond. Res. 2001, 15, 30–35. [Google Scholar]
- Baker, D. Differences in strength and power among junior-high, senior-high, college-aged, and elite professional rugby league players. J. Strength Cond. Res. 2002, 16, 581–585. [Google Scholar]
- Baker, D. A series of studies on the training of high-intensity muscle power in rugby league football players. J. Strength Cond. Res. 2001, 15, 198–209. [Google Scholar]
- Baker, D.; Newton, R. Comparison of lower body strength, power, acceleration, speed, agility and sprint momentum to describe and compare playing ranking among professional rugby league players. J. Strength Cond. Res. 2008, 22, 153–158. [Google Scholar] [CrossRef] [PubMed]
- Baker, D.; Nance, S. The relation between strength and power in professional rugby league players. J. Strength Cond. Res. 1999, 13, 224–229. [Google Scholar]
- Fernandes, J.F.T.; Lamb, K.L.; Twist, C. A comparison of load-velocity and load-power relationships between well-trained young and middle-aged males during three popular resistance exercises. J. Strength Cond. Res. 2018, 32, 1440–1447. [Google Scholar] [CrossRef] [PubMed]
- James, L.P.; Haff, G.G.; Kelly, V.G.; Connick, M.J.; Hoffman, B.W.; Beckman, E.M. The impact of strength level on adaptations to combined weightlifting, plyometric, and ballistic training. Scand. J. Med. Sci. Sports. 2018, 28, 1494–1505. [Google Scholar] [CrossRef]
- Hansen, K.T.; Cronin, J.B.; Pickering, S.L.; Douglas, L. Do force-time and power-time measures in a loaded jump squat differentiate between speed performance and playing level in elite and elite junior rugby union players? J. Strength Cond. Res. 2011, 25, 2382–2391. [Google Scholar] [CrossRef]
- Stock, M.; Beck, T.W.; DeFreitas, J.; Dillon, M. Test-retest reliability of barbell velocity during the free-weight bench-pres exercise. J. Strength Cond. Res. 2011, 25, 171–177. [Google Scholar] [CrossRef] [PubMed]
- Baechle, T.R.; Earle, R.W. Essentials of Strength Training and Conditioning, 4th ed.; Human Kinetics: Leed, UK, 2008. [Google Scholar]
- Fernandes, J.F.T.; Lamb, K.L.; Twist, C. The intra- and inter-day reproducibility of the FitroDyne as a measure of multi-jointed muscle function. Isokinet. Exerc. Sci. 2016, 24, 39–49. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive statistics for studies in sports medicine and exercise science. Med. Sci. Sports Exerc. 2009, 41, 3–12. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Science; Lawrence Earlbaum Associates: Hilsdale, NJ, YSA, 1988. [Google Scholar]
- Sainani, K. The problem with ‘Magnitude-Based Inference’. Med. Sci. Sports Exerc. 2018, 50, 2166–2176. [Google Scholar] [CrossRef] [PubMed]
- Till, K.; Jones, B.; Geeson-Brown, T. Do physical qualities influence the attainment of professional status within elite 16-19 year old rugby league players? J. Sci. Med. Sport 2016, 19, 585–589. [Google Scholar] [CrossRef] [PubMed]
- Veale, J.P.; Pearce, A.J.; Buttifant, D.; Carlson, J.S. Anthropometric profiling of elite junior and senior Australian football players. Int. J. Sports Physiol. Perform. 2010, 5, 509–520. [Google Scholar] [CrossRef] [PubMed]
- Baker, D. 10-Year changes in upper body strength and power in elite professional rugby league players-the effect of training age, stage, and content. J. Strength Cond. Res. 2013, 27, 285–292. [Google Scholar] [CrossRef]
- Malina, R.; Bar-Or, O.; Bouchard, C. Growth Maturation and Physical Activity; Human Kinetics: Champaign, IL, USA, 2004. [Google Scholar]
- Argus, C.K.; Gill, N.D.; Keogh, J.W.L. Characterization of the differences in strength and power between different levels of competition in rugby union athletes. J. Strength Cond. Res. 2012, 26, 2698–2704. [Google Scholar] [CrossRef] [PubMed]
- Till, K.; Tester, E.; Jones, B.; Emmonds, S.; Fahey, J.; Cooke, C. Anthropometric and physical characteristics of English academy rugby league players. J. Strength Cond. Res. 2014, 28, 319–327. [Google Scholar] [CrossRef]
- Gabbett, T.J.; Kelly, J.; Pezet, T. A comparison of fitness and skill among playing positions in sub-elite rugby league players. J. Sci. Med. Sport 2008, 11, 585–592. [Google Scholar] [CrossRef]
- Erskine, R.M.; Fletcher, G.; Folland, J.P. The contribution of muscle hypertrophy to strength changes following resistance training. Eur. J. Appl. Physiol. 2014, 114, 1239–1249. [Google Scholar] [CrossRef] [PubMed]
- Balshaw, T.G.; Massey, G.J.; Maden-Wilkinson, T.M.; Morales-Artacho, A.J.; McKeown, A.; Appleby, C.L.; Folland, J.P. Changes in agonist neural drive, hypertrophy and pre-training strength all contribute to the individual strength gains after resistance training. Eur. J. Appl. Physiol. 2017, 117, 631–640. [Google Scholar] [CrossRef]
- Bilsborough, J.C.; Greenway, K.G.; Opar, D.A.; Livingstone, S.G.; Cordy, J.T.; Bird, S.R.; Coutts, A.J. Comparison of anthropometry, upper-body strength and lower-body power characteristics in different levels of Australian Football players. J. Strength Cond. Res. 2015, 29, 826–834. [Google Scholar] [CrossRef] [PubMed]
- Behm, D.G. Neuromuscular implications and applications of resistance training. J. Strength Cond. Res. 1995, 9, 264–274. [Google Scholar]
- Tillin, N.A.; Jiménez-Reyes, P.; Pain, M.G.; Folland, J.P. Neuromuscular performance of explosive power athletes versus untrained individuals. Med. Sci. Sports Exerc. 2010, 42, 781–790. [Google Scholar] [CrossRef]
| Effect Size | ||||||
|---|---|---|---|---|---|---|
| First Grade (n = 26) | U’19s (n = 23) | U’16s (n = 16) | First vs. Academy | First vs. Scholarship | Academy vs. Scholarship | |
| Mass (kg) | 94.6 ± 9.5 | 85.9 ± 10.4 | 79.7 ± 10.8 | −0.89 ± 0.49 | −1.52 ± 0.57 | −0.58 ± 0.55 |
| Very likely | Most likely | Likely | ||||
| Sum of skinfolds (mm) | 81.0 ± 14.7 | 90.7 ± 23.9 | 88.2 ± 29.3 | 0.65 ± 0.64 | 0.48 ± 0.90 | −0.10 ± 0.60 |
| Likely | Unclear | Unclear | ||||
| Bench press 1RM (kg) | 135.2 ± 16.2 | 111.5 ± 14.3 | 82.2 ± 12.6 | −1.42 ± 0.44 | −3.18 ± 0.46 | −1.98 ± 0.50 |
| Most likely | Most likely | Most likely | ||||
| Relative bench press 1RM (kg·bm−1) | 1.43 ± 0.14 | 1.30 ± 0.15 | 1.03 ± 0.12 | −0.87 ± 0.50 | −2.76 ± 0.47 | −1.71 ± 0.46 |
| Very likely | Most likely | Most likely | ||||
| Squat 1RM (kg) | 183.3 ± 20.6 | 174.3 ± 27.0 | 140.0 ± 22.2 | −0.43 ± 0.53 | −2.04 ± 0.56 | −1.23 ± 0.48 |
| Possibly | Most likely | Most likely | ||||
| Relative squat 1RM (kg·bm−1) | 1.94 ± 0.22 | 2.04 ± 0.26 | 1.78 ± 0.32 | −0.78 ± 0.92 | −0.71 ± 0.70 | −0.94 ± 0.61 |
| Likely | Likely | Very likely | ||||
| 20 kg | 40 kg | 60 kg | 80 kg | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Velocity | Power | Velocity | Power | Velocity | Power | Velocity | Power | ||
| First grade vs. Academy | Bench press | −1.83 ± 0.46 | −1.85 ± 0.40 | −2.06 ± 0.54 | −1.97 ± 0.42 | −1.76 ± 0.54 | −1.32 ± 0.37 | −1.66 ± 0.55 | −1.56 ± 0.44 |
| Most likely | Most likely | Most likely | Most likely | Most likely | Most likely | Most likely | Most likely | ||
| Squat | −0.11 ± 0.36 | −1.04 ± 0.45 | −0.17 ± 0.46 | −0.81 ± 0.37 | −1.14 ± 0.67 | −1.03 ± 0.51 | −1.01 ± 0.52 | −1.31 ± 0.65 | |
| Unclear | Most likely | Unclear | Most likely | Very likely | Most likely | Very likely | Most likely | ||
| First grade vs. scholarship | Bench press | −3.07 ± 0.47 | −2.17 ± 0.43 | −3.72 ± 0.72 | −2.55 ± 0.49 | −3.32 ± 0.65 | −1.72 ± 0.39 | ||
| Most likely | Most likely | Most likely | Most likely | Most likely | Most likely | ||||
| Squat | −0.41 ± 0.36 | −1.75 ± 0.41 | −1.13 ± 0.44 | −1.39 ± 0.39 | −1.82 ± 0.48 | −2.61 ± 0.44 | −3.11 ± 0.54 | −2.71 ± 0.46 | |
| Unclear | Most likely | Most likely | Most likely | Most likely | Most likely | Most likely | Most likely | ||
| Academy vs. Scholarship | Bench press | −1.29 ± 0.49 | −0.47 ± 0.54 | −1.31 ± 0.61 | −0.73 ± 0.57 | −1.21 ± 0.55 | −0.75 ± 0.54 | ||
| Most likely | Likely | Most likely | Likely | Most likely | Very likely | ||||
| Squat | −0.66 ± 0.51 | −0.75 ± 0.43 | −1.00 ± 0.46 | −1.11 ± 0.55 | −0.39 ± 0.40 | −1.35 ± 0.43 | −1.28 ± 0.49 | −0.85 ± 0.39 | |
| Likely | Very likely | Most likely | Most likely | Likely | Most likely | Most likely | Most likely | ||
| Bench Press | Squat | |||
|---|---|---|---|---|
| 1RM | Velocity | 1RM | Velocity | |
| First team | 0.310 | 0.514 * | 0.365 | 0.117 |
| Academy | 0.310 | 0.546 * | 0.505 * | 0.256 |
| Scholarship | 0.635 * | 0.788 * | 0.332 | 0.484 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandes, J.F.T.; Daniels, M.; Myler, L.; Twist, C. Influence of Playing Standard on Upper- and Lower-Body Strength, Power, and Velocity Characteristics of Elite Rugby League Players. J. Funct. Morphol. Kinesiol. 2019, 4, 22. https://doi.org/10.3390/jfmk4020022
Fernandes JFT, Daniels M, Myler L, Twist C. Influence of Playing Standard on Upper- and Lower-Body Strength, Power, and Velocity Characteristics of Elite Rugby League Players. Journal of Functional Morphology and Kinesiology. 2019; 4(2):22. https://doi.org/10.3390/jfmk4020022
Chicago/Turabian StyleFernandes, John F. T., Matthew Daniels, Liam Myler, and Craig Twist. 2019. "Influence of Playing Standard on Upper- and Lower-Body Strength, Power, and Velocity Characteristics of Elite Rugby League Players" Journal of Functional Morphology and Kinesiology 4, no. 2: 22. https://doi.org/10.3390/jfmk4020022
APA StyleFernandes, J. F. T., Daniels, M., Myler, L., & Twist, C. (2019). Influence of Playing Standard on Upper- and Lower-Body Strength, Power, and Velocity Characteristics of Elite Rugby League Players. Journal of Functional Morphology and Kinesiology, 4(2), 22. https://doi.org/10.3390/jfmk4020022






