Interpretable Machine Learning for Osteopenia Detection: A Proof-of-Concept Study Using Bioelectrical Impedance in Perimenopausal Women
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Participants
2.3. Procedures
2.3.1. Interview and Categorical Data Collection
2.3.2. Height Measurement
2.3.3. Body Composition Assessment
Validation of BIA Against DXA
2.3.4. Bone Health Assessment
2.4. Machine Learning Workflow
3. Results
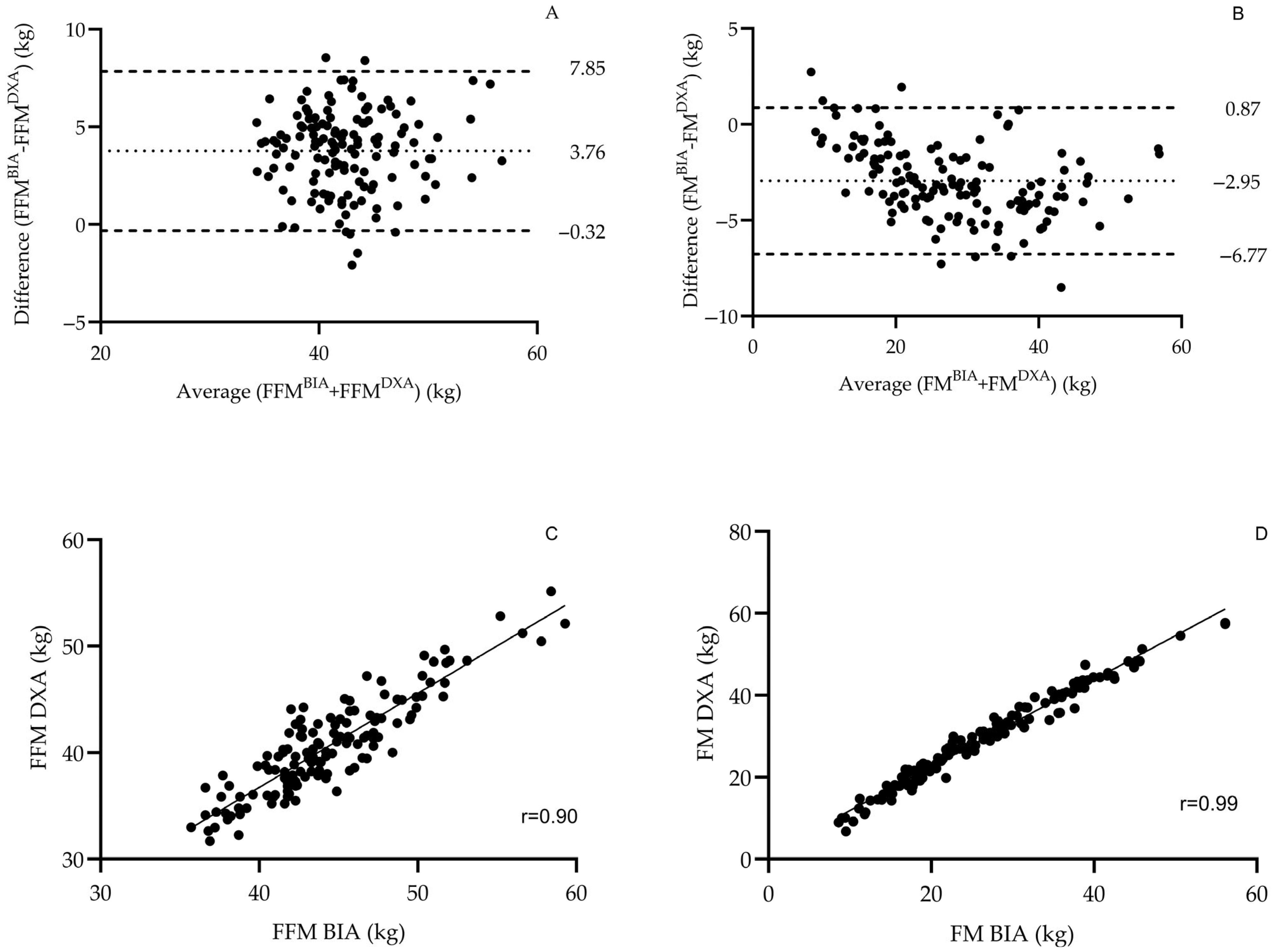
3.1. Validity of the BIA Device in the Study’s Population
Participant Characteristics
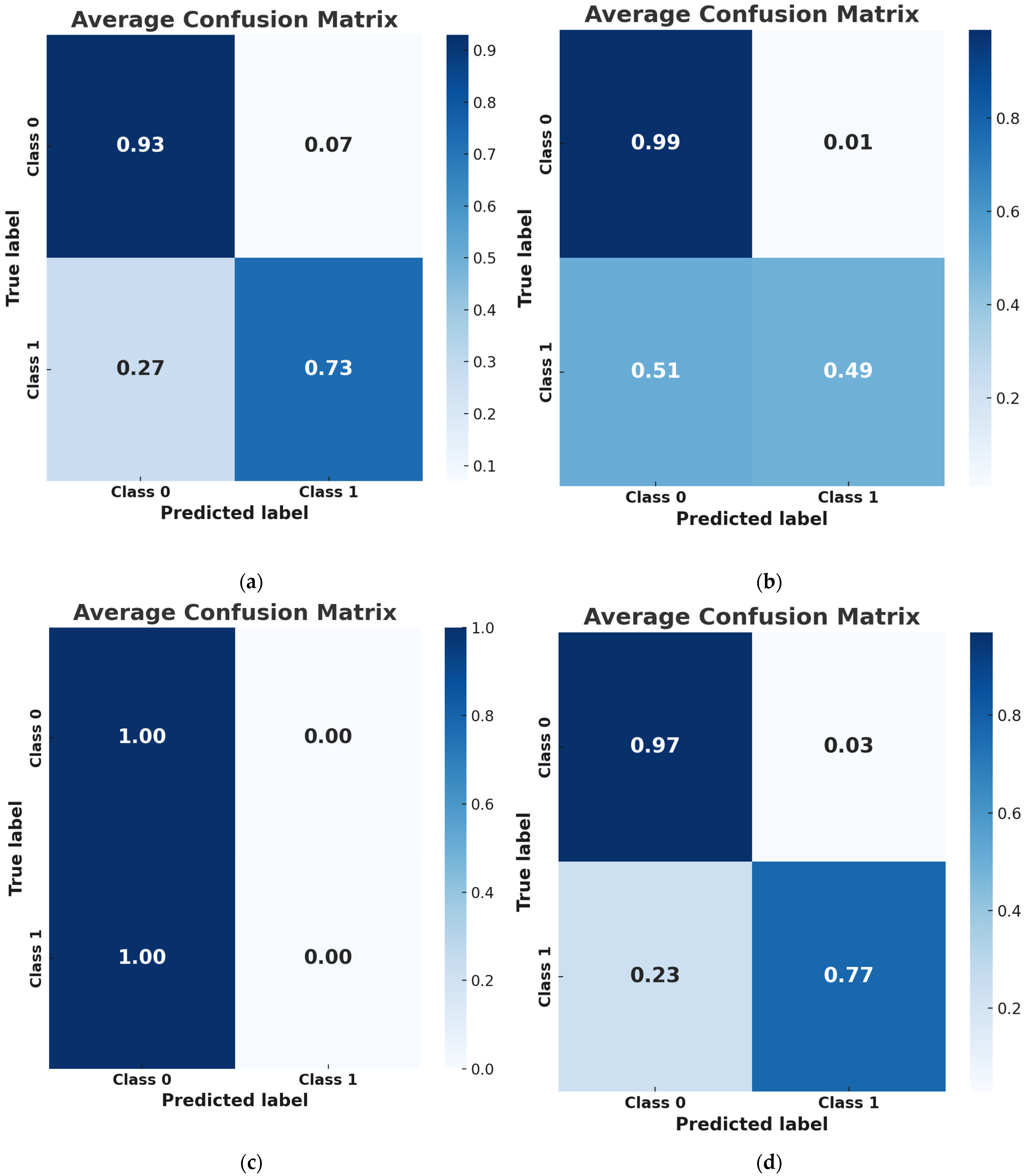
3.2. Performance Metrics
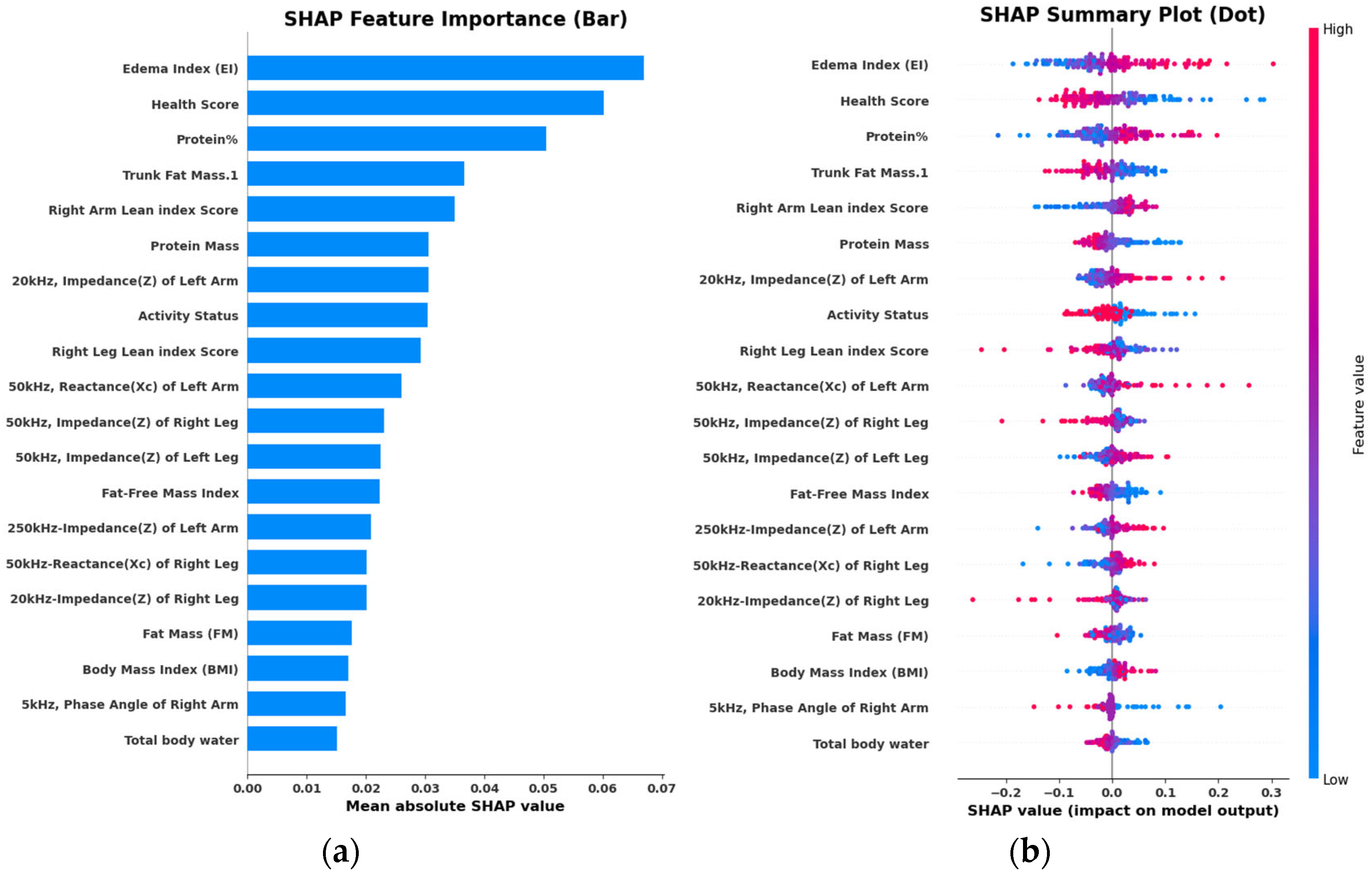
3.3. Feature Selection
3.4. Interpretation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ferrari, S.L. Osteoporosis: A Complex Disorder of Aging with Multiple Genetic and Environmental Determinants. World Rev. Nutr. Diet. 2005, 95, 35–51. [Google Scholar] [CrossRef]
- Yu, B.; Wang, C.-Y. Osteoporosis: The Result of an ‘Aged’ Bone Microenvironment. Trends Mol. Med. 2016, 22, 641–644. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.T.; Lane, J.M. Osteoporosis: A Review. Clin. Orthop. Relat. Res. (1976–2007) 2004, 425, 126–134. [Google Scholar] [CrossRef]
- Krum, S.A.; Brown, M. Unraveling Estrogen Action in Osteoporosis. Cell Cycle 2008, 7, 1348–1352. [Google Scholar] [CrossRef] [PubMed]
- Raisz, L.G. Pathogenesis of Osteoporosis: Concepts, Conflicts, and Prospects. J. Clin. Investig. 2005, 115, 3318–3325. [Google Scholar] [CrossRef]
- Rosen, C.J. The Epidemiology and Pathogenesis of Osteoporosis. In Endotext; MDText.com, Inc.: South Dartmouth, MA, USA, 2000. [Google Scholar]
- Ji, M.-X.; Yu, Q. Primary Osteoporosis in Postmenopausal Women. Chronic Dis. Transl. Med. 2015, 1, 9–13. [Google Scholar] [CrossRef]
- van der Voort, D.J.M.; Geusens, P.P.; Dinant, G.J. Risk Factors for Osteoporosis Related to Their Outcome: Fractures. Osteoporos. Int. 2001, 12, 630–638. [Google Scholar] [CrossRef]
- Shepherd, J.A.; Ng, B.K.; Sommer, M.J.; Heymsfield, S.B. Body Composition by DXA. Bone 2017, 104, 101–105. [Google Scholar] [CrossRef]
- Wojtys, E.M. Bone Health. Sports Health A Multidiscip. Approach 2020, 12, 423–424. [Google Scholar] [CrossRef]
- Cashman, K.D. Diet, Nutrition, and Bone Health. J. Nutr. 2007, 137, 2507S–2512S. [Google Scholar] [CrossRef]
- Torres-Costoso, A.; López-Muñoz, P.; Martínez-Vizcaíno, V.; Álvarez-Bueno, C.; Cavero-Redondo, I. Association Between Muscular Strength and Bone Health from Children to Young Adults: A Systematic Review and Meta-Analysis. Sports Med. 2020, 50, 1163–1190. [Google Scholar] [CrossRef] [PubMed]
- Withers, R.T.; LaForgia, J.; Pillans, R.K.; Shipp, N.J.; Chatterton, B.E.; Schultz, C.G.; Leaney, F. Comparisons of Two-, Three-, and Four-Compartment Models of Body Composition Analysis in Men and Women. J. Appl. Physiol. 1998, 85, 238–245. [Google Scholar] [CrossRef] [PubMed]
- Alemán-Mateo, H.; Esparza Romero, J.; Macías Morales, N.; Salazar, G.; Hernández Triana, M.; Valencia, M.E. Body Composition by Three-Compartment Model and Relative Validity of Some Methods to Assess Percentage Body Fat in Mexican Healthy Elderly Subjects. Gerontology 2004, 50, 366–372. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; You, X.; Zhang, L.; Zhang, C.; Zou, W. Mechanical Regulation of Bone Remodeling. Bone Res. 2022, 10, 16. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Liu, B.; Hou, Q.; Dai, Q.; Wang, D.; Xie, B.; Sun, Y.; Wang, B. Global and Local Fat Effects on Bone Mass and Quality in Obesity. Bone Jt. Res. 2023, 12, 580–589. [Google Scholar] [CrossRef]
- Morley, J.E. Sarcopenia: Diagnosis and Treatment. J. Nutr. Health Aging 2008, 12, 452. [Google Scholar] [CrossRef]
- Rosenberg, I.H. Sarcopenia: Origins and Clinical Relevance. Clin. Geriatr. Med. 2011, 27, 337–339. [Google Scholar] [CrossRef]
- Schoeler, D.A. Bioelectrical Impedance Analysis What Does It Measure? Ann. N. Y. Acad. Sci. 2000, 904, 159–162. [Google Scholar] [CrossRef]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.-C.; Pirlich, M.; et al. Bioelectrical Impedance Analysis—Part I: Review of Principles and Methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef]
- Shieh, A.; Karlamangla, A.S.; Karvonen-Guttierez, C.A.; Greendale, G.A. Menopause-Related Changes in Body Composition Are Associated With Subsequent Bone Mineral Density and Fractures: Study of Women’s Health Across the Nation. J. Bone Miner. Res. 2023, 38, 395–402. [Google Scholar] [CrossRef]
- Lee, J.; Jung, J.-H.; Kim, J.; Jeong, C.; Ha, J.; Kim, M.-H.; Lee, J.-M.; Chang, S.-A.; Baek, K.-H.; Han, K.; et al. Associations between Body Composition and the Risk of Fracture According to Bone Mineral Density in Postmenopausal Women: A Population-Based Database Cohort Study. Eur. J. Endocrinol. 2023, 189, 527–536. [Google Scholar] [CrossRef] [PubMed]
- Stampoulis, T.; Avloniti, A.; Draganidis, D.; Balampanos, D.; Chalastra, P.E.; Gkachtsou, A.; Pantazis, D.; Retzepis, N.-O.; Protopapa, M.; Poulios, A.; et al. New Bioelectrical Impedance-Based Equations to Estimate Resting Metabolic Rate in Young Athletes. Methods Protoc. 2025, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.; Bešević, J.; Conroy, M.; Omiyale, W.; Lacey, B.; Allen, N. Comparison of Body Composition Measures Assessed by Bioelectrical Impedance Analysis versus Dual-Energy X-Ray Absorptiometry in the United Kingdom Biobank. Clin. Nutr. ESPEN 2024, 63, 214–225. [Google Scholar] [CrossRef]
- Achamrah, N.; Colange, G.; Delay, J.; Rimbert, A.; Folope, V.; Petit, A.; Grigioni, S.; Déchelotte, P.; Coëffier, M. Comparison of Body Composition Assessment by DXA and BIA According to the Body Mass Index: A Retrospective Study on 3655 Measures. PLoS ONE 2018, 13, e0200465. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Kim, H.J.; Han, S.; Park, S.J.; Sim, M.; Lee, K.H. Reliability and Agreement Assessment of Sarcopenia Diagnosis through Comparison of Bioelectrical Impedance Analysis and Dual-Energy X-Ray Absorptiometry. Diagnostics 2024, 14, 899. [Google Scholar] [CrossRef]
- Aleixo, G.F.P.; Shachar, S.S.; Nyrop, K.A.; Muss, H.B.; Battaglini, C.L.; Williams, G.R. Bioelectrical Impedance Analysis for the Assessment of Sarcopenia in Patients with Cancer: A Systematic Review. Oncologist 2020, 25, 170–182. [Google Scholar] [CrossRef]
- Hernlund, E.; Svedbom, A.; Ivergård, M.; Compston, J.; Cooper, C.; Stenmark, J.; McCloskey, E.V.; Jönsson, B.; Kanis, J.A. Osteoporosis in the European Union: Medical Management, Epidemiology and Economic Burden. Arch. Osteoporos. 2013, 8, 136. [Google Scholar] [CrossRef]
- Ioannidis, G.; Papaioannou, A.; Hopman, W.M.; Akhtar-Danesh, N.; Anastassiades, T.; Pickard, L.; Kennedy, C.C.; Prior, J.C.; Olszynski, W.P.; Davison, K.S.; et al. Relation between Fractures and Mortality: Results from the Canadian Multicentre Osteoporosis Study. Can. Med. Assoc. J. 2009, 181, 265–271. [Google Scholar] [CrossRef]
- Becker, D.J.; Kilgore, M.L.; Morrisey, M.A. The Societal Burden of Osteoporosis. Curr. Rheumatol. Rep. 2010, 12, 186–191. [Google Scholar] [CrossRef]
- Luan, A.; Maan, Z.; Lin, K.-Y.; Yao, J. Application of Machine Learning to Osteoporosis and Osteopenia Screening Using Hand Radiographs. J. Hand Surg. Am. 2025, 50, 43–50. [Google Scholar] [CrossRef]
- Sebro, R.; De la Garza-Ramos, C. Machine Learning for the Prediction of Osteopenia/Osteoporosis Using the CT Attenuation of Multiple Osseous Sites from Chest CT. Eur. J. Radiol. 2022, 155, 110474. [Google Scholar] [CrossRef] [PubMed]
- Lim, H.K.; Ha, H.I.; Park, S.-Y.; Han, J. Prediction of Femoral Osteoporosis Using Machine-Learning Analysis with Radiomics Features and Abdomen-Pelvic CT: A Retrospective Single Center Preliminary Study. PLoS ONE 2021, 16, e0247330. [Google Scholar] [CrossRef]
- Chawla, S.K.; Malhotra, D. Prediction of Osteoporosis Using Artificial Intelligence Techniques: A Review. In The International Conference on Recent Innovations in Computing; Springer Nature: Singapore, 2023; pp. 181–198. [Google Scholar]
- Liu, R.W.; Ong, W.; Makmur, A.; Kumar, N.; Low, X.Z.; Shuliang, G.; Liang, T.Y.; Ting, D.F.K.; Tan, J.H.; Hallinan, J.T.P.D. Application of Artificial Intelligence Methods on Osteoporosis Classification with Radiographs—A Systematic Review. Bioengineering 2024, 11, 484. [Google Scholar] [CrossRef]
- Kokkotis, C.; Moustakidis, S.; Papageorgiou, E.; Giakas, G.; Tsaopoulos, D.E. Machine Learning in Knee Osteoarthritis: A Review. Osteoarthr. Cart. Open 2020, 2, 100069. [Google Scholar] [CrossRef] [PubMed]
- Shim, J.-G.; Kim, D.W.; Ryu, K.-H.; Cho, E.-A.; Ahn, J.-H.; Kim, J.-I.; Lee, S.H. Application of Machine Learning Approaches for Osteoporosis Risk Prediction in Postmenopausal Women. Arch. Osteoporos. 2020, 15, 169. [Google Scholar] [CrossRef]
- Kokkotis, C.; Giarmatzis, G.; Giannakou, E.; Moustakidis, S.; Tsatalas, T.; Tsiptsios, D.; Vadikolias, K.; Aggelousis, N. An Explainable Machine Learning Pipeline for Stroke Prediction on Imbalanced Data. Diagnostics 2022, 12, 2392. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, J.; Wu, Y.; Liu, H.; Meng, F.; Liu, Q.; Midgley, A.C.; Zhang, X.; Qi, T.; Kang, H.; et al. Prediction and Design of Nanozymes Using Explainable Machine Learning. Adv. Mater. 2022, 34, 2201736. [Google Scholar] [CrossRef] [PubMed]
- El Maghraoui, A.; Roux, C. DXA Scanning in Clinical Practice. QJM 2008, 101, 605–617. [Google Scholar] [CrossRef]
- Shepherd, J.A.; Fan, B.; Lu, Y.; Wu, X.P.; Wacker, W.K.; Ergun, D.L.; Levine, M.A. A Multinational Study to Develop Universal Standardization of Whole-Body Bone Density and Composition Using GE Healthcare Lunar and Hologic DXA Systems. J. Bone Miner. Res. 2012, 27, 2208–2216. [Google Scholar] [CrossRef]
- Slart, R.H.J.A.; Punda, M.; Ali, D.S.; Bazzocchi, A.; Bock, O.; Camacho, P.; Carey, J.J.; Colquhoun, A.; Compston, J.; Engelke, K.; et al. Updated Practice Guideline for Dual-Energy X-Ray Absorptiometry (DXA). Eur. J. Nucl. Med. Mol. Imaging 2025, 52, 539–563. [Google Scholar] [CrossRef]
- Jin, W.; Xu, L.; Yue, C.; Hu, L.; Wang, Y.; Fu, Y.; Guo, Y.; Bai, F.; Yang, Y.; Zhao, X.; et al. Development and Validation of Explainable Machine Learning Models for Female Hip Osteoporosis Using Electronic Health Records. Int. J. Med. Inf. 2025, 199, 105889. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Bai, Y.; Zhang, Z.; Lu, J. A Validated MiRNA Signature for the Diagnosis of Osteoporosis Related Fractures Using SVM Algorithm Classification. Exp. Ther. Med. 2020, 20, 2209–2217. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Dai, Z.; Lau, E.H.Y.; Cui, C.; Lin, H.; Qi, J.; Ni, W.; Zhao, L.; Lv, Q.; Gu, J.; et al. Prevalence of Bone Mineral Density Loss and Potential Risk Factors for Osteopenia and Osteoporosis in Rheumatic Patients in China: Logistic Regression and Random Forest Analysis. Ann. Transl. Med. 2020, 8, 226. [Google Scholar] [CrossRef] [PubMed]
- Dzierżak, R.; Omiotek, Z. Application of Deep Convolutional Neural Networks in the Diagnosis of Osteoporosis. Sensors 2022, 22, 8189. [Google Scholar] [CrossRef]
- Retzepis, N.-O.; Avloniti, A.; Kokkotis, C.; Protopapa, M.; Stampoulis, T.; Gkachtsou, A.; Pantazis, D.; Balampanos, D.; Smilios, I.; Chatzinikolaou, A. Identifying Key Factors for Predicting the Age at Peak Height Velocity in Preadolescent Team Sports Athletes Using Explainable Machine Learning. Sports 2024, 12, 287. [Google Scholar] [CrossRef]
- Kim, J.-K.; Bae, M.-N.; Lee, K.; Kim, J.-C.; Hong, S.G. Explainable Artificial Intelligence and Wearable Sensor-Based Gait Analysis to Identify Patients with Osteopenia and Sarcopenia in Daily Life. Biosensors 2022, 12, 167. [Google Scholar] [CrossRef]
- Koirala, A.; Pourafshar, N.; Daneshmand, A.; Wilcox, C.S.; Mannemuddhu, S.S.; Arora, N. Etiology and Management of Edema: A Review. Adv. Kidney Dis. Health 2023, 30, 110–123. [Google Scholar] [CrossRef]
- Lent-Schochet, D.; Jialal, I. Physiology, Edema. In StatPearls; StatPearls: Tampa, FL, USA, 2023. [Google Scholar]
- Epsley, S.; Tadros, S.; Farid, A.; Kargilis, D.; Mehta, S.; Rajapakse, C.S. The Effect of Inflammation on Bone. Front. Physiol. 2021, 11, 511799. [Google Scholar] [CrossRef]
- Bembey, A.K.; Bushby, A.J.; Boyde, A.; Ferguson, V.L.; Oyen, M.L. Hydration Effects on the Micro-Mechanical Properties of Bone. J. Mater. Res. 2006, 21, 1962–1968. [Google Scholar] [CrossRef]
- Gibon, E.; Lu, L.Y.; Nathan, K.; Goodman, S.B. Inflammation, Ageing, and Bone Regeneration. J. Orthop. Transl. 2017, 10, 28–35. [Google Scholar] [CrossRef]
- Mountziaris, P.M.; Spicer, P.P.; Kasper, F.K.; Mikos, A.G. Harnessing and Modulating Inflammation in Strategies for Bone Regeneration. Tissue Eng. Part. B Rev. 2011, 17, 393–402. [Google Scholar] [CrossRef] [PubMed]
- Ho-Pham, L.T.; Nguyen, N.D.; Lai, T.Q.; Nguyen, T.V. Contributions of Lean Mass and Fat Mass to Bone Mineral Density: A Study in Postmenopausal Women. BMC Musculoskelet. Disord. 2010, 11, 59. [Google Scholar] [CrossRef] [PubMed]
- Tomlinson, D.J.; Erskine, R.M.; Morse, C.I.; Onamb, G.L. Body Fat Percentage, Body Mass Index, Fat Mass Index and the Ageing Bone: Their Singular and Combined Roles Linked to Physical Activity and Diet. Nutrients 2019, 11, 195. [Google Scholar] [CrossRef]
- Leslie, W.D.; Orwoll, E.S.; Nielson, C.M.; Morin, S.N.; Majumdar, S.R.; Johansson, H.; Odén, A.; McCloskey, E.V.; Kanis, J.A. Estimated Lean Mass and Fat Mass Differentially Affect Femoral Bone Density and Strength Index but Are Not FRAX Independent Risk Factors for Fracture. J. Bone Miner. Res. 2014, 29, 2511–2519. [Google Scholar] [CrossRef] [PubMed]
- Ferretti, J. Bone Mass, Bone Strength, Muscle–Bone Interactions, Osteopenias and Osteoporoses. Mech. Ageing Dev. 2003, 124, 269–279. [Google Scholar] [CrossRef]
- Macintosh, B.; Phillip, G.; Alan, M. Skeletal Muscle: Form and Function; Human Kinetics: Champaign, IL, USA, 2006. [Google Scholar]
- Tatsumi, Y.; Higashiyama, A.; Kubota, Y.; Sugiyama, D.; Nishida, Y.; Hirata, T.; Kadota, A.; Nishimura, K.; Imano, H.; Miyamatsu, N.; et al. Underweight Young Women Without Later Weight Gain Are at High Risk for Osteopenia After Midlife: The KOBE Study. J. Epidemiol. 2016, 26, 572–578. [Google Scholar] [CrossRef]
- Coin, A.; Sergi, G.; Benincà, P.; Lupoli, L.; Cinti, G.; Ferrara, L.; Benedetti, G.; Tomasi, G.; Pisent, C.; Enzi, G. Bone Mineral Density and Body Composition in Underweight and Normal Elderly Subjects. Osteoporos. Int. 2001, 11, 1043–1050. [Google Scholar] [CrossRef]
- Uzogara, S.G.; Uzogara, S.G. Underweight, the Less Discussed Type of Unhealthy Weight and Its Implications: A Review. Am. J. Food Sci. Nutr. Res. 2016, 3, 126–142. [Google Scholar]
- Frost, H.M. Wolff’s Law and Bone’s Structural Adaptations to Mechanical Usage: An Overview for Clinicians. Angle Orthod. 1994, 64, 175–188. [Google Scholar]
- Schriefer, J.L.; Warden, S.J.; Saxon, L.K.; Robling, A.G.; Turner, C.H. Cellular Accommodation and the Response of Bone to Mechanical Loading. J. Biomech. 2005, 38, 1838–1845. [Google Scholar] [CrossRef]
- Carina, V.; Della Bella, E.; Costa, V.; Bellavia, D.; Veronesi, F.; Cepollaro, S.; Fini, M.; Giavaresi, G. Bone’s Response to Mechanical Loading in Aging and Osteoporosis: Molecular Mechanisms. Calcif. Tissue Int. 2020, 107, 301–318. [Google Scholar] [CrossRef] [PubMed]
- Sultana, S.; Hasan, M.N.; Taleb, M. The Correlation of Bone Mineral Density, Body Mass Index and Age. Asian J. Med. Biol. Res. 2021, 7, 76–81. [Google Scholar] [CrossRef]
- Michaëlsson, K.; Bergström, R.; Mallmin, H.; Holmberg, L.; Wolk, A.; Ljunghall, S. Screening for Osteopenia and Osteoporosis: Selection by Body Composition. Osteoporos. Int. 1996, 6, 120–126. [Google Scholar] [CrossRef] [PubMed]
- Bigaard, J.; Frederiksen, K.; Tjønneland, A.; Thomsen, B.L.; Overvad, K.; Heitmann, B.L.; Sørensen, T.I.A. Body Fat and Fat-Free Mass and All-Cause Mortality. Obes. Res. 2004, 12, 1042–1049. [Google Scholar] [CrossRef]
- Chang, S.-H.; Beason, T.S.; Hunleth, J.M.; Colditz, G.A. A Systematic Review of Body Fat Distribution and Mortality in Older People. Maturitas 2012, 72, 175–191. [Google Scholar] [CrossRef]
- Britton, K.A.; Massaro, J.M.; Murabito, J.M.; Kreger, B.E.; Hoffmann, U.; Fox, C.S. Body Fat Distribution, Incident Cardiovascular Disease, Cancer, and All-Cause Mortality. J. Am. Coll. Cardiol. 2013, 62, 921–925. [Google Scholar] [CrossRef]
- Elks, C.M.; Francis, J. Central Adiposity, Systemic Inflammation, and the Metabolic Syndrome. Curr. Hypertens. Rep. 2010, 12, 99–104. [Google Scholar] [CrossRef]
- Tian, L.; Yu, X. Lipid Metabolism Disorders and Bone Dysfunction-Interrelated and Mutually Regulated (Review). Mol. Med. Rep. 2015, 12, 783–794. [Google Scholar] [CrossRef]
- Valderrabano, V.; Nigg, B.M.; Hintermann, B.; Goepfert, B.; Dick, W.; Frank, C.B.; Herzog, W.; Tscharner, V. von Muscular Lower Leg Asymmetry in Middle-Aged People. Foot Ankle Int. 2007, 28, 242–249. [Google Scholar] [CrossRef]
- Drid, P.; Drapsin, M.; Trivic, T.; Lukač, D.; Obadov, S.; Milosevic, Z. Asymmetry of Muscle Strength in Elite Athletes. Biomed. Hum. Kinet. 2009, 1, 3–5. [Google Scholar] [CrossRef]
- Handsfield, G.G.; Knaus, K.R.; Fiorentino, N.M.; Meyer, C.H.; Hart, J.M.; Blemker, S.S. Adding Muscle Where You Need It: Non-uniform Hypertrophy Patterns in Elite Sprinters. Scand. J. Med. Sci. Sports 2017, 27, 1050–1060. [Google Scholar] [CrossRef] [PubMed]
- Kuruvilla, S.J.; Fox, S.D.; Cullen, D.M.; Akhter, M.P. Site Specific Bone Adaptation Response to Mechanical Loading. J. Musculoskelet. Neuronal Interact. 2008, 8, 71–78. [Google Scholar] [PubMed]
- Amirabdollahian, F.; Haghighatdoost, F. Anthropometric Indicators of Adiposity Related to Body Weight and Body Shape as Cardiometabolic Risk Predictors in British Young Adults: Superiority of Waist-to-Height Ratio. J. Obes. 2018, 2018, 8370304. [Google Scholar] [CrossRef]
- Xu, Y.; Yan, W.; Cheung, Y.B. Body Shape Indices and Cardiometabolic Risk in Adolescents. Ann. Hum. Biol. 2015, 42, 70–75. [Google Scholar] [CrossRef] [PubMed]
- Bertoli, S.; Leone, A.; Krakauer, N.Y.; Bedogni, G.; Vanzulli, A.; Redaelli, V.I.; De Amicis, R.; Vignati, L.; Krakauer, J.C.; Battezzati, A. Association of Body Shape Index (ABSI) with Cardio-Metabolic Risk Factors: A Cross-Sectional Study of 6081 Caucasian Adults. PLoS ONE 2017, 12, e0185013. [Google Scholar] [CrossRef]
- Lambert, C.; Beck, B.R.; Harding, A.T.; Watson, S.L.; Weeks, B.K. Regional Changes in Indices of Bone Strength of Upper and Lower Limbs in Response to High-Intensity Impact Loading or High-Intensity Resistance Training. Bone 2020, 132, 115192. [Google Scholar] [CrossRef]
- Young, A.; Sawka, M. Bioelectrical Impedance to Estimate Changes in Hydration Status. Int. J. Sports Med. 2002, 23, 361–366. [Google Scholar] [CrossRef]
- Brandi, M.L. Microarchitecture, the Key to Bone Quality. Rheumatology 2009, 48, iv3–iv8. [Google Scholar] [CrossRef]
- Gandhi, S.S.; Muraresku, C.; McCormick, E.M.; Falk, M.J.; McCormack, S.E. Risk Factors for Poor Bone Health in Primary Mitochondrial Disease. J. Inherit. Metab. Dis. 2017, 40, 673–683. [Google Scholar] [CrossRef]
- Catheline, S.E.; Kaiser, E.; Eliseev, R.A. Mitochondrial Genetics and Function as Determinants of Bone Phenotype and Aging. Curr. Osteoporos. Rep. 2023, 21, 540–551. [Google Scholar] [CrossRef]
- Ding, P.; Gao, C.; Zhou, J.; Mei, J.; Li, G.; Liu, D.; Li, H.; Liao, P.; Yao, M.; Wang, B.; et al. Mitochondria from Osteolineage Cells Regulate Myeloid Cell-Mediated Bone Resorption. Nat. Commun. 2024, 15, 5094. [Google Scholar] [CrossRef] [PubMed]
- Di Vincenzo, O.; Marra, M.; Di Gregorio, A.; Pasanisi, F.; Scalfi, L. Bioelectrical Impedance Analysis (BIA)-Derived Phase Angle in Sarcopenia: A Systematic Review. Clin. Nutr. 2021, 40, 3052–3061. [Google Scholar] [CrossRef] [PubMed]
- Kushner, R.F.; Gudivaka, R.; Schoeller, D.A. Clinical Characteristics Influencing Bioelectrical Impedance Analysis Measurements. Am. J. Clin. Nutr. 1996, 64, 423S–427S. [Google Scholar] [CrossRef]
- Garlini, L.M.; Alves, F.D.; Ceretta, L.B.; Perry, I.S.; Souza, G.C.; Clausell, N.O. Phase Angle and Mortality: A Systematic Review. Eur. J. Clin. Nutr. 2019, 73, 495–508. [Google Scholar] [CrossRef] [PubMed]
- Yamada, M.; Kimura, Y.; Ishiyama, D.; Nishio, N.; Otobe, Y.; Tanaka, T.; Ohji, S.; Koyama, S.; Sato, A.; Suzuki, M.; et al. Phase Angle Is a Useful Indicator for Muscle Function in Older Adults. J. Nutr. Health Aging 2019, 23, 251–255. [Google Scholar] [CrossRef]
- Olds, T.S.; Gomersall, S.R.; Olds, S.T.; Ridley, K. A Source of Systematic Bias in Self-Reported Physical Activity: The Cutpoint Bias Hypothesis. J. Sci. Med. Sport. 2019, 22, 924–928. [Google Scholar] [CrossRef]
- Ferguson, B. ACSM’s Guidelines for Exercise Testing and Prescription 9th Ed. 2014. J. Can. Chiropr. Assoc. 2014, 58, 328. [Google Scholar]
| Osteopenic (Mean ± SD, n) | Non-Osteopenic (Mean ± SD, n) | T-Score | p Value | |
|---|---|---|---|---|
| Age | 48.8 ± 3.9 (n = 33) | 46.6 ± 4.5 (n = 105) | −2.69 | 0.009 |
| Height (cm) | 164.2 ± 7.5 (n = 33) | 165.3 ± 5.9 (n = 104) | 0.80 | 0.428 |
| Weight (kg) | 62.0 ± 7.9 (n = 33) | 73.0 ± 13.8 (n = 105) | 5.67 | <0.001 |
| BMI (kg/m2) | 23.1 ± 3.5 (n = 33) | 26.6 ± 4.8 (n = 105) | 4.51 | <0.001 |
| Fat Mass (kg) | 19.9 ± 7.1 (n = 33) | 26.5 ± 10.4 (n = 103) | 4.10 | <0.001 |
| % Body Fat | 31.4 ± 7.8 (n = 33) | 35.1 ± 8.6 (n = 103) | 2.29 | 0.026 |
| Lean Mass (kg) | 39.6 ± 3.8 (n = 33) | 43.6 ± 4.4 (n = 103) | 5.04 | <0.001 |
| Model | Accuracy | Recall | Precision | F1-Score | ROC AUC | Best Hyperparameters | Features |
|---|---|---|---|---|---|---|---|
| NNs | 0.9212 | 0.7667 | 0.8914 | 0.8199 | 0.9311 | {‘activation’: ‘relu’, ‘alpha’: 0.0001, ‘hidden_layer_sizes’: (10, 20, 50), ‘learning_rate’: ‘constant’, ‘solver’: ‘adam’} | 34 |
| LR | 0.8701 | 0.4905 | 0.9500 | 0.6424 | 0.8626 | {‘C’: 0.1, ‘solver’: ‘newton-cg’} | 53 |
| SVM | 0.7611 | 0.0000 | 0.0000 | 0.0000 | 0.4749 | {‘C’: 0.1, ‘kernel’: linear’} | 1 |
| XGBoost | 0.8847 | 0.7333 | 0.7886 | 0.7547 | 0.8243 | {‘learning_rate’: 0.1, ‘max_depth’: 5, ‘min_child_weight’: 1, ‘n_estimators’: 200} | 13 |
| Predictors | Type of Predictor |
|---|---|
| Minerals | Numeric |
| Edema Index (EI) | Numeric |
| Total Body Water | Numeric |
| Right Leg Lean Index Score | Numeric |
| Mineral% | Numeric |
| Protein% | Numeric |
| 20 kHz, Impedance (Z) of Left Arm | Numeric |
| Edema Index | Numeric |
| Activity Status | Categorical |
| Athlete Status | Categorical |
| Free Fat Mass | Numeric |
| 50 kHz, Reactance (Xc) of Left Arm | Numeric |
| Fat Mass (FM) | Numeric |
| Protein Mass | Numeric |
| FM Normal Range Lower Limit | Numeric |
| Health Score | Numeric |
| Right Arm Lean Index Score | Numeric |
| Waist–Height Ratio (WHtR) | Numeric |
| Skeletal Muscle Index | Numeric |
| 20 kHz, Impedance (Z) of Left Arm | Numeric |
| 50 kHz, Impedance (Z) of Right Leg | Numeric |
| 250 kHz, Impedance (Z) of Left Arm | Numeric |
| Protein Mass.1 | Numeric |
| Body Mass Index (BMI) | Numeric |
| 50 kHz, Impedance (Z) of Left Leg | Numeric |
| TBW/FFM.1 | Numeric |
| Trunk Fat Mass.1 | Numeric |
| 50 kHz, Phase Angle of Right Arm | Numeric |
| Soft Lean Mass (SLM) | Numeric |
| 50 kHz, Reactance (Xc) of Right Leg | Numeric |
| Right Leg Fat Mass | Numeric |
| 5 kHz, Phase Angle of Right Arm | Numeric |
| Fat-Free Mass Index | Numeric |
| 20 kHz, Impedance (Z) of Right Leg | Numeric |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balampanos, D.; Kokkotis, C.; Stampoulis, T.; Avloniti, A.; Pantazis, D.; Protopapa, M.; Retzepis, N.-O.; Emmanouilidou, M.; Aggelakis, P.; Zaras, N.; et al. Interpretable Machine Learning for Osteopenia Detection: A Proof-of-Concept Study Using Bioelectrical Impedance in Perimenopausal Women. J. Funct. Morphol. Kinesiol. 2025, 10, 262. https://doi.org/10.3390/jfmk10030262
Balampanos D, Kokkotis C, Stampoulis T, Avloniti A, Pantazis D, Protopapa M, Retzepis N-O, Emmanouilidou M, Aggelakis P, Zaras N, et al. Interpretable Machine Learning for Osteopenia Detection: A Proof-of-Concept Study Using Bioelectrical Impedance in Perimenopausal Women. Journal of Functional Morphology and Kinesiology. 2025; 10(3):262. https://doi.org/10.3390/jfmk10030262
Chicago/Turabian StyleBalampanos, Dimitrios, Christos Kokkotis, Theodoros Stampoulis, Alexandra Avloniti, Dimitrios Pantazis, Maria Protopapa, Nikolaos-Orestis Retzepis, Maria Emmanouilidou, Panagiotis Aggelakis, Nikolaos Zaras, and et al. 2025. "Interpretable Machine Learning for Osteopenia Detection: A Proof-of-Concept Study Using Bioelectrical Impedance in Perimenopausal Women" Journal of Functional Morphology and Kinesiology 10, no. 3: 262. https://doi.org/10.3390/jfmk10030262
APA StyleBalampanos, D., Kokkotis, C., Stampoulis, T., Avloniti, A., Pantazis, D., Protopapa, M., Retzepis, N.-O., Emmanouilidou, M., Aggelakis, P., Zaras, N., Michalopoulou, M., & Chatzinikolaou, A. (2025). Interpretable Machine Learning for Osteopenia Detection: A Proof-of-Concept Study Using Bioelectrical Impedance in Perimenopausal Women. Journal of Functional Morphology and Kinesiology, 10(3), 262. https://doi.org/10.3390/jfmk10030262











