Abstract
To assist an individual with an amputation in regaining daily quality of life, a 2SPU-RU type parallel mechanism was developed based on ankle biomechanics. The inverse kinematic analysis of this mechanism was performed using the vector method. Subsequently, the Jacobian matrices were analyzed. The dynamic model of the mechanism was then created based on the principle of virtual work, and its theoretical solution was compared with numerical results obtained in a simulation environment. Additionally, the validity of the dynamic model and the inverse kinematics was verified by comparing theoretical and simulation results for the movements of plantarflexion–dorsiflexion, eversion–inversion, and abduction–adduction during the gait cycle.
1. Introduction
Transtibial amputations statistically account for more than 80% of lower limb amputations worldwide [1]. According to the WHO, it is estimated that 0.5% of the global population requires prostheses, orthoses, and rehabilitation treatment. The estimate of 0.5% of the world population corresponds to approximately 35–40 million people in need of orthotic and prosthetic services worldwide [2]. This prevalence underscores the importance of advanced research and development in prosthetics and rehabilitation for individuals undergoing this form of amputation. Various factors can precipitate the need for transtibial amputations, with vascular diseases being a principal cause [3]. Peripheral vascular diseases and complications stemming from diabetes can severely impair blood flow [4,5], leading to tissue necrosis and, consequently, amputations [6,7]. Similarly, traumatic events such as accidents and severe injuries can make transtibial amputations imperative to forestall further complications and safeguard the overall health of the individual [8]. Chronic and unresolved infections can result in extensive tissue damage and necrosis in certain instances, necessitating amputation to stop the infection’s progression [9]. Additionally, the presence of aggressive or treatment-resistant cancerous tumors in the lower leg may also warrant amputation as a life-preserving intervention [10].
The enduring repercussions of transtibial amputations significantly impact the lives and well-being of affected individuals [11]. Those who undergo such amputations confront substantial mobility challenges, necessitating the use of prosthetics to regain autonomy in movement [12]. The loss of a limb also imparts a profound psychological toll, necessitating extensive support and counseling to facilitate mental adjustment and maintain psychological well-being [13]. Furthermore, robust rehabilitation programs become imperative, emphasizing the strengthening of remaining muscles, training in mobility, and adaptation to new prosthetic limbs [14]. The integrated approach to addressing the physical and psychological ramifications is vital to enhancing the overall quality of life for individuals enduring transtibial amputations [15].
The functional needs of lower limb prosthesis users primarily focus on the ability to walk effectively across various environments, such as uneven and slippery surfaces, and in situations requiring agility, such as climbing stairs. Due to their potential to enhance balance and stability during walking, there is a high demand for advanced prosthetic technologies, including improvements in socket design, alignment, and microprocessor-controlled systems. However, significant challenges in overall gait and balance persist despite technological advancements [15].
Independence in daily activities is another critical aspect for users, directly linked to their quality of life and self-esteem. Additionally, maintaining or returning to work after an amputation is crucial, with a successful return often dependent on the job’s physical demands and the work environment’s adaptability [16]. More advanced devices offer better mobility, reduce energy expenditure, and help minimize productivity loss, thus supporting a more active and autonomous life.
The development of mechatronic lower limb prostheses has significantly improved aspects such as walking energy efficiency [17], mobility [14], independence [18], workplace productivity due to fewer absence days, as well as better balance and stability [19], increased safety and confidence [20], and reduced cognitive demands [21]. Moreover, these advancements have contributed to better limb health [22] and reduced costs, excluding the purchase price of devices [23]. However, there is still room for critical improvements, especially in maintaining balance comparable to healthy individuals [19] and the scarcity of fully electric devices that support activities such as standing up from a seated position, which impacts overall independence and mobility [24]. While balance confidence has improved, the number of trips and falls has not significantly decreased [21].
There is a notable absence of prostheses that utilize parallel mechanisms [25]. Parallel mechanisms, where components are arranged in a closed-loop configuration [26], can offer enhanced stability, precision [27], and load-bearing capacity [28]. This makes them integral to developing advanced, adaptive prosthetics [29]. These parallel mechanisms enable coordinated movements and adaptations to varied terrains, which are critical for the comprehensive restitution of limb function for transtibial amputees and support more dynamic and life-like mobility. The potential benefits of utilizing parallel mechanisms in ankle prostheses are diverse, from enabling more natural gait patterns to allowing users to navigate varied terrains quickly and confidently. Such advancements could significantly improve the quality of life for individuals reliant on ankle prostheses by offering increased mobility, comfort, and functionality. This apparent gap underscores the pressing need for continued research and development efforts to explore and integrate parallel mechanisms into the design and construction of ankle prostheses. Leveraging insights and advancements from rehabilitation studies can pave the way for innovative prosthetic solutions that more effectively meet the diverse needs of amputees [25,30,31,32,33,34,35]. Existing prosthetics often have limitations in accurately mimicking ankle movements, which motivates research to overcome these challenges by developing an anatomically accurate parallel mechanism that can replicate natural human movements, thereby significantly enhancing the quality of life for amputees.
This research is organized as follows: Section 2 presents the biomechanical principles. Section 3 illustrates the design of a parallel 2SPU-RU mechanism based on ankle biomechanics. Section 4 details the inverse kinematic analysis of this mechanism, which was performed using a closed-loop vector method. Subsequently, Section 5 analyzes the Jacobian matrices. Section 6 presents the inverse dynamic model of the mechanism, created based on the principle of virtual work. Section 7 compares its theoretical solution to numerical results obtained in a simulation environment. Section 8 presents the discussion and finally, the conclusion in Section 9.
The significant contributions of this work are as follows:
- The model uniquely simulates essential ankle movements, tailored specifically for ankle prostheses.
- The integration of parallel mechanisms to enhance prosthetic stability and adaptability using the innovative 2SPU-RU parallel mechanism.
- The design is rigorously validated against theoretical and simulation results to ensure its effectiveness and accuracy.
2. Biomechanical Principles
2.1. Planes, Axes, and Types of Movement
Understanding planes, axes, and types of movement is vital for designing transtibial prostheses that offer functional and natural motion for the user. Each movement must be carefully engineered to simulate the natural function of a human ankle while accommodating the user’s needs.
- Anatomical plane: The sagittal plane is a vertical division of the body into right and left sections, with movement occurring around a horizontal axis. The frontal plane, called the coronal plane, splits the body into anterior (front) and posterior (back) parts. Meanwhile, the horizontal transverse plane divides the body into superior (upper) and inferior (lower) sections, as shown in Figure 1a.
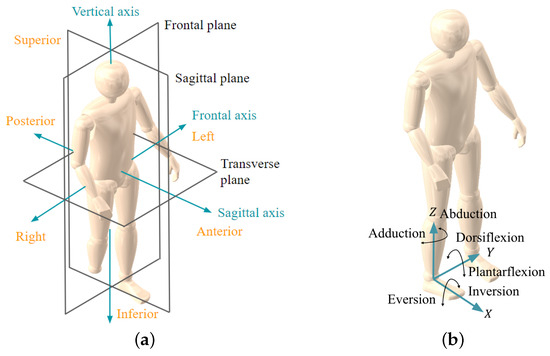 Figure 1. Biomechanics: (a) sagittal, frontal, and transverse planes and vertical, sagittal, and frontal axes, and (b) plantarflexion–dorsiflexion, eversion–inversion, and abduction–adduction movements.
Figure 1. Biomechanics: (a) sagittal, frontal, and transverse planes and vertical, sagittal, and frontal axes, and (b) plantarflexion–dorsiflexion, eversion–inversion, and abduction–adduction movements. - Anatomical axes: The vertical axis runs from top to bottom and serves as the axis of rotation for movements occurring in the transverse plane. The sagittal axis, which extends from front to back, is linked with movements in the frontal plane, such as lateral bending to the side. Meanwhile, the frontal axis runs from side to side through the body and facilitates movements in the sagittal plane, as shown in Figure 1a.
- Anatomical motions: Plantarflexion involves moving the foot away from the body by pointing the toes downward, while dorsiflexion is the opposite movement, flexing the foot upward toward the shin. Eversion occurs when the sole is turned outward, away from the body’s median plane, and inversion is when the sole turns inward toward the median plane. Abduction refers to moving the foot away from the body’s midline in the transverse plane, and adduction is the foot’s movement toward the body’s midline in the same plane, as shown in Figure 1b.
2.2. The Gait Cycle
The mechanism must replicate the phases of the gait cycle, which refer to the different stages involved in the walking action. The gait cycle is divided into two main phases: the stance phase and the swing phase, forming a complete cycle from when one foot touches the ground to when the same foot contacts the ground again [36]. The gait cycle is detailed in Figure 2 and Table 1.
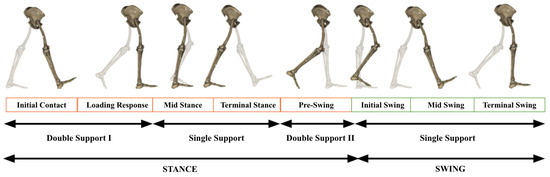
Figure 2.
Phases and periods of the gait cycle.

Table 1.
Phases of the gait cycle.
Stance phase: This phase begins when the foot touches the ground and ends when the foot lifts off the ground. It constitutes approximately 60% of the gait cycle and is subdivided into several subphases: initial contact (heel strike), loading response (foot flat), mid-stance, terminal stance (heel off), and pre-swing (toe off).
Swing phase: This phase covers the period when the foot is off the ground and moving forward to begin a new step. It represents approximately 40% of the gait cycle and is divided into subphases: initial swing (acceleration), mid-swing, and terminal swing (deceleration).
iSen inertial sensors and AMTI NetForce force platforms were used to test the gait data of inverse kinematics and kinetics of a 33-year-old female weighing approximately 50 kg with a height of 1.52 m and a gait velocity of 1.3 m/s. These advanced measurements allow us to capture a wide range of dynamic data crucial for understanding the movement patterns and forces involved during walking. The data obtained are presented in Figure 3, which is divided into several subfigures to illustrate different aspects of the movement. Figure 3a shows the angle of dorsiflexion–plantarflexion movement, vital for understanding how the foot interacts with the ground during walking. Figure 3b examines the angle of inversion–eversion movement, offering insights into lateral stability and balance throughout the gait cycle. Meanwhile, Figure 3c highlights the angle of abduction–adduction movement, providing details on the lateral movement of the foot and its influence on overall biomechanics. Finally, Figure 3d provides detailed information about the ground reaction forces over time during gait.
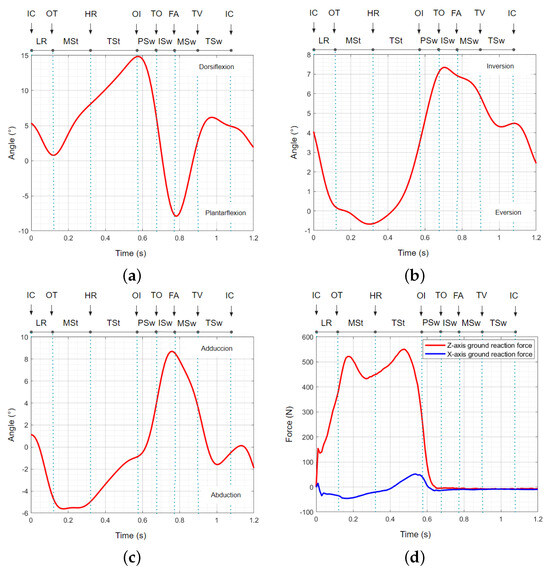
Figure 3.
The gait cycle: (a) angle of plantarflexion–dorsiflexion movement, (b) angle of inversion–eversion movement, (c) angle of abduction–adduction movement, and (d) reaction forces on the ground vs. time during a gait. IC: initial contact; OT: opposite toe off; HR: heel rise; OI: opposite initial contact; TO: toe off; FA: feet adjacent; TV: tibia vertical; LR: loading response; MSt: mid–stance; TSt: terminal stance; PSw: pre–swing; ISw: initial swing; MSw: mid–swing; TSw: terminal swing.
3. Design of a Parallel 2SPU-RU Mechanism
The engineering of a parallel mechanism necessitates carefully considering several critical components, as depicted in Figure 4a. These include the platforms constituting the fixed base and the moving platform, the power source propelling the mechanism’s motion, and the joints or kinematic pairs that link the platforms to the actuators and power source. Specifically, the 2SPU-RU parallel mechanism comprises three kinematic chains connecting a mobile platform to a fixed base.
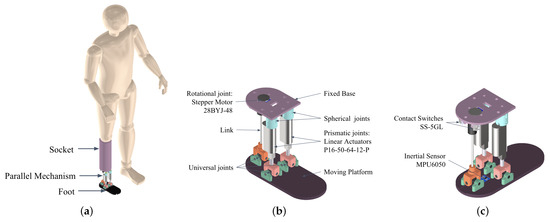
Figure 4.
Parallel mechanism type 2SPU-RU: (a) parallel mechanism with a prosthetic socket and foot, designed for a person with an amputation, (b) elements of mechanism, and (c) integration of inertial sensor and contact switches in the mechanism.
Kinematic chains: The first kinematic chain refers to an RU (revolute-universal)-type kinematic chain within the mechanism, where the R joint enables rotation around a single axis and the U joint allows for rotation around two axes. This kinematic chain comprises a 28BYJ-48 stepper motor, a rigid link, and a universal joint. The stepper motor is linked to the rigid link via one coupling, and the rigid link is connected to the universal joint through another coupling. The second and third kinematic chains are categorized as SPU (spherical–prismatic–universal) types. Each chain features a spherical joint (S) that allows three-dimensional movement at a fixed point, a prismatic joint (P) that facilitates linear motion, and a universal joint (U) that permits rotation around two axes. A linear actuator from Actuonix, the P16-50-64-12-P model, is positioned between the spherical and universal joints, as depicted in Figure 4b.
Moving platform: The moving platform replicates the multifaceted movements of the human ankle. Centrally situated on the upper portion of the mechanism’s moving platform is the Inertial Measurement Unit (IMU), model MPU6050. Its primary role is to ascertain the rotational angles of the prosthesis, as depicted in Figure 4c.
Fixed base: The mechanism’s design includes a fixed platform, also referred to as a stationary base, which ensures that it remains in a precise, unmoving position. The fixed base is the foundation where two spherical joints, a 28BYJ-48 stepper motor and SS-5GL contact switches, are mounted, as depicted in Figure 4c.
Figure 5 shows the Autodesk Inventor Professional 2021 modeling and simulation tool that evaluated and optimized the design.
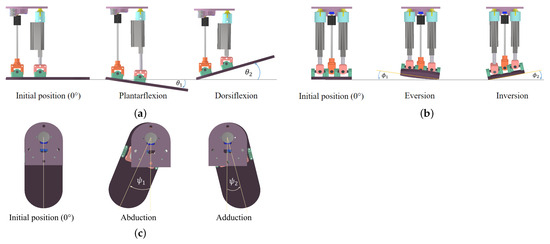
Figure 5.
Movements of the parallel mechanism: (a) in the sagittal plane, (b) in the frontal plane, and (c) in the transverse plane.
Ankle and foot movements are organized by the three principal anatomical planes. In the sagittal plane, two movements are described: plantar flexion, with an angle of , indicating a downward movement of the foot, and dorsiflexion, with an angle of , representing an upward movement of the foot. In the frontal plane, the movements of eversion and inversion are denoted, with angles of and , respectively, indicating the foot movement outward and inward. Lastly, in the transversal plane, abduction and adduction are listed, with angles of and , which signify the foot’s movement to the lateral and medial sides, respectively.
4. Inverse Kinematic Analysis
In this section, we apply the geometric method to establish the inverse kinematics model to know the actuators’ position based on the moving platform’s orientation. Therefore, in this section on kinematics, we will describe and explain the elements necessary for kinematic modeling. These elements include nomenclature, global and local reference systems, and geometric and angular parameters.
In parallel mechanisms, coordinates or joints are typically denoted using a specific notation system. For this study, the coordinates of the fixed platform are denoted by the points while those of the moving platform are indicated by the points , as illustrated in Figure 6a. The lead-colored cross shaft is attached to the moving platform, while the other white cross shaft is coupled to the prismatic joint (P) or rotational joint (R), as illustrated in Figure 6b.
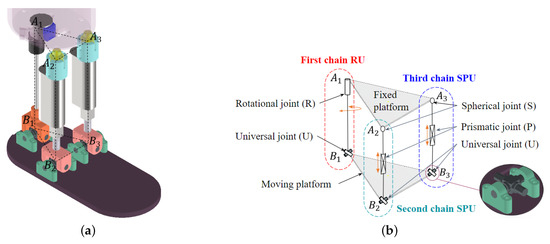
Figure 6.
Mechanism 2SPU-RU: (a) coordinates of the fixed base and moving platform, and (b) kinematic chains.
4.1. Global and Local Reference Frame
The global reference frame shown in Figure 7a is a three-dimensional coordinate system that remains fixed and serves as an absolute reference frame for describing the position and orientation of the parallel mechanism in its environment. It is located at the geometric center of the fixed platform, also called the fixed base of the parallel mechanism 2SPU-RU.
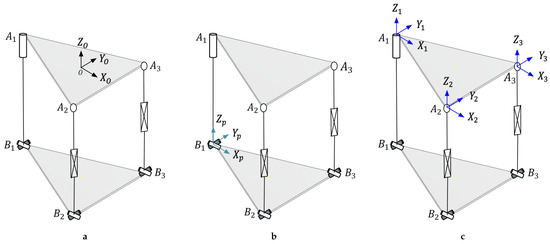
Figure 7.
Reference frame of the 2SPU-RU parallel mechanism: (a) global reference system O() in fixed platform, (b) local reference system in moving platform (), and (c) local reference system in joint (), (), ().
- The origin is located at the geometric center of the fixed platform.
- The axis in the anteroposterior direction (from the heel to the tip of the foot). It is the main direction of advance when walking.
- The axis in the mediolateral direction; that is, perpendicular to the sagittal plane of the body and horizontal to the ground, pointing toward the foot’s outer side.
- The axis in the vertical direction, upward. This axis will mainly align with the body weight and the reactive force of the ground.
The local reference frame , depicted in Figure 7b, is rigidly affixed to the moving platform (end effector) at point . This frame is essential for describing the platform’s rotation and position relative to the global reference frame . Similarly, the local reference frames , , and , shown in Figure 7c, are attached to points , , of kinematic chains 1, 2, and 3, respectively. These frames are used to track the rotation and position of the components in these chains relative to the global frame , as well as to monitor the displacements of rotary actuator 1 and linear actuators 2 and 3.
4.2. Geometric Parameters
Geometric parameters are the characteristics and measurements that define the structure and kinematics of the 2SPU-RU mechanism. These parameters determine how the moving parts of the mechanism move and are positioned, as shown in Figure 8.
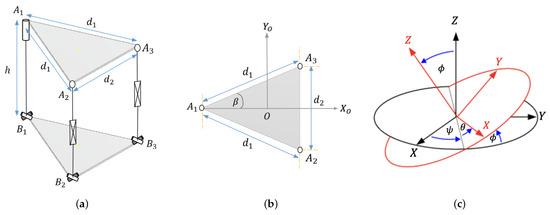
Figure 8.
2SPU-RU parallel mechanism: (a) distances of the elements, (b) cartesian coordinates of the joint points with respect to the global frame O(), and (c) Bryant–Cardan angles .
- (a)
- Distances Between JointsThe distances between the joints, as shown in Figure 8a, are linear measurements that indicate the separation between various connecting joints of the parallel mechanism. These distances define the geometric configuration of the mechanism and influence its range of movement. The platforms and are rigid elements shaped into an isosceles triangle. The triangles and are identical. The side lengths , and , are equal, respectively.
- (b)
- Joint CoordinatesThe coordinates of the joints in the parallel mechanism represent the spatial positions of the fixed and moving platforms’ kinematic pairs. These coordinates are defined within a global reference frame and are used to describe each joint’s position and relative orientation in space. Figure 8b details the coordinates of the points O, , , , which make up the 2SPU-RU parallel mechanism.
- (c)
- Angular Parameters of the Moving PlatformIn the parallel mechanism, the orientation of the moving platform is defined using the Bryant–Cardan ZXY angle sequence, as shown in Figure 8c. This method starts with a rotation around the Z axis by an angle , followed by a rotation around the X axis by an angle , and culminates with a rotation around the Y axis by an angle , as detailed in Equation (1). The choice of the ZXY sequence is supported by recommendations from the International Society of Biomechanics, which proposes this specific ZXY sequence to calculate ankle rotations. In anatomical terms, this sequence corresponds to the movements of adduction–abduction, inversion–eversion, and plantarflexion–dorsiflexion:
- (d)
- Angular Velocity of the Moving PlatformThe angular velocity vector depends on the time variation of the rotation matrix composed of the angles , , . In this case, the angular velocity is obtained through Equation (2):
- (e)
- Angular Acceleration of the Moving PlatformThe angular acceleration of the moving platform is obtained by differentiating the angular velocity for time, as shown in Equation (3):
4.3. First Kinematic Chain
This section presents the position analysis, followed by the linear and angular velocity analysis and the angular acceleration analysis of the RU kinematic chain in the parallel mechanism.
- (a)
- Position AnalysisThe position vectors of the RU kinematic chain are defined to the global reference frame O(), as shown in Figure 9a. The position vectors define the vector Equation (4).
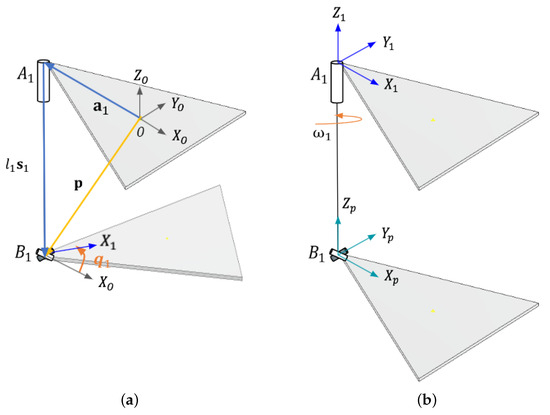 Figure 9. RU kinematic chain of the parallel mechanism: (a) vectors of the RU kinematic chain, and (b) angular velocity of the rotary actuator.Where the vectors , , and remain constant, which implies that their components do not change concerning time or any other variable, and is the ankle’s rotation angle in the rotation axis of the moving platform:where is the vector representing the position of the spherical joint to the origin O, is the vector representing the position of the rotary actuator to , and is the vector representing the position of P located at the universal joint U concerning the origin O.
Figure 9. RU kinematic chain of the parallel mechanism: (a) vectors of the RU kinematic chain, and (b) angular velocity of the rotary actuator.Where the vectors , , and remain constant, which implies that their components do not change concerning time or any other variable, and is the ankle’s rotation angle in the rotation axis of the moving platform:where is the vector representing the position of the spherical joint to the origin O, is the vector representing the position of the rotary actuator to , and is the vector representing the position of P located at the universal joint U concerning the origin O. - (b)
- Linear and Angular Velocity AnalysisThe linear and angular velocity of the kinematic chain RU is analyzed. It is important to note that all the bodies of each kinematic chain i (with ) move with the same angular velocity. The rotary actuator belongs to the kinematic chain RU and is at point . This implies that the vector connecting with maintains a constant magnitude and direction. Therefore, it is established that the derivative of the position vector = is equal to zero .Furthermore, due to the connection with the universal joint (U) of two degrees of freedom located at , it is established that the rotation on the axis of the rotary actuator coincides with the rotation of the moving platform concerning the axis. It corresponds to the first rotation of the three successive intrinsic rotations that define the rotation matrix of the moving platform through Equation (1). Thus, the angular velocity of the actuator is equal to the derivative of the rotation angle with respect to the axis (), as shown in Figure 9b.
- (c)
- Angular Acceleration AnalysisBy differentiating the equation that relates the angular velocity of the kinematic chain RU with the velocity of the moving platform projected onto the axis , it is obtained that . That is to say, the angular acceleration of the kinematic chain RU is equal to the angular acceleration of the second derivative of the rotation angle concerning the axis.
4.4. Second and Third SPU Kinematic Chains
This section presents the position, linear velocity, and angular velocity analysis of the ith SPU kinematic chain. Then, it presents a linear velocity analysis of the cylinder and piston in the linear actuator. Also, it presents a linear acceleration and angular acceleration analysis of the ith SPU kinematic chain, and finally, a linear acceleration analysis of the cylinder and piston of the linear actuator.
- (a)
- Position Analysis of the ith SPU Kinematic ChainThe position vectors of the SPU kinematic chain are established to the global reference frame O(), as depicted in Figure 10a. This results in Equation (5), which equals the sum of the vectors , , and the vectors and :where is the vector representing the position of the spherical joint to the origin O, is the vector representing the position of the rotary actuator to , and is the vector representing the position of the universal joint with respect to .
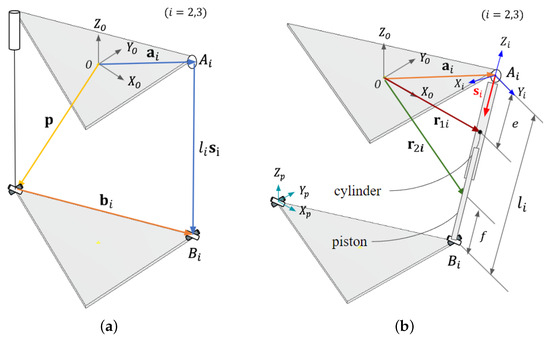 Figure 10. Parallel mechanism: (a) vectors of the SPU kinematic chain, and (b) free body diagram of the typical limb.From Equation (5), the vector has a magnitude presented in Equation (6) and a direction presented in Equation (7):In Figure 10b, a linear actuator composed of a cylinder and a piston is illustrated, where the latter moves along the axis, defined along the unit vector . The axis is defined along the second axis of rotation of the universal joint, which allows for relative rotation between the second kinematic chain and the universal joint.From the global reference frame O(, , ) of the fixed platform, the position vectors of the center of mass of the cylinder and the piston are defined, which are denominated and and are defined by Equation (8) and Equation (9), respectively. The distance between and the center of mass of the cylinder is represented by e, while the distance between and the center of mass of the piston is designated as f:
Figure 10. Parallel mechanism: (a) vectors of the SPU kinematic chain, and (b) free body diagram of the typical limb.From Equation (5), the vector has a magnitude presented in Equation (6) and a direction presented in Equation (7):In Figure 10b, a linear actuator composed of a cylinder and a piston is illustrated, where the latter moves along the axis, defined along the unit vector . The axis is defined along the second axis of rotation of the universal joint, which allows for relative rotation between the second kinematic chain and the universal joint.From the global reference frame O(, , ) of the fixed platform, the position vectors of the center of mass of the cylinder and the piston are defined, which are denominated and and are defined by Equation (8) and Equation (9), respectively. The distance between and the center of mass of the cylinder is represented by e, while the distance between and the center of mass of the piston is designated as f: - (b)
- Linear Velocity Analysis of the ith Kinematic Chain SPUThe velocity analysis aims to determine a mechanical element’s linear and angular velocities. Starting from Equation (5), the terms on the left side of the equality are derived, resulting in Equation (10).Where is the velocity vector of the universal joint , is the velocity of the universal joint (which is always zero), and the term represents the cross product between the angular velocity of the mobile platform and the vector :The velocity is transformed to the local reference frame of the ith kinematic chain , which is expressed with a left superscript, resulting in Equation (11).Where is the rotation matrix from the global reference frame O(,, ) to the local reference frame of the ith kinematic chain:Equation (12) is used to calculate :where is the rotation matrix from the local reference frame of the kinematic chain to the local reference frame of the moving platform . The rotation matrix is determined by two rotations: is the rotation around the axis, followed by the rotation around the axis, and it is calculated in Equation (13):It is noted that the third column of the matrix equals the negative of the vector expressed in the reference frame of the moving base . Therefore, to resolve Equation (13), the angles were calculated according to Equation (14):where is the negative vector of the vector , expressed in the reference frame of the moving platform .The terms found on the left side of Equation (5) are derived and equal to the velocity . This equality relates the speed of the universal joint with the angular velocity and the linear speed of the kinematic chain .The new equation expressed in the local reference frame allows us to obtain a direct expression of the angular velocity of the second kinematic chain according to Equation (17):
- (c)
- Angular Velocity Analysis of the ith Kinematic Chain SPUThe angular velocity of the ith kinematic chain with respect to the local reference frame is calculated by multiplying by the cross product of in both terms of Equation (17):The last term of Equation (19) is eliminated because the unit vectors are parallel, resulting in a cross product equal to zero. Similarly, in the Equation, the property of the vector cross product is applied, resulting in Equation (20):In Equation (20), the term is equal to one by the dot product between the unit vectors.
- (d)
- Linear Velocity Analysis of the Cylinder and Piston in the Linear ActuatorOnce the linear velocity of the universal joint and the angular velocity of the ith kinematic chain relative to the local reference frame (, , ) are known, it is possible to calculate the velocity of each component within the ith kinematic chain to the local reference frame (, , ). The cylinder’s velocity is denoted by and the piston’s velocity by .The terms and are replaced in Equation (26):The term is factored out in Equation (27):
- (e)
- Linear Acceleration Analysis of the ith Kinematic Chain SPUDifferentiating Equation (10) concerning time yields the acceleration of point as defined by Equation (28):The velocity is expressed in the reference frame of the kinematic chain (, , ), resulting in Equation (29):The acceleration of point in Equation (30) is expressed in terms of the kinematic chain acceleration using the derivative of Equation (17):The terms and from Equation (31) are zero because the dot product of two perpendicular vectors is zero.Likewise, for the term , the property is applied, and Equation (32) is obtained:
- (f)
- Angular Acceleration Analysis of the ith Kinematic Chain SPUThe term of Equation (35) is zero due to the cross product of two parallel vectors.In the terms , , and the property of the cross product , Equation (21), and deriving Equation (21) are applied, reducing to
- (g)
- Linear Acceleration Analysis of the Cylinder and Piston of the Linear Actuator
5. Jacobian Matrices
Once the positions, velocities, and accelerations are known, the calculation of the Jacobian matrices of the kinematic chains proceeds. The objective is to express the velocity of each body of the mechanism as a function of , as shown in Equation (39):
where is the six-row vector that represents the linear and angular velocities of the center of gravity of the mobile platform expressed in the global reference frame O().
5.1. Jacobian Matrix of Kinematic Chain RU
From the analysis of the linear velocity of the kinematic chain RU, it is found that and that it only has angular velocity on the axis . Therefore, the angular velocity of the link of the kinematic chain RU can be expressed according to Equation (40):
where the Jacobian matrix is expressed according to Equation (41):
Furthermore, it is known that the angular velocity of actuator 1 is the component along the axis of the angular velocity of the kinematic chain RU (). This analysis obtains the Jacobian matrix of actuator 1 according to Equation (42):
5.2. The Moving Platform
The moving platform (end effector) of the parallel mechanism is considered. The angular velocity of the moving platform is expressed as a function of the vector according to Equation (43):
It is observed that the linear velocity of the moving base is a function of its angular velocity, so the Jacobian relates the six vector with the angular velocity of the moving platform according to Equation (45):
5.3. Second and Third Kinematic Chain SPU
Starting from Equation (10), the linear velocity of the cross head of the ith kinematic chain concerning the center of gravity of the moving platform is expressed according to Equations (46) and (47):
where
Equation (47) is expressed in the reference frame of the ith kinematic chain (, , ), resulting in Equations (48) and (49):
where
The linear velocities of the cylinder and piston of the second kinematic chain are calculated, as expressed in Equations (52):
The Jacobian matrices of the cylinder and the piston of the kinematic chain are denoted by Equation (54):
Finally, the Jacobian matrix of the parallel mechanism is obtained according to Equation (55):
6. Inverse Dynamics Analysis
Inverse dynamics involves finding the forces and torques required in the mechanism’s actuators to achieve a specific movement of the mechanism. The dynamic equations of motion employ the principle of virtual work.
6.1. External Forces and Moments on the Moving Platform
The resultant of the forces and moments applied at the center of mass of the moving platform is denoted by Equation (56):
where is the vector of forces and resulting moments on the moving platform, is the external force exerted at the center of mass of the moving platform in [N], is the external moment exerted at the articulation between the moving platform and kinematic chain 1 in , is the mass of the moving platform in [kg], is the gravity vector , is the linear acceleration of the center of gravity of the moving platform in , and of Equation (57) is the inertia matrix of the moving platform taken about the center of mass in the fixed frame O in [kg·m2]:
where and represent orthogonal transformation matrices. is the inertia matrix of the platform in a local frame.
- (a)
- Forces and Inertia on the Kinematic Chain RUAssuming that gravitational force is the only external force, the resultant applied forces and inertia exerted at the center of mass of the link in the kinematic chain RU can be expressed in the local frame with Equation (58):where is the vector of resultant forces and moments on the link of the first kinematic chain, expressed from the local reference frame ; is the mass of the link of the kinematic chain RU in [kg]; and is the moment of inertia of the link of the kinematic chain RU [kg·m2].
- (b)
- Forces and Inertia on the Second Kinematic Chain (SPU)Similarly, assuming that gravitational force is the only external force, the resultant applied forces and inertia exerted on the centers of mass of the cylinder and piston can be expressed in the local frame of the second kinematic chain with Equations (59) and (60):where is the vector of resultant forces and moments on the cylinder of the second kinematic chain (SPU), expressed from the local reference frame ; is the mass of the cylinder of the second kinematic chain (SPU) in [kg]; and is the moment of inertia of the cylinder of the second kinematic chain (SPU) concerning the local reference frame , [kg·m2]:where is the vector of resultant forces and moments on the piston of the second kinematic chain (SPU), expressed from the local reference frame . is the mass of the piston of the second kinematic chain (SPU), [kg]. is the moment of inertia of the piston of the second kinematic chain (SPU) concerning the local reference frame , [kg·m2].
6.2. Motion Equations
The dynamic model of the parallel mechanism is obtained through the principle of virtual work, which allows for the determination of the torques of each joint based on the external forces and moments applied to the mechanism’s bodies. In this case, the bodies are a moving platform, a cylinder, and a piston for each linear actuator and the link of the kinematic chain RU.
According to this method, Equation (61) must be satisfied, which relates the resultant force on each body, the differential displacement it generates in each body, the virtual displacements of the joints, and the torque on each joint:
where is the vector of the rotation angle of the link of the kinematic chain RU, is the vector of the torques applied to the revolute joints and two prismatic joints, is the position vector of the moving platform, is the vector of forces and resulting moments on the moving platform, is the position vector of the link of the kinematic chain RU, is the vector of resultant forces and moments on the link of the first kinematic chain RU, is the vector of resultant forces and moments on the cylinder of the second kinematic chain (SPU), is the position vector of the cylinder of the kinematic chain i (2 or 3), is the vector of resultant forces and moments on the cylinder of the second kinematic chain (SPU), is the position vector of the piston of the kinematic chain i (2 or 3), and is the vector of resultant forces and moments on the piston of the second kinematic chain (SPU).
Equation (62) presents the vector of the rotation angle of the link of the kinematic chain RU :
where are the lengths of the second and third kinematic chains, respectively.
The resultant applied forces and inertia , , and their corresponding virtual displacements , , are expressed in their respective frames of reference. The input forces are intentionally isolated from the other forces to facilitate derivation.
The virtual displacements must be compatible with the kinematic constraints imposed by the joints. Therefore, it is necessary to relate the above virtual displacements with independent generalized virtual displacements. Hence, we have Equations (63) to (66):
Substituting Equations (63) to (66) into Equation (61) results in Equation (67). It is important to mention that the torques are written with respect to the center of mass of each link. However, if an external torque is applied at a point other than the center of mass, it must be transformed to one taken about the center of mass before substituting it into the motion equations:
7. Results
7.1. Simulation Parameters
A CAD model of the 2SPU-RU parallel mechanism was designed in Autodesk Inventor 2021 software to determine the simulation parameters accurately. This allowed for the acquisition of joint coordinates, inertial and mass properties, and the ankle’s motion conditions.
- (a)
- Joint coordinates: The coordinates of the fixed platform in millimeters were obtained from the global reference frame O(, , ):The moving platform’s coordinates were obtained from its reference frame (, , ).
- (b)
- Mass properties: The moving platform mass is 0.22 kg. The mass of the cylinder in the second kinematic chain is 0.085 kg, and the piston in the same chain has a mass of 0.010 kg. Similarly, the cylinder mass is 0.085 kg for the third kinematic chain, and the piston is 0.010 kg. Lastly, the mass of the link in the kinematic chain RU is 0.21 kg.
- (c)
- Center of mass of cylinder and piston: The distance between and the center of mass of cylinder 2 is e = 55 mm. The distance between and the center of mass of piston 2 is f = 27 mm. The distance between and the center of mass of cylinder 3 is e = 55 mm. The distance between and the center of mass of piston 3 is f = 27 mm.
- (d)
- Inertial properties in kg.mm2:
- (e)
- Gravity vector: .
- (f)
- External force: The reaction forces on the ground during a gait are forces external and . Here, force is the vertical force on the Z axis and force is the horizontal reaction force from the ground on the X axis. Additionally, the external moment = exists, as shown in Figure 3.
Based on these parameters and equations, the dynamic problem of the 2SPU-RU parallel mechanism was programmed and calculated using MATLAB to implement the algorithm and verification through simulation results. The following simulations were performed to validate the principle of virtual work. These simulations assumed that gravitational force is the only external force acting on the kinematics chains.
Based on the principle of virtual work, a methodology for solving the inverse dynamics of the 2SPU-RU parallel mechanism is developed. The methodology involves five basic steps. Step 1: solve the inverse kinematics of the parallel mechanism. Step 2: formulate the link Jacobian matrices. Step 3: calculate the inertia forces. Step 4: formulate the dynamical equations of motion. Step 5: solve the dynamical equations of motion. Several movements of the gait cycle of the moving platform are simulated. Using the principle of virtual work, the constraint forces are eliminated at the outset. This allows us to reduce the inverse dynamics of the 2SPU-RU parallel mechanism to solve a system of linear equations.
7.2. Inverse Kinematics Results in MATLAB R2022b
The results obtained through the model developed and implemented in Matlab R2022b were as follows. Biomechanical data from the gait cycle were utilized, focusing on the rotation angles of the ankle–foot joint during a gait cycle at a speed of 1.3 m/s. The angle corresponds to the abduction–adduction movement, angle to the eversion–inversion movement, and angle to the plantarflexion–dorsiflexion movement, as shown in Figure 3. The input data, which consist of the orientation of the moving platform, undergo an inverse kinematics process. Subsequently, the angular and linear displacements of the actuators are obtained. The angular and linear displacement of the actuators versus time is presented in Figure 11, where the horizontal axis represents time, expressed in seconds. Meanwhile, the vertical axis indicates the angular displacement, measured in degrees for the rotary actuator, and the linear displacement expressed in millimeters for linear actuators 2 and 3. The results are analyzed in Table 2.
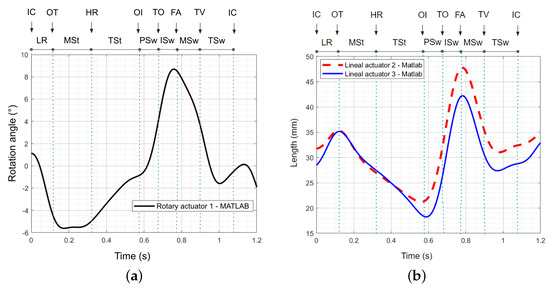
Figure 11.
Combined ankle movement (plantarflexion−dorsiflexion, inversion−eversion, and abduction−adduction): (a) rotation angle of the rotary actuator during a gait cycle, and (b) length of the linear actuators during a gait cycle. IC: initial contact; OT: opposite toe off; HR: heel rise; OI: opposite initial contact; TO: toe off; FA: feet adjacent; TV: tibia vertical; LR: loading response; MSt: mid−stance; TSt: terminal stance; PSw: pre−swing; ISw: initial swing; MSw: mid−swing; TSw: terminal swing.

Table 2.
Analysis of the combined ankle movement in the gait cycle phases.
The gait cycle comprises two main periods: the stance and swing periods, each characterized by different movement patterns. The stance period is represented by the phases initial contact (IC), loading response (LR), mid-stance (MSt), terminal stance (TSt), and pre-swing (PSw). The swing period is presented by the phases initial swing (ISw), mid-swing (MSw), and terminal swing (TSw). Critical moments within these periods include initial contact (IC), opposite toe off (OT), heel rise (HR), opposite initial contact (OI), toe off (TO), feet adjacent (FA), and vertical tibia (TV).
7.3. Inverse Kinematics Simulating in Simscape
In the Simscape program, the inverse kinematics are validated using the rotary and linear actuator displacements shown in Figure 12 as input data. The output data are the rotation angles of the moving platform in the sequence. When compared, these angles match the experimental data presented in Figure 3. Likewise, the results are analyzed in Table 3.
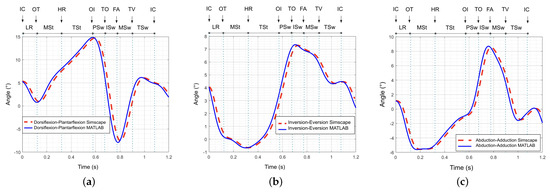
Figure 12.
Angle vs. time: (a) plantarflexion−dorsiflexion, (b) inversion−eversion, and (c) abduction−adduction. IC: initial contact; OT: opposite toe off; HR: heel rise; OI: opposite initial contact; TO: toe off; FA: feet adjacent; TV: tibia vertical; LR: loading response; MSt: mid−stance; TSt: terminal stance; PSw: pre−swing; ISw: initial swing; MSw: mid−swing; TSw: terminal swing.

Table 3.
Analysis of angle vs. time in the gait cycle phases.
7.4. Inverse Dynamics Results in MATLAB and Simscape
The results, based on the inverse dynamic model developed with MATLAB R2022b and Simscape, are a testament to our thorough analysis. The input data, including the plantar flexion–dorsiflexion, eversion–inversion, and abduction–adduction movement angles from Figure 3, as well as the external forces , and external moment , were meticulously considered. The results are shown in the Figure 13 and Figure 14, and are analyzed in Table 4, provide a comprehensive understanding of the system’s behavior.
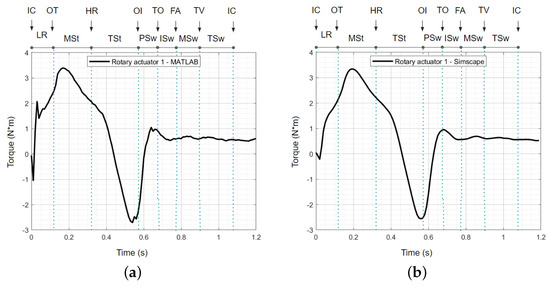
Figure 13.
Rotary actuator torque vs. time during the combined movement in a gait cycle: (a) based on MATLAB R2022b, and (b) based on Simscape. IC: initial contact; OT: opposite toe off; HR: heel rise; OI: opposite initial contact; TO: toe off; FA: feet adjacent; TV: tibia vertical; LR: loading response; MSt: mid−stance; TSt: terminal stance; PSw: pre−swing; ISw: initial swing; MSw: mid−swing; TSw: terminal swing.
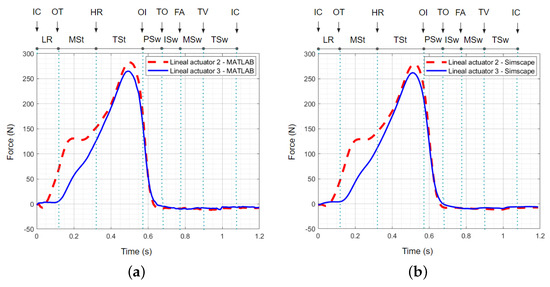
Figure 14.
Forces of linear actuators 2 and 3 vs. time during the combined movement in a gait cycle: (a) based on MATLAB R2022b, and (b) based on Simscape. IC: initial contact; OT: opposite toe off; HR: heel rise; OI: opposite initial contact; TO: toe off; FA: feet adjacent; TV: tibia vertical; LR: loading response; MSt: mid−stance; TSt: terminal stance; PSw: pre−swing; ISw: initial swing; MSw: mid−swing; TSw: terminal swing.

Table 4.
Analysis of the combined movement in the gait cycle phases.
8. Discussion
This study compared the responses of actuators using MATLAB and Simscape, providing detailed insight into the differences in torque, force, rotation angle, and length across the different phases of the gait cycle.
- Rotation angle of the rotary actuator: Figure 11a shows the rotation angle of the rotary actuator in MATLAB. During initial contact (IC) and load response (LR), the angle decreases to approximately −5.5°, followed by a significant increase to around 8.6° during the initial swing (ISw) phase. This behavior is crucial for replicating the natural ankle movement, where the combined ankle movement (plantarflexion–dorsiflexion, inversion–eversion, and abduction–adduction) is essential for efficient gait.
- Length of the linear actuators: Figure 11b shows the variation in the length of linear actuators 2 and 3 in MATLAB. The most notable differences are seen during the initial swing (ISw), where actuator 2 increases in length up to 48 mm, while actuator 3 reaches only 42 mm. This variation can be attributed to rotation angles of the biomechanical data from the gait cycle, which reflect differences in each actuator. These differences highlight how various parameters can influence ankle movement.
- Torque of the rotary actuator: Figure 13 compares torque from the rotary actuator obtained from MATLAB and Simscape. The observed torque patterns are remarkably similar between both simulations. During the initial contact (IC) and load response (LR) phases, a rapid increase in torque is observed, peaking around 3.5 Nm, followed by a drop to negative values during terminal stance (TSt) and pre-swing (PSw). This consistency suggests that both simulation environments can accurately model the torque dynamics in the rotary actuator.
- Force of the linear actuators: Figure 14 presents the forces generated by linear actuators 2 and 3 in MATLAB and Simscape. Similar to the torque analysis, the recorded forces show similar patterns in both simulations. During the load response (LR) phase, the force peaks around 280 N for actuator 2 and 260 N for actuator 3, consistent across both platforms. This behavior indicates that both MATLAB and Simscape can adequately replicate the forces involved in the gait cycle using linear actuators.
- Implications and limitations: The similarities observed between MATLAB and Simscape in modeling torque and force suggest that both environments can be reliably used for biomechanical studies of the gait cycle. However, the differences in the lengths of the linear actuators during the initial swing (ISw) phase indicate that fine-tuning parameters and configurations are needed to achieve precise replication of ankle movement. A limitation of the study is the reliance on simulation models, which may only capture some of the complexities of human movement. Future research could integrate experimental data to validate and adjust simulation models, ensuring greater accuracy in representing biomechanical behavior.
- Uncertainty: The 2SPU-RU parallel mechanism, used in three-degree-of-freedom ankle prostheses, can present significant challenges during its manufacturing process. These uncertainties may arise from various sources, such as errors in the manufacturing parameters of the mechanism’s components and unexpected flexibility of the elements within the kinematic chain that may deviate from the theoretical design. Such variations can affect the precision and dynamic behavior of the mechanism, complicating the prosthesis’s functionality. To mitigate these potential issues, it is crucial to adopt strategies such as rigorous calibration and integrating sensors for real-time feedback, enabling dynamic adjustments to control the parameters. A sensitivity analysis will also help understand how different uncertainties impact the mechanism’s performance.
- Specific application in ankle prostheses: Unlike general existing approaches applicable across a broad range of nonlinear systems, our model is designed and optimized for the biomechanics and needs of the human ankle. This includes the precise simulation of plantarflexion–dorsiflexion, eversion–inversion, and abduction–adduction movements, crucial for mimicking the natural ankle’s functionality.
- Integration of parallel mechanisms in ankle prostheses: Our study addresses a significant gap in the current literature by integrating parallel mechanisms into the design of ankle prostheses, which not only enhances stability and precision but also facilitates dynamic adaptation to different terrains and movements. This adaptability is achieved through the unique configuration of the 2SPU-RU mechanism, providing superior balance and control compared to traditional designs.
- Validation through dynamic modeling and simulation: We extensively validated our model, comparing theoretical and simulated results to ensure accuracy and applicability. This rigorous validation demonstrates the effectiveness of our design under realistic operating conditions, which is often a challenge with more abstract theoretical approaches.
9. Conclusions
This study develops and validates an inverse kinematic and dynamic model of a 2SPU-RU parallel mechanism for prosthetic ankles, capable of simulating the three critical degrees of ankle movement. Using Autodesk Inventor, MATLAB, and Simscape, this research demonstrates that the model accurately replicates natural gait movements across various planes, confirming its effectiveness through comparative MATLAB and Simscape simulations. This breakthrough provides a robust foundation for future advancements in prosthetic ankle design, emphasizing optimization in actuator control and design for rehabilitation and robotics applications.
Author Contributions
V.E.A. contributed to the conceptualization, methodology, validation, formal analysis, investigation, resources, writing—original draft preparation, and visualization. D.A.E. contributed to the conceptualization, review, editing, and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are available by contacting Victoria E. Abarca.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| a1 | the vector representing the position of the spherical joint to the origin O. |
| s1 | the vector representing the position of the rotary actuator to . |
| p | the vector representing the position of P located at the universal joint U with respect to the origin O |
| the rotation angle of the link of the kinematic chain RU. | |
| ai | the vector representing the position of the spherical joint to the origin O. |
| si | the vector representing the position of the rotary actuator to . |
| bi | the vector representing the position of the universal joint with respect to . |
| the velocity vector of the universal joint . | |
| the velocity of the universal joint (which is always zero). | |
| the angular velocity of the moving platform. | |
| the rotation matrix from the global reference frame O(,, ) to the local reference frame of the kinematic chain i. | |
| the six-row vector that represents the linear and angular velocities of the moving platform expressed in the global reference frame . | |
| the six-row vector that represents the linear and angular velocities of the link of the kinematic chain RU expressed in the local reference frame . | |
| the Jacobian matrix of the link of the kinematic chain RU. | |
| the Jacobian matrix such that . | |
| the Jacobian matrix such that . | |
| the third row of the Jacobian matrix . | |
| the Jacobian matrix of the ith kinematic chain. | |
| the Jacobian matrix of the ith kinematic chain expressed in its local reference frame (, , ). | |
| the Jacobian matrix of actuator i. | |
| the Jacobian matrices of the cylinder of the ith kinematic chain. | |
| the Jacobian matrices of the piston of the ith kinematic chain. | |
| the vector of forces and resulting moments on the moving platform. | |
| the external force exerted at the center of mass of the moving platform, [N]. | |
| the external moment exerted at the articulation between the moving platform and kinematic chain 1, . | |
| the mass of the moving platform, [kg]. | |
| the gravity vector . | |
| the inertia matrix of the moving platform taken about the center of mass and expressed in the fixed frame O , [kg·m2]. | |
| the linear acceleration of the center of gravity of the moving platform, . | |
| the vector of resultant forces and moments on the link of the first kinematic chain, expressed from the local reference frame . | |
| the mass of the link of the kinematic chain RU, [kg]. | |
| the moment of inertia of the link of the kinematic chain RU, [kg·m2]. | |
| the vector of resultant forces and moments on the cylinder of the second kinematic chain (SPU), expressed from the local reference frame . | |
| the vector of resultant forces and moments on the piston of the second kinematic chain (SPU), expressed from the local reference frame . | |
| the mass of the cylinder of the second kinematic chain (SPU), [kg]. | |
| the mass of the piston of the second kinematic chain (SPU), [kg]. | |
| the moment of inertia of the cylinder of the second kinematic chain (SPU) with respect to the local reference frame , [kg·m2]. | |
| the moment of inertia of the piston of the second kinematic chain (SPU) with respect to the local reference frame , [kg·m2]. | |
| the vector of the rotation angle of the link of the kinematic chain RU and the lengths of the second and third kinematic chains , respectively. | |
| the vector of the torques applied to the revolute joints and two prismatic joints. | |
| the position vector of the moving platform. | |
| the position vector of the link of the kinematic chain RU. | |
| the position vector of the cylinder of the kinematic chain i (2 or 3). | |
| the position vector of the piston of the kinematic chain i (2 or 3). |
References
- Sathsara, A.K.P.; Widanage, K.N.D.; Sooriyaperakasam, N.; Ranaweera, R.K.P.S.; Gopura, R.A.R.C. A Hybrid Powering Mechanism for a Transtibial Robotic Prosthesis. In Proceedings of the 2019 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 3–5 July 2019; pp. 447–453. [Google Scholar] [CrossRef]
- World Health Organization. WHO Standards for Prosthetics and Orthotics; World Health Organization: Geneva, Switzerland, 2017; ISBN 978-92-4-151248-0. License: CC BY-NC-SA 3.0 IGO; Available online: https://www.who.int/publications/i/item/9789241512480 (accessed on 24 June 2024).
- Ying, A.F.; Tang, T.Y.; Jin, A.; Chong, T.T.; Hausenloy, D.J.; Koh, W.P. Diabetes and other vascular risk factors in association with the risk of lower extremity amputation in chronic limb-threatening ischemia: A prospective cohort study. Cardiovasc. Diabetol. 2022, 21, 7. [Google Scholar] [CrossRef] [PubMed]
- Abarca, V.E.; Gallardo, N.J.; Elías, D.A. Mecanismo paralelo UPS-1S para la articulación de un tobillo protésico para personas con amputación transtibial. Col. Investig. Multidisc. 2019, 7, 1. [Google Scholar]
- Salazar, C.A.; Abarca, V.E. Design of a Mechanism for a Robotic Transtibial Prosthesis. Int. J. Sci. Technol. Res. 2019, 8, 1416–1422. [Google Scholar]
- Barnes, J.A.; Eid, M.A.; Creager, M.A.; Goodney, P.P. Epidemiology and Risk of Amputation in Patients with Diabetes Mellitus and Peripheral Artery Disease. Arterioscler. Thromb. Vasc. Biol. 2020, 40, 1808–1817. [Google Scholar] [CrossRef] [PubMed]
- Boyko, E.J.; Monteiro-Soares, M.; Wheeler, S.G.B. Peripheral Arterial Disease, Foot Ulcers, Lower Extremity Amputations, and Diabetes. In Diabetes in America; Cowie, C.C., Casagrande, S.S., Menke, A., Eds.; National Institute of Diabetes and Digestive and Kidney Diseases (US): Bethesda, MD, USA, 2018; Chapter 20. Available online: https://www.ncbi.nlm.nih.gov/books/NBK567977/ (accessed on 3 January 2024).
- Chihuri, S.; Wong, C.K. Factors Associated with the Likelihood of Fall-Related Injury among People with Lower Limb Loss. Inj. Epidemiol. 2018, 5, 42. [Google Scholar] [CrossRef] [PubMed]
- Itsiopoulos, I.; Vasiliadis, A.V.; Tsitouras, D.; Goulas, P.; Malliou, P.; Ktenidis, K. Amputation in Necrotizing Fasciitis - Dilemma or Reality: A Case Report and Literature Review. J. Orthop. Case Rep. 2020, 10, 54–58. [Google Scholar] [PubMed]
- Parsons, C.M.; Pimiento, J.M.; Cheong, D.; Marzban, S.S.; Gonzalez, R.J.; Johnson, D.; Letson, G.D.; Zager, J.S. The Role of Radical Amputations for Extremity Tumors: A Single Institution Experience and Review of the Literature. J. Surg. Oncol. 2012, 105, 149–155. [Google Scholar] [CrossRef]
- Alessa, M.; Alkhalaf, H.A.; Alwabari, S.S.; Alwabari, N.J.; Alkhalaf, H.; Alwayel, Z.; Almoaibed, F. The Psychosocial Impact of Lower Limb Amputation on Patients and Caregivers. Cureus 2022, 14, e31248. [Google Scholar] [CrossRef]
- Gonzales-Huisa, O.A.; Oshiro, G.; Abarca, V.E.; Chavez-Echajaya, J.G.; Elias, D.A. EMG and IMU Data Fusion for Locomotion Mode Classification in Transtibial Amputees. Prosthesis 2023, 5, 1232–1256. [Google Scholar] [CrossRef]
- Roșca, A.C.; Baciu, C.C.; Burtăverde, V.; Mateizer, A. Psychological Consequences in Patients with Amputation of a Limb. An Interpretative-Phenomenological Analysis. Front. Psychol. 2021, 12, 537493. [Google Scholar] [CrossRef]
- Gavette, H.; McDonald, C.L.; Kostick-Quenet, K.; Mullen, A.; Najafi, B.; Finco, M.G. Advances in Prosthetic Technology: A Perspective on Ethical Considerations for Development and Clinical Translation. Front. Rehabil. Sci. 2024, 4, 1335966. [Google Scholar] [CrossRef] [PubMed]
- Manz, S.; Valette, R.; Damonte, F.; Gaudio, L.A.; Gonzalez-Vargas, J.; Sartori, M.; Dosen, S.; Rietman, J. A Review of User Needs to Drive the Development of Lower Limb Prostheses. J. NeuroEng. Rehabil. 2022, 19, 119. [Google Scholar] [CrossRef] [PubMed]
- van Schaik, L.; Hoeksema, S.; Huvers, L.F.; Geertzen, J.H.B.; Dijkstra, P.U.; Dekker, R. The most important activities of daily functioning: The opinion of persons with lower limb amputation and healthcare professionals differ considerably. Int. J. Rehabil. Res. 2022, 43, 82–89. [Google Scholar] [CrossRef] [PubMed]
- Gardinier, E.S.; Kelly, B.M.; Wensman, J.; Gates, D.H. A Controlled Clinical Trial of a Clinically-Tuned Powered Ankle Prosthesis in People with Transtibial Amputation. Clin. Rehabil. 2018, 32, 319–329. [Google Scholar] [CrossRef] [PubMed]
- Tucker, M.R.; Olivier, J.; Pagel, A.; Bleuler, H.; Bouri, M.; Lambercy, O.; del R Millán, J.; Riener, R.; Vallery, H.; Gassert, R. Control Strategies for Active Lower Extremity Prosthetics and Orthotics: A Review. J. Neuroeng. Rehabil. 2015, 12, 1. [Google Scholar] [CrossRef] [PubMed]
- Bolger, D.; Ting, L.H.; Sawers, A. Individuals with transtibial limb loss use interlimb force asymmetries to maintain multi-directional reactive balance control. Clin Biomech. 2014, 29, 1039–1047. [Google Scholar] [CrossRef] [PubMed]
- Hafner, B.J. Clinical Prescription and Use of Prosthetic Foot and Ankle Mechanisms: A Review of the Literature. J. Prosthet. Orthot. 2005, 17, 5–11. [Google Scholar] [CrossRef]
- Blumentritt, S.; Schmalz, T.; Jarasch, R. The Safety of C-Leg: Biomechanical Tests. J. Prosthet. Orthot. 2009, 21, 2–15. [Google Scholar] [CrossRef]
- Gauthier-Gagnon, C.; Grisé, M.C.; Potvin, D. Enabling Factors Related to Prosthetic Use by People with Transtibial and Transfemoral Amputation. Arch. Phys. Med. Rehabil. 1999, 80, 706–713. [Google Scholar] [CrossRef]
- Seelen, H.A.M.; Hemmen, B.; Schmeets, A.J.; Ament, A.J.H.A.; Evers, S.M.A.A. Costs and consequences of a prosthesis with an electronically stance and swing phase controlled knee joint. Technol. Disabil. 2009, 21, 25–34. [Google Scholar] [CrossRef]
- Chadwell, A.; Diment, L.; Micó-Amigo, M.; Morgado Ramírez, D.Z.; Dickinson, A.; Granat, M.; Kenney, L.; Kheng, S.; Sobuh, M.; Ssekitoleko, R.; et al. Technology for Monitoring Everyday Prosthesis Use: A Systematic Review. J. Neuroeng. Rehabil. 2020, 17, 93. [Google Scholar] [CrossRef] [PubMed]
- Abarca, V.E.; Elias, D.A. A Review of Parallel Robots: Rehabilitation, Assistance, and Humanoid Applications for Neck, Shoulder, Wrist, Hip, and Ankle Joints. Robotics 2023, 12, 131. [Google Scholar] [CrossRef]
- Liao, Z.; Yao, L.; Lu, Z.; Zhang, J. Screw theory based mathematical modeling and kinematic analysis of a novel ankle rehabilitation robot with a constrained 3-PSP mechanism topology. Int. J. Intell. Robot. Appl. 2018, 2, 351–360. [Google Scholar] [CrossRef] [PubMed]
- Husty, M.; Birlescu, I.; Tucan, P.; Vaida, C.; Pisla, D. An algebraic parameterization approach for parallel robots analysis. Mech. Mach. Theory 2019, 140, 245–257. [Google Scholar] [CrossRef]
- Tsai, L.-W. Solving the Inverse Dynamics of a Stewart-Gough Manipulator by the Principle of Virtual Work. J. Mech. Des. 1999, 122, 3–9. [Google Scholar] [CrossRef]
- Song, M.; Guo, S.; Wang, X.; Qu, H. Dynamic Analysis and Performance Verification of a Novel Hip Prosthetic Mechanism. Chin. J. Mech. Eng. 2020, 33, 17. [Google Scholar] [CrossRef]
- Du, Y.; Li, R.; Li, D.; Bai, S. An ankle rehabilitation robot based on 3-RRS spherical parallel mechanism. Adv. Mech. Eng. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Saglia, J.A.; Tsagarakis, N.G.; Dai, J.S.; Caldwell, D.G. Control Strategies for Patient-Assisted Training Using the Ankle Rehabilitation Robot (ARBOT). IEEE/ASME Trans. Mechatron. 2013, 18, 1799–1808. [Google Scholar] [CrossRef]
- Zuo, S.; Li, J.; Dong, M.; Jiao, R.; Wang, S.; Ju, J.; Wang, Y. Design of Composite Parallel External Fixator for Multisegment Foot and Ankle Deformity Correction: A Correction Requirement-Dominated Approach. IEEE/ASME Trans. Mechatron. 2023, 28, 2271–2281. [Google Scholar] [CrossRef]
- Peng, B.; Zhu, S.; Khajepour, A.; Huang, Y. Kinematics and orientation capability of a family of 3-DOF parallel mechanisms. Mech. Mach. Theory 2019, 142, 103606. [Google Scholar] [CrossRef]
- Wang, C.; Fang, Y.; Guo, S.; Chen, Y. Design and Kinematical Performance Analysis of a 3-RUS/RRR Redundantly Actuated Parallel Mechanism for Ankle Rehabilitation. J. Mechan. Robot. 2013, 5, 041003. [Google Scholar] [CrossRef]
- Jamwal, P.K.; Hussain, S.; Xie, S.Q. Three-Stage Design Analysis and Multicriteria Optimization of a Parallel Ankle Rehabilitation Robot Using Genetic Algorithm. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1433–1446. [Google Scholar] [CrossRef]
- Stöckel, T.; Jacksteit, R.; Behrens, M.; Skripitz, R.; Bader, R.; Mau-Moeller, A. The Mental Representation of the Human Gait in Young and Older Adults. Front. Psychol. 2015, 6, 943. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).