Developing and Investigating the Analyzers of Kinematic Viscosity and Density of Petroleum Products on Throttle Bridge Transducers
Abstract
1. Introduction
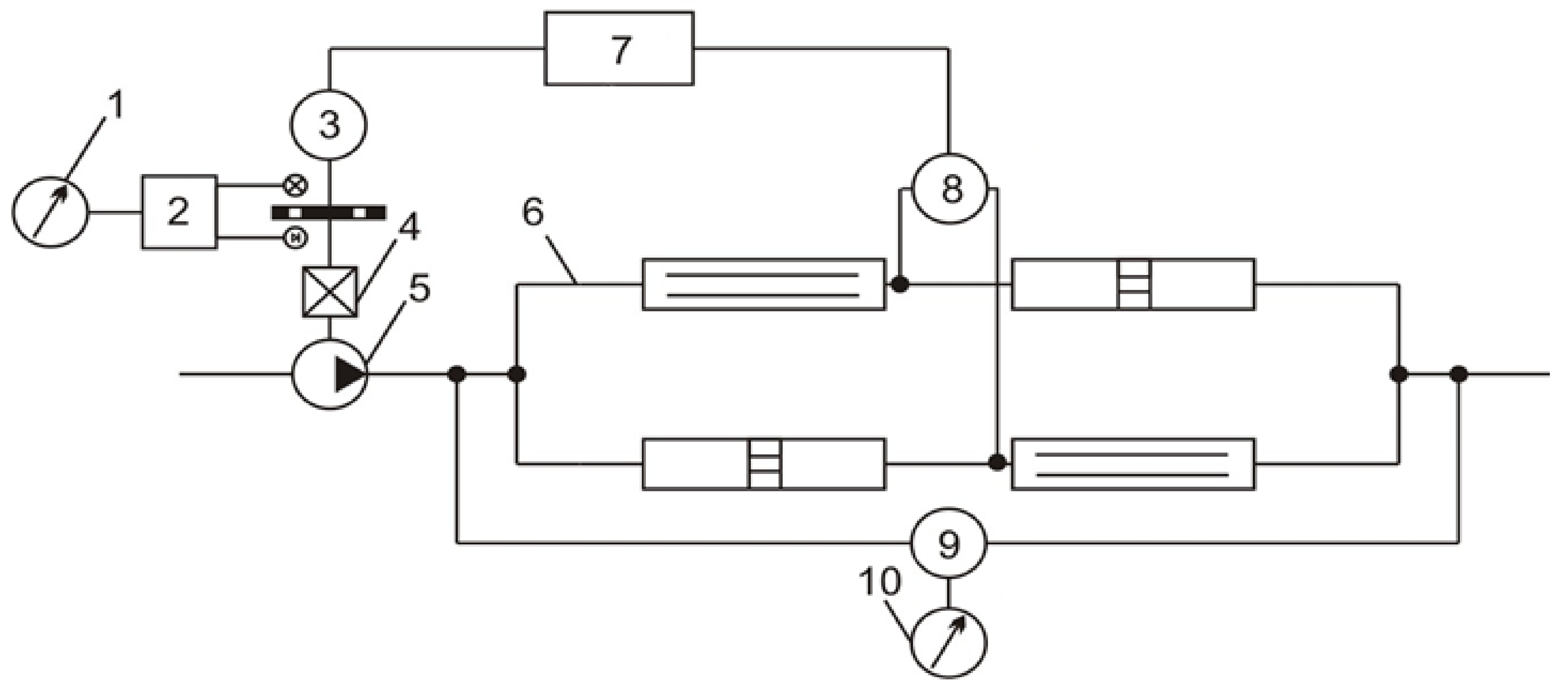
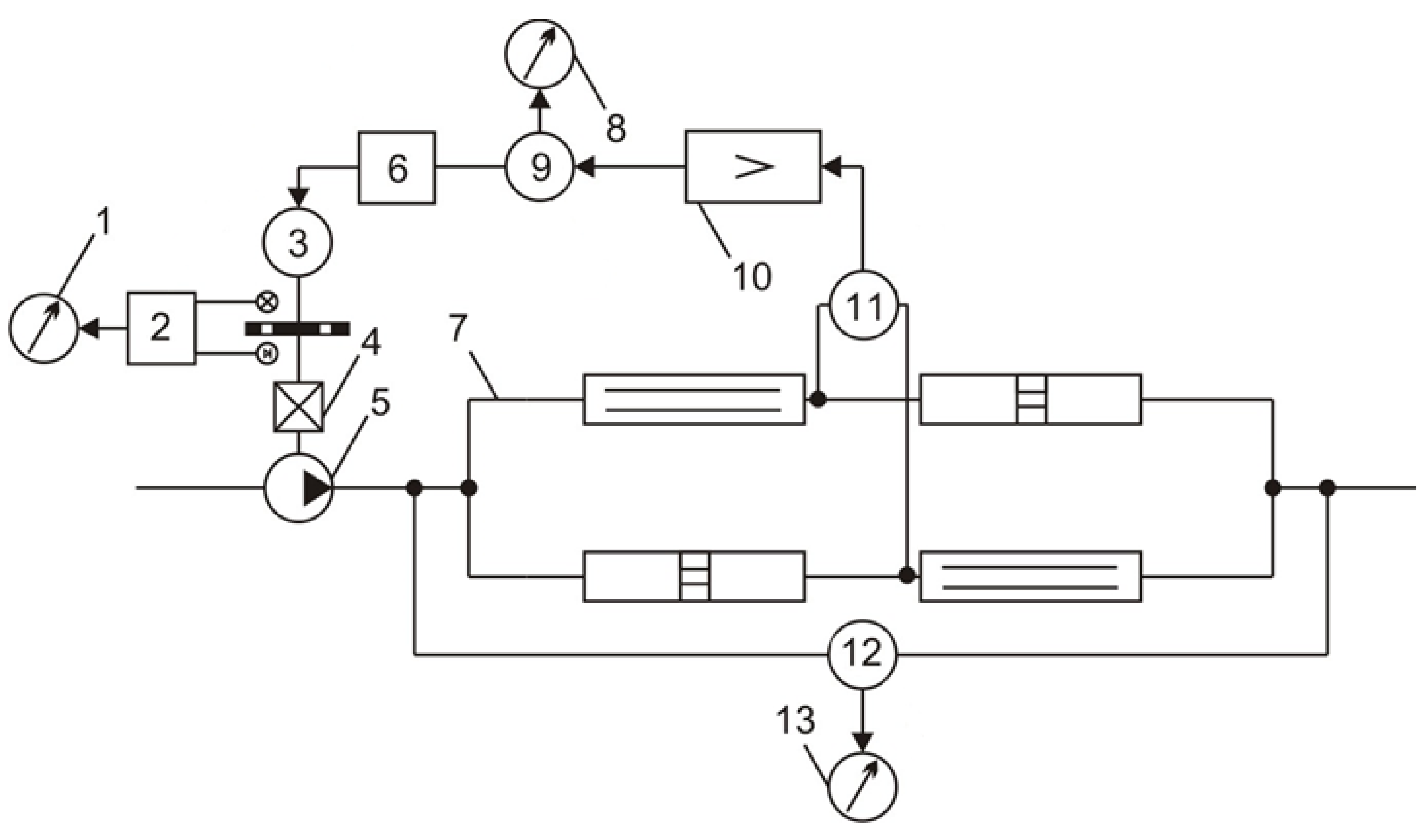
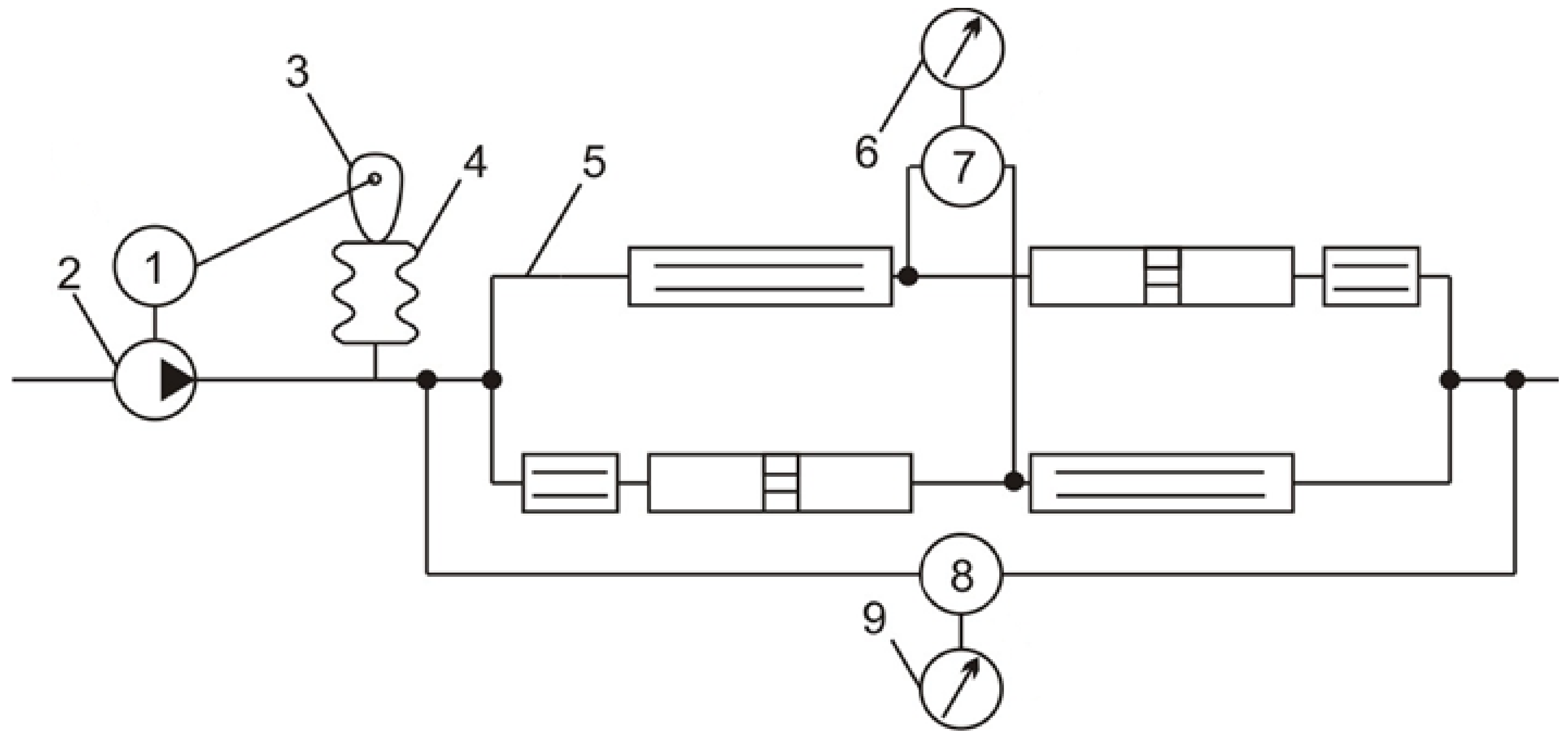
2. Materials and Methods
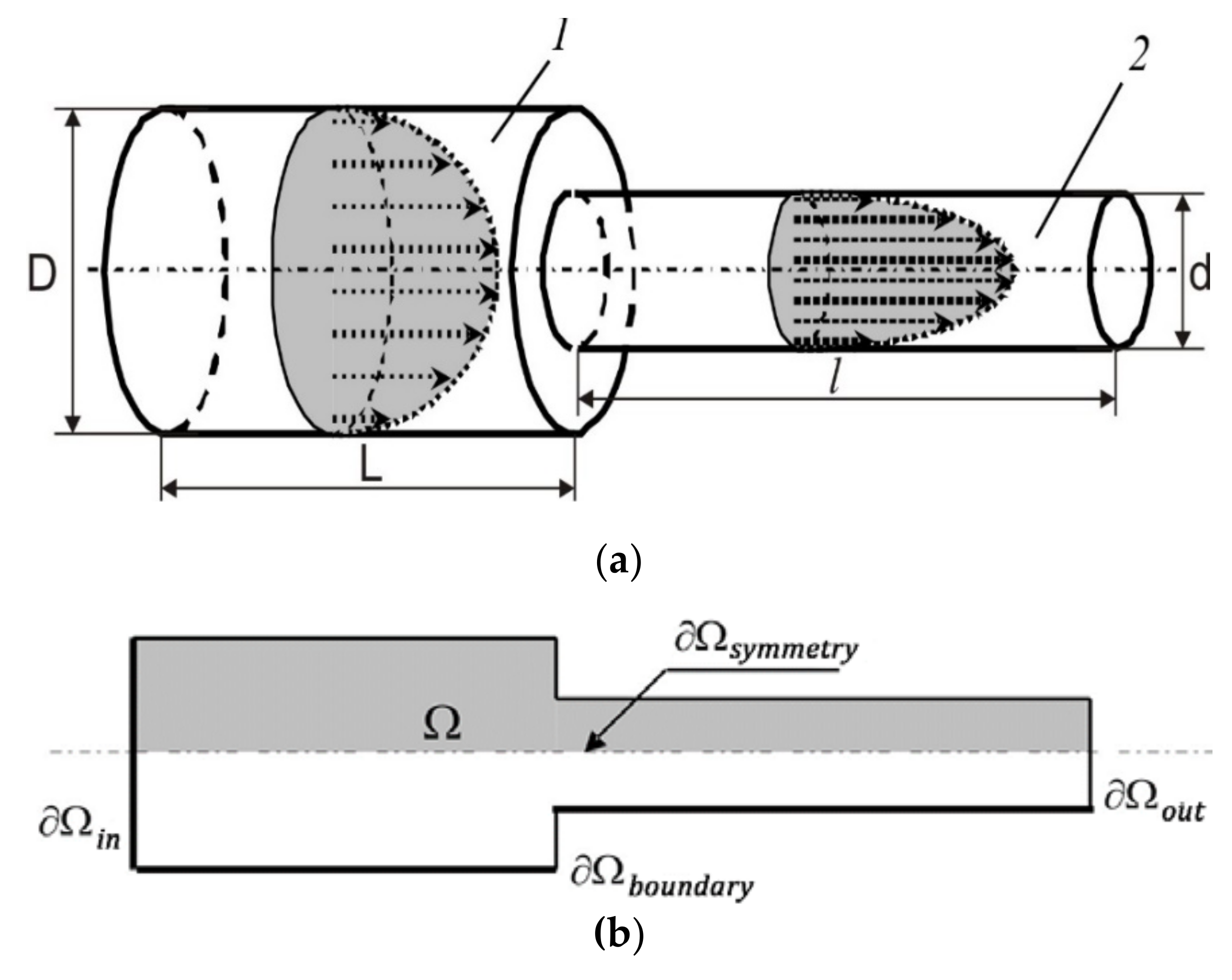
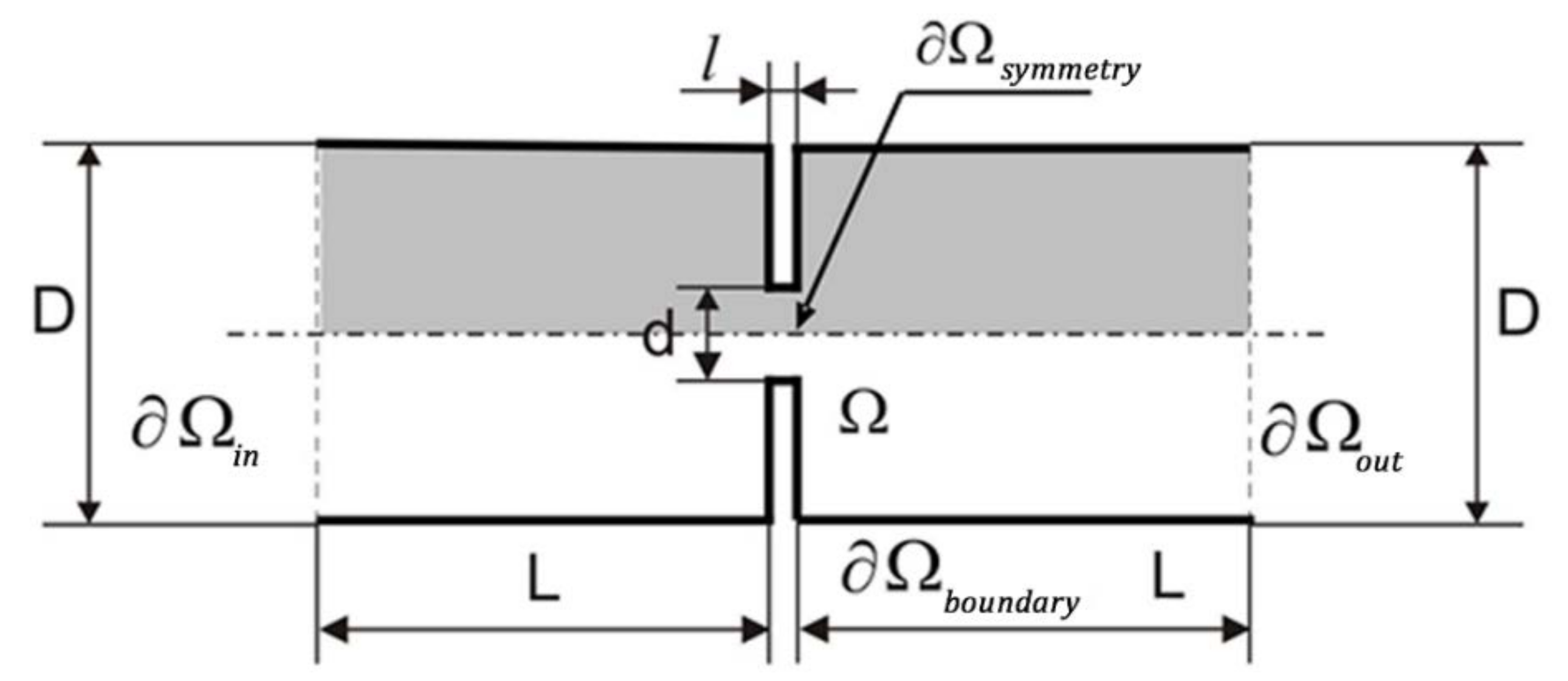
- the radial component of velocity on the axis of symmetry is zero
- at the inlet to the throttle, the fluid moves along its axis at the velocity
- at the outlet of the throttle there is no radial component of the velocity, and the zero pressure is maintained
- the fluid near the walls of the throttle is at the resting state
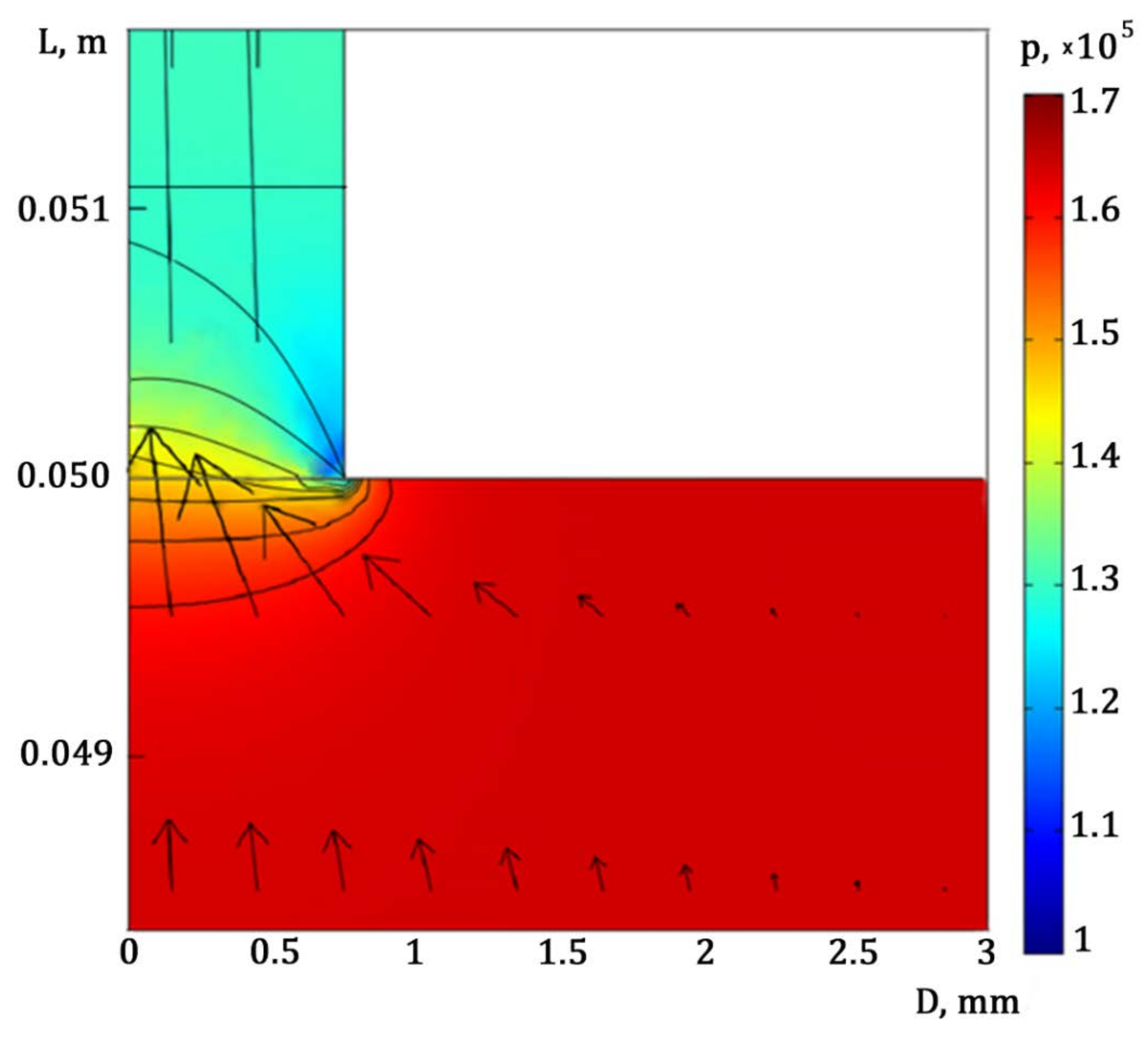
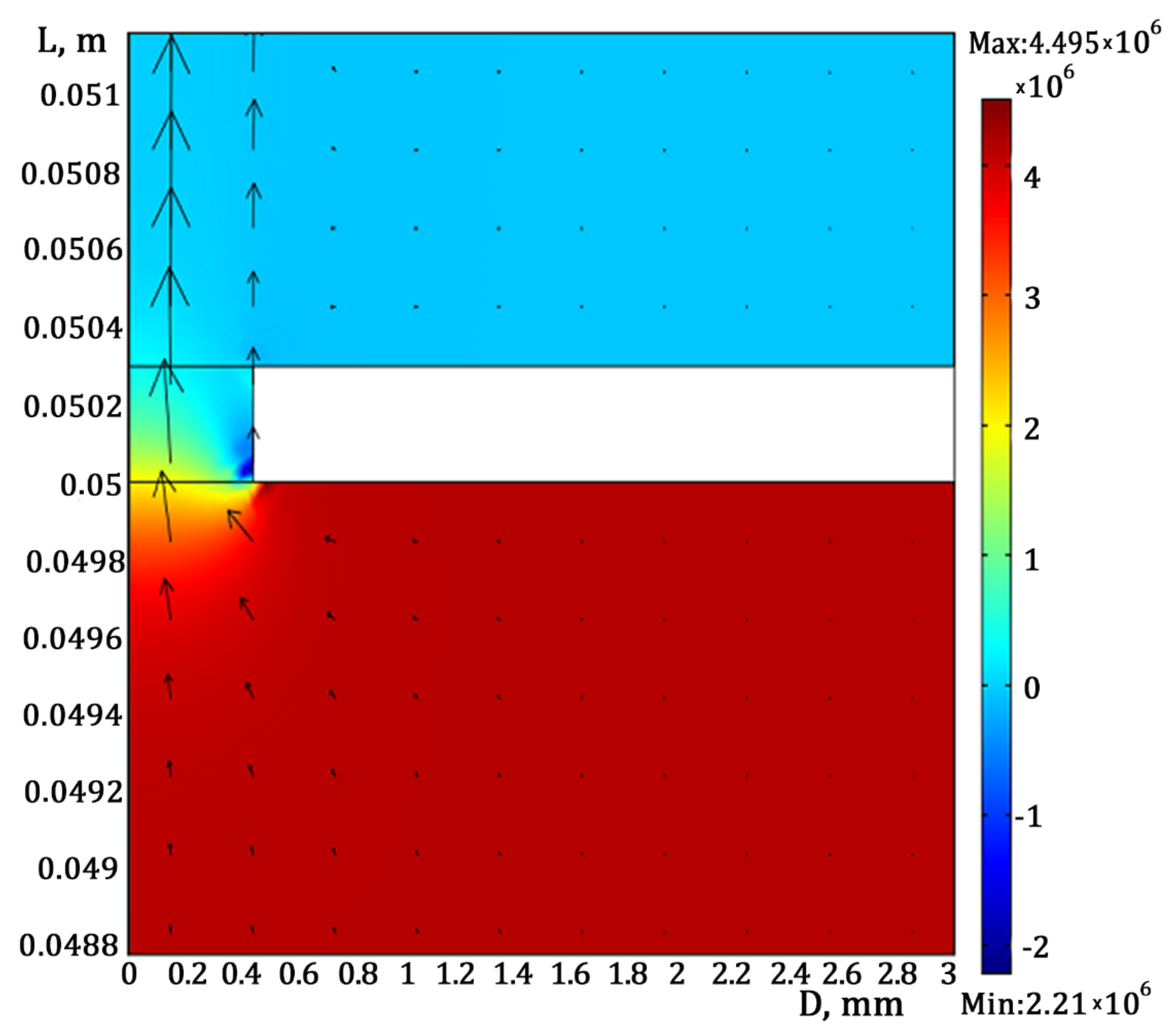
- The radial component of velocity on the axis of symmetry is zero (3);
- At the inlet of the throttle, the fluid moves along its axis with velocity , the energy value is maintained constant, and the energy dissipation along this axis is
- At the outlet of the throttle there is no radial component of velocity, a zero value of the pressure is maintained, the energy value is maintained constant, and the energy dissipation along this axis is
- The distribution of fluid velocity near the inner surface of the throttle is described by a logarithmic function. Kinetic energy and energy dissipation are functions of the velocity component tangential to the surfacewhere is the velocity component tangential to the surface of the throttle; is the von Kármán constant; is the distance from the point where the velocity is determined to the wall; is the constant of the model [4].
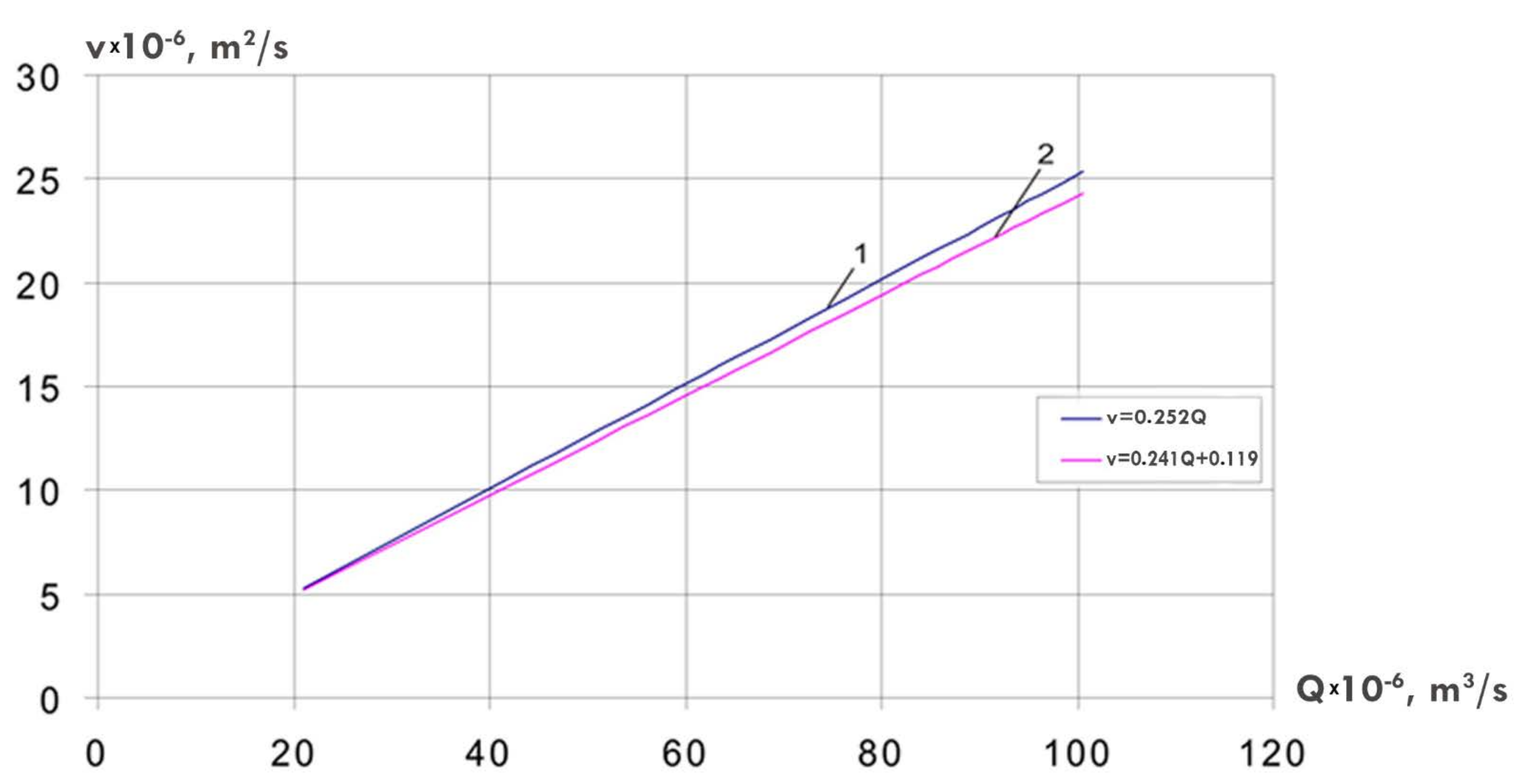
3. Results
- Turbine oil TP-22 with the density at the temperature 20 °C and the kinematic viscosity at the temperature 50 °C;
- Airplane oil M-20A with and ;
- Kerosene and ;
- Petrol A-95 with and .
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Panneerselvam, S.I.; Miranda, L.R. Biodiesel production from mutton tallow. In Proceedings of the 2011 IEEE Conference on Clean Energy and Technology (CET), Kuala Lumpur, Malaysia, 27–29 June 2011; pp. 83–86. [Google Scholar] [CrossRef]
- Borminskii, S.A.; Parshina, A.V. Metrological analysis of the system for complex control of the level, density and viscosity of multi-layer liquids in tanks. In Proceedings of the 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 6–9 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Grigoriev, B.A.; Koldaev, A.I.; Boldyrev, D.V. Neural network approach to prediction of the liquid petroleum products viscosity. In Proceedings of the 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 6–9 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Kalghatgi, G.; Aramco, S. Manufacture, Composition, and Properties of Practical Fuels for Internal Combustion Engines. In Fuel/Engine Interactions; SAE: Warrendale, PA, USA, 2014; pp. 33–62. [Google Scholar] [CrossRef]
- Akula, R.; Sai, B.R.; Jaswitha, K.; Kumar, M.S.; Yamini, V. Sensor based quality check and automated fuel level indication system. In Proceedings of the 2019 3rd International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 10–11 October 2019; pp. 164–168. [Google Scholar] [CrossRef]
- Osadchuk, O.V.; Semenov, A.O.; Zviahin, O.S.; Semenova, O.O.; Rudyk, A.V. Increasing the Sensitivity of Measurement of a Moisture Content in Crude Oil. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2021, 5, 49–53. [Google Scholar] [CrossRef]
- Jamal, D.N.; Shajahan, M.S.M.; Cruz, S.N.; Abhineshjayram, M.; Goutham, S. Empirical investigation and comparison of different viscosity liquids with increasing temperature. In Proceedings of the 2020 International Conference on Emerging Trends in Information Technology and Engineering (ic-ETITE), Vellore, India, 24–25 February 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Zhou, L. Toward prediction of kinematic viscosity of biodiesel using a robust approach. Energy Sources Part A Recovery Util. Environ. Eff. 2018, 40, 2895–2902. [Google Scholar] [CrossRef]
- Tan, F.; Ye, P.; Qiu, D.; Guo, L.; Huang, W.; Zeng, H.; Hou, D. A new method for measuring properties of liquid by using a single quartz crystal microbalance. In Proceedings of the 2017 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS), Besancon, France, 9–13 July 2017; pp. 649–651. [Google Scholar] [CrossRef]
- Riazi, M.R.; Eser, S. Properties, specifications, and quality of crude oil and petroleum products. In Petroleum Refining and Natural Gas Processing; Riazi, M., Eser, S., Agrawal, S., Peña, J.D., Eds.; ASTM International: West Conshohocken, PA, USA, 2013; pp. 79–100. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, T.; Zhou, Z. Experimental study on turbine flowmeter’s performance measuring fluids with different viscosities. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 5397–5401. [Google Scholar] [CrossRef]
- FY 2013 Progress Report for FUEL & LUBRICANT Technologies. Energy Efficiency and Renewable Energy. U.S. Department of Energy. Vehicle Technologies Office. Approved by Kevin Stork, DOE/EE-1042. 2014. Available online: https://www.energy.gov/sites/prod/files/2014/07/f17/fy2013_fuels_technologies.pdf (accessed on 29 October 2021).
- Khanchych, K.; Zhelezny, V.; Motovoy, I. Investigation of viscosity of O-xylene/Fullerene C60 solutions. In Proceedings of the 2020 IEEE 10th International Conference Nanomaterials: Applications & Properties (NAP), Sumy, Ukraine, 9–13 November 2020; pp. 01TPNS01-1–01TPNS01-4. [Google Scholar] [CrossRef]
- Osadchuk, A.V.; Semenov, A.A.; Zviahin, O.S.; Savytskyi, A.Y.; Komada, P.; Nurseitova, K. Numerical method for processing frequency measuring signals from microelectronic sensors based on transistor structures with negative differential resistance. Proc. SPIE 2019, 11176, 111765Y. [Google Scholar] [CrossRef]
- Ganesh, D.; Gowrishankar, G. Effect of nano-fuel additive on emission reduction in a biodiesel fuelled CI engine. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2011; pp. 3453–3459. [Google Scholar] [CrossRef]
- Schiffer, M.; Mackowiak, P.; Ngo, H.; Ehrmann, O.; Schneider-Ramelow, M.; Lang, K. Mems mass flow controller for liquid fuel supply to HCCI-driven engine. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 793–796. [Google Scholar] [CrossRef]
- Ye, Z.; Mao, X.; Huang, H. Investigation of a fuel oil viscosity and temperature control system based on state observation. In Proceedings of the 2018 11th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 8–9 December 2018; pp. 231–235. [Google Scholar] [CrossRef]
- Xin, Z.; Xin, W. Research on transformer oil kinematic viscosity detection method based on IWOA-RBF and multi-frequency ultrasonic technology. In Proceedings of the 2020 3rd International Conference on Control and Robots (ICCR), Tokyo, Japan, 26–29 December 2020; pp. 199–203. [Google Scholar] [CrossRef]
- Kuzma, O. The dynamic destruction aggregates in nano suspensions into rotary viscometer. In Proceedings of the 2017 IEEE 7th International Conference Nanomaterials: Application & Properties (NAP), Odessa, Ukraine, 10–15 September 2017; pp. 01PCSI32-1–01PCSI32-4. [Google Scholar] [CrossRef]
- Bunn, T.F.; Jones, M.G.; Wheeler, C.A. Pumping power station ash as a high concentration slurry. In Paste 2010: Proceedings of the Thirteenth International Seminar on Paste and Thickened Tailings; Jewell, R., Fourie, A.B., Eds.; Australian Centre for Geomechanics: Perth, Australia, 2010; pp. 515–527. [Google Scholar] [CrossRef]
- PRC Technologies. Viscometer—Covimat 105 DC. Available online: http://www.prctech-th.com/Covimat-105-DC.html (accessed on 29 October 2021).
- Brookfield Viscosity. Brookfield TT200 Viscometer. Available online: http://brookfield-benelux.com/Bookfield_TT200_Process_viscometer.html (accessed on 29 October 2021).
- Zhu, P.; Lai, J.; Wu, K.; Zhang, Z.; Huang, X.; Zhang, L.; Liu, J. An attenuated time measurement based on pulse interval for oscillating cup viscometer. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 3109–3111. [Google Scholar] [CrossRef]
- Akbay, C.; Koçak, O. Vibrational viscosimeter design for biomedical purposes. In Proceedings of the 2018 Medical Technologies National Congress (TIPTEKNO), Magusa, Cyprus, 8–10 November 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Kuntner, J.; Stangl, G.; Jakoby, B. Characterizing the rheological behavior of oil-based liquids: Microacoustic sensors versus rotational viscometers. IEEE Sens. J. 2005, 5, 850–856. [Google Scholar] [CrossRef]
- Hagenbach, E. Über die Bestimmung der Zähigkeit einer Flüssigkeit durch den Ausfluß der Röhren. Ann. Phys. 1860, 108, 385–426. [Google Scholar] [CrossRef]
- Sutera, S.P.; Skalak, R. The History of Poiseuille’s Law. Annu. Rev. Fluid Mech. 1993, 25, 1–19. [Google Scholar] [CrossRef]
- Pistun, Y.; Matiko, H.; Krykh, H. Mathematical models of throttle elements of gashydrodynamic measuring transducers. Energy Eng. Control Syst. 2019, 5, 94–107. [Google Scholar] [CrossRef]
- ISO 3104:2020. Petroleum Products—Transparent and Opaque Liquids—Determination of Kinematic Viscosity and Calculation of Dynamic Viscosity. Available online: https://www.iso.org/ru/standard/67965.html (accessed on 29 October 2021).
- Hongguang, X.; Mei, C. Study on the oil quantities calculation method of coriolis mass flow meter in oil dynamic measurement. In Proceedings of the 2017 13th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017; pp. 22–26. [Google Scholar] [CrossRef]
- Liu, T.; Leusheva, E.; Morenov, V.; Li, L.; Jiang, G.; Fang, C.; Zhang, L.; Zheng, S.; Yu, Y. Influence of Polymer Reagents in the Drilling Fluids on the Efficiency of Deviated and Horizontal Wells Drilling. Energies 2020, 13, 4704. [Google Scholar] [CrossRef]
- Gonzalez, M.; Seren, H.R.; Ham, G.; Buzi, E.; Bernero, G.; Deffenbaugh, M. Viscosity and Density Measurements Using Mechanical Oscillators in Oil and Gas Applications. IEEE Trans. Instrum. Meas. 2018, 67, 804–810. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, D.; He, X.; Wang, X. A Hydrodynamic Model for Measuring Fluid Density and Viscosity by Using Quartz Tuning Forks. Sensors 2020, 20, 198. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Dai, W.; Wu, H.; Dong, F. A Conductance Ring Coupled Cone Meter for Oil-Water Two-Phase Flow Measurement. IEEE Sens. J. 2014, 14, 1244–1252. [Google Scholar] [CrossRef]
- Cappa, F. Modelling fluid transfer and slip in a fault zone when integrating heterogeneous hydromechanical characteristics in its internal structure. Geophys. J. Int. 2009, 178, 1357–1362. [Google Scholar] [CrossRef]
- McComb, D. Renormalization methods applied to turbulence theory. In Theories of Turbulence; CISM Courses and Lectures No. 442; International Centre for Mechanical Sciences; Oberlack, M., Busse, F.H., Eds.; Springer: Vienna, Austria, 2002; pp. 123–195. [Google Scholar]
- Kolmogorov, A.N. Mathematical models of turbulent motion of an incompressible viscous fluid. Uspekhi Mat. Nauk. 2004, 59, 5–10. [Google Scholar] [CrossRef]
- ASTM D1298—12b. Standard Test Method for Density, Relative Density, or API Gravity of Crude Petroleum and Liquid Petroleum Products by Hydrometer Method. 2017. Available online: https://www.astm.org/Standards/D1298.htm (accessed on 29 October 2021).
- Semenov, A.; Baraban, S.; Semenova, O.; Voznyak, O.; Vydmysh, A.; Yaroshenko, L. Statistical Express Control of the Peak Values of the Differential-Thermal Analysis of Solid Materials. Solid State Phenom. 2019, 291, 28–41. [Google Scholar] [CrossRef]
- Kucheruk, V.; Palamarchuk, Y.; Kulakov, P. The statistical models of machinery milking duration by group milking machines. East. Eur. J. Enterp. Technol. 2014, 4, 13–17. [Google Scholar] [CrossRef]
- Kucheruk, V.; Palamarchuk, Y.; Kulakov, P.; Gnes, T. The statistical model of mechanical milking duration of farmyard milking installation. East. Eur. J. Enterp. Technol. 2014, 2, 31–37. [Google Scholar] [CrossRef][Green Version]
- Kucheruk, V.; Kurytnik, I.; Kulakov, P.; Lishchuk, R.; Moskvichova, Y.; Kulakova, A. Definition of dynamic characteristics of pointer measuring devices on the basis of automatic indications determination. Arch. Control Sci. 2018, 28, 401–418. [Google Scholar] [CrossRef]
- Judd, C.M.; McClelland, G.H.; Ryan, C.S. Data Analysis: A Model Comparison Approach to Regression, ANOVA, and Beyond, 3rd ed.; Taylor & Francis: New York, NY, USA, 2017; pp. 10–24. [Google Scholar]
- Rudyk, A.; Semenov, A.; Kryvinska, N.; Semenova, O. Study of phase and amplitude-phase methods for measuring a reactive element quality factor. Measurement 2022, 187, 110271. [Google Scholar] [CrossRef]
- Rudyk, A.V.; Semenov, A.O.; Kryvinska, N.; Semenova, O.O.; Kvasnikov, V.P.; Safonyk, A.P. Strapdown Inertial Navigation Systems for Positioning Mobile Robots—MEMS Gyroscopes Random Errors Analysis Using Allan Variance Method. Sensors 2020, 20, 4841. [Google Scholar] [CrossRef] [PubMed]






| Brand | Model | Viscosity Measurement Range, Pa·s | Maximal Flow Rate, 10−3 m3/s | Temperature Range |
|---|---|---|---|---|
| Brookfield | TT-200 | (10–50)·104 | immersive | −40 °C–150 °C |
| TT-100 | (10–50)·104 | 1.5 | up to 150 °C | |
| Bruss | System Bruss | (100–50)·107 | immersive | up to 120 °C |
| Contraves | Covlstat 1 | up to 2000 | 0.2 | up to 150 °C |
| DC43 | up to 4.5·106 | 0.7 | up to 350 °C | |
| DD | 0.4–12,000 | 0.1 | up to 90 °C | |
| TO | (1–5)·104 | immersive | up to 65 °C | |
| Crosfield | Viscomex 390 | 10–400 | 0.15 | 0 °C–150 °C |
| Eur-Controe | visc-21 E, P | 80–1500 | 0.2 | 40 °C–120 °C |
| Haake | Viscontro | 5·107 | 0.27 | up to 160 °C |
| VC-1, VC-2 | 1000 | 0.1 | up to 100 °C | |
| Rheometrics | On-Line | 104–107 | - | up to 150 °C |
| Solartron Mobley | Covimat 105 | (8–72)·104 | 0.05 | up to 120 °C |
| Brand | Model | Viscosity Measurement Range of the Viscometers, mPa·s | Note |
|---|---|---|---|
| Automation Product | Dynatro CL-10RL | 100–105 | Compensating T |
| Zendix Corporation | Ultra-Viscoson” | 50–50,000 | Compensating T |
| Nametre | 7.006 CЧP | 1–106 | Digital display T |
| Unipan | Type 505 | 50–50,000 | Compensating T |
| AND | SV-10A | 1–100,000 | Controlling T |
| Solartron Mobrey Limited | Solartron 7827 | 0.5–20,000 | Controlling T |
| Brand | Model | Range of Measurement, mPa·s | Maximal Operating Temperature, °C | Pressure, MPa |
|---|---|---|---|---|
| m-VROC | Type A | 0.2–100 | 70 | - |
| m-VROC | Type E | 1–100,000 | 70 | - |
| RHEOTEST | LK 2.2 | 1–10,000 | 80 | 0.75 |
| Ametek | TT100 | 10–500,000 | 150 | 2 |
| Rheotec | KV 100-F | 0–500 | 150 | 0.25 |
| TBT Schematic | Static Conversion Functions | Restrictions | |
|---|---|---|---|
| by Kinematic Viscosity | by Density | ||
 3L-1T | |||
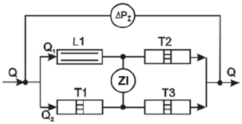 1L-3T | |||
 2L-2T | |||
| Type of the CBR Scheme | Static Conversion Factor of the TBT | Relative Uncertainty, % | |||||
|---|---|---|---|---|---|---|---|
| ν | ρ | ||||||
| Calculated | Experimental | Calculated | Experimental | ν | ρ | ||
| 1L-3T | symmetrical | 0.292 | 0.279 | 4.92·10−6 | 5.34·10−6 | 4.65 | 8.54 |
| asymmetrical | 0.402 | 0.383 | 4.56·10−6 | 4.96·10−6 | 4.96 | 8.76 | |
| 2L-2T | symmetrical | 0.252 | 0.241 | 5.51·10−6 | 5.85·10−6 | 4.64 | 6.17 |
| asymmetrical | 0.293 | 0.280 | 5.26·10−6 | 5.68·10−6 | 5.52 | 7.98 | |
| 3L-1T | symmetrical | 0.360 | 0.340 | 4.63·10−6 | 4.28·10−6 | 5.88 | 8.17 |
| asymmetrical | 0.314 | 0.297 | 4.19·10−6 | 3.86·10−6 | 5.72 | 8.55 | |
| Flow Rate at a Balancing Moment in the TBT | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.92 | 22.51 | 22.48 | 22.41 | 22.46 | 22.46 | 22.50 | 22.41 | 22.34 | 22.26 | 22.20 | 22.40 |
| 2.11 | 48.74 | 48.36 | 48.21 | 48.58 | 48.09 | 48.51 | 48.53 | 48.66 | 48.05 | 48.61 | 48.43 |
| 2.94 | 68.25 | 68.15 | 68.33 | 68.15 | 68.14 | 68.05 | 68.65 | 68.43 | 68.91 | 69.38 | 68.44 |
| 3.85 | 88.76 | 88.75 | 88.78 | 88.84 | 88.86 | 88.76 | 88.76 | 88.94 | 88.96 | 89.11 | 88.85 |
| 4.95 | 113.23 | 112.79 | 113.08 | 113.53 | 113.43 | 113.65 | 113.29 | 113.54 | 113.78 | 113.73 | 113.40 |
| Flow Rate at a Balancing Moment in the TBT | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5.12 | 20.98 | 20.85 | 20.83 | 20.68 | 20.89 | 21.06 | 21.14 | 20.99 | 21.11 | 20.99 | 20.95 |
| 10.34 | 41.76 | 41.59 | 41.69 | 41.68 | 41.93 | 41.99 | 41.58 | 41.44 | 41.49 | 41.81 | 41.69 |
| 14.87 | 61.41 | 61.59 | 61.41 | 61.76 | 62.03 | 62.20 | 62.03 | 62.23 | 61.91 | 61.60 | 61.82 |
| 21.57 | 89.49 | 89.14 | 90.06 | 90.18 | 90.18 | 90.45 | 90.28 | 90.20 | 90.11 | 89.98 | 90.01 |
| 24.55 | 100.55 | 100.39 | 100.38 | 100.11 | 100.21 | 100.70 | 101.00 | 101.05 | 101.04 | 100.59 | 100.60 |
| , kg/m3 | Pressure Drop in the TBT | , kP | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5.12 | 732 | 59 | 58 | 56 | 59 | 58 | 56 | 57 | 57 | 59 | 56 | 57.5 |
| 10.34 | 770 | 239 | 242 | 244 | 242 | 240 | 238 | 241 | 244 | 242 | 239 | 241.1 |
| 14.87 | 795 | 543 | 540 | 551 | 540 | 554 | 546 | 549 | 551 | 554 | 543 | 547.1 |
| 21.57 | 830 | 1212 | 1196 | 1187 | 1212 | 1222 | 1215 | 1218 | 1215 | 1222 | 1208 | 1210.7 |
| 24.55 | 836 | 1511 | 1516 | 1508 | 1526 | 1508 | 1530 | 1526 | 1523 | 1511 | 1536 | 1519.5 |
| 1.070 | 1.03 | 1.04 | 1.05 | 1.07 | 1.08 | 1.08 | 1.04 | 1.06 | 1.08 | 1.04 | 0.013 | 0.022 |
| 2.038 | 2.00 | 2.02 | 2.00 | 1.98 | 2.03 | 2.05 | 2.00 | 1.96 | 2.00 | 2.05 | 0.029 | 0.029 |
| 2.965 | 3.02 | 2.98 | 2.98 | 2.96 | 3.00 | 3.02 | 3.04 | 2.98 | 2.92 | 2.92 | −0.017 | 0.040 |
| 3.818 | 3.80 | 3.78 | 3.78 | 3.80 | 3.76 | 3.78 | 3.77 | 3.80 | 3.74 | 3.80 | 0.037 | 0.020 |
| 4.903 | 4.90 | 4.94 | 4.96 | 4.88 | 4.91 | 4.95 | 4.90 | 4.96 | 4.88 | 4.84 | −0.009 | 0.040 |
| 5.10 | 5.11 | 5.12 | 5.11 | 5.21 | 5.31 | 5.13 | 5.17 | 5.28 | 5.13 | 5.31 | −0.088 | 0.079 |
| 9.86 | 9.99 | 9.92 | 10.10 | 10.12 | 10.09 | 9.86 | 9.98 | 10.06 | 10.09 | 9.88 | −0.06 | 0.082 |
| 14.92 | 14.91 | 14.76 | 14.91 | 14.92 | 14.93 | 14.83 | 14.82 | 14.83 | 14.80 | 14.72 | 0.077 | 0.072 |
| 20.22 | 20.34 | 20.41 | 20.38 | 20.18 | 20.19 | 20.23 | 20.14 | 20.36 | 20.34 | 20.41 | −0.078 | 0.102 |
| 24.86 | 24.71 | 24.69 | 24.80 | 24.80 | 24.75 | 24.62 | 24.64 | 24.90 | 24.84 | 24.91 | 0.094 | 0.102 |
| , kg/m3 | Pressure Change in the TBT | , MPa | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5.10 | 730 | 0.061 | 0.061 | 0.061 | 0.063 | 0.066 | 0.061 | 0.062 | 0.065 | 0.061 | 0.066 | 0.063 |
| 9.86 | 763 | 0.244 | 0.240 | 0.249 | 0.250 | 0.249 | 0.237 | 0.243 | 0.247 | 0.249 | 0.238 | 0.245 |
| 11.92 | 786 | 0.559 | 0.548 | 0.559 | 0.560 | 0.561 | 0.553 | 0.552 | 0.553 | 0.551 | 0.545 | 0.554 |
| 20.22 | 818 | 1.083 | 1.090 | 1.087 | 1.066 | 1.067 | 1.071 | 1.062 | 1.085 | 1.083 | 1.090 | 1.078 |
| 24.86 | 840 | 1.641 | 1.639 | 1.653 | 1.653 | 1.647 | 1.629 | 1.632 | 1.667 | 1.659 | 1.668 | 1.649 |
| Results of Measurement | , kg/m3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 730 | 754.0 | 739.1 | 730.0 | 736.8 | 720.4 | 736.2 | 771.6 | 728.6 | 748.1 | 709.3 | −7.42 | 19.22 |
| 763 | 779.7 | 793.9 | 735.2 | 723.2 | 758.2 | 765.0 | 781.2 | 762.7 | 727.5 | 784.3 | 1.91 | 25.11 |
| 786 | 773.1 | 801.8 | 781.6 | 769.3 | 775.3 | 782.9 | 791.1 | 774.4 | 790.4 | 796.1 | 2.40 | 11.16 |
| 818 | 823.3 | 799.7 | 802.8 | 821.9 | 831.8 | 832.3 | 822.0 | 816.4 | 819.6 | 815.4 | −0.52 | 10.71 |
| 840 | 841.9 | 847.4 | 839.9 | 837.9 | 832.6 | 846.0 | 858.5 | 838.2 | 826.5 | 829.5 | 0.16 | 9.39 |
| 1.11 | 1.10 | 1.21 | 1.10 | 1.11 | 1.02 | 1.19 | 1.10 | 0.98 | 1.01 | 1.00 | 0.028 | 0.019 |
| 1.94 | 1.95 | 1.96 | 1.88 | 1.85 | 1.89 | 1.94 | 1.97 | 1.84 | 1.91 | 1.86 | 0.035 | 0.048 |
| 3.02 | 3.10 | 3.09 | 3.10 | 3.05 | 3.04 | 3.02 | 3.02 | 2.95 | 2.98 | 2.97 | −0.012 | 0.054 |
| 4.11 | 4.07 | 4.10 | 4.07 | 4.20 | 4.19 | 4.18 | 4.16 | 4.09 | 4.07 | 4.13 | −0.016 | 0.053 |
| 4.81 | 4.78 | 4.76 | 4.81 | 4.82 | 4.86 | 4.84 | 4.89 | 4.89 | 4.83 | 4.80 | −0.018 | 0.043 |
| 5.23 | 5.32 | 5.53 | 5.58 | 5.61 | 5.31 | 5.01 | 5.02 | 5.54 | 5.60 | 5.14 | −0.136 | 0.112 |
| 10.12 | 10.02 | 10.38 | 10.56 | 10.60 | 10.24 | 10.11 | 10.02 | 10.04 | 10.58 | 10.46 | −0.181 | 0.217 |
| 15.31 | 15.04 | 14.98 | 15.26 | 15.13 | 15.39 | 15.54 | 15.62 | 15.40 | 15.02 | 15.47 | 0.025 | 0.232 |
| 20.08 | 20.00 | 19.68 | 20.11 | 20.17 | 20.36 | 20.44 | 20.28 | 20.12 | 20.05 | 19.96 | −0.037 | 0.218 |
| 29.63 | 29.87 | 29.74 | 29.51 | 29.42 | 29.20 | 29.18 | 29.37 | 29.46 | 29.31 | 29.44 | 0.180 | 0.218 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semenov, A.; Drevetskyi, V.; Rudyk, A.; Semenova, O.; Komada, P. Developing and Investigating the Analyzers of Kinematic Viscosity and Density of Petroleum Products on Throttle Bridge Transducers. Inventions 2022, 7, 6. https://doi.org/10.3390/inventions7010006
Semenov A, Drevetskyi V, Rudyk A, Semenova O, Komada P. Developing and Investigating the Analyzers of Kinematic Viscosity and Density of Petroleum Products on Throttle Bridge Transducers. Inventions. 2022; 7(1):6. https://doi.org/10.3390/inventions7010006
Chicago/Turabian StyleSemenov, Andriy, Volodymyr Drevetskyi, Andrii Rudyk, Olena Semenova, and Paweł Komada. 2022. "Developing and Investigating the Analyzers of Kinematic Viscosity and Density of Petroleum Products on Throttle Bridge Transducers" Inventions 7, no. 1: 6. https://doi.org/10.3390/inventions7010006
APA StyleSemenov, A., Drevetskyi, V., Rudyk, A., Semenova, O., & Komada, P. (2022). Developing and Investigating the Analyzers of Kinematic Viscosity and Density of Petroleum Products on Throttle Bridge Transducers. Inventions, 7(1), 6. https://doi.org/10.3390/inventions7010006









