Strategic Placement of Solar Power Plant and Interline Power Flow Controllers for Prevention of Blackouts
Abstract
:1. Introduction
2. Mathematical Modelling
2.1. Mathematical Modelling of IPFC
2.2. Inequality Constraints
3. Problem Formulation
3.1. Placement of Solar Power Plant and IPFC
Proposed Line Severity Index
3.2. Tuning of IPFC
3.2.1. Minimization of Voltage Deviation
3.2.2. Improvement of Security Margin
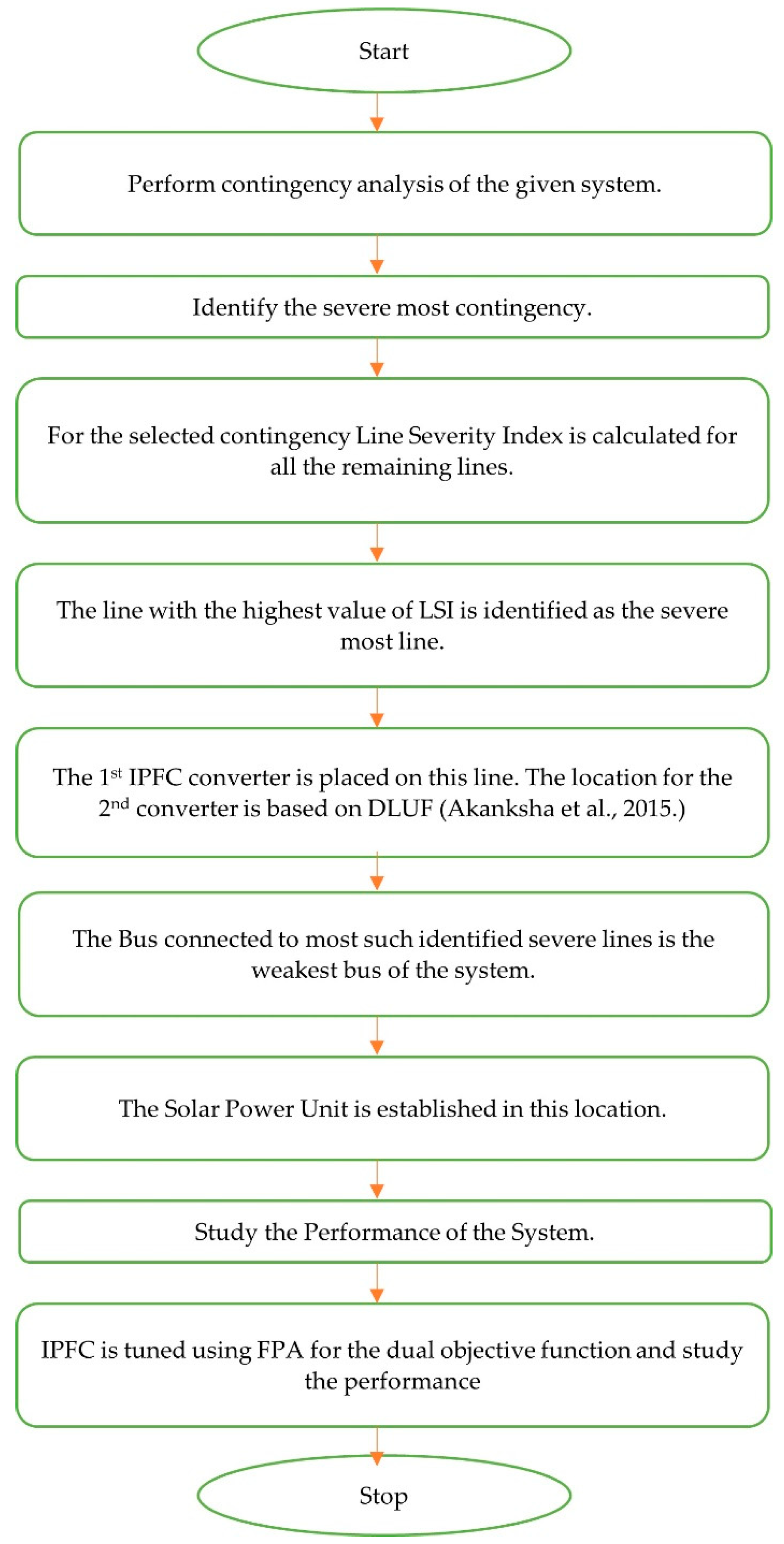
4. Methodology
5. Results
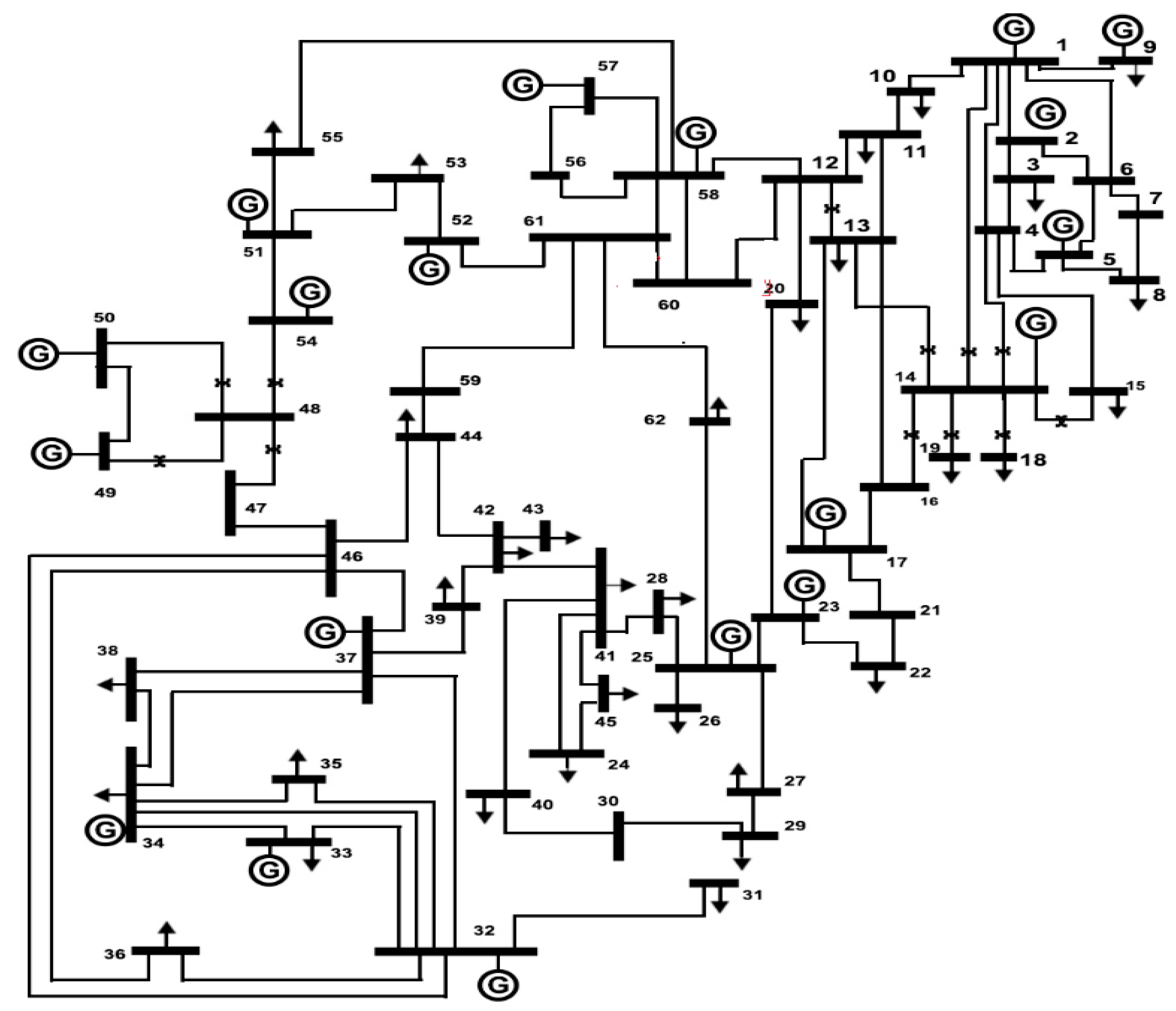
IEEE 57 Bus System
6. Conclusions
- Solar power systems can effectively reduce the stress on the existing system.
- The IPFC along with the solar power unit has reduced the active and reactive losses in the power system.
- The voltage deviation, security margin and line severity can be controlled within acceptable limits by the proposed method even in the situation of n-1 contingencies. This helps in avoiding any further disruptions in the power system. Thus, the proposed method is an effective means of avoiding blackouts in the country.
7. Future Prospects
- More Solar and wind units may be installed to study its effect.
- The more effective indices may be developed for the effective placement of solar and wind units.
- Other methods of placements may be incorporated into the system.
- The proposed method may be implemented on larger transmission systems to study its effectiveness.
8. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Pi, Qi | Inverter active and reactive power. |
| Vl—Vl∟θl (l = i, j, k) and Vl, θl | Magnitude and angle of Vl. |
| Vsein, ∟θsein | Magnitude and angle of Vsein |
| Vsein | Complex controllable series injected voltage source, series compensation of the series converter |
| n | bus j, k - common bus connected to IPFC. |
| Zsein | Series transformer impedance |
| Pni and Qni | Active and reactive power flows leaving bus n connected to IPFC |
| gin, bin | Conductance and susceptance of a transmission line respectively |
| S | Solar irradiance |
| L(S) | Lognormal function |
| P(s) | Solar electric power generated |
| Pmin | Minimum output power of the PV unit |
| Sst, Sc | Standard and critical point solar irradiance respectively |
| Sij | Apparent power flow in line ij |
| MVAij(max) | Maximum MVA rating of the line between bus i and bus j |
| MVAij | Actual MVA rating of the line between bus i and bus j |
| a | Multiplying factor. |
| Vk | Voltage magnitude at bus k |
| JL | No. of load buses |
| µ, σ | Mean and standard deviation of the log-normal probability function respectively |
References
- Clegg, S.; Mancarella, P. Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks. IEEE Trans. Sustain. Energy 2015, 6, 1234–1244. [Google Scholar] [CrossRef]
- Bai, L.; Li, F.; Jiang, T.; Jia, H. Robust scheduling for wind integrated energy systems considering gas pipeline and power transmission N–1 contingencies. IEEE Trans. Power Syst. 2017, 32, 1582–1584. [Google Scholar] [CrossRef]
- Yang, X.; Wang, X.; Liu, Z.; Luo, X.; Yan, J. Effect of fin number on the melting phase change in a horizontal finned shell-and-tube thermal energy storage unit. Sol. Energy Mater. Sol. Cells 2022, 236, 111527. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Z.; Du, Z.; Yu, J.; Yang, X.; Yan, J. Effect of fin-metal foam structure on thermal energy storage: An experimental study. Renew. Energy 2021, 172, 57–70. [Google Scholar] [CrossRef]
- Yang, X.; Guo, J.; Yang, B.; Cheng, H.; Wei, P.; He, Y.-L. Design of non-uniformly distributed annular fins for a shell-and-tube thermal energy storage unit. Appl. Energy 2020, 279, 115772. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Z.; Yang, B.; Yang, X.; Yan, J. Melting assessment on the angled fin design for a novel latent heat thermal energy storage tube. Renew. Energy 2022, 183, 406–422. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.; Yang, B.; Yang, X.; Li, M.-J. Thermal assessment on solid-liquid energy storage tube packed with non-uniform angled fins. Sol. Energy Mater. Sol. Cells 2022, 236, 111526. [Google Scholar] [CrossRef]
- Ahmad, A.; Ahmad Reza, S. Optimal placement and sizing of multi-type FACTS devices in power systems using metaheuristic optimisation techniques: An updated review. Ain Shams Eng. J. 2020, 11, 611–628. [Google Scholar] [CrossRef]
- Zhang, X.P. Modeling of the interline power flow controller and the generalized unified power flow controller in Newton power flow. IET Proc.-Gener. Transm. Distrib. 2003, 150, 268–274. [Google Scholar] [CrossRef]
- Teerthana, S.; Yokoyama, A. An optimal power flow control method of power system using interline power flow controller (IPFC). In Proceedings of the 2004 IEEE Region 10 Conference TENCON, Chiang Mai, Thailand, 24 November 2004; pp. 343–346. [Google Scholar]
- Velayutham, U.; Ponnusamy, L.; Venugopal, G. Minimization of cost and congestion management using interline power flow controller. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 1495–1512. [Google Scholar] [CrossRef]
- Daram, S.B.; Venkataramu, P.S.; Nagaraj, M.S. Performance index based contingency ranking under line outage condition incorporating IPFC. In Proceedings of the International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016. [Google Scholar]
- Yang, X.S. Firefly algorithm, Levy flights and global optimization. In Research and Development in Intelligent Systems XXVI; Springer: London, UK, 2009; pp. 209–218. [Google Scholar]
- Akanksha, M.; Nagesh Kumar, G.V. Line utilisation factor-based optimal allocation of IPFC and sizing using firefly algorithm for congestion management. IET Gener. Transm. Distrib. 2016, 10, 115–122. [Google Scholar]
- Oyekanmi, W.A.; Radman, G.; Babalola, A.A.; Ajewole, T.O. Power System Simulation and Contingency Ranking Using Load Bus Voltage Index. In Proceedings of the 2014 11th International Conference on Electronics, Computer and Computation (ICECCO), Abuja, Nigeria, 29 September–1 October 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Verma, R.; Rathore, A. Optimal Placement of Facts Device Considering Voltage Stability and Losses using Teaching Learning based Optimization. J. Inst. Eng. India Ser. B 2021, 102, 771–776. [Google Scholar] [CrossRef]
- Kumar, G.N.; Kalavathi, M.S. Cat Swarm Optimization for optimal placement of multiple UPFC’s in voltage stability enhancement under contingency. Electr. Power Energy Syst. 2014, 57, 97–104. [Google Scholar] [CrossRef]
- Adetokun, B.B.; Cristopher, M.M. Application and control of flexible alternating current transmission system devices for voltage stability enhancement of renewable-integrated power grid: A comprehensive review. Heliyon 2021, 7, e06461. [Google Scholar] [CrossRef] [PubMed]
- Nusair, K.; Alasali, F.; Ali, H.; William, H. Optimal placeent of FACTS devices and power-flow solutions for a power network system integrated with stochastic renewable energy resources using metaheuristic optimization techniques. Int. J. Energy Res. 2021, 45, 18786–18809. [Google Scholar] [CrossRef]
- Dawn, S.; Tiwari, P.K.; Goswami, A.K. An approach for long term economic operations of competitive power market by optimal combined scheduling of wind turbines and FACTS controllers. Energy 2019, 181, 709–723. [Google Scholar] [CrossRef]
- Aghdam, F.H.; Ghaemi, S.; Safari, A.; Farrokhifar, M. Profit-based evaluation of optimal FACTS devices planning for the large consumers and TRANSCO considering uncertainty. Int. Trans. Electr. Energy Syst. 2021, 31, e12828. [Google Scholar] [CrossRef]
- Ma, R.; Li, X.; Luo, Y.; Wu, X.; Jiang, F. Multi-objective Dynamic Optimal Power Flow of Wind Integrated Power Systems Considering Demand Response. CSEE J. Power Energy Syst. 2019, 5, 466–473. [Google Scholar] [CrossRef]
- Mishra, A.; Nagesh Kumar, G.V.; Rao, B.V.; Chowdary, D.D. Real power performance index and line stability index-based management of contingency using firefly algorithm. IET Gener. Transm. Distrib. 2016, 10, 2327–2335. [Google Scholar] [CrossRef]

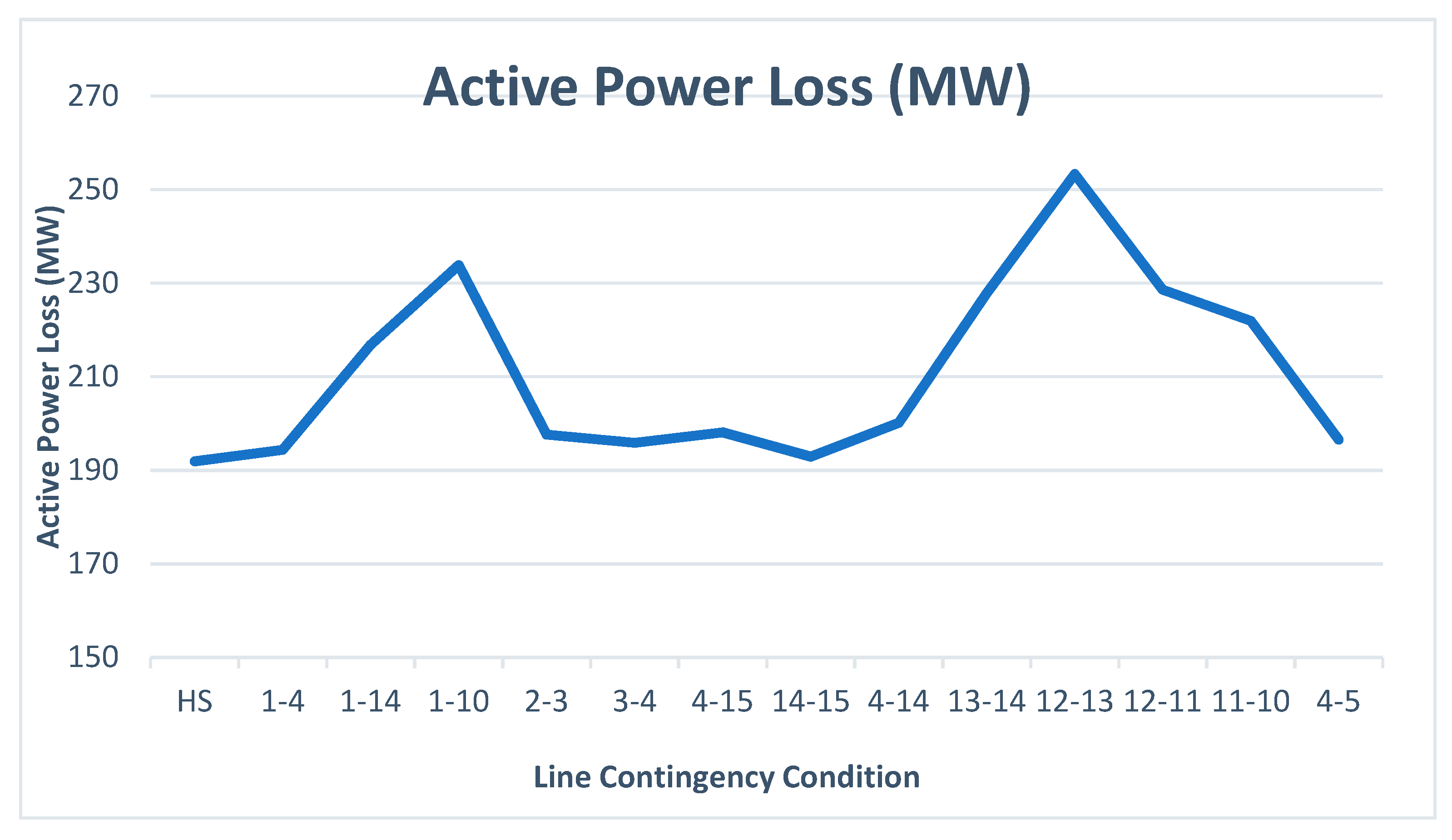
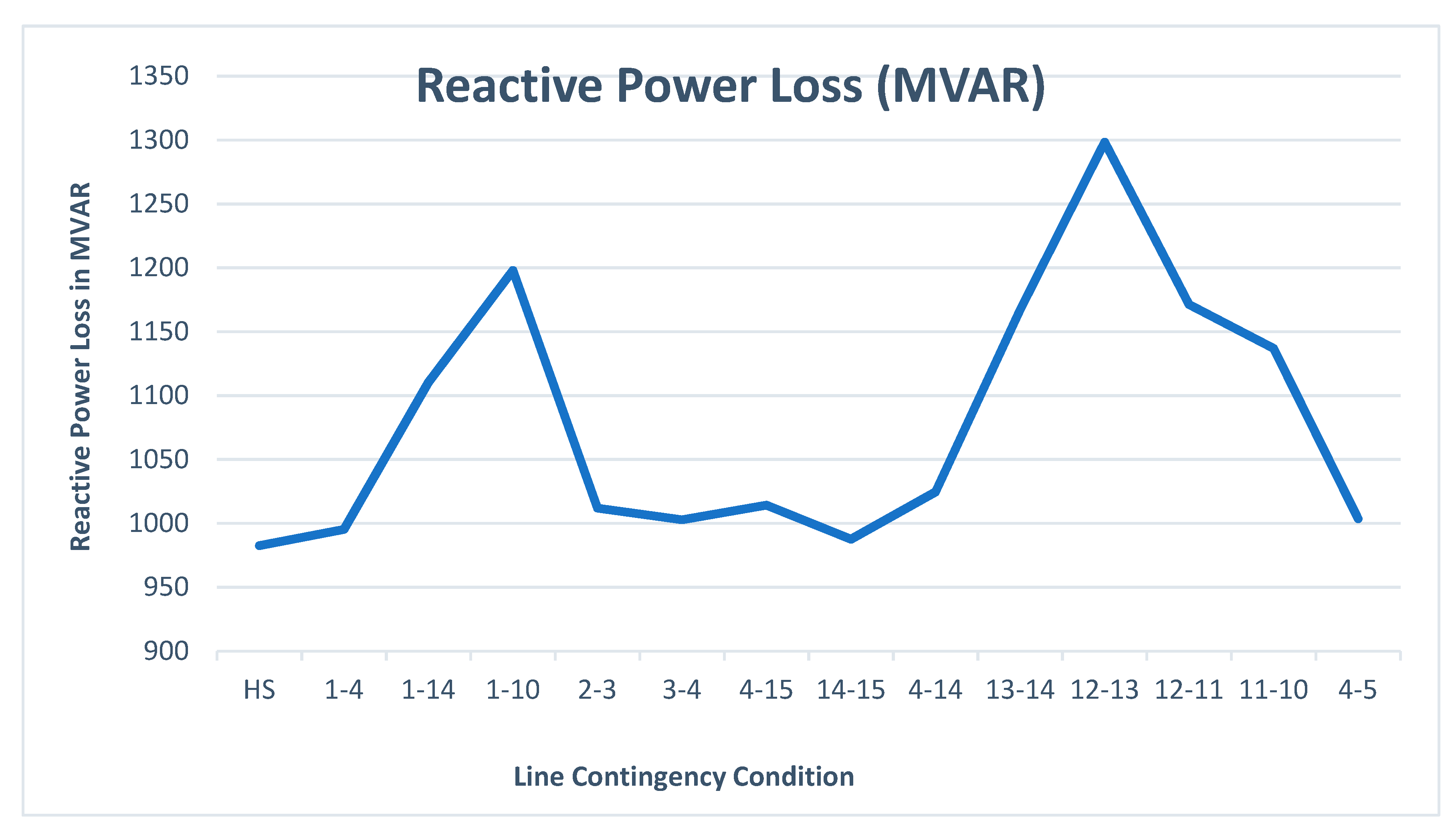
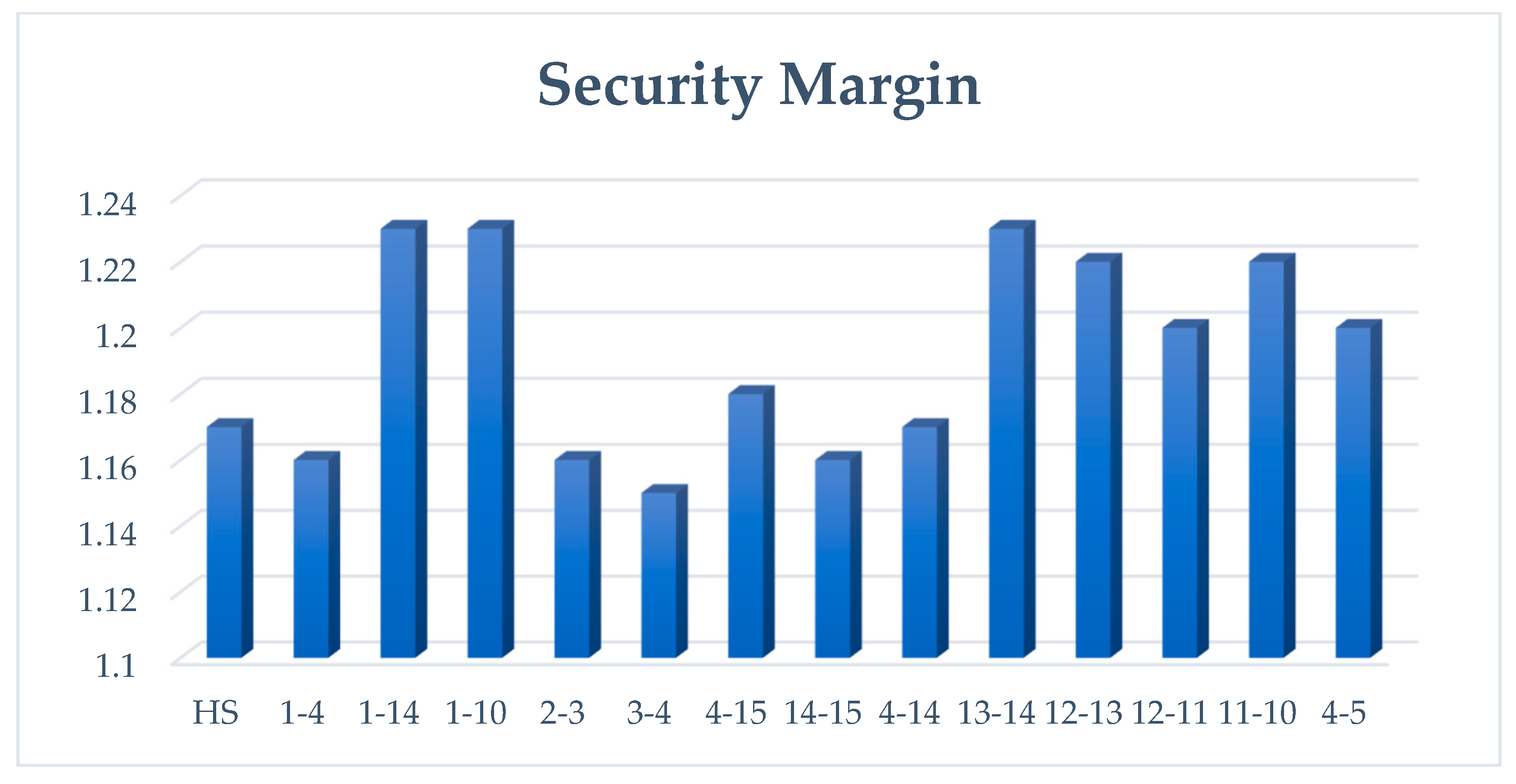
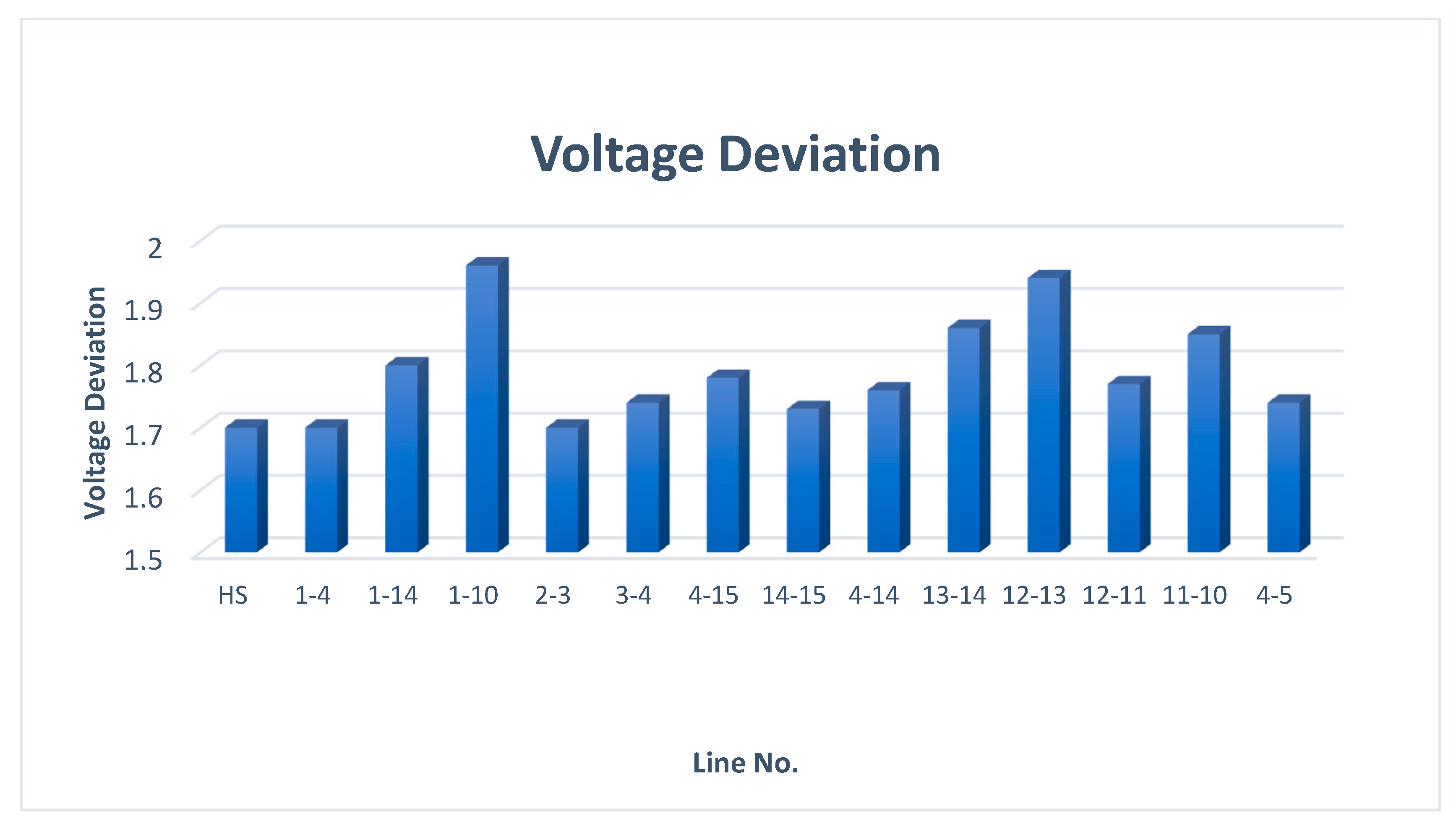
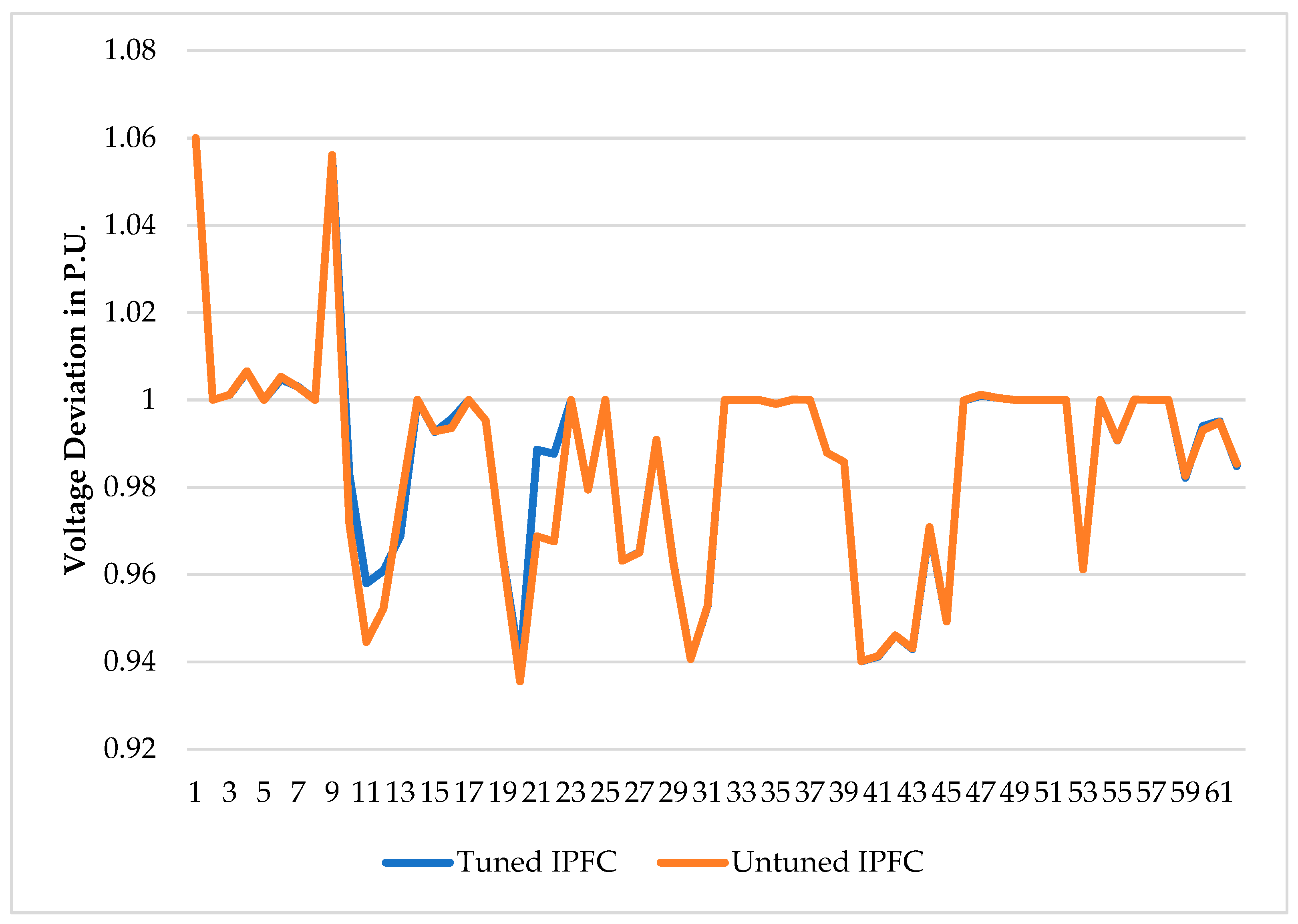
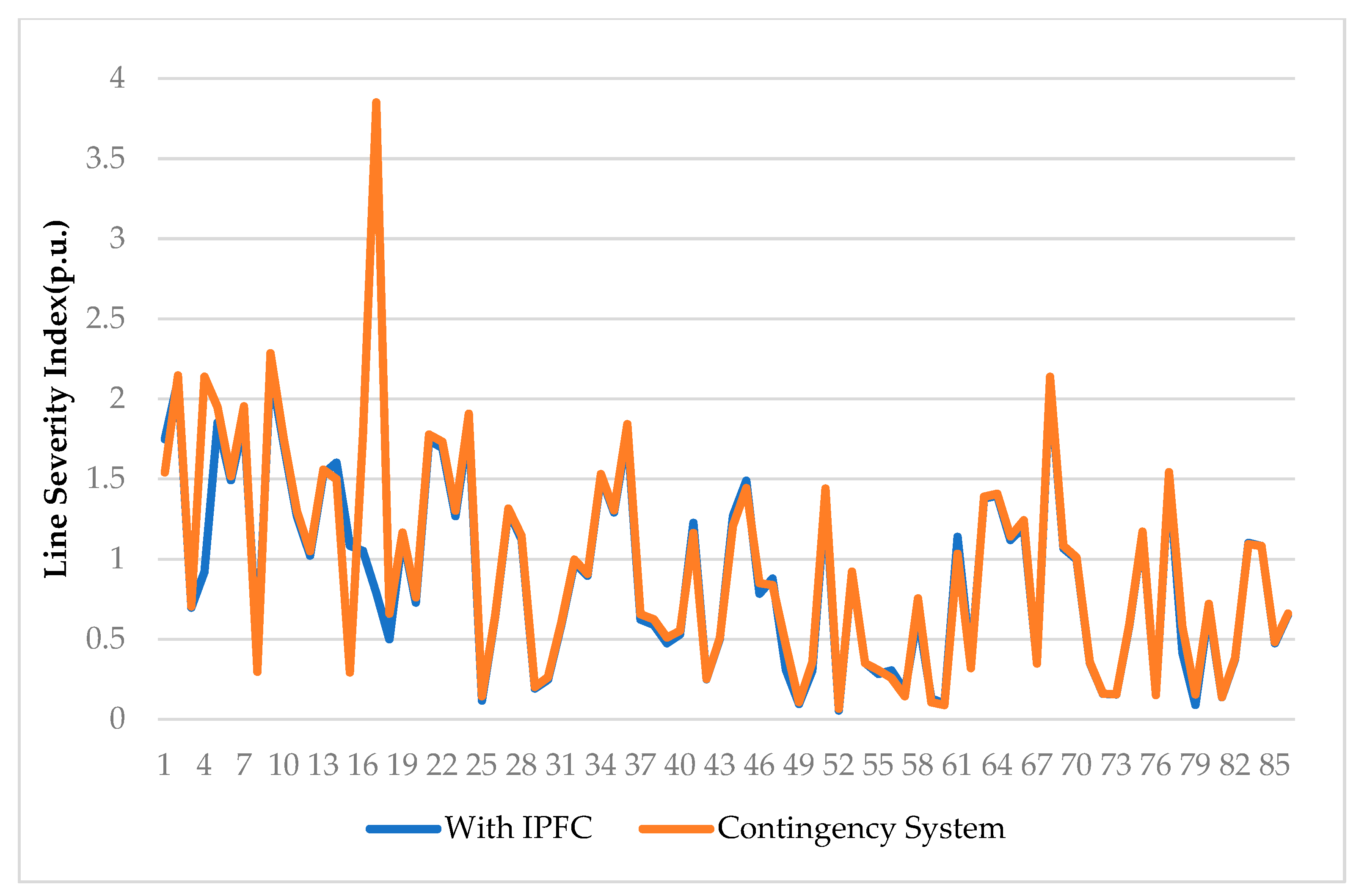
| S. No. | Contingency Condition | Active Power Loss (MW) | Reactive Power Loss (MVAR) | SM (p.u.) | VD (p.u.) |
|---|---|---|---|---|---|
| 1 | Healthy System | 191.9 | 982.5 | 1.17 | 1.7 |
| 2 | 1–4 | 194.3 | 995.3 | 1.16 | 1.7 |
| 3 | 1–14 | 216.8 | 1110.2 | 1.23 | 1.8 |
| 4 | 1–10 | 233.8 | 1198.0 | 1.23 | 1.96 |
| 5 | 2–3 | 197.6 | 1011.8 | 1.16 | 1.70 |
| 6 | 3–4 | 195.8 | 1002.8 | 1.15 | 1.74 |
| 7 | 4–15 | 198.1 | 1014.2 | 1.18 | 1.78 |
| 8 | 14–15 | 192.9 | 987.6 | 1.16 | 1.73 |
| 9 | 4–14 | 200.1 | 1024.6 | 1.17 | 1.76 |
| 10 | 13–14 | 227.8 | 1167.1 | 1.23 | 1.86 |
| 11 | 12–13 | 253.3 | 1298.3 | 1.22 | 1.96 |
| 12 | 12–11 | 228.6 | 1171.3 | 1.20 | 1.77 |
| 13 | 11–10 | 221.9 | 1136.9 | 1.22 | 1.85 |
| 14 | 4–5 | 196.5 | 1003.6 | 1.20 | 1.74 |
| S. No. | Contingency Condition | Line Severity Index (p.u.) |
|---|---|---|
| 1. | 3–4 | 3.49 |
| 2. | 4–15 | 5.12 |
| 3. | 12–13 | Contingency Line |
| 4. | 12–11 | 16.11 |
| 5. | 11–10 | 8.66 |
| 6. | 6–7 | 14 |
| 7. | 7–8 | 14.56 |
| 8. | 11–16 | 6.71 |
| 9. | 21–22 | 13.46 |
| 10. | 27–29 | 0.13 |
| 11. | 29–30 | 0.16 |
| 12. | 12–20 | 0.59 |
| 13. | 13–17 | 0.16 |
| 14. | 24–45 | 0.81 |
| 15. | 24–41 | 0.73 |
| 16. | 41–45 | 0.47 |
| 17. | 40–41 | 0.28 |
| 18. | 41–42 | 1.29 |
| 19. | 42–43 | 0.063 |
| 20. | 42–44 | 0.114 |
| Parameter | Healthy System | System Contingency | With Solar Unit &IPFC | IPFC Tuning |
|---|---|---|---|---|
| Active Power Loss (MW) | 87.372 | 102.126 | 98.747 | 91.139 |
| Reactive Power Loss (MVAR) | 445.172 | 523.159 | 500.62 | 467.78 |
| Voltage Deviation (p.u.) | 1.12 | 1.1828 | 1.1318 | 1.1105 |
| Security Margin (p.u.) | 0.92 | 1.79 | 1.41 | 1.35 |
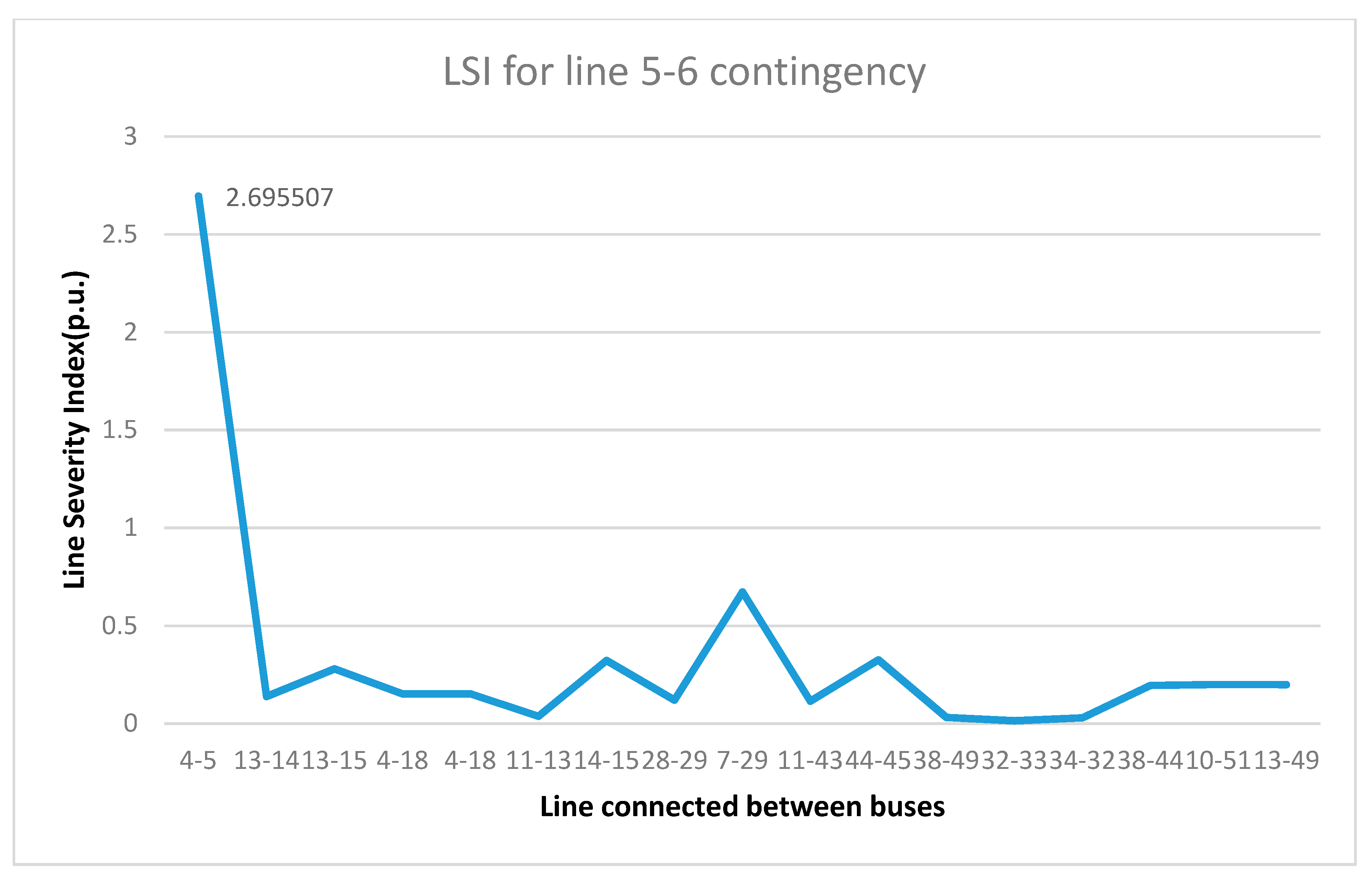
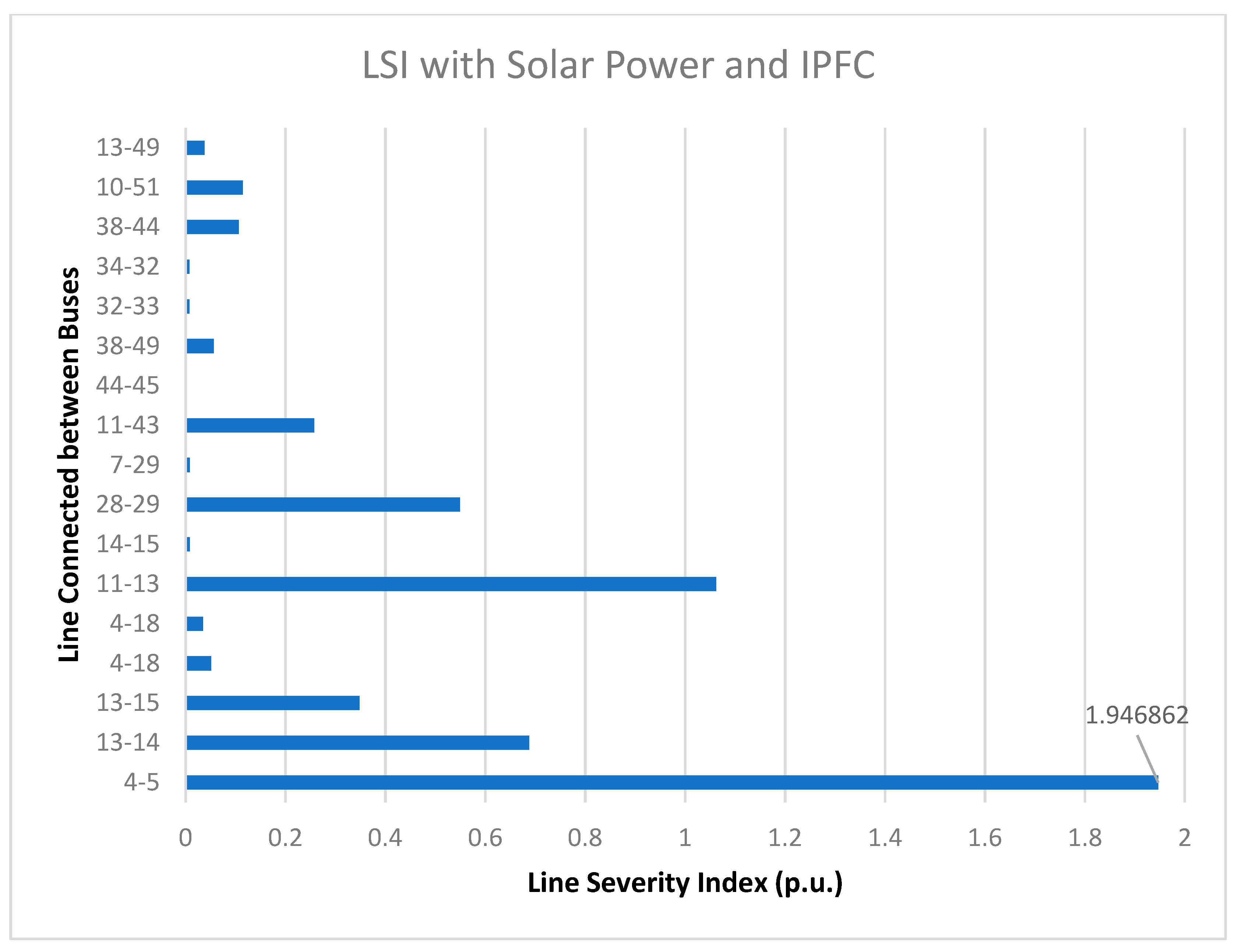
| S. No. | From Bus-To Bus | LSI for Line 5–6 Contingency (p.u.) | LSI with Solar Power and IPFC (p.u.) |
|---|---|---|---|
| 1. | 4–5 | 2.695507 | 1.946862 |
| 2. | 13–14 | 0.138384 | 0.68796 |
| 3. | 13–15 | 0.279629 | 0.347864 |
| 4. | 4–18 | 0.152256 | 0.051076 |
| 5. | 4–18 | 0.152256 | 0.034708 |
| 6. | 11–13 | 0.037133 | 1.06193 |
| 7. | 14–15 | 0.32251 | 0.008668 |
| 8. | 28–29 | 0.120062 | 0.549526 |
| 9. | 7–29 | 0.67322 | 0.008354 |
| 10. | 11–43 | 0.113771 | 0.257759 |
| 11. | 44–45 | 0.325242 | 0.000361 |
| 12. | 38–49 | 0.031542 | 0.056644 |
| 13. | 32–33 | 0.01428 | 0.007762 |
| 14. | 34–32 | 0.029207 | 0.007569 |
| 15. | 38–44 | 0.194922 | 0.10614089 |
| 16. | 10–51 | 0.199273 | 0.11418384 |
| 17. | 13–49 | 0.198919 | 0.037791 |
| S. No. | Parameter | Value of System Parameter for Line 5–6 Outage | Healthy System |
|---|---|---|---|
| 1 | Active Power Loss (MW) | 81.49 | 58.604 |
| 2 | Reactive Power Loss (MVAR) | 280.35 | 225.717 |
| 3 | Voltage Deviation (p.u.) | 1.1 | 1.01 |
| 4 | Security Margin (p.u.) | 1.9 | 1.12 |
| S. No. | Parameter | Healthy System | With Contingency | With Solar Power and IPFC | With Tuned IPFC |
|---|---|---|---|---|---|
| 1 | Active Power Loss (MW) | 58.604 | 81.49 | 73.106 | 65.24 |
| 2 | Reactive Power Loss (MVAR) | 225.717 | 280.35 | 249.050 | 231.12 |
| 3 | Voltage Deviation (p.u.) | 1.01 | 1.1 | 1.08 | 0.988 |
| 4 | Security Margin (p.u.) | 1.12 | 1.9 | 1.68 | 1.3 |
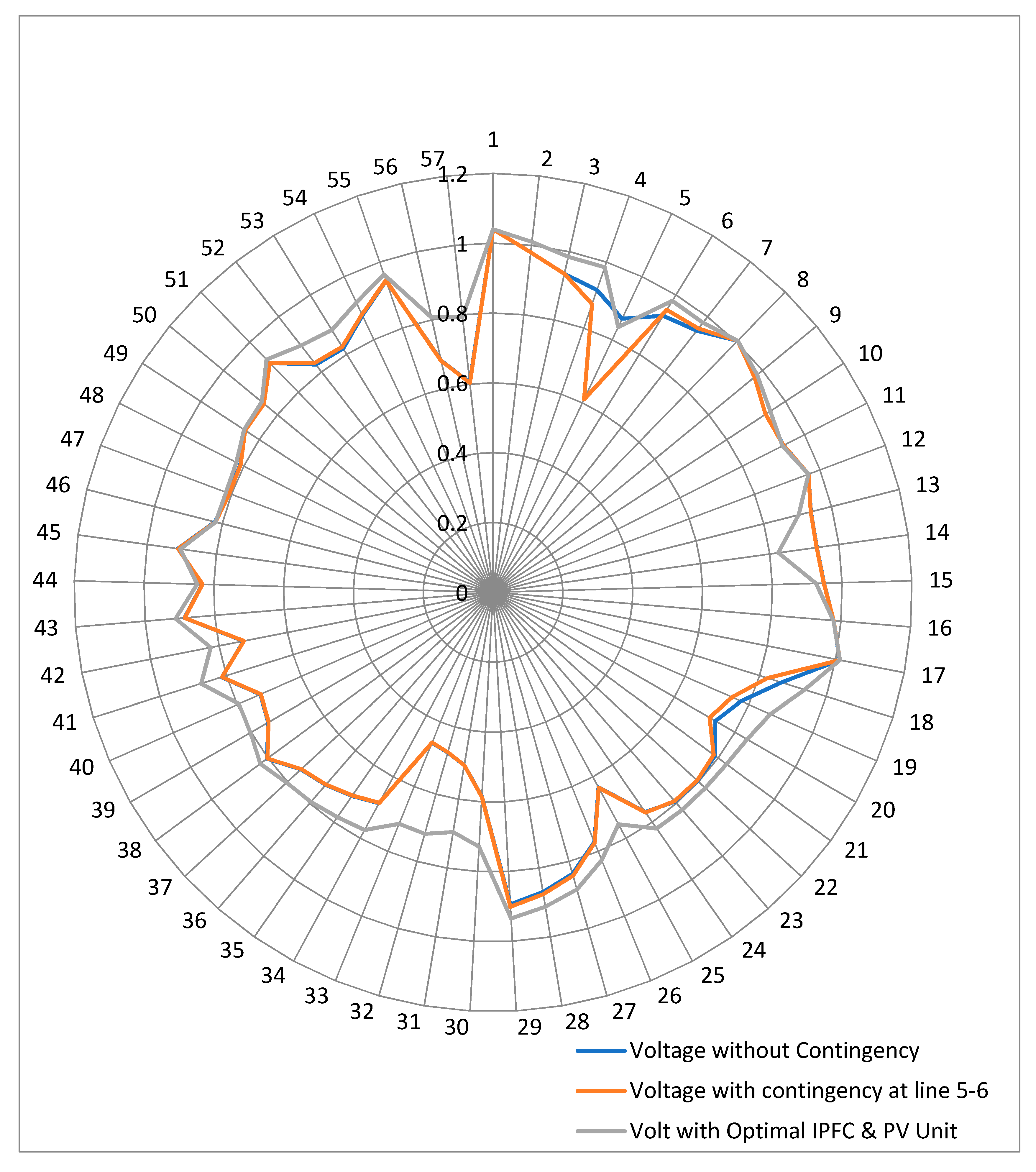
| S. No. | Volt without Contingency (p.u.) | Volt with Contingency at 5–6 (p.u.) | Volt with Optimal IPFC and Solar Unit (p.u.) |
|---|---|---|---|
| 1. | 1.04 | 1.04 | 1.04 |
| 2. | 0.98 | 0.98 | 1.01 |
| 3. | 0.935 | 0.935 | 0.985 |
| 4. | 0.9159 | 0.873 | 0.9841 |
| 5. | 0.8666 | 0.6111 | 0.8403 |
| 6. | 0.93 | 0.95 | 0.98 |
| 7. | 0.9501 | 0.9577 | 0.9789 |
| 8. | 1.005 | 1.005 | 1.005 |
| 9. | 0.97 | 0.97 | 0.98 |
| 10. | 0.9325 | 0.9324 | 0.9487 |
| 11. | 0.9326 | 0.9324 | 0.9291 |
| 12. | 0.965 | 0.965 | 0.965 |
| 13. | 0.9391 | 0.9388 | 0.9027 |
| 14. | 0.9361 | 0.9358 | 0.8249 |
| 15. | 0.9482 | 0.948 | 0.9255 |
| 16. | 0.9789 | 0.9786 | 0.9782 |
| 17. | 1.012 | 1.0122 | 1.0123 |
| 18. | 0.8649 | 0.8236 | 0.9346 |
| 19. | 0.7755 | 0.7475 | 0.8674 |
| 20. | 0.7352 | 0.7161 | 0.8404 |
| 21. | 0.7888 | 0.7842 | 0.8297 |
| 22. | 0.7963 | 0.7945 | 0.8261 |
| 23. | 0.7935 | 0.7919 | 0.8249 |
| 24. | 0.7646 | 0.7661 | 0.8221 |
| 25. | 0.6345 | 0.6355 | 0.7543 |
| 26. | 0.7711 | 0.7731 | 0.8269 |
| 27. | 0.837 | 0.8421 | 0.8835 |
| 28. | 0.8694 | 0.8756 | 0.9122 |
| 29. | 0.8944 | 0.9013 | 0.9348 |
| 30. | 0.5853 | 0.5861 | 0.7287 |
| 31. | 0.5011 | 0.5013 | 0.6952 |
| 32. | 0.476 | 0.4753 | 0.7181 |
| 33. | 0.4643 | 0.4636 | 0.715 |
| 34. | 0.6859 | 0.6846 | 0.7729 |
| 35. | 0.7085 | 0.7072 | 0.7825 |
| 36. | 0.7305 | 0.7292 | 0.7949 |
| 37. | 0.7478 | 0.7465 | 0.8036 |
| 38. | 0.8037 | 0.8023 | 0.8275 |
| 39. | 0.7436 | 0.7423 | 0.8025 |
| 40. | 0.7277 | 0.7263 | 0.7948 |
| 41. | 0.8142 | 0.8137 | 0.8761 |
| 42. | 0.7277 | 0.7269 | 0.8241 |
| 43. | 0.8867 | 0.8864 | 0.9127 |
| 44. | 0.8336 | 0.8325 | 0.8476 |
| 45. | 0.9109 | 0.9103 | 0.9043 |
| 46. | 0.8214 | 0.8203 | 0.8199 |
| 47. | 0.8078 | 0.8066 | 0.8168 |
| 48. | 0.8115 | 0.8103 | 0.8241 |
| 49. | 0.8492 | 0.8483 | 0.8519 |
| 50. | 0.8513 | 0.8506 | 0.8583 |
| 51. | 0.9167 | 0.9165 | 0.9305 |
| 52. | 0.8269 | 0.8328 | 0.8958 |
| 53. | 0.82 | 0.8253 | 0.8821 |
| 54. | 0.8772 | 0.8803 | 0.9177 |
| 55. | 0.9438 | 0.9447 | 0.9629 |
| 56. | 0.6805 | 0.6795 | 0.8073 |
| 57. | 0.605 | 0.6037 | 0.7929 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, A.; Venkata, N.K.G.; Bali, S.K.; Bathina, V.R.; Ramisetty, U.M.; Gollapudi, S.; Habib Fayek, H.; Rusu, E. Strategic Placement of Solar Power Plant and Interline Power Flow Controllers for Prevention of Blackouts. Inventions 2022, 7, 30. https://doi.org/10.3390/inventions7010030
Mishra A, Venkata NKG, Bali SK, Bathina VR, Ramisetty UM, Gollapudi S, Habib Fayek H, Rusu E. Strategic Placement of Solar Power Plant and Interline Power Flow Controllers for Prevention of Blackouts. Inventions. 2022; 7(1):30. https://doi.org/10.3390/inventions7010030
Chicago/Turabian StyleMishra, Akanksha, Nagesh Kumar Gundavarapu Venkata, Sravana Kumar Bali, Venkateswara Rao Bathina, Uma Maheswari Ramisetty, Srikanth Gollapudi, Hady Habib Fayek, and Eugen Rusu. 2022. "Strategic Placement of Solar Power Plant and Interline Power Flow Controllers for Prevention of Blackouts" Inventions 7, no. 1: 30. https://doi.org/10.3390/inventions7010030
APA StyleMishra, A., Venkata, N. K. G., Bali, S. K., Bathina, V. R., Ramisetty, U. M., Gollapudi, S., Habib Fayek, H., & Rusu, E. (2022). Strategic Placement of Solar Power Plant and Interline Power Flow Controllers for Prevention of Blackouts. Inventions, 7(1), 30. https://doi.org/10.3390/inventions7010030








