Duan–Rach Approach to Study Al2O3-Ethylene Glycol C2H6O2 Nanofluid Flow Based upon KKL Model
Abstract
1. Introduction
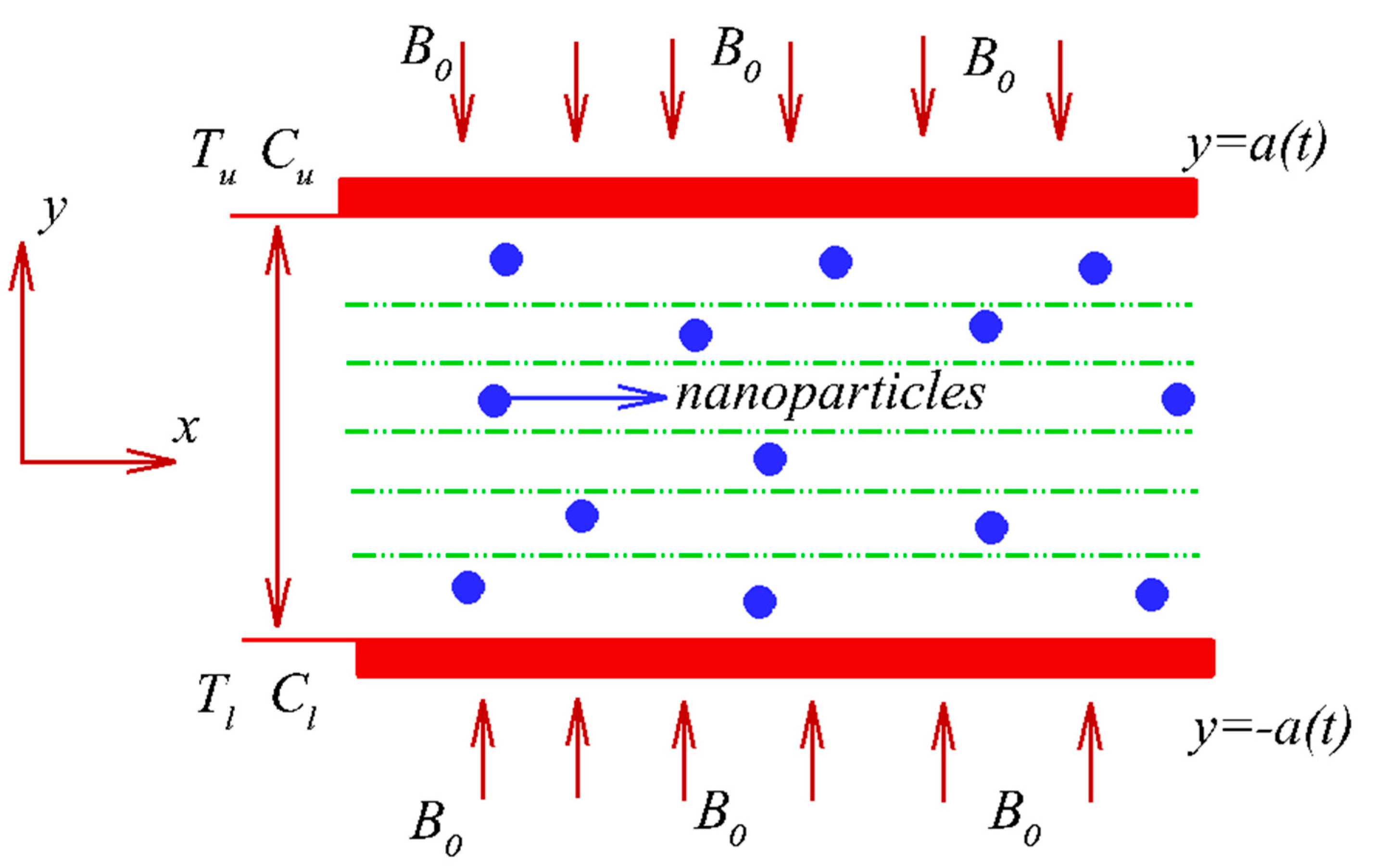
2. Mathematical Formulation
3. Formulation of Physical Quantities
4. Formulation of Duan–Rach Approach
5. Implementation of the Method
6. Discussion
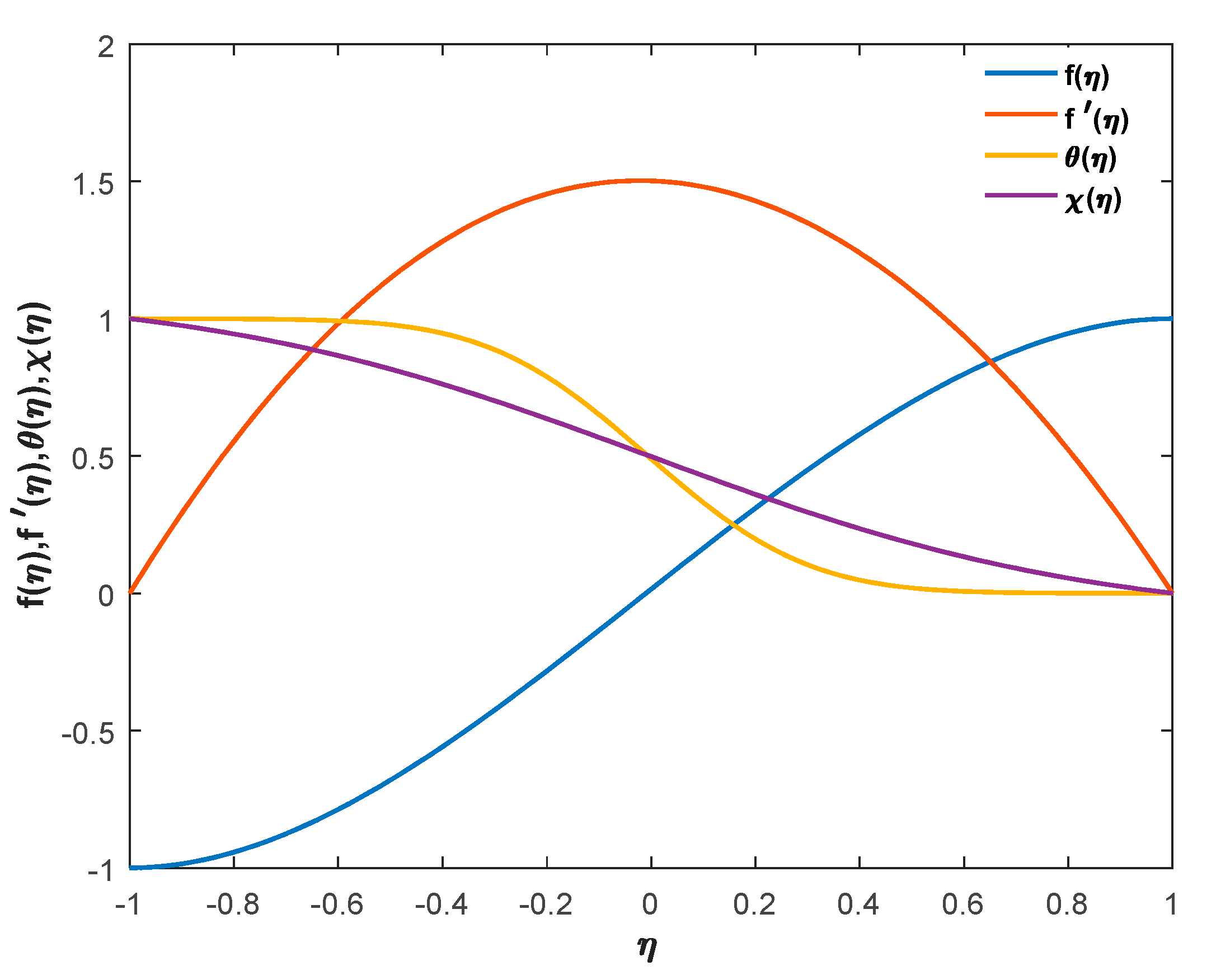
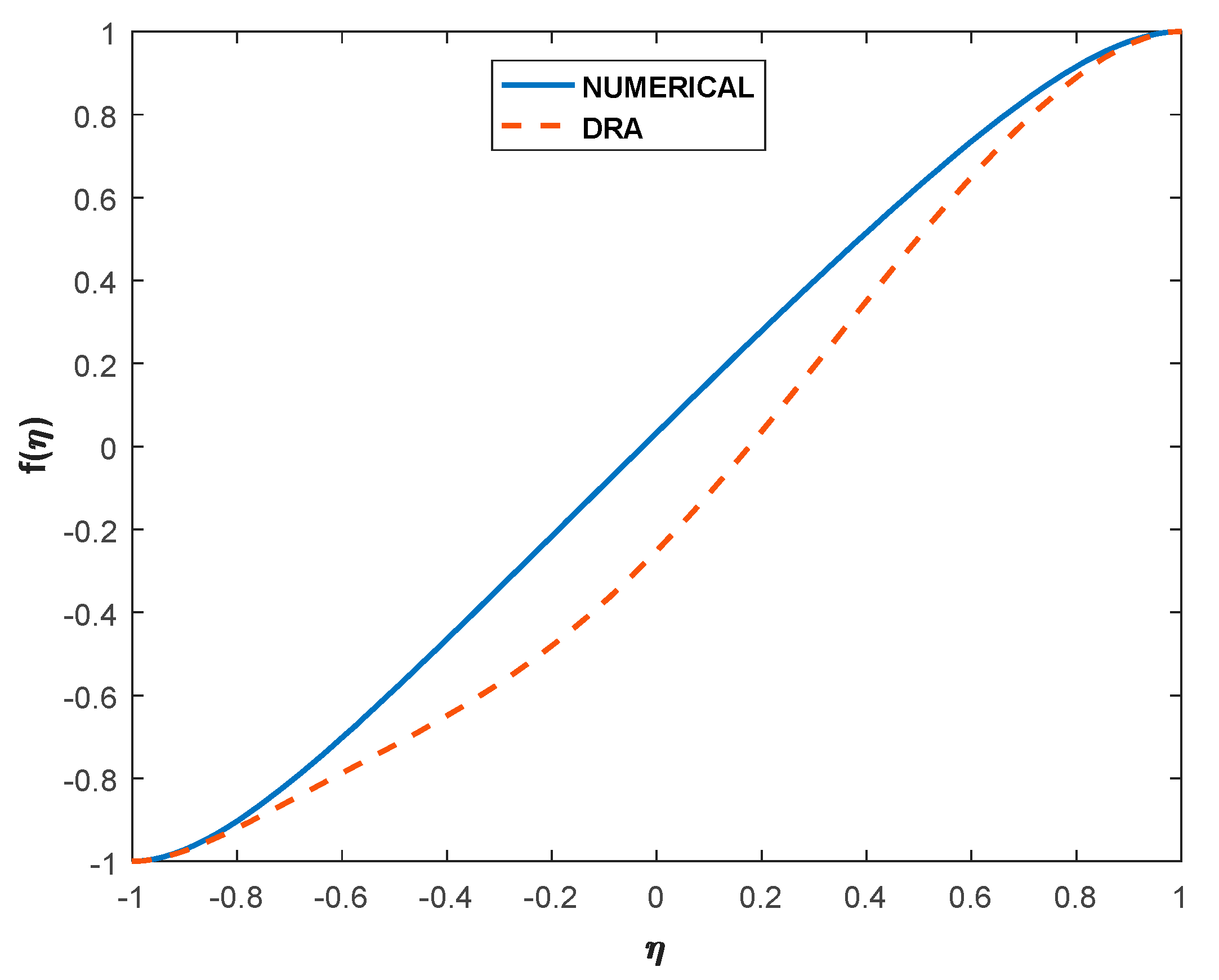
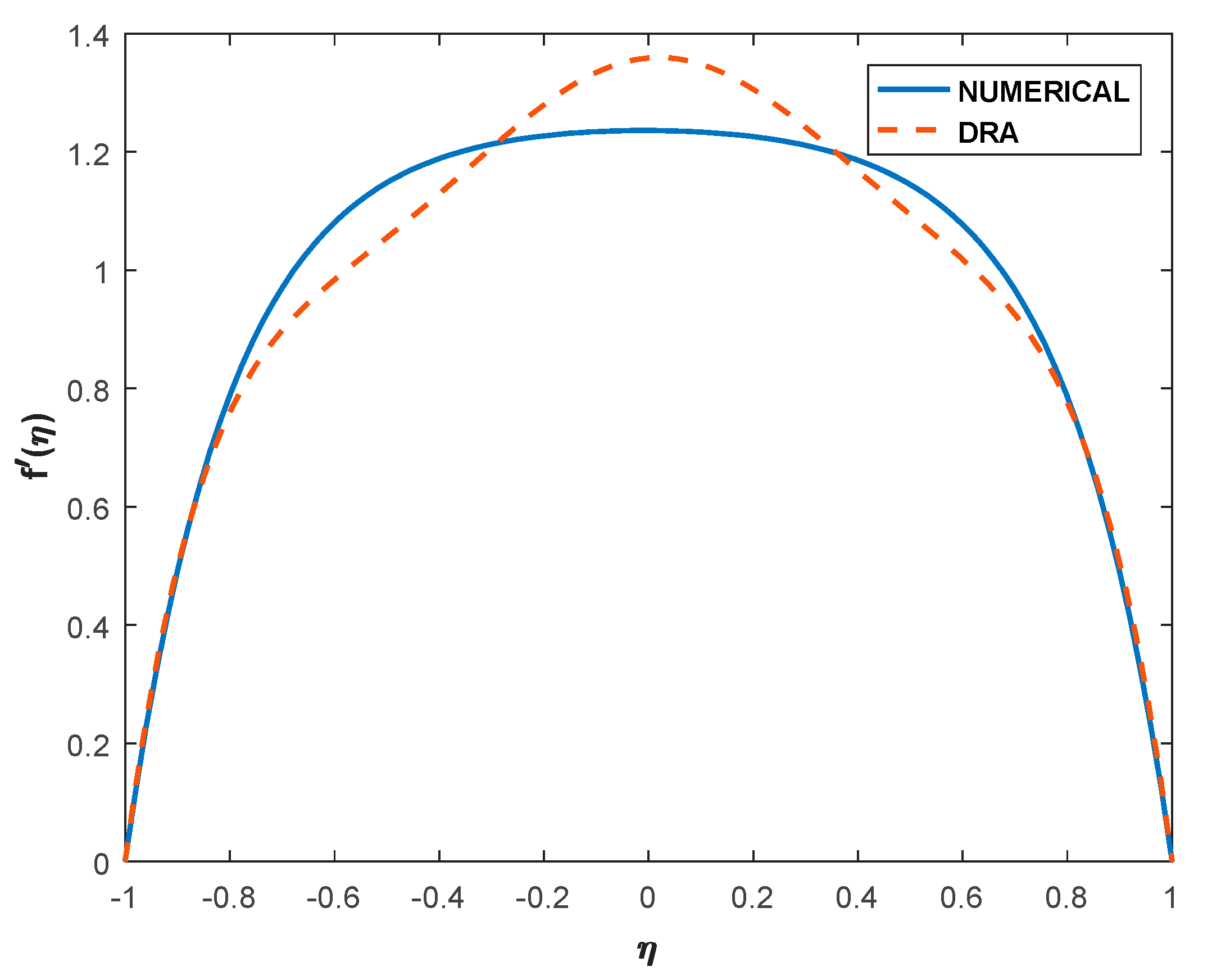
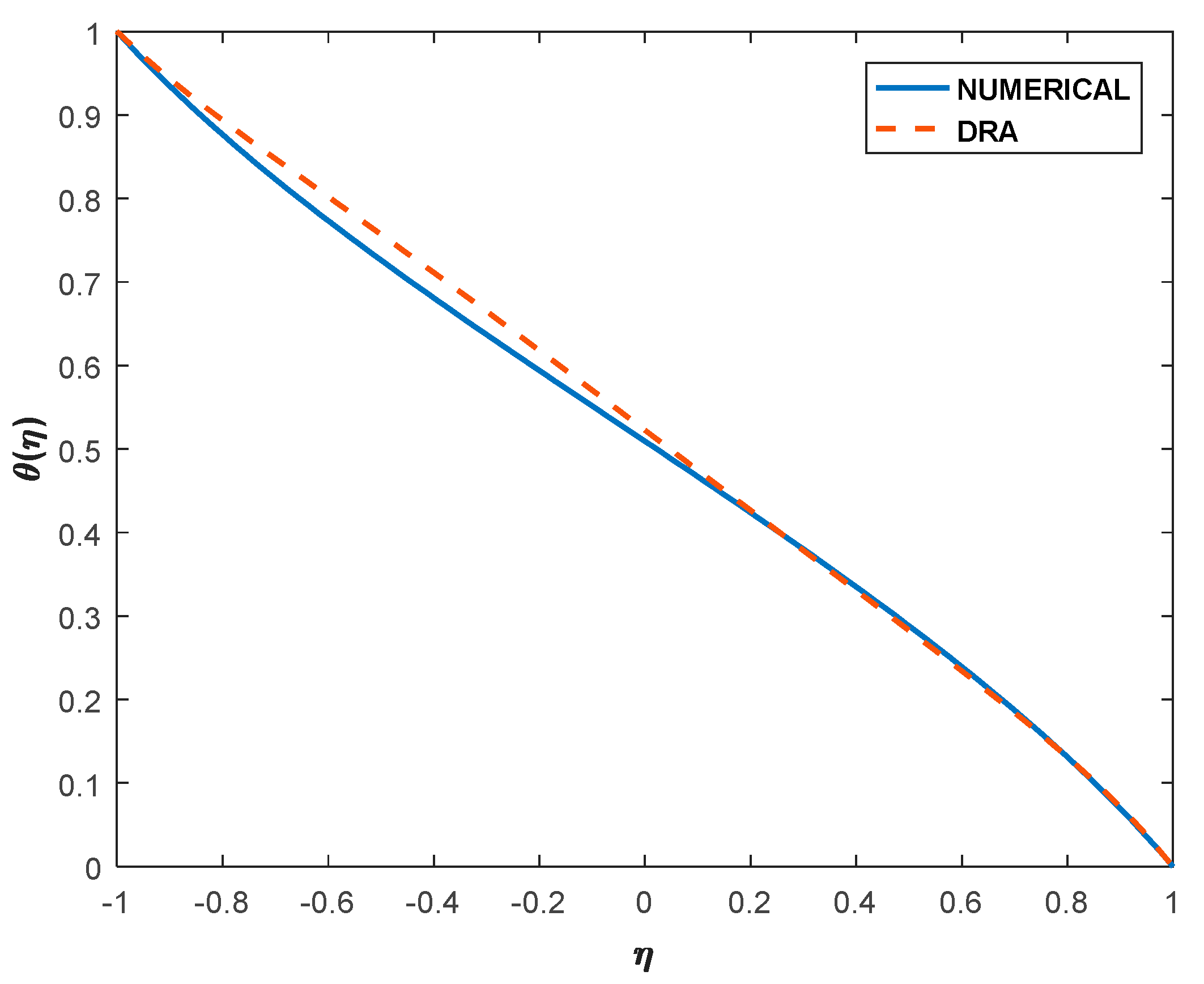
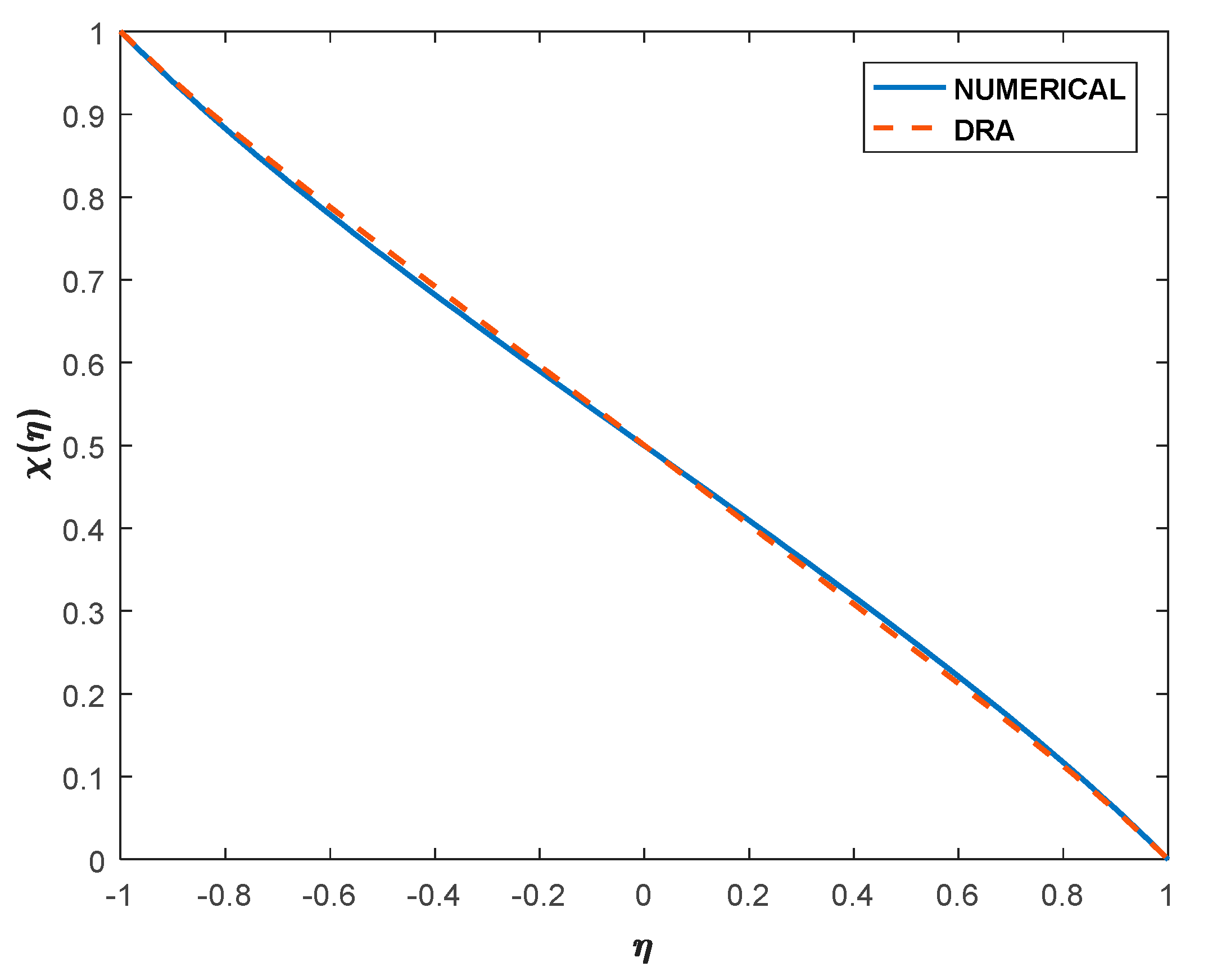
6.1. Validation and Comparative Study of Various Profiles
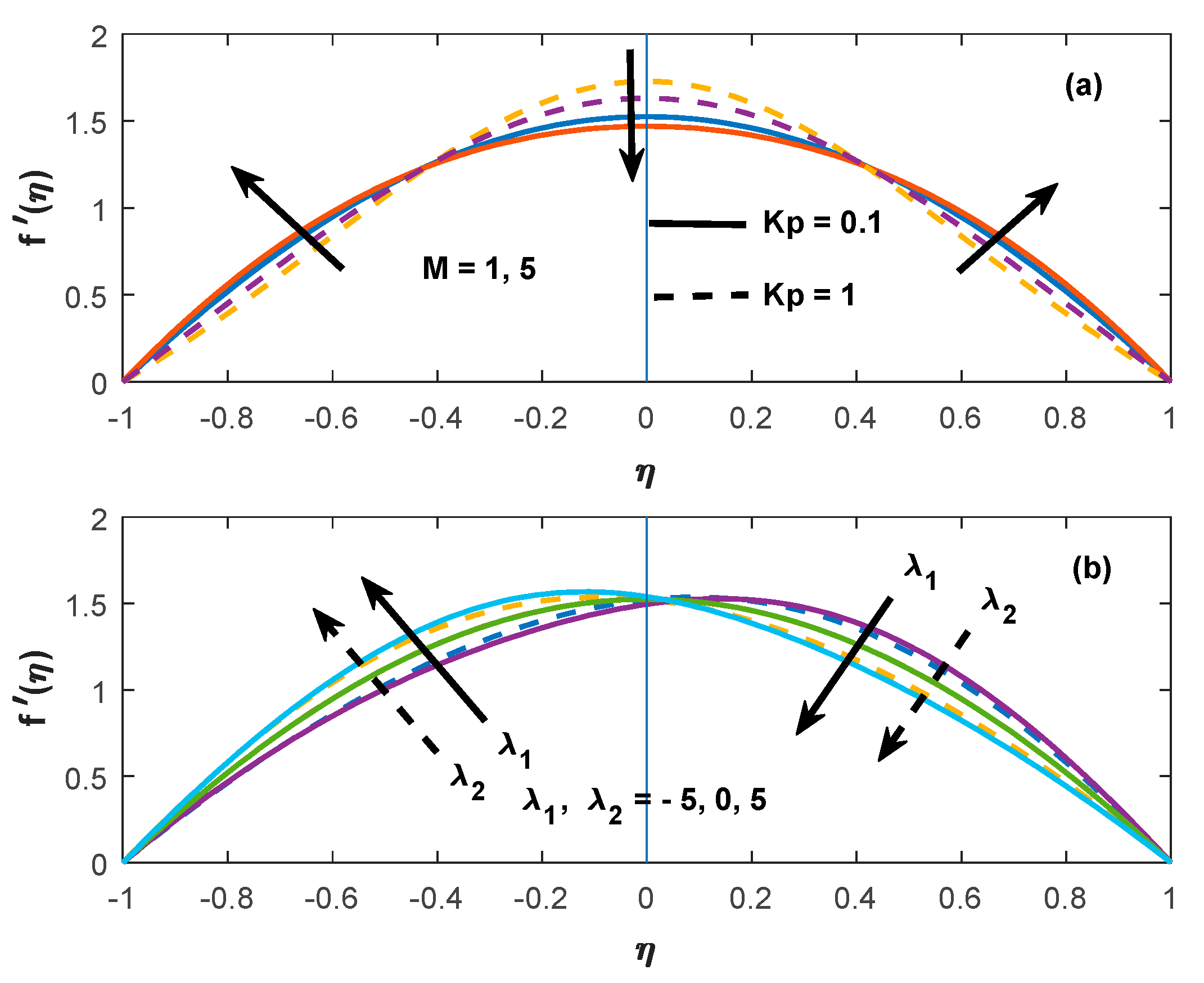
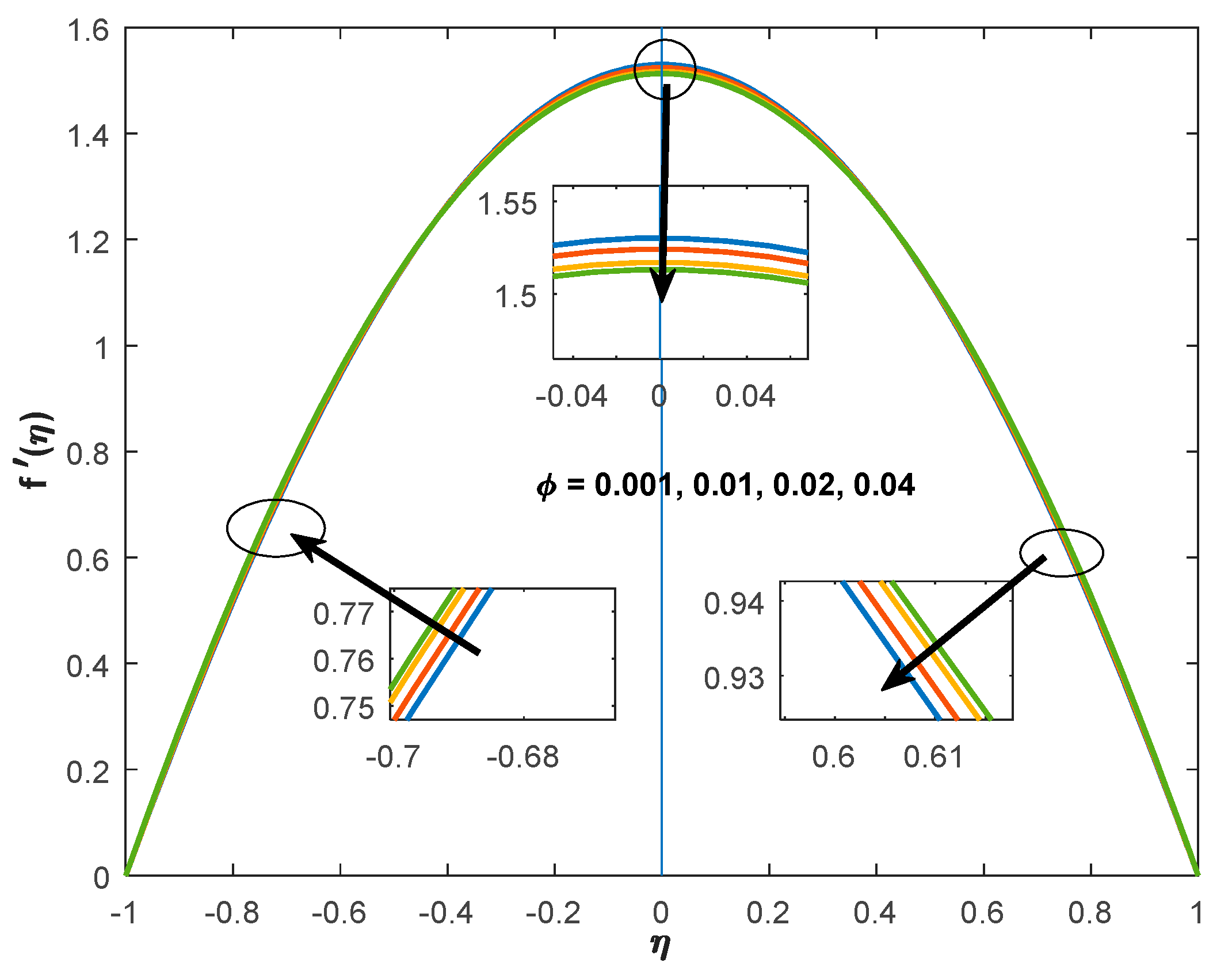
6.2. Variation of the Velocity Distribution
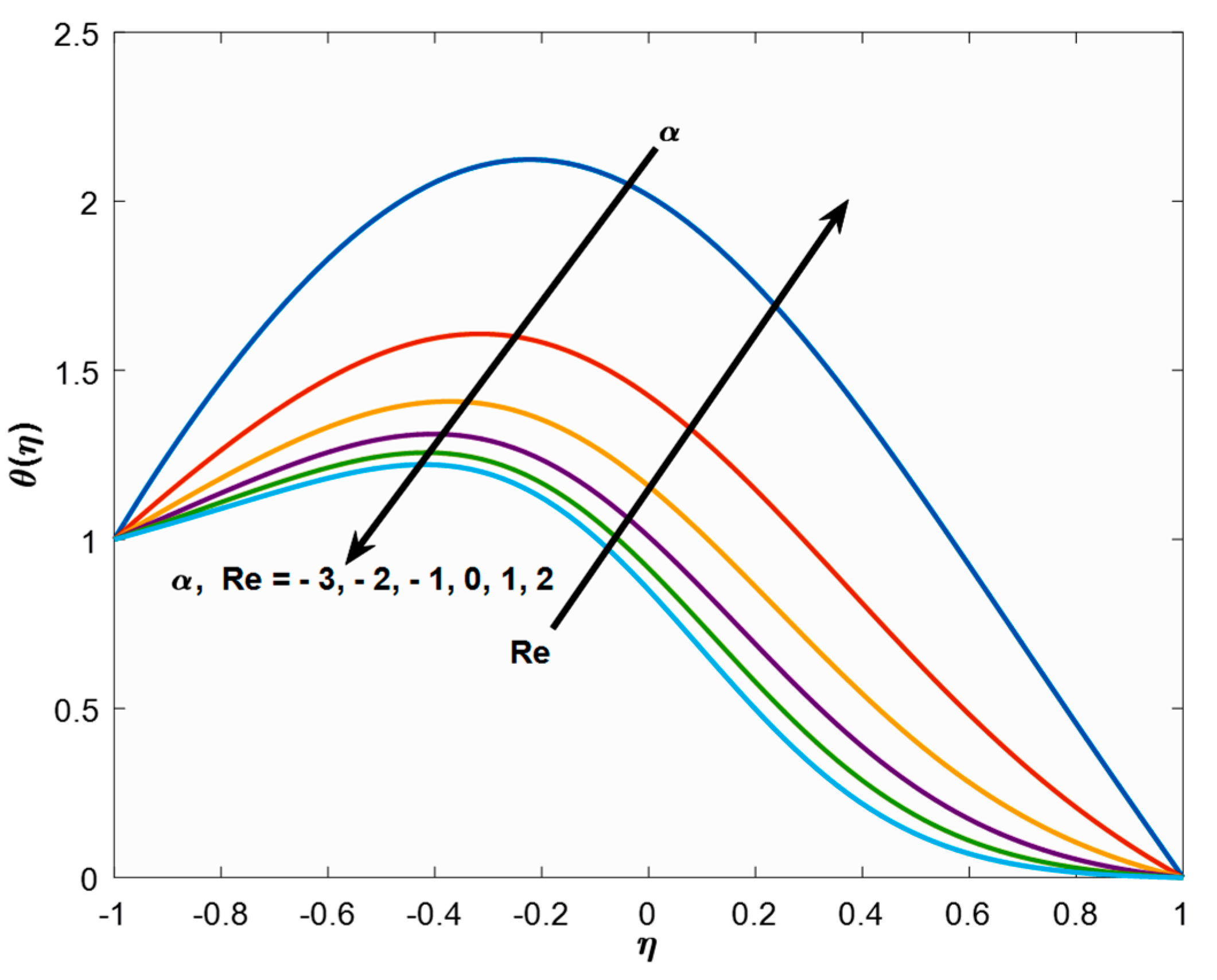
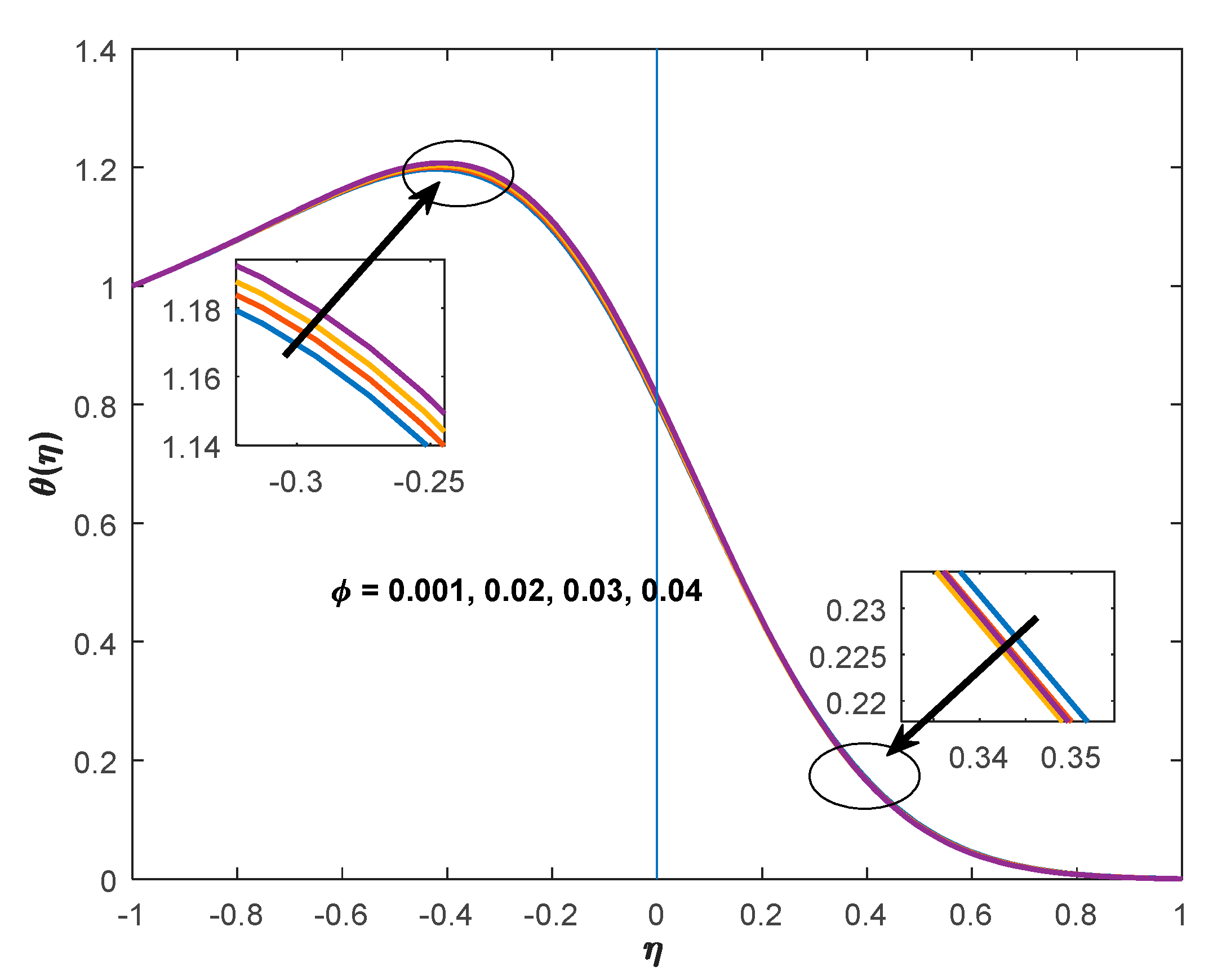
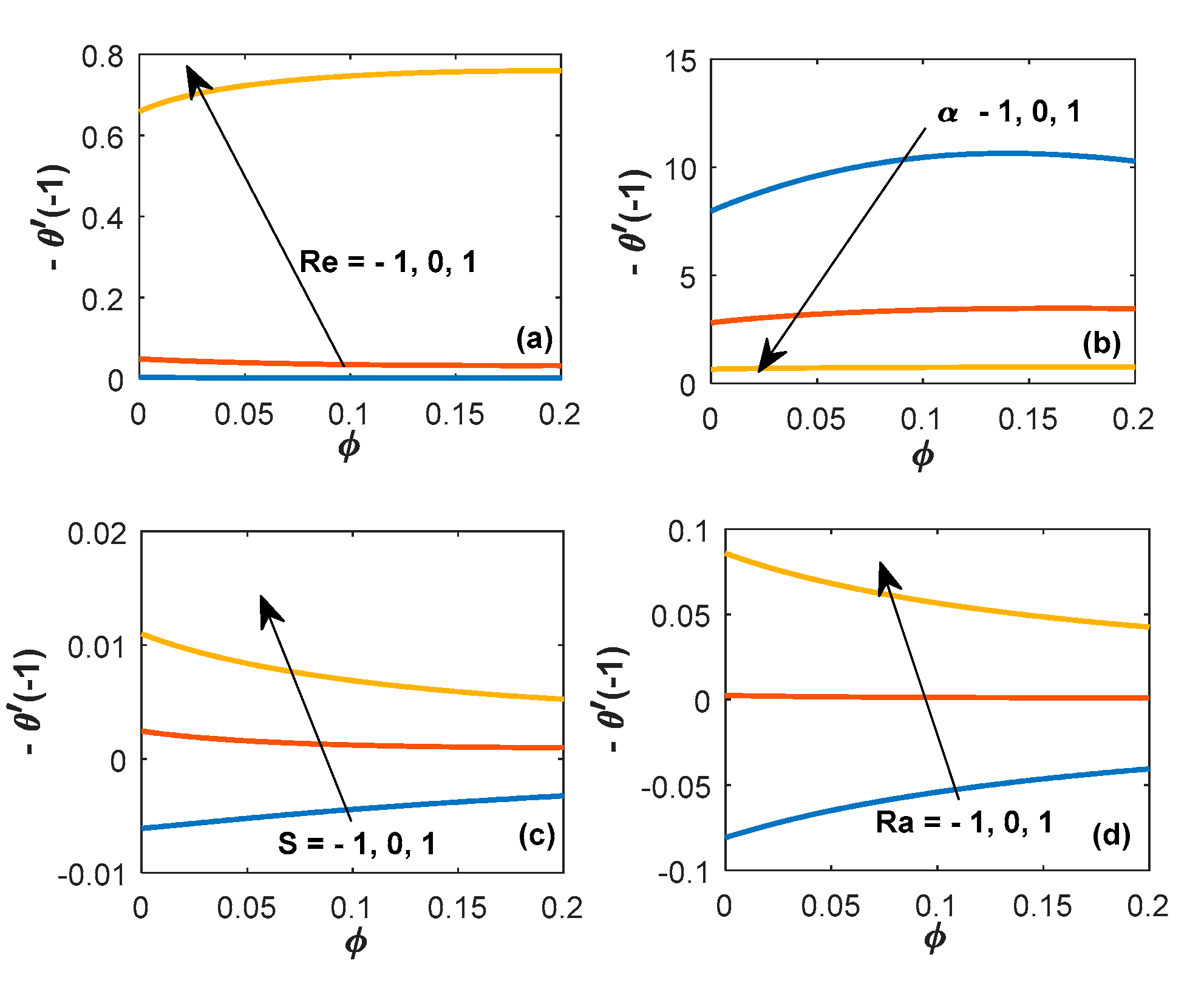
6.3. Variation of Temperature Distributions
6.4. Variation of Temperature Distributions
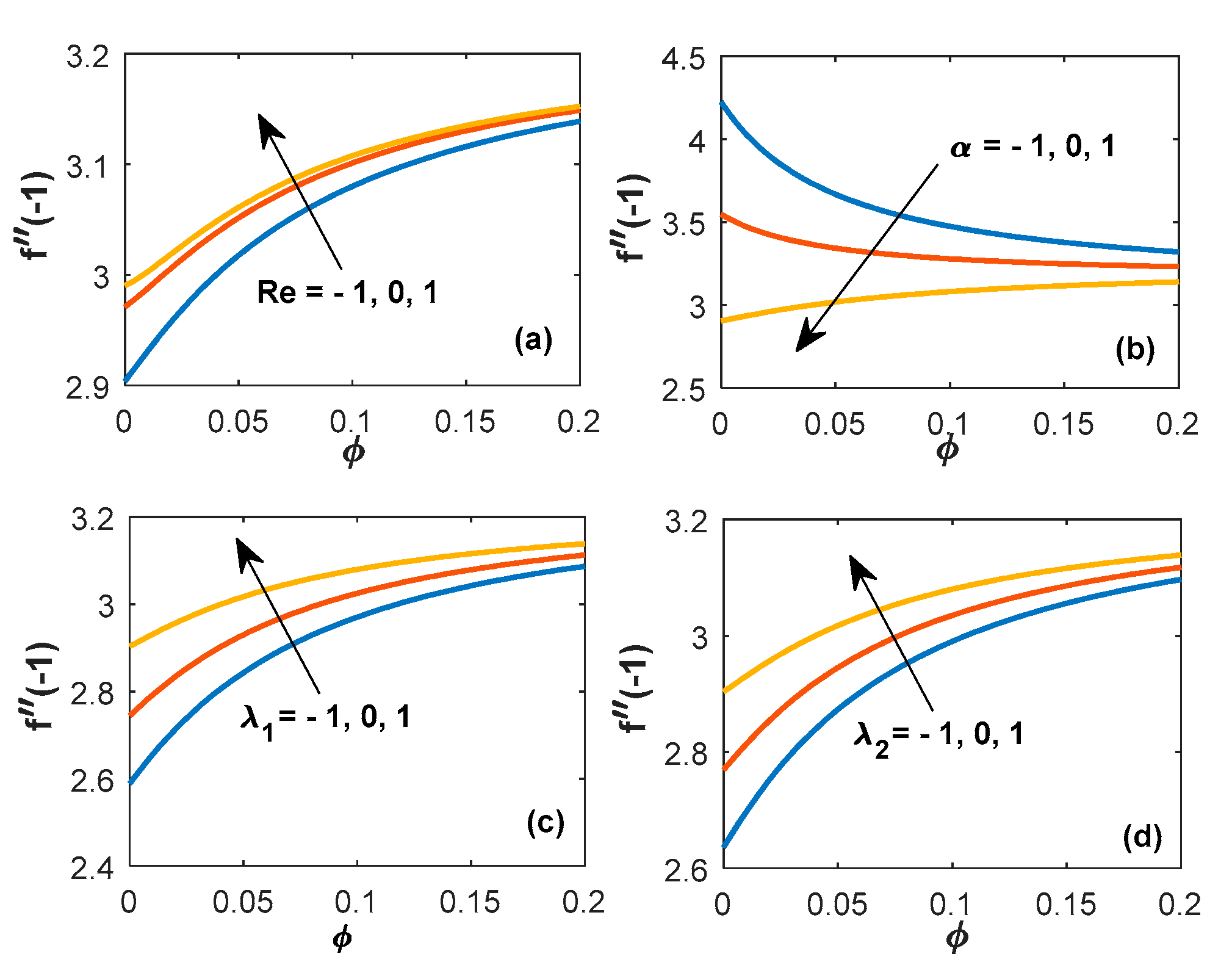
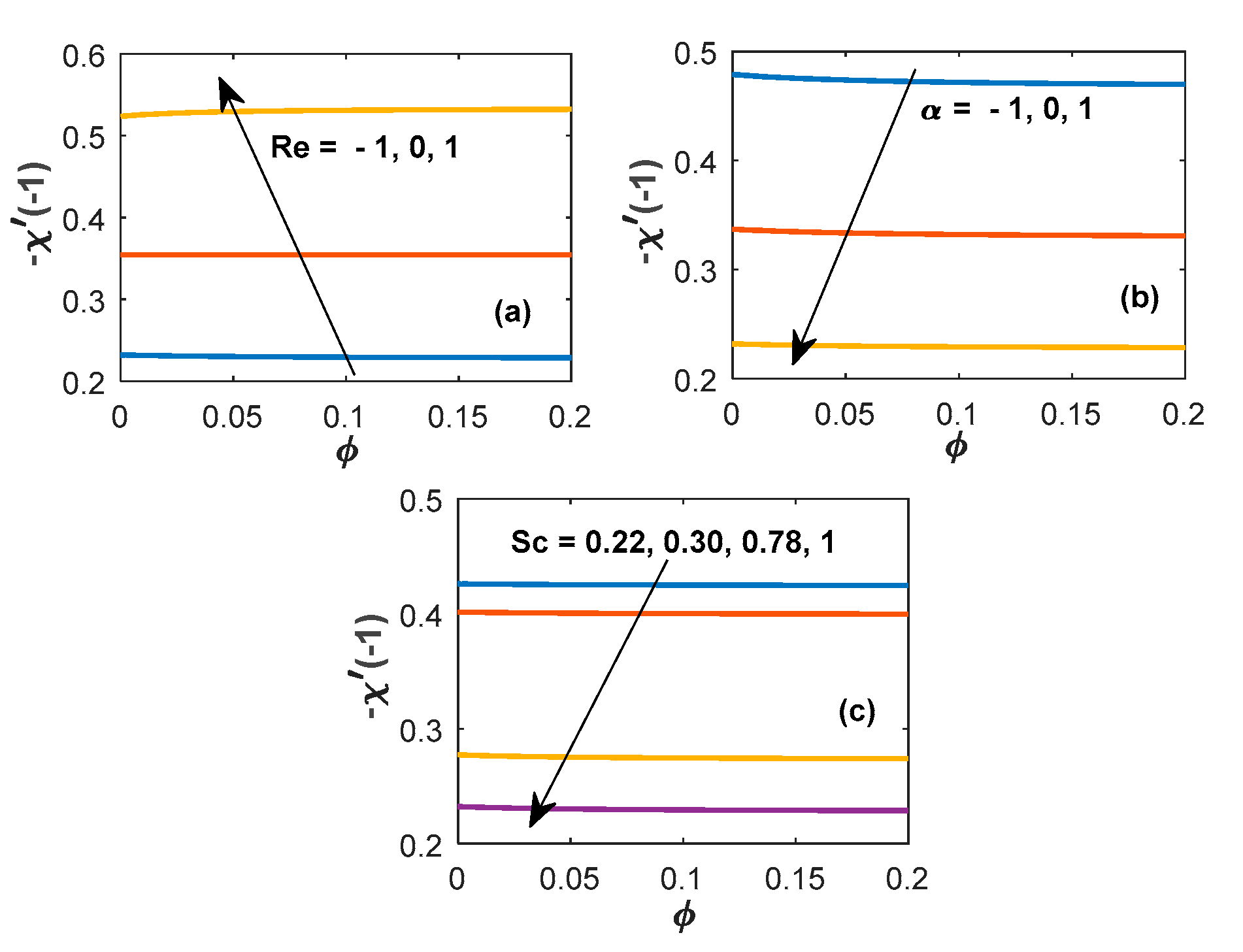
6.5. Variation of Engineering Coefficients
7. Conclusions
- It is noticed that a rapid decrease in temperature profile is observed when Alumina–EG nanofluids are contemplated.
- Porosity effects enhance the flow, whereas the magnetic field opposes the flow.
- Increase in buoyancy forces from heating to cooling, the enhancing nature of the profiles exhibits to lower down the thickness at the lower plate in the half region. In contrast, from the point of contact at the central area, the opposite effect is rendered near the upper plate region.
- It is found that increasing volume fraction retards the thickness at the lower plate; however, the expansion at the upper plate is more.
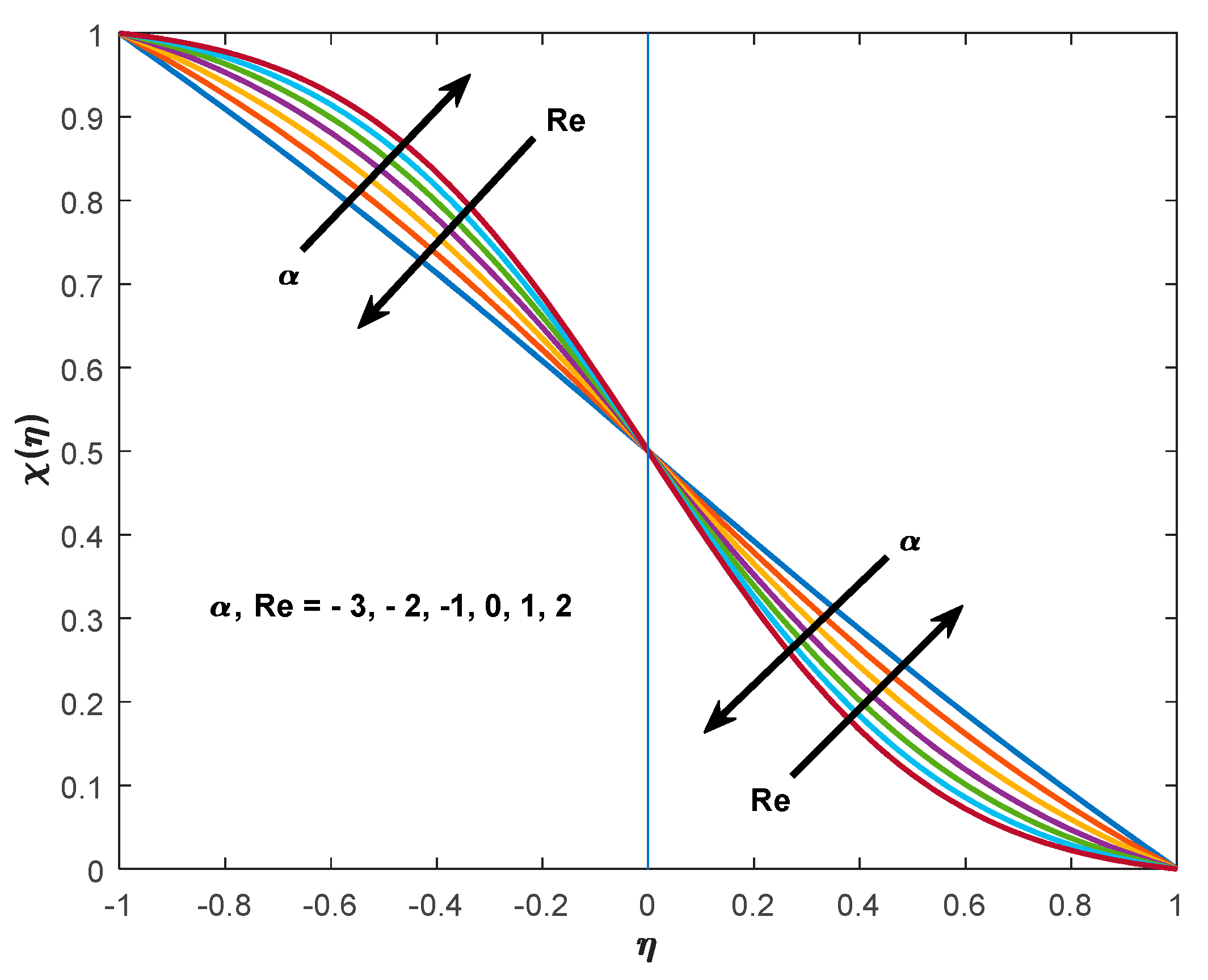
- It is seen that the profile overshoots with increasing suction Reynolds number i.e., for positive values and reverse impact is rendered for the injection where it indicates the negative Reynolds number.
- It is concluded that the growing volume fraction will cause a development in the heat transfer properties.
- Prandtl number shows converse behavior in the upper region as compared with the low area.
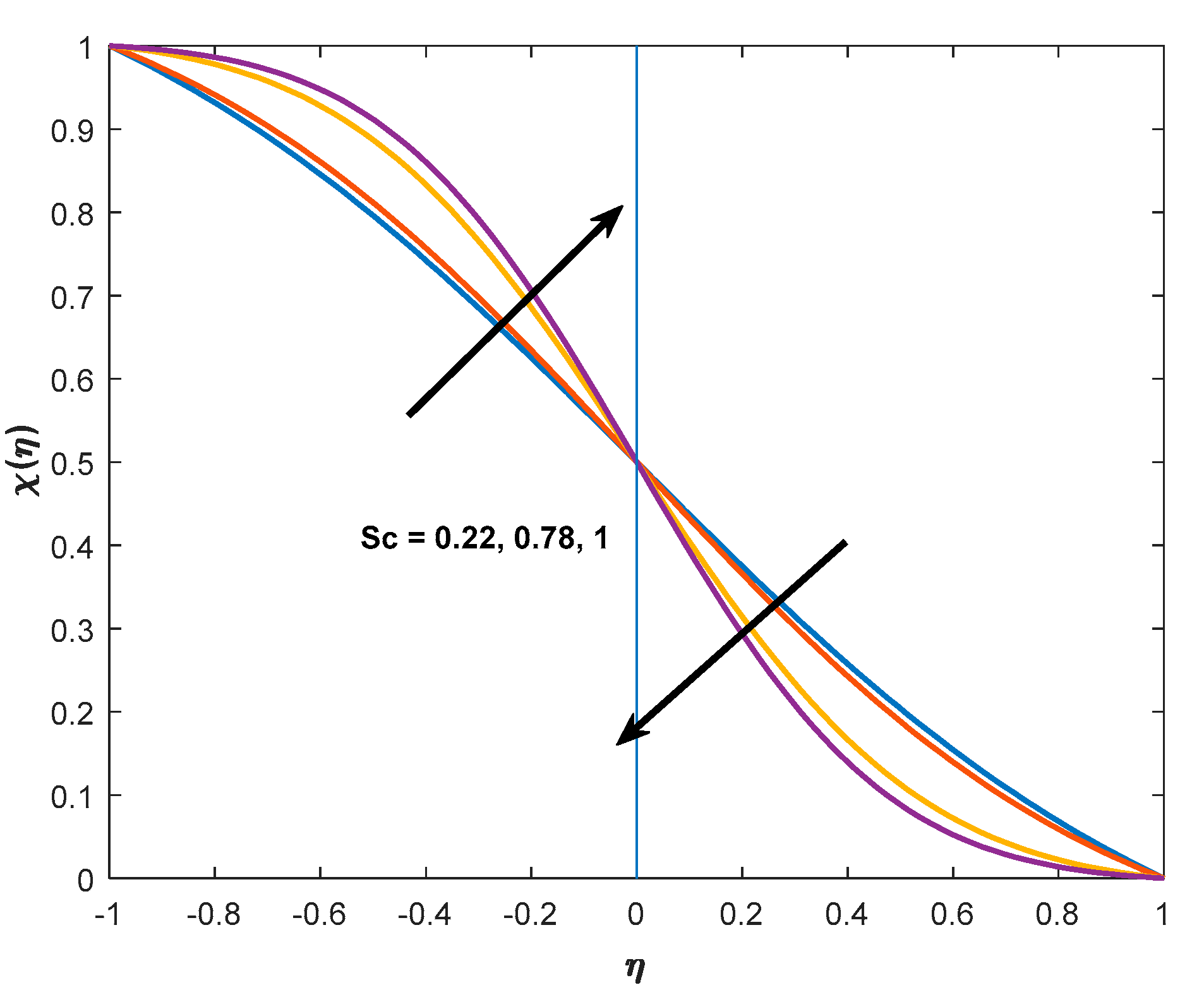
- Reynolds number and Schmidt number show converse behavior on the concentration profile.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Permeability | |
| magnetic field strength | |
| concentration fluid | |
| specific heat | |
| solutal diffusivity | |
| velocity profiles | |
| self-similar velocity | |
| gravity | |
| shape factor for nanoparticle | |
| magnetic parameter | |
| thermal conductivity of water | |
| porosity parameter | |
| horizontal and vertical co-ordinate axes | |
| pressure | |
| Prandtl number | |
| heat source parameter | |
| coefficient of radiation absorption | |
| non-dimensional radiation absorption | |
| Reynolds number | |
| non-dimensional source parameter | |
| Schmidt number | |
| Horizontal and vertical velocity | |
| Temperature | |
| Greek Symbols | |
| nanoparticle volume fraction | |
| sphericity of the nanoparticles | |
| kinematic viscosity | |
| fluid density | |
| electrical conductivity | |
| volumetric coefficient of expansion for heat transfer | |
| volumetric coefficient of expansion for mass transfer | |
| dynamic viscosity | |
| wall expansion/contraction parameter | |
| thermal diffusivity | |
| scaled boundary layer coordinate | |
| dimensionless temperature | |
| dimensionless concentration | |
| thermal buoyancy parameter | |
| solutal buoyancy parameter | |
| heat capacity | |
| Subscripts | |
| nf | nanofluid |
| f | base fluid |
| p | solid particle |
| l | lower walls |
| u | upper walls |
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Developments and Applications of Non-Newtonian Flows, FED-231/MD(66); Siginer, D.A., Wang, H.P., Eds.; ASME: New York, NY, USA, 1995; pp. 99–105. [Google Scholar]
- Choi, S.U.S. Nanofluids: From vision to reality through research. J. Heat Transf. 2009, 131, 1–9. [Google Scholar] [CrossRef]
- Barik, A.K.; Mishra, S.K.; Mishra, S.R.; Pattnaik, P.K. Multiple slip effects on MHD nanofluid flow over an inclined, radiative, and chemically reacting stretching sheet by means of FDM. Heat Transf. Asian Res. 2019, 1–25. [Google Scholar] [CrossRef]
- Mutuku, W.N. Ethylene glycol (EG)-based nanofluids as a coolant for automotive radiator. Asia Pac. J. Comput. Eng. 2016, 3, 1. [Google Scholar] [CrossRef]
- Mishra, S.R.; Pattnaik, P.K.; Bhatti, M.M.; Abbas, T. Analysis of heat and mass transfer with MHD and chemical reaction effects on viscoelastic fluid over a stretching sheet. Indian J. Phys. 2017. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Sheremet, M.A.; Chamkha, A.J.; Hashim, I. MHD convective heat transfer in a discretely heated square cavity with conductive inner block using two-phase nanofluid model. Sci. Rep. 2018, 8, 7410. [Google Scholar] [CrossRef] [PubMed]
- Mohammadein, S.A.; Raslan, K.; Abdel-Wahed, M.S.; Abedel-Aal, E.M. KKL-model of MHD CuO-nanofluid flow over a stagnation point stretching sheet with nonlinear thermal radiation and suction/injection. Results Phys. 2018, 10, 194–199. [Google Scholar] [CrossRef]
- Rahimi, A.; Kasaeipoor, A.; Malekshah, E.H.; Rashidi, M.M.; Purusothaman, A. Lattice Boltzmann simulation of 3D natural convection in a cuboid filled with KKL-model predicted nanofluid using Dual-MRT model. Int. J. Numer. Methods Heat Fluid Flow 2018. [Google Scholar] [CrossRef]
- Rout, B.C.; Mishra, S.R. Thermal energy transport on MHD nanofluid flow over a stretching surface: A comparative study. Eng. Sci. Technol. Int. J. 2018, 21, 60–69. [Google Scholar] [CrossRef]
- Rana, S.; Nawaz, M. Investigation of enhancement of heat transfer in Sutterby nanofluid using Koo–Kleinstreuer and Li (KKL) correlations and Cattaneo–Christov heat flux model. Phys. Scr. 2019, 94, 115213. [Google Scholar] [CrossRef]
- Mohamed, R.A. Modeling electrical properties of nanofluids using artificial neural network. Phys. Scr. 2019, 94, 105222. [Google Scholar] [CrossRef]
- Peng, Y.; Sulaiman, A.A.; Afrand, M.; Moradi, R. A numerical simulation for magnetohydrodynamic nanofluid flow and heat transfer in rotating horizontal annulus with thermal radiation. RSC Adv. 2019. [Google Scholar] [CrossRef]
- Prakash, J.; Siva, E.P.; Tripathi, D.; Kuharat, S.; Bég, O.A. Peristaltic pumping of magnetic nanofluids with thermal radiation and temperature-dependent viscosity effects: Modelling a solar magneto-biomimetic nanopump. Renew. Energy 2019, 133, 1308–1326. [Google Scholar] [CrossRef]
- Rout, B.C.; Mishra, S.R. Analytical approach to metal and metallic oxide properties of Cu-water and TiO2-water nanofluids over a moving vertical plate. Pramana-J. Phys. 2019, 93, 41. [Google Scholar] [CrossRef]
- Al-Khaled, K.; Khan, S.U. Thermal Aspects of Casson Nanoliquid with Gyrotactic Microorganisms, Temperature-Dependent Viscosity, and Variable Thermal Conductivity: Bio-Technology and Thermal Applications. Inventions. 2020, 5, 39. [Google Scholar] [CrossRef]
- Bhatta, D.P.; Mishra, S.R.; Dash, J.K.; Makinde, O.D. A semi-analytical approach to time dependent squeezing flow of Cu and Ag water-based nanofluids. Defect Diffus. Forum 2019, 393, 121–137. [Google Scholar]
- Khan, S.U.; Tlili, I. Significance of activation energy and effective Prandtl number in accelerated flow of Jeffrey nanoparticles with gyrotactic microorganisms. J. Energy Resour. Technol. 2020, 142, 112101. [Google Scholar] [CrossRef]
- Zhang, L.; Arain, M.B.; Bhatti, M.M.; Zeeshan, A.; Hal-Sulami, H. Effects of magnetic Reynolds number on swimming of gyrotactic microorganisms between rotating circular plates filled with nanofluids. Appl. Math. Mech. 2020, 41, 637–654. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Shahid, A.; Abbas, T.; Alamri, S.Z.; Ellahi, R. Study of activation energy on the movement of gyrotactic microorganism in a magnetized nanofluids past a porous plate. Processes 2020, 8, 328. [Google Scholar] [CrossRef]
- Ghasemi, H.; Aghabarari, B.; Alizadeh, M.; Khanlarkhani, A.; Abu-Zahra, N. High efficiency decolorization of wastewater by Fenton catalyst: Magnetic iron-copper hybrid oxides. J. Water Process Eng. 2020, 37, 101540. [Google Scholar] [CrossRef]
- Mozaffari, S. Rheology of Bitumen at the Onset of Asphaltene Aggregation and Its Effects on the Stability of Water-in-Oil Emulsion. Master’s Thesis, University of Alberta, Alberta, AB, Canada, 2015. [Google Scholar]
- Darjani, S.; Koplik, J.; Pauchard, V. Extracting the equation of state of lattice gases from random sequential adsorption simulations by means of the Gibbs adsorption isotherm. Phys. Rev. E 2017, 96, 052803. [Google Scholar] [CrossRef]
- Ellahi, R.; Hussain, F.; Abbas, S.A.; Sarafraz, M.M.; Goodarzi, M.; Shadloo, M.S. Study of Two-Phase Newtonian Nanofluid Flow Hybrid with Hafnium Particles under the Effects of Slip. Inventions 2020, 5, 6. [Google Scholar] [CrossRef]
- Ray, A.K.; Vasu, B.; Bég, O.A.; Gorla, R.S.R.; Murthy, P.V.S.N. Homotopy Semi-Numerical Modeling of Non-Newtonian Nanofluid Transport External to Multiple Geometries Using a Revised Buongiorno Model. Inventions 2019, 4, 54. [Google Scholar] [CrossRef]
- Abbas, M.A.; Hussain, I. Statistical Analysis of the Mathematical Model of Entropy Generation of Magnetized Nanofluid. Inventions 2019, 4, 32. [Google Scholar] [CrossRef]
- Safaei, M.R.; Safdari Shadloo, M.; Goodarzi, M.S.; Hadjadj, A.; Goshayeshi, H.R.; Afrand, M.; Kazi, S.N. A survey on experimental and numerical studies of convection heat transfer of nanofluids inside closed conduits. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Giwa, S.O.; Sharifpur, M.; Goodarzi, M.; Alsulami, H.; Meyer, J.P. Influence of base fluid, temperature, and concentration on the thermophysical properties of hybrid nanofluids of alumina–ferrofluid: Experimental data, modeling through enhanced ANN, ANFIS, and curve fitting. J. Therm. Anal. Calorim. 2020, 1–9. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Viscous dissipation effects in micro tubes and micro channels. Int. J. Heat Mass Transf. 2004, 47, 3159–3169. [Google Scholar] [CrossRef]
- Koo, J. Computational Nanofluid Flow and Heat Transfer Analyses Applied to Microsystems. Ph.D. Thesis, State University, Raleigh, NC, USA, 2004. [Google Scholar]
- Li, Z.X.; Khaled, U.; Al-Rashed, A.A.; Goodarzi, M.; Sarafraz, M.M.; Meer, R. Heat transfer evaluation of a micro heat exchanger cooling with spherical carbon-acetone nanofluid. Int. J. Heat Mass Transf. 2020, 149, 119124. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Laminar nanofluid flow in microheat-sinks. Int. J. Heat Mass Transf. 2005, 48, 2652–2661. [Google Scholar] [CrossRef]
- Uchida, S.; Aoki, H. Unsteady flows in a semi-infinite contracting or expanding pipe. J. Fluid Meach. 1977, 82, 371–387. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problem of Physics: The Decomposition Method; Springer Netherlands: Dordrecht, The Netherlands, 1994. [Google Scholar]
- KhakRah, H.; Hooshmand, P.; Ross, D.; Jamshidian, M. Numerical analysis of free convection and entropy generation in a cavity using compact finite-difference lattice Boltzmann method. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 977–995. [Google Scholar] [CrossRef]
- Duan, J.S.; Rach, R. A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations. Appl. Math. Comput. 2011, 218, 4090–4118. [Google Scholar] [CrossRef]
- Akbar, M.Z.; Ashraf, M.; Iqbal, M.F.; Ali, K. Heat and mass transfer analysis of unsteady MHD nanofluid flow through a channel with moving porous walls and medium. AIP Adv. 2016, 6, 045222. [Google Scholar] [CrossRef]


| Ethylene-Glycol | 1114 | 2415 | 0.252 |
| Alumina | 3970 | 765 | 40 |
| Coefficient Values | Alumina-Ethylene-Glycol |
|---|---|
| 52.813488759 | |
| 6.115637295 | |
| 0.6955745084 | |
| 4.17455552786 × 10−2 | |
| 0.176919300241 | |
| −298.19819084 | |
| −34.532716906 | |
| −3.9225289283 | |
| −0.2354329626 | |
| −0.999063481 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pattnaik, P.K.; Mishra, S.; Bhatti, M.M. Duan–Rach Approach to Study Al2O3-Ethylene Glycol C2H6O2 Nanofluid Flow Based upon KKL Model. Inventions 2020, 5, 45. https://doi.org/10.3390/inventions5030045
Pattnaik PK, Mishra S, Bhatti MM. Duan–Rach Approach to Study Al2O3-Ethylene Glycol C2H6O2 Nanofluid Flow Based upon KKL Model. Inventions. 2020; 5(3):45. https://doi.org/10.3390/inventions5030045
Chicago/Turabian StylePattnaik, Pradyumna Kumar, Satyaranjan Mishra, and Muhammad Mubashir Bhatti. 2020. "Duan–Rach Approach to Study Al2O3-Ethylene Glycol C2H6O2 Nanofluid Flow Based upon KKL Model" Inventions 5, no. 3: 45. https://doi.org/10.3390/inventions5030045
APA StylePattnaik, P. K., Mishra, S., & Bhatti, M. M. (2020). Duan–Rach Approach to Study Al2O3-Ethylene Glycol C2H6O2 Nanofluid Flow Based upon KKL Model. Inventions, 5(3), 45. https://doi.org/10.3390/inventions5030045







