The Impact of the Covariance Matrix Sampling on the Angle of Arrival Estimation Accuracy
Abstract
1. Introduction
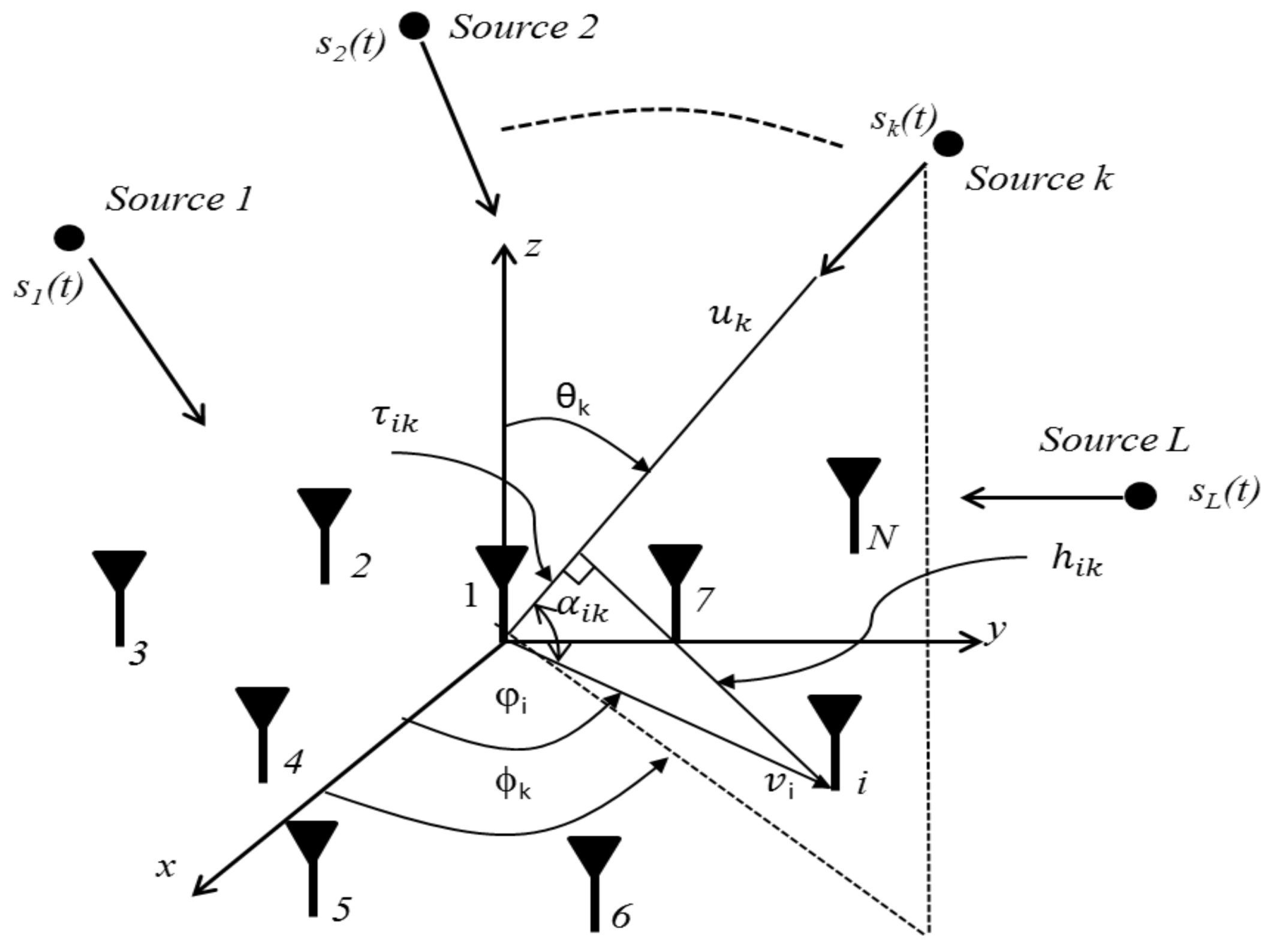
2. AoA Model and Problem Formulation
- is a Binary Phase Shift Keying (BPSK) modulated signal.
- is an AWGN for each channel.
- is the M × L matrix of steering vectors and is defined as follows:
3. The Projection Matrix Construction
4. The Methodology of Matrix Sampling
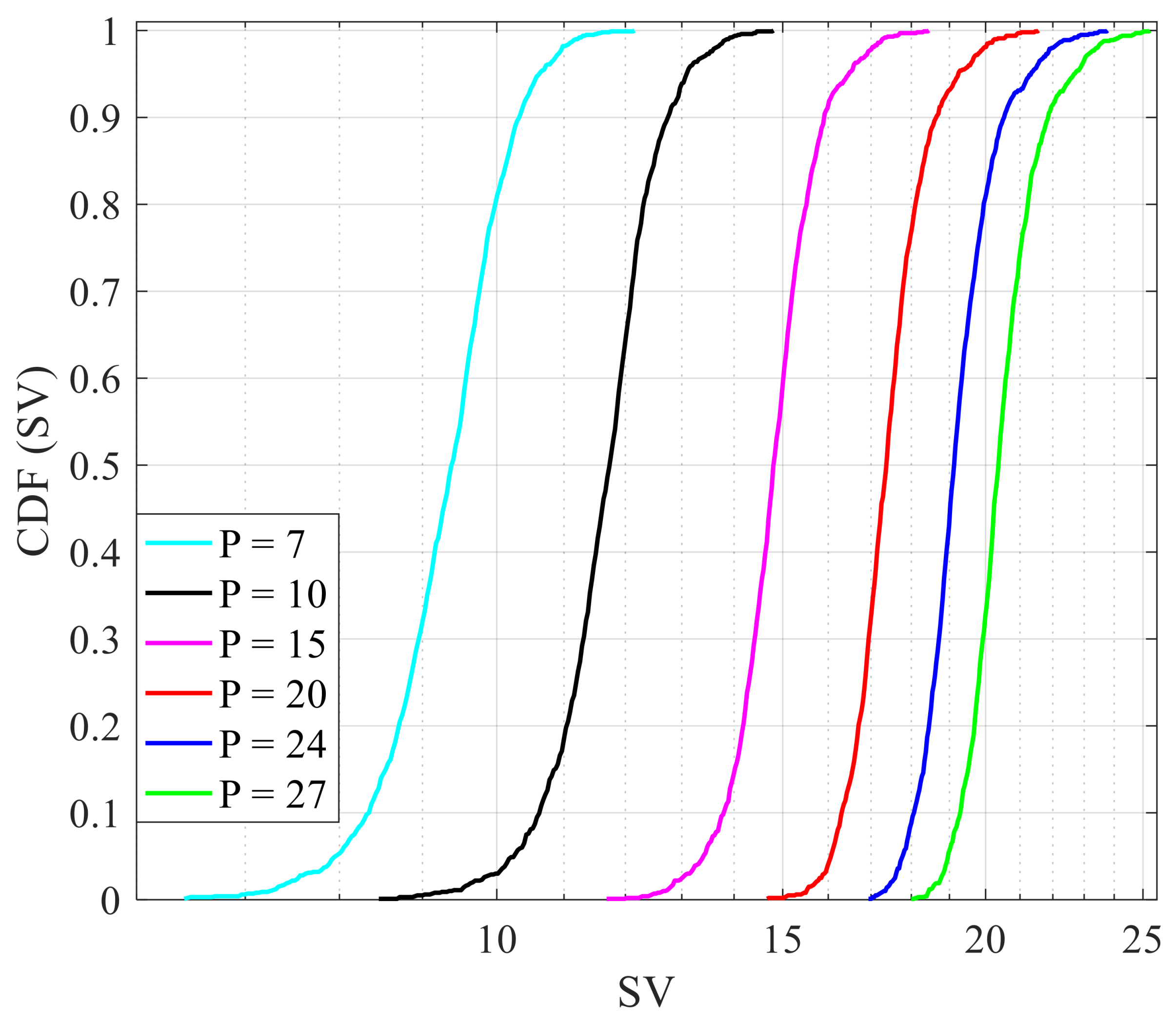
4.1. Estimation Accuracy Analysis
4.2. The Computational Complexity Analysis
5. Numerical Simulations and Discussions
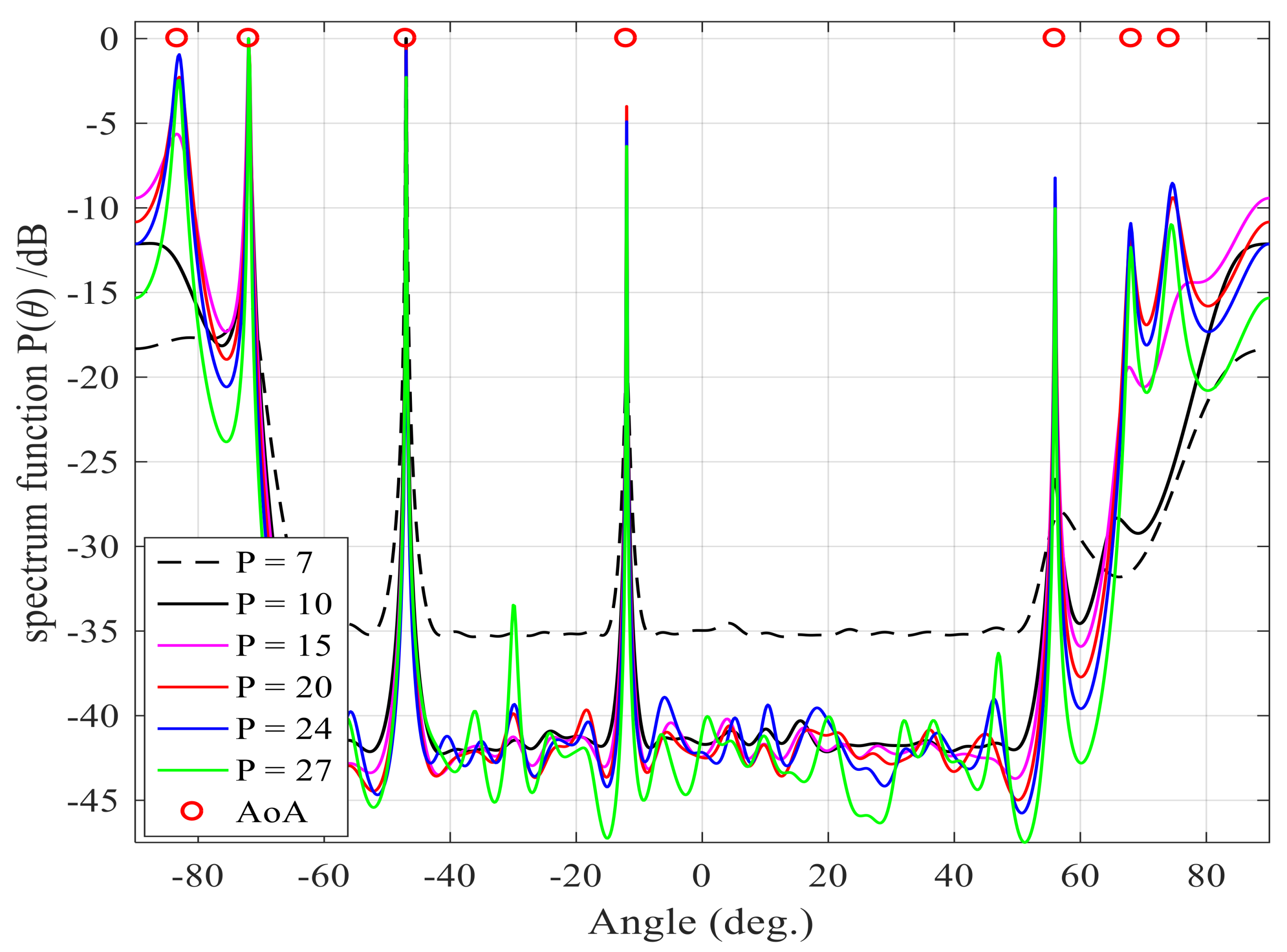
5.1. Intercomparison: Numerical Example
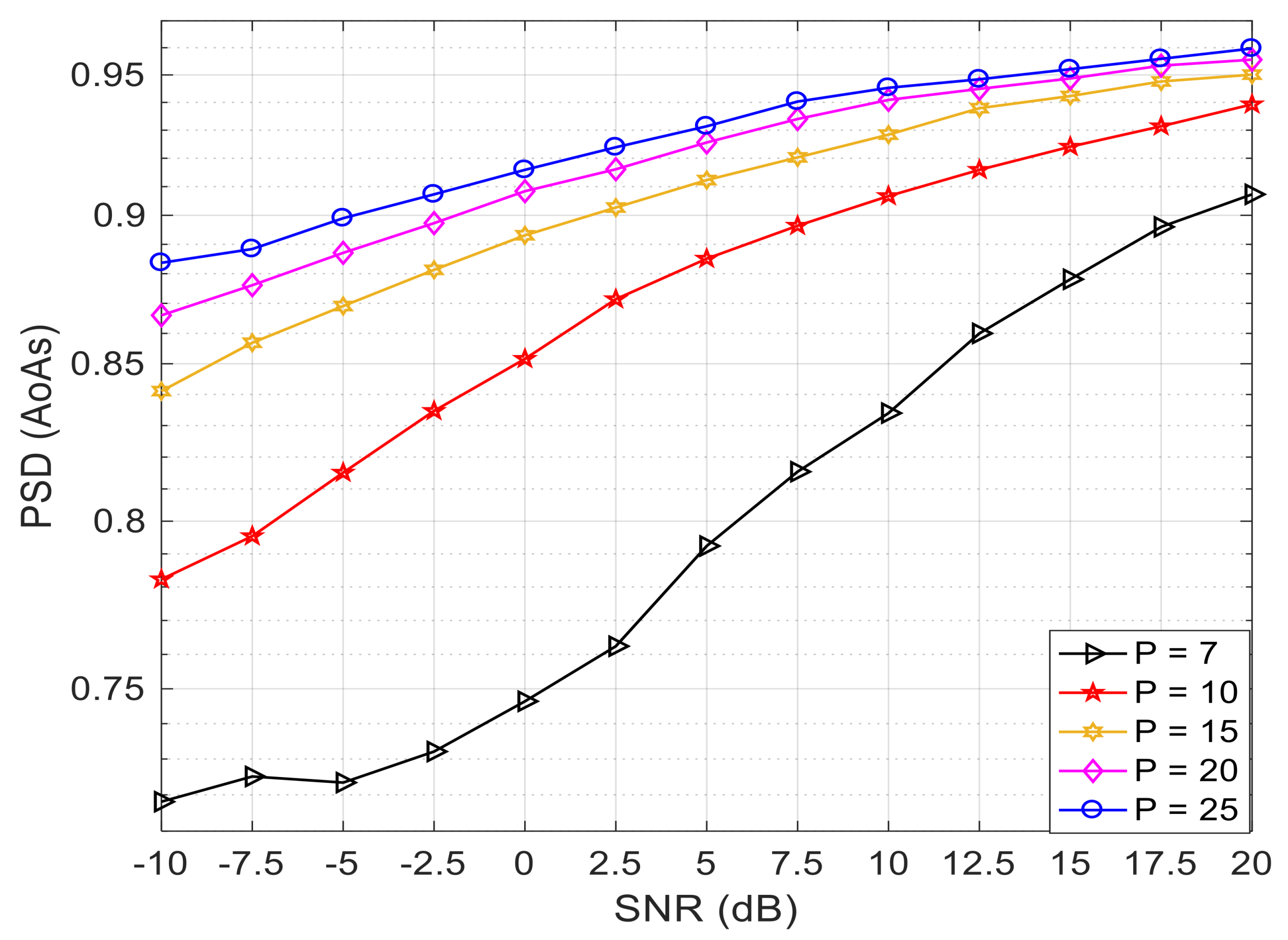
5.2. The Performance Comparison Based on the Various Signal-to-Noise Ratios (SNRs)
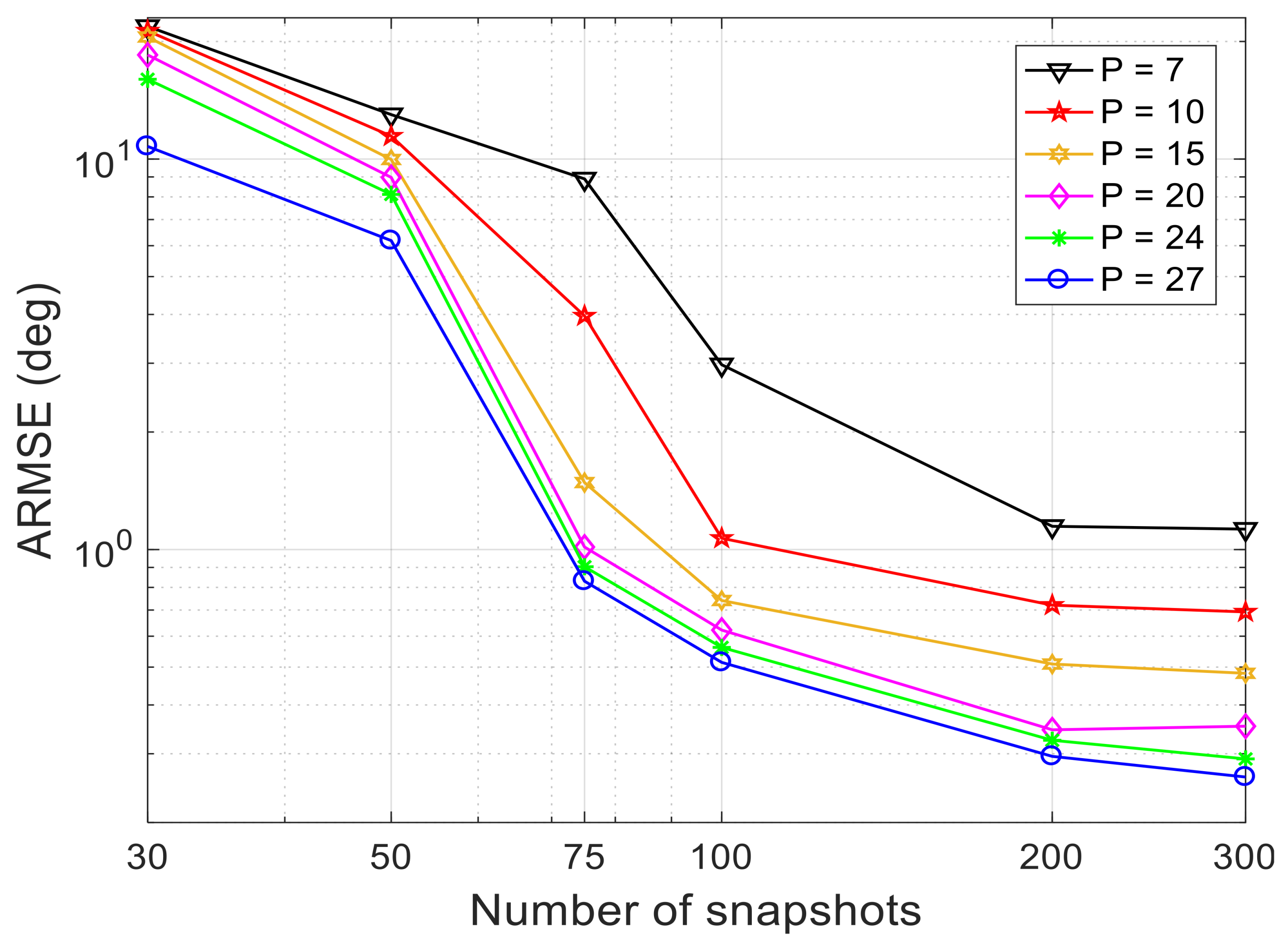
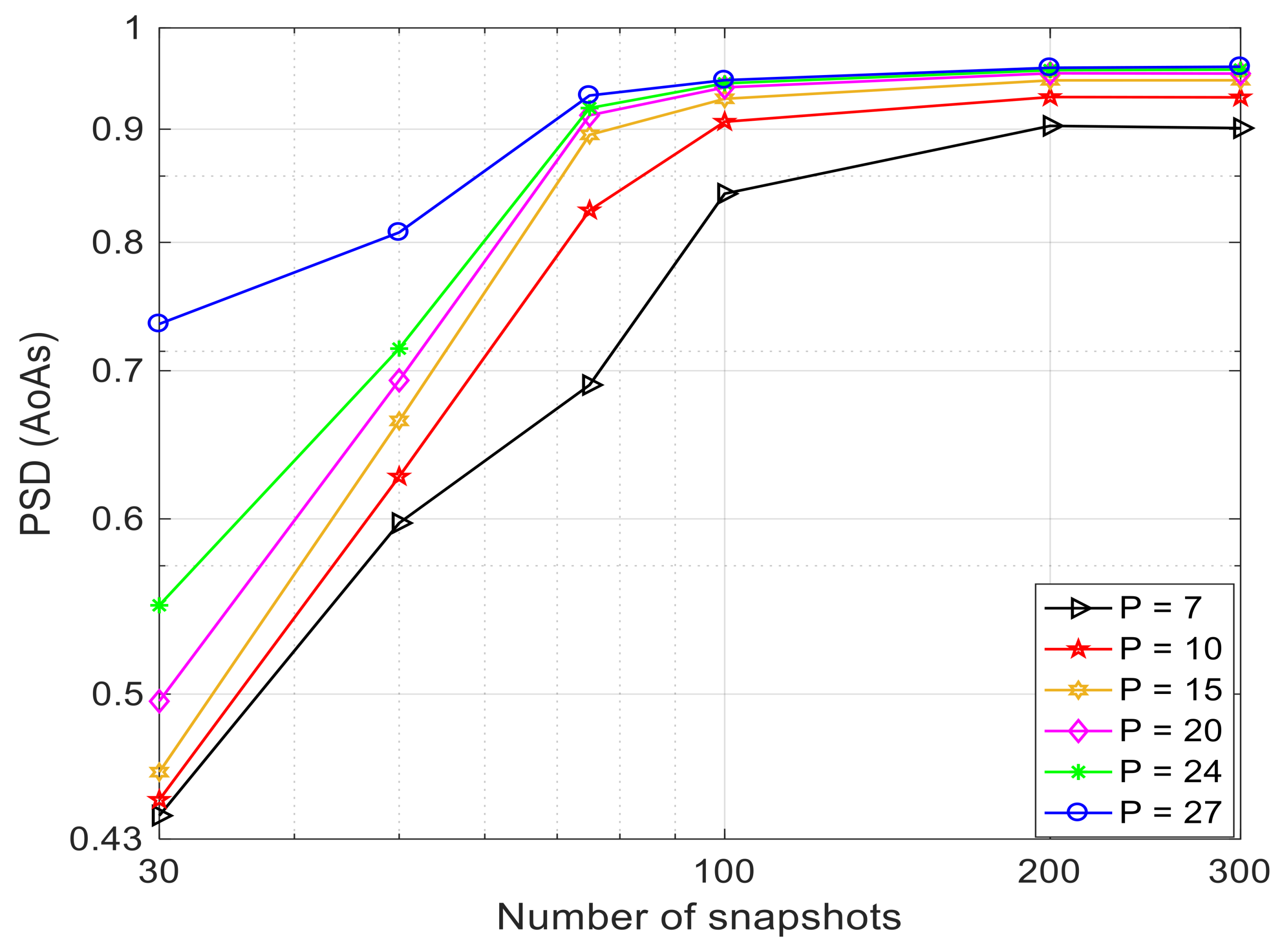
5.3. Performance Comparison Based on Different Numbers of Snapshots
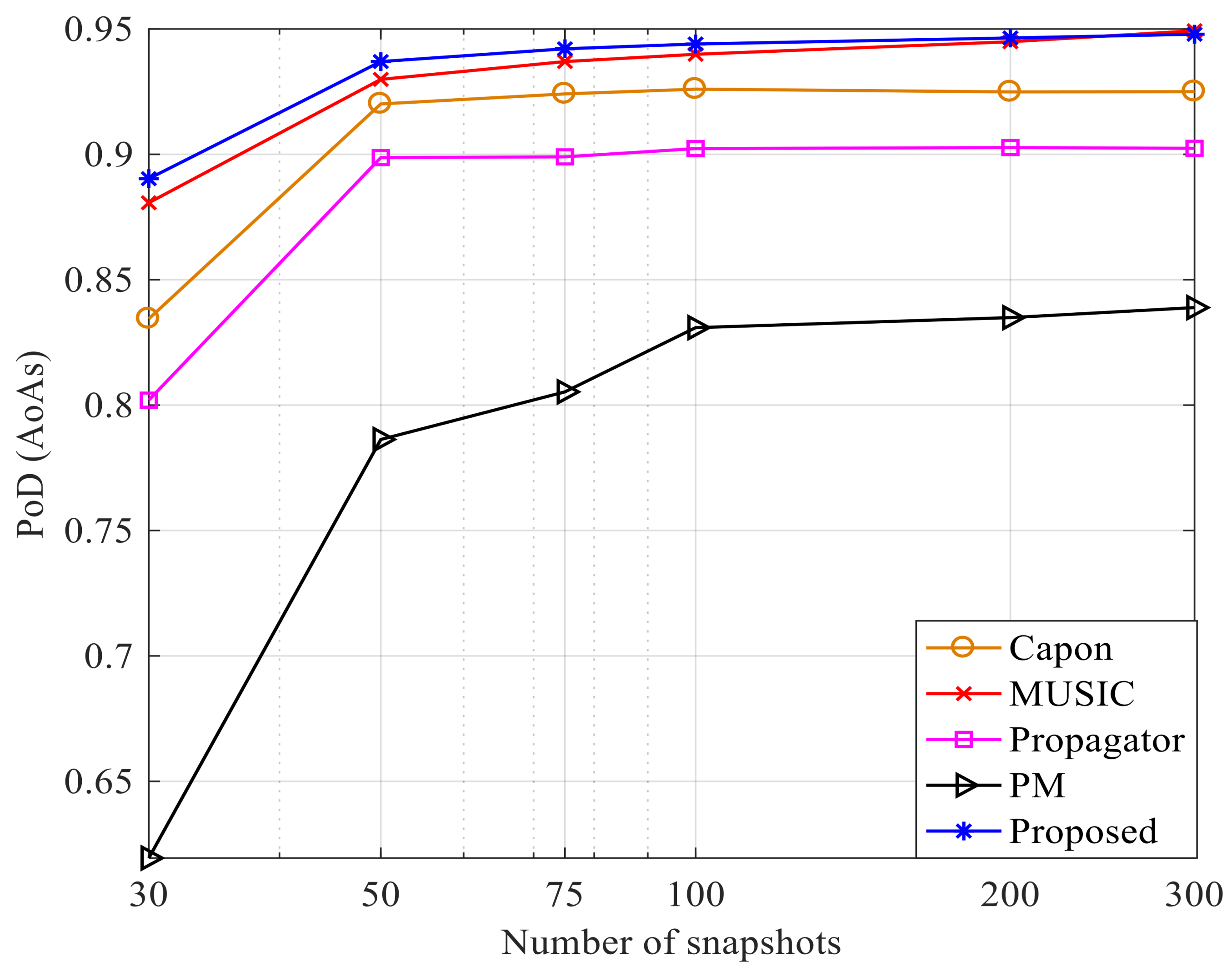
5.4. Comparison with Other AoA Methods
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wan, L.; Han, G.; Shu, L.; Chan, S.; Zhu, T. The Application of DOA Estimation Approach in Patient Tracking Systems with High Patient Density. IEEE Trans. Ind. Inf. 2016, 12, 353–2364. [Google Scholar] [CrossRef]
- Cremer, M.; Dettmar, U.; Hudasch, C.; Kronberger, R.; Lerche, R.; Pervez, A. Localization of Passive UHF RFID Tags Using the AoAct Transmitter Beamforming Technique. IEEE Sens. J. 2016, 16, 1762–1771. [Google Scholar] [CrossRef]
- Hameed, K.W.; Al-Sadoon, M.; Jones, S.M.R.; Noras, J.M.; Dama, Y.A.S.; Masri, A.; Abd-Alhameed, R.A. Low complexity single snapshot DoA method. In Proceedings of the 2017 Internet Technologies and Applications (ITA), Wrexham, UK, 12–15 September 2017; pp. 244–248. [Google Scholar]
- Zhang, X.; Xu, D. Angle estimation in MIMO radar using reduced-dimension capon. Electron. Lett. 2010, 46, 860–861. [Google Scholar] [CrossRef]
- Kabir, A.L.; Saha, R.; Khan, M.A.; Sohul, M.M. Locating Mobile Station Using Joint TOA/AOA. In Proceedings of the 4th International Conference on Ubiquitous Information Technologies & Applications, Fukuoka, Japan, 20–22 December 2009; pp. 1–6. [Google Scholar]
- Raghavan, V.; Cezanne, J.; Subramanian, S.; Sampath, A.; Koymen, O. Beamforming Tradeoffs for Initial UE Discovery in Millimeter-Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 543–559. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R. Millimeter Wave MIMO With Lens Antenna Array: A New Path Division Multiplexing Paradigm. IEEE Trans. Commun. 2016, 64, 1557–1571. [Google Scholar] [CrossRef]
- Al-Sadoon, M.A.G.; Abdullah, A.S.; Ali, R.S.; Tu, Y.; Abd-Alhameed, R.A.; Jones, S.M.R.; Noras, J.M. The effects of mutual coupling within antenna arrays on angle of arrival methods. In Proceedings of the 2016 Loughborough Antennas & Propagation Conference (LAPC), Loughborough, UK, 14–15 November 2016; pp. 1–5. [Google Scholar]
- Al-Sadoon, M.; Danjuma, I.; Abdussalam, F.; Elfergani, I.; Rodriguez, J.; Abd-Alhameed, R.; Jones, S.M.R. Dual-band compact-size antenna array for angle of arrival estimation. In Proceedings of the Loughborough Antennas & Propagation Conference (LAPC 2017), Loughborough, UK, 13–14 November 2017. [Google Scholar]
- Al-Sadoon, M.A.G.; Asif, R.; Obeidat, H.; Bin-Melha, M.S.; Obeidat, H.; Zweid, A.; Abd-Alhameed, R.A. Low Complexity Antenna Array DOA System for Localization Applications. In Proceedings of the 6th International Conference on Wireless Networks and Mobile Communications 2018 (WINCOM), Marrakesh, Morocco, 16–19 October 2018. [Google Scholar]
- Bartlett, M. An Introduction to Stochastic Processes with Special References to Methods and Applications; Cambridge University Press: New York, NY, USA, 1961. [Google Scholar]
- Capon, J. High-Resolution Frequency-Wavenumber Spectrum Analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Gross, F. Smart Antennas for Wireless Communications; McGraw-Hill Companies Inc.: New York, NY, USA, 2005. [Google Scholar]
- Burg, J.P. The Relationship between Maximum Entropy Spectra and Maximum Likelihood Spectra. Geophysics 1972, 37, 375–376. [Google Scholar] [CrossRef]
- Pisarenko, V.F. The Retrieval of Harmonics from a Covariance Function. Geophys. J. R. Astrono. Soc. 1973, 33, 347–366. [Google Scholar] [CrossRef]
- Wax, M.; Tie-Jun, S.; Kailath, T. Spatio-temporal spectral analysis by eigenstructure methods. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 817–827. [Google Scholar] [CrossRef]
- Al-Sadoon, M.A.G.; Hameed, K.W.; Zweid, A.; Jones, S.; Abd-Alhameed, R.A.; Abusitta, M. Analysis and investigation the estimation accuracy and reliability of Pisarenko Harmonic Decomposition algorithm. In Proceedings of the 2017 Internet Technologies and Applications (ITA), Wrexham, UK, 12–15 September 2017; pp. 249–253. [Google Scholar]
- Al-Sadoon, M.; Bin-Melha, M.; Zubo, R.; Asharaa, A.; Asif, R.; Shepherd, S. Partial Noise Subspace Method for DOA Estimation Applications. In Proceedings of the 2018 IEEE 2nd International Conference for Engineering, Technology and Sciences of Al-Kitab (2ndICETS-2018), Karkuk, Iraq, 4–6 December 2018. [Google Scholar]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Reddi, S.S. Multiple Source Location-A Digital Approach. IEEE Trans. Aerosp. Electron. Syst. 1979, AES-15, 95–105. [Google Scholar] [CrossRef]
- Barabell, A. Improving the resolution performance of eigenstructure-based direction-finding algorithms. In Proceedings of the ICASSP ’83. IEEE International Conference on Acoustics, Speech, and Signal Processing, Boston, MA, USA, 14–16 April 1983; pp. 336–339. [Google Scholar]
- Roy, R.; Kailath, T. ESPRIT-Estimation of Signal Parameters via Rotational Invariance Techniques. IEEE Trans. ASSP 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Munier, J.; Delisle, G.Y. Spatial analysis using new properties of the cross-spectral matrix. IEEE Trans. Signal Process. 1991, 39, 746–749. [Google Scholar] [CrossRef]
- Marcos, S.; Marsal, A.; Benidir, M. The propagator method for source bearing estimation. Signal Process. 1995, 42, 121–138. [Google Scholar] [CrossRef]
- Fleury, B.H.; Dahlhaus, D.; Heddergott, R.; Tschudin, M. Wideband angle of arrival estimation using the SAGE algorithm. In Proceedings of the ISSSTA’95 International Symposium on Spread Spectrum Techniques and Applications, Mainz, Germany, 25 September 1996; Volume 1, pp. 79–85. [Google Scholar]
- Fleury, B.H.; Tschudin, M.; Heddergott, R.; Dahlhaus, D.; Pedersen, K.I. Channel parameter estimation in mobile radio environments using the SAGE algorithm. IEEE J. Sel. Areas Commun. 1999, 17, 434–450. [Google Scholar] [CrossRef]
- Yilmazer, N.; Koh, J.; Sarkar, T.K. Utilization of a unitary transform for efficient computation in the matrix pencil method to find the direction of arrival. IEEE Trans. Antennas Propag. 2006, 54, 175–181. [Google Scholar] [CrossRef]
- Yan, F.G.; Jin, T.; Jin, M.; Shen, Y. Subspace-based direction-of-arrival estimation using centro-symmetrical arrays. Electron. Lett. 2016, 52, 1895–1896. [Google Scholar] [CrossRef]
- Yan, F.G.; Shen, Y.; Jin, M. Fast DOA estimation based on a split subspace decomposition on the array covariance matrix. Signal Process. 2015, 115, 1–8. [Google Scholar] [CrossRef]
- Yan, F.G.; Cao, B.; Liu, S.; Jin, M.; Shen, Y. Reduced-complexity direction of arrival estimation with centro-symmetrical arrays and Its performance analysis. Signal Process. 2018, 142, 388–397. [Google Scholar] [CrossRef]
- Jiang, G.; Mao, X.; Liu, Y. Direction-of-arrival estimation for uniform circular arrays under small sample size. J. Syst. Eng. Electron. 2016, 27, 1142–1150. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Zheng, G.; Feng, C.; Tang, J. Improved DOA estimation algorithm for co-prime linear arrays using root-MUSIC algorithm. Electron. Lett. 2017, 53, 1277–1279. [Google Scholar] [CrossRef]
- Yan, F.G.; Wang, J.; Liu, S.; Shen, Y.; Jin, M. Reduced-Complexity Direction of Arrival Estimation Using Real-Valued Computation with Arbitrary Array Configurations. Int. J. Antennas Propag. 2018, 2018, 3284619. [Google Scholar] [CrossRef]
- Al-Sadoon, M.A.; Abdullah, A.S.; Ali, R.S.; Al-Abdullah, A.S.; Abd-Alhameed, R.A.; Jones, S.M.R.; Noras, J.M. New and Less Complex Approach to Estimate Angles of Arrival. In Proceedings of the 8th International Conference on Wireless and Satellite Services, WiSATS 2016, Cardiff, UK, 19–20 September 2016; pp. 18–27. [Google Scholar]
- Al-Sadoon, M.; Abduljabbar, N.; Ali, N.; Asif, R.; Zweid, A.; Alhassan, H.; Noras, J.M.; Abd-Alhameed, R.A. A More Efficient AOA Method for 2D and 3D Direction Estimation with Arbitrary Antenna Array Geometry. In Proceedings of the 8th International Conference on Broadband Communications, Networks and Systems, Faro, Portugal, 19–20 September 2018; pp. 419–430. [Google Scholar]
- Al-Sadoon, M.A.; Ali, N.T.; Dama, Y.; Zuid, A.; Jones, S.M.R.; Abd-Alhameed, R.A.; Noras, J.M. A New Low Complexity Angle of Arrival Algorithm for 1D and 2D Direction Estimation in MIMO Smart Antenna Systems. Sensors 2017, 17, 2631. [Google Scholar] [CrossRef] [PubMed]
- Gross, F. Smart Antennas with Matlab: Principles and Applications in Wireless Communication; McGraw-Hill Professional: New York, NY, USA, 2015. [Google Scholar]
- Si, W.; Zeng, F.; Hou, C.; Peng, Z. A sparse-based off-grid DOA estimation method for coprime arrays. Sensors 2018, 18, 3025. [Google Scholar] [CrossRef] [PubMed]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Deshpande, A.; Rademacher, L. Efficient volume sampling for row/column subset selection. In Proceedings of the 2010 IEEE 51st Annual Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 23–26 October 2010; pp. 329–338. [Google Scholar]
- Mestre, X. Improved estimation of eigenvalues and eigenvectors of covariance matrices using their sample estimates. IEEE Trans. Inf. Theory 2008, 54, 5113–5129. [Google Scholar] [CrossRef]
- Deshpande, A.; Rademacher, L.; Vempala, S.; Wang, G. Matrix approximation and projective clustering via volume sampling. In Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithm, Miami, Florida, 22–26 January 2006; pp. 1117–1126. [Google Scholar]
- Yeh, C.C. Projection approach to bearing estimations. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1347–1349. [Google Scholar]
- Godara, L.C. Application of antenna arrays to mobile communications. II. Beam-forming and direction-of-arrival considerations. Proc. IEEE 1997, 85, 1195–1245. [Google Scholar] [CrossRef]


| Input: | The measured data matrix, , with M receivers, N number of measurements, L incident signals. |
| Output: | The estimated AoAs. |
| Step 1: | Calculate the CM using (25) |
| Step 2: | Sample matrix based on a specific P as follows: |
| Step 3: | Construct the projection matrix (i.e., ) using (32) |
| Step 4: | Construct the pseudo spectrum using (33) |
| Step 5: | Find the locations of the produced peaks to determine the AoAs |
| Algorithm | The Needed Computational Operations |
|---|---|
| Capon | O (M3 + M2) |
| MUSIC | O (M3 + M2) |
| Propagator | O (M2 L + M2) |
| Original PM | O (M2 L + M2) |
| Proposed | O (M2 P + M2) |
| No. of Sampled Columns | The Computational Load |
|---|---|
| P = 7 | O (3.3 × 105) |
| P = 10 | O (3.33 × 105) |
| P = 15 | O (3.37 × 105) |
| P = 20 | O (3.42 × 105) |
| P = 24 | O (3.45 × 105) |
| P = 27 | O (3.48 × 105) |
| Algorithm | Number of Multiplications |
|---|---|
| Capon | O (3.5 × 105) |
| MUSIC | O (3.5 × 105) |
| Propagator | O (3.3 × 105) |
| Original PM | O (3.3 × 105) |
| Proposed | O (3.4 × 105) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sadoon, M.A.G.; Abd-Alhameed, R.A.; McEwan, N.J. The Impact of the Covariance Matrix Sampling on the Angle of Arrival Estimation Accuracy. Inventions 2019, 4, 43. https://doi.org/10.3390/inventions4030043
Al-Sadoon MAG, Abd-Alhameed RA, McEwan NJ. The Impact of the Covariance Matrix Sampling on the Angle of Arrival Estimation Accuracy. Inventions. 2019; 4(3):43. https://doi.org/10.3390/inventions4030043
Chicago/Turabian StyleAl-Sadoon, Mohammed A. G., Raed A. Abd-Alhameed, and Neil J. McEwan. 2019. "The Impact of the Covariance Matrix Sampling on the Angle of Arrival Estimation Accuracy" Inventions 4, no. 3: 43. https://doi.org/10.3390/inventions4030043
APA StyleAl-Sadoon, M. A. G., Abd-Alhameed, R. A., & McEwan, N. J. (2019). The Impact of the Covariance Matrix Sampling on the Angle of Arrival Estimation Accuracy. Inventions, 4(3), 43. https://doi.org/10.3390/inventions4030043






