Abstract
This paper presents a deep neural network (DNN)-embedded mixed-integer linear programming (MILP) model for fault prediction and production optimization in tablet pressing machines. The DNN predicts the probability of failures during the tablet pressing process by analyzing key operational parameters such as pressure, temperature, humidity, speed, vibration, and number of maintenance cycles. The MILP model optimizes the temperature and humidity settings, production schedules, and maintenance planning to maximize total profit while minimizing penalties for fault pressing, energy consumption, and maintenance costs. To integrate DNN into the MILP framework, Big-M constraints are applied to linearize the Rectified Linear Unit (ReLU) activation functions, ensuring solvability and global optimality of the optimization problem. A case study using the Kaggle dataset demonstrates the model’s ability to dynamically adjust production and maintenance schedules, enhancing profitability and resource utilization under fluctuating electricity prices. Sensitivity analyses further highlight the model’s robustness to variations in maintenance and energy costs, striking an effective balance between cost efficiency and production quality, which makes it a promising solution for intelligent scheduling and optimization in complex manufacturing environments.
1. Introduction
The rapid evolution of manufacturing industries has underscored the necessity for flexible, reliable, and cost-effective systems capable of adapting to dynamic production demands. Researchers and practitioners have increasingly turned to advanced technologies to address the challenges posed by complex interrelations and stringent operational constraints. Among these, artificial intelligence (AI) [1], optimization theory (OT) [2], and predictive maintenance (PdM) skills [3] have emerged as key methods for minimizing downtime and enhancing operational efficiency.
Artificial intelligence, especially deep learning, has significantly transformed modern manufacturing by enabling fault prediction, process monitoring, and real-time decision making [4]. Deep neural networks (DNNs) are particularly effective at capturing nonlinear relationships and uncovering hidden patterns in production data, offering valuable insights into operational dynamics. However, although DNNs are good at predictions, they have difficulty meeting strict constraints and achieving optimal solutions, which are essential in high-risk industries [5]. In contrast, mixed-integer linear programming (MILP) has been a key approach in industrial optimization, excelling in problems involving discrete decision variables and stringent operational constraints. Nevertheless, MILP models heavily depend on precise mathematical representations of system behavior, which can be challenging when process dynamics are complex or poorly understood [6].
To bridge the gap between data-driven insights and mathematical optimization, this study proposes an innovative framework that integrates DNNs into MILP models, offering an intelligent solution for production scheduling and operational optimization. By combining the predictive power of DNNs with the optimization strengths of MILP, the approach ensures global optimality while satisfying strict operational constraints. While applicable to various manufacturing contexts, this paper demonstrates its effectiveness through a case study of tablet pressing machines, a typical example of highly constrained, mission-critical production processes.
The integration of MILP and a DNN leverages MILP’s global optimization and the DNN’s capability to recognize complex patterns, ensuring robust and reliable solutions for industrial challenges. Building upon this foundation, this paper makes the following key contributions:
(1): Development of a DNN Model for Fault Prediction: A DNN-based fault prediction model is developed for tablet pressing machines, utilizing key parameters from real-world production environments to enhance predictive accuracy and enable proactive maintenance.
(2): DNN-MILP Integration via ReLU Linearization: The DNN is seamlessly integrated into the MILP framework by linearizing ReLU activation functions using Big-M constraints, ensuring both model solvability and solution precision.
(3): Multi-level Scheduling Optimization Methodology and Cost Analysis: The scheduling methodology integrates production scheduling, fault prediction, maintenance planning, and energy management for optimal resource allocation. A comprehensive cost analysis framework evaluates the impact of maintenance, energy consumption, and production failures on profitability, balancing cost efficiency and production quality.
2. Literature Review
Accurate fault prediction is crucial for reducing unplanned downtime, optimizing maintenance, and improving efficiency in production. Traditional methods, which rely on empirical knowledge or physical models, often struggle with real-time accuracy in complex, high-dimensional environments. Recent advancements in AI have addressed these challenges by effectively handling nonlinear and multidimensional data. For example, [7] integrated DNNs with LSTM networks to analyze historical data, significantly improving fault classification and Remaining Useful Life (RUL) prediction. Similarly, [8] proposed a DNN-based low-latency Intrusion Detection and Prevention System (IDPS) with a distributed architecture enabled real-time monitoring and efficient classification, while enhancing security and response speed in mission-critical applications. Reference [9] addresses task randomness and dynamic resource changes in smart manufacturing by proposing a deep reinforcement learning (DRL)-based optimization method for dynamic scheduling. This method builds a DSSM mathematical model to handle nonlinear scheduling relationships and improves training stability using a dual-network architecture with a prediction and a target network. Experimental results demonstrate its effectiveness in optimizing task allocation and improving scheduling efficiency.
MILP is a widely recognized and versatile optimization method that can address multi-constraint, multi-objective problems while ensuring global optimality. Its applications span various domains, including manufacturing [10,11,12], fleet optimization [13,14], and energy systems [15]. For instance, [10] employed MILP to optimize production, inventory, and transportation decisions within industrial supply chains, leading to substantial cost reductions. Similarly, [13] proposed an MILP-based optimization model to maximize operator profit by optimizing order selection, fleet rebalancing, and charging/discharging strategies for autonomous electric vehicle fleets. However, the effectiveness of MILP approaches is inherently dependent on the accuracy of input data and their high computational complexity remains a significant challenge, particularly in large-scale applications.
Heuristic algorithms play a crucial role in the industrial scheduling, particularly in addressing complex and dynamic production environments by providing efficient optimization solutions. In [16], the authors proposed a Hyper-Heuristics (HH) approach to tackle scheduling challenges in the pharmaceutical industry, enabling production tasks to autonomously adjust scheduling strategies in response to task variations and resource fluctuations. By comparing 168 scheduling rules, this method effectively optimized the mean completion time (MCT), enhancing both production efficiency and system adaptability. Reference [17] proposes a hybrid metaheuristic algorithm based on MILP and Tabu Search (TS) for scheduling optimization in manufacturing systems. By integrating Simulated Annealing (SA) and Variable Neighborhood Search (VNS), the method enhances search efficiency and reduces production costs. Experimental results demonstrate that TS-SA outperforms traditional approaches in manufacturing scheduling optimization, effectively minimizing inventory costs. Although heuristic algorithms can quickly solve complex optimization problems, these methods tend to get stuck in local optimal, and their performance depends heavily on parameters and problem characteristics. Therefore, in practical applications, it is necessary to balance efficiency and accuracy while further improving the algorithms.
The combination of DNNs and MILP has gained attention in energy management and decision making. The authors of [18] formulated DNNs as 0-1 MILP problems by modeling ReLU activation constraints, enabling feature visualization and adversarial example generation but increasing computational complexity. The authors of [19] applied a similar approach to verify quantized deep neural networks (QDNNs) for safety-critical systems. In energy management, Ref. [20] proposed a hybrid method for optimizing residential HVAC systems, using MILP to generate optimal historical data for training DNNs. This approach outperforms predictive MILP, PSO, and DDPG in energy optimization and temperature control while reducing computation time, offering a practical solution for real-time decision making.
In recent years, the application of machine learning in pharmaceutical equipment has increasingly become a research focus. However, the existing studies primarily concentrate on fault prediction and have not achieved deep integration with optimization systems. For example, the study in [21] proposed a machine learning-based predictive calibration fault detection method to optimize the calibration management of tablet press machines to reduce the impact of pressure, speed, weight control, and thickness consistency deviations on tablet quality. This study employed Random Forest (RF), Support Vector Machine (SVM), and Neural Networks (NNs) for fault prediction, with experimental results indicating that the neural network model achieved the highest detection accuracy of 94.1%. However, this method mainly focuses on fault prediction, with limitations in computational efficiency, and does not further explore how to utilize prediction results to optimize production scheduling. Similarly, the study in [22] proposed a Transformer-based predictive maintenance model, ManuTrans, for fault prediction in pharmaceutical equipment. The results showed that this method is better than LSTM, SVM, and ARIMA in terms of fault prediction accuracy. However, the model still has limited generalization capability and high computational. Moreover, it does not explore leveraging prediction results to optimize production scheduling and maintenance strategies dynamically.
To the best of the authors’ knowledge, no existing research has integrated artificial intelligence with optimization methods by combining predictive maintenance with optimization strategies to enable fault detection and dynamic optimization of equipment. This study aims to bridge this gap by leveraging the capability of DNNs to process large-scale datasets and the advantage of MILP in handling multi-constraint optimization. The proposed approach is applied to the production scheduling optimization of tablet press machines, ensuring stable equipment operation while maximizing production efficiency and reducing operational costs.
3. Methodology
This section details the implementation and evaluation of the proposed DNN-embedded MILP framework. The process includes training the DNN for fault prediction, embedding its outputs into the MILP model, and performing optimization across various operational scenarios. The evaluation focuses on prediction performance and production scheduling, ensuring the robustness of the model under varying conditions.
3.1. Research Problem Statement
In the pharmaceutical industry, tablet press machines can be classified into single and multi-station tablet presses. The former is primarily used for small-scale production and falls outside the scope of this study. In contrast, multi-station tablet press machines are highly suitable for large-scale production, feature a high level of automation, and have been widely adopted in pharmaceutical manufacturing [23].
The DNN component predicts the success or failure of the tablet press machine by analyzing key operational factors, including pressure (pressure levels within the machine during operation, in kN), temperature (temperature variations in the environment, in °C), speed (rotational speed of the machine, in ), vibration (vibration levels in mm/s), humidity (humidity variations in the environment, in ), and number of maintenance cycles (number of maintenance completed by the machine).
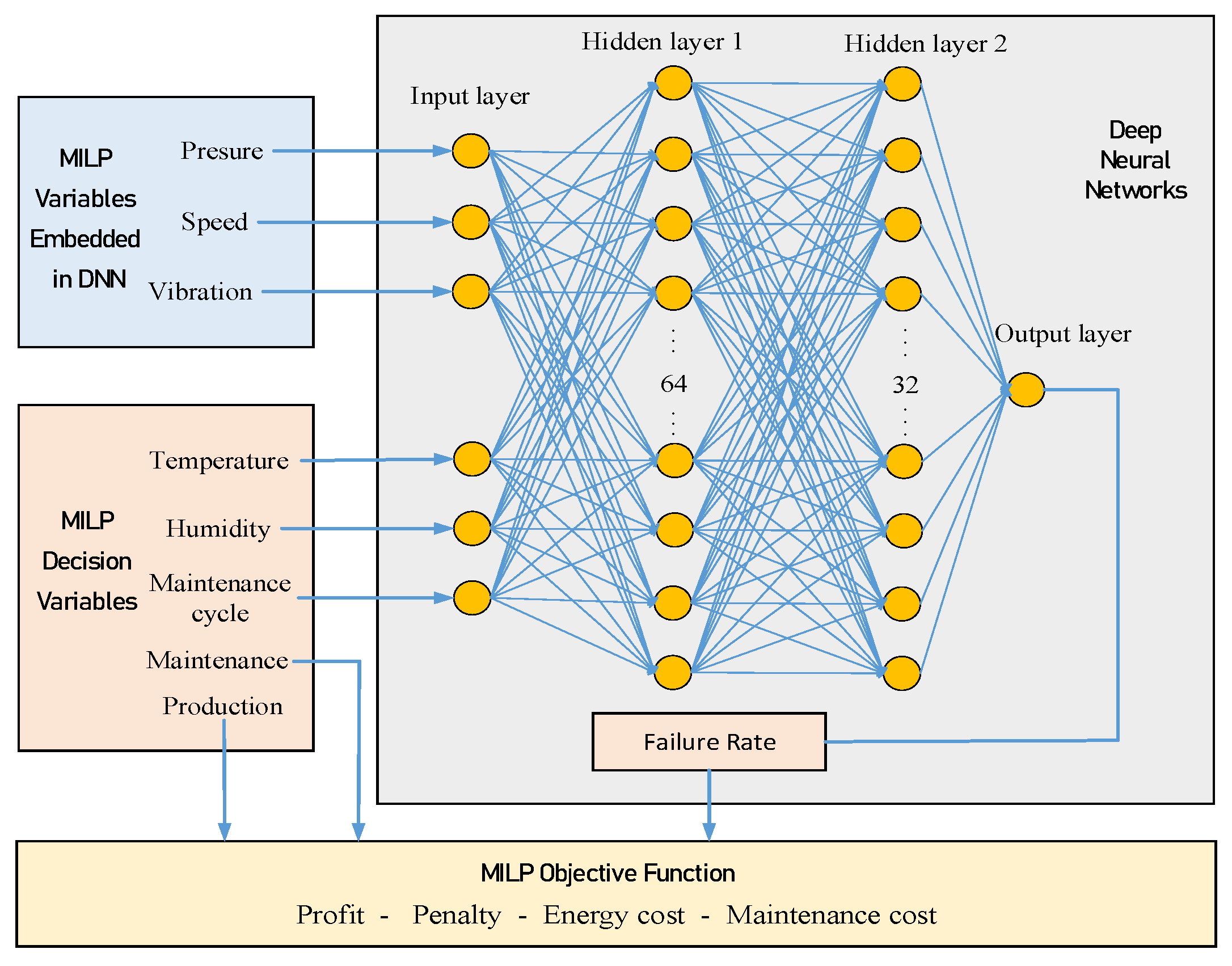
The MILP model optimizes machine operations by determining the hourly temperature and humidity settings alongside maintenance schedules to maximize overall profitability. This profitability metric accounts for revenue (in USD),calculated as the product of the number of successfully tableted units per time interval and the unit revenue per tablet; penalties (in USD), determined by the product of the number of failed tableted units per time interval and the unit penalty per tablet; and energy costs (in USD), which include expenses associated with both air conditioning (for temperature and humidity regulation) and machine operations (considering pressure, speed, vibration, and the quantity of tablets produced), with energy costs calculated as the product of consumed energy and real-time electricity prices. Figure 1 illustrates the comprehensive structure of the proposed model, and the nomenclature is summarized in Table 1.
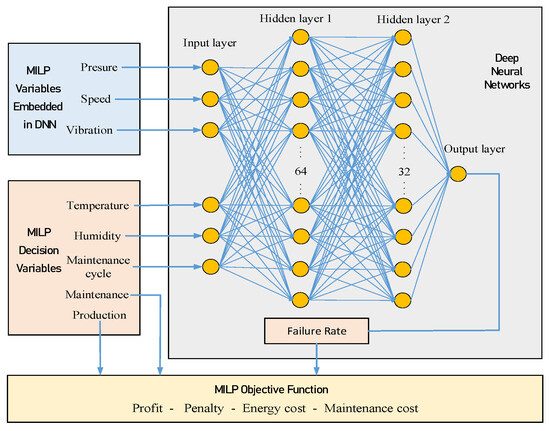
Figure 1.
The overall structure of the DNN-embedded MILP model used for fault prediction and production optimization in tablet press equipment.

Table 1.
Nomenclature of the model.
3.2. Model
3.2.1. DNN Model for Fault Prediction
The DNN serves as a predictive tool for estimating the likelihood of failure during the tablet pressing process, leveraging key machine parameters such as pressure (P), temperature (), speed (S), vibration (V), humidity (), and the number of maintenance cycles (). As an integral component of the proposed framework, the DNN provides critical inputs for the MILP optimization model, enabling more informed decision making. The design of the DNN comprises the following components:
- Input Feature Selection: The DNN model utilizes key operational parameters as inputs, including pressure (P), temperature (), speed (S), vibration (V), humidity (), and number of maintenance cycles (). These features are identified based on historical data as critical factors influencing the success rate of tablet pressing.
- Model Architecture: The DNN consists of an input layer, two hidden layers, and an output layer. Hidden layer 1 contains 64 neurons that receive data from the input layer through full connection and extract the features of the data. Hidden layer 2 contains 32 neurons and uses Rectified Linear Unit (ReLU) as the activation function to pass the extracted features to the output layer.
- ReLU activation constraints: In this paper, to integrate ReLU into the MILP framework, binary variables are introduced to control the activation state, and Big-M constraints are used to encode the ReLU logic. This transforms the nonlinear characteristics of the original ReLU function into constraints that can be incorporated into the optimization problem. By approximating or replacing the nonlinearity of ReLU with linear constraints, this approach not only ensures the solvability of the optimization problem but also retains the expressive power of the original nonlinear model [24,25].
- Training Data and Preprocessing: Historical operational data are used for training the DNN, with the weights () and biases () being extracted during the process. Input features are scaled to the range using a Min–Max scaler to mitigate discrepancies in feature scales and enhance convergence speed. The model is trained using a cross-entropy loss function and the Adam optimizer, ensuring robust predictive performance and computational efficiency.
- Output and Role: The output layer predicts the failure probability () for each time interval. This probability dynamically influences the MILP-based scheduling and maintenance optimization to achieve cost-effectiveness and operational efficiency.
The ReLU activation constraints and the input are related through the following four constraints. These constraints ensure that the activation logic of ReLU can be effectively transformed into solvable constraints in the optimization problem.
First, Equation (1) indicates that when , the output equals the input , while when , the output can be a large constant M. Equation (2) ensures that when ReLU is activated, the output is at least equal to the input . Next, Equation (3) guarantees that when , the output is zero, and when , the output can be any non-negative value. Finally, Equation (4) ensures that the output is always non-negative. These constraints, by introducing binary variables and a large constant M, transform the nonlinear characteristics of ReLU into linear constraints, making it solvable in optimization problems.
3.2.2. MILP Model for Optimization
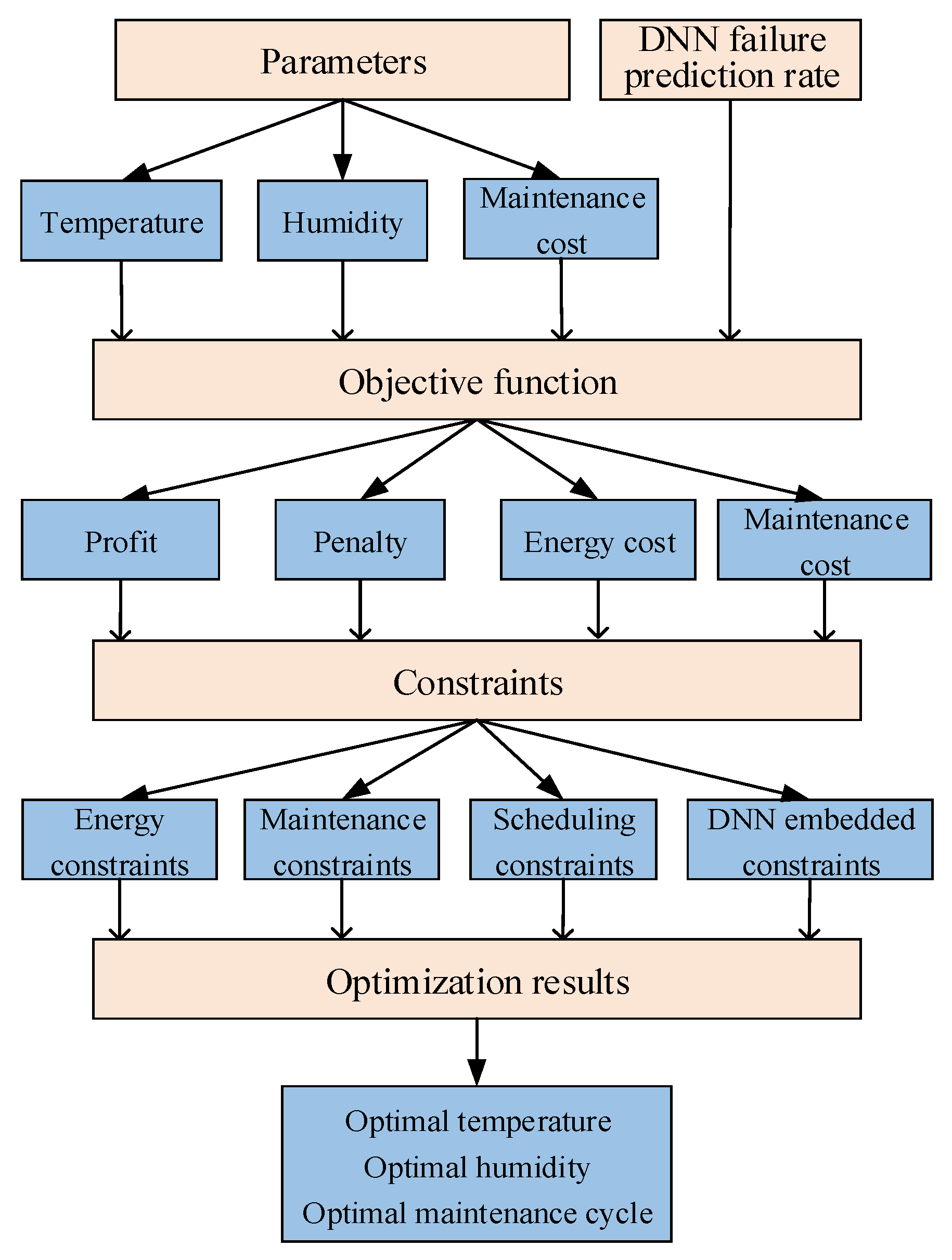
The MILP model is formulated to optimize tablet pressing machine operations by determining the temperature and humidity levels (, ), adjusting the tablet pressing amount (), and scheduling maintenance (). The objective is to maximize total profit by balancing production efficiency, maintenance costs, and energy consumption while ensuring compliance with operational constraints. The flowchart of Figure 2 illustrates the MILP optimization framework.
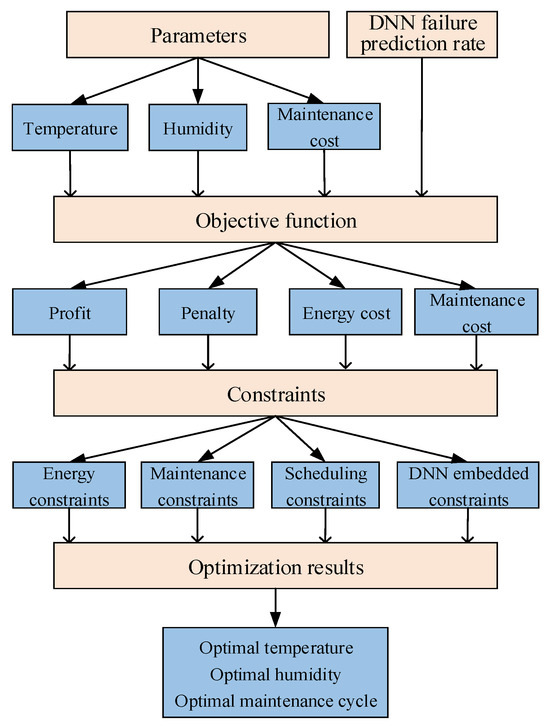
Figure 2.
MILP optimization flowchart.
- Objective function:
The objective function combines the fault predictions from the DNN with the operational constraints modeled by the MILP to ensure a balanced optimization between maximizing profits and minimizing penalties, energy costs, and maintenance expenses.
In the objective function, the term represents the revenue generated from successful tablet pressing, where denotes the probability of success and is the profit per successful tablet. Conversely, captures the penalties associated with failed tablet pressing, with representing the probability of failure and denoting the penalty per failure. In addition to these terms, accounts for the energy costs required for various operational processes, including temperature and humidity adjustments as well as the pressing operations, while accounts for the maintenance costs incurred throughout the process.
- Maintenance and tablet pressing schedule constraints:
The scheduling framework prioritizes the synchronization of maintenance activities with the production demands by dynamically adjusting the number of maintenance cycles and tablet pressing targets to achieve the optimal utilization of resources throughout the production timeline.
Equation (6) defines the total maintenance cycle as the sum of maintenance activities across all time intervals within a day. Equation (7) specifies that the total number of tablets pressed during the day must meet the production target (), ensuring the machine achieves its operational goals. Equation (8) restricts the hourly tablet production () when maintenance occurs, where the production capacity is reduced proportionally to the maintenance duration (m) if maintenance () is scheduled in a given time interval. Finally, Equation (9) represents the maintenance cost as a product of a binary variable indicating maintenance and the unit maintenance cost.
- Energy constraints:
Energy usage modeling focuses on quantifying the power consumption required for temperature and humidity adjustments, as well as the operational load of the tablet pressing machine. Approaching ensures cost management while upholding production quality and efficiency.
Equation (10) quantifies the energy consumption required for temperature adjustments. This energy is determined by the temperature difference between the outside temperature and optimized inside temperature (), scaled by the temperature adjustment cost coefficient (). Similarly, Equation (11) captures the energy used for humidity regulation, which depends on the change in humidity across intervals, scaled by the humidity adjustment cost coefficient ().
The energy cost of operating the machine for tablet pressing is represented by Equation (12). It is a function of the number of tablets pressed () and the machine’s pressure (P), speed (S), and vibration (V), each weighted by their respective coefficients (, , ). Finally, Equation (13) computes the total energy cost within a time interval by summing the energy costs for temperature adjustment (), humidity adjustment (), and machine operation (). This total is then multiplied by the electricity price () to reflect the cost for that interval.
- DNN-embedded constraints:
The DNN-embedded MILP constraints integrate predictive analytics into the optimization process, converting parameters like pressure, temperature, and maintenance cycles into constraints that improve adaptability to complex and dynamic production environments.
Equation (14) describes the input to the DNN model, comprising the machine’s operational parameters, including pressure (P), temperature (), speed (S), vibration (V), humidity (), and the maintenance cycle count (). In Equation (15), the activations of the input layer () are defined as identical to the input values (). Forward propagation through the DNN is represented in Equation (16), where the pre-activation value of a node in layer h () is computed as the weighted sum of activations from the previous layer, scaled by the weight matrix () and then with bias vector added.
ReLU activation function constraints are enforced through Equations (17)–(20). Specifically, Equation (17) sets an upper bound on the activation value () based on the pre-activation value () and a binary indicator (). Equation (18) ensures that the activation value is no less than the pre-activation value. Equation (19) limits the activation value to a large constant (M) when the ReLU output is active (), while Equation (20) guarantees the non-negativity of the activation values. The output of the DNN () is linked to the failure probability () through Equation (21), and Equation (22) constrains the failure probability to lie within the range [0, 1], consistent with its probabilistic interpretation.
4. Case Study
The Kaggle dataset “Fault Prediction in Tablet Press Equipment” in [26] offers a rich collection of sensor readings and fault indicators from the tablet press machinery widely used in pharmaceutical manufacturing. It contains real-time measurements such as pressure, temperature, vibration, and speed, along with binary fault labels and timestamps that align data points with equipment behavior over time. This dataset provides a comprehensive representation of the operational conditions and fault occurrences, capturing the key fault characteristics and machine behaviors commonly observed in real-world pharmaceutical manufacturing. This makes it a representative and reliable source for validating the proposed model.
The key model parameters and cost-related variables are defined to establish the settings for the DNN and MILP framework. The parameters include the pressure value P, which is set to 62; a speed S, assigned the value of 758; the velocity V, specified as 0.3; a daily tablet demand of 600; the maximum tablet pressing amount per interval is 36; the maintenance duration m, equal to 0.5 h; and a large constant M, defined as , used for linearizing ReLU activation functions. Furthermore, the weight coefficients are given as , , and . For cost-related components, the parameters include , set at USD 100, , determined to be USD 200, and , valued at USD 1000. Additionally, the cost coefficients for temperature and humidity adjustments are and , taking values of USD 500 and USD 300, respectively. The electricity price data are sourced from the real-world dataset provided by Energy Online [27].
The proposed model was solved using Gurobi Optimizer (version 10.0.3, Gurobi Optimization, LLC, Houston, TX, USA), with an optimality gap tolerance set to 0.01%. The computational experiments were conducted on a system equipped with an Intel Core i7-1365U processor (Intel Corporation, Santa Clara, CA, USA), supporting SSE2, AVX, and AVX2 instruction sets. This processor features 10 cores and 12 threads, providing efficient support for parallel computation. The system was also configured with 16 GB of RAM and operated under Windows 11 (Microsoft Corporation, Redmond, WA, USA). Under this computational setup, the solver explored 1679 nodes and performed 119,206 simplex iterations, reaching an optimal solution within 217 s.
5. Results
The results of the proposed DNN-embedded MILP model for fault prediction and production optimization in tablet pressing machines are introduced in this section through prediction and optimization results and sensitivity analysis. The model’s performance in production scheduling and fault prediction is presented, and its robustness under varying cost parameters is evaluated.
5.1. Prediction and Optimization Results
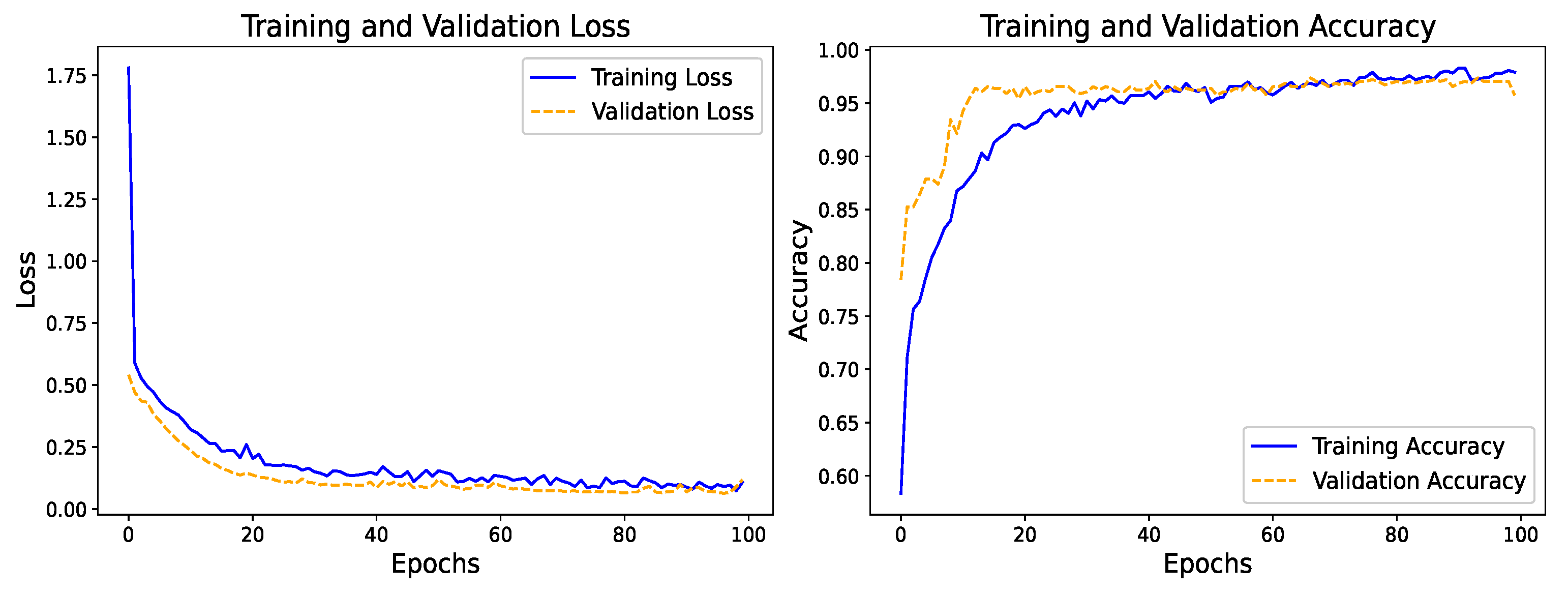
Figure 3 depicts the progression of the model’s training process, highlighting changes in the loss function and accuracy. Both training and validation losses decrease steadily with increasing epochs and stabilize in the later stages. Concurrently, the training accuracy improves from approximately 60% to nearly 100%, with validation accuracy following a similar trend, reaching around 90% early on and converging closely with the training accuracy. These results confirm the model’s strong convergence, robust generalization, and consistent performance on training and validation datasets.
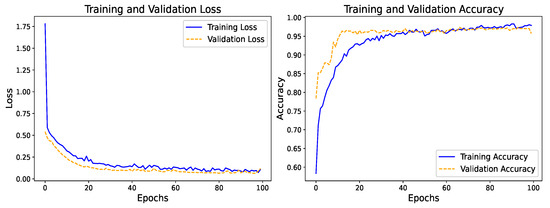
Figure 3.
DNN training and validation loss and accuracy curves.
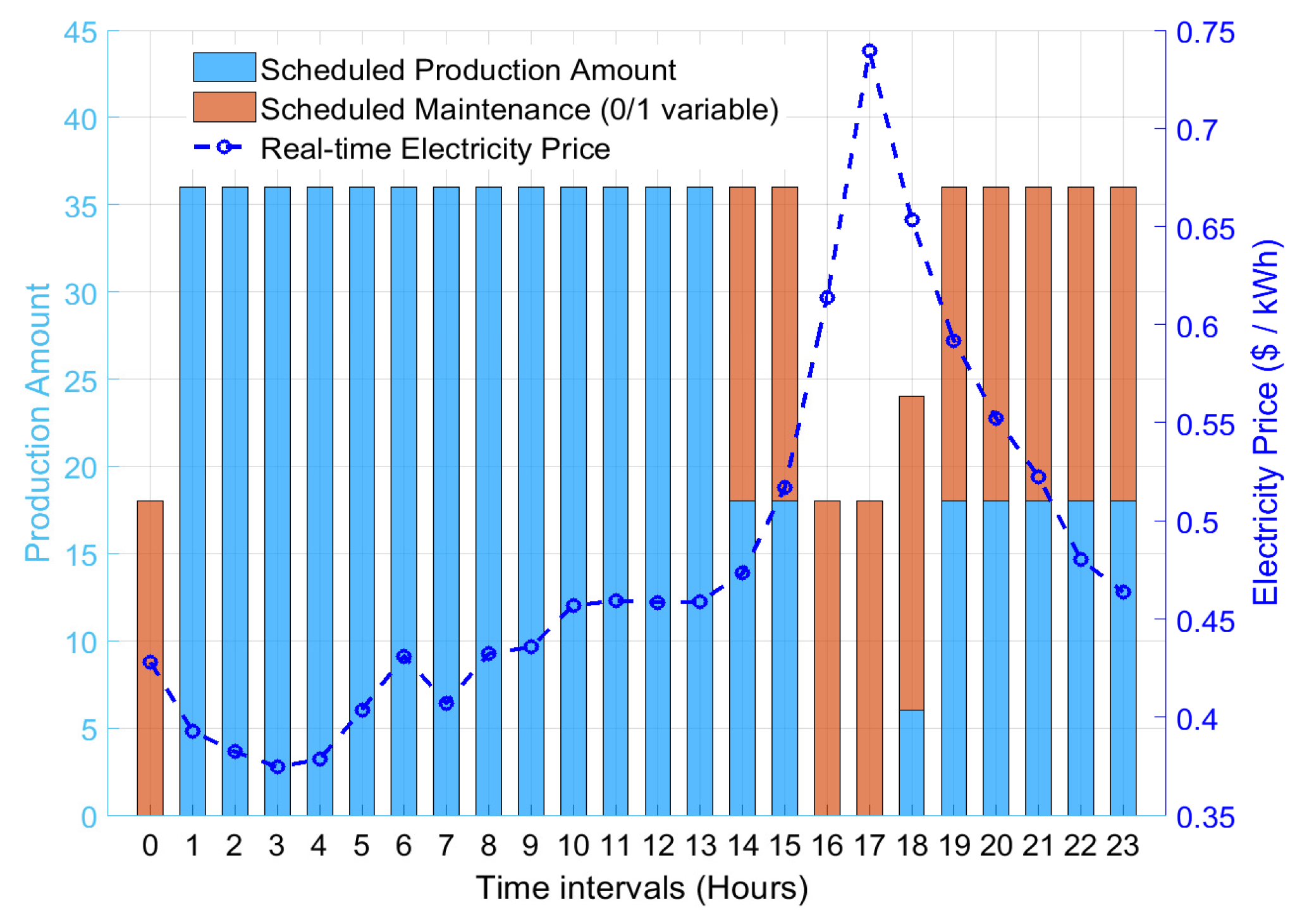
Figure 4 illustrates the optimization results of production scheduling and maintenance planning based on the DNN-embedded MILP model. Maintenance activities are subject to two operational constraints of the tablet pressing machine: at most, one maintenance session can occur per hour (modeled as binary variables), and the total number of maintenance sessions within a day must meet the requirement in [26], which is closely tied to the production success rate. The optimization results demonstrate that the model prioritizes production tasks during periods of low electricity prices to maximize profitability while strategically scheduling maintenance during peak electricity price periods. This dynamic adjustment not only effectively reduces high-cost operational periods but also ensures the machine’s reliability and overall operational efficiency.
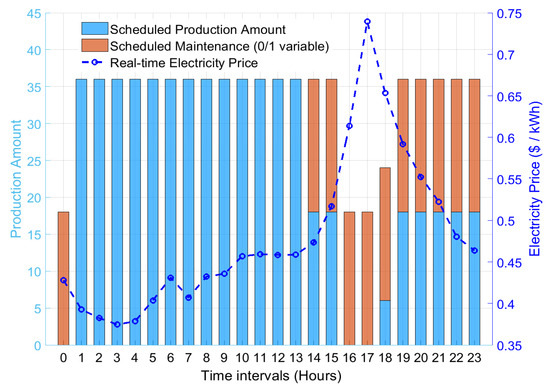
Figure 4.
Optimized production and maintenance scheduling with real-time electricity pricing.
5.2. Sensitivity Analysis
To assess the robustness of the proposed DNN-embedded MILP model, sensitivity analyses were performed by varying the cost of single maintenance, temperature adjustment, and humidity adjustment. Each parameter was systematically scaled between 0.5 and 1.5 times its baseline value to evaluate the model’s adaptability to parameter fluctuations and their subsequent effects on profit and cost components, including penalty cost, energy cost, and maintenance cost.
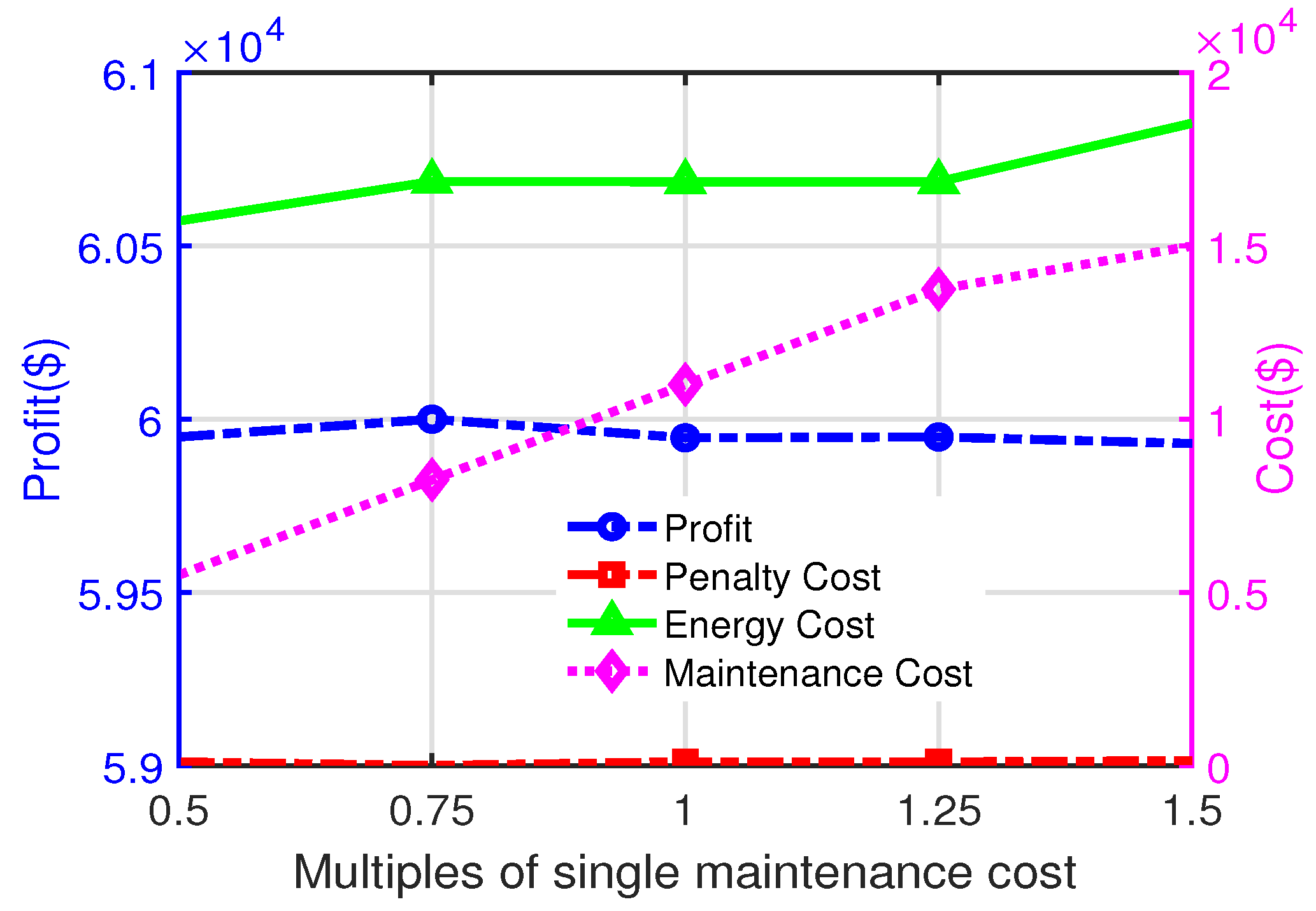
Figure 5 illustrates the impact of varying the cost of a single maintenance session on profit and cost components. As the cost of a single maintenance session increases, the overall maintenance costs rise significantly, resulting in a noticeable decline in overall profit. The high accuracy of the DNN’s predictions effectively reduces failure rates and minimizes associated penalties. Meanwhile, energy costs exhibit a gradual upward trend, reflecting the increased energy demands for the production adjustments necessitated by maintenance activities. Notably, beyond 1.25 times the baseline cost, the growth of total maintenance costs begins to slow, indicating that the model strategically adjusts maintenance schedules to control further cost escalation. These results highlight the model’s ability to dynamically balance maintenance and production activities, effectively mitigating the adverse effects of increased maintenance costs while maintaining profitability and operational efficiency.
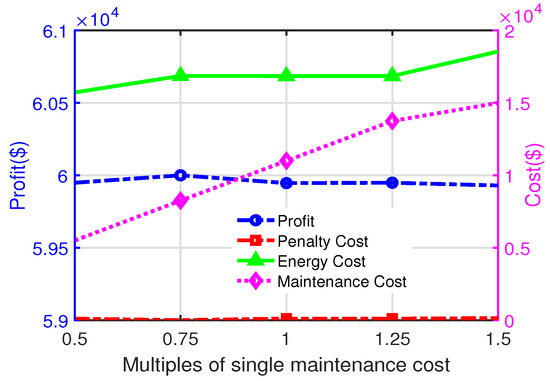
Figure 5.
The effect of the changed multiple of maintenance cost on profit, penalty cost, energy cost, and maintenance cost.
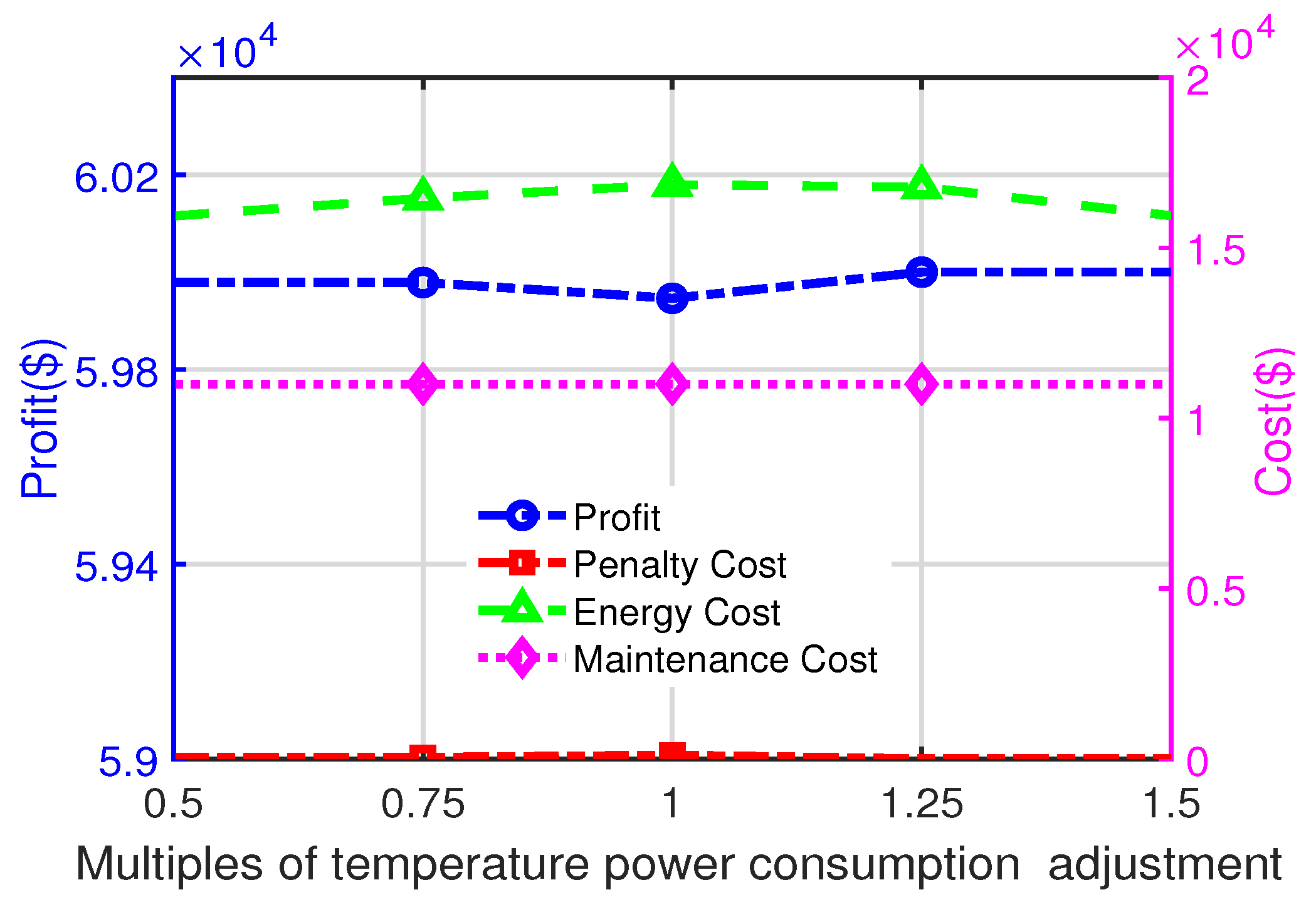
Figure 6 illustrates the impact of temperature adjustment cost on profit and cost components. As the adjustment cost increases, energy costs rise initially due to the higher expense of maintaining optimal temperature settings. However, beyond 1.25 times the baseline cost, energy costs begin to decline. This reflects the model’s strategy to reduce the frequency and magnitude of temperature adjustments, prioritizing profit maximization while controlling operational expenses. Penalty costs remain consistently low thanks to the high accuracy of the DNN’s predictions, which minimize failures and maintain production quality. Maintenance costs show no noticeable variation, suggesting that the temperature adjustment costs do not directly influence maintenance schedules. These findings demonstrate the model’s adaptability in optimizing energy usage and balancing cost efficiency under varying adjustment cost scenarios, ensuring stable profitability.
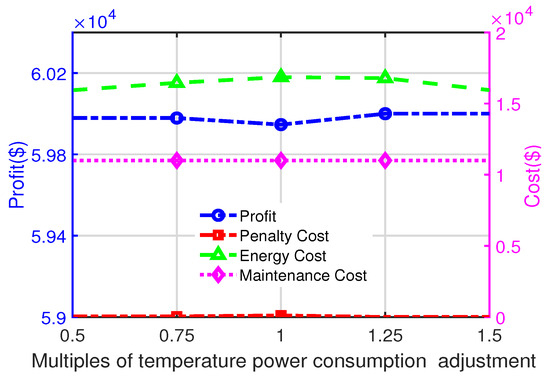
Figure 6.
The effect of the changed multiple of temperature adjustment on profit, penalty cost, energy cost, and maintenance cost.
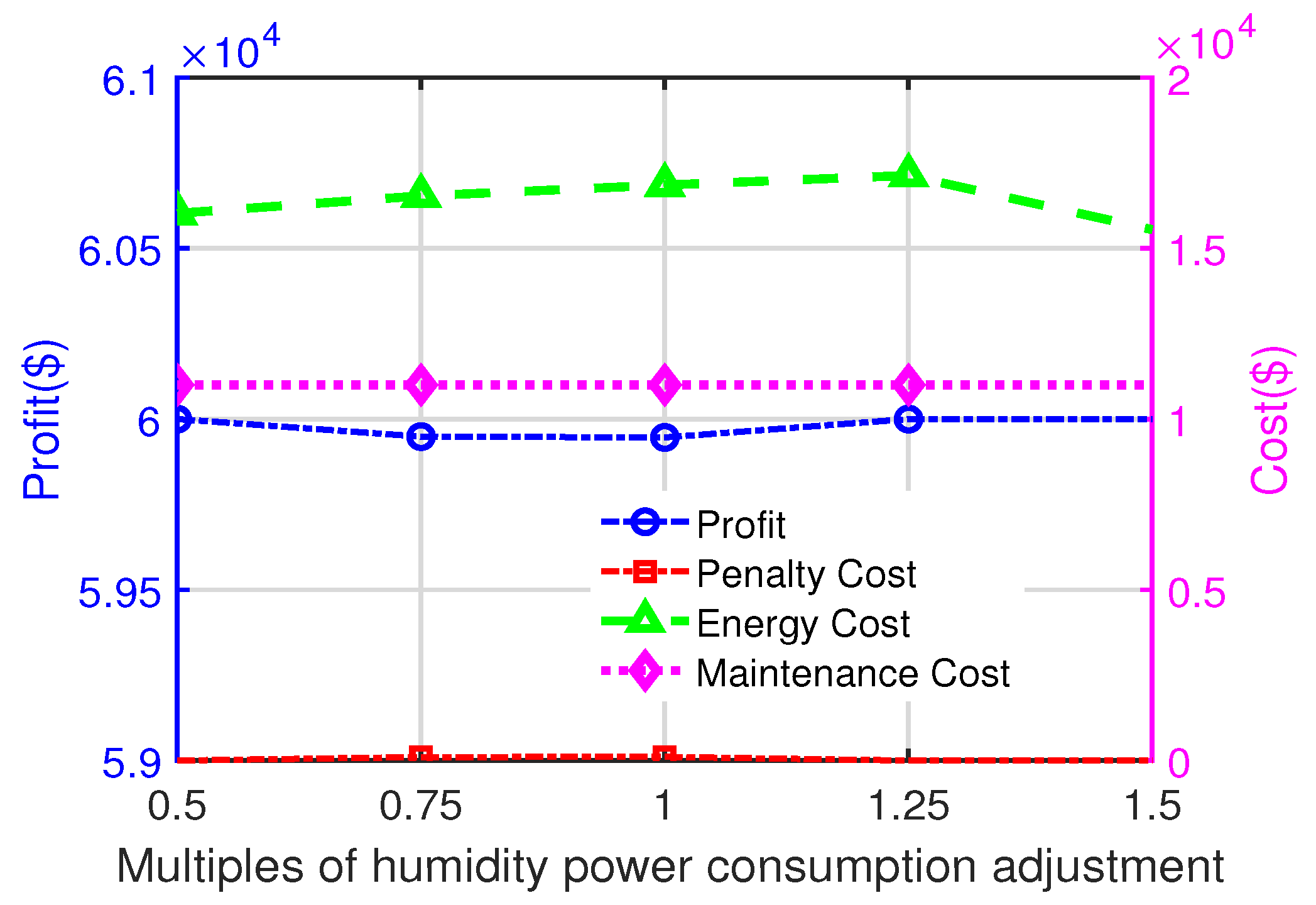
Figure 7 illustrates the impact of humidity adjustment cost on profit and cost components. As the adjustment cost increases, the energy costs initially rise due to the higher expense of frequent adjustments, but they begin to decrease beyond 1.25 times the baseline cost. Compared to Figure 6, the energy costs under humidity adjustment costs exhibit greater fluctuations, indicating higher sensitivity to cost changes.
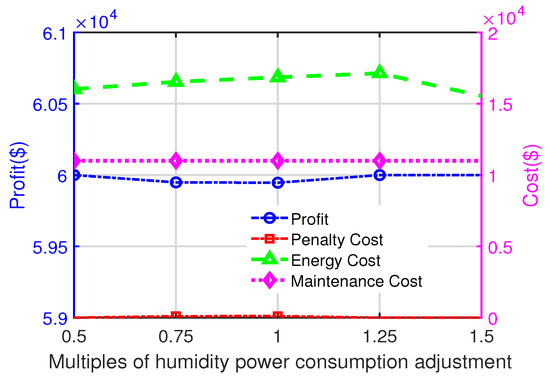
Figure 7.
The effect of the changed multiple of humidity adjustment on profit, penalty cost, energy cost, and maintenance cost.
6. Conclusions
This paper presents a novel framework that integrates DNNs with mixed-integer linear programming (MILP) for fault prediction and production optimization in tablet pressing machines. By embedding a DNN for failure probability estimation within the MILP model, the proposed approach effectively bridges the gap between data-driven predictive analytics and mathematical optimization. This integration enhances predictive accuracy and ensures globally optimal decision making in complex manufacturing environments. Big-M constraints transform ReLU activation functions into linear constraints, ensuring that the model can be efficiently solved while preserving the key properties of the original nonlinear structure.
Based on real-world datasets, the case study demonstrates the framework’s ability to dynamically adjust production schedules, temperature and humidity settings, and maintenance planning. The results highlight significant improvements in operational efficiency, resource utilization, and overall profitability under fluctuating energy prices. Sensitivity analyses further confirm the model’s robustness and adaptability, showing that it effectively balances production quality and cost efficiency even amid variations in energy and maintenance costs. The proposed framework offers substantial practical value for manufacturing systems. Adapting production and maintenance schedules to real-time electricity prices further enhances cost-effectiveness and operational resilience.
However, this study also reveals certain limitations. The DNN inference process is efficient, and the MILP model requires solving a high-dimensional optimization problem with multiple constraints. In large-scale manufacturing systems involving various machines, the computational complexity of the proposed DNN-MILP framework increases significantly due to the expanded decision space and the additional constraints introduced by ReLU linearization. Distributed optimization techniques such as Benders decomposition can be applied to enhance scalability, allowing for parallelized decision making across multiple machines. A hierarchical optimization approach can also be employed, where a high-level controller determines resource allocation and maintenance schedules. In contrast, lower-level optimizations fine-tune individual machine operations. Hybrid methods combining heuristic algorithms with MILP can further reduce computational burdens.
Addressing real-world deployment challenges, such as data acquisition, computational cost, and industrial applicability, is crucial for practical implementation. Industrial settings often involve heterogeneous data sources with missing values and sensor noise, necessitating robust preprocessing and real-time sensor integration. The computational burden of the proposed DNN-MILP framework may increase in large-scale applications, requiring distributed optimization techniques and lightweight neural networks to enhance efficiency. Furthermore, integrating this framework with existing industrial control systems (e.g., SCADA, MES) and extending it to multi-machine scheduling would improve its scalability and adaptability in real-world manufacturing environments. These aspects present promising directions for future research.
Author Contributions
Conceptualization, J.L. and L.W.; methodology, J.L. and L.W.; software, J.L.; validation, J.L., L.W., and Y.Q.; data curation, J.L. and H.Z.; writing—original draft preparation, J.L. and H.Z.; writing—review and editing, J.L. and Y.Q.; visualization, J.L. and Y.Q.; supervision, L.W.; project administration, L.W.; funding acquisition, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
At present, this research has not received any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data Availability Statement
The data for fault prediction in tablet press equipment: https://www.kaggle.com/datasets/thegoanpanda/fault-prediction-in-tablet-press-equipment (accessed on 9 November 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ponnusamy, V.; Ekambaram, D.; Zdravkovic, N. Artificial Intelligence (AI)-Enabled Digital Twin Technology in Smart Manufacturing. In Industry 4.0, Smart Manufacturing, and Industrial Engineering; CRC Press: Boca Raton, FL, USA, 2025; pp. 248–270. [Google Scholar]
- Georgiadis, G.P.; Elekidis, A.P.; Georgiadis, M.C. Optimization-based scheduling for the process industries: From theory to real-life industrial applications. Processes 2019, 7, 438. [Google Scholar] [CrossRef]
- Tiddens, W.; Braaksma, J.; Tinga, T. Exploring predictive maintenance applications in industry. J. Qual. Maint. Eng. 2022, 28, 68–85. [Google Scholar]
- Yu, J.; Zhang, Y. Challenges and opportunities of deep learning-based process fault detection and diagnosis: A review. Neural Comput. Appl. 2023, 35, 211–252. [Google Scholar]
- Al-Hamzi, Y.M.; Sahibuddin, S.B. A Comprehensive Crucial Review of Re-Purposing DNN-Based Systems: Significance, Challenges, and Future Directions. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 562–582. [Google Scholar] [CrossRef]
- Bragin, M.A. Survey on Lagrangian relaxation for MILP: Importance, challenges, historical review, recent advancements, and opportunities. Ann. Oper. Res. 2024, 333, 29–45. [Google Scholar]
- He, J.; Yu, X.; Li, Q.; Zhang, B.; Wang, X.; Zhao, Q.; Qiang, X.; Wang, Q.; Huo, Z.; Ye, T. DNN-based error level prediction for reducing read latency in 3D NAND flash memory. Microelectron. Reliab. 2023, 147, 115008. [Google Scholar]
- Illy, P.; Kaddoum, G. A collaborative DNN-based low-latency IDPS for mission-critical smart factory networks. IEEE Access 2023, 11, 96317–96329. [Google Scholar]
- Zhou, L.; Zhang, L.; Horn, B.K. Deep reinforcement learning-based dynamic scheduling in smart manufacturing. Procedia Cirp. 2020, 93, 383–388. [Google Scholar]
- Kallrath, J. Solving planning and design problems in the process industry using mixed integer and global optimization. Ann. Oper. Res. 2005, 140, 339–373. [Google Scholar]
- Wirtz, M.; Neumaier, L.; Remmen, P.; Müller, D. Temperature control in 5th generation district heating and cooling networks: An MILP-based operation optimization. Appl. Energy 2021, 288, 116608. [Google Scholar]
- Kunath, S.; Kühn, M.; Völker, M.; Schmidt, T.; Rühl, P.; Heidel, G. MILP performance improvement strategies for short-term batch production scheduling: A chemical industry use case. SN Appl. Sci. 2022, 4, 87. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, D.; Han, B.; Xue, F.; Lu, S.; Jiang, L. Urban Autonomous Electric Vehicles Fleet Operation Strategy—From the Perspective of Operators. In Proceedings of the 2024 IEEE 34th Australasian Universities Power Engineering Conference (AUPEC), Sydney, Australia, 20–22 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Dukpa, A.; Butrylo, B. MILP-based profit maximization of electric vehicle charging station based on solar and EV arrival forecasts. Energies 2022, 15, 5760. [Google Scholar] [CrossRef]
- Shao, C.; Wang, X.; Shahidehpour, M.; Wang, X.; Wang, B. An MILP-based optimal power flow in multicarrier energy systems. IEEE Trans. Sustain. Energy 2016, 8, 239–248. [Google Scholar] [CrossRef]
- Bouazza, W.; Sallez, Y.; Trentesaux, D. Dynamic scheduling of manufacturing systems: A product-driven approach using hyper-heuristics. Int. J. Comput. Integr. Manuf. 2021, 34, 641–665. [Google Scholar]
- Daneshdoost, F.; Hajiaghaei-Keshteli, M.; Sahin, R.; Niroomand, S. Tabu search based hybrid meta-heuristic approaches for schedule-based production cost minimization problem for the case of cable manufacturing systems. Informatica 2022, 33, 499–522. [Google Scholar] [CrossRef]
- Fischetti, M.; Jo, J. Deep neural networks and mixed integer linear optimization. Constraints 2018, 23, 296–309. [Google Scholar] [CrossRef]
- Mistry, S.; Saha, I.; Biswas, S. An MILP encoding for efficient verification of quantized deep neural networks. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2022, 41, 4445–4456. [Google Scholar]
- Dinh, H.T.; Kim, D. MILP-based imitation learning for HVAC control. IEEE Internet Things J. 2021, 9, 6107–6120. [Google Scholar] [CrossRef]
- Katta, S. Predictive Machine Learning Models for Calibration Failure Detection in Pharmaceutical Manufacturing. J. Artif. Intell. Mach. Learn. Data Sci. 2023, 1, 2152–2160. [Google Scholar] [CrossRef]
- Kavasidis, I.; Lallas, E.; Gerogiannis, V.C.; Charitou, T.; Karageorgos, A. Predictive maintenance in pharmaceutical manufacturing lines using deep transformers. Procedia Comput. Sci. 2023, 220, 576–583. [Google Scholar] [CrossRef]
- Begum, S.G.; Bai, A.S.; Kalpana, G.; Mounika, P.; Chandini, J.A. Review on tablet manufacturing machines and tablet manufacturing defects. Indian Res. J. Pharm. Sci. 2018, 5, 1479–1490. [Google Scholar]
- Zhao, C.; Li, X. Linearization of ReLU Activation Function for Neural Network-Embedded Optimization: Optimal Day-Ahead Energy Scheduling. arXiv 2023, arXiv:2310.01758. [Google Scholar]
- Grimstad, B.; Andersson, H. ReLU networks as surrogate models in mixed-integer linear programs. Comput. Chem. Eng. 2019, 131, 106580. [Google Scholar]
- TheGoanPanda. Fault Prediction in Tablet Press Equipment Dataset. Kaggle. 2025. Available online: https://www.kaggle.com/datasets/thegoanpanda/fault-prediction-in-tablet-press-equipment (accessed on 9 November 2024).
- EnergyOnline. Generic Data—U.S. Electricity Prices. 2024. Available online: https://www.energyonline.com/Data/GenericData.aspx?DataId=21 (accessed on 8 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).