XGBoost-Based Heuristic Path Planning Algorithm for Large Scale Air–Rail Intermodal Networks
Abstract
1. Introduction
2. Methodology
2.1. Problem Description
2.2. Network Design
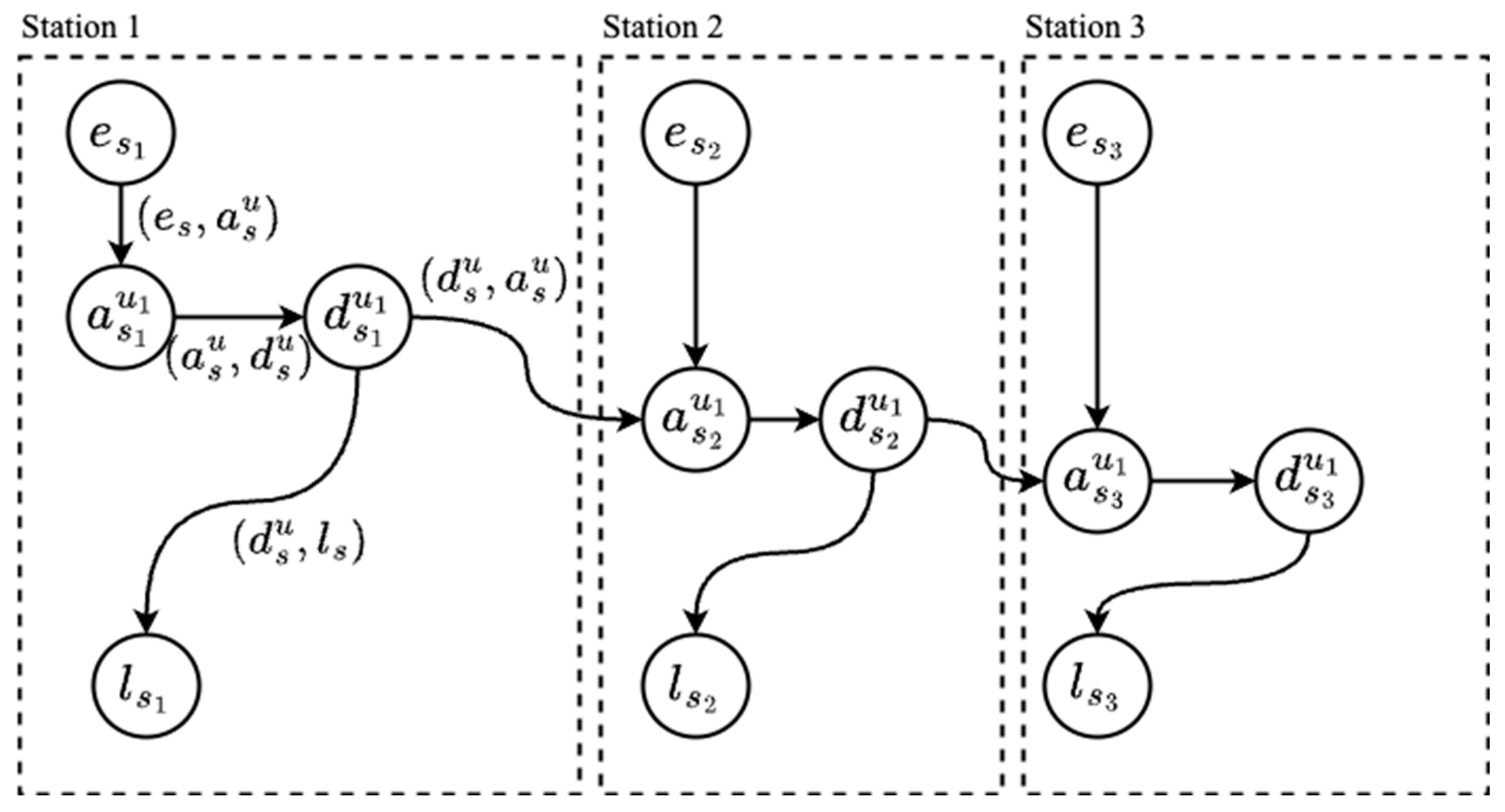
2.2.1. Time-Expanded Graph Based Network
- , represents the set of events corresponding to passengers entering a station or airport .
- , represents the set of events corresponding to passengers leaving a station or airport .
- , represents the set of events corresponding to vehicle arriving at a station or airport .
- , represents the set of events corresponding to vehicle departing from a station or airport .
- represents the entering process in which a passenger enters a station and waits for the arrival of the train or airplane.
- represents the leaving process in which a passenger gets off a train or airplane and ultimately leaves the station or airport.
- represents the waiting process in which a train or an airplane arrives at a station or airport, stops for a period of time and departs, during which the passenger remains inside the vehicle without leaving.
- represents the hopping process in which a passenger travels in a vehicle from one station or airport to the next.
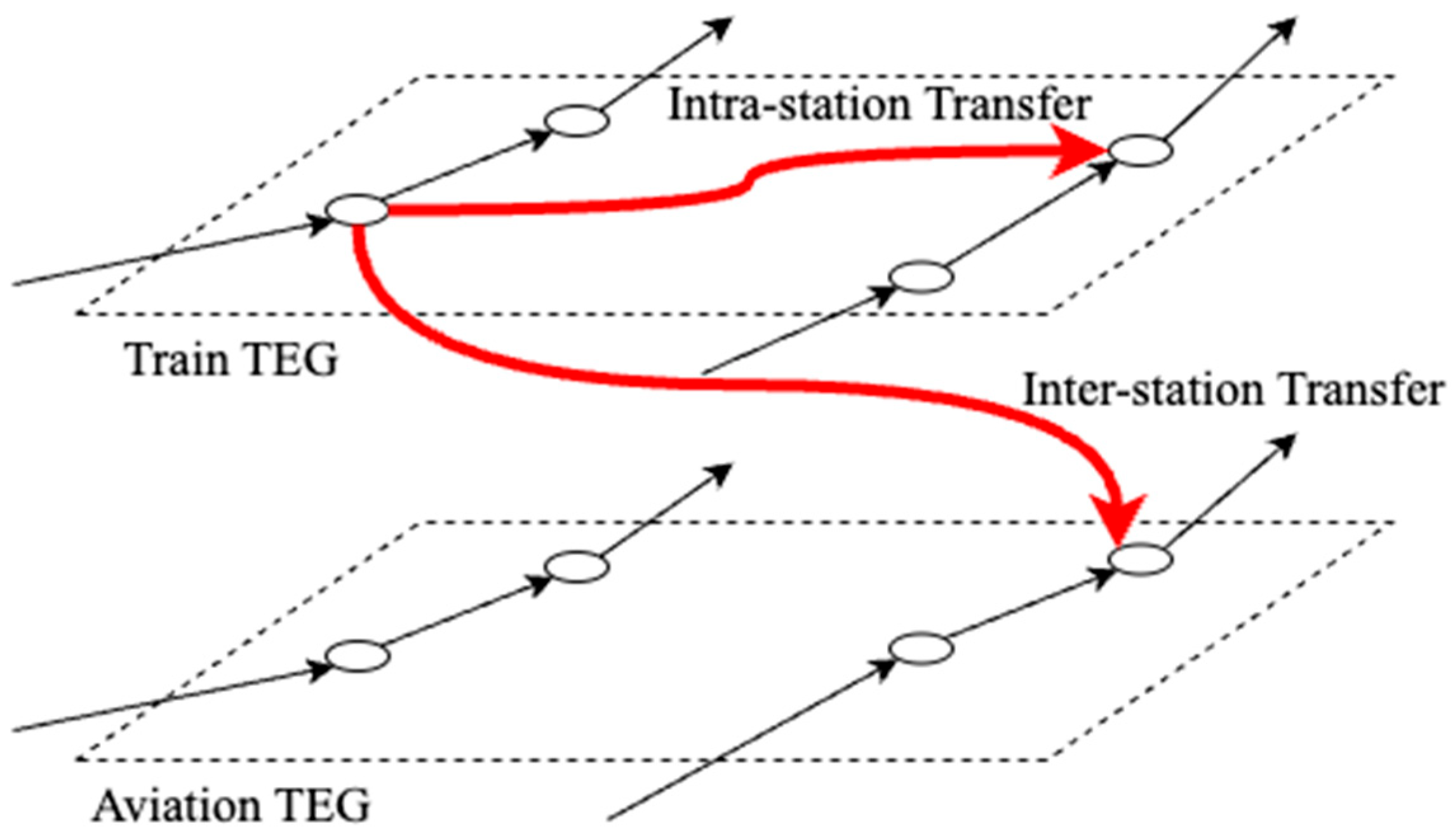
- represents the intra-station transfer process in which a passenger transfers to a different mode of transportation without leaving the station or airport.
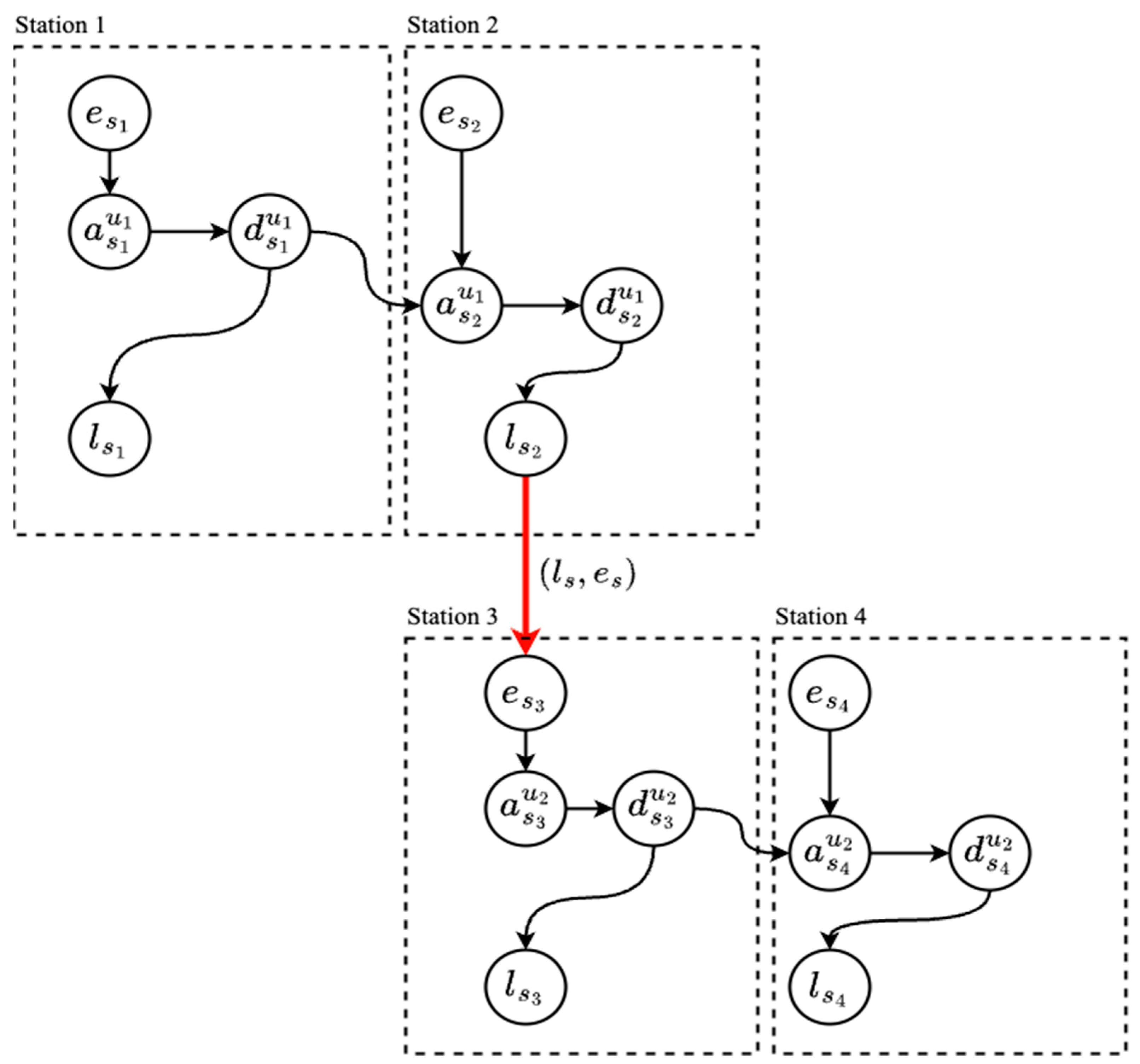
- represents the inter-station transfer process in which a passenger transfers between two different stations or an airport to continue their journey on different modes of transportation.
2.2.2. Transfer Edge Generation
2.3. General Travel Cost
2.4. The Mathematical Model
2.5. XGBoost-Based Heuristic Path Planning Algorithm
2.5.1. General Travel Cost Function with Heuristic Factor
2.5.2. XGBoost Algorithm
2.5.3. Evaluation Index Construction
- Accuracy is the ratio of correct prediction. The formula is expressed as:
- Recall is the possibility of finding all positive samples. The formula is expressed as:
- Precision as the correlation of classifying a negative sample as a positive is measured. The formula is expressed as:
- F-Score considers both precision and recall indicators and is expressed as:
- When the parameter , the most common F1 is the harmonic mean of precision and recall. The formula is expressed as:
2.5.4. Heuristic Route Algorithm
- Load railway and airplane operation plan data, generate TEG for train and airplane.
- Establish transfer edges between train and airplane TEG to form an air–rail integrated TEG.
- Load users’ historical data.
- Train the XGBoost model and perform parameter tuning.
- Use the pre-trained XGBoost model to determine which transfer edges can be kept based on the user’s query conditions.
- Update of the edges that will be kept to 1 and set the of the other transfer edges to .
- Run K shortest path algorithm, this paper utilizes the bidirectional Dijkstra for the K shortest path search process.
3. Numerical Experiments and Analysis
3.1. Data Prepareation
3.1.1. Air–Rail Intermodal Network Construction Dataset
3.1.2. XGBoost Model Training Dataset
- The first segment and the second segment of the journey are by train and by airplane separately.
- The arrival time of the first segment of the journey and the departure time of the second segment differ by less than 4 h.
- The straight-line distance between the destination of the first segment of the journey and the origin of the second segment is within 50 km.
3.2. XGBoost Model Training
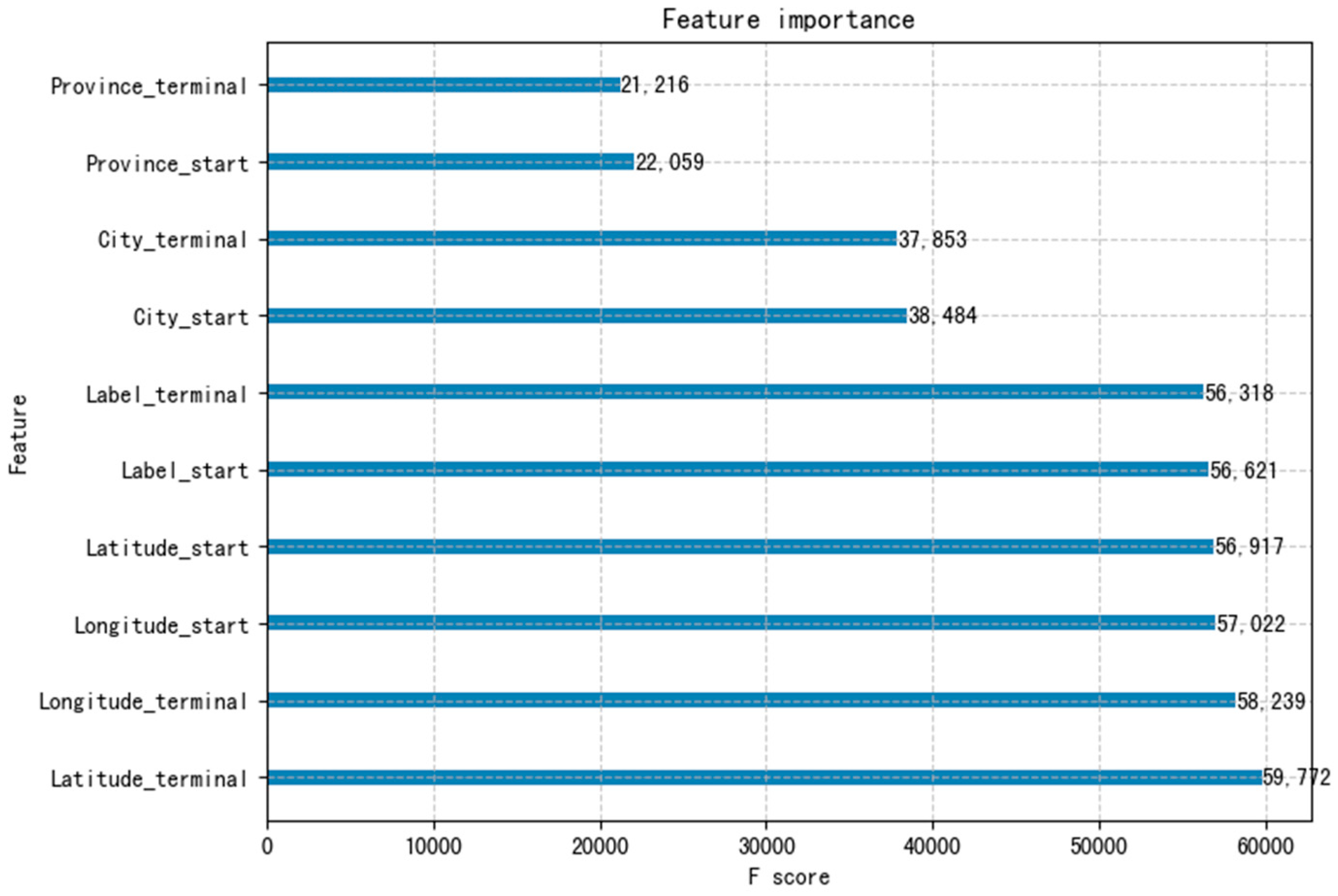
3.2.1. Feature Selection and Processing
3.2.2. Parameter Tuning
3.2.3. Robust Validation
3.3. XGBoost Acceleration Analysis
- Run K shortest path planning algorithm directly Without XGBoost.
- Use XGB-HPPA.
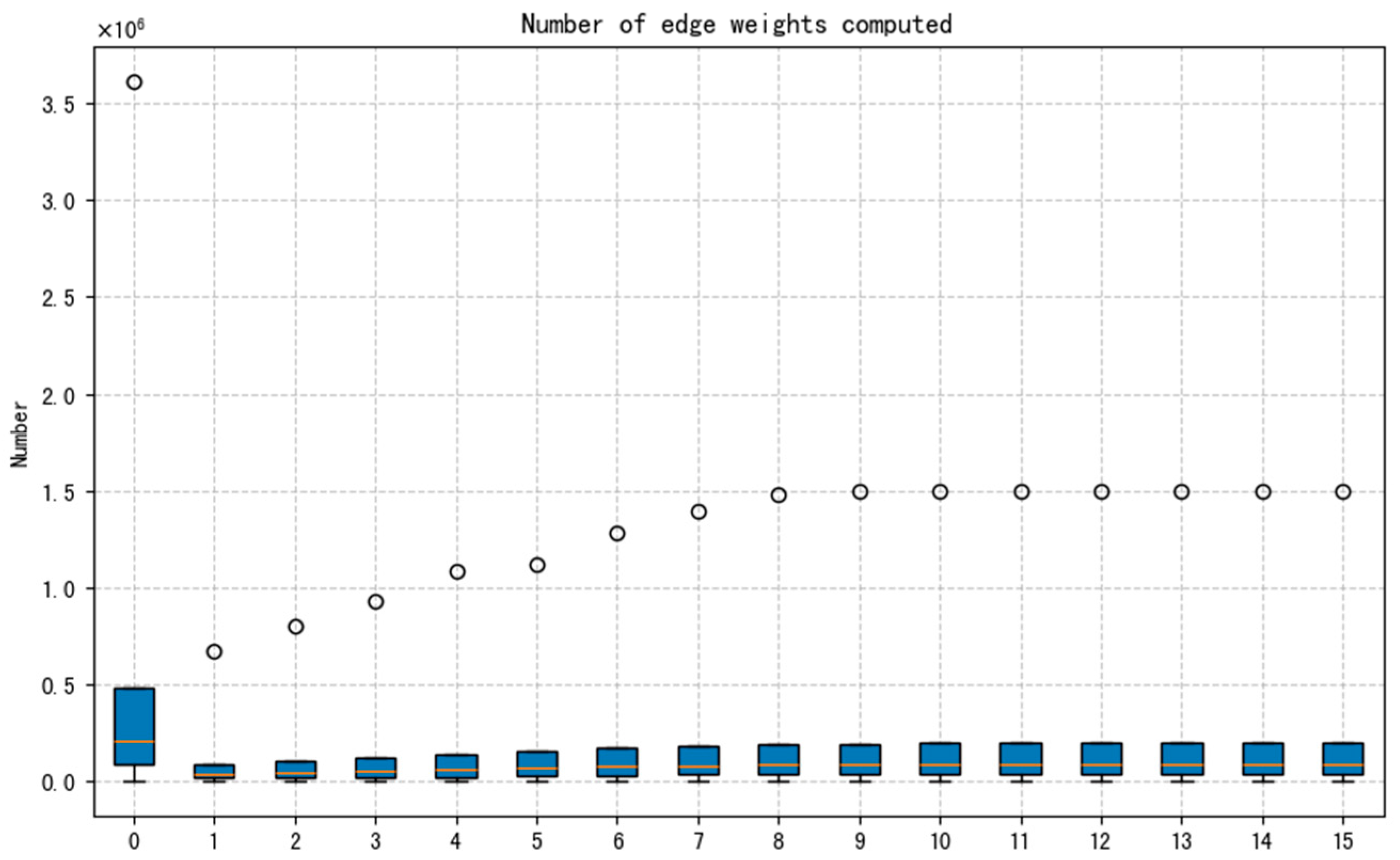
3.3.1. Analysis of Algorithm Complexity and Scalability
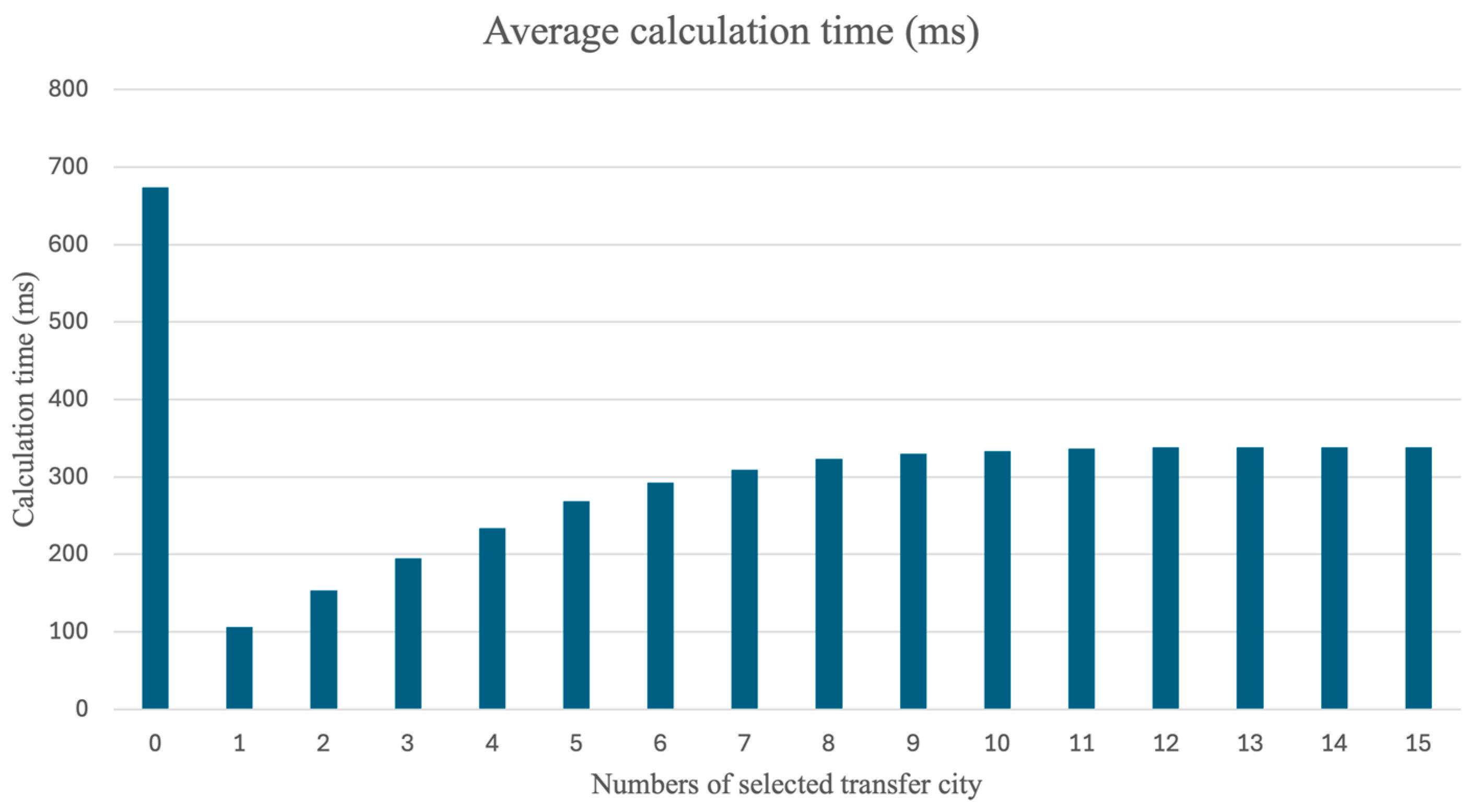
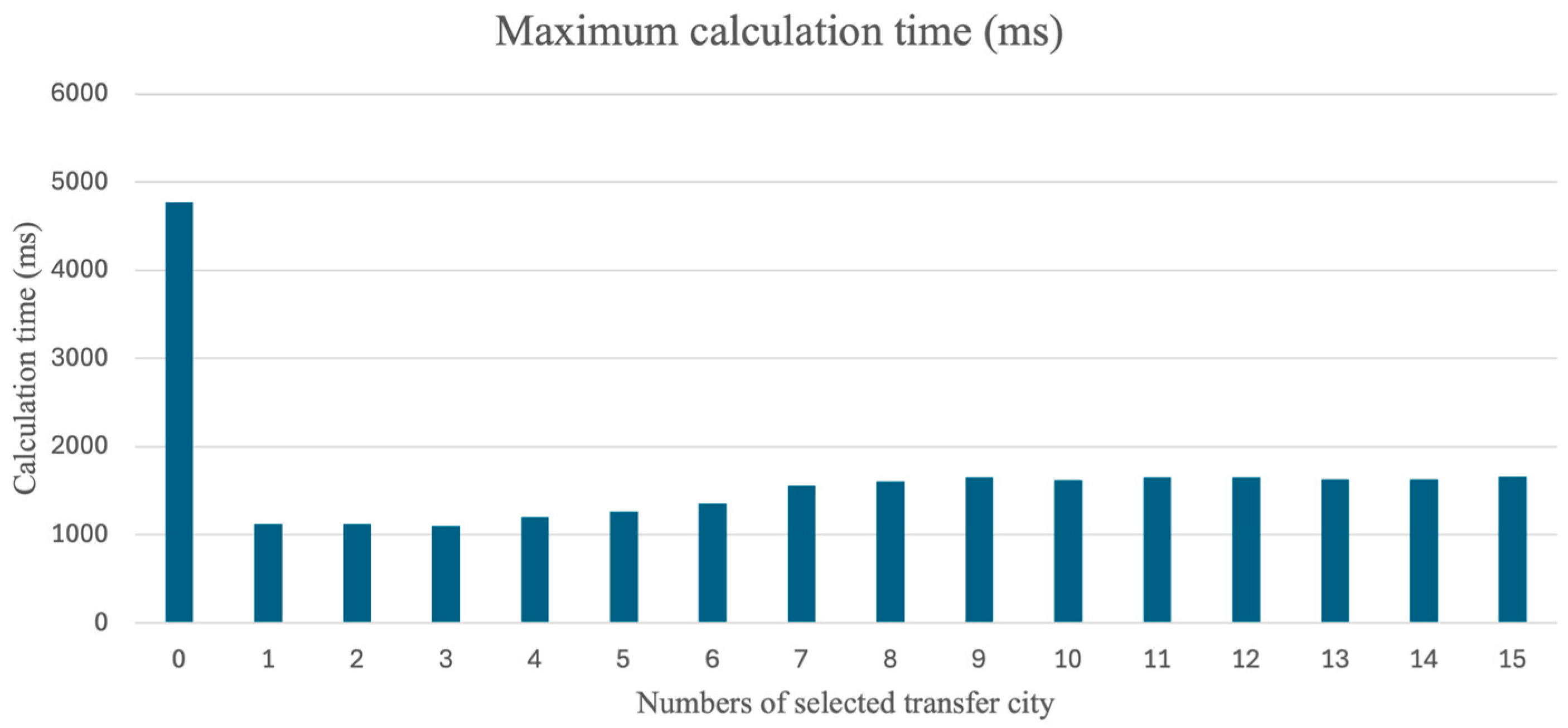
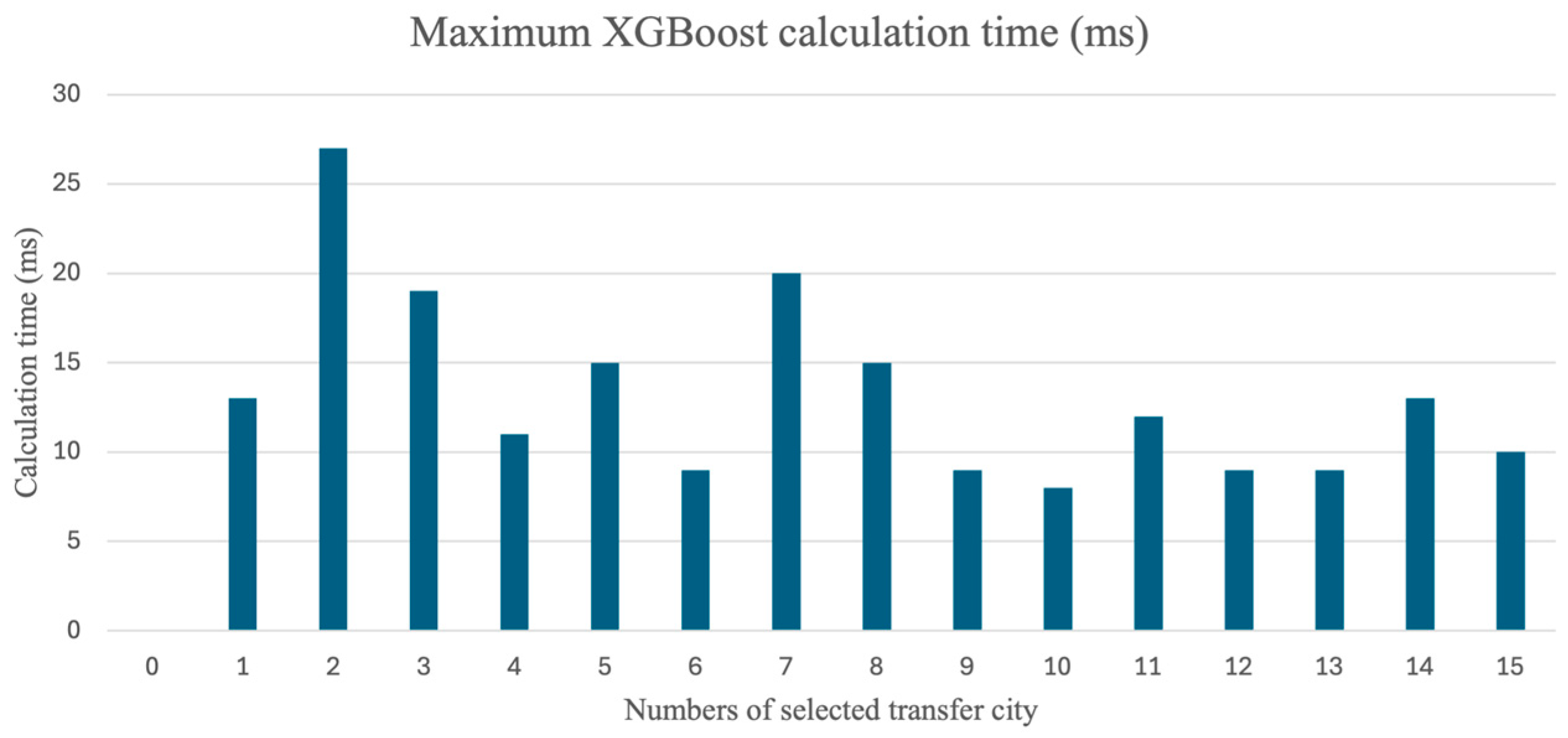
3.3.2. Comparison of Calculation Time
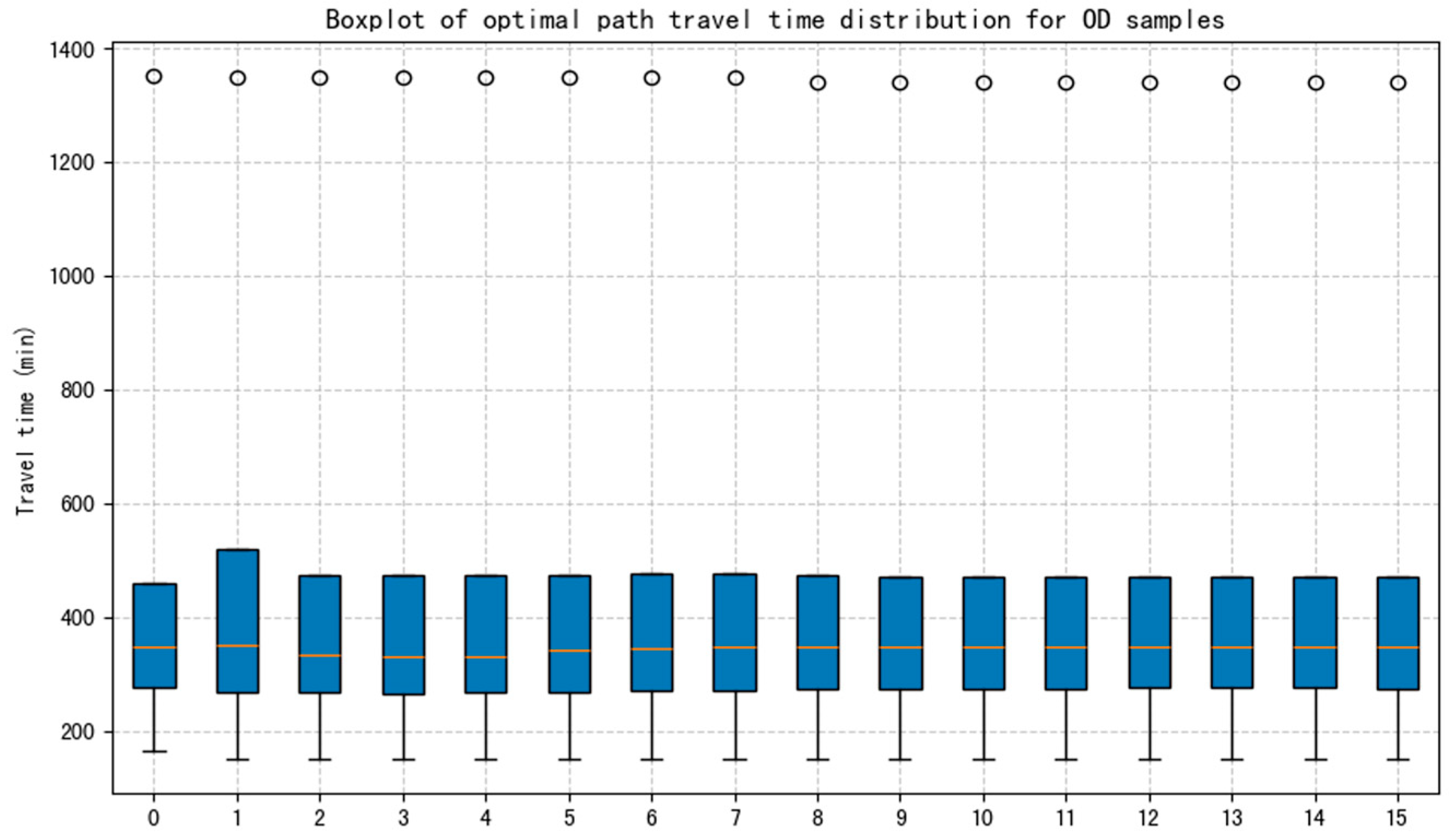
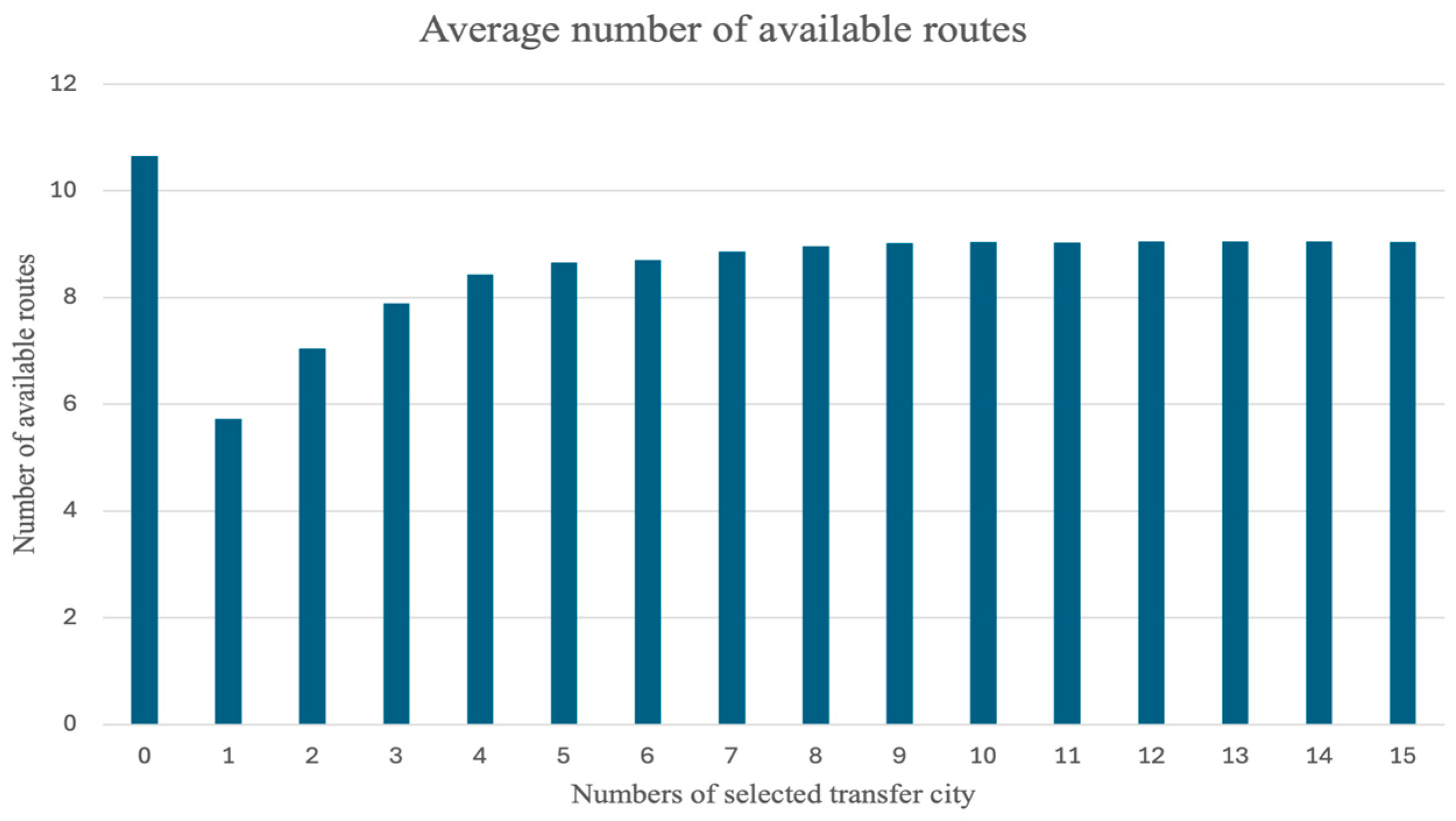
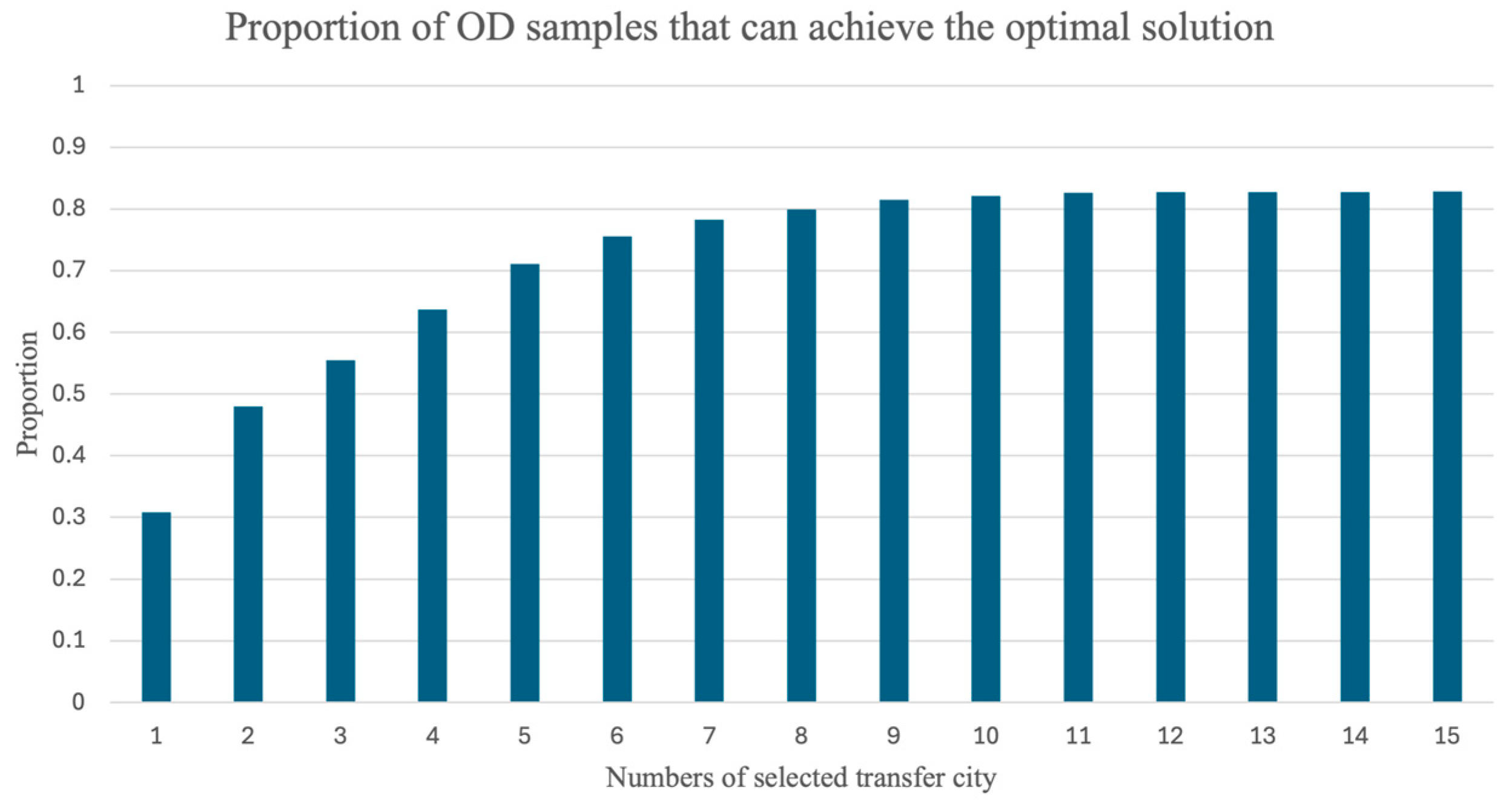
3.3.3. Comparison of Path Planning Results Quality
4. Conclusions
- The coordinate features of starting and terminal stations are more influential than unique identification label features.
- The XGBoost model can significantly enhance the computational speed of the path planning algorithm, reducing the average computation time by 50% in this paper’s experiments, with the maximum time reduction reaching 31%.
- The XGBoost model introduces a degree of compromise in path planning outcomes. This is observed through a modest decrease in the average number of viable paths for OD pairs. Additionally, there are instances where certain OD pairs may not readily reach the optimal routes. However, these effects are generally outweighed by the substantial gains in computational efficiency and the enhanced ability to manage complex path planning scenarios within acceptable time frames.
- Selecting a greater number of cities for transfers using XGBoost can lead to improved results, although this also increases the time required for path planning. Optimal results are generally achieved when selecting between seven and ten cities for transfers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, K.; Jiang, C.; Ng, A.K.; Zhu, Z. Air and rail connectivity patterns of major city clusters in China. Transp. Res. Part A Policy Pract. 2020, 139, 35–53. [Google Scholar] [CrossRef]
- Xu, T.; Ding, X.; Li, J. Research on the Connecting Path Search Algorithm for Air-Rail Integration. J. Softw. 2013, 8, 8. [Google Scholar] [CrossRef]
- Xu, F.; Zhu, J.F.; Miao, J.J.; Ding, R.R. Simulation of Two Stages-Variant Growth Evolution Model of High-speed Railway and Civil Aviation Compound Network. J. Syst. Simul. 2018, 30, 1369–1375. [Google Scholar]
- Xu, W.; He, S.; Song, R.; Chaudhry, S.S. Finding the K shortest paths in a schedule-based transit network. Comput. Oper. Res. 2012, 39, 1812–1826. [Google Scholar] [CrossRef]
- Magzhan, K.; Jani, H.M. A review and evaluations of shortest path algorithms. Int. J. Sci. Technol. Res 2013, 2, 99–104. [Google Scholar]
- Wang, S.X. The improved dijkstra’s shortest path algorithm and its application. Procedia Eng. 2012, 29, 1186–1190. [Google Scholar]
- Donald, G.; Hao, J.X.; Kai, S.R. Shortest path algorithms using dynamic breadth-first search. Networks 1991, 21, 29–50. [Google Scholar]
- Aranski, A.W. Depth First Search Algorithm In Solving the Shortest Route Using the Concept of Generate and Test. Int. J. Inf. Syst. Technol. 2022, 6, 353–360. [Google Scholar]
- Liu, L.; Wang, B.; Xu, H. Research on path-planning algorithm integrating optimization A-star algorithm and artificial potential field method. Electronics 2022, 11, 3600. [Google Scholar] [CrossRef]
- Dirk, S.; Christian, T. Running time analysis of ant colony optimization for shortest path problems. J. Discret. Algorithms 2012, 10, 165–180. [Google Scholar]
- Lin, L.; Gen, M. Priority-based genetic algorithm for shortest path routing problem in OSPF. In Intelligent and Evolutionary Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 91–103. [Google Scholar]
- Fu, L.; Sun, D.; Rilett, L.R. Heuristic shortest path algorithms for transportation applications: State of the art. Comput. Oper. Res. 2006, 33, 3324–3343. [Google Scholar] [CrossRef]
- Xu, F.; Zhu, J.F.; Miao, J.J. Optimization Design of Air-rail Network Based on Algorithm of Traversal and Search. In 2016 International Conference on Service Science, Technology and Engineering (SSTE 2016). Available online: https://scholar.archive.org/work/zsoehcritvgnpfxfxdkjp3rvyi/access/wayback/http://dpi-proceedings.com/index.php/dtetr/article/download/6493/6089 (accessed on 10 November 2024).
- Zheng, L.X.; Si, B.F. Hyper-graph based stochastic multimodal traffic network assignment problem. Shandong Sci. 2013, 26, 78–83. [Google Scholar]
- Gendreau, M.; Ghiani, G.; Guerriero, E. Time-dependent routing problems: A review. Comput. Oper. Res. 2015, 64, 189–197. [Google Scholar] [CrossRef]
- Nurhidayat, A.Y.; Widyastuti, H.; Sutikno; Upahita, D.P. Research on passengers’ preferences and impact of high-speed rail on air transport demand. Sustainability 2023, 15, 3060. [Google Scholar] [CrossRef]
- Fischer, F.; Helmberg, C. Dynamic graph generation for the shortest path problem in time expanded networks. Math. Program. 2014, 143, 257–297. [Google Scholar] [CrossRef]
- Geisberger, R.; Sanders, P.; Schultes, D.; Vetter, C. Exact routing in large road networks using contraction hierarchies. Transp. Sci. 2012, 46, 388–404. [Google Scholar] [CrossRef]
- Shi, H.; Cao, W.; Zhu, S.; Zhu, B. Applications of the Improved A* Algorithm for Route Planning. In Proceedings of the Second International Conference on Intelligent Computation Technology & Automation. IEEE Computer Society, Changsha, China, 10–11 October 2009. [Google Scholar]
- Chen, T. Xgboost: Extreme Gradient Boosting, R Package Version 0.4-2. 2015; Volume 1, p. 464. 2015. Available online: https://cran.ms.unimelb.edu.au/web/packages/xgboost/vignettes/xgboost.pdf (accessed on 23 December 2024).
- Chen, Z.; Fan, W. A freeway travel time prediction method based on an XGBoost model. Sustainability 2021, 13, 8577. [Google Scholar] [CrossRef]
- Ren, Q.; Wang, J. Research on Enterprise Digital-Level Classification Based on XGBoost Model. Sustainability 2023, 15, 2699. [Google Scholar] [CrossRef]



| Positive | Negative | |
|---|---|---|
| True | True Positive (TP) | True Negative (TN) |
| False | False Positive (FP) | False Negative (FN) |
| Feature | Definition | Attribute |
|---|---|---|
| The unique identification label of start station. | Categorical | |
| The unique identification label of terminal station. | Categorical | |
| The unique identification label of start city. | Categorical | |
| The unique identification label of terminal city. | Categorical | |
| The unique identification label of start province. | Categorical | |
| The unique identification label of terminal province. | Categorical | |
| The latitude of the start station. | Float | |
| The longitude of the start station. | Float | |
| The latitude of the terminal station. | Float | |
| The longitude of the terminal station. | Float | |
| The unique identification label of transfer station. | Categorical | |
| The unique identification label of transfer city. | Categorical | |
| The unique identification label of transfer province. | Categorical |
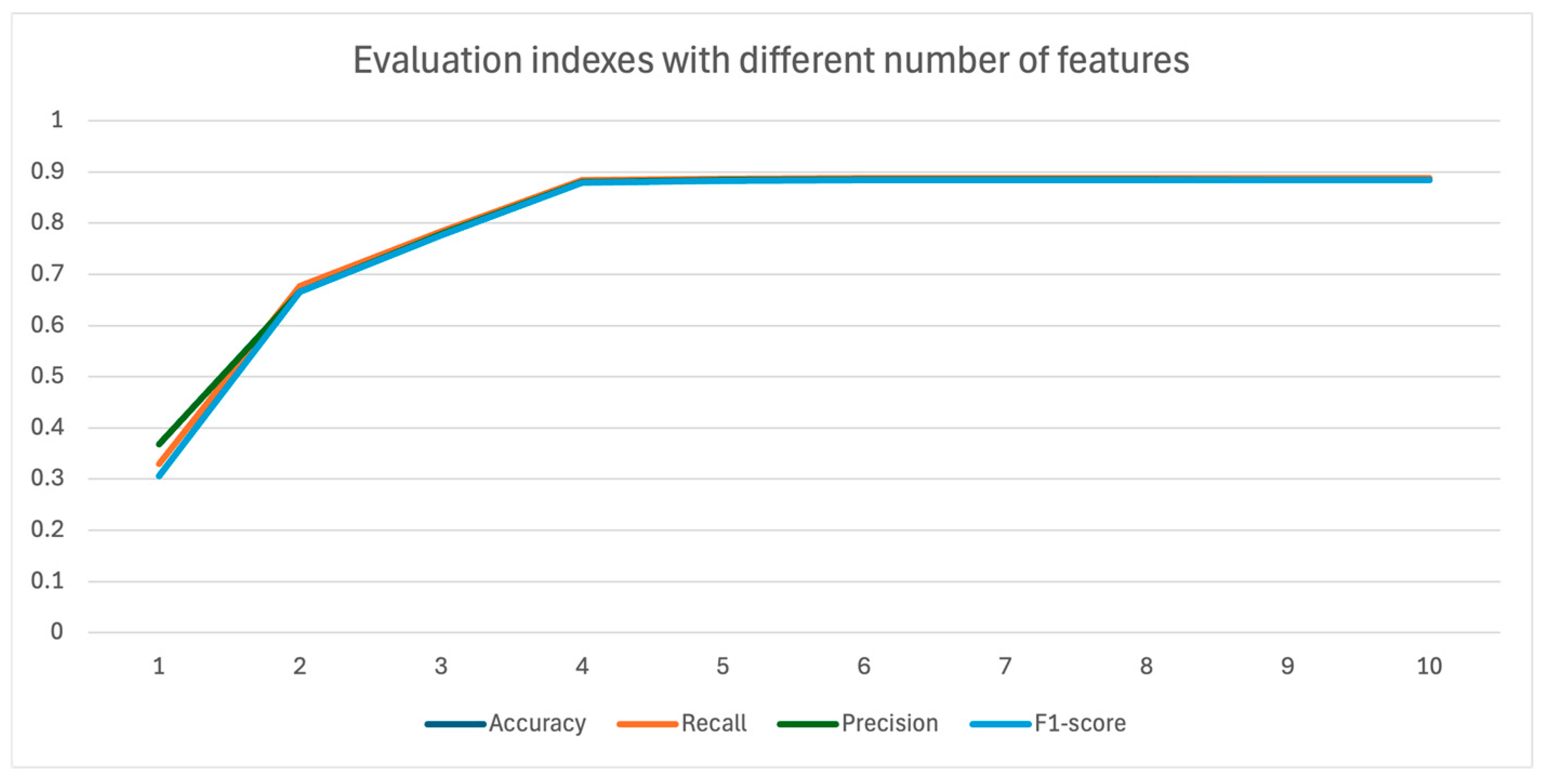
| Number of Features | Accuracy | Recall | Precision | F1-Score |
|---|---|---|---|---|
| 1 | 0.3297 | 0.3297 | 0.3686 | 0.3061 |
| 2 | 0.6768 | 0.6768 | 0.6653 | 0.6664 |
| 3 | 0.7831 | 0.7831 | 0.7787 | 0.7767 |
| 4 | 0.8836 | 0.8836 | 0.8798 | 0.8796 |
| 5 | 0.8865 | 0.8865 | 0.8842 | 0.8827 |
| 6 | 0.8873 | 0.8873 | 0.8851 | 0.8837 |
| 7 | 0.8875 | 0.8875 | 0.8853 | 0.8838 |
| 8 | 0.8879 | 0.8879 | 0.8849 | 0.8842 |
| 9 | 0.8877 | 0.8877 | 0.8841 | 0.8841 |
| 10 | 0.8880 | 0.8880 | 0.8844 | 0.8843 |
| Evaluation Index | Before Parameter Adjustment | After Parameter Adjustment |
|---|---|---|
| Accuracy | 0.8836 | 0.8903 |
| Recall | 0.8836 | 0.8904 |
| Precision | 0.8798 | 0.8877 |
| F1-Score | 0.8796 | 0.8876 |
| Fold | Accuracy |
|---|---|
| 1 | 0.8848 |
| 2 | 0.8835 |
| 3 | 0.8846 |
| 4 | 0.8857 |
| 5 | 0.8855 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weng, S.; Shan, X.; Bai, G.; Wu, J.; Zhao, N. XGBoost-Based Heuristic Path Planning Algorithm for Large Scale Air–Rail Intermodal Networks. Inventions 2025, 10, 27. https://doi.org/10.3390/inventions10020027
Weng S, Shan X, Bai G, Wu J, Zhao N. XGBoost-Based Heuristic Path Planning Algorithm for Large Scale Air–Rail Intermodal Networks. Inventions. 2025; 10(2):27. https://doi.org/10.3390/inventions10020027
Chicago/Turabian StyleWeng, Shengyuan, Xinghua Shan, Guangdong Bai, Jinfei Wu, and Nan Zhao. 2025. "XGBoost-Based Heuristic Path Planning Algorithm for Large Scale Air–Rail Intermodal Networks" Inventions 10, no. 2: 27. https://doi.org/10.3390/inventions10020027
APA StyleWeng, S., Shan, X., Bai, G., Wu, J., & Zhao, N. (2025). XGBoost-Based Heuristic Path Planning Algorithm for Large Scale Air–Rail Intermodal Networks. Inventions, 10(2), 27. https://doi.org/10.3390/inventions10020027






