Analysis of Contact Noise Due to Elastic Recovery of Surface Asperities for Spherical Contact
Abstract
:1. Introduction
2. Theoretical Model for Contact Noise
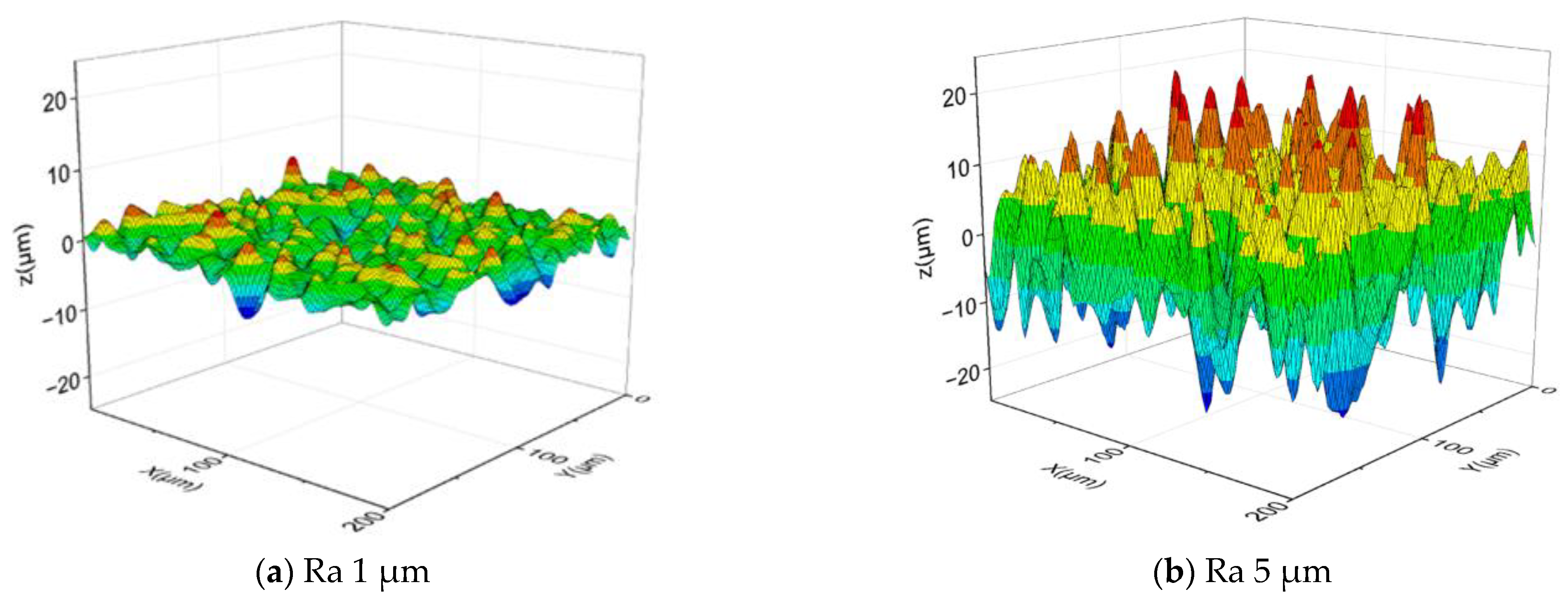
2.1. Rough Surface Generation
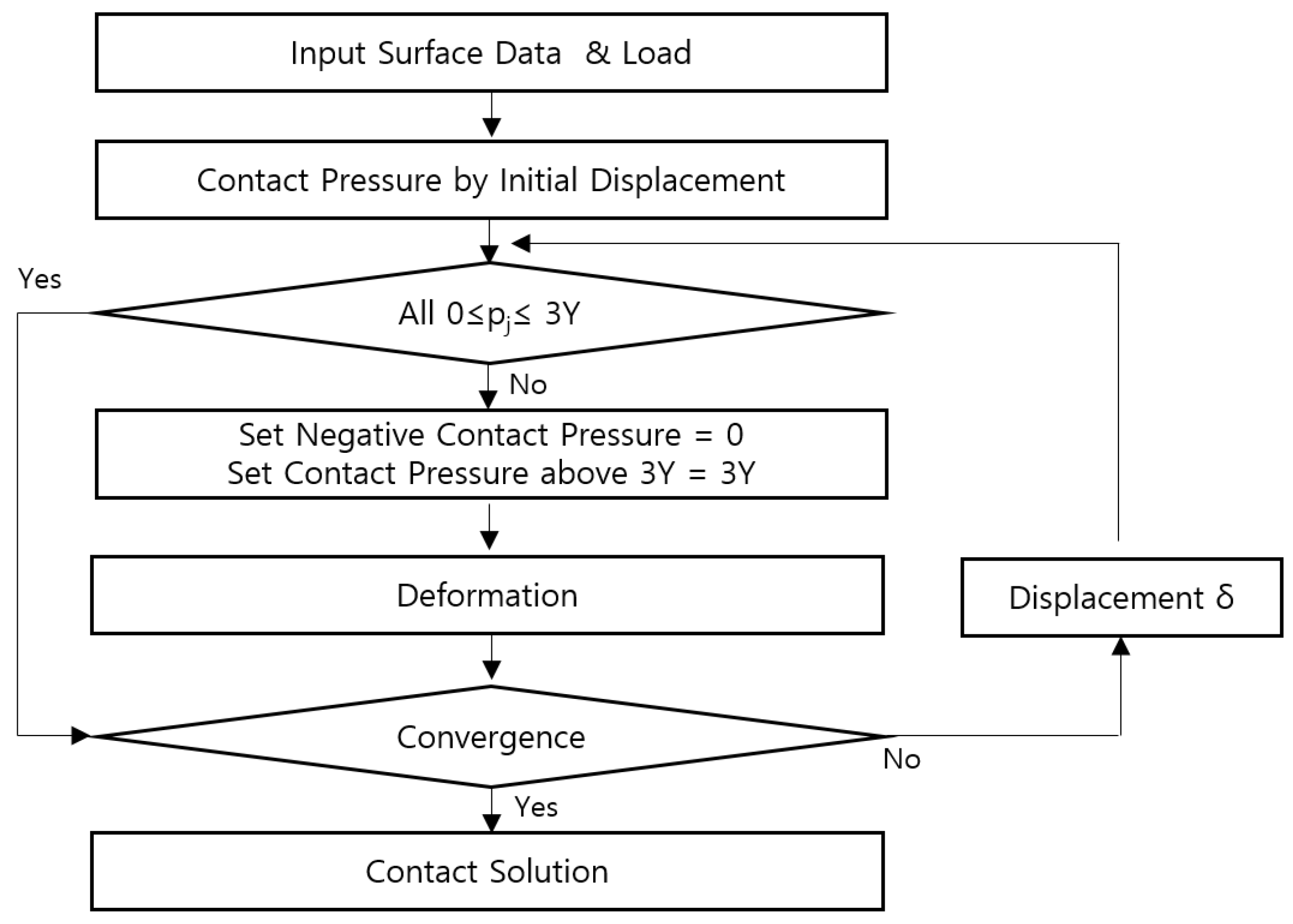
2.2. Contact Analysis
2.3. Contact Noise Analysis
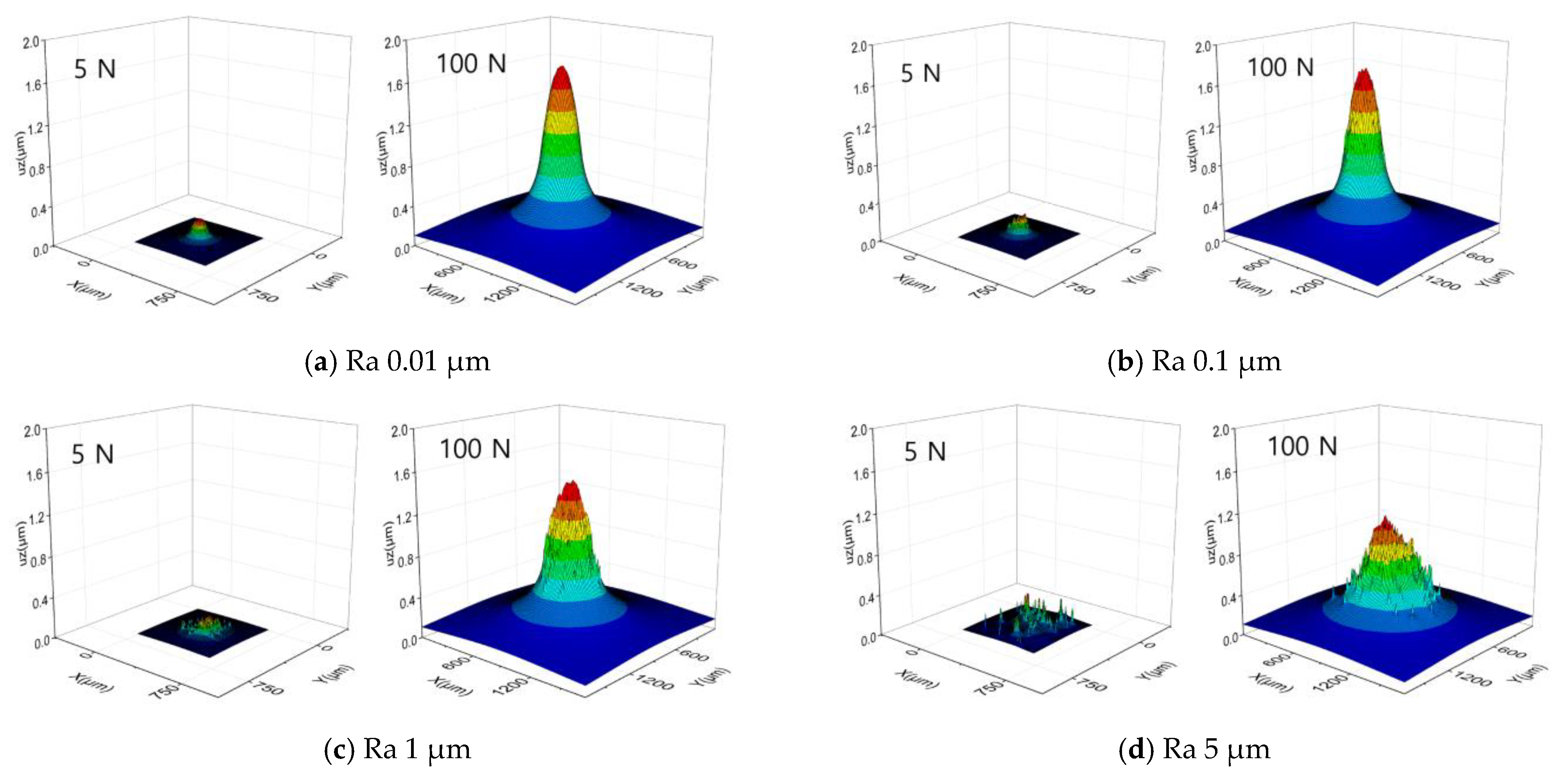
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ananthapadmanaban, T.; Radhakrishnan, V. An investigation of the role of surface irregularities in the noise spectrum of rolling and sliding contacts. Wear 1982, 83, 399–409. [Google Scholar] [CrossRef]
- Baranov, V.; Kudryavtsev, E.; Sarychev, G.; Schavelin, V. Friction of solids and nature of acoustic emission. In Acoustic Emission in Friction; Baranov, V., Kudryavtsev, E., Sarychev, G., Schavelin, V., Eds.; Elsevier: Moscow, Russia, 2007; Volume 53, pp. 1–36. [Google Scholar]
- Fan, Y.; Gu, F.; Ball, A. Modelling acoustic emissions generated by sliding friction. Wear 2010, 268, 811–815. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of Nominally Flat Surfaces. Proc. Roy. Soc. 1966, A295, 300–319. [Google Scholar]
- Sharma, R.B.; Parey, A.; Tandon, N. Modelling of acoustic emission generated in involute spur gear pair. J. Sound Vib. 2017, 393, 353–373. [Google Scholar] [CrossRef]
- Sharma, R.B.; Parey, A. Modelling of acoustic emission generated due to pitting on spur gear. Eng. Fail. Anal. 2018, 86, 1–20. [Google Scholar] [CrossRef]
- Sharma, R.B.; Parey, A. Modelling of acoustic emission generated in rolling element bearing. Appl. Acoust. 2019, 144, 96–112. [Google Scholar] [CrossRef]
- Abdo, J.A. Investigation of contact stiffness and its relation to friction-induced noise and vibration. Int. J. Model. Simul. 2006, 26, 295–302. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Li, J.; Liu, K. Effect of textured surface on the frictional noise under line contact and sliding–rolling conditions. P. I. Mech. Eng. C-J. Mec. 2018, 232, 1679–1689. [Google Scholar] [CrossRef]
- Kozupa, M.; Kolusz, G.; Świątkowski, M. Acoustic radiation efficiency parameter in assessment of transformer noise. In Proceedings of the Euronoise 2018, Heraklion, Greece, 27–31 May 2018. [Google Scholar]
- Feng, P.; Borghesani, P.; Smith, W.A.; Randall, R.B.; Peng, Z. A review on the relationships between acoustic emission, friction and wear in mechanical systems. Appl. Mech. Rev. 2020, 72, 020801. [Google Scholar] [CrossRef]
- Feng, P.; Borghesani, P.; Smith, W.A.; Peng, Z. Model-based surface roughness prediction using acoustic emission signals. Tribol. Int. 2020, 144, 106101. [Google Scholar] [CrossRef]
- Lontin, K.; Khan, M.A. Wear and Airborne Noise Interdependency at Asperitical Level: Analytical Modelling and Experimental Validation. Materials 2021, 14, 7308. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.Y.; Mo, J.L.; Wang, X.C.; Zhu, M.H.; Zhou, Z.R. Effect of surface roughness on friction-induced noise: Exploring the generation of squeal at sliding friction interface. Wear 2018, 402–403, 80–90. [Google Scholar] [CrossRef]
- Sun, J.; Yang, H.; Li, D.; Xu, C. Analysis of friction-related acoustic emission in bolted joint structures. Int. J. Mech. Syst. Dyn. 2023, 3, 383–396. [Google Scholar] [CrossRef]
- Borghesani, P.; Smith, W.A.; Zhang, X.; Feng, P.; Antoni, J.; Peng, Z. A new statistical model for acoustic emission signals generated from sliding contact in machine elements. Tribol. Int. 2018, 127, 412–419. [Google Scholar] [CrossRef]
- Nahornyi, V.; Panda, A.; Valíček, J.; Harničárová, M.; Kušnerová, M.; Pandová, I.; Legutko, S.; Palková, Z.; Lukáč, O. Method of Using the Correlation between the Surface Roughness of Metallic Materials and the Sound Generated during the Controlled Machining Process. Materials 2022, 15, 823. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Kim, S.; Seo, Y.H.; Song, W. Acoustic emission analysis for monitoring tribological behaviors of steel coated with zinc phosphate/stearate for cold forging. Tribol. Int. 2024, 196, 109641. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Qu, Y.; He, D. Gear pitting fault diagnosis using integrated cnn and gru network with both vibration and acoustic emission signals. Appl. Sci. 2019, 9, 768. [Google Scholar] [CrossRef]
- Leaman, F.; Vicuña, C.; Clausen, E. A review of gear fault diagnosis of planetary gearboxes using acoustic emissions. Acoust. Aust. 2021, 49, 265–272. [Google Scholar] [CrossRef]
- Patir, N. A numerical procedure for random generation of rough surfaces. Wear 1978, 47, 263–277. [Google Scholar] [CrossRef]
- Lee, S.C.; Cheng, H.S. On the relation of load to average gap in the contact between surfaces with longitudinal roughness. Tribol. Trans. 1992, 35, 523–529. [Google Scholar] [CrossRef]
- Kim, T.W.; Bhushan, B.; Cho, Y.J. The contact behavior of elastic/plastic non-Gaussian rough surfaces. Tribol. Lett. 2006, 22, 1–13. [Google Scholar] [CrossRef]
- Love, A.E.H. The stress produced in a semi-infinite solid by pressure on part of the boundary. Proc. Roy. Soc. London 1929, A228, 377–420. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, B.; Kim, K.; Kim, T. Analysis of Contact Noise Due to Elastic Recovery of Surface Asperities for Spherical Contact. Inventions 2025, 10, 17. https://doi.org/10.3390/inventions10010017
Lee B, Kim K, Kim T. Analysis of Contact Noise Due to Elastic Recovery of Surface Asperities for Spherical Contact. Inventions. 2025; 10(1):17. https://doi.org/10.3390/inventions10010017
Chicago/Turabian StyleLee, Bora, Kyungseob Kim, and Taewan Kim. 2025. "Analysis of Contact Noise Due to Elastic Recovery of Surface Asperities for Spherical Contact" Inventions 10, no. 1: 17. https://doi.org/10.3390/inventions10010017
APA StyleLee, B., Kim, K., & Kim, T. (2025). Analysis of Contact Noise Due to Elastic Recovery of Surface Asperities for Spherical Contact. Inventions, 10(1), 17. https://doi.org/10.3390/inventions10010017





