A Two-Plane Proton Radiography System Using ATLAS IBL Pixel-Detector Modules
Abstract
1. Introduction
2. Materials and Methods
2.1. ATLAS IBL Pixel-Detector Module
2.2. Experimental Setup and Working Principle
2.2.1. The Two-Plane Imaging System Prototype
2.2.2. Beam Characteristics and Imaging Dose
2.2.3. Phantoms
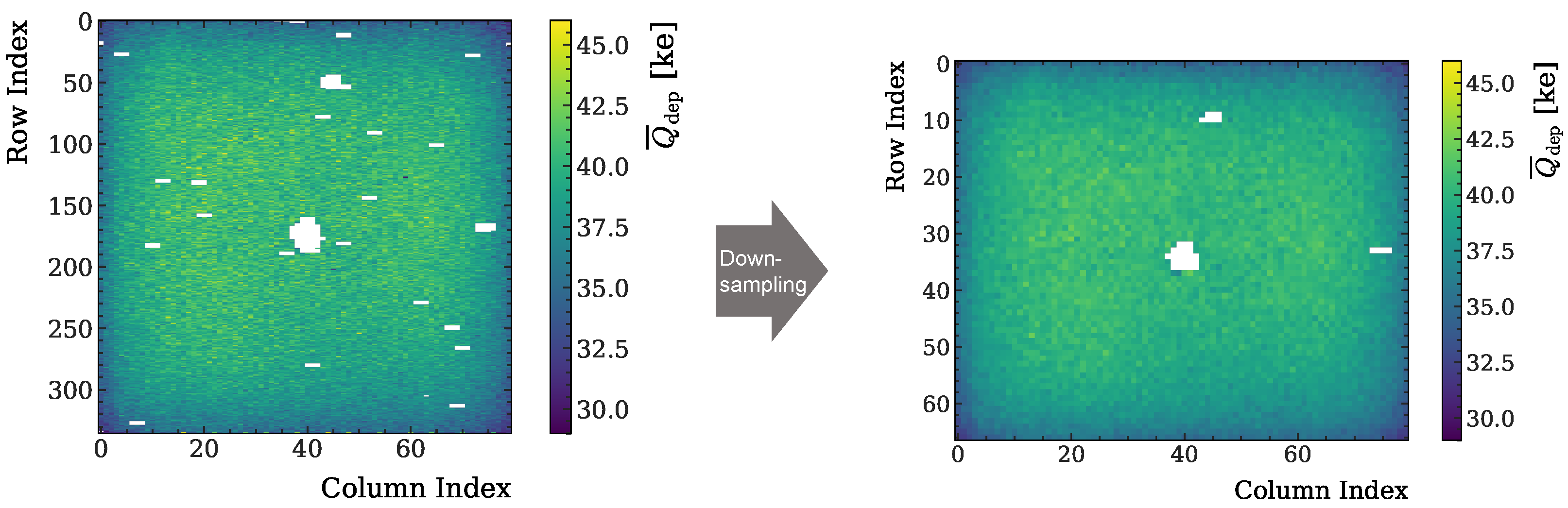
2.2.4. Data Post-Processing
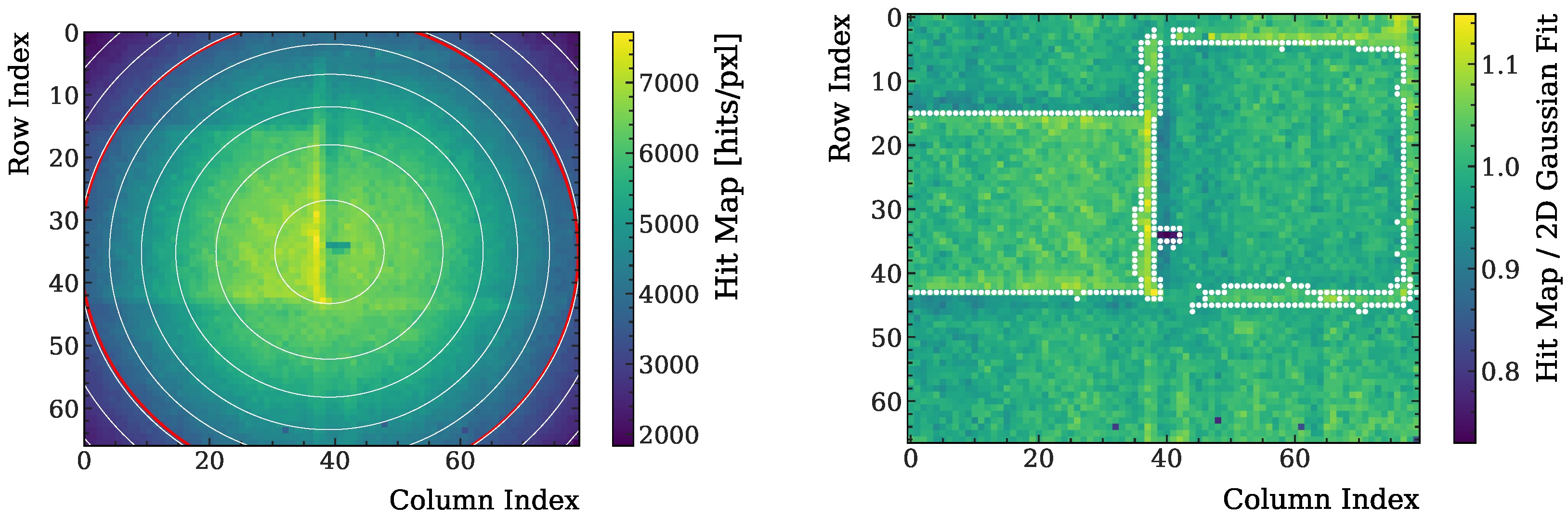
2.3. First Detector: Determining Image Contours
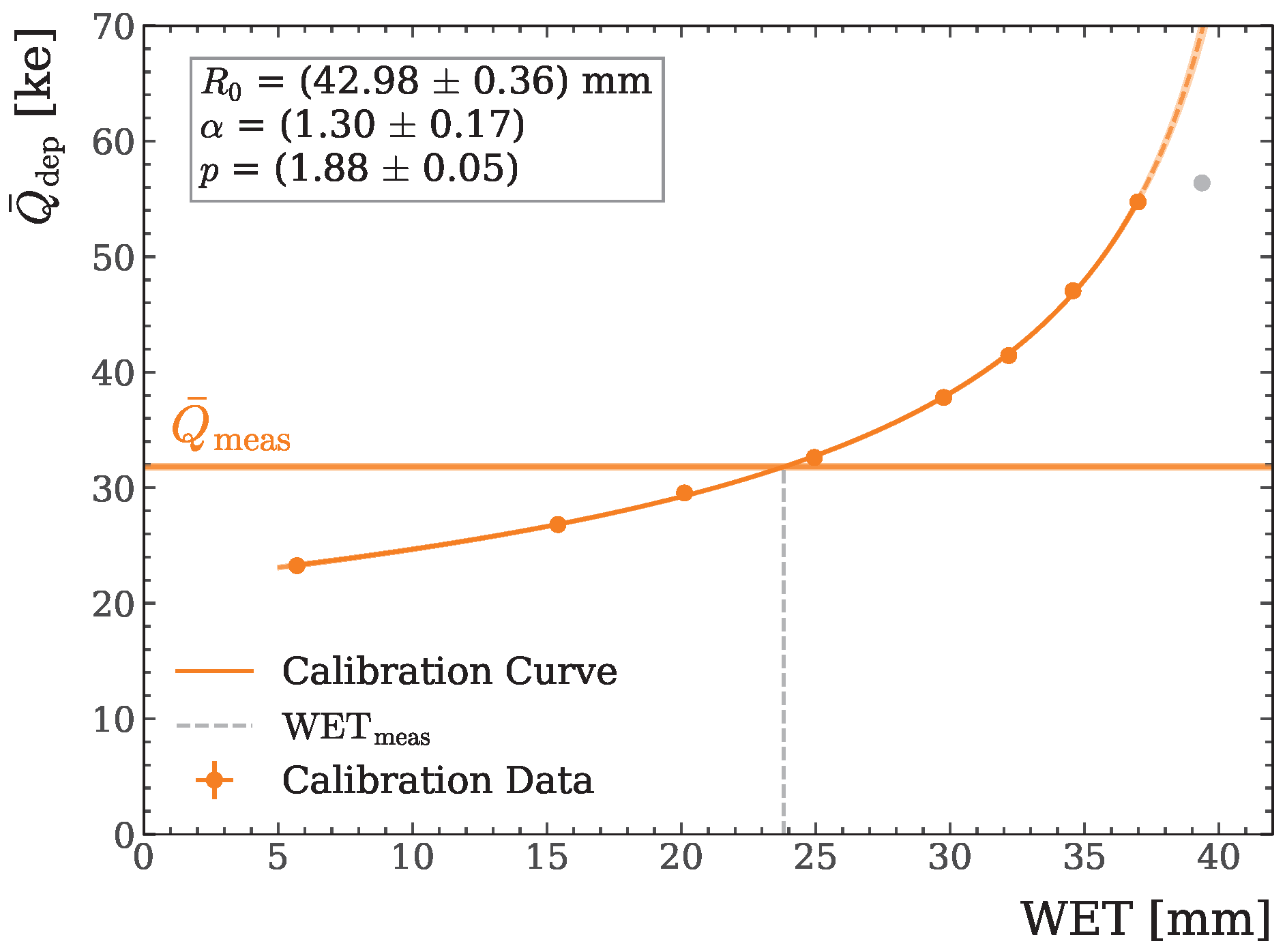
2.4. Second Detector: WET Image Calculation
2.5. WET Accuracy Study
2.6. WET Contrast Study
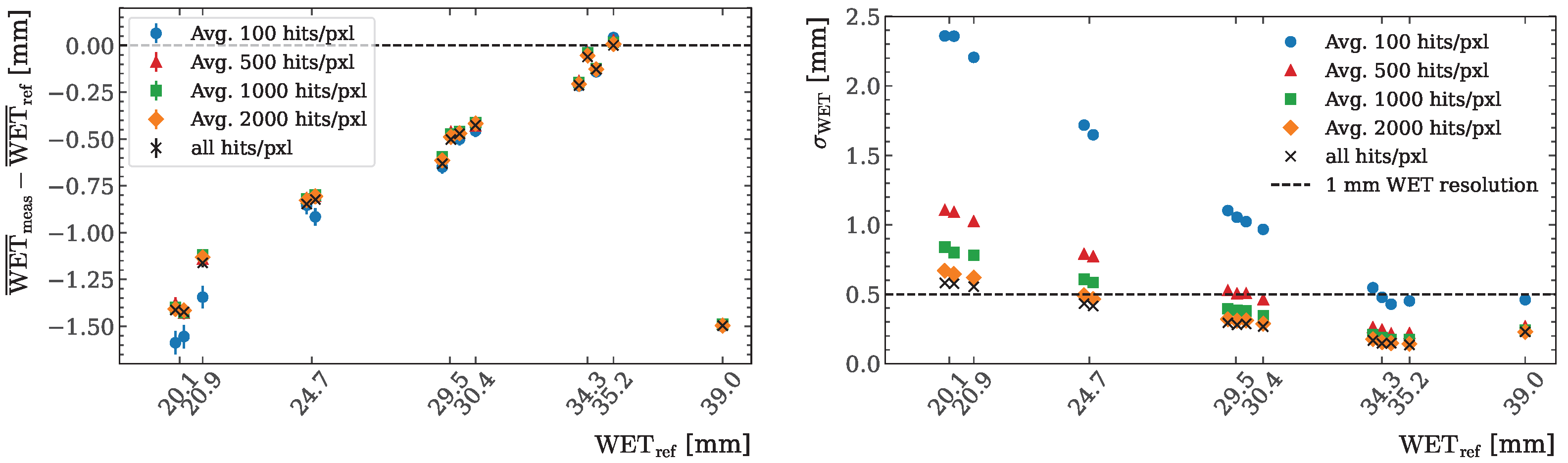
2.7. Varying Hits per Pixel Study
2.8. Changing WET Study
3. Results
3.1. WET Accuracy Study
3.2. WET Contrast Study
3.3. Varying Hits per Pixel Study
3.4. Changing WET Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IBL | Insertable B-Layer |
| ROI | Region of interest |
| SEM | Standard error of the mean |
| TLU | Trigger logic unit |
| ToT | Time over Threshold |
| TPIS | Two-Plane Imaging System |
| WER | Water equivalent ratio |
| WET | Water equivalent thickness |
Appendix A. Varying Hits per Pixel Study

References
- Lomax, A. SFUD, IMPT, and Plan Robustness. In Particle Radiotherapy: Emerging Technology for Treatment of Cancer; Rath, A.K., Sahoo, N., Eds.; Springer: New Delhi, India, 2016; pp. 169–194. [Google Scholar] [CrossRef]
- Van De Water, S.; Albertini, F.; Weber, D.C.; Heijmen, B.J.M.; Hoogeman, M.S.; Lomax, A.J. Anatomical Robust Optimization to Account for Nasal Cavity Filling Variation during Intensity-Modulated Proton Therapy: A Comparison with Conventional and Adaptive Planning Strategies. Phys. Med. Biol. 2018, 63, 025020. [Google Scholar] [CrossRef] [PubMed]
- Albertini, F.; Matter, M.; Nenoff, L.; Zhang, Y.; Lomax, A. Online Daily Adaptive Proton Therapy. Br. J. Radiol. 2020, 93, 20190594. [Google Scholar] [CrossRef]
- Paganetti, H.; Botas, P.; Sharp, G.C.; Winey, B. Adaptive Proton Therapy. Phys. Med. Biol. 2021, 66, 22TR01. [Google Scholar] [CrossRef]
- Sarosiek, C.; DeJongh, E.A.; Coutrakon, G.; DeJongh, D.F.; Duffin, K.L.; Karonis, N.T.; Ordoñez, C.E.; Pankuch, M.; Rykalin, V.; Winans, J.R.; et al. Analysis of characteristics of images acquired with a prototype clinical proton radiography system. Med. Phys. 2021, 48, 2271–2278. [Google Scholar] [CrossRef]
- Parodi, K. Latest developments in in-vivo imaging for proton therapy. Br. J. Radiol. 2020, 93, 20190787. [Google Scholar] [CrossRef]
- Knopf, A.C.; Lomax, A. In Vivo Proton Range Verification: A Review. Phys. Med. Biol. 2013, 58, 131–160. [Google Scholar] [CrossRef]
- Schneider, U.; Besserer, J.; Pemler, P.; Dellert, M.; Moosburger, M.; Pedroni, E.; Kaser-Hotz, B. First Proton Radiography of an Animal Patient. Med. Phys. 2004, 31, 1046–1051. [Google Scholar] [CrossRef]
- Esposito, M.; Waltham, C.; Taylor, J.T.; Manger, S.; Phoenix, B.; Price, T.; Poludniowski, G.; Green, S.; Evans, P.M.; Allport, P.P.; et al. PRaVDA: The first solid-state system for proton computed tomography. Phys. Med. 2018, 55, 149–154. [Google Scholar] [CrossRef]
- Johnson, R.P.; Bashkirov, V.; DeWitt, L.; Giacometti, V.; Hurley, R.F.; Piersimoni, P.; Plautz, T.E.; Sadrozinski, H.F.W.; Schubert, K.; Schulte, R.; et al. A Fast Experimental Scanner for Proton CT: Technical Performance and First Experience with Phantom Scans. IEEE Trans. Nucl. Sci. 2016, 63, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Amato, C.; Martisikova, M.; Gehrke, T. A technique for spatial resolution improvement in helium-beam radiography. Med. Phys. 2020, 47, 2212–2221. [Google Scholar] [CrossRef] [PubMed]
- DeJongh, E.A.; DeJongh, D.F.; Polnyi, I.; Rykalin, V.; Sarosiek, C.; Coutrakon, G.; Duffin, K.L.; Karonis, N.T.; Ordoñez, C.E.; Pankuch, M.; et al. Technical Note: A Fast and Monolithic Prototype Clinical Proton Radiography System Optimized for Pencil Beam Scanning. Med. Phys. 2021, 48, 1356–1364. [Google Scholar] [CrossRef]
- Landry, G.; Dedes, G.; Collins-Fekete, C.A.; Krah, N.; Simard, M.; Rit, S. Ion and secondary imaging. Phys. Med. Biol. 2024, 69, 240301. [Google Scholar] [CrossRef]
- Metzner, M.; Zhevachevska, D.; Schlechter, A.; Kehrein, F.; Schlecker, J.; Murillo, C.; Brons, S.; Jäkel, O.; Martišíková, M.; Gehrke, T. Energy Painting: Helium-Beam Radiography with Thin Detectors and Multiple Beam Energies. Phys. Med. Biol. 2024, 69, 055002. [Google Scholar] [CrossRef] [PubMed]
- Grinstein, S. Overview of the ATLAS insertable B-layer (IBL) project. Nucl. Instrum. Methods Phys. Res. 2013, 699, 61–66. [Google Scholar] [CrossRef]
- Krah, N.; Khellaf, F.; Létang, J.M.; Rit, S.; Rinaldi, I. A Comprehensive Theoretical Comparison of Proton Imaging Set-Ups in Terms of Spatial Resolution. Phys. Med. Biol. 2018, 63, 135013. [Google Scholar] [CrossRef] [PubMed]
- Schilling, I.; Bäcker, C.M.; Bäumer, C.; Behrends, C.; Hötting, M.; Hohmann, J.; Kröninger, K.; Timmermann, B.; Weingarten, J. Measuring the Beam Energy in Proton Therapy Facilities Using ATLAS IBL Pixel Detectors. Instruments 2022, 6, 80. [Google Scholar] [CrossRef]
- Lascaud, J.; Dash, P.; Schnürle, K.; Bortfeldt, J.; Niepel, K.; Maas, J.; Würl, M.; Vidal, M.; Hérault, J.; Landry, G.; et al. Fabrication and Characterization of a Multimodal 3D Printed Mouse Phantom for Ionoacoustic Quality Assurance in Image-Guided Pre-Clinical Proton Radiation Research. Phys. Med. Biol. 2022, 67, 205001. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sciveres, M.; Arutinov, D.; Barbero, M.; Beccherle, R.; Dube, S.; Elledge, D.; Fleury, J.; Fougeron, D.; Gensolen, F.; Gnani, D.; et al. The FE-I4 pixel readout integrated circuit. Nucl. Instrum. Methods Phys. Res. 2011, 636, S155–S159. [Google Scholar] [CrossRef]
- International Commission on Radiation Units and Measurements. Stopping Powers and Ranges for Protons and Alpha Particles; Technical report; ICRU Report 49; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 1993. [Google Scholar]
- FE-I4 Collaboration. The FE-I4B Integrated Circuit Guide; The FE-I4 Collaboration; CERN: Geneva, Switzerland, 2012. [Google Scholar]
- Commissioning Data provided by the West German Proton Therapy Centre Essen, 2024.
- Behrends, C.; Bäcker, C.M.; Schilling, I.; Zwiehoff, S.; Weingarten, J.; Kröninger, K.; Rehbock, C.; Barcikowski, S.; Wulff, J.; Bäumer, C.; et al. The Radiosensitizing Effect of Platinum Nanoparticles in Proton Irradiations Is Not Caused by an Enhanced Proton Energy Deposition at the Macroscopic Scale. Phys. Med. Biol. 2022, 67, 155023. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Newhauser, W.D. Calculation of Water Equivalent Thickness of Materials of Arbitrary Density, Elemental Composition and Thickness in Proton Beam Irradiation. Phys. Med. Biol. 2009, 54, 1383–1395. [Google Scholar] [CrossRef]
- Barlow, R. Statistics: A Guide to the Use of Statistical Methods in the Physical Sciences, 1st ed.; John Wiley & Sons Ltd.: Chichester, England, 1989. [Google Scholar]
- Campbell, M.; Havranek, V.; Heijne, E.; Holy, T.; Idarraga, J.; Jakubek, J.; Lebel, C.; Leroy, C.; Llopart, X.; Novotny, J.; et al. Charge collection from proton and alpha particle tracks in silicon pixel detector devices. In Proceedings of the 2007 IEEE Nuclear Science Symposium Conference Record, Honolulu, HI, USA, 26 October–3 November 2007; Volume 2, pp. 1047–1050. [Google Scholar] [CrossRef]
- Cookson, J. Radiography with protons. Naturwissenschaften 1974, 61, 184–191. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Bortfeld, T. An Analytical Approximation of the Bragg Curve for Therapeutic Proton Beams. Med. Phys. 1997, 24, 2024–2033. [Google Scholar] [CrossRef]
- Bäumer, C.; Koska, B.; Lambert, J.; Timmermann, B.; Mertens, T.; Talla, P.T. Evaluation of Detectors for Acquisition of Pristine Depth-dose Curves in Pencil Beam Scanning. J. Appl. Clin. Med. Phys. 2015, 16, 151–163. [Google Scholar] [CrossRef]
- Dhanesar, S.; Sahoo, N.; Kerr, M.; Taylor, M.B.; Summers, P.; Zhu, X.R.; Poenisch, F.; Gillin, M. Quality Assurance of Proton Beams Using a Multilayer Ionization Chamber System. Med. Phys. 2013, 40, 092102. [Google Scholar] [CrossRef]
- Metzner, M.; Longarino, F.K.; Ackermann, B.; Schlechter, A.; Saphörster, M.; Xu, Y.; Schlecker, J.; Wohlfahrt, P.; Richter, C.; Brons, S.; et al. Accuracy of a Helium-beam Radiography System Based on Thin Pixel Detectors for an Anthropomorphic Head Phantom. Med. Phys. 2025, 52, 4757–4768. [Google Scholar] [CrossRef]
- Pottier, L.L.; Heim, T.; Garcia-Sciveres, M. Testing the limits of ITkPixV2: The ATLAS inner tracker pixel detector readout chip. arXiv 2025, arXiv:2502.05097. [Google Scholar] [CrossRef]
- Seller Oria, C.; Free, J.; Marmitt, G.G.; Knäusl, B.; Brandenburg, S.; Knopf, A.C.; Meijers, A.; Langendijk, J.A.; Both, S. Technical Note: Flat Panel Proton Radiography with a Patient Specific Imaging Field for Accurate WEPL Assessment. Med. Phys. 2023, 50, 1756–1765. [Google Scholar] [CrossRef] [PubMed]
- Mumot, M.; Algranati, C.; Hartmann, M.; Schippers, J.M.; Hug, E.; Lomax, A.J. Proton Range Verification Using a Range Probe: Definition of Concept and Initial Analysis. Phys. Med. Biol. 2010, 55, 4771–4782. [Google Scholar] [CrossRef] [PubMed]
- Farace, P.; Righetto, R.; Meijers, A. Pencil Beam Proton Radiography Using a Multilayer Ionization Chamber. Phys. Med. Biol. 2016, 61, 4078–4087. [Google Scholar] [CrossRef]
- Hammi, A.; Placidi, L.; Weber, D.C.; Lomax, A.J. Positioning of Head and Neck Patients for Proton Therapy Using Proton Range Probes: A Proof of Concept Study. Phys. Med. Biol. 2017, 63, 015025. [Google Scholar] [CrossRef] [PubMed]
- Hammi, A.; Koenig, S.; Weber, D.C.; Poppe, B.; Lomax, A.J. Patient Positioning Verification for Proton Therapy Using Proton Radiography. Phys. Med. Biol. 2018, 63, 245009. [Google Scholar] [CrossRef] [PubMed]
- Lim-Reinders, S.; Keller, B.M.; Al-Ward, S.; Sahgal, A.; Kim, A. Online Adaptive Radiation Therapy. Int. J. Radiat. Oncol. Biol. Phys. 2017, 99, 994–1003. [Google Scholar] [CrossRef] [PubMed]











| Calibration Phantom | Step Phantom | Complex Phantom | ||||
|---|---|---|---|---|---|---|
| t [mm] | WET [mm] | WER | WET [mm] | t [mm] | WET [mm] | |
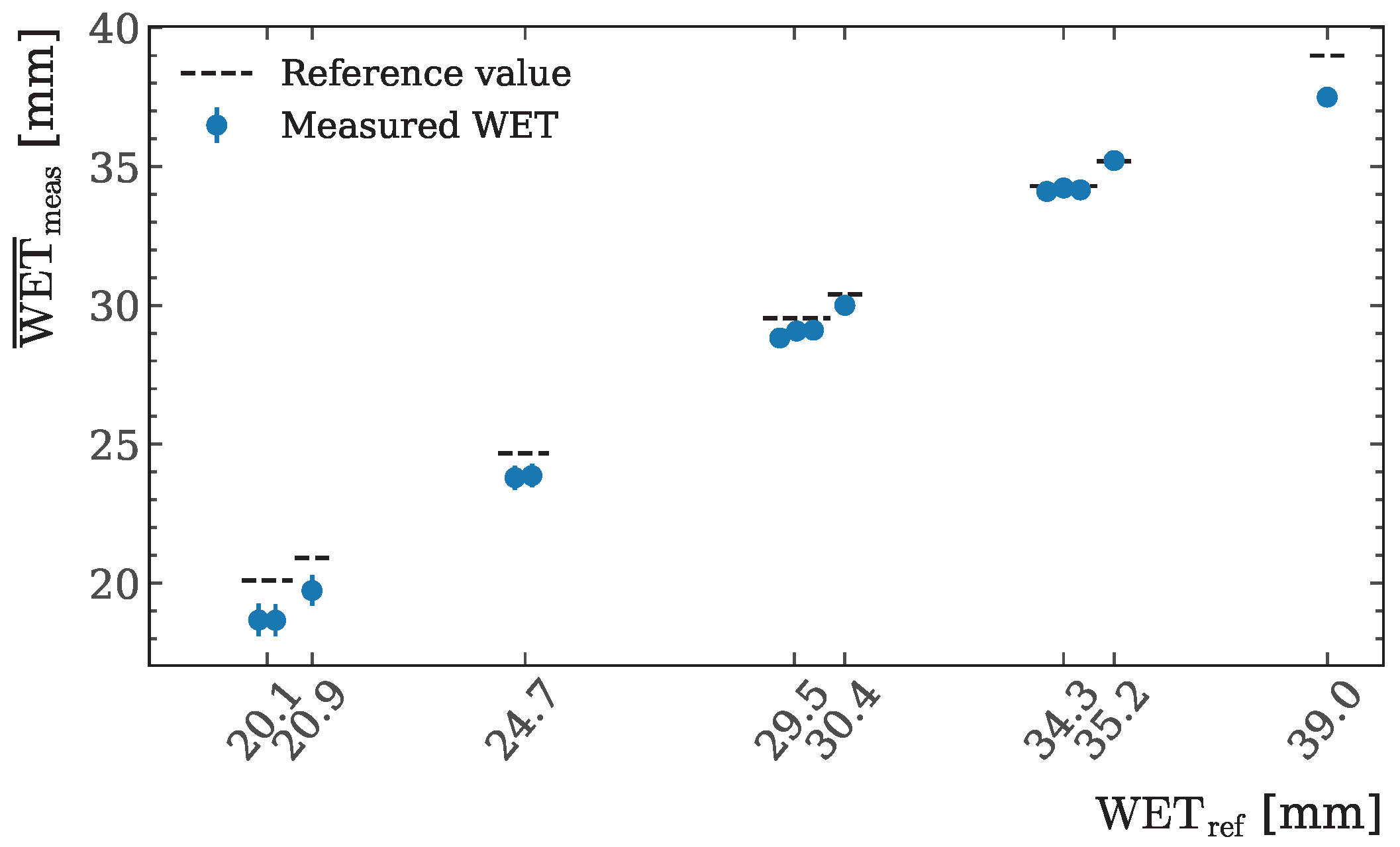
| 4.89(4) | 5.70(1) | 1.165(11) | 20.08(2)/20.89(2) | Pos. 1 | 5.26(1) | 6.12(2) |
| 9.13(5) | 10.56(1) | 1.157(6) | 20.08(2)/24.64(2) | Pos. 2 | 8.28(1) | 9.63(2) |
| 13.2(1) | 15.41(1) | 1.165(5) | 24.69(2)/29.46(2) | Pos. 3 | 12.24(1) | 14.23(3) |
| 17.3(1) | 20.12(1) | 1.164(5) | 29.58(2)/30.43(2) | Pos. 4 | 12.21(1) | 14.20(3) |
| 21.4(1) | 24.95(2) | 1.167(5) | 29.58(2)/34.32(2) | Pos. 5 | 9.33(1) | 10.85(2) |
| 25.7(1) | 29.76(2) | 1.160(4) | 34.29(2)/35.22(2) | Pos. 6 | 9.20(1) | 10.70(2) |
| 27.7(1) | 32.18(2) | 1.161(4) | 34.29(2)/39.00(2) | 9.96(1) | 12.5(1) | |
| 29.8(1) | 34.57(2) | 1.162(4) | 9.86(1) | 11.47(2) | ||
| 31.8(1) | 36.99(2) | 1.162(4) | 3.80(5) | 4.75(7) | ||
| 34.1(1) | 39.37(2) | 1.156(4) | 3.30(5) | 3.84(6) | ||
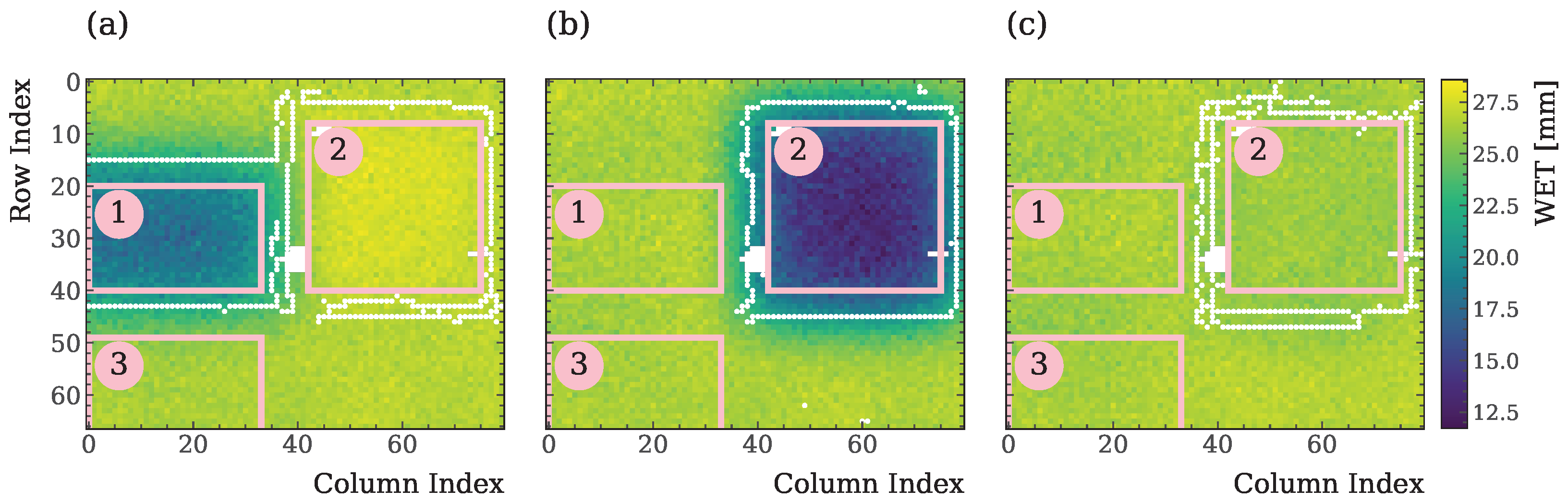
| ROI | Positions | WETsetup (a) [mm] | WETsetup (b) [mm] | WETsetup (c) [mm] |
|---|---|---|---|---|
| 1 | 2 & 5 | 20.48(4) | 29.06(10) | 29.06(10) |
| 2 | 1 & 6 | 29.26(11) | 16.81(4) | 28.28(6) |
| 3 | 3 & 4 | 28.43(5) | 28.43(5) | 28.43(5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Speiser, H.; Bäcker, C.M.; Esser, J.; Hild, A.; Iampieri, M.; Lüvelsmeyer, A.-K.; Tappe, A.; Thews, H.; Kröninger, K.; Weingarten, J. A Two-Plane Proton Radiography System Using ATLAS IBL Pixel-Detector Modules. Instruments 2025, 9, 23. https://doi.org/10.3390/instruments9040023
Speiser H, Bäcker CM, Esser J, Hild A, Iampieri M, Lüvelsmeyer A-K, Tappe A, Thews H, Kröninger K, Weingarten J. A Two-Plane Proton Radiography System Using ATLAS IBL Pixel-Detector Modules. Instruments. 2025; 9(4):23. https://doi.org/10.3390/instruments9040023
Chicago/Turabian StyleSpeiser, Hendrik, Claus Maximillian Bäcker, Johannes Esser, Alina Hild, Marco Iampieri, Ann-Kristin Lüvelsmeyer, Annsofie Tappe, Helen Thews, Kevin Kröninger, and Jens Weingarten. 2025. "A Two-Plane Proton Radiography System Using ATLAS IBL Pixel-Detector Modules" Instruments 9, no. 4: 23. https://doi.org/10.3390/instruments9040023
APA StyleSpeiser, H., Bäcker, C. M., Esser, J., Hild, A., Iampieri, M., Lüvelsmeyer, A.-K., Tappe, A., Thews, H., Kröninger, K., & Weingarten, J. (2025). A Two-Plane Proton Radiography System Using ATLAS IBL Pixel-Detector Modules. Instruments, 9(4), 23. https://doi.org/10.3390/instruments9040023






