Faraday Cups: Principles, Designs, and Applications Across Scientific Disciplines—A Review
Abstract
1. Introduction
2. Operating Principle
- Leakage currents from the suppressor electrode: If the isolation between the FC and the suppressor electrode is poor, it may create a conducting path [36]. This can be improved by using high purity insulating bushes and isolators (such as Alumina, Teflon, Polyetheretherketone (PEEK), Garolite (G-10), etc.).
- Charged particles from residual gas: This is typical for broad beam ion sources operating at higher background pressures [24]. Here, the chances of trapped gas remnants inside the FC cavity are quite high. The incoming particle can ionize the gas within the FC cavity and lead to a falsification of the measured signal due to the collection of these low-energy ions. A good background vacuum can minimize this effect; however, some errors due to background ionization may prevail in the measurements. The geometric design of the FC should be optimized to reduce the ionization and trapping of the residual gas inside its cavity.
- Thermal emission of electrons from the heated surface: In very rare cases (for, e.g., high power beams [37] or lasers [39]), the temperature of the FC material can exceed the limit for thermionic emission of the electrons, which can be avoided using a coolant to maintain the surface temperatures below the thermionic limits.
3. FC Design Considerations
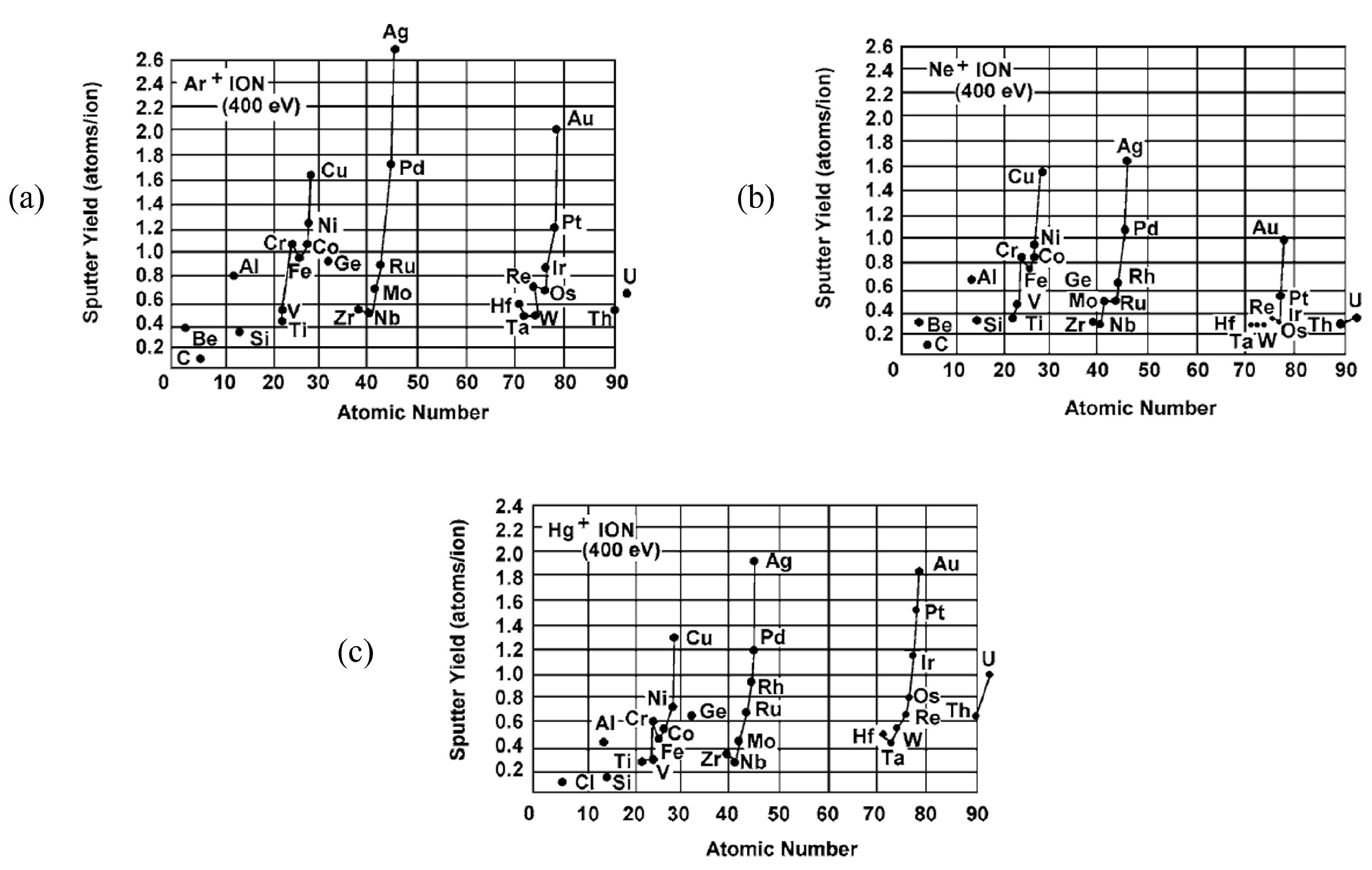
3.1. Sputtering of the FC Material


3.2. Secondary Electron Emission
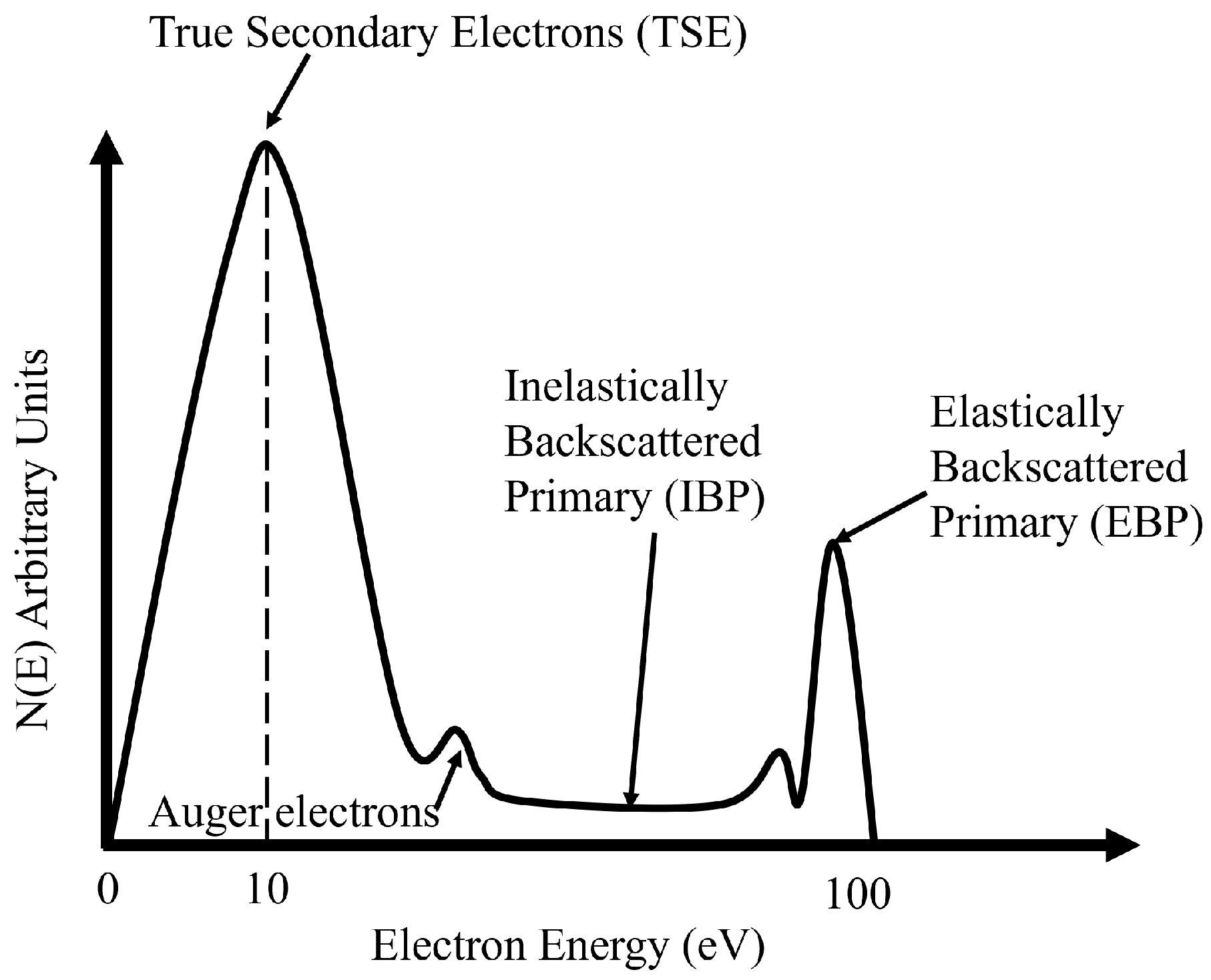
- is the maximum energy of the ejected secondary electrons from the material.
- is the maximum energy of the incident particle beam.
- is the electron mass in amu.
- is the emission angle of the electron with respect to the surface normal.
- is the mass of the incident ion particle.
| Author/Model | Formula/Key Idea | Key Takeaway |
|---|---|---|
| Huerta et al. (2019) [61] | Monte Carlo approach for ion-induced SEY considering surface morphology; Poisson-distributed emission. | |
| Vaughan (1989) [62] | Empirical SEY model for electron tubes, valid up to . | |
| Furman (2002) [63] | Empirical fits for Cu and stainless steel | Categorizes secondary electrons into backscattered, re-diffused, and true electrons. |
| Svensson et al. (1981) [64] | Experimental study | Studied angular dependence of SEY for noble gases on polycrystalline Cu. |
| Habl et al. (2021) [65] | Experimental study | Investigated SEY from iodine bombardment for space propulsion applications. |
| Fernandez-Coppe et al. (2024) [66] | Monte Carlo-based simulation | Tracks ion and recoil trajectories using stopping power databases; applied to Ar, Kr, and Xe on W and Fe. |
| Beuhler & Friedman (1977, 1986) [67] | Models ion-induced SEY but does not account for plasmons or recoil energy losses. | |
| Schou (1980) [69] | Improves the B & F model by incorporating recoil energy losses, but relies on empirical constants. |

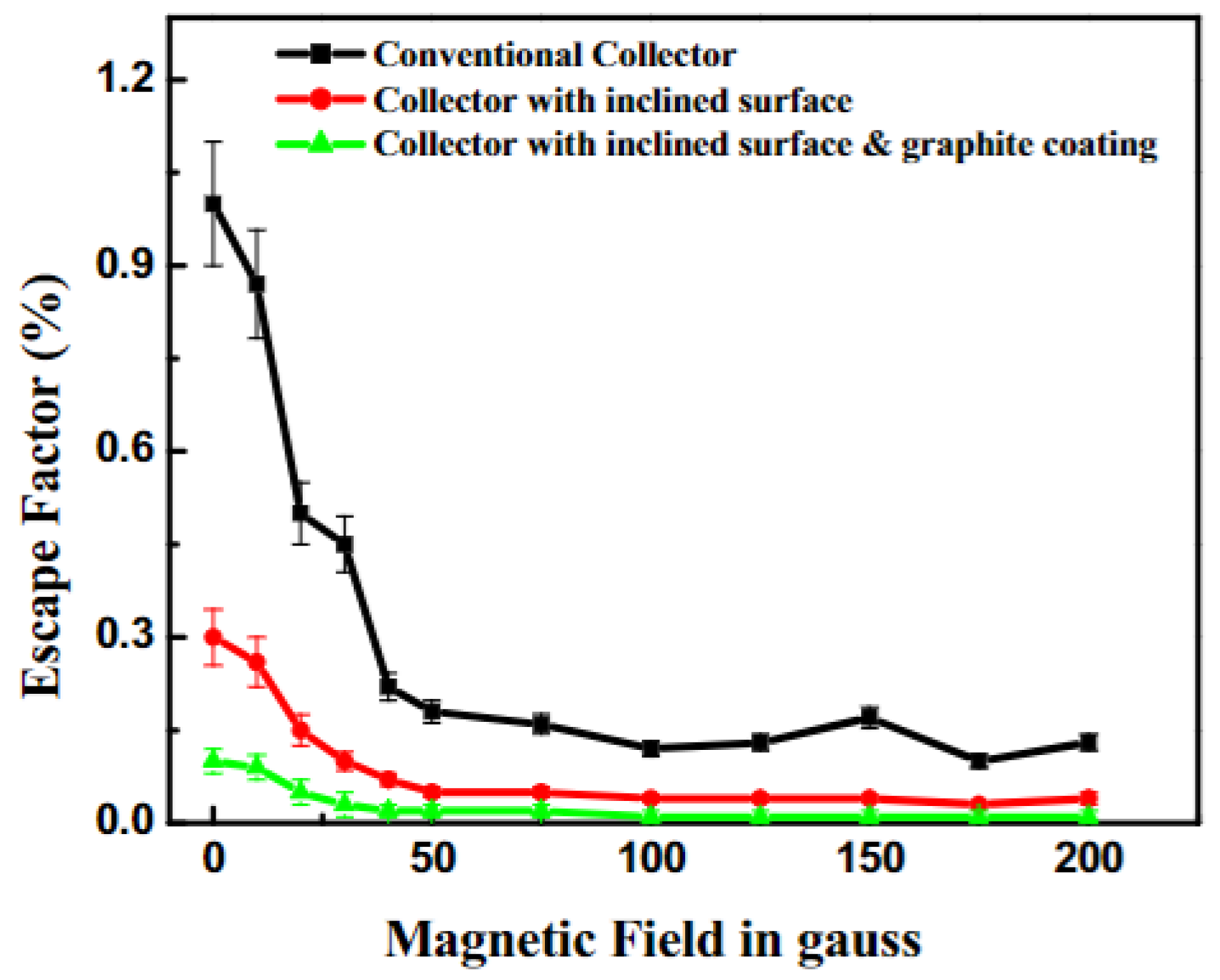
3.3. Backscattering of Particles
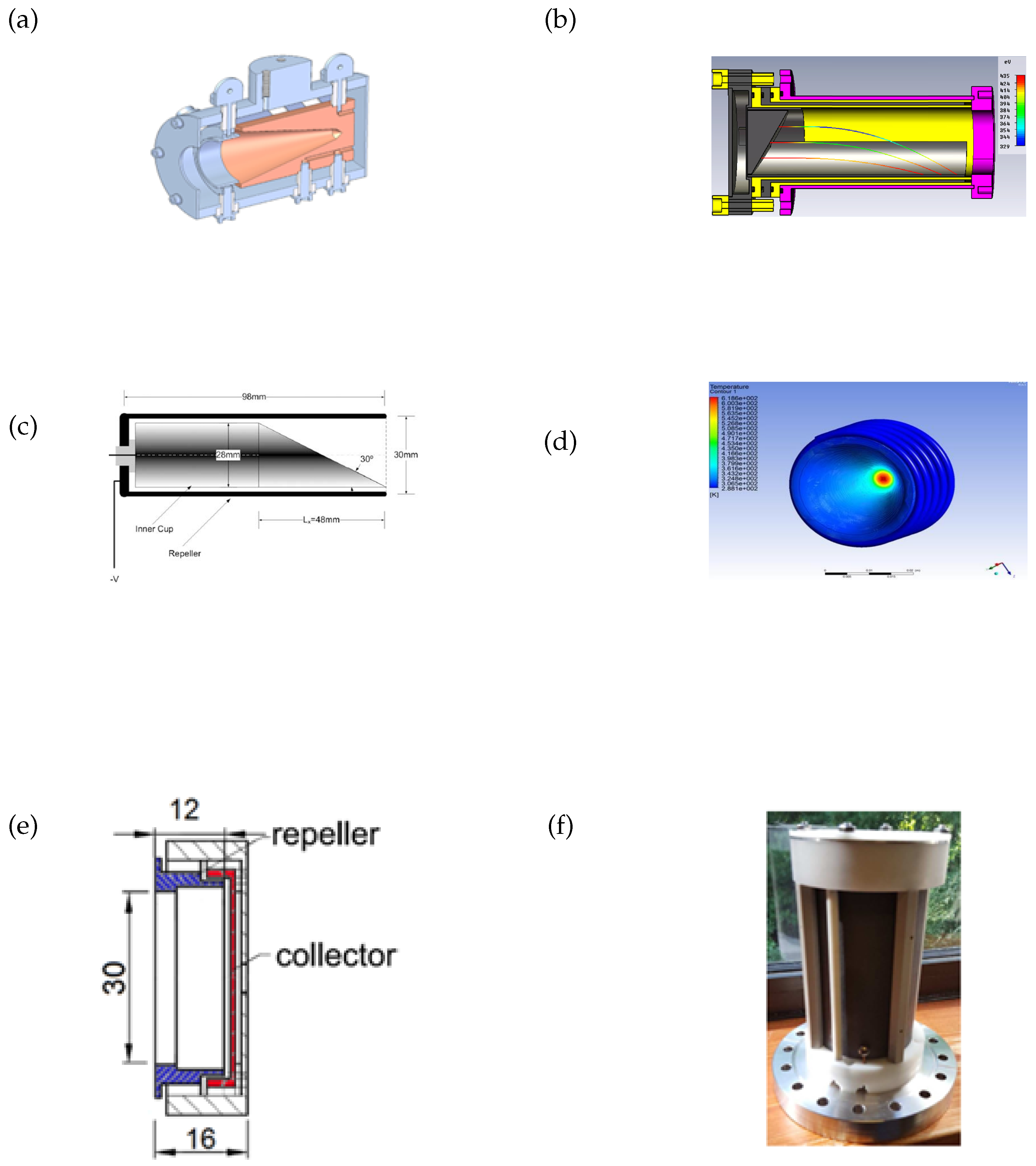
3.4. Stopping Distance and Different FC Designs

3.5. Shielding
| Sr. No. | Energy | Material | Current/Charge | Particle | Reference |
|---|---|---|---|---|---|
| 1 | 200 keV | OFHC Cu | 3.2 pC | /p/e− | Harasimowicz et al. [5] |
| 2 | 200 keV | Cu | 500 A | p+ | Ebrahimibasabi et al. [98] |
| 3 | 20 keV | – | – | p+ | Naieni et al. [99] |
| 4 | 300 keV | OFHC Cu | 30 mA | D+ | Rawat et al. [6] |
| 5 | 10 MeV/u | SS | 1 pA–1 nA | Ions () | Sosa et al. [100] |
| 6 | 10–60 MeV | Cu/Ta | ∼150 mA | e−/e+ | Godlove et al. [113] |
| 7 | 25 keV | Cu | pA | p+ | Thomas et al. [76] |
- Electromagnetic shielding
- Faraday cage effect: Conductive enclosures redirect external electric fields around the shielded area, primarily mitigating the electric field components [114].
- Magnetic field attenuation: For effective EM shielding, magnetic field attenuation is crucial. This requires the following aspects: high-permeability materials (e.g., mu-metal) [115] for low-frequency magnetic fields; eddy current induction in conductive materials for high-frequency magnetic fields [116].
- Grounding: A proper grounding technique is essential in ensuring that the shield effectively dissipates unwanted electromagnetic fields.
- Materials selection:For electric fields, highly conductive materials like copper or aluminum are required;For magnetic fields, high-permeability alloys (e.g., mu-metal, nickel–iron alloys) are effective at low frequencies, while composite or layered shields can be used for broadband shielding, offering attenuation over both low and high-frequency ranges.
- Thickness and skin depth: The thickness of the shielding must consider the skin depth of EM waves at different frequencies.
- Radioactive shielding
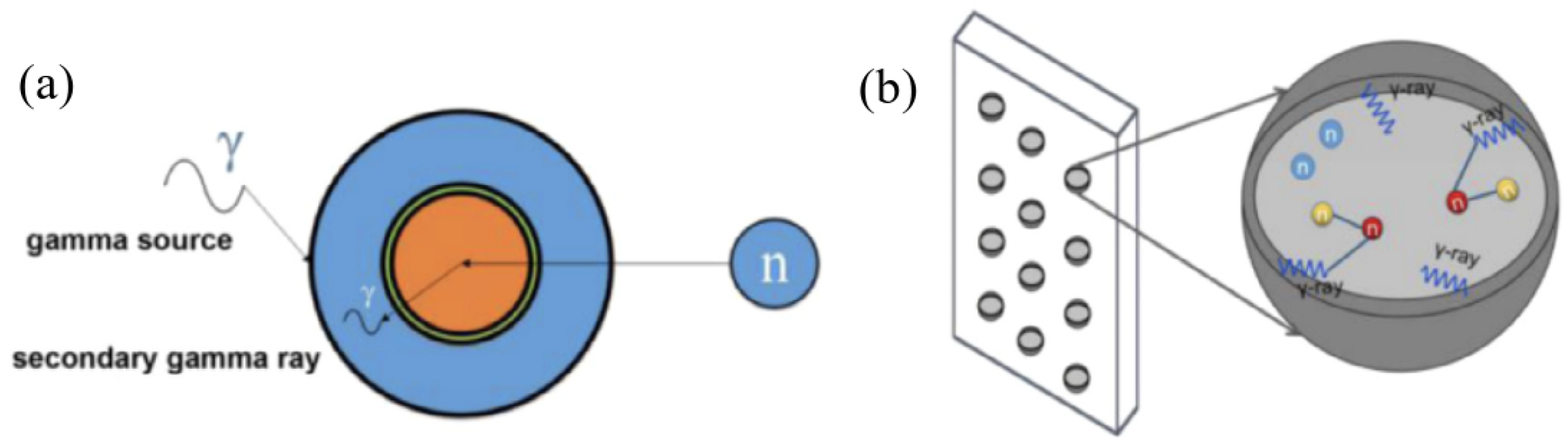
- Materials selection: The choice of materials for FC construction must balance several factors like electrical properties, radiation resistance, secondary emission, and heat dissipation.For FCs used in high-radiation environments, copper alloys or aluminum may be preferred for their conductivity and radiation resistance; tungsten or molybdenum could be better choices for parts exposed to very high energy beams due to their high melting points and density; ceramic insulators like alumina might be employed for their radiation hardness.To protect the sensitive electronics of the FC, additional shielding materials such as lead or tungsten are commonly incorporated to attenuate X-rays and gamma rays. In neutron-rich environments, materials like borated polyethylene, water, or concrete are preferred due to their cost-effectiveness and strong neutron-absorption properties [117], as illustrated schematically in Figure 15. It shows a core–shell particle structure, where a neutron-absorbing gadolinium oxide () core is encapsulated by a tungsten (W) shell. The tungsten shell acts as a primary barrier for gamma radiation, while the Gd2O3 core captures incident neutrons, often emitting secondary gamma rays in the process. This configuration exemplifies a “double shielding” system, with enhanced protection against both gamma rays and neutrons.
- Shield thickness: This is generally calculated based on the type and energy of the radiation. Monte Carlo simulations can help optimize the thickness and configuration of the shielding.
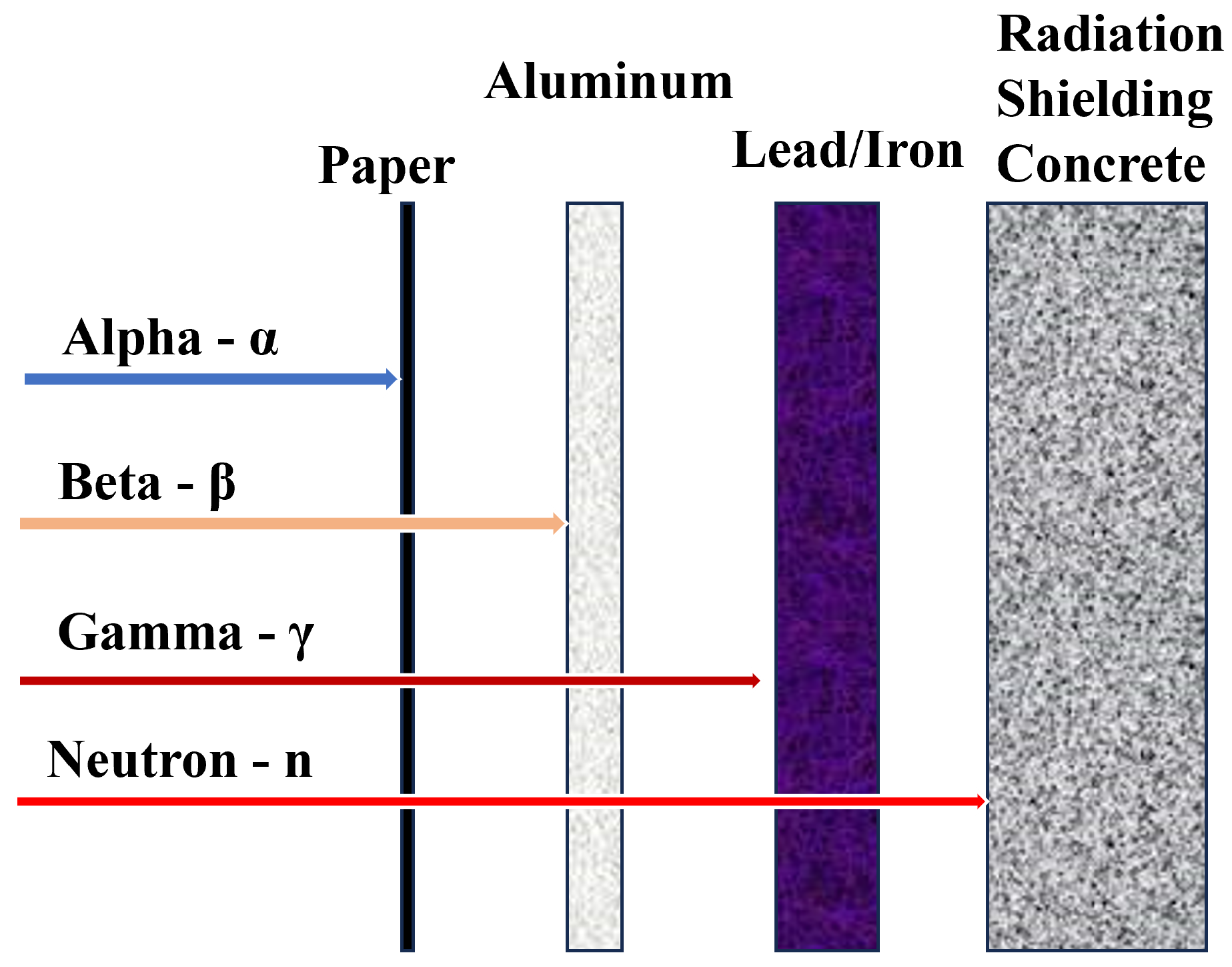
- Layering: As shown in Figure 16, using multiple layers of different materials to absorb different types of radiation (for example, lead for gamma rays, borated polyethylene for neutrons).
4. Signal Processing and Data Acquisition
4.1. Signal Processing
4.1.1. Current–Voltage Conversion
4.1.2. Noise Reduction
- Radiation Shielding
- Filtering

4.1.3. Integration and Digitization
- Analog Integration
- Offset nulling: Using potentiometers or digital correction to counteract the initial offset.
- Chopper stabilization: Modulating the input signal to reduce the impact of op-amp offset voltage [134].
- Auto zeroing: Periodically resetting the integrator’s output to zero.
- Digital integration: For applications requiring high accuracy and long integration times, digital signal processors (DSPs) can be used to perform the integration digitally.
- Digital Integration
- High resolution analog to digital conversion (ADC), such as AD7606, ADS1256, typically with 16 to 24 bit resolution. Their purpose is to convert the amplified and filtered analog signal into a digital form for processing and analysis. The design considerations are high-resolution, with fast sampling rates to accurately capture the signal dynamics.
- Microcontrollers or FPGAs to perform the integration.
- Software algorithms for post processing.
- Integration time: The choice of integration time depends on the beam characteristics and the required measurement precision. Longer integration times can improve the signal-to-noise ratio but may limit the temporal resolution of the measurement.
- Reset mechanism: For continuous measurements, a reset mechanism is necessary to prevent integrator saturation. This can be achieved through periodic discharge of the integrating capacitor in analog systems or by resetting the accumulator in digital systems [138].
- Baseline correction: To handle DC offsets and low-frequency noise, baseline correction techniques may be employed, such as chopper stabilized integrators or digital baseline subtraction algorithms [139].
- Calibration: Regular calibration of the integration system is a key factor in ensuring accurate charge measurements. This can be performed using known current sources or calibrated pulse generators.
4.1.4. Dynamic Signal Analysis
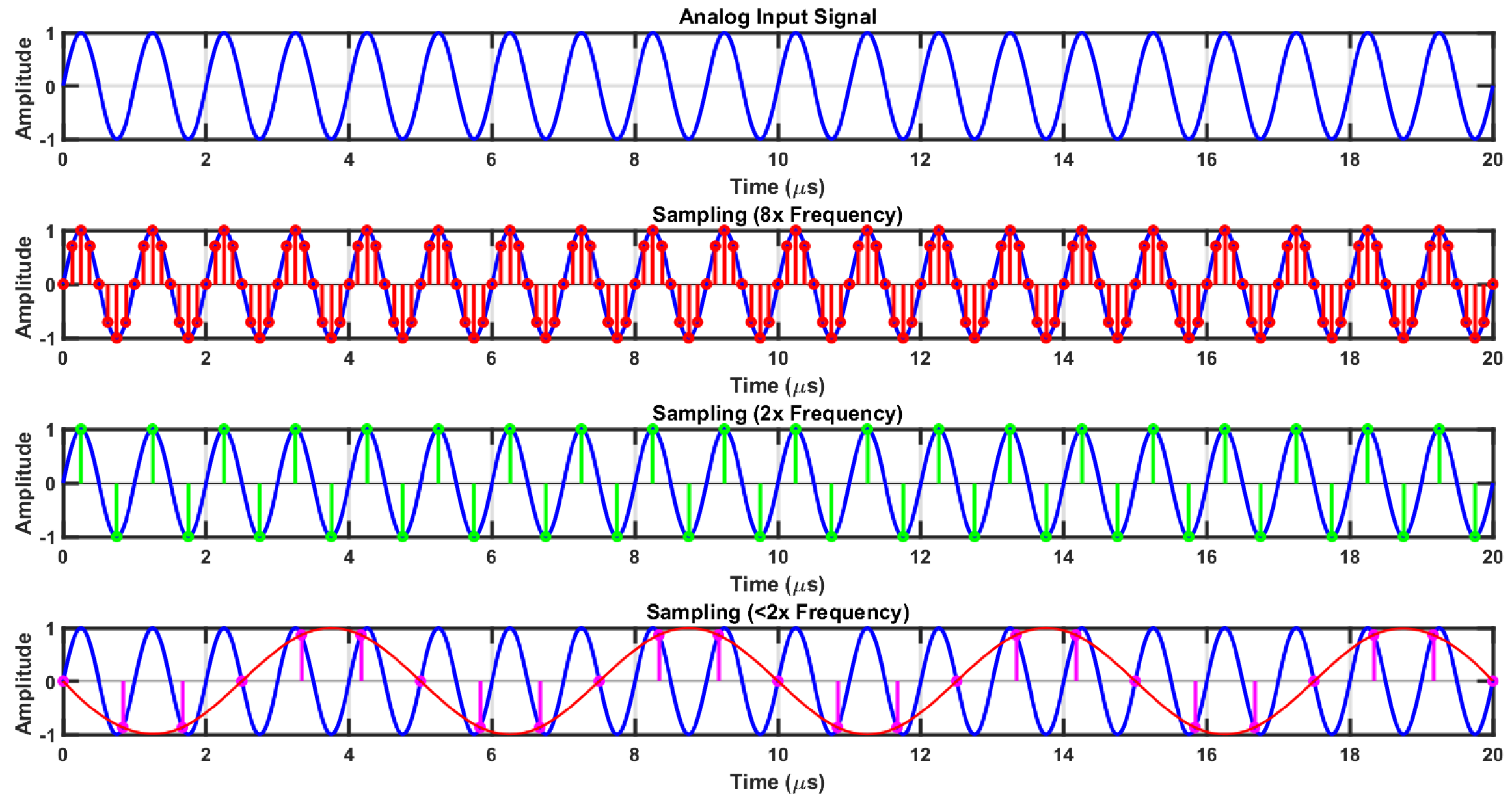
4.2. Data Acquisition
4.2.1. Data Acquisition System (DAQ)
4.2.2. Real-Time Processing
4.2.3. Synchronization
4.2.4. Data Analysis
4.2.5. DAQ System Design
5. Fast Faraday Cup
- : perfect matching, no reflections. : short circuit, the reflected signal has the same amplitude but opposite sign. : open circuit, the reflected signal has the same amplitude and sign.
6. Conventional FCs in Antimatter Research
7. FCs for Mass Spectrometry
8. FCs for Broad Ion Beams
8.1. Electric Propulsion
8.2. Thermonuclear Fusion Reactors
9. FCs for Nuclear, Particle and High-Energy Physics
9.1. FCs in Nuclear and Particle Physics
9.1.1. Use and Significance
- Beam intensity measurement
- Calibration of detectors
- Beam profiling
9.1.2. Applications in Nuclear Physics
- Nuclear reaction studies
9.1.3. Applications in Particle Physics
- Particle accelerator experiments
- Quantifying beam losses:By comparing intensity measurements at different points, it can be accurately determined where and to what extent beam particles are lost [223].
- Calculating interaction efficiencies:Intensity measurements prior to and following interaction regions allow for precise calculations of interaction cross-sections, efficiencies, etc. [224].
- Monitoring beam quality:Intermediate measurements along the beamlines of the facilities provide insight into the change in intensity [225,226], which could help identify issues such as misalignment. However, as FCs are destructive devices in nature (the beam is absorbed when measured), their use is typically limited to intermittent or dedicated periods, for example, during machine setup, calibration, or to cross check non-destructive diagnostics along the beamline.
- Optimizing accelerator performance:The data collected from FCs contribute to the general optimization of accelerator parameters during the initial stages of accelerator tuning, ensuring optimal beam delivery and experimental conditions [9,227]. In these cases, temporarily stopping the beam with an FC is acceptable to ensure a reliable setup and calibration of the system. Once optimal conditions are achieved, routine optimization and feedback rely mainly on non destructive diagnostics, with FCs serving as a reference or calibration points.
- Decay rate measurements
9.2. FCs in High-Energy Physics
9.2.1. Use and Significance
- Beam diagnostics in particle accelerators
- Radiation protection
- Calibration of beamline instruments
- Secondary particle detection
9.2.2. Challenges in High-Energy Applications
- Bremsstrahlung radiation:For high-energy electron beams, bremsstrahlung radiation becomes significant. This requires additional shielding and considerations in the cup design [234].
- Pair production:At energies above the pair production threshold, electron–positron pairs can be created. The cup design must account for this to prevent charge loss [38].
- Material selection:For high-energy applications, materials with high melting points and low atomic numbers are preferred to minimize secondary particle production and heat load [235].
- Data acquisition:Handling high data rates and ensuring accurate real-time processing are critical in experiments involving high-energy beams. To overcome these challenges, innovative FC designs have been developed. Segmented FCs (these allow for spatial resolution of the beam profile while measuring current) [110], cooled FCs (for high-power beams, water or cryogenic cooling systems are integrated into the cup design to manage heat loads), and choosing materials with high thermal conductivity, such as copper or tungsten, can help in efficient heat dissipation.
9.2.3. Applications in Collider Experiments
- Proton–Proton colliders
- Electron–Positron colliders
9.2.4. Applications in Fixed-Target Experiments
- High-Intensity Beamlines
- Neutrino experiments
10. FCs for Medical Accelerators
11. Alternative Diagnostics
12. Conclusions
- Advanced materials [270]: Development of nanostructured or composite materials that can withstand higher temperatures while reducing secondary electron emission.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| ADC | analog-to-digital converter |
| AEIS | Antimatter Experiment: Gravity, Interferometry and Spectroscopy |
| AI | Artificial Intelligence |
| ALPHA | Antihydrogen Laser Physics Apparatus |
| ALPI | Acceleratore Lineare Per Ioni |
| ATRAP | Antihydrogen Trap |
| BASE | Baryon Antibaryon Antisymmetry Experiment |
| CERN | Conseil Européen pour la Recherche Nucléaire |
| CFD | Computational Fluid Dynamics |
| CMOS | Complementary Metal Oxide Semiconductor |
| DAQ | data acquisition system |
| DC | direct current |
| DSA | dynamic signal analysis |
| ELBE | Electron Linac for Beams with High Brilliance and Low Emittance |
| EMI | Electro Magnetic Interference |
| EPICS | Experimental Physics and Industrial Control System |
| ESP | Elastically Backscattered Primary |
| FBCT | Fast Beam Current Transformer |
| FCC | Future Circular Collider |
| FC | Faraday Cup |
| FCA | Faraday Cup Array |
| FFC | Fast Faraday Cup |
| FLUKA | FLUktuierende KAskade |
| FPGA | Field-Programmable Gate Array |
| GG | Ground Grid |
| GPS | Global Positioning System |
| GPU | Graphics Processing Unit |
| HEP | high-energy physics |
| HOLMES | HOlmium MEasurement of Electron capture for Neutrino mass Search |
| IFIN-HH | Horia Hulubei National Institute for Research and Development |
| in Physics and Nuclear Engineering | |
| INFN | Istituto Nazionale di Fisica Nucleare |
| ISOLDE | Isotope Separator On Line Device |
| ISE | Inelastically Backscattered Electron |
| JN | Johnson–Nyquist |
| KEK | Kō Enerugī kasokuki Kenkyū kikō |
| KOMAC | Korea Multi-purpose Accelerator Complex |
| LabVIEW | LABoratory Virtual Instrument Engineering Workbench |
| LEIS | low-energy ion scattering |
| LHC | Large Hadron Collider |
| LINAC | linear accelerator |
| LNS | Laboratori Nazionali del Sud |
| MATLAB | MATrix LABoratory |
| MC | Monte Carlo |
| MCNP | Monte Carlo N Particle Transport |
| MCP | Micro Channel Plate |
| MLFC | Multi-Layer Faraday Cup |
| MIT | Massachusetts Institute of Technology |
| MPFC | Multi-Pinhole Faraday Cup |
| NBI | Neutral Beam Injector |
| NuMI | Neutrinos at Main Injector |
| PCB | printed circuit board |
| PCI | Peripheral Component Interconnect |
| PIC | Particle In Cell |
| PMFC | Poor Man’s Faraday Cup |
| PXI | PCI eXtension |
| RAID | Redundant Array of Independent Disks |
| RF | radio frequency |
| RTIA | Resistor Transimpedance Amplifier |
| SAR | Successive Approximation Register |
| SD | Standard Deviation |
| SEY | secondary electron yield |
| SG | Suppressor Grid |
| SHINE | SPS Heavy Ion and Neutrino Experiment |
| SPS | Super Proton Synchrotron |
| SRIM | Stopping Range of Ions in Matter |
| TES | Transition Edge Sensor |
| TOKAMAK | Toroidal Chamber with Magnetic Coils (transliteration from russian) |
| TOPAS | Tool for Particle Simulation |
| TRIM | TRansport of Ions in Matter |
| TSE | true secondary electron |
| UHDR | Ultra-High Dose Rate |
| VME | Virtual Machine Environment |
References
- Brown, L.; Beynon, J.H. Ion-Trap Methods. 2024. Available online: https://www.britannica.com/science/mass-spectrometry/Ion-trap-methods#ref619943 (accessed on 22 August 2025).
- Jean, P. New experiments on the kathode rays. Nature 1896, 53, 298–299. [Google Scholar] [CrossRef]
- Cockcroft, J.D.; Walton, E.T.S. Experiments with high velocity positive ions.―(I) Further developments in the method of obtaining high velocity positive ions. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1932, 136, 619–630. [Google Scholar] [CrossRef]
- Bellato, M.; Dainelli, A.; Poggi, M. Design and tests for the fast Faraday cup of the ALPI post-accelerator. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1996, 382, 118–120. [Google Scholar] [CrossRef]
- Harasimowicz, J.; Welsch, C.P. Development of Instrumentation for Low Energy Beams. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 2013. Available online: https://www.liverpool.ac.uk/media/livacuk/quasargroup/files/downloads/JanuszHarasimowicz_Thesis.pdf (accessed on 22 August 2025).
- Rawat, B.S.; Vala, S.; Abhangi, M.; Kumar, R.; Chauhan, S. Design and Simulation of 10kW Faraday cup for Ion beam current measurement. In Proceedings of the International Conference on Nuclear Engineering, American Society of Mechanical Engineers. Shanghai, China, 2–6 July 2017; Volume 57878, p. V009T15A051. [Google Scholar] [CrossRef]
- Cantero, E.; Lanaia, D.; Fraser, M.; Sosa, A.; Bravin, E.; Voulot, D.; Andreazza, A.W. Performance Tests of a short Faraday Cup designed for HIE-ISOLDE. In Proceedings of the IPAC2013, Shanghai, China, 12–17 May 2013; Available online: https://accelconf.web.cern.ch/ipac2013/papers/mopme072.pdf (accessed on 22 August 2025).
- Lazerson, S.A.; Ellis, R.; Freeman, C.; Ilagan, J.; Wang, T.; Shao, L.; Allen, N.; Gates, D.; Neilson, H. Development of a Faraday cup fast ion loss detector for keV beam ions. Rev. Sci. Instrum. 2019, 90, 093504. [Google Scholar] [CrossRef] [PubMed]
- Winterhalter, C.; Togno, M.; Nesteruk, K.P.; Emert, F.; Psoroulas, S.; Vidal, M.; Meer, D.; Weber, D.C.; Lomax, A.; Safai, S. Faraday cup for commissioning and quality assurance for proton pencil beam scanning beams at conventional and ultra-high dose rates. Phys. Med. Biol. 2021, 66, 124001. [Google Scholar] [CrossRef]
- Raza, U.; Akbar, S.; Yaqub, K.; Zeeshan, S.; Khan, M.A.; Farooqi, I.; Javeed, S.; Ahmed, M. Faraday Cup for high current and duty cycle electron LINACs. Vacuum 2020, 175, 109242. [Google Scholar] [CrossRef]
- Brown, K.L.; Tautfest, G.W. Faraday-Cup Monitors for High-Energy Electron Beams. Rev. Sci. Instrum. 1956, 27, 696–702. [Google Scholar] [CrossRef]
- Yuksel, A.N.; Turemen, G.; Bulut, S.; Serin, N.O.; Yavas, O. Design of beam instrumentation for in-vacuum materials irradiation and testing in a 30 MeV medical cyclotron. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 977, 164290. [Google Scholar] [CrossRef]
- Kunert, C.; Bundesmann, J.; Damerow, T.; Denker, A.; Weber, A. A Multi-Leaf Faraday Cup especially for proton therapy of ocular tumors. In Proceedings of the 5th International Particle Accelerator Conference (IPAC’14), Dresden, Germany, 15–20 June 2014; pp. 2149–2152. Available online: https://accelconf.web.cern.ch/cyclotrons2013/papers/th2pb04.pdf (accessed on 22 August 2025).
- Husain, A.; Ryser, J.; Pakela, J.; Huang, M.; Shoniyozov, K.; Stappen, F.V.; Koumenis, C.; Dong, L.; Fan, Y.; Diffenderfer, E.; et al. An efficient dosimetry method with a Faraday cup for small animal, small-field proton irradiation under conventional and ultra-high dose rates. arXiv 2022, arXiv:2209.07354. [Google Scholar]
- Scuderi, V.; Amato, A.; Amico, A.G.; Borghesi, M.; Cirrone, G.A.P.; Cuttone, G.; Fajstavr, A.; Giuffrida, L.; Grepl, F.; Korn, G.; et al. Diagnostics and dosimetry solutions for multidisciplinary applications at the ELIMAIA beamline. Appl. Sci. 2018, 8, 1415. [Google Scholar] [CrossRef]
- Akio, M.; Eizo, N. Calibration of Faraday cup efficiency in a multicollector mass spectrometer. Chem. Geol. Isot. Geosci. Sect. 1991, 94, 105–110. [Google Scholar] [CrossRef]
- Scheidemann, A.A.; Darling, R.B.; Schumacher, F.J.; Isakharov, A. Faraday cup detector array with electronic multiplexing for multichannel mass spectrometry. J. Vac. Sci. Technol. A Vacuum Surfaces Film. 2002, 20, 597–604. [Google Scholar] [CrossRef]
- Imrie, D.C.; Pentney, J.M.; Cottrell, J.S. A Faraday cup detector for high-mass ions in matrix-assisted laser desorption/ionization time-of-flight mass spectrometry. Rapid Commun. Mass Spectrom. 1995, 9, 1293–1296. [Google Scholar] [CrossRef]
- Grigoryan, R.; Costas-Rodríguez, M.; Santens, P.; Vanhaecke, F. Multicollector Inductively Coupled Plasma–Mass Spectrometry with 1013 Ω Faraday Cup Amplifiers for Ultrasensitive Mg Isotopic Analysis of Cerebrospinal Fluid Microsamples. Anal. Chem. 2020, 92, 15975–15981. [Google Scholar] [CrossRef]
- Bernasconi, S.M.; Hu, B.; Wacker, U.; Fiebig, J.; Breitenbach, S.F.; Rutz, T. Background effects on Faraday collectors in gas-source mass spectrometry and implications for clumped isotope measurements. Rapid Commun. Mass Spectrom. 2013, 27, 603–612. [Google Scholar] [CrossRef]
- Fitzakerley, D.W. Antihydrogen Via Two-Stage Charge Exchange. Master’s Thesis, York University, Toronto, ON, Canada, 2015. Available online: https://yorkspace.library.yorku.ca/bitstream/10315/32118/2/Fitzakerley_Daniel_W_2015_PhD.pdf (accessed on 22 August 2025).
- Hugonnaud, V.; Mazouffre, S.; Krejci, D. Faraday cup sizing for electric propulsion ion beam study: Case of a field-emission-electric propulsion thruster. Rev. Sci. Instrum. 2021, 92, 084502. [Google Scholar] [CrossRef]
- Hugonnaud, V.; Mazouffre, S. Optimization of a Faraday cup collimator for electric propulsion device beam study: Case of a Hall thruster. Appl. Sci. 2021, 11, 2419. [Google Scholar] [CrossRef]
- Rawat, B.S.; Sharma, S.K.; Choksi, B.; Prahlad, V.; Baruah, U.K. Measurement system for ion beam profiles using fixed parallel wires and Faraday cup array. Aip Adv. 2022, 12, 125103. [Google Scholar] [CrossRef]
- Brown, D.L.; Walker, M.L.; Szabo, J.; Huang, W.; Foster, J.E. Recommended practice for use of Faraday probes in electric propulsion testing. J. Propuls. Power 2017, 33, 582–613. [Google Scholar] [CrossRef]
- Trottenberg, T.; Bansemer, F.; Böttcher, S.; Feili, D.; Henkel, H.; Hesse, M.; Kersten, H.; Krüger, T.; Laube, J.; Lazurenko, A.; et al. An in-flight plasma diagnostic package for spacecraft with electric propulsion. EPJ Tech. Instrum. 2021, 8, 16. [Google Scholar] [CrossRef]
- Réfy, D.I.; Zoletnik, S.; Dunai, D.; Anda, G.; Lampert, M.; Hegedűs, S.; Nagy, D.; Palánkai, M.; Kádi, J.; Leskó, B.; et al. Micro-Faraday cup matrix detector for ion beam measurements in fusion plasmas. Rev. Sci. Instrum. 2019, 90, 033501. [Google Scholar] [CrossRef]
- Ogawa, K.; Bozhenkov, S.A.; Äkäslompolo, S.; Killer, C.; Grulke, O.; Nicolai, D.; Satheeswaran, G.; Isobe, M.; Osakabe, M.; Yokoyama, M.; et al. Energy-and-pitch-angle-resolved escaping beam ion measurements by Faraday-cup-based fast-ion loss detector in Wendelstein 7-X. J. Instrum. 2019, 14, C09021. [Google Scholar] [CrossRef]
- Darrow, D.S.; Bäumel, S.; Cecil, F.E.; Kiptily, V.; Ellis, R.; Pedrick, L.; Werner, A. Design and construction of a fast ion loss Faraday cup array diagnostic for Joint European Torus. Rev. Sci. Instrum. 2004, 75, 3566–3568. [Google Scholar] [CrossRef]
- Bonofiglo, P.J.; Kiptily, V.; Horton, A.; Beaumont, P.; Ellis, R.; Cecil, F.E.; Podesta, M.; Contributors JET. Improvements to the Faraday cup fast ion loss detector and magnetohydrodynamic induced fast ion loss measurements in Joint European Torus plasmas. Rev. Sci. Instrum. 2020, 91, 093502. [Google Scholar] [CrossRef]
- Atsushi, O.; Isono, T.; Nishiuchi, T.; Takahashi, H.; Kitajima, S.; Sasao, M. Charge-Exchanged Beam Measurement by Using a Grid-Biased Faraday Cup. Plasma Fusion Res. 2010, 5, S2088. [Google Scholar] [CrossRef]
- McKenna, C.M. Faraday cup designs for ion implantation. In Springer Series in Electrophysics; Springer: Berlin, Germany, 1982; pp. 73–103. [Google Scholar] [CrossRef]
- Brogden, V.; Johnson, C.; Rue, C.; Graham, J.; Langworthy, K.; Golledge, S.; McMorran, B. Material Sputtering with a Multi-Ion Species Plasma Focused Ion Beam. Adv. Mater. Sci. Eng. 2021, 2021, 8842777. [Google Scholar] [CrossRef]
- Catapang, A.V.; Herndez, I.J.; Vasquez, M.R.; Wada, M. Performance of a reactive magnetron sputtering ion source using water vapor plasma. J. Phys. Conf. Ser. 2022, 2244, 012099. [Google Scholar] [CrossRef]
- Hellborg, R. Electrostatic Accelerators; Springer: Berlin, Germany, 2005. [Google Scholar] [CrossRef]
- Liu, J.; Yu, D.; Ruan, F.; Xue, Y.; Wang, W. Note: A real-time beam current density meter. Rev. Sci. Instrum. 2013, 84, 036107. [Google Scholar] [CrossRef]
- Shaw, J.; Averill, R.; Kowalski, S.; Sarkar, S.; Sibley, C.; Sobczynski, S.; Turchinetz, W. A high power Faraday cup to measure extracted beam current from the Bates South Hall Ring. In Proceedings of the 1997 Particle Accelerator Conference (Cat. No. 97CH36167), Vancouver, BC, Canada, 16 May 1997; Volume 2, pp. 2274–2275. [Google Scholar] [CrossRef]
- Strehl, P. Beam Instrumentation and Diagnostics; Springer: Berlin/Heidelberg, Germany, 2006; Volume 120. [Google Scholar] [CrossRef]
- Nassisi, V.; Delle Side, D.; Velardi, L.; Buccolieri, G.; De Benedittis, A.; Paladini, F. A study of the secondary electrons yield produced by laser induced ions on Faraday cups as a function of beam angle. J. Phys. Conf. Ser. 2014, 508, 012021. [Google Scholar] [CrossRef]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Materials Processing; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Carter, G.; Colligon, J.S. Ion Bombardment of Solids; Heinemann Educational: London, UK, 1968. Available online: https://search.catalog.loc.gov/instances/cb86489c-4293-555b-bad7-a8e140d3101f?option=lccn&query=75380561 (accessed on 22 August 2025).
- Wolf, B. Handbook of Ion Sources; CRC Press: Boca Raton, FL, USA, 1995; Available online: https://books.google.com/books?hl=en&lr=&id=qoQHMSBNFsAC&oi=fnd&pg=PA2&dq=Handbook+of+ion+sources&ots=5lZvm1Da1A&sig=kd2xjjX9ZcCga__He5j7_cHlC8M (accessed on 22 August 2025).
- Wasa, K. Sputtering Phenomena. In Handbook of Sputtering Technology (Second Edition); William Andrew Publishing: Oxford, UK, 2012; pp. 41–75. [Google Scholar] [CrossRef]
- Lewis, M.A.; Glocker, D.A.; Jorne, J. Measurements of secondary electron emission in reactive sputtering of aluminum and titanium nitride. J. Vac. Sci. Technol. A Vacuum Surfaces Film. 1989, 7, 1019–1024. [Google Scholar] [CrossRef]
- Ikuse, K.; Yoshimura, S.; Hine, K.; Kiuchi, M.; Hamaguchi, S. Sputtering yields of Au by low-energy noble gas ion bombardment. J. Phys. D Appl. Phys. 2009, 42, 135203. [Google Scholar] [CrossRef]
- McHugh, J.A. Ion beam sputtering-the effect of incident ion energy on atomic mixing in subsurface layers. Radiat. Eff. 1974, 21, 209–215. [Google Scholar] [CrossRef]
- Sasaki, T.; Yoshida, N.; Takahashi, M.; Tomita, M. The optimization of incident angles of low-energy oxygen ion beams for increasing sputtering rate on silicon samples. Appl. Surf. Sci. 2008, 255, 1357–1359. [Google Scholar] [CrossRef]
- Kitani, H.; Toyoda, N.; Matsuo, J.; Yamada, I. Incident angle dependence of the sputtering effect of Ar-cluster-ion bombardment. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 1997, 121, 489–492. [Google Scholar] [CrossRef]
- Glöersen, P.G. Ion—beam etching. J. Vac. Sci. Technol. 1975, 12, 28–35. [Google Scholar] [CrossRef]
- Sano, N.; Bellew, A.; Blenkinsopp, P. Comparing sputter rates, depth resolution, and ion yields for different gas cluster ion beams (GCIB): A practical guide to choosing the best GCIB for every application. J. Vac. Sci. Technol. A 2023, 41, 053204. [Google Scholar] [CrossRef]
- Sigmund, P. Theory of sputtering. I. Sputtering yield of amorphous and polycrystalline targets. Phys. Rev. 1969, 184, 383. [Google Scholar] [CrossRef]
- Seah, M.P. An accurate semi-empirical equation for sputtering yields, II: For neon, argon and xenon ions. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2005, 229, 348–358. [Google Scholar] [CrossRef]
- Jeynes, C.; Barradas, P.N. Pitfalls in ion beam analysis. In Handbook of Modern Ion Beam Materials Analysis; Number 15; Materials Research Society: Warrendale, PA, USA, 2009; pp. 347–383. Available online: https://openresearch.surrey.ac.uk/esploro/outputs/bookChapter/Pitfalls-in-Ion-Beam-Analysis/99514015402346 (accessed on 22 August 2025).
- Whetten, T.J.; Armstead, A.A.; Grzybowski, T.A.; Ruoff, A.L. Etching of diamond with argon and oxygen ion beams. J. Vac. Sci. Technol. A 1984, 2, 477–480. [Google Scholar] [CrossRef]
- Austin, L.; Starke, H. Ueber die Reflexion der Kathodenstrahlen und eine damit verbundene neue Erscheinung secundärer Emission. Ann. Der Phys. 1902, 314, 271–292. [Google Scholar] [CrossRef]
- Bruining, H. Physics and Applications of Electron Secondary Emission; Mc Graw Hill: Columbus, OH, USA, 1954; Available online: https://www.sciencedirect.com/book/9780080090146/physics-and-applications-of-secondary-electron-emission (accessed on 22 August 2025).
- Lenard, P. Zur Entwicklung der Kenntnis von den Geschwindigkeitsverlusten der Kathodenstrahlen in der Materie. Annalen der Physik 1926, 385, 1–16. [Google Scholar] [CrossRef]
- Ritter, M. A Landmark-Based Method for the Geometrical 3D Calibration of Scanning Microscopes. Ph.D. Thesis, Technische Universitat Berlin, Berlin, Germany, 2007. [Google Scholar] [CrossRef]
- Swanson, C.; Kaganovich, I.D. Modeling of reduced secondary electron emission yield from a foam or fuzz surface. J. Appl. Phys. 2018, 123, 023302. [Google Scholar] [CrossRef]
- Main, D.; Jenkins, T.G.; Theis, J.G.; Werner, G.R.; Cary, J.R.; Lanham, E.; Veitzer, S.A.; Kruger, S.E. Modeling the Role of Secondary Electron Emission in Direct Current Magnetron Sputtering using Explicit Energy-Conserving Particle-in-Cell Methods. arXiv 2025, arXiv:2507.10727. [Google Scholar]
- Huerta, C.E.; Wirz, R.E. Ion-induced electron emission reduction via complex surface trapping. Aip Adv. 2019, 9, 125009. [Google Scholar] [CrossRef]
- Vaughan, J.; Rodney, M. A new formula for secondary emission yield. IEEE Trans. Electron Devices 1989, 36, 1963–1967. [Google Scholar] [CrossRef]
- Furman, M.A.; Pivi, M.T.F. Probabilistic model for the simulation of secondary electron emission. Phys. Rev. Spec. Top. Beams 2002, 5, 124404. [Google Scholar] [CrossRef]
- Svensson, B.; Holmén, G.; Burén, A. Angular dependence of the ion-induced secondary-electron yield from solids. Phys. Rev. B 1981, 24, 3749. [Google Scholar] [CrossRef]
- Habl, L.; Rafalskyi, D.; Lafleur, T. Secondary electron emission due to multi-species iodine ion bombardment of different target materials. J. Appl. Phys. 2021, 129, 153302. [Google Scholar] [CrossRef]
- Fernandez-Coppel, J.; Wirz, R.; Marian, J. Fully discrete model of kinetic ion-induced electron emission from metal surfaces. J. Appl. Phys. 2024, 135, 083301. [Google Scholar] [CrossRef]
- Beuhler, R.J.; Friedman, L. Low noise, high voltage secondary emission ion detector for polyatomic ions. Int. J. Mass Spectrom. Ion Phys. 1977, 23, 81–97. [Google Scholar] [CrossRef]
- Beuhler, R.; Friedman, L. Larger cluster ion impact phenomena. Chem. Rev. 1986, 86, 521–537. [Google Scholar] [CrossRef]
- Schou, J. Transport theory for kinetic emission of secondary electrons from solids. Phys. Rev. B 1980, 22, 2141–2174. [Google Scholar] [CrossRef]
- Dassault Systèmes. CST Studio Suite. Available online: https://www.3ds.com/products-services/simulia/products/cst-studio-suite/solvers (accessed on 22 August 2025).
- Dahl, D.A. SIMION for the personal computer in reflection. Int. J. Mass Spectrom. 2000, 200, 3–25. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Available online: https://www.comsol.com/ (accessed on 22 August 2025).
- Hasselkamp, D.; Rothard, H.; Groeneveld, K.O.; Kemmler, J.; Varga, P.; Winter, H. Particle Induced Electron Emission II; Springer: Berlin/Heidelberg, Germany, 2006; Volume 123. [Google Scholar] [CrossRef]
- Sternglass, E.J. Theory of secondary electron emission by high-speed ions. Phys. Rev. 1957, 108, 1. [Google Scholar] [CrossRef]
- Cantero, E.D.; Sosa, A.; Andreazza, W.; Bravin, E.; Lanaia, D.; Voulot, D.; Welsch, C.P. Design of a compact Faraday cup for low energy, low intensity ion beams. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 807, 86–93. [Google Scholar] [CrossRef]
- Thomas, J.D.; Hodges, G.S.; Seely, D.G.; Moroz, N.A.; Kvale, T.J. Performance enhancement study of an electrostatic Faraday cup detector. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2005, 536, 11–21. [Google Scholar] [CrossRef]
- Rawat, B.S. Studies on Extraction of an Ion Beam and Its Transport from a Multi-Cusp Gridded Ion Source. Ph.D. Thesis, Homi Bhabha National Institute/Institute for Plasma Research, Mumbai, India, 2024. [Google Scholar] [CrossRef]
- Zalm, P.C.; Beckers, L.J. Ion-induced secondary electron emission from copper and zinc. Surf. Sci. 1985, 152, 135–141. [Google Scholar] [CrossRef]
- Baragiola, R.A.; Alonso, E.V.; Ferron, J.; Oliva-Florio, A. Ion-induced electron emission from clean metals. Surf. Sci. 1979, 90, 240–255. [Google Scholar] [CrossRef]
- Carlston, C.E.; Magnuson, G.D.; Mahadevan, P.; Harrison, D.E., Jr. Electron ejection from single crystals due to 1-to 10-keV noble-gas ion bombardment. Phys. Rev. 1965, 139, A729. [Google Scholar] [CrossRef]
- Bogaerts, A.; Gijbels, R. The ion-and atom-induced secondary electron emission yield: Numerical study for the effect of clean and dirty cathode surfaces. Plasma Sources Sci. Technol. 2002, 11, 27. [Google Scholar] [CrossRef]
- Holmén, G.; Svensson, B.; Burén, A. Ion induced electron emission from polycrystalline copper. Nucl. Instrum. Methods Phys. Res. 1981, 185, 523–532. [Google Scholar] [CrossRef]
- Zhang, H.B.; Hu, X.C.; Wang, R.; Cao, M.; Zhang, N.; Cui, W.Z. Note: Measuring effects of Ar-ion cleaning on the secondary electron yield of copper due to electron impact. Rev. Sci. Instrum. 2012, 83, 066105. [Google Scholar] [CrossRef]
- Phelps, A.V.; Petrovic, Z.L. Cold-cathode discharges and breakdown in argon: Surface and gas phase production of secondary electrons. Plasma Sources Sci. Technol. 1999, 8, R21. [Google Scholar] [CrossRef]
- Pruitt, J.S. Secondary electron trajectories in a Faraday cup magnetic field. Nucl. Instrum. Methods 1966, 39, 329–334. [Google Scholar] [CrossRef]
- Bhatia, R.K.; Yadav, V.K.; Kumar, Y.; Gonde, B.R.; Ravisankar, E.; Saha, T.K.; Nataraju, V.; Gupta, S.K. Improved Faraday collector for magnetic sector mass spectrometers. Int. J. Mass Spectrom. 2015, 393, 58–62. [Google Scholar] [CrossRef]
- Tan, I.H.; Ueda, M.; Dallaqua, R.S.; Rossi, J.O. Magnetic field effects on secondary electrons emitted during ion implantation in vacuum arc plasmas. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2006, 242, 332–334. [Google Scholar] [CrossRef]
- Friedrich, M. Equipment for Beam Diagnostics. In Electrostatic Accelerators. Particle Acceleration and Detection; Hellborg, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; p. 317. [Google Scholar] [CrossRef]
- Mack, M.E.; Holsinger, R.F. Zero Deflection Magnetically-Suppressed Faraday for Ion Implanters. 1998. Available online: https://patents.google.com/patent/US5757018A/en (accessed on 22 August 2025).
- Nam, K.Y.; Kim, K.R.; Park, B.S.; Lee, W.R. A development of Faraday cup for the application to the SNU tandem accelerator beam line. In Proceedings of the 2003 Spring Meeting of the KNS, Gyeongju, Republic of Korea, 29–30 May 2003; Available online: https://www.kns.org/files/pre_paper/21/481%EB%82%A8%EA%B8%B0%EC%9A%A9.pdf (accessed on 22 August 2025).
- von Jagwitz-Biegnitz, H.; Faircloth, D.; Holmes, A.J.; Selway, R.G.; Beasley, P.; Heid, O. 2D wire grid integrated with Faraday Cup for low energy H-Beam analysis at SIEMENS Novel electrostatic accelerator. In Proceedings of the IBIC, Oxford, UK, 16–19 September 2013; Available online: https://accelconf.web.cern.ch/IBIC2013/papers/tupf06.pdf (accessed on 22 August 2025).
- Bisson, J.; Zhao, Z.; Gammel, G.; Alvarado, D.; Walker, C. Faraday System for Ion Implanters. 2004. Available online: https://patents.google.com/patent/US6723998B2/en (accessed on 22 August 2025).
- Cohen, A.J.; Koral, K.F. Backscattering and Secondary-Electron Emission from Metal Targets of Various Thicknesses; National Aeronautics and Space Administration: Washington, DC, USA, 1965. Available online: https://ntrs.nasa.gov/api/citations/19650012044/downloads/19650012044.pdf (accessed on 22 August 2025).
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM–The stopping and range of ions in matter. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Adıgüzel, A.; Çetinkaya, H.; Esen, Ş.; Halis, D.; İlhan, T.B.; Kılıçgedik, A.; Oğur, S.; Öz, S.; Özbey, A.Y.D.I.N.; Özcan, V.E.; et al. Low-energy ion beam diagnostics: An integrated solution. J. Instrum. 2024, 19, T03002. [Google Scholar] [CrossRef]
- Brongersma, H.H. Low-energy ion scattering. Charact. Mater. 2012, 2044, 1–23. [Google Scholar] [CrossRef]
- Salvat, F. Bethe stopping-power formula and its corrections. Phys. Rev. A 2022, 106, 032809. [Google Scholar] [CrossRef]
- Ebrahimibasabi, E.; Feghhi, H.S.A. Design and construction of a secondary electron suppressed Faraday Cup for measurement of beam current in an electrostatics proton accelerator. Int. J. Mass Spectrom. 2015, 386, 1–5. [Google Scholar] [CrossRef]
- Naieni, A.K.; Bahrami, F.; Yasrebi, N.; Rashidian, B. Design and study of an enhanced Faraday cup detector. Vacuum 2009, 83, 1095–1099. [Google Scholar] [CrossRef]
- Bravin, E.; Welsch, C.P.; Cantero, E.D.; Garcia, S.A. Optimization of a short Faraday cup for low-energy ions using numerical simulations. In Proceedings of the IBIC 2014, Monterry, CA, USA, 14–18 September 2014; Available online: https://accelconf.web.cern.ch/ibic2014/papers/wepf07.pdf (accessed on 22 August 2025).
- Johnston, R.; Bernauer, J.; Cooke, C.M.; Corliss, R.; Epstein, C.S.; Fisher, P.; Friščić, I.; Hasell, D.; Ihloff, E.; Kelsey, J.; et al. Realization of a large-acceptance Faraday Cup for 3 MeV electrons. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 922, 157–160. [Google Scholar] [CrossRef]
- Masoumzadeh, A.; Habibi, M.; Afsharmanesh, M. Design, construction and test of an optimized Faraday cup for beam current determination of a helicon ion source. Vacuum 2019, 159, 99–104. [Google Scholar] [CrossRef]
- Vala, S.; Kumar, R.; Abhangi, M.; Swami, H.L.; Bandyopadhyay, M.; Kumar, R. Installation, commissioning and testing of a low energy accelerator based 14-MeV neutron generator for lab scale fusion neutronics experiment. Fusion Eng. Des. 2025, 217, 115158. [Google Scholar] [CrossRef]
- Stockli, M.P.; Welton, R.F.; Keller, R.; Leitner, M. Emittance studies with an Allison scanner. Rev. Sci. Instrum. 2006, 77, 03B706. [Google Scholar] [CrossRef]
- Allison, P.W.; Sherman, J.D.; Holtkamp, D.B. An emittance scanner for intense low-energy ion beams. IEEE Trans. Nucl. Sci. 2007, 30, 2204–2206. [Google Scholar] [CrossRef]
- Laxdal, A.; Ames, F.; Baartman, R.A.; Brennan, D.; Koscielniak, S.R.; Morris, D.; Rawnsley, W.R.; Vincent, P.; Waters, G.; Yosifov, D. High Power Allison Scanner for Electrons. In Proceedings of the BIW2012, Newport News, VA, USA, 17 April 2012; Available online: https://accelconf.web.cern.ch/BIW2012/talks/tucp04_talk.pdf (accessed on 22 August 2025).
- Kima, D.H.; Dang, J.J.; Kwon, H.J.; Lee, S.H.; Kimb, H.S.; Chunga, K.J.; Hwanga, Y.S. Design and Installation of A Prototype Multi-pinhole Faraday Cup. In Proceedings of the Transactions of the Korean Nuclear Society Virtual Spring Meeting, Virtual, 9–10 July 2020; Available online: https://journal-home.s3.ap-northeast-2.amazonaws.com/site/kns2020spring/presentation/20S-525.pdf (accessed on 22 August 2025).
- Zuo, C.; Huang, J.; Yang, J.; Zhang, L.G. Design and analysis of a beam uniformity detector based on Faraday cup array. In Proceedings of the 4th Internamtional Beam Instrumentation Conference (IBIC), Barcelona, Spain, 11–15 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Rosing, M.; Hummer, C.; Zolecki, R. The measurement of Twiss parameters using segmented Faraday Cups. In Proceedings of the IEEE Particle Accelerator Conference, Accelerator Science and Technology, Chicago, IL, USA, 20–23 March 1989; pp. 1586–1588. [Google Scholar] [CrossRef]
- Knolle, D.; Ratschko, D.D.; Gläser, M. A segmented Faraday cup for two-dimensional representation of the current distribution of an ion beam. Rev. Sci. Instrum. 1996, 67, 3082–3084. [Google Scholar] [CrossRef]
- Kosonen, S.T.; Kalvas, T.; Tarvainen, O.; Toivanen, V. Empirical study of multidimensional Child-Langmuir law with plasma ion source extraction using round apertures. J. Phys. Conf. Ser. 2022, 2244, 012079. [Google Scholar] [CrossRef]
- Huo, W.; Hu, J.; Qin, L.; Cao, X.; Zhao, W. Variable beam entrance Faraday cup system for pulsed electron beam current profile characterization. Rev. Sci. Instrum. 2020, 91, 113303. [Google Scholar] [CrossRef]
- Godlove, T.F.; Toms, M.E.; Jones, D.W.; Murray, K.M. Faraday cup and secondary-emission monitor calibration. IEEE Trans. Nucl. Sci. 1967, 14, 215–216. [Google Scholar] [CrossRef]
- Chapman, S.J.; Hewett, D.P.; Trefethen, L.N. Mathematics of the Faraday cage. Siam Rev. 2015, 57, 398–417. [Google Scholar] [CrossRef]
- Conecici, L.M.; Munteanu, C.; Purcar, I.M. Study of the shielding performances of different materials regarding Electromagnetic Field Interference. Iop Conf. Ser. Mater. Sci. Eng. 2017, 200, 012045. [Google Scholar] [CrossRef]
- Becherini, G.; Di Fraia, S.; Schneider, M.; Ciolini, R.; Tellini, B. Shielding of high magnetic fields. In Proceedings of the 2008 14th Symposium on Electromagnetic Launch Technology, Victoria, BC, Canada, 10–13 June 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Abdullah, M.A.H.; Rashid, R.S.M.; Amran, M.; Hejazii, F.; Azreen, N.M.; Fediuk, R.; Voo, Y.L.; Vatin, N.I.; Idris, M.I. Recent Trends in Advanced Radiation Shielding Concrete for Construction of Facilities: Materials and Properties. Polymers 2022, 14, 2830. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Ma, L.; Yang, C.; Bian, Z.; Zhang, D.; Cui, S.; Wang, M.; Chen, Z.; Li, X. Recent Progress in Gd-Containing Materials for Neutron Shielding Applications: A Review. Materials 2023, 16, 4305. [Google Scholar] [CrossRef] [PubMed]
- Brenner, K.; Zimmermann, M.; Butterling, M.; Wagner, A.; Hugenschmidt, C.; Guatieri, F. Spatially-resolved charge detectors for particle beam optimization with femtoampere resolution achieved by in-vacuum signal preamplification. arXiv 2024, arXiv:2402.06902. [Google Scholar] [CrossRef]
- Harrison, R.G.; Robert, D. A Faraday cup for charge measurements in biophysical and environmental fieldwork. J. Electrost. 2025, 135, 104062. [Google Scholar] [CrossRef]
- Texas Instruments. OPA129 Precision FET-Input Op Amp. 2020. Available online: https://datasheet.octopart.com/OPA129U-Texas-Instruments-datasheet-8443484.pdf (accessed on 22 August 2025).
- FEMTO Messtechnik GmbH. DLPCA-200 Variable Gain Transimpedance Amplifier. 2022. Available online: https://www.femto.de/en/products/current-amplifiers/dlpca-200.html (accessed on 22 August 2025).
- Koornneef, J.M.; Bouman, C.; Schwieters, J.B.; Davies, G.R. Measurement of small ion beams by thermal ionisation mass spectrometry using new 1013 Ohm resistors. Anal. Chim. Acta 2014, 819, 49–55. [Google Scholar] [CrossRef]
- Cox, S.E.; Hemming, S.R.; Tootell, D. The Isotopx NGX and ATONA Faraday amplifiers. Geochronology 2020, 2, 231–243. [Google Scholar] [CrossRef]
- Brown, F.B.; Mosteller, R.D.; Sood, A. Verification of MCNP 5. Available online: https://mcnp.lanl.gov/pdf_files/TechReport_2002_LANL_LA-UR-02-3199_BoothBrownEtAl.pdf (accessed on 22 August 2025).
- Battistoni, G.; Boehlen, T.; Cerutti, F.; Chin, P.W.; Esposito, L.S.; Fasso, A.; Ferrari, A.; Lechner, A.; Empl, A.; Mairani, A.; et al. Overview of the FLUKA code. Ann. Nucl. Energy 2015, 82, 10–18. [Google Scholar] [CrossRef]
- Donegani, E.M.; Olsson, A.; Page, L.; Ruelas, M. Design and performance of the shielded DTL4 Faraday cup for the commissioning of the high-power ESS proton linac. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2023, 1057, 168727. [Google Scholar] [CrossRef]
- Frasca, A.; Kersevan, R.; Lerner, G.; Welsch, C.; Ciarma, A.; Kumar, N.; Boscolo, M.; Calviani, M.; Calzolari, D.; Perillo Marcone, A.; et al. Energy deposition and radiation level studies for the FCC ee experimental insertions. In Proceedings of the 15th International Particle Accelerator Conference, Nashville, TN, USA, 19–24 May 2024; pp. 1152–1155. [Google Scholar] [CrossRef]
- PIC Wire. Triaxial Cables for Low-Current Measurements. 2022. Available online: https://picwire.com/Resources/Technical/Technical-Articles/Coaxial-Cable-vs-Triaxial-Cable (accessed on 22 August 2025).
- Tektronix. Triaxial Cables for Low-Current Measurements. Available online: https://www.tek.com/en/documents/application-note/making-stable-low-current-measurements-high-test-connection-capacitance (accessed on 22 August 2025).
- Nyquist, H. Thermal Agitation of Electric Charge in Conductors. Phys. Rev. 1928, 32, 110–113. [Google Scholar] [CrossRef]
- Nouzák, L.; James, D.; Němeček, Z.; Šafránková, J.; Pavlů, J.; Nováková, J.; Vaverka, J.; Sternovsky, Z. Detection of Dust Particles Using Faraday Cup Instruments. Astrophys. J. 2021, 909, 132. [Google Scholar] [CrossRef]
- Gavin, H.P.; Morales, R.; Reilly, K. Drift-free integrators. Rev. Sci. Instrum. 1998, 69, 2171–2175. [Google Scholar] [CrossRef]
- Chen, H.L.; Chen, P.S.; Chiang, J.S. A Low-Offset Low-Noise Sigma-Delta Modulator with Pseudorandom Chopper-Stabilization Technique. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 2533–2543. [Google Scholar] [CrossRef]
- CAEN DT5730—8-Channel, 14-bit, 500 MS/s Digitizer. 2022. Available online: https://www.caen.it/products/dt5730/ (accessed on 22 August 2025).
- Adaptive Computing Support. Available online: https://www.xilinx.com/support/download.html (accessed on 22 August 2025).
- Altera featured products. Available online: https://www.altera.com/ (accessed on 22 August 2025).
- Kamil, M. Simple digital integration algorithm with saturation and drift elimination based Second-Order Generalized Integrator. In Proceedings of the 2015 9th International Conference on Compatibility and Power Electronics (CPE), Lisbon, Portugal, 24–26 June 2015; pp. 312–316. [Google Scholar] [CrossRef]
- Hung-Chie, C. Stable baseline correction of digital strong-motion data. Bull. Seismol. Soc. Am. 1997, 87, 932–944. [Google Scholar] [CrossRef]
- El Pro Cus. What is Analog to Digital Converter and Its Working. 2025. Available online: https://www.elprocus.com/analog-to-digital-converter (accessed on 22 August 2025).
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 2010; Available online: https://research.iaun.ac.ir/pd/naghsh/pdfs/UploadFile_2230.pdf (accessed on 22 August 2025).
- Harris, F.J. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Mandal, S.; Sau, S.; Chakrabarti, A.; Chattopadhyay, S. FPGA based High Speed Data Acquisition System for High Energy Physics Application. arXiv 2015, arXiv:1503.08819. [Google Scholar] [CrossRef]
- Seifert, B.; Eizinger, M.; Hörbe, T.; Gerger, J.; Fries, J.; Bettiol, L. From Analog to Digital Faraday Cups: An Overview of FOTEC’s Plasma Diagnostics Equipment Evolution. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; p. 1667. [Google Scholar] [CrossRef]
- Villamarín, D. Design of a high performance Digital data AcquIsition SYstem (DAISY) for innovative nuclear experiments. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2023, 1055, 168526. [Google Scholar] [CrossRef]
- Xilinx. Zynq-7000 SoC Overview. 2022. Available online: https://www.xilinx.com/products/silicon-devices/soc/zynq-7000.html (accessed on 22 August 2025).
- Liu, G.; Bao, Y.; Yue, N.; Wang, S.; Wu, H.; Liu, Q.; Yang, W. A GPU-based real-time processing system for frequency division multiple-input-multiple-output radar. Iet Radar Sonar Navig. 2023, 17, 1524–1537. [Google Scholar] [CrossRef]
- The White Rabbit Project. 2024. Available online: https://white-rabbit.web.cern.ch/ (accessed on 22 August 2025).
- Kester, W. Mixed Signal and DSP Design Techniques; Analog Devices: Wilmington, MA, USA, 2002; Available online: https://www.analog.com/en/resources/technical-books/mixed_signal_dsp_design_book.html (accessed on 29 June 2025).
- Brun, R.; Rademakers, F. ROOT—An object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1997, 389, 81–86. [Google Scholar] [CrossRef]
- National Instruments. Introduction to EPICS. 2025. Available online: https://www.ni.com/en/shop/seamlessly-connect-to-third-party-devices-and-supervisory-system/introduction-to-epics.html?srsltid=AfmBOooC6Wah9oSiORPsE2K2nuaZuyqRyKC3f80-ADvr6HjrhYBasmaY (accessed on 22 August 2025).
- Singh, R.; Klaproth, S.; Forck, P.; Reichert, T.; Reiter, A.; Rodrigues, G. Simulation and Measurements of the Fast Faraday Cups at GSI UNILAC. In Proceedings of the 11th International Beam Instrumentation Conference (IBIC’22), Kraków, Poland, 1–15 September 2022; JACOW Publishing: Geneva, Switzerland, 2022; pp. 286–290. [Google Scholar] [CrossRef]
- Mal, K.; Kumar, S.; Rodrigues, G.; Singh, R. Study and improvements of a radially coupled coaxial Fast Faraday cup design toward lower intensity beams. Aip Adv. 2022, 12, 125223. [Google Scholar] [CrossRef]
- Shemyakin, A. Estimation of Dilution of a Fast Faraday Cup Response Due to the Finite Particles Speed; Technical Report; Fermilab: Batavia, IL, USA, 2016. Available online: https://lss.fnal.gov/archive/test-tm/2000/fermilab-tm-2641-ad.pdf (accessed on 22 August 2025).
- Sefkow, A.B.; Davidson, R.C.; Efthimion, P.C.; Gilson, E.P.; Yu, S.S.; Roy, P.K.; Bieniosek, F.M.; Coleman, J.E.; Eylon, S.; Greenway, W.G.; et al. Fast Faraday cup to measure neutralized drift compression in intense ion charge bunches. Phys. Rev. Spec. Top. Beams 2006, 9, 052801. [Google Scholar] [CrossRef]
- Singh, R.; Barth, W.; Forck, P.; Lauber, S.; Miski-Oglu, M.; Reichert, T.; Scarpine, V.; Sieber, T.; Sun, D. Comparison of Feschenko BSM and Fast Faraday Cup with Low Energy Ion Beams. JACoW 2021, IBIC2021, WEPP16. [Google Scholar] [CrossRef]
- Caravita, R. Towards Measuring Gravity on Neutral Antimatter. Ph.D. Thesis, Genoa University, Genoa, Italy, 2018. Available online: https://cds.cern.ch/record/2640201 (accessed on 22 August 2025).
- Johnson, M.A. Design and Commissioning of Beamlines for the ALPHA Antihydrogen Experiment. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2019. Available online: https://search.proquest.com/openview/24c156b0a071c869db79c73a4fe9d960/1?pqorigsite=gscholar&cbl=18750&diss=y (accessed on 29 June 2025).
- Cerchiari, G.; Kellerbauer, A.; Safronova, M.S.; Safronova, U.I.; Yzombard, P. Ultracold anions for high-precision antihydrogen experiments. Phys. Rev. Lett. 2018, 120, 133205. [Google Scholar] [CrossRef]
- Latacz, B.M.; Fleck, M.; Jäger, J.I.; Umbrazunas, G.; Arndt, B.P.; Erlewein, S.R.; Wursten, E.J.; Devlin, J.A.; Micke, P.; Abbass, F.; et al. Orders of Magnitude Improved Cyclotron-Mode Cooling for Nondestructive Spin Quantum Transition Spectroscopy with Single Trapped Antiprotons. Phys. Rev. Lett. 2024, 133, 053201. [Google Scholar] [CrossRef]
- Fischer, J.; Schmidt, A.; Azaryan, N.; Butin, F.; Somoza, J.F.; Husson, A.; Klink, C.; Obertelli, A.; Schlaich, M.; Sinturel, A.; et al. Design and characterization of an antiproton deceleration beamline for the PUMA experiment. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2024, 550, 165318. [Google Scholar] [CrossRef]
- Andresen, G.; ALPHA Collaboration. Antimatter Plasmas in a Multipole Trap for Antihydrogen. Phys. Rev. Lett. 2007, 98, 023402. [Google Scholar] [CrossRef]
- Andresen, G.; ALPHA Collaboration. Antiproton, positron, and electron imaging with a microchannel plate/phosphor detector. Rev. Sci. Instrum. 2009, 80, 123701. [Google Scholar] [CrossRef]
- Kornakov, G.; Cerchiari, G.; Zieliński, J.; Lappo, L.; Sadowski, G.; Doser, M. Synthesis of cold and trappable fully stripped highly charged ions via antiproton-induced nuclear fragmentation in traps. Phys. Rev. C 2023, 107, 034314. [Google Scholar] [CrossRef]
- Butler, B. Antihydrogen Formation, Dynamics and Trapping. Ph.D. Thesis, Swansea University, Swansea, UK, 2011. Available online: https://cds.cern.ch/record/1350519 (accessed on 22 August 2025).
- Smorra, C.; Blaum, K.; Bojtar, L.; Borchert, M.; Franke, K.A.; Higuchi, T.; Leefer, N.; Nagahama, H.; Matsuda, Y.; Mooser, A.; et al. BASE–the baryon antibaryon symmetry experiment. Eur. Phys. J. Spec. Top. 2015, 224, 3055–3108. [Google Scholar] [CrossRef]
- Gabrielse, G. Trapped antihydrogen in its ground state. Phys. Rev. Lett. 2012, 108, 113002. [Google Scholar] [CrossRef]
- Vallis, N.; Auchmann, B.; Craievich, P.; Duda, M.; Garcia-Rodrigues, H.; Kosse, J.; Schaer, M. P3: A Positron source demonstrator for FCC-ee. In Proceedings of the 65th ICFA Advanced Beam Dynamics Workshop High Luminosity Circular e+ e− Colliders, Frascati, Italy, 12–15 September 2022. [Google Scholar] [CrossRef]
- Rienäcker, B.; Mariazzi, S.; Povolo, L.; Guatieri, F.; Caravita, R.; Penasa, L.; Pino, F.; Nebbia, G.; Brusa, R.S. Method for measuring positron number in high intensity nanosecond positron bunches based on Poisson statistic. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2022, 1033, 166661. [Google Scholar] [CrossRef]
- Watson, T.L. Accumulation and Manipulation of Positron Plasmas for Antihydrogen Production. Ph.D. Thesis, University of Wales Swansea, Swansea, UK, 2003. Available online: https://books.google.co.uk/books?id=61B50AEACAAJ (accessed on 22 August 2025).
- Aghion, S.; Amsler, C.; Ariga, A.; Ariga, T.; Belov, A.S.; Bonomi, G.; Bräunig, P.; Bremer, J.; Brusa, R.S.; Cabaret, L.; et al. Positron bunching and electrostatic transport system for the production and emission of dense positronium clouds into vacuum. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2015, 362, 86–92. [Google Scholar] [CrossRef]
- Dubov, L.; Akmalova, Y.; Stepanov, S.; Shtotsky, Y.; Shtotsky, Y. Evaluation of Positron Implantation Profiles in Various Materials for 22Na Source. Acta Phys. Pol. A 2017, 132, 1482–1485. [Google Scholar] [CrossRef]
- Li, X.; Barbiellini, B.; Di Noto, V.; Pagot, G.; Zheng, M.; Ferragut, R. A Positron Implantation Profile Estimation Approach for the PALS Study of Battery Materials. Condens. Matter 2023, 8, 48. [Google Scholar] [CrossRef]
- Maher, S.; Jjunju, F.P.; Taylor, S. Colloquium: 100 years of mass spectrometry: Perspectives and future trends. Rev. Mod. Phys. 2015, 87, 113–135. [Google Scholar] [CrossRef]
- Dempster, A.J. A new Method of Positive Ray Analysis. Phys. Rev. 1918, 11, 316–325. [Google Scholar] [CrossRef]
- Aston, F.W. A new mass-spectrograph and the whole number rule. Proc. R. Soc. Lond. A 1927, 115, 487–514. [Google Scholar] [CrossRef]
- Alvarez, L.W. Ernest Orlando Lawrence. 1967. Available online: https://history.aip.org/phn/11604030.html (accessed on 22 August 2025).[Green Version]
- Revesz, K.M.; Wehr, J.M.; Keybl, J. Measurement of Delta13C and Delta18O Isotopic Ratios of CaCO3 Using a Thermoquest Finnigan GasBench II Delta Plus XL Continuous Flow Isotope Ratio Mass Spectrometer with Application to Devils Hole Core DH-11 Calcite; Technical report; US Geological Survey, National Center: Reston, VA, USA, 2001. [Google Scholar] [CrossRef]
- Yang, Z.; Ren, Z.; Cheng, Y.; Sun, W.; Xi, Z.; Jia, W.; Li, G.; Wang, Y.; Guo, M.; Li, D. Review and prospect on portable mass spectrometer for recent applications. Vacuum 2022, 199, 110889. [Google Scholar] [CrossRef]
- Gilchrist, K.H.; Bower, C.A.; Lueck, M.R.; Piascik, J.R.; Stoner, B.R.; Natarajan, S.; Parker, C.B.; Glass, J.T. A Novel Ion Source and Detector for a Miniature Mass Spectrometer. In Proceedings of the SENSORS, Atlanta, GA, USA, 28–31 October 2007; pp. 1372–1375. [Google Scholar] [CrossRef]
- Schneider, J.M.; Kleine, T. Effects of Faraday cup deterioration on Sr and Cr isotope analyses by thermal ionization mass spectrometry. J. Anal. At. Spectrom. 2024, 39, 1910–1918. [Google Scholar] [CrossRef]
- Panitzsch, L.; Stalder, M.; Wimmer-Schweingruber, R.F. Direct high-resolution ion beam-profile imaging using a position-sensitive Faraday cup array. Rev. Sci. Instrum. 2009, 80. [Google Scholar] [CrossRef]
- Goebel, D.M.; Katz, I.; Mikellides, I.G. Fundamentals of Electric Propulsion; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Hilton, H.H.; Stevens, J.R. Faraday Cup Detectors. The Aerospace Corporation Rept. TR-0172 (2260-20)-3, El Segundo, CA. 1971. Available online: https://apps.dtic.mil/sti/tr/pdf/AD0732284.pdf (accessed on 22 August 2025).
- Habl, L.; Rafalskyi, D.; Lafleur, T. Ion beam diagnostic for the assessment of miniaturized electric propulsion systems. Rev. Sci. Instrum. 2020, 91, 093501. [Google Scholar] [CrossRef]
- Pioch, R.; Désangles, V.; Chabert, P. Investigation of the directional Faraday cup and improvement of the comparison between direct and indirect thrust measurements of a magnetic nozzle ECR thruster. Phys. Plasmas 2024, 31, 043516. [Google Scholar] [CrossRef]
- Hey, F.G.; Vaupel, M.; Groll, C.; Tajmar, M.; Sell, A.; Eckert, K.; Weise, D.; Saks, N.; Johann, U. Development of a Gridless Retarding Potential Analyser. In Proceedings of the 35th International Electric Propulsion Conference, Atlanta, GA, USA, 8–12 October 2017; Available online: https://electricrocket.org/IEPC/IEPC_2017_271.pdf (accessed on 22 August 2025).
- Bramanti, C.; Fearn, D. The design and operation of beam diagnostics for the dual stage 4-grid ion thruster. In Proceedings of the 30th International Electric Propulsion Conference, Florence, Italy, 17–20 September 2007; pp. 17–20. Available online: https://electricrocket.org/IEPC/IEPC-2007-050.pdf (accessed on 22 August 2025).
- Brown, D.L.; Gallimore, A.D. Evaluation of ion collection area in Faraday probes. Rev. Sci. Instrum. 2010, 81, 063504. [Google Scholar] [CrossRef] [PubMed]
- Hallouin, T.; Guglielmi, A.; Gurciullo, A.; Moriconi, B.; Mazouffre, S. Far-field plume properties of a cluster of 100 W-class permanent magnets Hall thrusters. In Proceedings of the 37th International Electric Propulsion Conference, Boston, MA, USA, 19–23 June 2022; Available online: https://hal.science/hal-03797516v1 (accessed on 22 August 2025).
- Rakhimov, R.G.; Kharlan, Y.Y.; Uzhinsky, I.; Milov, A.E.; Aypov, R.E.; Cherniy, I.A. Numerical simulation of plasma discharge in RF ion thruster. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019; pp. 15–20. Available online: https://www.researchgate.net/publication/336013173_Numerical_simulation_of_plasma_discharge_in_RF_ion_thruster (accessed on 22 August 2025).
- Taploo, A.; Lin, L.; Keidar, M. Air ionization in self-neutralizing air-breathing plasma thruster. J. Electr. Propuls. 2022, 1, 25. [Google Scholar] [CrossRef]
- Scharmann, S.; Keil, K.; Zorn, J.; Dietz, P.; Nauschütt, B.; Holste, K.; Hannemann, K.; Klar, P.J.; Kloss, S.; Graubner, S.; et al. Thrust measurement of an ion thruster by a force probe approach and comparison to a thrust balance. Aip Adv. 2022, 12, 045218. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z.; Tang, H.; Ling, W.Y.L.; Chen, Z.; Ren, J.; Cao, J. Measurement of the distribution of charge exchange ions in a Hall-effect thruster plume. Plasma Sources Sci. Technol. 2020, 29, 085001. [Google Scholar] [CrossRef]
- Mühlich, N.S.; Seifert, B.; Ceribas, E.; Gerger, J.; Aumayr, F. High-precision digital Faraday cups for FEEP thrusters. J. Instrum. 2022, 17, P08008. [Google Scholar] [CrossRef]
- Hofer, R.R.; Gallimore, A.D. A Comparison of Nude and Collimated Faraday Probes for Use with Hall Thrusters. In Proceedings of the 27th International Electric Propulsion Conference, Pasadena, CA, USA, 14–19 October 2001; Available online: https://api.semanticscholar.org/CorpusID:15143357 (accessed on 22 August 2025).
- Tsui, C.K.; Boedo, J.A.; Stangeby, P.C.; TCV Team. Accounting for Debye sheath expansion for proud Langmuir probes in magnetic confinement fusion plasmas. Rev. Sci. Instrum. 2018, 89, 013505. [Google Scholar] [CrossRef]
- Chen, F.F. Langmuir probe analysis for high density plasmas. Phys. Plasmas 2001, 8, 3029–3041. [Google Scholar] [CrossRef]
- Karamcheti, A.; Steinbrüchel, C. Parametrization of Laframboise’s results for spherical and cylindrical Langmuir probes. J. Vac. Sci. Technol. A 1999, 17, 3051–3056. [Google Scholar] [CrossRef]
- Rawat, B.S.; Sharma, S.K.; Prahlad, V.; Choksi, B.; Baruah, U.K. Experimental Studies on the Roles of Space Charge Neutralization in a Ring Cusp Ion Source. IEEE Trans. Plasma Sci. 2023, 51, 2218–2224. [Google Scholar] [CrossRef]
- Kucerovsky, D.; Kucerovsky, Z. Analysis of the dynamic Faraday cup. J. Phys. D Appl. Phys. 2003, 36, 2407. [Google Scholar] [CrossRef]
- Sotnikov, O.; Ivanov, A.; Belchenko, Y.; Gorbovsky, A.; Deichuli, P.; Dranichnikov, A.; Emelev, I.; Kolmogorov, V.; Kondakov, A.; Sanin, A.; et al. Development of high-voltage negative ion based neutral beam injector for fusion devices. Nucl. Fusion 2021, 61, 116017. [Google Scholar] [CrossRef]
- Rostoker, N.; Fisher, A.; Leader, J.C. High Flux Neutral Beams. Technical report; University of California: Los Angeles, CA, USA, 1990; Available online: https://apps.dtic.mil/sti/html/tr/ADA236994/ (accessed on 22 August 2025).
- Sasao, M.; Nishitani, T.; Krasilnilov, A.; Popovichev, S.; Kiptily, V.; Kallne, J. Chapter 9: Fusion product diagnostics. Fusion Sci. Technol. 2008, 53, 604–639. [Google Scholar] [CrossRef]
- Yamamoto, S.; Ogawa, K.; Isobe, M.; Darrow, D.S.; Kobayashi, S.; Nagasaki, K.; Okada, H.; Minami, T.; Kado, S.; Ohshima, S.; et al. Faraday-cup-type lost fast ion detector on Heliotron J. Rev. Sci. Instrum. 2016, 87. [Google Scholar] [CrossRef]
- Lei, G.J.; Yan, L.W.; Liu, D.P.; Zhang, X.M.; Zhao, M.; Geng, S.F.; Li, M.; Zhang, Y.X.; Bi, Z.H.; Bu, Y.N.; et al. Development of megawatt radiofrequency ion source for the neutral beam injector on HL-2A tokamak. Nucl. Fusion 2021, 61, 036019. [Google Scholar] [CrossRef]
- Arcimovich, L.A.; Bobrovskij, G.L.; Gorbunov, E.P.; Ivanov, D.P.; Kirillov, V.D.; Kuznecov, J.I.; Mirnov, S.V.; Petrov, M.P.; Razumova, K.A.; Strelkov, V.; et al. Experiments in Tokamak Devices. In Proceedings of the International Conference on Plasma Physics and Controlled Nuclear Fusion Research, Novosibirsk, Russia, 1–7 August 1968; pp. 157–171. Available online: https://inis.iaea.org/records/210rf-1g491 (accessed on 22 August 2025).
- Wesson, J.; Campbell, J.D. Tokamaks; Oxford University Press: Oxford, UK, 2011; Volume 149, Available online: https://books.google.com/books?hl=en&lr=&id=XJssMXjHUr0C&oi=fnd&pg=PP2&dq=Wesson,+John+and+Campbell,+David+J+TOKAMAKS&ots=EDmi0K5iDe&sig=Yt8r4Du8Suz8XhP36aafrMY3Ffo (accessed on 22 August 2025).
- Manchanda, R.; Chowdhuri, M.B.; Ghosh, J.; Ramaiya, N.; Yadava, N.; Patel, S.; Shukla, G.; Shah, K.; Dey, R.; Jadeja, K.A.; et al. Physics studies of ADITYA & ADITYA-U tokamak plasmas using spectroscopic diagnostics. Nucl. Fusion 2022, 62, 042014. [Google Scholar] [CrossRef]
- Mantica, P.; Bonanomi, N.; Mariani, A.; Carvalho, P.; Delabie, E.; Garcia, J.; Hawkes, N.; Johnson, T.; Keeling, D.; Sertoli, M.; et al. The role of electron-scale turbulence in the JET tokamak: Experiments and modelling. Nucl. Fusion 2021, 61, 096014. [Google Scholar] [CrossRef]
- ITER. External Heating Systems—Supporting Systems. 2024. Available online: https://www.iter.org/machine/supporting-systems/external-heating-systems (accessed on 22 August 2025).
- Dlougach, E.; Panasenkov, A.; Kuteev, B.; Serikov, A. Neutral beam coupling with plasma in a compact fusion neutron source. Appl. Sci. 2022, 12, 8404. [Google Scholar] [CrossRef]
- Sharma, S.K.; Vattilli, P.; Choksi, B.; Punyapu, B.; Sidibomma, R.; Bonagiri, S.; Aggrawal, D.; Baruah, U.K. Design of a Prototype Positive Ion Source with Slit Aperture Type Extraction System. J. Phys. Conf. Ser. 2017, 823, 012025. [Google Scholar] [CrossRef]
- Knoll, G.F. Radiation Detection and Measurement; John Wiley and Sons: Hoboken, NJ, USA, 2010; p. 864. Available online: https://books.google.com/books?hl=en&lr=&id=4vTJ7UDel5IC&oi=fnd&pg=PA1&dq=Radiation+Detection+and+Measurement,+4th+Edition+Share+Icon+Glenn+F.+Knoll+&ots=VyDSEVGJaB&sig=w35uM2hySopxJ-8GVQ0RCbPYZTw (accessed on 22 August 2025).
- Kak, A.; Kher, A.; Vishwakarma, S.C.; Kumar, A.; Gandhi, M.; Radheshyam, P.; Kumar, A.; Abhinandan, L. Fabrication of an Ultra High Vacuum Compatible Faraday Cup for Qualification of Electron Gun for 10 kW Industrial LINAC. J. Phys. Conf. Ser. 2012, 390, 012069. [Google Scholar] [CrossRef]
- Boromiza, M.; Borcea, C.; Dessagne, P.; Ghita, D.; Glodariu, T.; Henning, G.; Kerveno, M.; Marginean, N.; Mihai, C.; Negret, A.; et al. Proton inelastic scattering cross section measurements on 16 O and 28 Si. EPJ Web Conf. 2017, 146, 11015. [Google Scholar] [CrossRef]
- Wiedemann, H. Particle Accelerator Physics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- You, H.J.; Jang, S.O.; Choo, W.I. Beam Profile Measurements with a Slit-Faraday Cup and a Wire Scanner for a Newly Developed 18 GHz Superconducting ECR Ion Source and its LEBT. In Proceedings of the 4th International Beam Instrumentation Conference, Barcelona, Spain, 11–15 September 2016; p. MOPB035. [Google Scholar] [CrossRef]
- Laschinsky, L.; Karsch, L.; Leßmann, E.; Oppelt, M.; Pawelke, J.; Richter, C.; Schürer, M.; Beyreuther, E. Radiobiological influence of megavoltage electron pulses of ultra-high pulse dose rate on normal tissue cells. Radiat. Environ. Biophys. 2016, 55, 381–391. [Google Scholar] [CrossRef]
- Morita, K.; Morimoto, K.; Kaji, D.; Akiyama, T.; Goto, S.I.; Haba, H.; Ideguchi, E.; Kanungo, R.; Katori, K.; Koura, H.; et al. Experiment on the Synthesis of Element 113 in the Reaction 209 Bi(70 Zn, n) 278113. J. Phys. Soc. Jpn. 2004, 73, 2593–2596. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, D.; dos Santos , R.; Liang, J.; Qin, Z.; Liu, J.; Liu, Z. Production Review of Accelerator-Based Medical Isotopes. Molecules 2022, 27, 5294. [Google Scholar] [CrossRef]
- Evans, L.; Bryant, P. LHC Machine. J. Instrum. 2008, 3, S08001. [Google Scholar] [CrossRef]
- Dabrowski, A.; Lefevre, T.; Velasco, M.; Wood, M. Beam Loss Monitoring. 2007. Available online: https://indico.cern.ch/event/17870/session/26/contribution/203/attachments/235310/329275/CLIC_workshop_BeamLossMonitor.pdf (accessed on 22 August 2025).
- Anh, N.T.; Chung, L.X.; Anh, L.T.; Anh, T.T.; La Cognata, M.; Dien, M.V.; Hoa, B.T.; Hung, N.T.; Khue, P.D.; Linh, D.T.K.; et al. Faraday Cup Development for Beam Monitoring and Cross-Sectional Measurement of p+12C Elastic Scattering with Ep = 0.95–3.2 MeV. IEEE Trans. Nucl. Sci. 2025, 72, 608–613. [Google Scholar] [CrossRef]
- Gambaryan, V.V.; Gubin, K.V.; Levichev, A.E.; Maltseva, Y.I.; Martyshkin, P.V.; Pachkov, A.A.; Peshekhonov, S.N.; Trunov, V.I. Design and test of a Faraday cup for low-charge measurement of electron beams from laser wakefield acceleration. Rev. Sci. Instrum. 2018, 89, 063303. [Google Scholar] [CrossRef] [PubMed]
- Hu, H. The design of faraday cup for C-ADS injector I. J. Phys. Conf. Ser. 2025, 2964, 012017. [Google Scholar] [CrossRef]
- Margarone, D.; Krása, J.; Giuffrida, L.; Picciotto, A.; Torrisi, L.; Nowak, T.; Musumeci, P.; Velyhan, A.; Prokůpek, J.; Láska, L.; et al. Full characterization of laser-accelerated ion beams using Faraday cup, silicon carbide, and single-crystal diamond detectors. J. Appl. Phys. 2011, 109. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Ahmed, S.; Albrecht, M.; Alekseev, M.; Amoroso, A.; An, F.F.; An, Q.; Bai, J.Z.; Bai, Y.; et al. Measurement of branching fractions for ψ(3686)→γη′, γη, and γπ0. Phys. Rev. D 2017, 96, 052003. [Google Scholar] [CrossRef]
- Adamson, P.; Anderson, K.; Andrews, M.; Andrews, R.; Anghel, I.; Augustine, D.; Aurisano, A.; Avvakumov, S.; Ayres, D.S.; Baller, B.; et al. The NuMI neutrino beam. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 806, 279–306. [Google Scholar] [CrossRef]
- Abgrall, N.; Andreeva, O.; Aduszkiewicz, A.; Ali, Y.; Anticic, T.; Antoniou, N.; Baatar, B.; Bay, F.; Blondel, A.; Blumer, J.; et al. NA61/SHINE facility at the CERN SPS: Beams and detector system. J. Instrum. 2014, 9, P06005. [Google Scholar] [CrossRef]
- Forck, P. Lecture Notes on Beam Instrumentation and Diagnostics. 2022. Available online: https://indico.cern.ch/event/569714/contributions/2303731/attachments/1415057/2166101/juas_script.pdf (accessed on 22 August 2025).
- Ponce, A.; Aguilar, J.A.; Tate, J.; Yacamán, M.J. Advances in the electron diffraction characterization of atomic clusters and nanoparticles. Nanoscale Adv. 2021, 3, 311–322. [Google Scholar] [CrossRef]
- Barrett, R.J.; Anderson, B.D.; Willard, H.B.; Anderson, A.N.; Jarmie, N. Testing and calibration of a Faraday cup and other intensity monitors for the external proton beam at LAMPF. Nucl. Instrum. Methods 1975, 129, 441–445. [Google Scholar] [CrossRef]
- Criegee, L. Untersuchung der direkten Paarbildung durch Elektronen. Zeitschrift für Physik 1960, 158, 433–443. [Google Scholar] [CrossRef]
- Elmer, J.W.; Teruya, A.T. An enhanced Faraday cup for rapid determination of power density distribution in electron beams. Weld. J. 2001, 80, 288-s. Available online: https://s3.us-east-1.amazonaws.com/WJ-www.aws.org/supplement/WJ_2001_12_s288.pdf (accessed on 22 August 2025).
- Gras, J.J.; Belohrad, D.; Barschel, C.; Odier, P.; Ludwig, M. Optimization of the LHC beam current transformers for accurate luminosity determination. In Proceedings of the 2nd International Particle Accelerator Conferenc, San Sebastian, Spain, 4–9 September 2011; Available online: https://cds.cern.ch/record/1379466 (accessed on 22 August 2025).
- Abe, T.; Akai, K.; Akasaka, N.; Akemoto, M.; Akiyama, A.; Arinaga, M.; Cai, Y.; Ebihara, K.; Egawa, K.; Enomoto, A.; et al. Achievements of KEKB. Prog. Theor. Exp. Phys. 2013, 2013. [Google Scholar] [CrossRef]
- Roy, P.K.; Taller, S.; Toader, O.; Naab, F.; Dwaraknath, S.; Was, G.S. A Multi-Pinhole Faraday Cup Device for Measurement of Discrete Charge Distribution of Heavy and Light Ions. In Proceedings of the 6th International Particle Accelerator Conference, Richmond, VA, USA, 3–8 May 2015; p. MOPWI009. [Google Scholar] [CrossRef]
- Borghesi, M. The first neutrino massmeasurement of HOLMES. 2023. Available online: https://indico.cern.ch/event/1199289/contributions/5447083/attachments/2703332/4692480/TAUP23_Holmes.pdf (accessed on 22 August 2025).
- DeWerd, L.A.; Smith, B.R. Ionization Chamber Instrumentation. CRC Press: Boca Raton, FL, USA, 2021; Available online: https://www.taylorfrancis.com/chapters/edit/10.1201/9781351005388-2/ionization-chamber-instrumentation-larry-dewerd-blake-smith (accessed on 22 August 2025).
- Papa, A.; Bertschi, S.; Künzi, L.; Signorelli, G. A pixelated Faraday cup for proton beam diagnostics. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 936, 25–26. [Google Scholar] [CrossRef]
- Wulff, J.; Paul, A.; Bäcker, C.M.; Baumann, K.S.; Esser, J.N.; Koska, B.; Timmermann, B.; Verbeek, N.G.; Bäumer, C. Consistency of Faraday cup and ionization chamber dosimetry of proton fields and the role of nuclear interactions. Med. Phys. 2024, 51, 2277–2292. [Google Scholar] [CrossRef]
- Verhey, L.J.; Koehler, A.M.; McDonald, J.C.; Goitein, M.; Ma, I.C.; Schneider, R.J.; Wagner, M. The Determination of Absorbed Dose in a Proton Beam for Purposes of Charged-Particle Radiation Therapy. Radiat. Res. 1979, 79, 34–54. Available online: https://pubmed.ncbi.nlm.nih.gov/472125/ (accessed on 22 August 2025). [CrossRef]
- Cascio, E.W.; Gottschalk, B. A Simplified Vacuumless Faraday Cup for the Experimental Beamline at the Francis H. Burr Proton Therapy Center. In Proceedings of the 2009 IEEE Radiation Effects Data Workshop, Québec City, QC, Canada, 20–24 July 2009; pp. 161–165. [Google Scholar] [CrossRef]
- Ehwald, J.; Togno, M.; Lomax, A.J.; Weber, D.C.; Safai, S.; Winterhalter, C. Detailed Monte-Carlo characterization of a Faraday cup for proton therapy. Med. Phys. 2023, 50, 5828–5841. [Google Scholar] [CrossRef] [PubMed]
- Perl, J.; Shin, J.; Schümann, J.; Faddegon, B.; Paganetti, H. TOPAS: An innovative proton Monte Carlo platform for research and clinical applications. Med. Phys. 2012, 39, 6818–6837. [Google Scholar] [CrossRef]
- Cambria, R.; Hérault, J.; Brassart, N.; Silari, M.; Chauvel, P. Proton beam dosimetry: A comparison between the Faraday cup and an ionization chamber. Phys. Med. Biol. 1997, 42, 1185. [Google Scholar] [CrossRef] [PubMed]
- Tesfamicael, B.; Athar, B.; Bejarano Buele, A.; Kozlyuk, V.; Nichiporov, D.; Watts, D.A.; Arjomandy, B. Technical Note: Use of commercial multilayer Faraday cup for offline daily beam range verification at the McLaren Proton Therapy Center. Med. Phys. 2019, 46, 1049–1053. [Google Scholar] [CrossRef]
- Yeap, P.L.; Lew, K.S.; Koh, W.Y.; Chua, C.G.; Wibawa, A.; Master, Z.; Lee, J.C.; Park, S.Y.; Tan, H.Q. Proton Beam Range and Charge Verification Using Multilayer Faraday Collector. Technol. Cancer Res. Treat. 2024, 23, 1–9. [Google Scholar] [CrossRef]
- Schoenauen, L.; Coos, R.; Colaux, J.L.; Heuskin, A. Design and optimization of a dedicated Faraday cup for UHDR proton dosimetry: Implementation in a UHDR irradiation station. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2024, 1064, 169411. [Google Scholar] [CrossRef]
- Marshall, C.; Meisel, Z.; Montes, F.; Wagner, L.; Hermansen, K.; Garg, R.; Chipps, K.A.; Tsintari, P.; Dimitrakopoulos, N.; Berg, G.P.A.; et al. Measurement of Charge State Distributions using a Scintillation Screen. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2023, 1056, 168661. [Google Scholar] [CrossRef]
- Jones, A.Z.; Bloch, C.D.; Hall, E.R.; Hashemian, R.; Klein, S.B.; Przewoski, B.v.; Murray, K.M.; Foster, C.C. Comparison of Indiana University Cyclotron Facility Faraday cup proton dosimetry with radiochromic films, a calorimeter, and a calibrated ion chamber. IEEE Trans. Nucl. Sci. 1999, 46, 1762–1765. [Google Scholar] [CrossRef]
- Dell, G.F.; Fotino, M. A Compraision of CEA and SLAC Faraday Cup Calibration by Means of a Secondary Emission Monitor; Technical report; Cambridge Electron Accelerator, Mass.: Cambridge, UK, 1968. [CrossRef][Green Version]
- Ghergherehchi, M.; Afarideh, H.; Ghannadi, M.; Mohammadzadeh, A.; Aslani, G.R.; Boghrati, B. Proton beam dosimetry: A comparison between a plastic scintillator, ionization chamber and Faraday cup. J. Radiat. Res. 2010, 51, 423–430. [Google Scholar] [CrossRef]
- Delacroix, S.; Mazal, A.; Daures, J.; Ostrowsky, A.; Nauraye, C.; Kacperek, A.; Vynkier, S.; Brassard, N.; Habrand, J. Proton dosimetry comparison involving ionometry and calorimetry. Int. J. Radiat. Oncol. Biol. Phys. 1997, 37, 711–718. [Google Scholar] [CrossRef]
- Ajit, A.; Seeger, S.; Gottschalk, M.; Tuch, T.; Wiedensohler, A. Observation of systematic deviations between Faraday cup aerosol electrometers for varying particle sizes and flow rates—results of the AEROMET FCAE workshop. Metrologia 2021, 58, 055006. [Google Scholar] [CrossRef]
- Spieler, H. Semiconductor Detector Systems; Oxford University Press: Oxford, UK, 2005; Available online: https://inspirehep.net/literature/700866 (accessed on 22 August 2025).[Green Version]
- Sauli, F. The gas electron multiplier (GEM): Operating principles and applications. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 805, 2–24. [Google Scholar] [CrossRef]
- Halvorsen, M.M.; Coco, V.; Gkougkousis, E.L.; Collins, P.; Girard, O. The Silicon Electron Multiplier sensor. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2022, 1041, 167325. [Google Scholar] [CrossRef]
- Grishin, V.; Dehning, B.; Effinger, E.; Emery, J.; Holzer, B. A family of gas ionization chambers and SEM for beam loss monitoring of LHC and other accelerators. In Proceedings of the 26th Russian Particle Accelerator Conference (RuPAC’18), Protvino, Russia, 1–5 October 2018; pp. 44–48. [Google Scholar] [CrossRef]
- Gschwendtner, E.; Assmann, R.W.; Dehning, B.; Ferioli, G.; Kain, V. Ionization chambers for the LHC beam loss detection. In Proceedings of the DIPAC 2003, Mainz, Germany, 5–7 May 2003; Available online: https://cds.cern.ch/record/923970?ln=en (accessed on 22 August 2025).
- Lecoq, P. Scintillation detectors for charged particles and photons. In Particle Physics Reference Library: Volume 2: Detectors for Particles and Radiation; Springer: Berlin, Germany, 2020; pp. 45–89. [Google Scholar] [CrossRef]
- Joukainen, H.; Sarén, J.; Ruotsalainen, P. Position sensitive plastic scintillator for beta particle detection. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2022, 1027, 166253. [Google Scholar] [CrossRef]
- Mezek, G.K. Semiconductor detectors for detection of elementary particles. Available online: https://www2.ung.si/~sstanic/teaching/MEM/2013_Eksp_metode_2_Gasper_Kukec_V2.pdf (accessed on 22 August 2025).
- Togawa, M.; Fujii, S.; Imura, M.; Itabashi, K.; Isobe, T.; Miyahara, M.; Nishinaga, J.; Okumura, H. The CIGS semiconductor detector for particle physics. J. Instrum. 2024, 19, C05042. [Google Scholar] [CrossRef]
- Zorzetti, S. Digital Signal Processing and Generation for a DC Current Transformer for Particle Accelerators; Technical report; Fermi National Accelerator Lab. (FNAL): Batavia, IL, USA, 2013. [CrossRef]
- Unser, K. A Toroidal DC Beam Current Transformer with High Resolution. IEEE Trans. Nucl. Sci. 1981, 28, 2344–2346. [Google Scholar] [CrossRef]
- Webber, R.C. Charged particle beam current monitoring tutorial. In Proceedings of the AIP Conference Proceedings, Vancouver, BC, USA, 3–6 October 1994; American Institute of Physics: College Park, MA, USA, 1995; Volume 333, pp. 3–23. [Google Scholar] [CrossRef]
- Suwada, T.; Tamiya, K.; Urano, T.; Kobayashi, H.; Asami, A. New analysis and performance of a wall-current monitor. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1997, 396, 1–8. [Google Scholar] [CrossRef]
- Ahire, S.A.; Bachhav, A.A.; Pawar, T.B.; Jagdale, B.S.; Patil, A.V.; Koli, P.B. The Augmentation of nanotechnology era: A concise review on fundamental concepts of nanotechnology and applications in material science and technology. Results Chem. 2022, 4, 100633. [Google Scholar] [CrossRef]
- Ebrahimibasabi, E.; Feghhi, S.A.H.; Khorsandi, M. Design and simulation of a new Faraday Cup for ES-200 electrostatic accelerator. In Proceedings of the 23rd Russian Particle Accelerator Conference, RuPAC’12—Russian Particle Accelerator Conference, St. Petersburg, Russia, 27–28 September 2012; pp. 682–684. Available online: https://accelconf.web.cern.ch/rupac2012/papers/weppd061.pdf (accessed on 22 August 2025).
- Bower, C.A.; Gilchrist, K.H.; Lueck, M.R.; Stoner, B.R. Microfabrication of fine-pitch high aspect ratio Faraday cup arrays in silicon. Sens. Actuators A Phys. 2007, 137, 296–301. [Google Scholar] [CrossRef]
- Letcher, E.; Stanton, D.; Novak, D.; Bunnell, K.; Peters, C.; Blomberg, B. Automated Faraday Cup reading at ATLAS. In Proceedings of the 14th International Particle Accelerator Conference (IPAC’14), Venice, Italy, 7–12 May 2023. [Google Scholar] [CrossRef]
- Kasper, J.C.; Lazarus, A.J.; Steinberg, J.T.; Ogilvie, K.W.; Szabo, A. Physics-based tests to identify the accuracy of solar wind ion measurements: A case study with the Wind Faraday Cups. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Goutierre, E. Machine Learning-Based Particle Accelerator Modeling. Ph.D. Thesis, Université Paris-Saclay, Paris, France, 2024. [Google Scholar]
- Garcia, A.S.; Eichler, A.; Xu, C.; Kaiser, J.; Scomparin, L.; Schenk, M.; Pochaba, S.; Hirlaender, S. The reinforcement learning for autonomous accelerators collaboration. JACoW 2024, IPAC2024, TUPS62. [Google Scholar] [CrossRef]
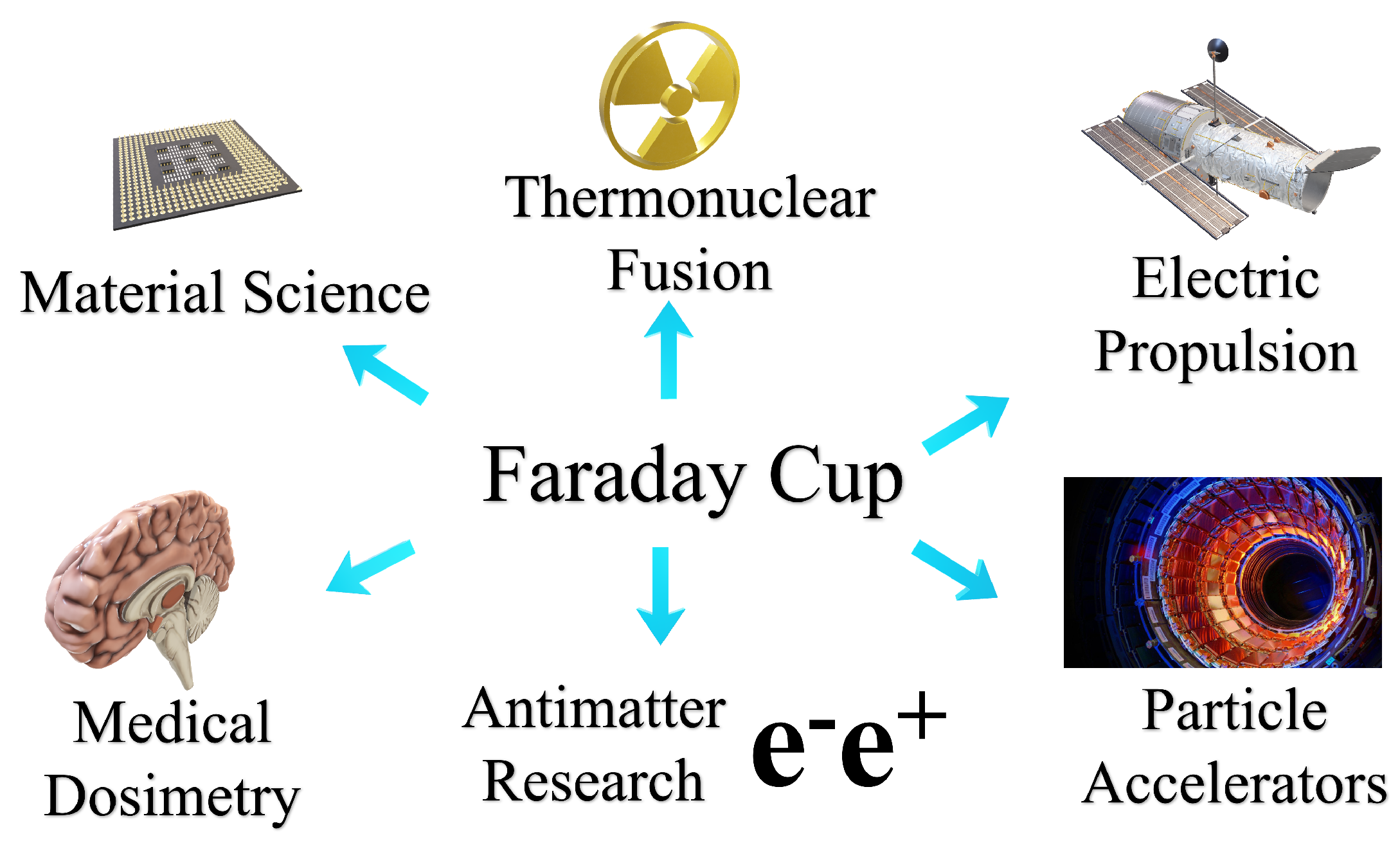






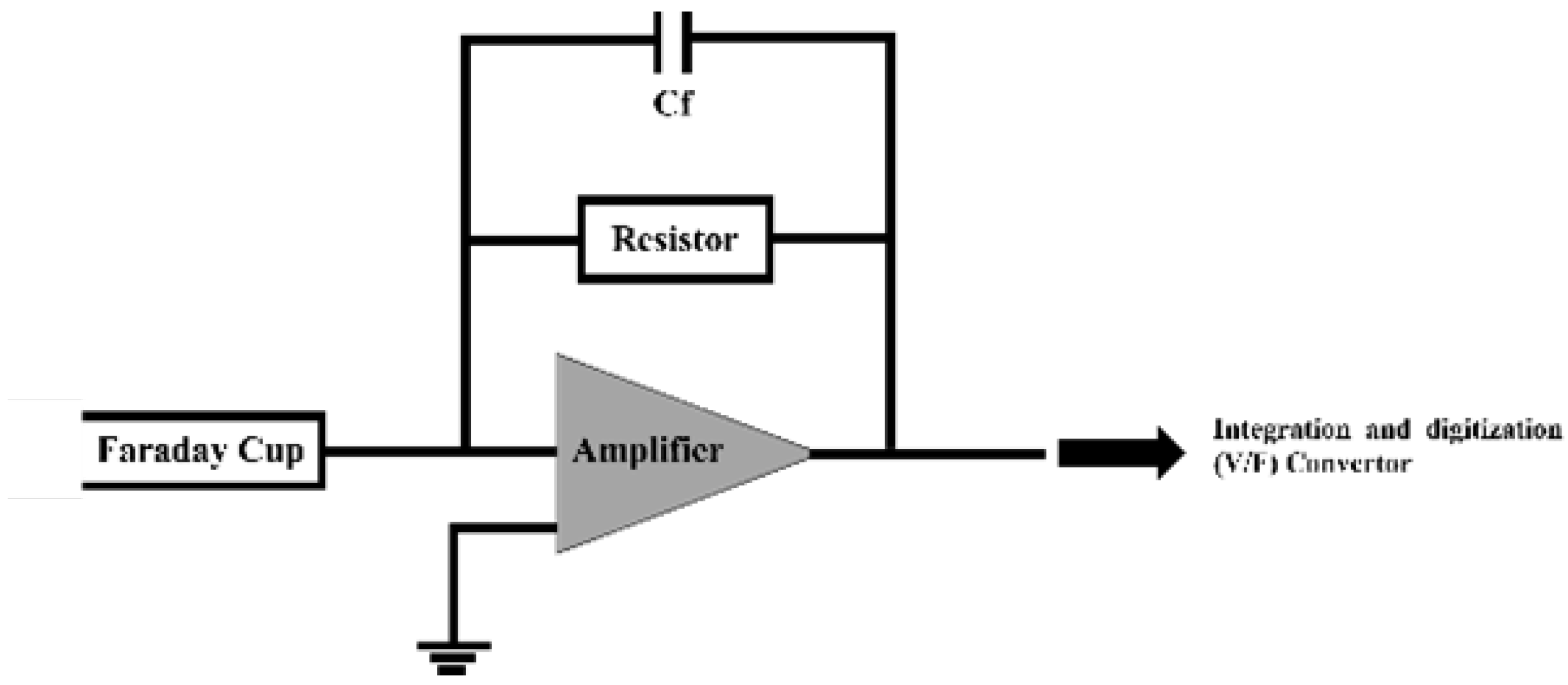
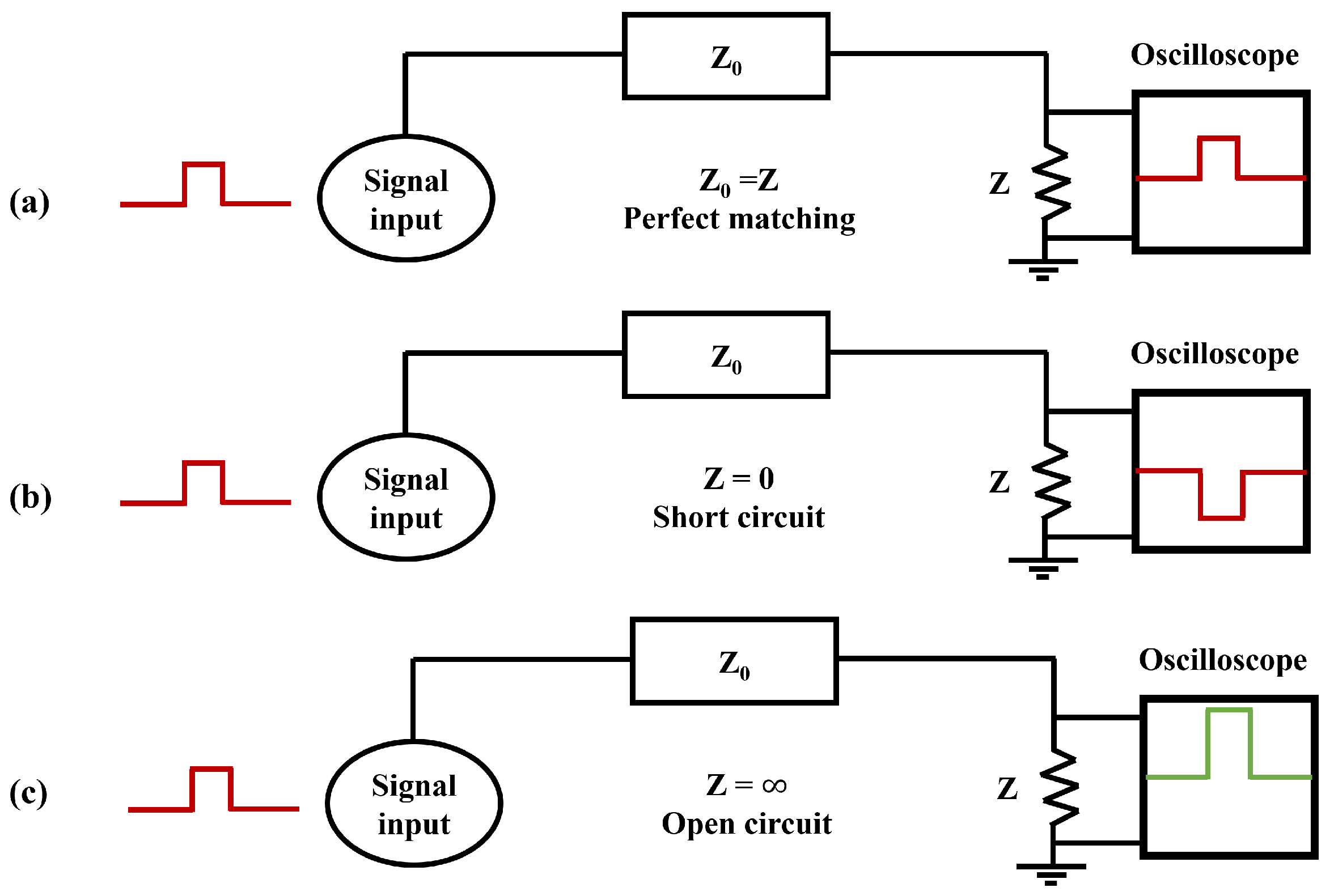

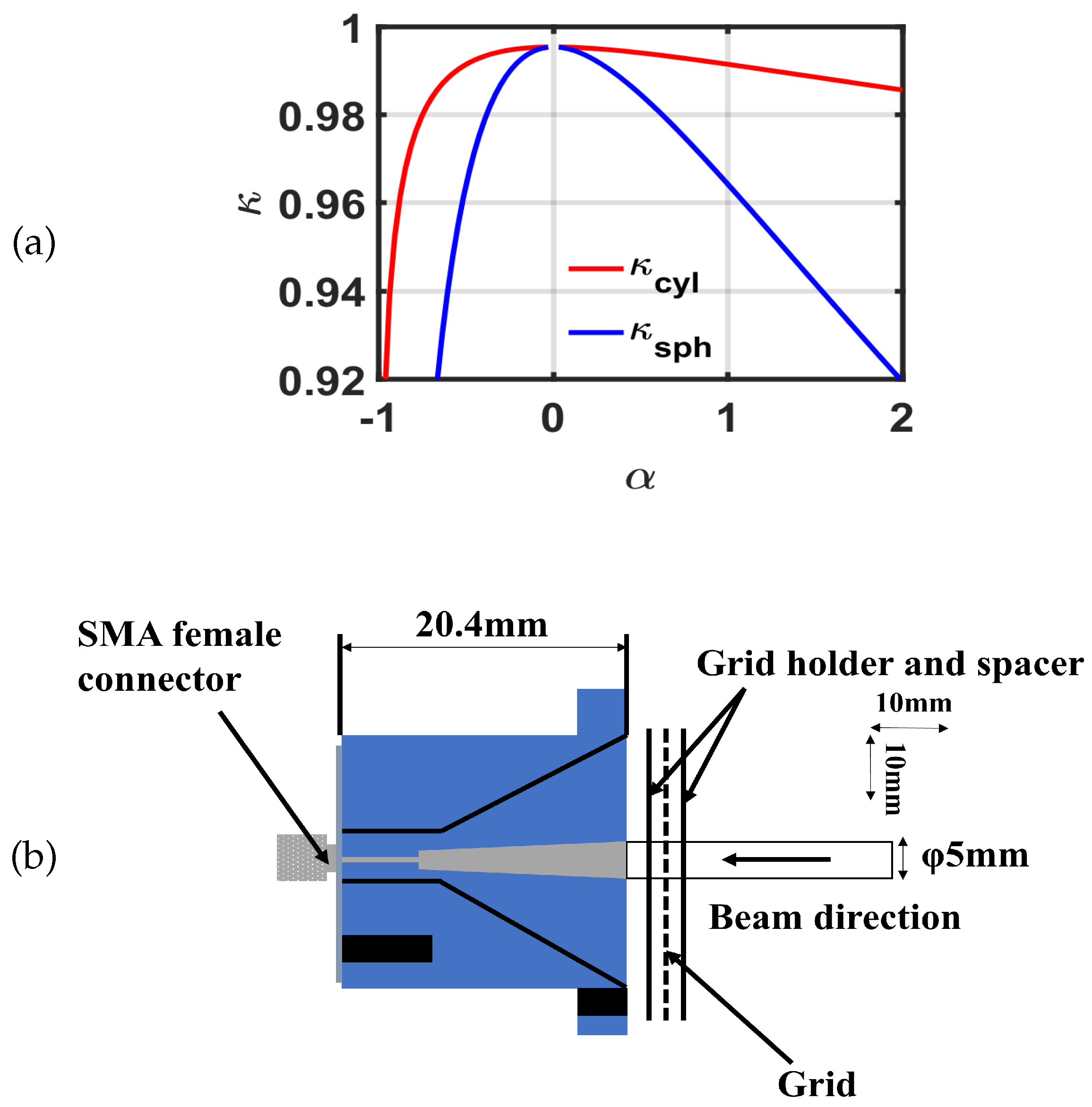




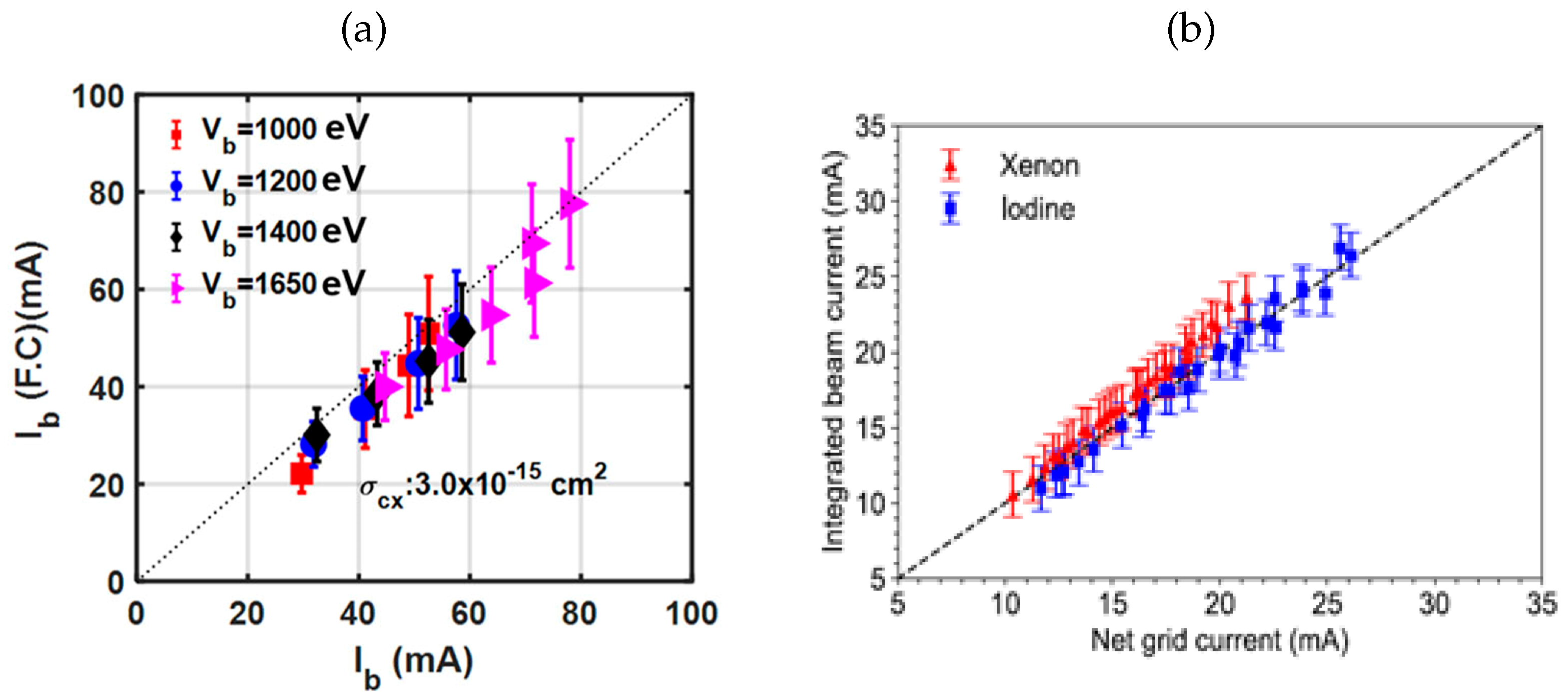
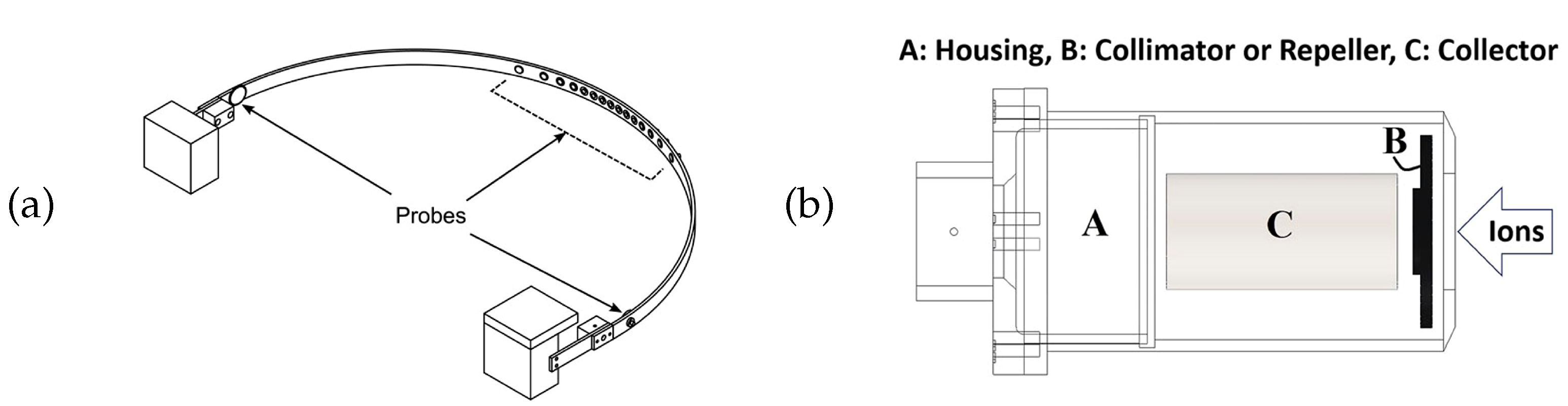

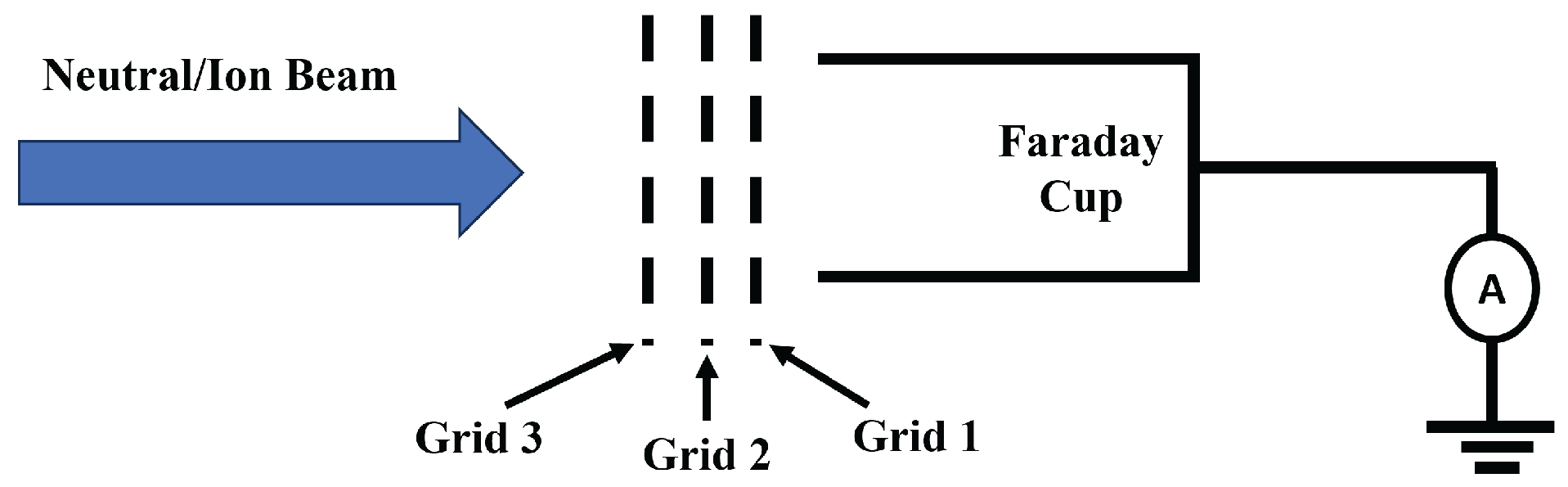


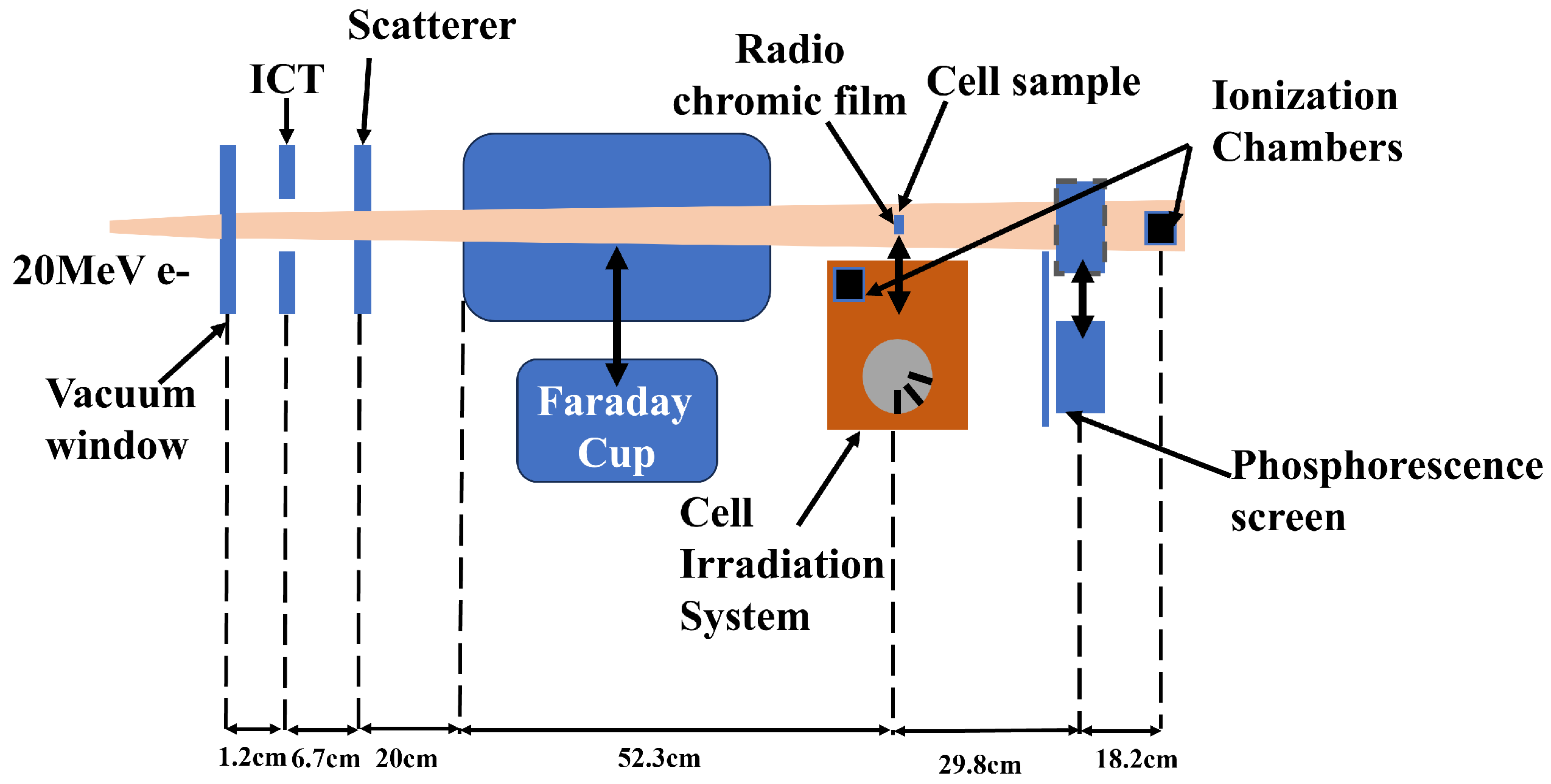

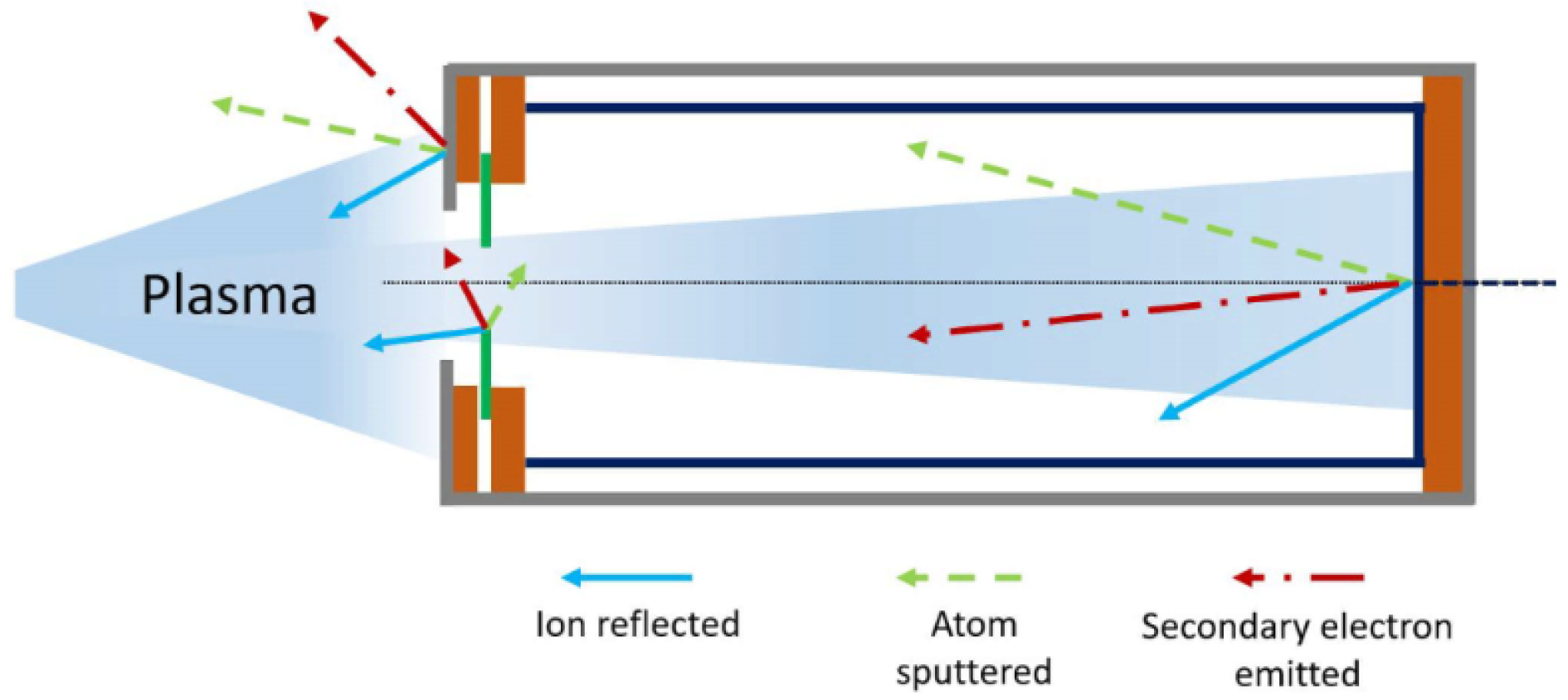
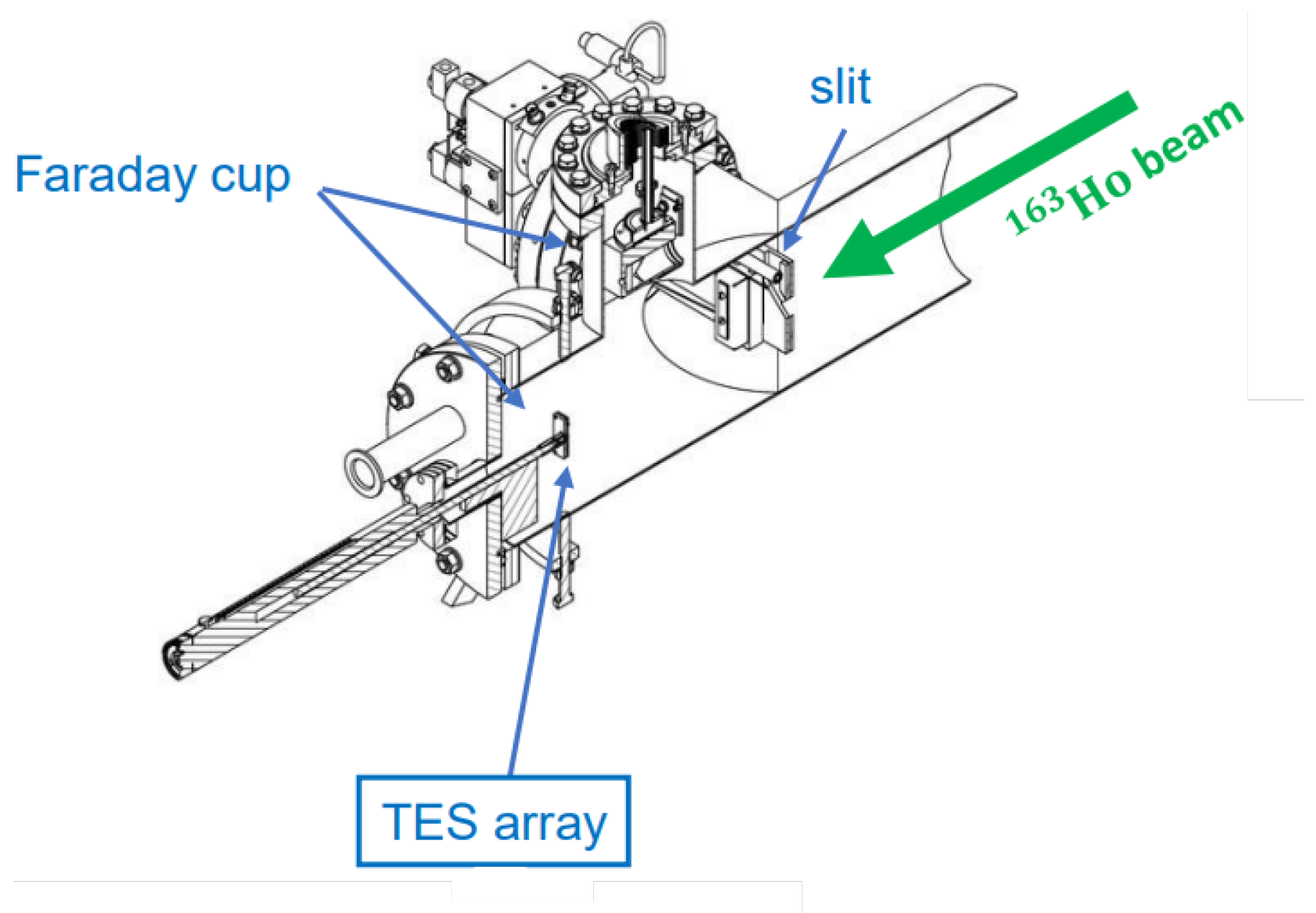


| Material | Advantages | Disadvantages |
|---|---|---|
| Copper (Cu) | Cheap, good heat dissipation, high electrical and thermal conductivity, easily machinable, and corrosion resistant | Prone to oxidation |
| Aluminum (Al) | Cheap, lightweight, good thermal conductivity, and corrosion resistant | Lower mechanical strength and melting point compared to Cu |
| Graphite (C) | Lightweight, radiation resistant, and high melting point | Brittle, difficult to machine, and average thermal conductivity |
| Tungsten (W) | High melting point, excellent for high-power beams | Very dense and heavy, expensive, and difficult to machine |
| Titanium (Ti) | Strong, lightweight, and corrosion resistant | Expensive and difficult to machine |
| Component | Example Model / Specification |
|---|---|
| Operational Amplifier | OPA129 (TI), DLPCA-200 (FEMTO), OPA627 (Burr-Brown) |
| ADC Module | CAEN DT5730 (14-bit, 500 MS/s), NI PXIe-5162 (10-bit, 5 GS/s) |
| DAQ System | NI PXI, CAEN VME, Keysight Infiniium Oscilloscope |
| FPGA Platform | Xilinx Zynq-7000, Altera Cyclone V |
| Shielded Cable | RG-223 Coaxial, Triaxial with Driven Shield |
| Shielding Materials | µ-metal, lead composite, copper mesh |
| Device | Advantages | Limitations |
|---|---|---|
| FCs [5,6,100] | Simple and robust design, direct current measurement, wide dynamic range, radiation hardness, absolute measurements without calibration, suitable for high-intensity beams | Low sensitivity for low currents, slow response times, no energy resolution, secondary electron emission can affect accuracy, destructive measurement |
| Electron multipliers [258,259] | High sensitivity, capable of detecting single ions, fast response times | Limited dynamic range, gain instability over time, requires high-voltage power supplies and complex signal processing |
| Ionization chambers [260,261] | Gas amplification increases sensitivity, non-destructive measurement | Requires careful gas handling and calibration, lower resolution compared to electron multipliers, slower response times, saturation at Ultra-High Dose Rates. |
| Scintillation detectors [262,263] | Fast response times, good energy resolution | Requires careful calibration, can be affected by radiation damage, involves complex photomultiplier tubes or photodiodes for signal readout |
| Semiconductor detectors [264,265] | High energy resolution, capable of detecting individual particles | Complex and expensive, sensitive to radiation damage, requires cooling systems for optimal performance |
| Current transformers (CTs) [266,267] | Non-destructive measurement, continuous monitoring without intercepting the beam | Limited to pulsed beams, lower sensitivity for DC beams |
| Beam current transformers (BCTs) | Non-invasive, real-time measurement, high accuracy | Limited by bandwidth, sensitive to external magnetic fields |
| Wall current monitors [268,269] | Non-interceptive measurement, can measure the image current induced on beam pipe walls | Limited–high-energy beams, requires precise calibration and alignment |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rawat, B.S.; Kumar, N.; Ghosal, D.; Aflyatunova, D.; Rienäcker, B.; Welsch, C.P. Faraday Cups: Principles, Designs, and Applications Across Scientific Disciplines—A Review. Instruments 2025, 9, 20. https://doi.org/10.3390/instruments9030020
Rawat BS, Kumar N, Ghosal D, Aflyatunova D, Rienäcker B, Welsch CP. Faraday Cups: Principles, Designs, and Applications Across Scientific Disciplines—A Review. Instruments. 2025; 9(3):20. https://doi.org/10.3390/instruments9030020
Chicago/Turabian StyleRawat, Bharat Singh, Narender Kumar, Debdeep Ghosal, Daliya Aflyatunova, Benjamin Rienäcker, and Carsten. P. Welsch. 2025. "Faraday Cups: Principles, Designs, and Applications Across Scientific Disciplines—A Review" Instruments 9, no. 3: 20. https://doi.org/10.3390/instruments9030020
APA StyleRawat, B. S., Kumar, N., Ghosal, D., Aflyatunova, D., Rienäcker, B., & Welsch, C. P. (2025). Faraday Cups: Principles, Designs, and Applications Across Scientific Disciplines—A Review. Instruments, 9(3), 20. https://doi.org/10.3390/instruments9030020









