X-Ray and UV Detection Using Synthetic Single Crystal Diamond
Abstract
1. Introduction
2. Survey of Diamond Properties
3. Diamond-Radiation Interactions
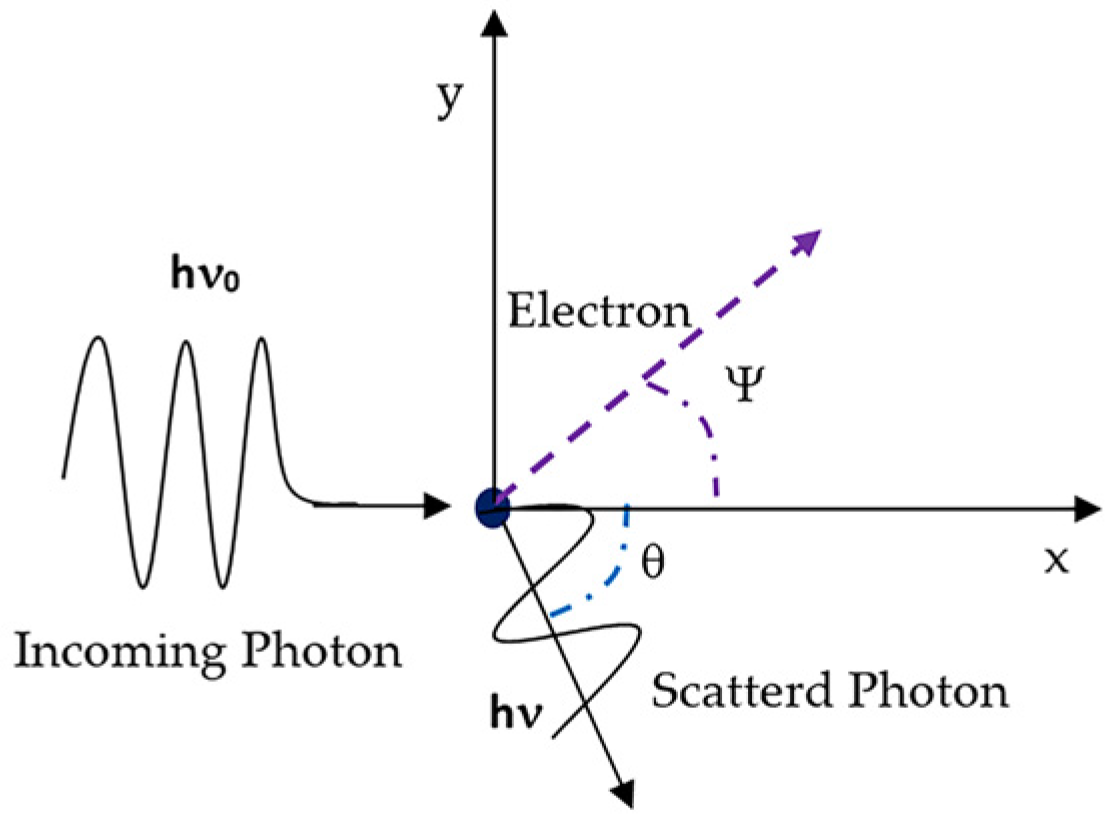
3.1. Photon Interactions
- γ + A → A* (excitation)
- γ + A → γ + A (Coherent or Rayleigh scattering)
- γ + A → γ’ + A* (Incoherent or Raman scattering)
- γ + A → A+ + e− (Ionization or Photoelectric effect)
- γ + A → γ’ + A+ + e− (Incoherent or Compton scattering)
- γ + A → A +(e− + e+) (pair production)
Photon Attenuation
3.2. Optical Photons Attenuation
4. Photodetectors
4.1. Photodetection in Semiconductors: Sketch of Theory
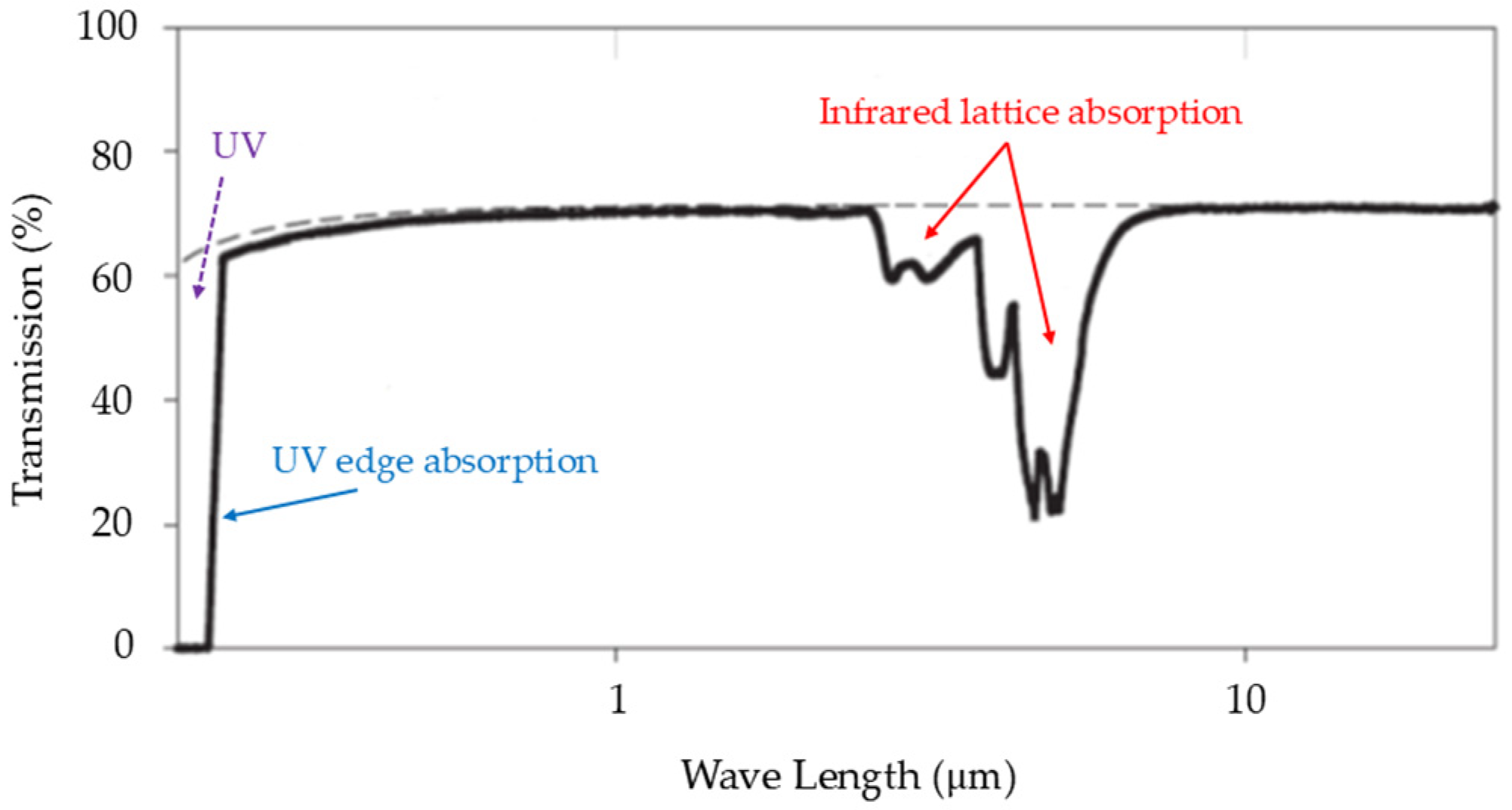
4.1.1. UV Absorption in Diamond
4.1.2. Carriers Production and Recombination
4.1.3. Charge Carriers Transport and Ramo–Shockley Theorem
4.2. Performance Characteristics of a Photodetector
4.2.1. Response Time
- the charge collection time (τCC), which is the time required for the electric field to sweep out charge carriers generated inside the semiconductor sensitive region;
- the diffusion time (τD), which is the time needed for charge carriers to diffuse inside the semiconductor volume;
- the rise time associated with the RC time constant (τRC), which is the time required to charge or discharge the photodiode’s junction capacitance through the external load resistance.
5. Diamond UV and X-Ray Photodetectors
5.1. SCD Diamond Photodetectors
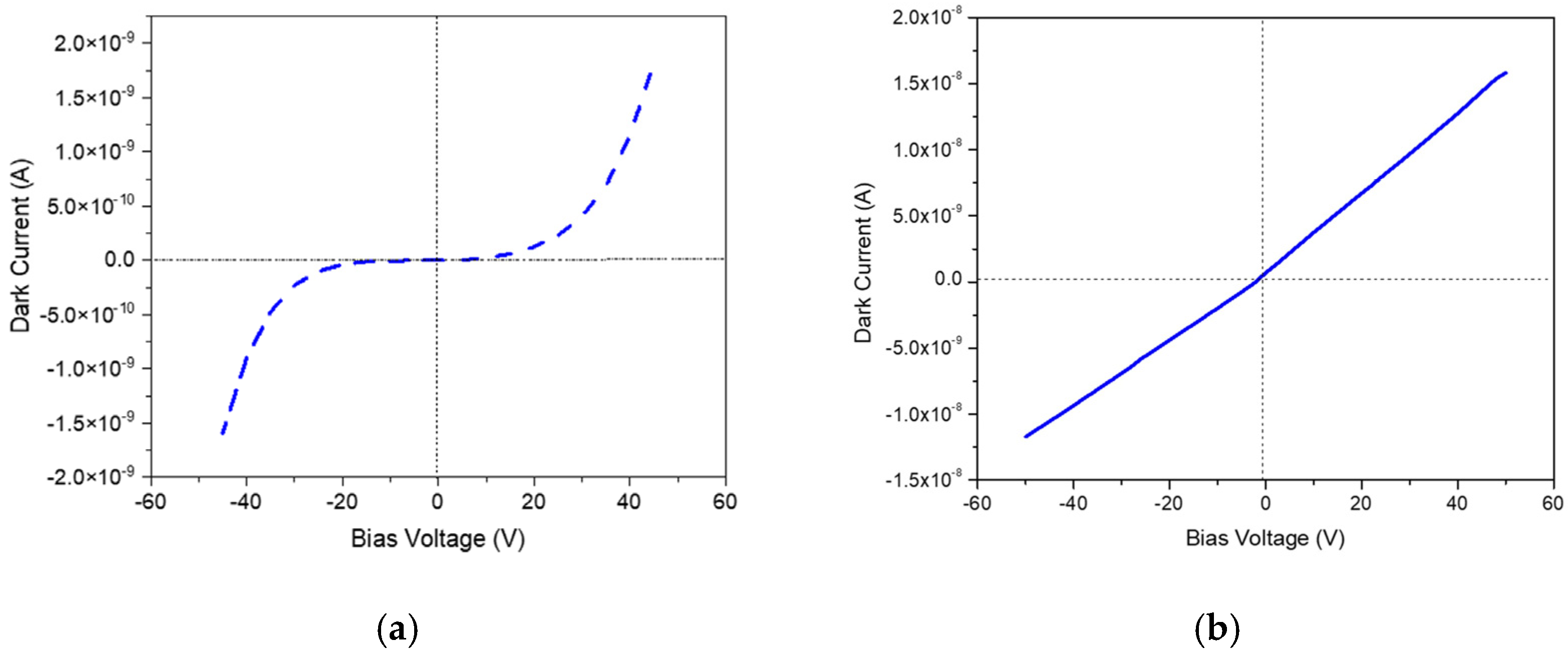
5.2. Ohmic and Schottky Electrical Contacts
5.3. SCD Layered Photodetectors
5.3.1. PIM Schottky Photodetector in Transverse Configuration
- a conductive boron-doped diamond homo-epitaxial layer, used as a backing contact, is deposited by MWPECVD technique on a commercial low-cost synthetic HPHT <100> type Ib SCD substrate (typically of 4 × 4 mm2 in size and approximately 300–400 μm thick), Figure 12a,b. Boron doping is achievedby adding dyborane-hydrogen gas mixture (100 ppm B2H6 in hydrogen) to the CH4/H2 source gases mixture routinely used for growing the intrinsic diamond (the purity of CH4 and H2 gases are 99.9995% and 99.9999%, respectively). P-type conductive diamond with an activation energy of 0.37 eV, is obtained. The boron concentration in the p-type diamond is estimated by fitting the resistivity-temperature curve obtaining values > 1020 cm−3. Depending on the application, the boron concentration can be varied as well as the thickness of the p-doped layer (0.5–2 nm).
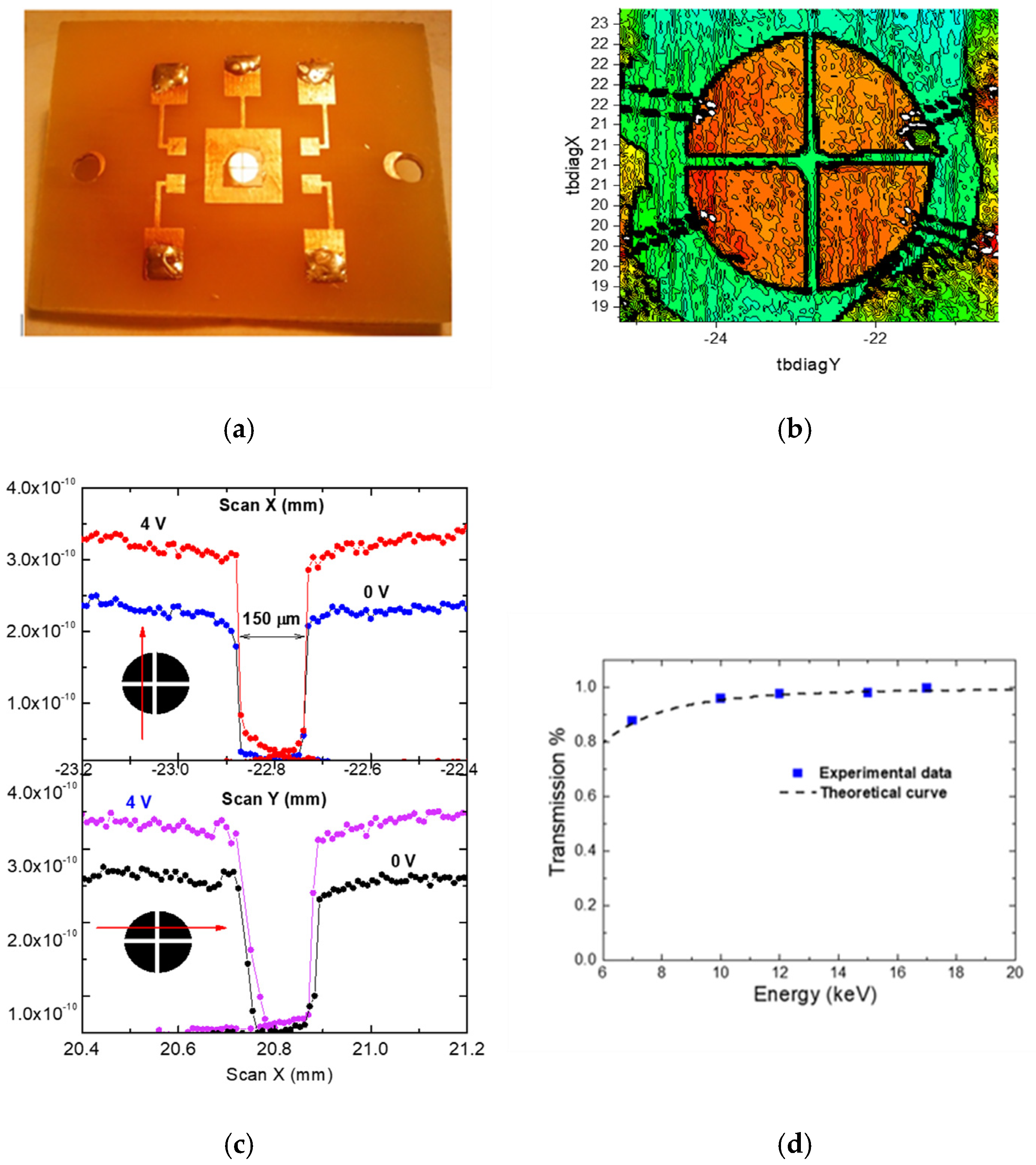
- In a second step, a nominally intrinsic diamond layer, which will act as the detecting region, is homo-epitaxially grown on top of the p-doped layer (Figure 12c). This process is performed in a separate growing apparatus to avoid boron contamination of the intrinsic SCD layer. The thickness of the intrinsic SCD layer can be varied from 0.5 μm up to a few hundred of microns. For UV photodiodes, owing to the small penetration depth of the UV radiation, the detecting region has a thickness of approximately 0.5–2 μm [95]. In the case of soft X-ray detection, a higher thickness of the intrinsic SCD, usually > 15 μm, can be chosen. After the intrinsic diamond growth, the PIM photodetector is oxidized by isothermal annealing at 500 °C for 1h in air to remove the H2 surface conductive layer formed during the growing phase. Eventually, a metal electrode, about 2–3 mm in diameter or side length is deposited by thermal evaporation on the top intrinsic diamond surface while an annealed silver paint is used to provide an almost ohmic contact to the boron–doped SCD layer (Figure 12d). Figure 13 shows two SEM pictures of a PIM photodetector.
5.3.2. PIM in Planar Configuration and Interdigitated Finger Electrodes
5.4. Characterization of Layered Photodetectors
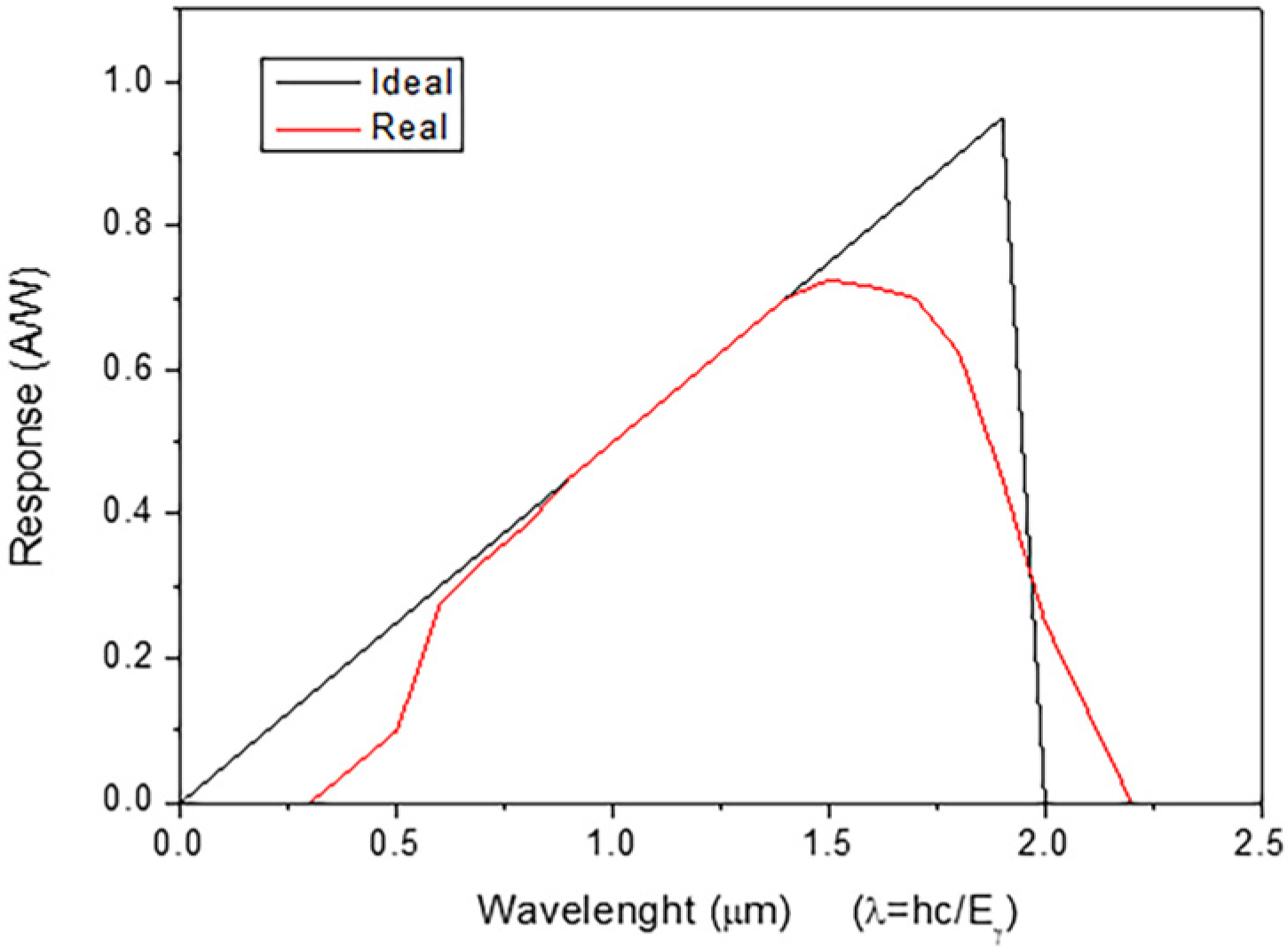
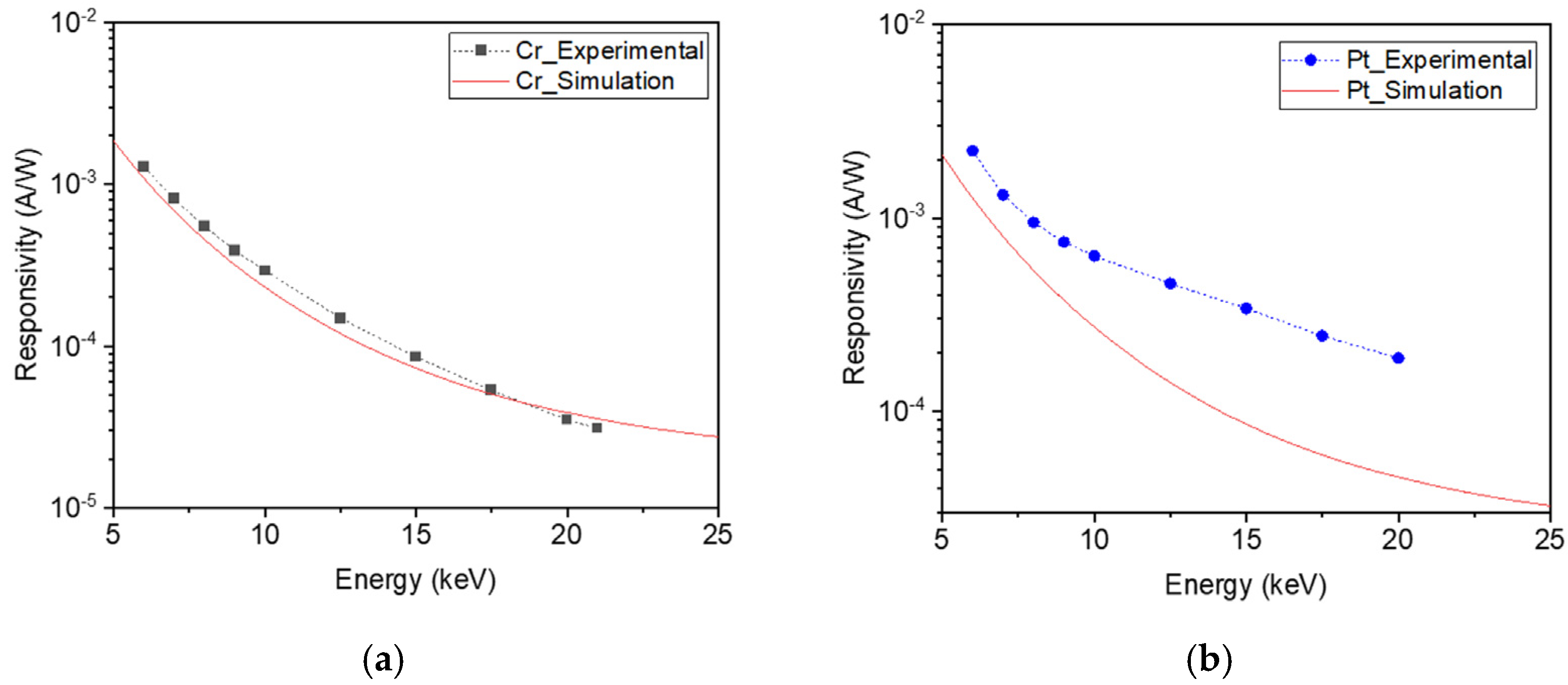
5.4.1. Responsivity of Layered Detectors
5.4.2. Time Dependent Response of Layered Detectors
6. Applications
6.1. Plasma Physics
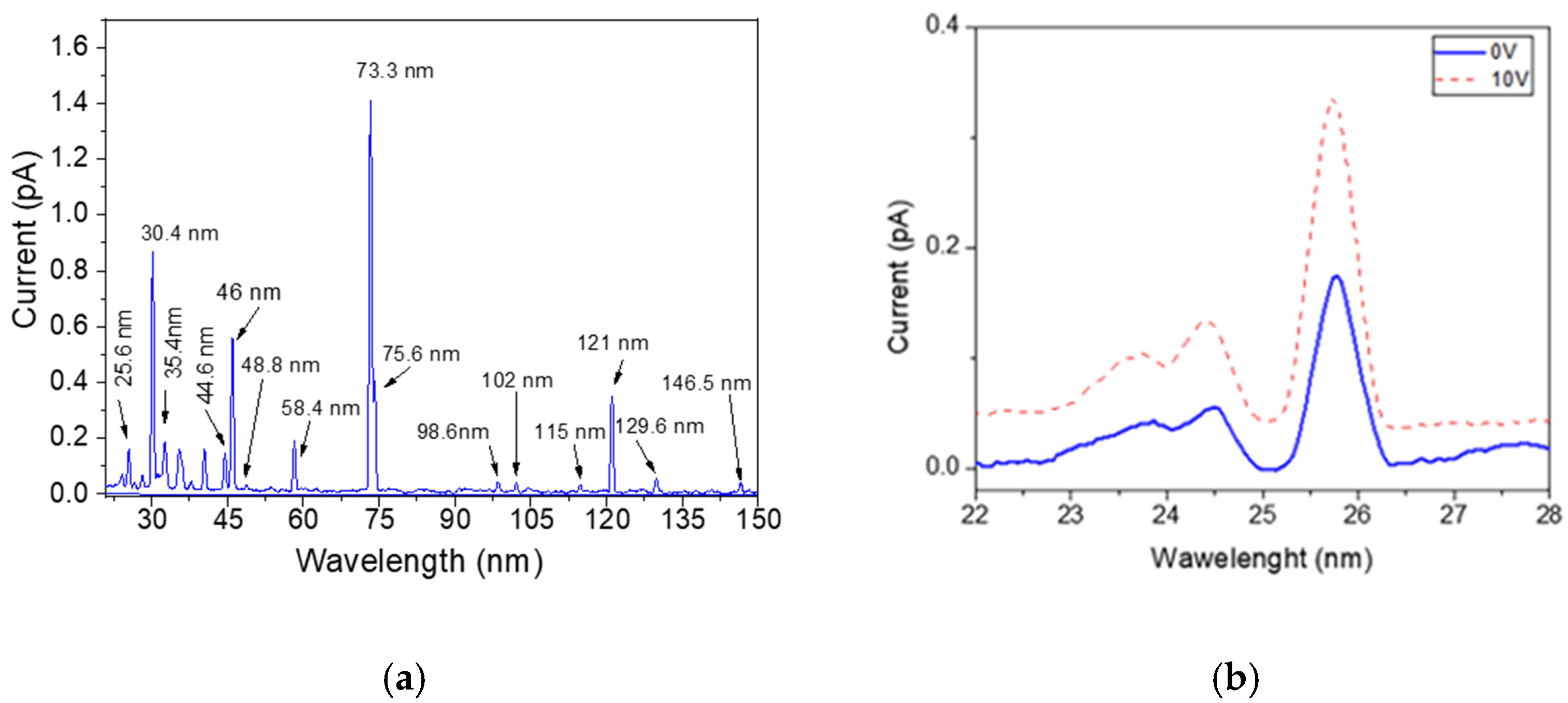
6.2. Syncrotrons, FEL and Space
7. Open Issues and Future Developments
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koizumi, S.; Nebel, C.E.; Nesladek, M. (Eds.) Physics and Application of CVD Diamond; Wiley-VCH GmbH Co. KGaA: Wetnhetm, Germany, 2008; ISBN 978-3-527-40801-6. [Google Scholar]
- Paoletti, A.; Tucciarone, A. (Eds.) The physics of diamond. In Proceedings of the International School of Physics Enrico Fermi—Course CXXXV, Varenna, Italy, 23 July–2 August 1996; IOS Press: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Nebel, C.E. Electronic properties of diamond. Semicon. Sci. Technol. 2003, 18, S1–S11. [Google Scholar] [CrossRef]
- Nebel, C.E.; Ristein, J. (Eds.) Thin-Film Diamond I; Elsevier: Amsterdam, The Netherlands, 2003; Volume 76, ISBN 978-0-12-752185-5. [Google Scholar]
- Balkanski, M.; Wallis, R.F. Semiconductor Physics and Applications; Oxford University Press: Oxford, UK, 2000; ISBN -10: 0198517408. [Google Scholar]
- Kozlov, S.; Belcarz, E.; Hage-Ali, M.; Stuck, R.; Siffert, P. Diamond nuclear radiation detectors. Nucl. Instrum. Methods 1974, 117, 277–283. [Google Scholar] [CrossRef]
- Tapper, R.J. Diamond detectors in particle physics. Rep. Prog. Phys. 2000, 63, 1273–1316. [Google Scholar] [CrossRef]
- Wort, C.J.H.; Balmer, R.S. Diamond as an electronic material. Mater. Today 2008, 11, 22–28. [Google Scholar] [CrossRef]
- Angelone, M.; Verona, C. Properties of Diamond-Based Neutron Detectors Operated in Harsh Environment. J. Nucl. Eng. 2021, 2, 422–470. [Google Scholar] [CrossRef]
- Laub, W.U.; Kaulich, T.W.; Nüsslin, F. A diamond detector in the dosimetry of high-energy electron and photon beams. Phys. Med. Biol. 1999, 44, 2183–2192. [Google Scholar] [CrossRef]
- Marinelli, M.; Prestopino, G.; Verona, C.; Verona-Rinati, G. Experimental determination of the PTW 60019 micro Diamond dosimeter active area and volume. Med. Phys. 2016, 43, 5205–5212. [Google Scholar] [CrossRef]
- Rollet, S.; Angelone, M.; Magrin, G.; Marinelli, M.; Milani, E.; Pillon, M.; Prestopino, G.; Verona, C.; Verona-Rinati, G. A novel microdisimeter based upon artificial single crystal diamond. IEEE Trans. Nucl. Sci. 2012, 59, 2409. [Google Scholar] [CrossRef]
- Verona, C.; Magrin, G.; Solevi, P.; Bandorf, M.; Marinelli, M.; Stock, M.; Rinati, G.V. Toward the use of single crystal diamond based detector for ion-beam therapy microdosimetry. Radiat. Meas. 2018, 110, 25–31. [Google Scholar] [CrossRef]
- Hostader, R. Crystal counters. Nucleonics 1949, 4, 29. [Google Scholar]
- Gudden, B.; Pohl, R. Das quantenaquivalent bei der lichtelektrischen leitung. Z. Phys. 1923, 17, 331–346. [Google Scholar] [CrossRef]
- Werner, M.; Locher, R. Growth and application of undoped and doped diamond films. Rep. Prog. Phys. 1998, 61, 1665–1710. [Google Scholar] [CrossRef]
- Schwander, M.; Partes, K. A review of diamond synthesis by CVD processes. Diam. Relat. Mater. 2011, 20, 1287–1301. [Google Scholar] [CrossRef]
- Dossa, S.S.; Ponomarev, I.; Feigelson, B.N.; Hainke, M.; Kranert, C.; Friedrich, J.; Derby, J.J. Analysis of the High-Pressure High-Temperature (HPHT) growth of single crystal diamond. J. Cryst. Growth 2023, 609, 127150. [Google Scholar] [CrossRef]
- Angelone, M.; Pillon, M.; Bertalot, L.; Orsitto, F.; Marinelli, M.; Milani, E.; Pucella, G.; Tucciarone, A.; Rinati, G.V.; Popovichev, S.; et al. Time dependent 14 MeV neutrons measurement using a polycrystalline chemical vapor deposited diamond detector at the JET tokamak. Rev. Sci. Instrum. 2005, 76, 013506. [Google Scholar] [CrossRef]
- Pomorski, M.; Berdermann, E.; Caragheorgheopol, A.; Ciobanu, M.; Kiš, M.; Martemiyanov, A.; Nebel, C.; Moritz, P.; For the NoRHDia Collaboration. Development of single-crystal CVD-diamond detectors for spectroscopy and timing. Phys. Stat. Solid. 2006, 203, 3152. [Google Scholar] [CrossRef]
- Schmid, G.J.; Griffith, R.L.; Izumi, N.; Koch, J.A.; Lerche, R.A.; Moran, M.J.; Phillips, T.W.; Turner, R.E.; Glebov, V.Y.; Sangster, T.C.; et al. CVD diamond as a high bandwidth neutron detector for inertial confinement fusion diagnostics. Rev. Sci. Instrum. 2003, 74, 1828–1831. [Google Scholar] [CrossRef]
- Adam, W.; de Boer, W.; Borchi, E.; Bruzzi, M.; Colledani, C.; D’Angelo, P.; Dabrowski, V.; Dulinski, W.; van Eijk, B.; Eremin, V.; et al. Radiation hard diamond sensors for future tracking applications. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2006, 565, 278–283. [Google Scholar] [CrossRef]
- Adam, W.; Bauer, C.; Berdermann, E.; Bergonzo, P.; Bogani, F.; Borchi, E.; Brambilla, A.; Bruzzi, M.; Colledani, C.; Conway, J.; et al. Review of the development of diamond radiation sensors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 434, 131–145. [Google Scholar] [CrossRef]
- Pernegger, H. High mobility diamonds and particle detectors. Phys. Status Sol. 2006, 203, 3299–3314. [Google Scholar] [CrossRef]
- Stoupin, S.; Krawczyk, T.; Liu, Z.; Franck, C. Selection of CVD Diamond Crystals for X-ray Monochromator Applications Using X-ray Diffraction Imaging. Crystals 2019, 9, 396. [Google Scholar] [CrossRef]
- Sang, L.; Liao, M.; Sumiya, M. A Comprehensive Review of Semiconductor Ultraviolet Photodetectors: From Thin Film to One-Dimensional Nanostructures. Sensors 2013, 13, 10482–10518. [Google Scholar] [CrossRef]
- Mainwood, A. Recent developments of diamond detectors for particles and UV radiation. Semicond. Sci. Technol. 2000, 15, R55–R63. [Google Scholar] [CrossRef]
- Barberini, L.; Cadeddu, S.; Caria, M. A new material for imaging in the UV: CVD Diamond. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 460, 127–137. [Google Scholar] [CrossRef]
- Koide, Y.; Liao, M.; Alvarez, J. Thermally stable solar-blind diamond UV photodetector. Diam. Relat. Mater. 2006, 15, 1962–1966. [Google Scholar] [CrossRef]
- Meyer, O.; Guirlet, R.; Haquin, S.; Monier-Garbet, P. X-UV spectroscopy for nuclear magnetic fusion diagnostic. UVX 2010, 2011, 115–121. [Google Scholar] [CrossRef][Green Version]
- Angelone, M.; Pillon, M.; Marinelli, M.; Milani, E.; Prestopino, G.; Verona, C.; Verona-Rinati, G.; Coffey, I.; Murari, A.; Tartoni, N. Single crystal artificial diamond detectors for VUV and soft X-rays measurements on JET thermonuclear fusion plasma. Nucl. Instrum. Methods Phys. Res. 2010, 623, 726–730. [Google Scholar] [CrossRef]
- Caiffi, B.; Coffey, I.; Pillon, M.; Osipenko, M.; Prestopino, G.; Ripani, M.; Taiuti, M.; Verona, C.; Verona-Rinati, G.; JET-EFDA contributors. Analysis of the response of CVD Diamond Detectors for UV and X-Ray plasma diagnostics installed at JET. Phys. Procedia 2015, 62, 79–83. [Google Scholar] [CrossRef][Green Version]
- Cesaroni, S.; Angelone, M.; Apruzzese, G.; Bombarda, F.; Gabellieri, L.; Marinelli, M.; Milani, E.; Palomba, S.; Pucella, G.; Romano, A.; et al. CVD diamond photodetectors for FTU plasma diagnostics. Fusion. Eng. Des. 2021, 166, 112323. [Google Scholar] [CrossRef]
- Snyders, R.; Hegemann, D.; Thiry, D.; Zabeida, O.; Klemberg-Sapieha, J.; Martinu, L. Foundations of plasma enhanced chemical vapor deposition of functional coatings. Plasma Sources Sci. Technol. 2023, 32, 07400. [Google Scholar] [CrossRef]
- Dobrinets, I.A.; Vins, V.G.; Zaitsev, A.M. HPHT-Treated Diamonds; Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 181, ISBN 978-3-642-37489-0. [Google Scholar] [CrossRef]
- Burns, R.; Hansen, J.; Spits, R.; Sibanda, M.; Welbourn, C.; Welch, D. Growth of high purity large synthetic diamond crystals. Diam. Relat. Mater. 1999, 8, 1433–1437. [Google Scholar] [CrossRef]
- Matsumoto, S.; Sato, Y.; Kamo, M.; Setaka, N. Vapor Deposition of Diamond Particles from Methane. Jpn. J. Appl. Phys. 1982, 21, L183–L185. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley and Sons (WIE): Hoboken, NJ, USA, 2004; ISBN -10. [Google Scholar]
- Koike, J.; Parkin, D.M.; Mitchell, T.E. Displacement threshold energy for type IIa diamond. Appl. Phys. Lett. 1992, 60, 1450–1452. [Google Scholar] [CrossRef]
- Angelone, M. Diamond Detectors for Neutrons; International Atomic Energy: Vienna, Austria, 2020; Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/52/019/52019798.pdf (accessed on 3 April 2025).
- Attix, F.H. Introduction to Radiological Physics and Radiation Dosimetry; John Wiley & Sons: Hoboken, NJ, USA, 1986; ISBN 9780471011460. [Google Scholar]
- Seely, J.F. Quantum Theory of Inverse Bremsstrahlung Absorption and Pair Production. In Laser Interaction and Related Plasma Phenomena; Schwarz, H.J., Hora, H., Eds.; Springer: Boston, MA, USA, 1974. [Google Scholar] [CrossRef]
- Motz, J.W.; Olsen, H.A.; Koch, H.W. Pair production by photons. Rev. Mod. Phys. 1969, 41, 581. [Google Scholar] [CrossRef]
- Andrews, D.L. Rayleigh Scattering and Raman Effect, Theory. In Encyclopedia of Spectroscopy and Spectrometry, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 978-0-12-803224-4. [Google Scholar]
- Klein, O.; Nishina, Y. Über die Streuung von Strahlung durch freie Elektronen nach der neuen relativistischen Quantendynamik von Dirac. Z. Phys. 1929, 52, 853–869. [Google Scholar] [CrossRef]
- Chen, S.-H.; Kotlarchyk, M. Interactions of Photons and Neutrons with Matter, 2nd ed.; World Scientific: Singapore, 2007; p. 271. ISBN 9789810242145. [Google Scholar]
- Hubbel, J.H. Attenuation Coefficients and Energy Absorption Coefficients from 10 keV to 100 GeV; NBS Report NSRDS-NBS 29; National Bureau of Standards: Gaithersburg, MD, USA, 1981. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/NSRDS/nbsnsrds29.pdf (accessed on 3 April 2025).
- Hubbel, J.H. Review and history of photon cross section calculations. Phys. Med. Biol. 2006, 51, R245–R262. [Google Scholar] [CrossRef]
- Weinberg, S. The Quantum Theory of Fields; Cambridge University Press: Cambridge, UK, 1995; Volume I, ISBN -13: 978-0521550017. [Google Scholar]
- Qian, W. On the Physical Process and Essence of the Photoelectric Effect. J. Appl. Math. Phys. 2023, 11, 1580–1597. [Google Scholar] [CrossRef]
- Available online: https://pubchem.ncbi.nlm.nih.gov/ptable/atomic-mass/ (accessed on 30 January 2025).
- Marinelli, M.; Felici, G.; Galante, F.; Gasparini, A.; Giuliano, L.; Heinrich, S.; Pacitti, M.; Prestopino, G.; Vanreusel, V.; Verellen, D.; et al. Design, realization, and characterization of a novel diamond detector prototype for FLASH radiotherapy dosimetry. Med. Phy. 2022, 49, 1902–1910. [Google Scholar] [CrossRef]
- Yin, Z.; Akkerman, Z.; Yang, B.X.; Smith, F.W. Optical properties and microstructure of CVD diamond films. Diam. Relat. Matyerials 1997, 6, 153–158. [Google Scholar] [CrossRef]
- Nalwa, H.S. Photodetectors and Fiber Optics; Academic Press: Cambridge, MA, USA, 2001; ISBN -10: 012513908X. [Google Scholar]
- Hummel, R.E. Electronic Properties of Materials, 4th ed.; Appendix-4; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Mildren, R.P.; Rabeau, J.R. (Eds.) Optical Engineering of Diamond; Chapter 1; Wiley-VCH Verlag GmbH & Co.: Hoboken, NJ, USA, 2013; ISBN 9783527411023. [Google Scholar] [CrossRef]
- Clark, C.D.; Dean, P.J.; Harris, P.V. Intrinsic edge absorption in diamond. Proc. R. Soc. A Math. Phys. Eng. Sci. 1964, 277, 312–329. [Google Scholar] [CrossRef]
- Grahn, H.T. Introduction to Semiconductor Physics; World Scientific Publishing: Singapore, 1999; ISBN -10: 9810233027. [Google Scholar]
- Drude, P. Zur Elektronentheorie der Metalle. Ann. Der Phys. 1900, 306, 566–613. [Google Scholar] [CrossRef]
- Li, Z.; Kraner, H. Modeling and simulation of charge collection properties for neutron irradiated silicon detectors. Nucl. Phys. B-Proc. Suppl. 1993, 32, 398–409. [Google Scholar] [CrossRef]
- Sze, S.M.; Mattis, D.C. Physics of Semiconductor Devices. Phys. Today 1970, 23, 75. [Google Scholar] [CrossRef]
- Pernegger, H.; Roe, S.; Weilhammer, P.; Eremin, V.; Frais-Kölbl, H.; Griesmayer, E.; Kagan, H.; Schnetzer, S.; Stone, R.; Trischuk, W.; et al. Charge-carrier properties in synthetic single-crystal diamond measured with the transient-current technique. J. Appl. Phys. 2005, 97, 073704. [Google Scholar] [CrossRef]
- Ramo, S. Currents Induced by Electron Motion. Proc. IRE 1939, 27, 584–585. [Google Scholar] [CrossRef]
- Shockley, W. Currents to Conductors Induced by a Moving Point Charge. J. Appl. Phys. 1938, 9, 635–636. [Google Scholar] [CrossRef]
- Weiss, C.; Frais-Kölbl, H.; Griesmayer, E.; Kavrigin, P. Ionization signals from diamond detectors in fast-neutron fields. Eur. Phys. J. A 2016, 52, 269. [Google Scholar] [CrossRef]
- Monroy, E.; Omnes, M.; Calle, F. Wide-bandgap semiconductor ultraviolet photodetectors. Semicond. Sci. Technol. 2003, 18, R33. [Google Scholar] [CrossRef]
- Lin, C.H.; Liu, C.W. Metal-insulator-semiconductor photodetectors. Sensors 2010, 10, 8797–8826. [Google Scholar] [CrossRef]
- Omnes, F.; Monroy, E.; Munoz, E.; Reverchon, J.L. Wide bandgap UV photodetectors: A short review of devices and applications. Proc. SPIE 2007, 6473E, 1–15. [Google Scholar] [CrossRef]
- Pallab, B. Semiconductor Optoelectronic Devices; Person Education Limited Publisher: London, UK, 1996; ISBN -10: 0134956565. [Google Scholar]
- BenMoussa, A.; Soltani, A.; Schühle, U.; Haenen, K.; Chong, Y.; Zhang, W.; Dahal, R.; Lin, J.; Jiang, H.; Barkad, H.; et al. Recent development of wide-bandgap semiconductor based UV sensors. Diam. Relat. Mater. 2009, 18, 860–864. [Google Scholar] [CrossRef]
- Verona, C. Single Crystal Diamond Schottky Photodiode. In Photodiodes-World Activities in 2011; Park, J.-W., Ed.; IntechOpen Ltd.: London, UK, 2011. [Google Scholar] [CrossRef]
- Almaviva, S.; Marinelli, M.; Milani, E.; Prestopino, G.; Tucciarone, A.; Verona, C.; Verona-Rinati, G.; Angelone, M.; Pillon, M. Extreme UV photodetectors based on CVD single crystal diamond in a p-type/intrinsic/metal configuration. Diam. Relat. Mater. 2009, 18, 101–105. [Google Scholar] [CrossRef]
- Liao, M.Y.; Sang, L.W.; Teraji, T.; Imura, M.; Alvarez, J.; Koide, Y. Comprehensive investigation of single crystal diamond deep-ultraviolet detectors. Jpn. J. Appl. Phys. 2012, 51, 090115:1–090115:7. [Google Scholar] [CrossRef]
- Balducci, A.; Marinelli, M.; Milani, E.; Morgada, M.E.; Tucciarone, A.; Verona-Rinati, G.; Angelone, M.; Pillon, M. Extreme ultraviolet single-crystal diamond detectors by chemical vapor deposition. Appl. Phys. Lett. 2005, 86, 193509. [Google Scholar] [CrossRef]
- Teraji, T.; Yoshizaki, S.; Wada, H.; Hamada, M.; Ito, T. Highly sensitive UV photodetectors fabricated using high-quality single-crystalline CVD diamond films. Diam. Relat. Mater. 2004, 13, 858–862. [Google Scholar] [CrossRef]
- Polyakov, V.I.; Rukovishnikov, A.I.; Rossukanyi, M.N.; Krikunov, A.I.; Ralchenko, V.G.; Smolin, A.A.; Varnin, V.P.; Teremetskaya, I.G. Photodetectors with CVD diamond films: Electrical and photoelectrical properties photoconductive and photodiode structures. Diam. Relat. Mater. 1998, 7, 821–825. [Google Scholar] [CrossRef]
- Thaiyotin, L.; Ratanaudompisut, E.; Phetchakul, T.; Cheirsirikul, S.; Supadech, S. UV photodetectors from Schottky diode diamond film. Diam. Relat. Mater. 2002, 11, 442–445. [Google Scholar] [CrossRef]
- McKeag, R.D.; Jackman, R.B. Diamond UV photodetectors: Sensitivity and speed for visible blind applications. Diam. Relat. Mater. 1998, 7, 513–518. [Google Scholar] [CrossRef]
- Pace, E.; Di Benedetto, R.; Scuderi, S. Fast stable visible-blind and highly sensitive CVD diamond UV photodetectors for laboratory and space applications. Diam. Relat. Mater. 2000, 9, 987–993. [Google Scholar] [CrossRef]
- Almaviva, S.; Marinelli, M.; Milani, E.; Prestopino, G.; Tucciarone, A.; Verona, C.; Verona-Rinati, G.; Angelone, M.; Pillon, M. Extreme UV UV single crystal diamond Schottky photodiode in a planar and transverse configuration. Diam. Relat. Mater. 2000, 19, 78–82. [Google Scholar] [CrossRef]
- Werner, M. Diamond metallization for device applications. Semicond. Sci. Technol. 2003, 18, S41. [Google Scholar] [CrossRef]
- Sze, S.M. Semiconductor Devices: Physics and Technology; John Wiley and Sons (WIE): Hoboken, NJ, USA, 1985; ISBN 0-471-33372-7. [Google Scholar]
- Tung, R.T. The physics and chemistry of Schottky barrier height. Appl. Phys. Rev. 2014, 1, 011304. [Google Scholar] [CrossRef]
- Tatsumi, N.; Ikeda, K.; Umezawa, H.; Shikata, S. Development of diamond Schottky barrier diode. SEI Tech. Rev. 2009, 68, 54. [Google Scholar]
- Teraji, T.; Koide, Y.; Ito, T. Schottky barrier height and thermal stability of p-diamond (100). Thin Solid Film. 2014, 557, 241. [Google Scholar] [CrossRef]
- Evans, D.A.; Roberts, O.R.; Williams, G.T.; Vearey-Roberts, A.R.; Bain, F.; Evans, S.; Langstaff, D.P.; Twitchen, D.J. Diamond-metal contacts: Interface barriers and real-time characterization. J. Phys. Condens. Matter 2009, 21, 364223. [Google Scholar] [CrossRef]
- Galbiati, A.; Lynn, S.; Oliver, K.; Schirru, F.; Nowak, T.; Marczewska, B.; Duenas, J.; Berjillos, R.; Martel, I.; Lavergne, L. Performance of Monocrystalline Diamond Radiation Detectors Fabricated Using TiW, Cr/Au and a Novel Ohmic DLC/Pt/Au Electrical Contact. IEEE Trans. Nucl. Sci. 2009, 56, 1863–1874. [Google Scholar] [CrossRef]
- Moazed, K.L.; Nguyen, R.; Zeidler, J.R. Ohmic contacts to semiconducting diamond. IEEE Electron. Device Lett. 1988, 9, 350–351. [Google Scholar] [CrossRef]
- Ueda, K.; Kawamoto, K.; Soumiya, T.; Asano, H. High-temperature characteristics of Ag and Ni/diamond Schottky diodes. Diam. Relat. Mater. 2013, 38, 41–44. [Google Scholar] [CrossRef]
- Ueda, K.; Kawamoto, K.; Asano, H. High-temperature and high voltage characteristics of Cu/diamond Schottky diodes. Diam. Relat. Mater. 2015, 57, 28–31. [Google Scholar] [CrossRef]
- Huffman, F. Thermoionic Energy Conversion. In Encyclopedia of Physical Science and Technology, 3rd ed.; Academic Press: Tarzana, CA, USA, 2003; pp. 627–638. [Google Scholar] [CrossRef]
- Moazed, K.L.; Zeidler, J.; Taylor, M.J. A thermally activated solid state reaction process for fabricating ohmic contacts to semiconducting diamond. J. Appl. Phys. 1990, 68, 2246–2254. [Google Scholar] [CrossRef]
- Prins, J.F. Preparation of ohmic contacts to semiconducting diamond. J. Phys. D Appl. Phys. 1989, 22, 1562–1564. [Google Scholar] [CrossRef]
- Latto, M.N.; Riley, D.; May, P.W. Impedance studies of boron-doped CVD diamond electrodes. Diam. Relat. Mater. 2000, 9, 1181–1183. [Google Scholar] [CrossRef]
- Verona, C. Development and Characterization of Extreme UV and Soft X-Ray Schottky Diodes Based on Synthetic Single Crystal Diamond for Plasma Diagnostic at the Joint European Torus (JET) Tokamak. Ph.D. Thesis, Mechanical Engineering Department, Tor Vergata University of Rome, Rome, Italy, 2010. [Google Scholar]
- Brezeanu, M.; Butler, T.; Rupesinghe, N.; Rashid, S.J.; Avram, M.; Amaratunga, G.A.J.; Udrea, F.; Dixon, M.; Twitchen, D.; Garraway, A.; et al. Single crystal diamond M–i–P diodes for power electronics. IEEE Proc. Circuits Devices Syst. 2007, 1, 380. [Google Scholar] [CrossRef]
- Almaviva, S.; Marinelli, M.; Milani, E.; Prestopino, G.; Tucciarone, A.; Verona, C.; Verona-Rinati, G.; Angelone, M.; Pillon, M.; Dolbnya, I.; et al. Chemical vapor deposition diamond based multilayered radiation detector: Physical analysis of detection properties. J. Appl. Phy. 2010, 107, 014511. [Google Scholar] [CrossRef]
- Palik, D. Handbook of Optical Constants of Solids II; Academic Press: Cambridge, MA, USA, 1991; Volume 2, ISBN 0125444222, 9780125444224. [Google Scholar]
- Bombarda, F.; Angelone, M.; Apruzzese, G.; Centioli, C.; Cesaroni, S.; Gabellieri, L.; Grosso, A.; Marinelli, M.; Milani, E.; Palomba, S.; et al. CVD diamond detectors for fast VUV and SX-ray diagnostics on FTU. Nucl. Fusion. 2021, 61, 116004. [Google Scholar] [CrossRef]
- Ciancaglioni, I.; Di Venanzio, C.; Marinelli, M.; Milani, E.; Prestopino, G.; Verona, C.; Verona-Rinati, G.; Angelone, M.; Pillon, M.; Tartoni, N. Influence of the metallic contact in extreme-ultraviolet and soft x-ray diamond based Schottky photodiodes. J. Appl. Phys. 2011, 110, 054513. [Google Scholar] [CrossRef]
- X-5 Monte Carlo Team: MCNP—A General Monte Carlo N-Particle Transport Code, Version 5, LANL Report LA-UR-03-1987, Los Alamos National Laboratory, Los Alamos—New Mexico (USA)(2004). Available online: https://mcnp.lanl.gov/pdf_files/TechReport_2003_LANL_LA-UR-03-1987Revised212008_SweezyBoothEtAl.pdf (accessed on 3 April 2025).
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50-30,000 eV, Z. = 1-92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Phillip, H.R.; Taft, E.A. Kramers-Kronig Analysis of Reflectance Data for Diamond. Phys. Rev. 1964, 136, A1445. [Google Scholar] [CrossRef]
- Ciancaglioni, I.; Marinelli, M.; Milani, E.; Prestopino, G.; Verona, C.; Verona-Rinati, G.; Angelone, M.; Pillon, M. Secondary electron emission in extreme-UV detectors: Application to diamond based devices. J. Appl. Phys. 2011, 110, 014501. [Google Scholar] [CrossRef]
- For Information on Refractive Index and Data. Available online: https://refractiveindex.info/?shelf=main&book=C&page=Phillip (accessed on 3 April 2025).
- Baccarani, G.; Rudan, M.; Spadini, G.; Maes, H.; Vandervorst, W.; Van Overstraeten, R. Interpretation of C-V measurements for determining the doping profile in semiconductors. Solid State Electron. 1980, 23, 65–71. [Google Scholar] [CrossRef]
- Keister, J.W.; Smedley, J. Single crystal diamond photodiode for soft X-ray radiometry. Nucl. Instrum. Meth. Phys. Res. 2009, 606, 774–779. [Google Scholar] [CrossRef]
- Ishihara, H.; Sugio, S.; Kanno, T.; Matsuoka, M.; Hayashi, K.J.S. Characterization of Photoconductive Diamond Detectors Candidate Vacuum Ultraviolet Radiation and Extreme Ultraviolet Radiation Light Source Detectors for Lithography. Sens. Mater. 2010, 22, 357–364. [Google Scholar] [CrossRef][Green Version]
- Antonelli, M.; Di Fraia, M.; Carrato, S.; Cautero, G.; Menk, R.; Jark, W.; Ganbold, T.; Biasiol, G.; Callegari, C.; Coreno, M.; et al. Fast synchrotron and FEL beam monitors based on single-crystal diamond detectors and InGaAs/InAlAs quantum well devices. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 730, 164–167. [Google Scholar] [CrossRef]
- Venot, O.; Fray, N.; Bénilan, Y.; Gazeau, M.-C.; Hébrard, E.; Larcher, G.; Schwell, M.; Dobrijevic, M.; Selsis, F. High-temperature measurements of VUV-absorption cross sections of CO2 and their application to exoplanets. Astron. Astrophys. 2013, 551, A131. [Google Scholar] [CrossRef]
- Liu, K.; Dai, B.; Ralchenko, V.; Xia, Y.; Quan, B.; Zhao, J.; Shu, G.; Sun, M.; Gao, G.; Yang, L.; et al. Single crystal diamond UV detector with a groove-shaped electrode structure and enhanced sensitivity. Sens. Actuators A 2017, 259, 121–126. [Google Scholar] [CrossRef]
- Kang, P.; Bing, D.; Ralchenko, V.; Yuanqin, X.; Baogang, Q.; Jiwen, Z.; Guoyang, S.; Mingqi, S.; Ge, G.; Lei, S.; et al. Diamond-based all-carbon photodetectors for solar-blind imaging. Adv. Opt. Mater. 2018, 6, 1800068. [Google Scholar] [CrossRef]
- Saito, T.; Hayashi, K.; Ishihara, H.; Saito, I. Characterization of photoconductive diamond detectors as a candidate of FUV/VUV transfer standard detectors. Metrologia 2006, 43, S5. [Google Scholar] [CrossRef]
- Trucchi, D.M.; Ascarelli, P. X-ray Spectrum Reconstruction by Diamond Detectors with Linear Response to Dose Rate. Crystals 2021, 11, 1258. [Google Scholar] [CrossRef]
- Griesmayer, E.; Kavrigin, P.; Weiss, C. The use of single crystal CVD diamond as position sensitive X-raydetector. In Proceedings of the 5th International Beam Instrumentation Conference IBIC, Barcelona, Spain, 11–15 September 2016; ISBN 978-3-95450-177-9. [Google Scholar]
- Girolami, M.; Allegrini, P.; Conte, G.; Trucchi, D.-M.; Ralchenko, V.G.; Salvatori, S. Diamond detectors for UV and X-ray source imaging. IEEE Electron Device Lett. 2012, 33, 224–226. [Google Scholar] [CrossRef]
- Normile, S.; Vezinet, D.; Perks, C.; Bombarda, F.; Verona-rinati, G.; Rice, J.E.; Verona, C.; Raso, A.M.; Angelone, M. Design of a diamond-based in-vessel soft x-ray detector for the SPARC tokamak. Rev. Sci. Instrum. 2024, 95, 093102. [Google Scholar] [CrossRef]
- Schühle, U.; Hochedez, J.F. Solar-blind UV detectors based on wide band gap semiconductors. In Observing Photons in Space; ISSI Scientific Report Series; Huber, M.C.E., Pauluhn, A., Culhane, J.L., Timothy, J.G., Wilhelm, K., Zehnder, A., Eds.; Springer: New York, NY, USA, 2013; Volume 9. [Google Scholar] [CrossRef]
- Jia, L.; Zhu, S.; Zhang, N.; Lin, Z.; Cai, W.; Cheng, L.; Lu, X.; Zheng, W. Ultrafast Diamond Photodiodes for vacuum Ultraviolet Imaging in Space-Based Applications. Adv. Opt. Mater. 2025, 13, 2402601. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, D.; Zhu, T.; Wang, J.; Yi, W.; Min, T.; Wang, H. Enhanced Responsivity of Diamond UV Detector Based on Re-grown Lens Structure. IEEE Electron Device Lett. 2020, 41, 1829–1832. [Google Scholar] [CrossRef]
- Pillon, M.; Angelone, M.; Aielli, G.; Almaviva, S.; Marinelli, M.; Milani, E.; Prestopino, G.; Tucciarone, A.; Verona, C.; Rinati, G.V. Radiation tolerance of a high quality synthetic single crystal chemical vapor deposition diamond detector irradiated by 14.8 MeV neutrons. J. Appl. Phys. 2008, 104, 054513. [Google Scholar] [CrossRef]
- Passeri, M.; Pompili, F.; Esposito, B.; Pillon, M.; Angelone, M.; Marocco, D.; Pagano, G.; Podda, S.; Riva, M. Assessment of single crystal diamond detector radiation hardness to 14 MeV neutrons. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2021, 1010, 165574. [Google Scholar] [CrossRef]
- Raso, A.M.; Verona, C.; Angelone, M.; Cesaroni, S.; Loreti, S.; Marinelli, M.; Verona-Rinati, G. Measure and Monte Carlo Simulation of Thin Diamond Detector Sensitivity to 14 MeV Neutrons. In Engineering Methodologies for Medicine and Sports, EMMS 2024; Conference Proceedings; Montanari, R., Richetta, M., Febbi, M., Staderini, E.M., Eds.; Springer Nature: Berlin/Heidelberg, Germany, 2024; Volume 162. [Google Scholar] [CrossRef]
- Martone, M.; Angelone, M.; Pillon, M. The 14 MeV Frascati neutron generator. J. Nucl. Mater. 1994, 212–215, 1661–1664. [Google Scholar] [CrossRef]
- Rebut, P.H. The Joint European Torus (JET). Eur. Phys. J. H. 2018, 43, 459–597. [Google Scholar] [CrossRef]
- De Sio, A.; Pace, E.; Cinque, G.; Marcelli, A.; Achard, J.; Tallaire, A. Diamond detectors for synchrotron radiation X-ray applications. Spectrochim. Acta Part. B 2007, 62, 558–561. [Google Scholar] [CrossRef]
- Tartoni, N.; Angelone, M.; Pillon, M.; Almaviva, S.; Marinelli, M.; Milani, E.; Prestopino, G.; Verona, C.; Verona-Rinati, G.; Roberts, M.A. X-ray detection by using CVD single crystal diamond detector. IEEE Trans. Nucl. Sci. 2009, 56, 849–852. [Google Scholar] [CrossRef]
- Marinelli, M.; Milani, G.E.; Prestopino, C.; Verona, G.; Verona-Rinati, M.; Angelone, M.; Pillon, K.V.; Tartoni, N.; Benetti, M.; Cannata, D.; et al. X-ray beam monitor made by thin-film CVD single-crystal diamond. J. Syncr. Rad. 2012, 19, 1015–1020. [Google Scholar] [CrossRef]
- Bohon, J.; Muller, E.; Smedley, J. Development of diamond-based X-ray detection for high-flux beamline diagnostics. J. Synchrotron Rad. 2010, 17, 711–718. [Google Scholar] [CrossRef]
- Dou, W.; Lin, C.; Fan, W.; Yang, X.; Fang, C.; Zang, H.; Wang, S.; Zh, C.; Zheng, Z.; Zhou, W.; et al. Highly sensitive diamond X-ray detector array for high-temperature applications. Chip 2024, 3, 100106. [Google Scholar] [CrossRef]
- Bloomer, C.; Newton, M.E.; Rehmb, G.; Salter, P.S. A single-crystal diamond X-ray pixel detector with embedded graphitic electrodes. J. Synchrotron Rad. 2020, 27, 599–607. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Ding, W.; Gaowei, M.; De Geronimo, G.; Bohon, J.; Smedley, J.; Muller, E. Pixelated transmission-mode diamond X-ray detector. J. Synchrotron Rad. 2015, 22, 1396–1402. [Google Scholar] [CrossRef] [PubMed]
- Houghton, C.; Bloomer, C.; Bobb, L. A direct experimental comparison of single-crystal CVD diamond and silicon carbide X-ray beam position monitors. J. Synchrotron Rad. 2023, 30, 876–884. [Google Scholar] [CrossRef] [PubMed]
- Desjardins, K.; Bordessoule, M.; Pomorski, M. X-ray position-sensitive duo-lateral diamond detectors at SOLEIL. J. Synchrotron Rad. 2018, 25, 399–406. [Google Scholar] [CrossRef]
- Morse, J.; Solar, B.; Graafsma, H. Diamond X-ray beam-position monitoring using signal readout at the synchrotron radiofrequency. J. Synchrotron Rad. 2010, 17, 456–464. [Google Scholar] [CrossRef]
- Desjardins, K.; Pomorski, K.; Morse, J. Ultra-thin optical grade scCVD diamond as X-ray beam position monitor. J. Synchrotron Rad. 2014, 21, 1217–1223. [Google Scholar] [CrossRef]
- Muller, E.; Smedley, J.M.; Bohon, J.; Yang, X.; Gaowei, M.; Skinner, J.; De Geronimo, G.; Sullivan, M.; Allaire, M.; Keister, J.W.; et al. Transmission-mode diamond white-beam position monitor at NSLS. J. Synchrotron Rad. 2012, 19, 381–387. [Google Scholar] [CrossRef]
- Yıldız, T.C.; Freund, W.; Liu, J.; Schreck, M.; Khakhulin, D.; Yousef, H.; Milnea, C.; Grunert, J. Diamond sensors for hard X-ray energy and position resolving measurements at the European XFEL. J. Synchrotron Rad. 2024, 31, 1029–1036. [Google Scholar] [CrossRef]
- Roth, T.; Freund, W.; Boesenberg, U.; Carini, G.; Song, S.; Lefeuvre, G.; Goikhman, A.; Fischer, M.; Schreck, M.; Grunerta, J.; et al. Pulse-resolved intensity measurements at a hard X-ray FEL using semi-transparent diamond detectors. J. Synchrotron Rad. 2018, 25, 177–188. [Google Scholar] [CrossRef]
- Bloomer, C.; Bobb, L.; Freund, W.; Grünert, J.; Liu, J.; Newton, M. XFEL Photon Pulse Measurement Using an All-Carbon Diamond Detector. In Proceedings of the 11th International Beam Instrumentation Conference IBIC-2022, Kraków, Poland, 11–15 September 2022. [Google Scholar] [CrossRef]
- De Feudis, M.; Caricato, A.P.; Chiodini, G.; Martino, M.; Maruccio, G.; Monteduro, A.G.; Ossi, P.M.; Perrino, R.; Spagnolo, S. Diamond detectors with electrodes graphitized by means of laser. Il Nuovo C. 2016, 39C, 254–257. [Google Scholar] [CrossRef]
- Pace, E.; De Sio, A. Diamond detectors for space applications. Nucl. Instrum. Meth. Phys. Res. 2003, A514, 93–99. [Google Scholar] [CrossRef]
- Pace, E.; De Sio, A. Innovative diamond space photodetectors for UV astrophysics. Mem. Della Soc. Astron. Ital. Suppl. 2010, 14, 84. [Google Scholar]
- BenMoussa, A.; Dammasch, I.E.; Hochedez, J.-F.; Schühle, U.; Koller, S.; Stockman, Y.; Scholze, F.; Richter, M.; Kroth, U.; Laubis, C.; et al. Pre-flight calibration of LYRA, the solar VUV radiometer on board PROBA2. Astron. Astrophys. 2009, 508, 1085–1094. [Google Scholar] [CrossRef]
- BenMoussa, A.; Hochedez, J.; Schühle, U.; Schmutz, W.; Haenen, K.; Stockman, Y.; Soltani, A.; Scholze, F.; Kroth, U.; Mortet, V.; et al. Diamond detectors for LYRA, the solar VUV radiometer on board PROBA2. Diam. Relat. Mater. 2006, 15, 802–806. [Google Scholar] [CrossRef]
- BenMoussa, A.; Schühle, U.; Haenen, K.; Nesládek, M.; Koizumi, S.; Hochedez, J.-F. PIN diamond detector development for LYRA, the solar VUV radiometer on board PROBA II. Phys. Stat. Sol. 2004, A201, 2536–2541. [Google Scholar] [CrossRef][Green Version]
- Cesaroni, S.; Bombarda, F.; Bollanti, S.; Cianfarani, C.; Claps, G.; Cordella, F.; Flora, F.; Marinelli, M.; Mezi, L.; Milani, E.; et al. Conceptual design of CVD diamond tomography systems for fusion devices. Fus. Engin. Des. 2023, 197, 114037. [Google Scholar] [CrossRef]
- Liu, B.; Liu, K.; Zhang, S.; Ralchenko, V.G.; Zhang, X.; Xue, J.; Wen, D.; Qiao, P.; Zhao, J.; Dai, B.; et al. Self-Powered Solar-Blind UV Detectors Based on O-Terminated Vertical Diamond Schottky Diode with Low Dark Current, High Detectivity, and High Signal-to-Noise Ratio. ACS Appl. Electron. Mater. 2022, 4, 5996–6003. [Google Scholar] [CrossRef]
- Girolami, M.; Serpente, V.; Mastellone, M.; Tardocchi, M.; Rebai, M.; Xiu, Q.; Liu, J.; Sun, Z.; Zhao, Y.; Valentini, V.; et al. Self-powered solar-blind ultrafast UV-C diamond detectors with asymmetric Schottky contacts. Carbon 2022, 189, 27–36. [Google Scholar] [CrossRef]
- Claps, G.; Murtas, F.; Foggetta, L.; Di Giulio, C.; Alozy, J.; Cavoto, G. Diamondpix: A CVD diamond detector with timePix3 chip interface. IEEE Trans. Nucl. Sci. 2018, 65, 2743–2753. [Google Scholar] [CrossRef]
- Gromov, V.; van Beuzekom, M.; Kluit, R.; Zappon, F.; Zivkovic, V.; Campbell, M.; Poikela, T.; Llopart, X.; Brezina, C.; Desch, K.; et al. Development and applications of the Timepix3 readout chip. In Proceedings of the 20th Anniversary International Workshop on Vertex detectors (VERTEX 2011), Rust, Austria, 19–24 June 2011. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, P.; Creely, A.; Greenwald, M.; Brunner, D.; Ballinger, S.; Chrobak, C.; Garnier, D.; Granetz, R.; Hartwig, Z.; Howard, N.; et al. Overview of the SPARC physicis basis toward the exploration of burning-plasma regimes in high field, compact tokamaks. Nucl. Fusion 2022, 62, 042003. [Google Scholar] [CrossRef]
- Romanelli, F.; Contributors, O.B.O.D.; Abate, D.; Acampora, E.; Agguiaro, D.; Agnello, R.; Agostinetti, P.; Agostini, M.; Aimetta, A.; Albanese, R.; et al. Divertor Tokamak Test facility project: Status of design and implementation. Nucl. Fusion. 2024, 64, 112015. [Google Scholar] [CrossRef]



















| 300 K | 500 K | 600 K | ||
|---|---|---|---|---|
| Atomic number 6 | 6 | |||
| Density (g cm−3) | 3.515 | |||
| Fusion Temperature (°C) 4100 | 4100 | |||
| Thermal conductivity (W cm−1 K−1) | 21.9 | 11.2 | 9.6 | |
| Resistivity (Ω cm) | 1013 | |||
| Dielectric constant | 5.7 | |||
| Break-down voltage (V cm−1) | >107 | |||
| Band gap (eV) | 5.47 | 5.42 | 5.38 | |
| Intrinsic carrier density (cm−3) | <103 | |||
| Energy to create e-h pair (eV) | 13 | |||
| Electron mobility (cm2V−1 s−1) 1 | 1800–2200 | |||
| Hole mobility (cm2V−1 s−1) 1 | 1200–1600 | |||
| Saturation velocity vsat (cm s−1) | 2.7 × 107 | |||
| Energy to displace an atom (eV) 2 | 43.3 |
| Spectral Region | Wave Length (nm) | Photon Energy Eγ (eV) |
|---|---|---|
| Infra Red | >780 | Eγ <1.75 |
| Visible | 750 ÷ 400 | 1.75 < Eγ < 3.1 |
| UV-A * | 400 ÷ 320 | 3.1 < Eγ < 3.85 |
| UV-B | 320 ÷ 280 | 3.85 < Eγ < 4.43 |
| UV-C | 280 ÷ 200 | 4.43 < Eγ < 6.20 |
| Far UV | 200 ÷ 10 | 6.20 < Eγ < 120 |
| X-Ray | <10 | Eγ > 100 |
| Material | Direct/Indirect Band-Gap | Band-Gap at 300 K (eV) |
|---|---|---|
| Diamond | Indirect | 5.47 |
| Ge | Indirect | 0.66 |
| Si | Indirect | 1.12 |
| GaAs | Direct | 1.42 |
| GaP | Indirect | 2.26 |
| α-SiC | Indirect | 2.99 |
| ZnO | Direct | 3.35 |
| ZnS | Direct | 3.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angelone, M.; Bombarda, F.; Cesaroni, S.; Marinelli, M.; Raso, A.M.; Verona, C.; Verona-Rinati, G. X-Ray and UV Detection Using Synthetic Single Crystal Diamond. Instruments 2025, 9, 9. https://doi.org/10.3390/instruments9020009
Angelone M, Bombarda F, Cesaroni S, Marinelli M, Raso AM, Verona C, Verona-Rinati G. X-Ray and UV Detection Using Synthetic Single Crystal Diamond. Instruments. 2025; 9(2):9. https://doi.org/10.3390/instruments9020009
Chicago/Turabian StyleAngelone, Maurizio, Francesca Bombarda, Silvia Cesaroni, Marco Marinelli, Angelo Maria Raso, Claudio Verona, and Gianluca Verona-Rinati. 2025. "X-Ray and UV Detection Using Synthetic Single Crystal Diamond" Instruments 9, no. 2: 9. https://doi.org/10.3390/instruments9020009
APA StyleAngelone, M., Bombarda, F., Cesaroni, S., Marinelli, M., Raso, A. M., Verona, C., & Verona-Rinati, G. (2025). X-Ray and UV Detection Using Synthetic Single Crystal Diamond. Instruments, 9(2), 9. https://doi.org/10.3390/instruments9020009







