Design and Uncertainty Analysis of an AC Loss Measuring Instrument for Superconducting Magnets
Abstract
1. Introduction
2. Application Domains
Metrological Requirements
3. Proposal
3.1. Conceptual Design
3.2. Physical Design
3.3. Simulation Setup
4. Instrument Validation
4.1. Case Study
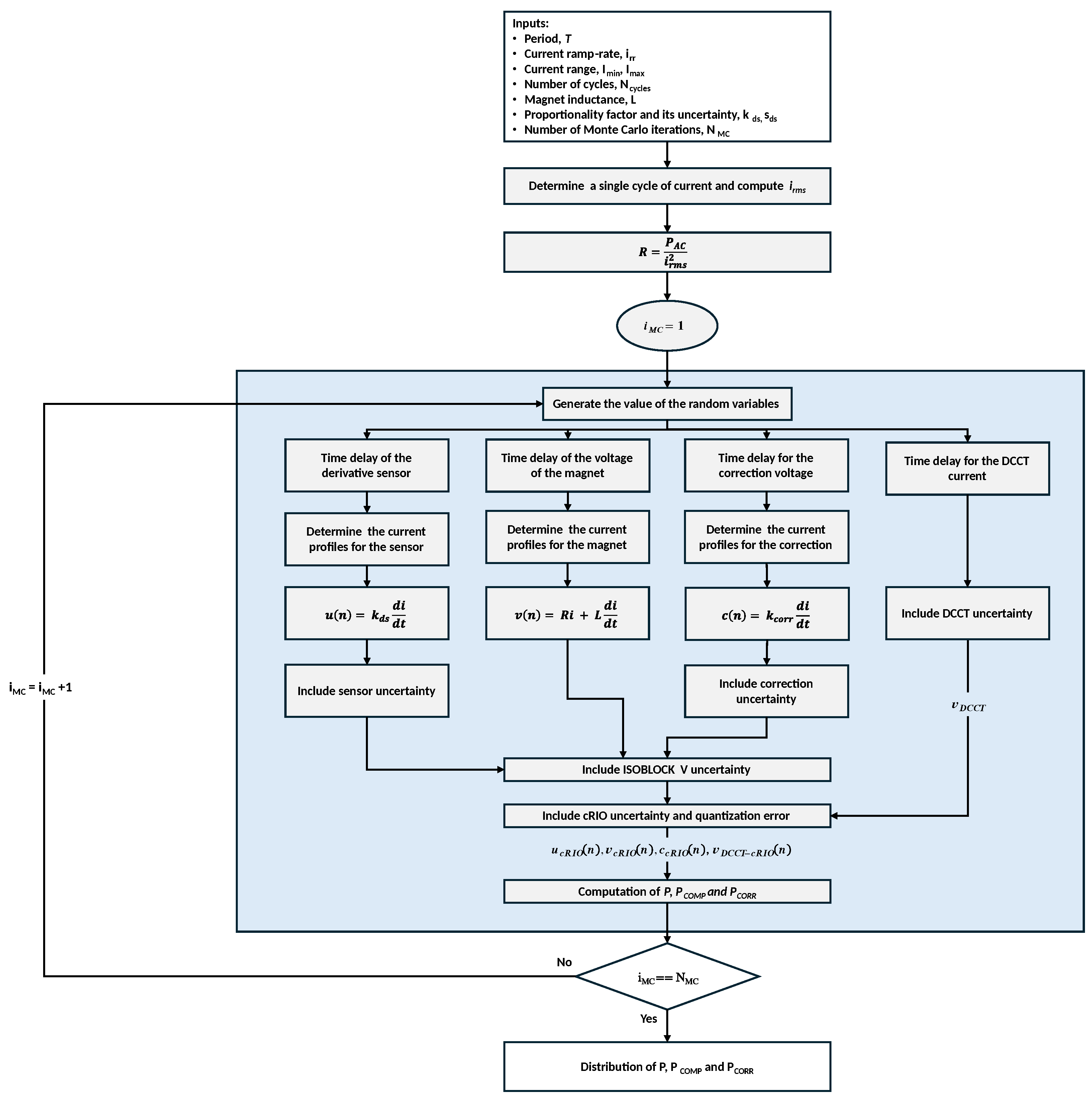
4.2. Uncertainty Analysis
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADC | Analog-to-Digital Converter |
| AC | Alternated Current |
| AIL | Advanced Instrumentation Laboratory |
| CCT | Canted Cosine Theta |
| cRIO | Compact Reconfigurable Input Output |
| DCCT | Direct-Current Current Transformer |
| FAIR | Facility for Antiproton and Ion Research |
| FPGA | Field-Programmable Gate Array |
| HTS | High-Temperature Superconductors |
| IFAST | Innovation Fostering in Accelerator Science and Technology |
| IRIS | Innovative Research Infrastructure on Applied Superconductivity |
| HITRIplus | Heavy-Ion Therapy Research Integration plus |
| RAM | Random-Access Memory |
| SIG | Superconducting Ion Gantry Mechanics |
References
- Ang, Z.; Bejar, I.; Bottura, L.; Richter, D.; Sheahan, M.; Walckiers, L.; Wolf, R. Measurement of AC loss and magnetic field during ramps in the LHC model dipoles. IEEE Trans. Appl. Supercond. 1999, 9, 742–745. [Google Scholar] [CrossRef]
- Di Castro, M.; Bottura, L.; Richter, D.; Sanfilippo, S.; Wolf, R. Coupling current and AC loss in LHC superconducting quadrupoles. IEEE Trans. Appl. Supercond. 2008, 18, 108–111. [Google Scholar] [CrossRef]
- Hatanaka, K.; Nakagawa, J.; Fukuda, M.; Yorita, T.; Saito, T.; Sakemi, Y.; Kawaguchi, T.; Noda, K. A HTS scanning magnet and AC operation. Nucl. Instruments Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2010, 616, 16–20. [Google Scholar] [CrossRef]
- Fischer, E.; Schnizer, P.; Sugita, K.; Meier, J.P.; Mierau, A.; Bleile, A.; Szwangruber, P.; Müller, H.; Roux, C. Fast-ramped superconducting magnets for FAIR production status and first test results. IEEE Trans. Appl. Supercond. 2015, 25, 4003805. [Google Scholar] [CrossRef]
- Amano, S.; Takayama, S.; Orikasa, T.; Nakanishi, K.; Hirata, Y.; Iwata, Y.; Mizushima, K.; Abe, Y.; Noda, E.; Urata, M.; et al. Thermal design and test results of the superconducting magnet for a compact heavy-ion synchrotron. IEEE Trans. Appl. Supercond. 2022, 32, 4401305. [Google Scholar] [CrossRef]
- Vulusala G, V.S.; Madichetty, S. Application of superconducting magnetic energy storage in electrical power and energy systems: A review. Int. J. Energy Res. 2018, 42, 358–368. [Google Scholar] [CrossRef]
- Ozelis, J.; Delchamps, S.; Gourlay, S.; Jaffery, T.; Kinney, W.; Koska, W.; Kuchnir, M.; Lamm, M.; Mazur, P.; Orris, D.; et al. AC loss measurements of model and full size 50 mm SSC collider dipole magnets at Fermilab. IEEE Trans. Appl. Supercond. 1993, 3, 678–681. [Google Scholar] [CrossRef]
- Volpini, G.; Alessandria, F.; Bellomo, G.; Fabbricatore, P.; Farinon, S.; Gambardella, U.; Manfreda, G.; Musenich, R.; Quadrio, M.; Sorbi, M. AC losses measurement of the DISCORAP model dipole magnet for the SIS300 synchrotron at FAIR. IEEE Trans. Appl. Supercond. 2013, 24, 4000205. [Google Scholar] [CrossRef]
- Felcini, E.; Pullia, M.; Sabbatini, L.; Vannozzi, A.; Trigilio, A.; Pivi, M.; De Cesaris, I.; Rossi, L.; Prioli, M.; Schwarz, P.; et al. Characterization of hysteretic behavior of a FeCo magnet for the design of a novel ion gantry. IEEE Trans. Appl. Supercond. 2024, 34, 4402105. [Google Scholar] [CrossRef]
- Yang, Y.; Matsuba, S.; Mizushima, K.; Fujimoto, T.; Iwata, Y.; Noda, E.; Urata, M.; Shirai, T.; Nishijima, G.; Takayama, S.; et al. Design and test of a 0.4-m long short model of a conduction-cooled superconducting combined function magnet for a compact, rapid-cycling heavy-ion synchrotron. Nucl. Instruments Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2023, 1050, 168165. [Google Scholar] [CrossRef]
- Karppinen, M.; Ferrentino, V.; Kokkinos, C.; Ravaioli, E. Design of a curved superconducting combined function bending magnet demonstrator for hadron therapy. IEEE Trans. Appl. Supercond. 2022, 32, 4400705. [Google Scholar] [CrossRef]
- Marchevsky, M. Quench detection and protection for high-temperature superconductor accelerator magnets. Instruments 2021, 5, 27. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, Z.; Grilli, F.; Gyftakis, K.; Mueller, M. Alternating current loss of superconductors applied to superconducting electrical machines. Energies 2021, 14, 2234. [Google Scholar] [CrossRef]
- Ashworth, S.; Suenaga, M. Local calorimetry to measure ac losses in HTS conductors. Cryogenics 2001, 41, 77–89. [Google Scholar] [CrossRef]
- Ghoshal, P.; Coombs, T.; Campbell, A. Calorimetric method of ac loss measurement in a rotating magnetic field. Rev. Sci. Instruments 2010, 81, 074702. [Google Scholar] [CrossRef]
- Wilson, M. Superconducting Magnets; Monographs on cryogenics; Clarendon Press: Oxford Science Publications, UK, 1983. [Google Scholar]
- Willering, G. Loss measurements in superconducting magnets at CERN. In Proceedings of the HFM Meeting, Zurich, Switzerland, 26 September 2024. [Google Scholar]
- Li, X.; Ren, L.; Guo, S.; Xu, Y.; Shi, J.; Tan g, Y.; Li, J. A novel AC loss measurement method for HTS coils based on parameter identification. Supercond. Sci. Technol. 2022, 35, 065021. [Google Scholar] [CrossRef]
- Verweij, A.; Leroy, D.; Walckiers, L.; Wolf, R.; Ten Kate, H. Analysis of the AC loss measurements on the one-metre dipole model magnets for the CERN LHC. IEEE Trans. Magn. 1994, 30, 1758–1761. [Google Scholar] [CrossRef]
- Yuan, W.; Coombs, T.; Kim, J.H.; Han Kim, C.; Kvitkovic, J.; Pamidi, S. Measurements and calculations of transport AC loss in second generation high temperature superconducting pancake coils. J. Appl. Phys. 2011, 110. [Google Scholar] [CrossRef]
- Shen, B.; Li, C.; Geng, J.; Zhang, X.; Gawith, J.; Ma, J.; Liu, Y.; Grilli, F.; Coombs, T. Power dissipation in HTS coated conductor coils under the simultaneous action of AC and DC currents and fields. Supercond. Sci. Technol. 2018, 31, 075005. [Google Scholar] [CrossRef]
- Zhu, K.; Guo, S.; Ren, L.; Xu, Y.; Wang, F.; Yan, S.; Liang, S.; Tang, Y.; Shi, J.; Li, J. AC loss measurement of HTS coil under periodic current. Phys. Supercond. Appl. 2020, 569, 1353562. [Google Scholar] [CrossRef]
- Šouc, J.; Pardo, E.; Vojenčiak, M.; Gömöry, F. Theoretical and experimental study of AC loss in high temperature superconductor single pancake coils. Supercond. Sci. Technol. 2008, 22, 015006. [Google Scholar] [CrossRef]
- Liao, Y.; Tang, Y.; Shi, J.; Shi, X.; Ren, L.; Li, J.; Wang, Z.; Xia, Z. An automatic compensation method for measuring the AC loss of a superconducting coil. IEEE Trans. Appl. Supercond. 2016, 26, 9001805. [Google Scholar] [CrossRef]
- De Bruyn, B.; Jansen, J.; Lomonova, E. AC losses in HTS coils for high-frequency and non-sinusoidal currents. Supercond. Sci. Technol. 2017, 30, 095006. [Google Scholar] [CrossRef]
- Breschi, M.; Macchiagodena, A.; Ribani, P.L.; Bellina, F.; Stacchi, F.; Bermudez, S.I.; Bajas, H. Experimental and Numerical Investigation on Losses in Electrodynamic Transients in a Nb3Sn Prototype Racetrack Coil. IEEE Trans. Appl. Supercond. 2018, 28, 4000605. [Google Scholar] [CrossRef]
- Rossi, L.; Arpaia, P.; Attanasio, C.; Avallone, G.; Avitabile, F.; Balconi, L.; Bellingeri, E.; Beneduce, E.; Benson, T.; Bernini, C.; et al. IRIS-a new distributed research infrastructure on applied superconductivity. IEEE Trans. Appl. Supercond. 2023, 34, 9500309. [Google Scholar] [CrossRef]
- Rossi, L.; Balconi, L.; Campana, P.; Felis, S.M.; Sorti, S.; Statera, M. IRIS—The Italian research infrastructure on Applied Superconductivity for Particle Accelerators and Societal Applications. J. Phys. Conf. Ser. 2024, 2687, 092012. [Google Scholar] [CrossRef]
- Fabbricatore, P.; Alessandria, F.; Bellomo, G.; Farinon, S.; Gambardella, U.; Kaugerts, J.; Marabotto, R.; Musenich, R.; Moritz, G.; Sorbi, M.; et al. Development of a curved fast ramped dipole for FAIR SIS300. IEEE Trans. Appl. Supercond. 2008, 18, 232–235. [Google Scholar] [CrossRef]
- De Matteis, E.; Barna, D.; Ceruti, G.; Kirby, G.; Lecrevisse, T.; Mariotto, S.; Perini, D.; Prioli, M.; Rossi, L.; Scibor, K.; et al. Straight and curved canted cosine theta superconducting dipoles for ion therapy: Comparison between various design options and technologies for ramping operation. IEEE Trans. Appl. Supercond. 2023, 33, 4401205. [Google Scholar] [CrossRef]
- Prioli, M.; De Matteis, E.; Farinon, S.; Felcini, E.; Gagno, A.; Mariotto, S.; Musenich, R.; Pullia, M.; Rossi, L.; Sorbi, M.; et al. Design of a 4 T Curved Demonstrator Magnet for a Superconducting Ion Gantry. IEEE Trans. Appl. Supercond. 2023, 33, 1–5. [Google Scholar] [CrossRef]
- Toral, F.; Barna, D.; Calzolaio, C.; Carloni, A.; Ceruti, G.; De Matteis, E.; Kirby, G.; Lecrevisse, T.; Mariotto, S.; Munilla, J.; et al. Status of Nb-Ti CCT Magnet EU Programs for Hadron Therapy. IEEE Trans. Appl. Supercond. 2024, 34, 4401705. [Google Scholar] [CrossRef]
- De Matteis, E.; Ballarino, A.; Barna, D.; Carloni, A.; Echeandia, A.; Kirby, G.; Lecrevisse, T.; Lucas, J.; Mariotto, S.; van Nugteren, J.; et al. Conceptual Design of an HTS Canted Cosine Theta Dipole Magnet for Research and Hadron Therapy Accelerators. IEEE Trans. Appl. Supercond. 2024, 34, 4402505. [Google Scholar] [CrossRef]
- Levi, F.; Bersani, A.; Bianchi, E.; Carloni, A.G.; Cereseto, R.; De Matteis, E.; Farinon, S.; Felcini, E.; Gagno, A.; Georgiadis, G.; et al. Mechanical Design of the 4 T Curved Demonstrator Dipole for the SIG Gantry. IEEE Trans. Appl. Supercond. 2024, 34, 4400505. [Google Scholar] [CrossRef]
- Steckert, J.; Kopal, J.; Bajas, H.; Denz, R.; Georgakakis, S.; De Matteis, E.; Spasic, J.; Siemko, A. Development of a digital quench detection system for nb 3 Sn magnets and first measurements on prototype magnets. IEEE Trans. Appl. Supercond. 2018, 28, 4703304. [Google Scholar] [CrossRef]
- Courts, S.S.; Swinehart, P.R. Review of Cernox™(Zirconium Oxy-Nitride) Thin-Film Resistance Temperature Sensors. In Proceedings of the AIP Conference Proceedings. American Institute of Physics, Chicago, IL, USA, 21–24 October 2022; Volume 684, pp. 393–398. [Google Scholar] [CrossRef]
- De Matteis, E.; Calcoen, D.; Denz, R.; Siemko, A.; Steckert, J.; Storkensen, M. New method for magnet protection systems based on a direct current derivative sensor. IEEE Trans. Appl. Supercond. 2018, 28, 4700505. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, C.H.; Iyyani, G.; Kvitkovic, J.; Pamidi, S. Transport AC loss measurements in superconducting coils. IEEE Trans. Appl. Supercond. 2010, 21, 3269–3272. [Google Scholar] [CrossRef]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of measurement data—Supplement 1 to the “Guide to the expression of uncertainty in measurement” —Propagation of distributions using a Monte Carlo method. Jt. Comm. Guid. Metrol. 2008, 111, 17. [Google Scholar] [CrossRef]
- Saltelli, A. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]









| Quantity | Symbol | Value |
|---|---|---|
| relative permeability (Vitroperm) | ||
| core cross section | ||
| secondary turns | ||
| air gap | ||
| magnetic length in the core |
| Gain | Offset | Time Delay | |
|---|---|---|---|
| DCCT | 37 | −70 to 70 | 1 to 5 |
| isolation module | −0.2% to 0.2% | −500 to 500 | 0 to 5.7 |
| acquisition module | −0.03% to 0.03% | −842 to 842 | 200 1% |
| (compensation) | 0.63% | 10% | 0 to 6 |
| (correction) | 10% | 0.0 to 0.2 | |
| ADC quantization error: 24 bit | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arpaia, P.; Cuneo, D.; De Matteis, E.; Esposito, A.; Ramos, P. Design and Uncertainty Analysis of an AC Loss Measuring Instrument for Superconducting Magnets. Instruments 2025, 9, 8. https://doi.org/10.3390/instruments9020008
Arpaia P, Cuneo D, De Matteis E, Esposito A, Ramos P. Design and Uncertainty Analysis of an AC Loss Measuring Instrument for Superconducting Magnets. Instruments. 2025; 9(2):8. https://doi.org/10.3390/instruments9020008
Chicago/Turabian StyleArpaia, Pasquale, Davide Cuneo, Ernesto De Matteis, Antonio Esposito, and Pedro Ramos. 2025. "Design and Uncertainty Analysis of an AC Loss Measuring Instrument for Superconducting Magnets" Instruments 9, no. 2: 8. https://doi.org/10.3390/instruments9020008
APA StyleArpaia, P., Cuneo, D., De Matteis, E., Esposito, A., & Ramos, P. (2025). Design and Uncertainty Analysis of an AC Loss Measuring Instrument for Superconducting Magnets. Instruments, 9(2), 8. https://doi.org/10.3390/instruments9020008









