Abstract
Highly intense bunches of protons and ions with energies of several MeV/u can be generated with ultra-short laser pulses focused on solid targets. In the most common interaction regime, target normal sheath acceleration, the spectra of these particles are spread over a wide range following a Maxwellian distribution. We report on the design and testing of a magnetic chicane for the selection of protons within a limited energy window. This consisted of two successive, anti-parallel dipole fields generated by cost-effective permanent C-magnets with customized configuration and longitudinal positions. The chicane was implemented into the target vessel of a petawatt laser facility with constraints on the direction of the incoming laser beam and guidance of the outgoing particles through a vacuum port. The separation of protons and carbon ions within distinct energy intervals was demonstrated and compared to a ray tracing code. Measurements with radiochromic film stacks indicated the selection of protons within [2.4, 6.9] MeV, [5.0, 8.4] MeV, or ≥6.9 MeV depending on the lateral dispersion. A narrow peak at 4.8 MeV was observed with a time-of-flight detector.
1. Introduction
Ion acceleration by ultra-intense laser–plasma interactions has evolved as a core technique for compact sources of energetic particles [1,2]. In so-called target normal sheath acceleration (TNSA), intense pulses of protons and light ions are released at laser intensities W/cm2 [3]. In this regime, particle spectra cover a wide interval up to a sharp maximum energy, , typically of several MeV/u, with an exponentially decreasing population. The generation of protons or light ions with comparatively narrow spectral distributions has been reported [4,5,6,7], albeit under experimental conditions in terms of laser pulse contrast or target properties that are not routinely met at present terawatt or petawatt laser facilities, especially when stable operation over a large number of shots is mandatory. Nevertheless, some applications of laser-accelerated particle beams require narrow ion spectra, e.g., radiobiological studies with cell cultures [8], tissues [9], or higher organisms [10,11]. These studies usually rely on the selection of mono-energetic ions out of the initial, broad distribution by means of magnetic beam control elements. Resistive dipole and quadrupole fields can be tuned to the desired ion species, charge states, and energies [12,13]. However, their application is restricted to dedicated beamlines at large facilities. Compact arrangements of permanent magnets can be more flexibly implemented in a general-purpose laboratory for short-term experimental campaigns. The design of such devices has previously been reported [14,15,16,17], and energy selection and particle guidance have been demonstrated using simulations, mono-energetic proton beams from radiofrequency accelerators, or laser-accelerated protons.
Combinations of permanent quadrupole magnets (PQMs) are suitable for the selective focusing of protons of a certain energy [18]. Such devices have been realized at various laser laboratories with two [19,20,21], four [22], or more [23] individual magnet blocks. Protons within narrow energy bands between 2 MeV and 14 MeV have been obtained, in some cases at a high fluence corresponding to high, single-shot doses in radiobiology studies. For higher energies, combinations of quadrupole and dipole magnets have been proposed [24,25]. The use of pulsed solenoids has also been reported [9,26].
Permanent dipole magnets have been widely used for the selection of proton energies in laser-based radiobiology experiments. Three basic designs can be distinguished, with the simplest comprising a single field orientation perpendicular to the particle trajectories, Figure 1a [27,28,29,30]. A small portion of the initial beam along the target normal direction is selected by a collimator, to reduce its angular spread. rays (moving along the initial beam axis) and electrons are efficiently separated from protons, and the trajectories of the latter are split according to the energies. This allows for selection of a narrow energy interval by means of a second collimator behind the dipole field. It is also possible to select several distinct intervals at the same time [31]. Two anti-parallel magnetic fields can be used to control the direction of the outgoing ions and to reduce their angular spread in the space between the fields and the cell samples, Figure 1b [32,33]. With a combination of four field orientations and an intermediate collimator, the mono-energetic beam can be redirected to the initial axis, Figure 1c [14,15,16,34].
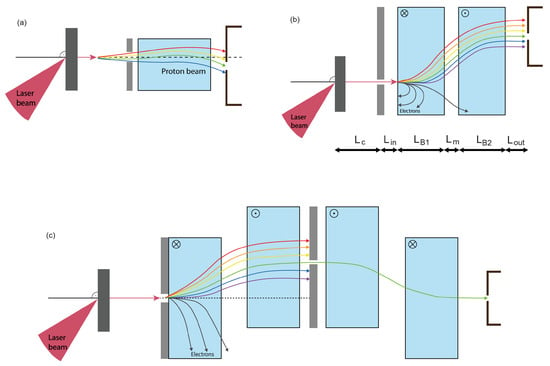
Figure 1.
Dipole chicanes with (a) one, (b) two, or (c) four anti-parallel magnetic fields and proton trajectories of different energies. For symbols in part (b) see text.
Here, the design of an energy selector based on two anti-parallel magnetic dipole fields is presented (Section 2) and its performance is demonstrated with laser-accelerated ions (Section 3). This chicane consists of cost-effective, permanent C-magnets, whose positions and orientations can be freely configured according to the actual experimental geometry and the particle energy of interest.
2. Materials and Methods
The magnetic field of the energy selector was generated by a set of identical, permanent C-magnets, Figure 2a. Each C-magnet consisted of two neodymium blocks (NdFeB N40, Webcraft GmbH, Gottmadingen, Germany; 60 (W) × 30 (L) × 15 (H) mm3) attached to a steel yoke with outer dimensions 100 (W) × 30 (L) × 90 (H) mm3. The yokes were nickelized for improved vacuum compatibility. With thin steel plates on top of each of the neodymium blocks, the remaining gap height was reduced to 7 mm. The main component of the magnetic field strength, , on the central plane of a single magnet is shown in Figure 2b. This was measured with a motorized Hall probe on a mesh of mm2 and interpolated for the graphical representation. The field strength was at the center between the pole shoes; previous simulations with the software COMSOL Multiphysics 5.3a gave a similar value of .
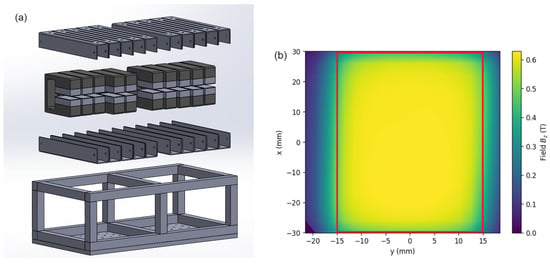
Figure 2.
(a) Exploded view of the energy selector; the outer dimensions of the support frame were 225 (W) × 446 (L) × 135 (H) mm3. (b) Two-dimensional field map of the central plane measured with a Hall probe; the red rectangle indicates the space between the pole shoes.
The overall field-filled space along the particle trajectories is generated by up to ten consecutive C-magnets in a support structure with outer dimensions 225 (W) × 446 (L) × 135 (H) mm3. It consists of a stable frame made of aluminum profiles of 20 mm width. Each C-magnet is inserted into a pair of channel profiles screwed to the frame to fix the position in the longitudinal (y) direction. The lateral (x) placement of each C-magnet can be freely adjusted. Here too, the selected position is blocked by two sets of screws that can be moved along a groove. This arrangement allows for safe mounting of neighboring magnets with strong, repulsive forces. The magnet gap can be oriented towards either side of the profiles. The design and materials applied enable customized configuration of the field geometry within the following limits:
- The field orientations can be parallel or antiparallel.
- The minimum longitudinal distance of the adjacent magnet yokes is 5 mm.
- A maximum of ten C-magnets can be installed.
- The gaps can reach a maximum lateral distance of mm from the central axis.
Two examples of this flexible arrangement will be presented in Section 3, where several magnets with parallel field orientation form one or two main blocks. The entire set of C-magnets has a total weight of 18 kg. The outer frame is mounted on an aluminum breadboard and a lab jack for precise height adjustment.
The total magnetic field of such an arrangement was modeled through the successive fields of individual magnets. This approximation is illustrated in Figure 3, which shows the measured values of on a mesh of mm2 distance, which were interpolated for the graphical representation. These data were obtained using five consecutive blocks with 4–5 mm spacing along the selector axis (y) and a lateral (x) displacement of 2–7 mm between adjacent magnets. The mesh space was limited by the range and mechanical degrees of freedom of the motorized stages carrying the Hall probe. A 1D cut along the red path of Figure 3a is plotted in Figure 3b; this shows the similar field strengths T in the intervals corresponding to the pole shoes and lower field values in the intermediate spaces. This was compared to a second dataset that was constructed from a 1D cut through the center of a single magnet, Figure 2b, applied five times in the respective z positions. In the block of five C-magnets, the field between the pole shoes appeared less uniform than the single one, and differences of the order 0.2 T were observed among the five units. In addition, the succession of individual magnets did not account for interactions between fields, and therefore suggests a more pronounced drop between each two neighbors than actually observed. The field integrals along this path within z = 0–154 mm amounted to Tm for the five-magnet dataset, and Tm for the simplified model, respectively. The calculations reported throughout the following sections were carried out with the field data of Figure 2b, adapted to the corresponding magnet positions inside the selector. This approximation can be quickly adapted to a new geometrical arrangement, without the need for time consuming field measurements, and allows the reproduction of the particle trajectories with reasonable precision.
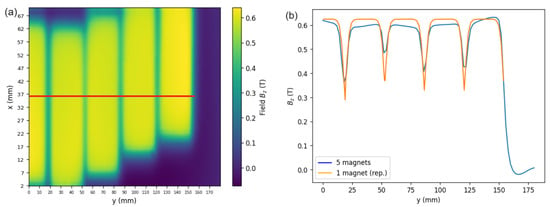
Figure 3.
(a) Two-dimensional field map of the central plane in a group of five consecutive magnets measured with a Hall probe. The red line indicates the position of a 1D cut along which the main field component is plotted in part (b) (in blue). In orange, model composed of repeated fields of one magnet, Figure 2b.
The trajectories of particles within this energy selector were simulated with a Python code based on the following assumptions: the particles (protons and ions) originated from a point-like source, with the laser focal spot on a solid target foil. A collimator at distance from the target defined the maximum angles of acceptance for particles entering the selector (see Figure 1b and Figure 4b). This collimator was placed in a target normal direction corresponding to the highest ion energies and flux in TNSA. A magnetic field acted on the charged particles at longitudinal coordinates within the yokes. In addition, fringe fields up to mm from the borders of the yokes were taken into account. Some spaces were not affected by the fields, namely the interval between the collimator and the first magnet, , the distance between the two main blocks, , and the interval behind the last magnet, . With these calculations, we obtained the particle spectral distributions inside a rectangular area at the distance of the detector or sample.
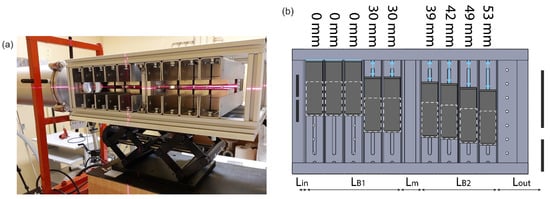
Figure 4.
(a) Energy selector at the external beamline of the CNA cyclotron. (b) Positions of the C-magnets for the 5+4 configuration (top view).
The simulation code allowed for a horizontal rotation of the selector with respect to the target normal axis. The trajectories of carbon ions in different charge states from C+ to C6+ were also simulated, for comparison with the experimental findings presented in Section 3.3. Furthermore, for beam tests at a cyclotron, the energy loss of protons in air, obtained from SRIM [35], was implemented into the Python code.
3. Results
To validate the simulated trajectories, the guidance of a mono-energetic proton beam was tested at an accelerator facility, Section 3.1. The dipole configuration was adapted to the experimental setup inside the target vessel of the VEGA-3 laser at the Spanish Pulsed Laser Center (CLPU, Salamanca), Section 3.2. The initial experimental data from the laser–plasma interactions, Section 3.3, showed the spectral separation of protons and carbon ions at this laboratory.
3.1. Test at CNA Cyclotron in Air
The guidance of particles through the selector was tested with a monoenergetic proton beam from a radiofrequency accelerator. The specific arrangement for this verification was motivated by its subsequent use at the VEGA-3 facility. Two anti-parallel magnetic fields were generated with five dipoles in the first block, and four in the second, as shown in Figure 4. Measurements were performed at the external beamline of the 18 MeV cyclotron of Centro Nacional de Aceleradores, Seville [36]. After passage through an aluminum attenuator of 500 µm thickness and a vacuum window consisting of a 100 µm thin aluminum foil, the proton beam energy in air was 14.49 MeV. The selector was placed 15.5 cm behind the beam outlet, Figure 4a. Two consecutive, circular collimators of 3 mm and 1 mm aperture, the smaller one close in front of the first dipole magnet, were used to delimit the beam diameter at the entrance of the selector. The beam entrance position and the horizontal orientation were adjusted with alignment lasers.
Radiochromic film (RCF) samples were placed between consecutive C-magnets, i.e., at various longitudinal coordinates y in the initial beam direction, to trace the lateral beam position, x, through the entire device. Only one sample was irradiated at the same time. The spots visible in Figure 5a were obtained with beam currents of 4–10 nA and irradiation times of 1–4 min. The results are summarized in Table 1. Due to the beam divergence and particle scatter in air, the spot size increased significantly along the beam path. We measured the distribution of optical density (OD) on the RCF using a transmission scan and thereby obtained the central position corresponding to the lateral displacement, , and the width of the spots where the OD dropped to 50%, . The spot positions were compared to the simulated displacement, . Since the measured data were obtained with respect to the border of the outer frame, the absolute values were subject to the non-zero rotation angle, , of the selector in the horizontal plane with respect to the beam axis. We therefore calculated the central trajectory of the protons and their final position for several rotation angles. The experimental data were best reproduced for ° with differences between 0.07 and 0.68 mm and . These results confirmed the validity of the applied ray tracing code with a simulated field configuration composed of identical, consecutive dipole fields.
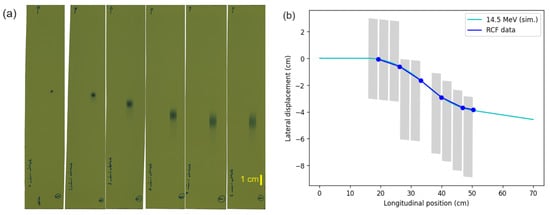
Figure 5.
(a) RCF sheets with beam spots indicating lateral hit positions. (b) Comparison of the measured positions (dots) with the simulated proton trajectory. The shaded areas indicate the dipole positions.

Table 1.
Comparison of the measured and simulated lateral displacements on RCF in the beam test at the CNA cyclotron.
3.2. Specific Configuration for VEGA-3
The 1 PW laser facility VEGA-3 provides up to 30 J beam energy in pulses with a minimum duration of 30 fs. The laser is focalized by a off-axis parabola located inside a dedicated vacuum chamber. The focal point lies at a fixed position inside a second, rectangular vessel with inner dimensions of mm2 in the horizontal plane. The laser entrance is along the central axis of the interaction chamber, Figure 6.
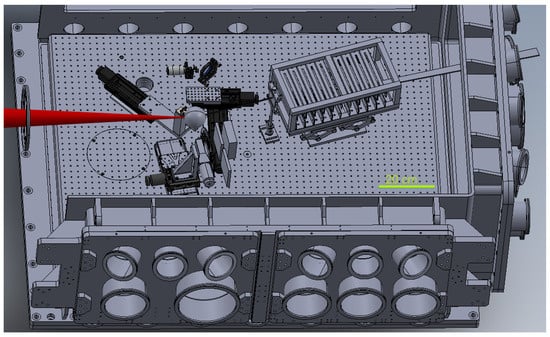
Figure 6.
Energy selector and proton trajectories with the 5+4 configuration inside the VEGA-3 target chamber.
Several side conditions had to be fulfilled for the present experiment, with the aim of generating laser-accelerated proton beams and demonstrating the spatial separation of particles after passage through the energy selector. First, the target foil had to be rotated by 10–20° with respect to the incoming laser beam, to avoid back reflection and potential damage of the optical systems. This implied a rotation of the target normal direction and, by consequence, of the selector with respect to the central axis of the vacuum chamber. The second condition was imposed by the optical system necessary for adjusting the target precisely to the focal spot position. These components were mounted on motorized stages and placed between the target wheel and the selector before each series of shots. The front side of the selector was 332 mm away from the focal spot, to allow for this operation. Third, the outgoing, monoenergetic proton beam had to leave the chamber through one of the ports on the rear wall, inside the horizontal plane and pointing towards the focal spot. This port was equipped with a vacuum window of 50 mm width and 5 mm height sealed with a 12.7 µm thin kapton foil to allow for particle passage to the atmosphere. In the simulations, this was implemented to study the angular dependence of the particle energies and fluence behind the selector.
For several magnet combinations, the trajectories of protons within the envisaged range of energies (4–8 MeV) were simulated and combined with a 3D CAD model of the entire setup. At this stage, only protons emitted on the target normal axis were considered. An asymmetric configuration introduced a non-zero angle between the outgoing particles and the initial, target normal direction. This feature was exploited to guide the protons through the ports. A large lateral deviation could be obtained with a single block of five parallel C-magnets, Figure 7. However, the divergence of protons with different energies would lead to a low fluence on the detector plane. Instead, a 5+4 combination as shown in Figure 4b and Figure 6 was chosen to guide the protons towards the port at 12.2° with respect to the chamber axis.
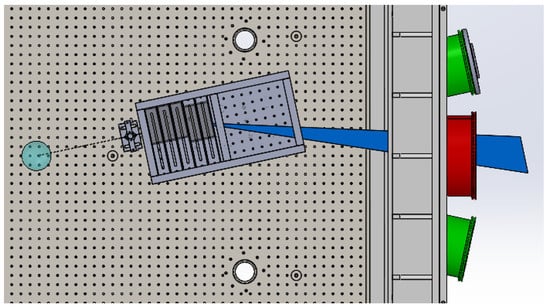
Figure 7.
Simulated proton trajectories inside the VEGA-3 target chamber for an alternative, 5+0 configuration of the selector.
The spatial separation of proton trajectories under passage through the 5+4 configuration is shown in Figure 8. Protons were released from a point-like source with energies uniformly distributed within the interval [2, 14] MeV. Their angular spread behind the target was uniform within the aperture of a collimator in front of the first dipole. The collimator lay in the target normal direction, which defined the reference system for the simulations. The position of the vacuum window in this system is illustrated by a blue rectangle. Protons of MeV (in black) fell close to the center of the window. With this particular magnet arrangement, protons of less than ∼3 MeV underwent a strong deflection in the first group of magnets and left the chicane laterally before the end of the second group.
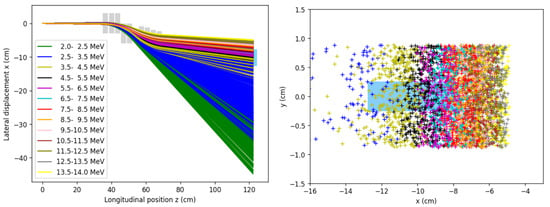
Figure 8.
Spatial separation of proton trajectories inside the VEGA-3 target chamber for the 5+4 configuration of the selector. (Left) Top view. (Right) Hit distribution on the exit plane (same color code as in part (left)). The grey rectangles illustrate the positions of the dipole magnets, and the light blue ones, the vacuum window.
With the 5+4 configuration, Figure 9 right shows the simulated proton spectra at three horizontal positions, , on the vacuum window with mm, corresponding to the limit closest to the initial beam axis where the highest proton energies were expected. For these calculations, the angular acceptance of a slit collimator of 5 mm width in front of the first C-magnet was used, in agreement with the measurements presented in Section 3.3. The simulated energies were uniformly distributed within [2, 14] MeV; protons with MeV were deflected far from the window. The typical, exponential distribution of ions generated in TNSA was emulated by applying a factor to each energy bin, with MeV close to the measured results from VEGA-3. The three energy intervals of Figure 9 range from 2.9–4.1 MeV ( mm), 3.6–5.5 MeV ( mm), and 5.0–8.6 MeV ( mm), respectively. Particles at low energies showed the smallest spectral width within a predefined detection interval, due to their comparatively strong deflection.
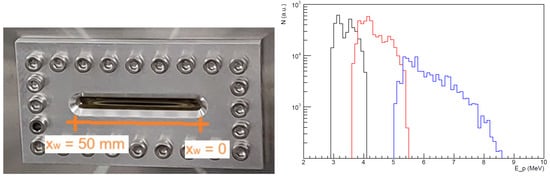
Figure 9.
(Left) Exterior view of the vacuum window and reference coordinate . (Right) Simulated energy distributions of protons at three positions of the vacuum window: mm (blue), mm (red), mm (black).
3.3. Experiment at VEGA-3
The energy selector was implemented into the VEGA-3 target chamber, as sketched in Figure 6, to test the generation of mono-energetic bunches of laser-accelerated protons. Aluminum membranes of 7 µm thickness were placed at the focal spot position through use of a motorized target wheel assembly [37], allowing for 808 individual shots in a single vacuum cycle. The target was rotated 17° with respect to the incoming laser direction. Protons were generated in the interaction of 240 fs laser pulses of 13 J (before compression; the energy on the target was 10.7 J). The focal spot diameter was 15.8 µm FWHM, resulting in a intensity of W/cm2. In a first series of measurements, the particles were detected on a plastic scintillator placed at the end of a 4.47 m long vacuum pipe mounted on the 12.2° port [38]. This allowed obtaining the proton energies by the time-of-flight (TOF) method. The flux was reconstructed from the signal height on a 3 GHz oscilloscope [39]. A slit collimator of 7.5 mm width was mounted in front of the scintillator to detect only particles within a small horizontal interval. These measurements were carried out two times, to detect the full spectrum emitted from the target (without the selector) or the protons passing through the chicane (with the selector in the predefined position). Without the selector, allowing for a direct view from the TOF detector to the target, a sharp peak close to ns was observed, Figure 10a, caused by high-energy photons from the laser–plasma interaction. In addition, visible light from the plasma was detected on a photodiode, whose output pulse was recorded on a different oscilloscope channel and that, by prior calibration with the peak, provided a reference time for all subsequent measurements. The peak was followed by a broad pulse from protons with time-of-flight in the range 100-500 ns. High-frequency fluctuations of the signal height, especially within the first 100 ns of the signal, caused by an electromagnetic pulse (EMP) generated in the laser–plasma interaction [40], were partly filtered out by a fast Fourier transform. The corresponding spectral distribution with a maximum energy of 5 MeV is shown in Figure 10b.
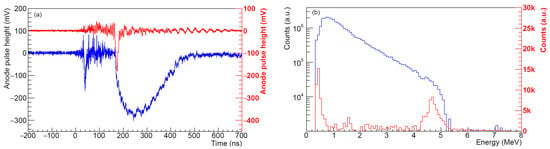
Figure 10.
(a) Oscilloscope signals from a time-of-flight detector and (b) reconstructed proton spectra. Colors indicate data taken with direct target view (blue, left scales) or with the energy selector inserted (red, right scales).
In a second step, the energy selector was inserted as shown in Figure 6, i.e., in target normal direction and with a pinhole collimator of 2 mm diameter in front of the first dipole. A 1.5 mm thick lead shielding covered the front side of the selector to absorb radiation at larger angles, including the straight connecting line between the target and the TOF detector. By consequence, the peak was not visible there. Instead, only one sharp peak was observed (same Figures, in red). Its timing with respect to the laser–plasma interaction was determined with the previously calibrated photodiode. The reconstructed proton energies indicated a quasi-mono-energetic peak at about 4.8 MeV. These data were obtained with 12 J laser pulses; mono-energetic peaks at the same position were also observed with 17 J and 20 J.
Additional data were taken after removing the TOF detector setup and mounting a vacuum window on the same port of the interaction chamber. Here, a slit collimator of 5 mm width was positioned at the selector entrance. The laser energy per 200 fs pulse was 27 J (22.1 J on target) which, focused in a spot of 14.5 µm diameter, corresponded to W/cm2. The distribution of proton energies right outside the window was measured with radiochromic films (RCF) of type Gafchromic EBT3-U, a material with a 28 µm thick sensitive layer on top of a 125 µm substrate. A stack of four RCF was placed directly behind the kapton window, with 44 µm aluminum foils on top of each EBT3-U film, to obtain a depth–dose profile from 20 accumulated laser shots. Figure 11a shows these four layers, with the right end oriented towards the biggest magnetic deflection, mm. The corresponding dose values, obtained from the previously calibrated relation between optical density (OD) and radiation dose and normalized to a single shot, are shown for each layer as solid curves in Figure 11b. In layers 2–4, a maximum OD was visible whose position moved towards the high-energy (left) end at increasing depths. We calculated the energy loss in the kapton window, aluminum foils, and the radiochromic films with SRIM [35] to obtain the minimum energies of protons necessary to reach the active layers of RCF 2 (5.0 MeV), RCF 3 (6.9 MeV), and RCF 4 (8.4 MeV), respectively. The corresponding limits of the hit positions, obtained with our ray tracing code, are indicated by the arrows. Their coordinates at a 1221 mm target distance coincided within mm with the peaks in the dose profiles, confirming qualitatively the expected spatial separation of protons with different energies.
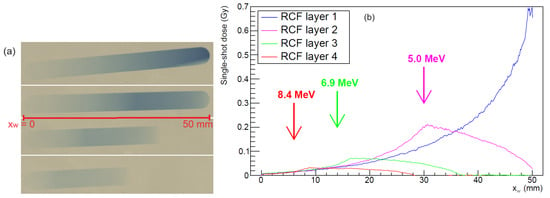
Figure 11.
(a) Transmission scan image of RCF stack on the vacuum window exposed to 20 laser shots. The vertical size of the irradiated areas is 5 mm. (b) Measured dose distributions in the horizontal direction; arrows indicate the positions of the maximum deflection for protons with minimum energies to reach the sensitive layers.
The measured dose values were used to retrieve the spectral components of the proton beam, making use of the known relation between the linear energy transfer in water, , the proton fluence, , and the dose deposition, D,
In layer 4, all the protons were assigned a common energy beyond the previously indicated limit of 8.4 MeV. The number of particles per cm2 required producing the observed dose calculated using Equation (1). For layer 3, the calculation was repeated within the corresponding energy interval but accounting for the dose deposited by the transient protons, and accordingly for layers 2 and 1. Figure 12 shows three examples: at mm, the dose in layer 4 indicated the presence of protons beyond 8.4 MeV; the limit of the highest-energy bin at 12.0 MeV was arbitrary. A contribution from protons of [6.9, 8.4] MeV was required to reproduce the signal in layer 3. The dose deposition in layers 1 and 2 was caused by the same particles; protons below 6.9 MeV were not observed in that position. At mm, the upper limit of proton energies was 8.4 MeV, as no dose was measured in layer 4. The proton fluence at [6.9, 8.4] MeV corresponded to layer 3. Here, the distribution peaked at [5.0, 6.9] MeV (layer 2); additional protons with <5.0 MeV were not required to reproduce the measured value of layer 1. Further towards the low-energy end of the window, at mm, the leading contribution stemmed from energies within [2.4, 5.0] MeV.
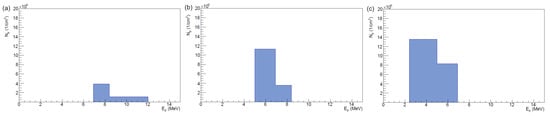
Figure 12.
Proton spectra retrieved at three horizontal positions on the vacuum window: (a) mm, (b) mm, (c) mm. Data refer to the RCF stack of Figure 11.
In order to investigate the presence of ions heavier than hydrogen, five PADC plates of 1 cm2 size (Tastrak, TASL, UK) were placed close behind the kapton window. They were exposed to particles from a single shot with 27 J laser energy. After etching (2 h at 90 °C in 6.25 M NaOH), a variation in the track density, visualized with a transmission scan, along the horizontal direction was observed, Figure 13a. The region of highest optical density was close to the target normal direction. For protons generated in TNSA with exponentially decaying spectra, the opposite tendency would be expected, as those of lower energies undergo stronger deflection inside the selector. Under a track microscope (Radosys PT10), two classes of patterns with very different diameters could be perceived, Figure 13b. The density of the larger ones decreased from the left to the right end of Figure 13a; individual pits can only be distinguished on the two rightmost plates. Due to their size, and taking into account the etching conditions, these tracks could be attributed to carbon ions [41]. Indeed, the simultaneous acceleration of protons and light ions was characteristic of the TNSA process. According to the SRIM simulation code [35] carbon ions of more than 12 MeV penetrated through the 12.7 µm kapton foil and potentially reached the PADC plates.

Figure 13.
(a) Transmission scan image of five PADC plates after a single laser shot. (b) Microscope image of plate 123.
We simulated the trajectories of carbon ions in different charge states (C+ to C6+) and with energies of 12–84 MeV. Taking into account the beam divergence due to the finite angular acceptance of the collimator, these calculations indicated that C6+ ions were spread over the entire width of the vacuum window, albeit with a higher abundance at coordinates corresponding to the plates with serial numbers 119–121 of Figure 13a. C5+ ions could only be found on the left half of the vacuum window, and C4+ ions only on plate 119. The lateral deflection of carbon ions with charge states lower than 4+ was insufficient to reach the kapton window. These simulations confirmed the classification of the large pits and provided a plausible explanation for the gradient in large track densities from the left to the right end of the beam window. Note that the carbon ions did not contribute to the dose distributions in the RCF of Figure 11 as they were stopped by the aluminum layer in front.
On PADC plates 122 and 123, the tiny tracks of Figure 13b were counted within selected regions. For these, the track densities were highest close to the right end of the vacuum window (/cm2) and decreased to 2.5–2.89 /cm3 at about 20 mm from the right end. This gradient is expected for protons with an exponential energy distribution typical for TNSA, as those of lower energies undergo stronger deflection. From Equation (1), the highest single-shot dose as determined with PADC amounted to 0.135 Gy.
4. Conclusions
A magnetic dipole chicane for the spectral separation of laser-accelerated protons was tested at the VEGA-3 facility. It consisted of a series of identical C-magnets mounted inside a stable frame, allowing for customized implementation into an experimental setup. Beam transport through a vacuum window was achieved through choice of the longitudinal dimensions of the two anti-parallel field regions. The guidance of a mono-energetic proton beam through the field was tested in air by comparing the measured horizontal displacement of the beam center with simulated trajectories. The energetic separation of protons from highly intense laser–plasma interactions was demonstrated. Carbon ions released in the same reactions were also detected, in agreement with the simulations.
The present study focused on the energy range between 4 MeV and 8 MeV. Protons of lower energies can be guided with fewer dipoles. For an effective separation of higher energies, it may be advantageous to increase the number of C-magnets with only one field orientation; a maximum of 10 dipoles fit inside the existing frame. Similarly, permanent C-magnets with higher field strength could be realized by reducing the gap size between the neodymium blocks. A H-shaped magnet design [14,15] might result in somewhat higher field strengths. However, with an asymmetric C-shape, the dead space occupied by the return yoke is avoided on one side, thus allowing for a wider range of lateral displacements within the given dimensions of the outer support frame.
The energy selector was designed for in vitro radiobiology experiments with laser-accelerated protons and ions. The irradiation of biological samples must be carried out with particles of limited spectral width, to guarantee a comparable dose deposition in all the cells. This can be achieved by choosing a small horizontal interval for the vacuum exit window. In practice, a compromise between the spectral width (dose uniformity) and particle fluence (single-shot dose) must be made. As an example, the spatial separation between protons of different energies was higher in the 5+0 configuration of Figure 7 but the fluence on the target plane was much lower than with the 5+4 combination, Figure 6.
The large spectral width of ions released in laser–plasma interactions is one of its distinctive features compared to radiofrequency accelerators. Mono-energetic particle beams are advantageous for many applications. For instance, protons above a specific energy threshold can induce nuclear reactions on a secondary target. Those at lower energies and with large populations in the initial spectra can be filtered out with magnetic fields to avoid unnecessary heat deposition and background generation. Our dipole chicane may be adapted to experimental requirements, especially at laser facilities that do not provide a permanent, dedicated beamline with magneto-optical elements.
Author Contributions
Conceptualization, M.S.; methodology, A.R., D.E. and M.S.; software, A.R., D.E. and J.J.-M.; validation, A.A., J.B., J.I.A. and M.E.; formal analysis, A.R. and M.S.; investigation, A.R., D.E., A.A., J.I.A., A.B., J.B., M.E., J.G.L., C.M., D.P., M.R.R. and M.S.; resources, M.C.J.-R.; data curation, A.R. and M.S.; writing—original draft preparation, M.S.; writing—review and editing, A.A. and J.B.; visualization, J.J.-M. and M.S.; supervision, A.A., J.B., M.E. and M.S.; project administration, J.B. and M.S.; funding acquisition, J.B., M.D.R.F. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
Project CIAICO/2022/008 funded by the regional government (Generalitat Valenciana) within the program “I+D+i Subvenciones para grupos de investigación consolidados AICO”. Additional support by Generalitat Valenciana in the Garantía Juvenil program, ref. EDGJID/2021/204. The authors would like to thank the Spanish Center of Pulsed Lasers (CLPU) and the members of the Consortium (Central Government, Regional Government of Castilla y León and Universidad de Salamanca) for considering experiment 00562-0101 as a strategic proposal that develops new potentialities for CLPU and, therefore, for financing the access to its facilities; they also acknowledge the results obtained with its petawatt laser system (VEGA-3) and its scientific and technical assistance. Supported by the Government of Castilla y León under the project CLP263P20 “Transport and manipulation of particles in laser accelerators: New scenarios in flash radiotherapy (TYMPAL)”, co-financed with FEDER funds. M. Carmen Jiménez-Ramos acknowledges the support of this work through a VI PPIT-US contract. Work supported by the Xunta de Galicia grant ED431F2023/21, by “la Caixa” Foundation (ID 100010434) (fellowship code LCF/BQ/PI20/11760027) and grant RYC2021-032654I funded by MICIU/AEI/10.13039/501100011033 and by “European Union NextGenerationEU”.
Data Availability Statement
Data supporting the conclusions are presented in the article. Additional data are available on request from the authors.
Acknowledgments
M.S. greatly acknowledges logistic support provided by Mavi Campos Lleó and Elisa Arias Campos for the realization of the experimental studies.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Daido, H.; Nishiuchi, M.; Pirozhkov, A.S. Review of laser-driven ion sources and their applications. Rep. Prog. Phys. 2012, 75, 056401. [Google Scholar] [CrossRef] [PubMed]
- Macchi, A.; Borghesi, M.; Passoni, M. Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 2013, 85, 751–793. [Google Scholar] [CrossRef]
- Roth, M.; Schollmeier, M. Ion Acceleration-Target Normal Sheath Acceleration. CERN Yellow Rep. 2016, 1, 231. [Google Scholar]
- Schwoerer, H.; Pfotenhauer, S.; Jäckel, O.; Amthor, K.U.; Liesfeld, B.; Ziegler, W.; Sauerbrey, R.; Ledingham, K.; Esirkepov, T. Laser-plasma acceleration of quasi-monoenergetic protons from microstructured targets. Nature 2006, 439, 445. [Google Scholar] [CrossRef] [PubMed]
- Henig, A.; Steinke, S.; Schnürer, M.; Sokollik, T.; Hörlein, R.; Kiefer, D.; Jung, D.; Schreiber, J.; Hegelich, B.M.; Yan, X.Q.; et al. Radiation-Pressure Acceleration of Ion Beams Driven by Circularly Polarized Laser Pulses. Phys. Rev. Lett. 2009, 103, 245003. [Google Scholar] [CrossRef]
- Haberberger, D.; Tochitsky, S.; Fiuza, F.; Gong, C.; Fonseca, R.A.; Silva, L.O.; Mori, W.B.; Joshi, C. Collisionless shocks in laser-produced plasma generate monoenergetic high-energy proton beams. Nat. Phys. 2012, 8, 95. [Google Scholar] [CrossRef]
- Palaniyappan, S.; Huang, C.; Gautier, D.C.; Hamilton, C.E.; Santiago, M.A.; Kreuzer, C.; Sefkow, A.B.; Shah, R.C.; Fernández, J.C. Efficient quasi-monoenergetic ion beams from laser-driven relativistic plasmas. Nat. Commun. 2015, 6, 10170. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, P.; Milluzzo, G.; Ahmed, H.; Odlozilik, B.; McMurray, A.; Prise, K.M.; Borghesi, M. Radiobiology Experiments With Ultra-high Dose Rate Laser-Driven Protons: Methodology and State-of-the-Art. Front. Phys. 2021, 9, 75. [Google Scholar] [CrossRef]
- Brack, F.E.; Kroll, F.; Gaus, L.; Bernert, C.; Beyreuther, E.; Cowan, T.E.; Karsch, L.; Kraft, S.; Kunz-Schughart, L.A.; Lessmann, E.; et al. Spectral and spatial shaping of laser-driven proton beams using a pulsed high-field magnet beamline. Sci. Rep. 2020, 10, 9118. [Google Scholar] [CrossRef]
- Rösch, T.F.; Szabó, Z.; Haffa, D.; Bin, J.; Brunner, S.; Englbrecht, F.S.; Friedl, A.A.; Gao, Y.; Hartmann, J.; Hilz, P.; et al. A feasibility study of zebrafish embryo irradiation with laser-accelerated protons. Rev. Sci. Instrum. 2020, 91, 063303. [Google Scholar] [CrossRef]
- Kroll, F.; Brack, F.E.; Bernert, C.; Bock, S.; Bodenstein, E.; Brüchner, K.; Cowan, T.E.; Gaus, L.; Gebhardt, R.; Helbig, U.; et al. Tumour irradiation in mice with a laser-accelerated proton beam. Nat. Phys. 2022, 18, 316–322. [Google Scholar] [CrossRef]
- Aymar, G.; Becker, T.; Boogert, S.; Borghesi, M.; Bingham, R.; Brenner, C.; Burrows, P.N.; Ettlinger, O.C.; Dascalu, T.; Gibson, S.; et al. LhARA: The Laser-hybrid Accelerator for Radiobiological Applications. Front. Phys. 2020, 8, 567738. [Google Scholar] [CrossRef]
- Cirrone, G.A.P.; Petringa, G.; Catalano, R.; Schillaci, F.; Allegra, L.; Amato, A.; Avolio, R.; Costa, M.; Cuttone, G.; Fajstavr, A.; et al. ELIMED-ELIMAIA: The First Open User Irradiation Beamline for Laser-Plasma-Accelerated Ion Beams. Front. Phys. 2020, 8, 564907. [Google Scholar] [CrossRef]
- Chen, S.N.; Gauthier, M.; Higginson, D.P.; Dorard, S.; Mangia, F.; Riquier, R.; Atzeni, S.; Marquès, J.R.; Fuchs, J. Monochromatic short pulse laser produced ion beam using a compact passive magnetic device. Rev. Sci. Instrum. 2014, 85, 043504. [Google Scholar] [CrossRef] [PubMed]
- Scuderi, V.; Jia, S.B.; Carpinelli, M.; Cirrone, G.; Cuttone, G.; Korn, G.; Licciardello, T.; Maggiore, M.; Margarone, D.; Pisciotta, P.; et al. Development of an energy selector system for laser-driven proton beam applications. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2014, 740, 87–93. [Google Scholar] [CrossRef]
- Schillaci, F.; Maggiore, M.; Cirrone, G.; Cuttone, G.; Pisciotta, P.; Costa, M.; Rifuggiato, D.; Romano, F.; Scuderi, V. Design of the prototype of a beam transport line for handling and selection of low energy laser-driven beams. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2016, 837, 80–87. [Google Scholar] [CrossRef]
- Zhu, J.G.; Zhu, K.; Tao, L.; Xu, X.H.; Lin, C.; Ma, W.J.; Lu, H.Y.; Zhao, Y.Y.; Lu, Y.R.; Chen, J.E.; et al. Distribution uniformity of laser-accelerated proton beams. Chin. Phys. C 2017, 41, 097001. [Google Scholar] [CrossRef][Green Version]
- Lim, J.K.; Frigola, P.; Travish, G.; Rosenzweig, J.B.; Anderson, S.G.; Brown, W.J.; Jacob, J.S.; Robbins, C.L.; Tremaine, A.M. Adjustable, short focal length permanent-magnet quadrupole based electron beam final focus system. Phys. Rev. ST Accel. Beams 2005, 8, 072401. [Google Scholar] [CrossRef]
- Schollmeier, M.; Becker, S.; Geißel, M.; Flippo, K.A.; Blažević, A.; Gaillard, S.A.; Gautier, D.C.; Grüner, F.; Harres, K.; Kimmel, M.; et al. Controlled Transport and Focusing of Laser-Accelerated Protons with Miniature Magnetic Devices. Phys. Rev. Lett. 2008, 101, 055004. [Google Scholar] [CrossRef] [PubMed]
- Nishiuchi, M.; Daito, I.; Ikegami, M.; Daido, H.; Mori, M.; Orimo, S.; Ogura, K.; Sagisaka, A.; Yogo, A.; Pirozhkov, A.S.; et al. Focusing and spectral enhancement of a repetition-rated, laser-driven, divergent multi-MeV proton beam using permanent quadrupole magnets. Appl. Phys. Lett. 2009, 94, 061107. [Google Scholar] [CrossRef]
- Bin, J.; Allinger, K.; Assmann, W.; Dollinger, G.; Drexler, G.A.; Friedl, A.A.; Habs, D.; Hilz, P.; Hoerlein, R.; Humble, N.; et al. A laser-driven nanosecond proton source for radiobiological studies. Appl. Phys. Lett. 2012, 101, 243701. [Google Scholar] [CrossRef]
- Pommarel, L.; Vauzour, B.; Mégnin-Chanet, F.; Bayart, E.; Delmas, O.; Goudjil, F.; Nauraye, C.; Letellier, V.; Pouzoulet, F.; Schillaci, F.; et al. Spectral and spatial shaping of a laser-produced ion beam for radiation-biology experiments. Phys. Rev. Accel. Beams 2017, 20, 032801. [Google Scholar] [CrossRef]
- Brandi, F.; Labate, L.; Palla, D.; Kumar, S.; Fulgentini, L.; Koester, P.; Baffigi, F.; Chiari, M.; Panetta, D.; Gizzi, L.A. A Few MeV Laser-Plasma Accelerated Proton Beam in Air Collimated Using Compact Permanent Quadrupole Magnets. Appl. Sci. 2021, 11, 6358. [Google Scholar] [CrossRef]
- Romano, F.; Schillaci, F.; Cirrone, G.; Cuttone, G.; Scuderi, V.; Allegra, L.; Amato, A.; Amico, A.; Candiano, G.; De Luca, G.; et al. The ELIMED transport and dosimetry beamline for laser-driven ion beams. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2016, 829, 153–158. [Google Scholar] [CrossRef]
- Scisciò, M.; Migliorati, M.; Palumbo, L.; Antici, P. Design and optimization of a compact laser-driven proton beamline. Sci. Rep. 2018, 8, 6299. [Google Scholar] [CrossRef]
- Busold, S.; Schumacher, D.; Deppert, O.; Brabetz, C.; Frydrych, S.; Kroll, F.; Joost, M.; Al-Omari, H.; Blažević, A.; Zielbauer, B.; et al. Focusing and transport of high-intensity multi-MeV proton bunches from a compact laser-driven source. Phys. Rev. ST Accel. Beams 2013, 16, 101302. [Google Scholar] [CrossRef]
- Metzkes, J.; Cowan, T.; Karsch, L.; Kraft, S.; Pawelke, J.; Richter, C.; Richter, T.; Zeil, K.; Schramm, U. Preparation of laser-accelerated proton beams for radiobiological applications. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2011, 653, 172–175. [Google Scholar] [CrossRef]
- Doria, D.; Kakolee, K.F.; Kar, S.; Litt, S.K.; Fiorini, F.; Ahmed, H.; Green, S.; Jeynes, J.C.G.; Kavanagh, J.; Kirby, D.; et al. Biological effectiveness on live cells of laser driven protons at dose rates exceeding 109 Gy/s. AIP Adv. 2012, 2, 011209. [Google Scholar] [CrossRef]
- Hanton, F.; Chaudhary, P.; Doria, D.; Gwynne, D.; Maiorino, C.; Scullion, C.; Ahmed, H.; Marshall, T.; Naughton, K.; Romagnani, L.; et al. DNA DSB Repair Dynamics following Irradiation with Laser-Driven Protons at Ultra-High Dose Rates. Sci. Rep. 2019, 9, 4471. [Google Scholar] [CrossRef]
- Milluzzo, G.; Ahmed, H.; Romagnani, L.; Doria, D.; Chaudhary, P.; Maiorino, C.; McIlvenny, A.; McMurray, A.; Polin, K.; Katzir, Y.; et al. Dosimetry of laser-accelerated carbon ions for cell irradiation at ultra-high dose rate. J. Phys. Conf. Ser. 2020, 1596, 012038. [Google Scholar] [CrossRef]
- Manti, L.; Perozziello, F.; Borghesi, M.; Candiano, G.; Chaudhary, P.; Cirrone, G.; Doria, D.; Gwynne, D.; Leanza, R.; Prise, K.M.; et al. The radiobiology of laser-driven particle beams: Focus on sub-lethal responses of normal human cells. J. Instrum. 2017, 12, C03084. [Google Scholar] [CrossRef][Green Version]
- Yogo, A.; Sato, K.; Nishikino, M.; Mori, M.; Teshima, T.; Numasaki, H.; Murakami, M.; Demizu, Y.; Akagi, S.; Nagayama, S.; et al. Application of laser-accelerated protons to the demonstration of DNA double-strand breaks in human cancer cells. Appl. Phys. Lett. 2009, 94, 181502. [Google Scholar] [CrossRef]
- Raschke, S.; Spickermann, S.; Toncian, T.; Swantusch, M.; Boeker, J.; Giesen, U.; Iliakis, G.; Willi, O.; Boege, F. Ultra-short laser-accelerated proton pulses have similar DNA-damaging effectiveness but produce less immediate nitroxidative stress than conventional proton beams. Sci. Rep. 2016, 6, 32441. [Google Scholar] [CrossRef]
- Yogo, A.; Maeda, T.; Hori, T.; Sakaki, H.; Ogura, K.; Nishiuchi, M.; Sagisaka, A.; Kiriyama, H.; Okada, H.; Kanazawa, S.; et al. Measurement of relative biological effectiveness of protons in human cancer cells using a laser-driven quasimonoenergetic proton beamline. Appl. Phys. Lett. 2011, 98, 053701. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Biersack, J.P. SRIM—The Stopping Range of Ions in Matter. In Treatise on Heavy-Ion Science; Bromley, D.A., Ed.; Springer: Boston, MA, USA, 1985. [Google Scholar] [CrossRef]
- Baratto-Roldán, A.; Jiménez-Ramos, M.d.C.; Jimeno, S.; Huertas, P.; García-López, J.; Gallardo, M.I.; Cortés-Giraldo, M.A.; Espino, J.M. Preparation of a radiobiology beam line at the 18 MeV proton cyclotron facility at CNA. Phys. Med. Eur. J. Med. Phys. 2020, 74, 19–29. [Google Scholar] [CrossRef]
- Peñas, J.; Bembibre, A.; Cortina-Gil, D.; Martín, L.; Reija, A.; Ruiz, C.; Seimetz, M.; Alejo, A.; Benlliure, J. A multi-shot target wheel assembly for high-repetition-rate, laser-driven proton acceleration. High Power Laser Sci. Eng. 2024, 12, e22. [Google Scholar] [CrossRef]
- Seimetz, M.; Bellido, P.; Soriano, A.; García López, J.; Jiménez-Ramos, M.C.; Fernández, B.; Conde, P.; Crespo, E.; González, A.J.; Hernández, L.; et al. Calibration and Performance Tests of Detectors for Laser-Accelerated Protons. IEEE Trans. Nucl. Sci. 2015, 62, 3216–3224. [Google Scholar] [CrossRef]
- Bellido, P.; Lera, R.; Seimetz, M.; de la Cruz, A.R.; Torres-Peirò, S.; Galán, M.; Mur, P.; Sánchez, I.; Zaffino, R.; Vidal, L.; et al. Characterization of protons accelerated from a 3 TW table-top laser system. J. Instrum. 2017, 12, T05001. [Google Scholar] [CrossRef]
- Seimetz, M.; Bellido, P.; Mur, P.; Lera, R.; de la Cruz, A.R.; Sánchez, I.; Zaffino, R.; Benlliure, J.; Ruiz, C.; Roso, L.; et al. Electromagnetic pulse generation in laser-proton acceleration from conductive and dielectric targets. Plasma Phys. Control. Fusion 2020, 62, 115008. [Google Scholar] [CrossRef]
- Seimetz, M.; Peñas, J.; Llerena, J.; Benlliure, J.; García López, J.; Millán-Callado, M.; Benlloch, J. PADC nuclear track detector for ion spectroscopy in laser-plasma acceleration. Phys. Med. Eur. J. Med. Phys. 2020, 76, 72–76. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).