Abstract
The spatiotemporal resolution of diagnostic X-ray images obtained with rotating-anode X-ray tubes has remained limited as the development of rigid, high-performance target materials has slowed down. However, novel imaging techniques using finer detector pixels and orthovolt cancer therapy employing narrow X-ray focal spots demand improved output from brilliant keV X-ray sources. Since its advent in 1929, rotating-anode technology has become the greatest bottleneck to improvement. To overcome this limitation, the current authors have devised a novel X-ray generation technology based on tungsten microparticle targets. The current study investigated a hybrid solution of a stream of fast tungsten microparticles and a rotating anode to both harvest the benefits of the improved performance of the new solution and to reuse known technology. The rotating anode captures energy that may pass a partially opaque microparticle stream and thereby contributes to X-ray generation. With reference to fast-rotating anodes and a highly appreciated small focal spot of a standardized size of 0.3 for an 8° target angle (physical: 0.45 mm × 4.67 mm), we calculated a potential output gain of at least 85% for non-melting microparticles and of 124% if melting is envisioned. Microparticle charging can be remediated by electron backscattering and electron field emission. The adoption of such a solution enables substantially improved image resolution.
1. Introduction
Rotating-anode X-ray sources are the workhorses of medical diagnostic imaging. Recently, an extension of their use has been suggested for the novel concept of high-flux photon therapy [1], which demands high power density in the source. Despite an urgent quest to increase the brilliance, the basic target technology has remained stagnant since the advent of the first commercially available spinning anode rotor in an ultra-high vacuum in 1929 [2,3]. A top layer of a high-atomic-number material, typically an alloy of tungsten and rhenium, outputs about one percent of the kinetic energy of the impacting electrons as bremsstrahlung and characteristic X-rays. Such materials are typically very dense, and thus the anodes have a high mass. This limits the angular velocity that may be achieved before the forces exerted on the anode cause it to fail mechanically. Furthermore, the electron beam causes the extreme heating of part of the anode, which then cools when not exposed to the beam, and the rapid spinning leads to high-frequency thermal cycling during each revolution. This eventually causes the cracking and melting of the (typically) sintered, rigid conversion layer and thus restricts the focal-spot size, which constrains the image resolution that may be achieved.
Contemporary computed tomography (CT) systems comprise compact rotating an-odes about 200 mm in diameter that are produced from molybdenum-based alloys of high-yield strengths, such as titanium–zirconium–molybdenum–carbon (TZM) or molybdenum–hafnium–carbon (MHC) subjected to bulk temperatures of up to 1600 °C, topped by a tungsten–rhenium layer (Figure 1). For safety reasons, the angular velocities must be limited to about 12,000 rpm to avoid excessive stresses. X-rays are generated in the focal spot (FS) by a focused high-energy electron beam impacting the conversion layer. For medical diagnostic imaging in the tube voltage range of between 30 kV and 150 kV, the conversion rate from electrical power to X-ray intensity is far below 0.1%, including losses in apertures and X-ray filters. An anode input power of up to 120 kW per tube is typically required to produce a sufficient X-ray intensity in cardiac CT applications, as well as to limit Poisson and electronic noise in the detector behind the attenuating patient. However, the necessary FS size is then larger than appreciated.
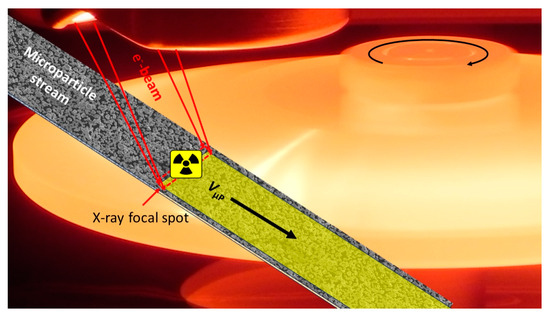
Figure 1.
Schematic of a hybrid target system. Bremsstrahlung is emitted from the rectangular focal spot where a focused beam of electrons with energies of up to 150 keV for medical imaging intersects with the rotating target material (circular arrow), which is covered with a µP layer in this schematic. The cathode at negative potential with respect to the rotor is visible at the top. The µP stream is shown flying over the rotating anode in a tangential direction parallel to the focal-spot width (straight arrow).
Due to the heat exhaust limitations of rotating anodes, enhancing the X-ray output while reducing the FS size is extremely challenging. Doubling the input power for a given FS would produce a 16-fold increase in centrifugal stress from the faster rotation that adds to the thermo-mechanical stress. Thus, progress has recently been slow and novel concepts would be highly appreciated [4,5]. Although X-ray sources with high brilliance are available, for example, Thomson scatter sources [6], synchrotron sources [7,8,9], laser plasma sources [10], and X-ray tubes based on liquid-metal jet anodes [11,12], alternative sources producing both the sufficient intensity and the total output required in medical CT do not exist.
Fortunately, the cathode of a more powerful X-ray source does not constitute a limiting difficulty. The generation of a higher electron flux and current density would be feasible if the residual-gas pressure in the cathode region could be substantially lower than that for the rotating anodes. It is the limited thermo-mechanical capability of rotating targets, particularly the erosion of the conversion layer, that constitutes the primary bottleneck.
We propose circumventing the deficits of the rigid target by replacing or supplementing it with a stream of tungsten (W) microparticles (µPs) (see Figure 1), with, as disclosed in the patent [13], a number of benefits:
- Separated µPs do not erode, as rigid targets do;
- Surface heating within a limited erosion temperature range of a dense sintered body is replaced by volume heating up to the melting point [14] or beyond;
- We propose abandoning the classic paradigm that the target is to be conductively coupled with the current source. The target would not then constitute an anode according to the normal definition. It is concluded from our finding that for sufficiently high electron energy, small tungsten µPs backscatter most of the charge that they receive. Electron field emission may contribute as well to balancing the charging state;
- Microparticles may be accelerated to velocities far exceeding the present FS track velocities of rotors, which are limited to approximately 100 ms−1. The results of initial investigations promise a potential achievable power density gain of up to an order of magnitude for very small FS sizes and tube voltages in the upper CT range and, notably, beyond.
The details of the manipulation of fast-streaming tungsten µPs in a vacuum will be the subject of future publications. Here, we investigate the concept of a hybrid target, sketched in Figure 2. It comprises a classic rotating anode with a dual function: firstly, to mechanically accelerate the µPs, and secondly, to convert the residual electron energy into X-rays that a shielding and X-ray-generating stream with limited density flying on top would let pass.
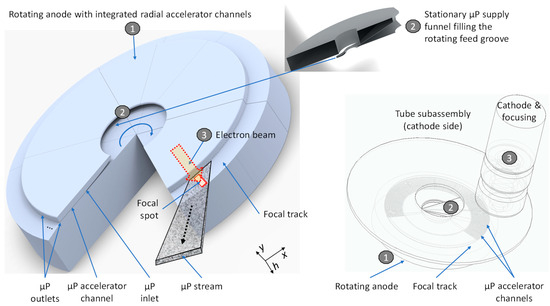
Figure 2.
Sketch of hybrid rotating µP target system. Radial accelerator channels are integrated into the rotating anode (1) that connect inlets in a circular µP supply groove (2) and outlets close to the recessed planar focal-spot track that shape the µP stream. Microparticles are supplied through a stationary feed channel (2) into the rotating groove and exit (arrow) in the vicinity of the focal spot where the focused electron beam from the cathode (3) excites the Ps and the underlying anode material to generate X-rays.
A multitude of radial accelerator channels with inlets that open in the form of funnels into a circular µP feed groove run through the rotating-anode body [Figure 2, (1)] and end in outlets close to the recessed planar focal-spot track. Microparticles are supplied through a stationary feed channel (2) into the rotating feed groove and exit close to the focal spot. The position of the feed funnel is asymmetric and adjusted to deliver µPs to an inlet funnel or a group of inlets such that the particles exit after the time of acceleration in each filled channel at the desired position of the focal spot. The cross sections decrease with the increasing radial position (not shown) to enable sufficient particle flux at the outlet, where the particle density is minimal. The focused electron beam excites the µPs in the stream and the underlying anode material to generate X-rays in the focal spot. The cross sections of the outlets define the thickness and width of the generated µP stream that covers the focal-spot track of the rotating anode.
2. Materials and Methods
2.1. Depth Distribution of Electronic Power Input
The combined thermal loadability of a hybrid target can be improved by shielding the rigid body from excessive electron bombardment by a stream of µPs, as shown in Figure 3. H denotes the thickness of a µP stream, vµP denotes its velocity, and dgap denotes its distance from the focal-spot track of the rotating anode that moves with the tangential velocity (va). The stream should have a mass density of more than 10% of solid tungsten to avoid the widening of typical medical diagnostic focal spots by electron scattering. During its transit through the electron beam, each µP charges from zero to QµP in a linear fashion if discharging other than electron backscattering is absent and contributes to an electric field with a dominating macroscopic normal component at each position (x) if the µP stream is sufficiently thin and sufficiently far from the rotating anode. Ideally, the velocity vectors of the µPs and elements of the FS track are aligned parallel or anti-parallel to the (short) FS width direction to minimize the µP residence time under the WCS wide beam of electrons that are accelerated with the tube voltage (Utube). As shown in the inserted chart, µPs may generate a potential shift (ΔUstream) and an electric field (E) and experience electrical mirror forces (FµP).
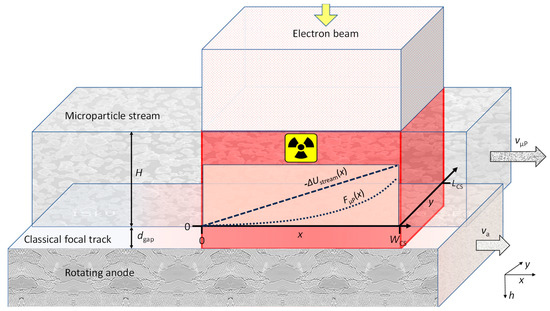
Figure 3.
Sketch of a hybrid target comprising a stream of µPs, traveling at a distance (dgap) (~µm) with a speed (vµP) of 102–103 m/s, and a rigid target moving with velocity (va) (~102 m/s) underneath. The combined thermal loadability can be improved by the shielding effect of the µPs. H (~1–100 µm) denotes the thickness of the µP stream. The P charge increases monotonically from zero to QµP during the P transit through the beam of electrons with energy (−e∙Utube). The µPs experience an electric-field increase with the time and position in the electron beam, a potential ΔUstream, and an attractive force (FµP), typically directed towards the rotating anode (see the inserted schematic graph).
The thermal-shielding effect grows with the thickness and density of the P stream. However, those µPs streaming at the short distance to the anode surface underneath a thick cloud of other µPs experience the impact of decelerated scattered electrons and the backscatter ratio declines with the reduced electron energy. These µPs will accumulate relatively high negative charges that will grow with the µP stream thickness and density. As the resulting voltage of realistic streams is relevant in comparison with the tube voltage, we chose to minimize the density of the investigated stream and selected the equivalent of a single monolayer of closely packed, commercially available monodisperse W spheres of a 5 µm diameter. This selection combines moderate thermal shielding for the underlying FS track and moderate charging. As the dgap is irrelevant for the shielding if the dimensions of the FS are much larger, we simulated the shielding and charging characteristics of a monolayer placed directly on top of the rotating anode in three dimensions with the Monte Carlo (MC) software Casino v3 [15], and we applied these data to a somewhat thicker stream with an accordingly reduced density in the non-vanishing distance.
A typical FS for medical imaging is line-shaped and much longer in the radial direction of the rotating anode than it is wide in the tangential direction, as indicated in Figure 1. In view of their isotropic angular intensity distribution, it is beneficial to use X-rays emerging radially under a small angle of typically <10° from the target. The width and length of the projected FS, as seen from the detector, may then be comparable, while the power density and necessary electron current density in the FS are minimal [16]. Such a line focus allowed us to simplify the simulation to two dimensions and concentrate on the plane parallel to the rotor axis comprising the tangent of the FS track through the FS. We further assumed a normal electron impact and negligible lateral electron scattering, such that the FS size is well represented by the electron beam cross section at the target surface.
To mimic isotropic energy input and minimize errors from lateral backscattering without exceeding the available computational capacity during the MC simulation, the center tungsten microsphere was surrounded by 22 equally sized, hexagonal, closely packed tungsten spheres embedded in a 100 µm × 100 µm × 5 µm box on top of a semi-infinite tungsten half-space. An electron beam with a circular cross section and an isotropic current density of a 50 µm radius for the 300 kV evaluation and 38.5 µm otherwise impacted the model arrangement depicted in Figure 4. The test beam radii were larger than the lateral electronic stopping range for 99% power absorption in the W.
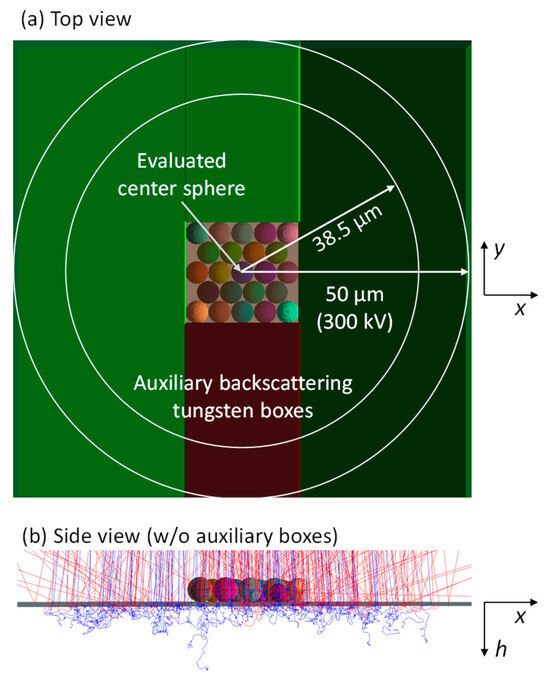
Figure 4.
Model arrangement for MC simulation of the input power distribution and the charge accumulated by the electron impact in a closely packed array of W spheres. The test 5 µm diameter center W sphere was surrounded in the x-y plane by 22 equally sized neighbors and embedded in extended W boxes of equal height to avoid errors from peripheral electron backscattering. This arrangement was placed directly on top of a W half space. (a) Top view from the electron source, (b) side view in perspective with primary (red) and selected scatter traces (blue) in the depth (h) (shown without shields to avoid clutter).
While spheres at the perimeter of the model array may experience a lateral loss of electrons by backscattering into a vacuum, towards the scattering tungsten boxes and the substrate, the center sphere is assumed to be representative of an arbitrary member of an infinite monolayer and is subject to an electron beam that is much wider than the layer thickness and its distance to the anode. The MC software outputs the energy accumulated in each voxel and allows us to assess the lateral and depth distribution of the electron power.
2.2. Simulation of the Electric Potential and Field
The electric potential of the µPs associated with charge accumulation has implications for the dynamics of the stream, electron focusing, the X-ray spectrum, and the intensity of the emitted X-rays. In the absence of discharging effects other than backscattering, the individual charges of the µPs grow along their trajectories in the electron beam. The absolute charge peaks at the exit of the focal spot, where x = WCS, as indicated in the chart inserted in Figure 3. We simulated the potential and electric fields with COMSOL Multiphysics® 6.2 [17] using the MC simulated charge accumulation that was obtained using MC simulations in Casino v3 from the number difference between the impacting primary electrons and all outgoing electrons in the center sphere. Electron transport data were exported from Casino and evaluated with an Excel®-based tool.
The simplest hybrid target system uses the rotating anode as the mechanical accelerator. µPs may be supplied into grooves near the center and accelerated by centrifugal forces in radial funnels. To avoid unwanted particle accretion, the feed funnels must be much wider than the particle diameter. A funnel placed on a plane normal to the rotor axis may be as wide as the focal spot and, thus, exceed the particle diameter by nearly two orders of magnitude for a medical diagnostic FS. The axial direction, however, determines the X-ray optical FS length of the hybrid target as well as the electrical potential in the possibly charged µP stream. We chose to model a 20 µm thick stream of µPs flying over the rigid planar anode (i.e., ). The stream was modeled as five layers with pseudo-randomly distributed microspheres in the axial h-direction, as shown in Figure 5. In the model, adjacent auxiliary electrodes serve to flatten the equipotential lines laterally. Figure 5 shows five electrode layers, shown for a sample stream of a 45 µm thickness. Instead, to avoid overlapping, for this study, we used only two auxiliary electrode layers to simulate a 20 µm stream also comprising five µP layers. The potentials of the auxiliary electrodes were optimized for a minimal difference in the potential as a function of the h along the normal to the anode center axis through the µP stream comprising the center sphere and a 60 µm distance normal (probing the spatial potential through the electrodes). The model arrangement was enclosed by a 1 × 1 × 1 mm3 grounded box.
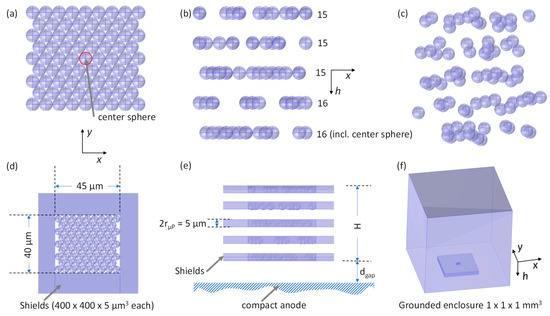
Figure 5.
Model for the FEM simulation of electric parameters in a sample array of 5 µm diameter µPs that fly over a compact anode. (a) Assumed hexagonal close packing of 77 spheres viewed from the electron source with the tested microsphere in the center. (b) Cross section with the spheres pseudo-randomly distributed along the depth h-direction in 5 layers, shown expanded to a thickness of H = 45 µm for clarity. (c) View in perspective. (d) As in (a), showing auxiliary electrodes for each µP layer that flatten the lateral equipotential lines in the center. (e) As in (b), with auxiliary electrodes and the compact anode showing the distance (dgap) of one sphere radius: 2.5 µm. (f) Overall view, including the grounded enclosure in perspective.
While the extension of a monolayer along the h has no influence on the absorbed power if the stream thickness (H) and distance (dgap) are much smaller than the width of the line focus (WCS), the electric potential will depend on these parameters. The distance (dgap) and the thickness (H) are assumed to be small compared with the WCS and the length (LCS) of the interaction region, thus allowing a two-dimensional macroscopic approximation and evaluation of the potential in the same plane, as discussed for the power distribution (Section 2.1). Further, in this approximation, the charging by primary and backscattered electrons is independent of the distance of the monolayer of µPs from the rigid anode, as the distribution of scattered electrons may be assumed to be isotropic at all distances. In the absence of further discharging effects, the space potential at the exit of the FS (ΔUstream(h)) is proportional to the ratio of the charge deposited in each µP per incident of primary electrons impacting on its cross section (qµP), which itself depends on the tube voltage. The ratio further depends on the electron scatter conditions that determine the energy distribution of the entirety of the impacting electrons. The qµP value is also assumed to be equal for all µPs in the (three-dimensional) stream irrespective of their h-positions. This assumption is justified for assessing the maximum of the absolute of the stream potential that is given primarily by the integrated macroscopic space charge. Microparticles contacting the rotating anode and mechanically scattered homogenize the charge distribution along the h.
3. Results
3.1. Power Distributions
Figure 6 shows the depth (h) distribution of the dissipated electron power, integrated normal to the imaging plane, for a monolayer of hexagonal, closely packed µPs and the compact substrate underneath and for selected primary-electron energies. Figure 6 depicts the same for selected thin slices through the structure.
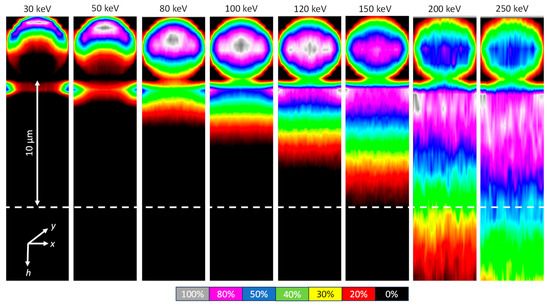
Figure 6.
Input power distributions for the of 5 µm diameter center W sphere, representing an arbitrary member of a closely packed monolayer, on top of a planar semi-infinite W substrate, for selected primary-electron impact energies. Color code: iso-regions of the individually maximum-normed power distributions, integrated over 5 µm along y.
While Figure 6 depicts the y-integrated power, Figure 7 shows the cross sections through a single center sphere and its direct neighbors for a 100 kV tube voltage. The color code is identical to that in Figure 6.
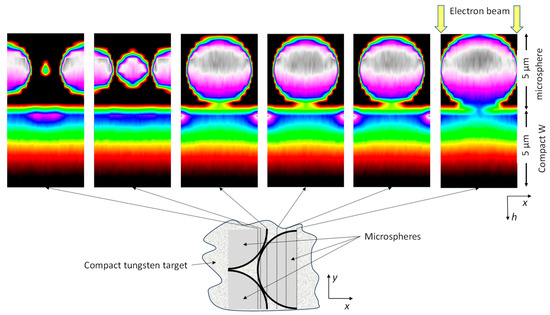
Figure 7.
Cross sections of the input power distribution for normal impact of 100 keV electrons with isotropic current density from the top (shown only for the center slice of a µP) on a hexagonal, densely packed monolayer of W µPs on a compact W target. The stopping power distribution in the depth direction is shown for a selection of slices. Here, the non-integrated distribution is shown per slice. The color code is identical to Figure 6.
As shown in Figure 6 and for the cross sections in Figure 7 and Figure 8, for a sample electron energy of 100 keV, the stopping power peaks close to the electron input. A beam diameter of 30 µm was used for Figure 8 to improve the statistics of the MC calculation. Table 1 gives the total absorbed power.
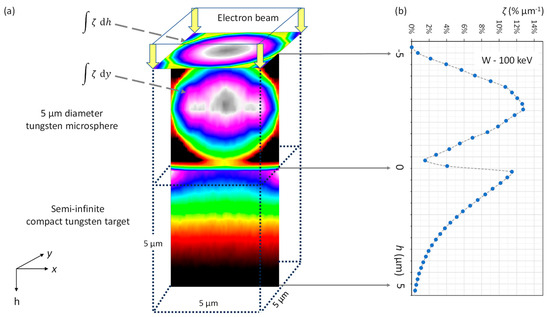
Figure 8.
Power distribution integrated in depth (h) (top) and in y direction (graph underneath). (a) Normal input of 100 keV electrons on a W µP on top of a compact W target. The color code is identical to Figure 6. (b) Power distribution (ζ), integrated across a quadratic surface cross section of 5 µm × 5 µm comprising the sphere. Values are at half-bin.

Table 1.
Energetic shielding coefficients (SµP), percentages of power absorbed by the rotating anode (Sanode), and entire hybrid structure (1 − ηE (hybrid)) for a rigid W target covered with a closely packed monolayer of 5 µm diameter W microspheres for the normal impact of electrons energized by the tube voltage (Utube).
The heat diffusion time across the P diameter is less than a microsecond and thus less than the dwell time of µPs under the electron impact, typically of the order of a few microseconds. In addition, the rotation of the µPs homogenizes the temperature distribution within the µPs further. The latter contribution depends on the uncontrolled spinning rate, however. Therefore, the total heat capacity of the layer of spheres limits the possible energy input rather than hot spots on the micrometer scale. Compared with compact W, the average heat capacity of the 2r-thick monolayer of W spheres with radii (r) is reduced to π/(3√3) = 60.5% of the bulk value. The permitted input power (Pinput) for the hybrid of the monolayer and the compact target is the minimum defined by, first, the power uptake of the µP stream and its energy absorption capacity, and second, by the permitted FS power of the referenced rotating-anode tube (Pinput,ref). Although it does not contribute to FS heating and X-ray generation, the power taken out into a vacuum by backscattered electrons, characterized by the energy backscattering coefficient (ηE), is usually included in published Panode data. If SµP and Sanode denote the ratio of the power absorbed in a stream of µPs and the rigid anode, respectively, dividing each by the input power, tube voltage (Utube), and width (WCS) and length (LCS) of the focal spot, vµP is the velocity of the µP stream, ρW is the mass density of tungsten, cW(T) is the temperature-dependent specific heat capacity, is the mass latent heat of fusion, and Panode = Sanode∙Pinput is the input power entering the rotating anode, whereas the power (PµP = SµP∙Pinput) goes to the shielding µPs. Table 1 lists the relevant coefficients from the MC simulation for selected tube voltages (Utube).
The maximal permitted power input for the rotating anode is given as follows:
The considered monolayer P stream can receive a maximal power input (Pmax,µP) of the following:
T0 denotes the P temperature entering the interaction region, Tm,W denotes the maximal permitted temperature, such as the melting temperature (Tm), ΔHf is the enthalpy change of all the phase transitions during heating from T0 to Tm,W and is zero if melting is not envisioned, as is the case for tungsten if it does not reach its melting temperature, and is expressed by the multiplication of the step function (s()). If the tungsten µPs do melt, ΔHf is then the latent heat of fusion. The rotating anode is overloaded when Pinput > (1, Pinput,ref/Sanode, while the P stream is overloaded when Pinput > Pmax,µP/SµP.
Provided that the P stream moves parallel or anti-parallel to the FS width direction, (i.e., the short dimension) such that the P residence time is WCS/vµP, the permitted power input (Pmax) is as follows:
Figure 9 shows the permitted input power as a function of the tube voltage for a nominal 0.3 FS of maximal size and an isotropic current density according to the standard IEC 60336 with an 8° target angle, corresponding to a maximal WCS of 450 µm, an LCS of 4670 µm, and a 650 µm projected X-ray optical FS length. We included the temperature-dependent W thermophysical properties [18]. The power was compared with the estimated maximal anode input power permitted for a high-performance rotating-anode CT reference tube (iMRC®, Philips, the Netherlands). Published data were adapted using the Müller–Oosterkamp formalism [19,20] to yield the estimated 25 kW CT anode input power that applies for a standardized 4-s-long scan in a cycle every 10 min. Derived from a simple thermal model, we assumed a bulk anode temperature of 1200 °C at the end of each scan and assumed 800 °C as the initial temperature of the µPs entering the FS. The µPs may enter the central region of the rotating anode at 100 °C and heat up to about 800 °C during their transit through the accelerator funnels at 1200 °C in a rotating anode.
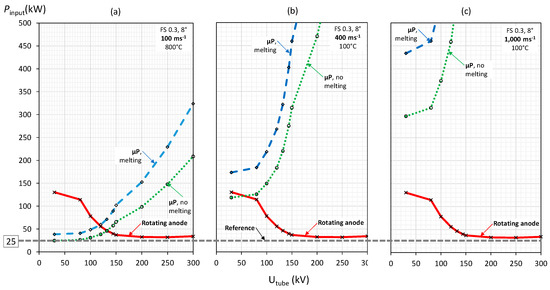
Figure 9.
Power limits from MC simulations for a nominal focal spot of 0.3 and an 8° anode angle according to IEC 60336, given by a closely packed µP stream monolayer if melting is envisioned (rhombi) or not envisioned (circles), and the rotating anode underneath (crosses). (a) Power limits for µPs that are mechanically accelerated with the help of the anode rotor in a hybrid configuration with an assumed body temperature of 1200 °C and a P temperature entering the FS of 800 °C that crosses the FS with a tangential velocity component of 100 ms−1. (b) Power limits for µPs that are mechanically accelerated by auxiliary means to a 400 ms−1 tangential velocity and crossing the FS parallel to the width direction (0°) with an assumed initial temperature of 100 °C. (c) As in (b), assuming a velocity of 1000 ms−1, the hybrid target allows for an input according to the weakest sub-component. To avoid clutter, the chart legend of (b) also applies for (a,c); dotted lines are added to guide the eye.
Power curves are given with the melting of µPs excluded (circles) and permitted (rhombi). The limit given by the thermally shielded rotating anode underneath is shown as well (crosses). Figure 9a is valid if the µPs are mechanically accelerated by, for example, the centrifugal force within the radial funnels in the anode rotor, as shown in Figure 10, and if they then cross the FS under an angle of about 45° with a tangential velocity component parallel to the FS width direction of 100 ms−1.
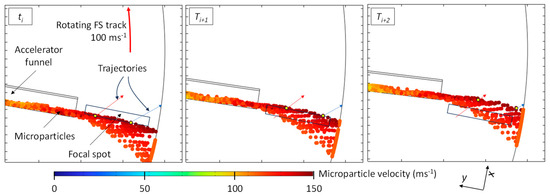
Figure 10.
Hybrid concept comprising a rotating anode to mechanically accelerate µPs and capture the unconsumed electron energy. Assumed FS track and tangential P speed of 100 ms−1. µPs are shown at sequential time points from ti to ti+2 spilling out of a radial accelerator funnel and covering the FS. A few trajectories are sketched as arrows. The simulation was performed with the COMSOL Multiphysics® 6.2 cpt module. µPs are assumed to elastically bounce in the accelerator and to eventually freeze to the outer periphery. The µP inlet close to the rotor center axis (to the left of the graph) is omitted for clarity.
For this example, non-melting µPs would enable a power increase from 25 kW to 46.2 kW (85% gain) for a tube voltage (Utube) of 132 kV. The performance limitation by the P stream, particularly below 132 kV, where the power absorption is high, is due to its low speed. The rotating anode remains cool while the P stream tends to overheat.
A better performance is shown in Figure 9b. The µPs were assumed to be mechanically accelerated separately from the anode rotor. For example, an auxiliary magnetic rotor that operates at a low temperature, such as is used for vacuum turbomolecular pumps, may allow for speeds exceeding 400 ms−1 and a low initial temperature of 100 °C. The thermal burden is better balanced between the µPs and the rotating anode than it is for (a), and it enables the power to increase from the 25 kW rotating-anode reference to 118 kW (a 375% gain) for a 30 kV tube voltage. Figure 9c assumes a P velocity of 1000 ms−1. The rotating-anode rotor is limiting, as in Figure 9b. Using a denser µP stream would be more effective at cooling the rotating anode by exploiting the heat capacity of the stream better. The higher µP velocity not only improves the thermal performance but also reduces the µP charging and the associated space charge potential. However, the extra mechanical accelerator may add complexity. As a starting case, further discussion in the current study shall be based on the situation in Figure 9a.
3.2. Electrical Charging
Figure 11a summarizes the thermal performance shown in absolute values in Figure 9a as the percentage of the permitted input power of the reference tube for the melting and non-melting scenarios. A denser stream than considered here would shield the rotating anode better for higher tube voltages (bold arrow). Figure 11b (curve A) depicts the charging coefficient (qµP) from the MC simulations of Section 2.2 for the equivalent of a closely packed monolayer of 5 µm diameter W spheres placed 2.5 µm in front of a rigid planar W anode. The high backscattering from the underlying anode causes higher charging by low-energy electrons compared with the freestanding monolayer simulated for comparison, as shown by curve B. The reduced X-ray conversion rate of the latter would have to be compensated for by enhancing the electron current. Figure 11b, curve C, shows the resulting higher charging. A freely flying stream may be advised if the electrical capacitance and the resulting potential in comparison with the tube voltage can be managed. Depending on the desired X-ray spectrum, it may even be beneficial to exclude undesired low-energy backscattered electrons, which heat the target without contributing to the filtered X-ray output.
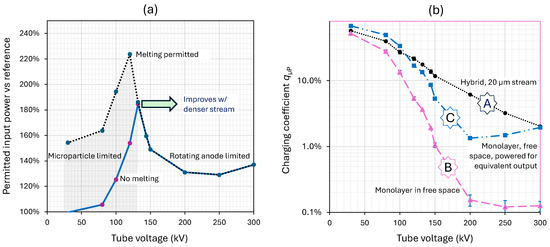
Figure 11.
Permitted input power and charging for a hybrid target with 5 µm diameter W µPs as a function of the tube voltage. (a) Permitted input power for a hybrid target with µPs of a 100 ms−1 speed compared with a rotating-anode reference tube if µP melting is permitted (peak: 224% at 120 kV) or forbidden (peak: 186% at 132 kV). Shaded area: power limited by the µP stream; clear area: power limited by the rotating anode. The shielding of the rotating anode would improve using a denser P stream with high tube voltages (bold arrow). (b) Charging coefficients for a closely packed monolayer of 5 µm diameter W spheres streaming in front of a rotating anode (curve A) or in free space (curve B). Curve C applies if the stream in free space is additionally powered to yield a hybrid-equivalent output.
3.3. Electrical Potential of the µP Stream
3.3.1. Discharging by Backscattering Only
In the absence of discharge channels other than electron backscattering, the electrical potential (∆Ustream(h)) within the tungsten P stream would reach unacceptable levels for the relevant current densities and tube voltages in the medical diagnostic range. We simulated a 20 µm thick stream of 5 µm diameter spheres by randomly normal h-shifting µPs that initially originated from a closely packed monolayer, similar to Figure 5, using a short minimal stream distance from the anode of only the µP radius (dgap = rµP) to assess the smallest realistic electric potential. All µPs have the same x-velocity but five different h-positions. If the model stream is subject to the maximal permitted loading at a 132 kV tube voltage, as shown in Figure 11a (nominal FS: 0.3; input power: 46.2 kW), the absolute value of the potential reaches about two-thirds of the tube voltage. For medical imaging, tube voltage fluctuations of only about a 10% percentage ripple with short reductions from the maximum of up to 30% are typically acceptable to still achieve a sufficient X-ray output and radiation quality. Therefore, such a charge buildup causing variations in the electron impact energy seem unacceptably high. However, the further discharge mechanisms described in the following subsections mitigate this problem.
3.3.2. Microparticle Stream in Free Space
Without any neighboring backscattering body, P charging in free space is much smaller than is discussed in Section 3.3.1, Figure 11b (curve B). As the P speed and initial temperature are not limited by the rotating anode, a higher power input may be permitted, but the charging would rise as well (Figure 11b, curve C). However, the capacitance of the stream with respect to electrodes at a greater distance would rise, and, therefore, the electric potential may become unacceptable. Liquid-metal jets or other thermally stable electrodes proximal, upstream, downstream, or sideways to the P stream may reduce its potential to acceptable levels. Materials like gallium eutectics, carbon, beryllium, or similar materials have low backscattering coefficients and reduce charging [21].
3.3.3. Impact Charge Equilibration and Charge Reversal
According to our model, all µPs are attracted by the anode. The image force grows quadratically with the accumulated charge (see the insert in Figure 3). A rough estimation reveals, however, that for a 100 ms−1 velocity, the first impact on the anode occurs at between one-half of the FS width and FS exit. Since the charge equilibration time scales of W are orders of magnitude smaller than the impact duration [22], charge reversal during impacts with the anode and charge equilibration during inter-µP impacts may reduce the lowest modeled negative potential, but the realistic values still seem far too high.
3.3.4. Electron Field Emission Discharge
However, all these scenarios are unrealistic due to the extreme electric-field strengths obtained of between 7 MV mm−1 for µPs that traverse the FS distant from the anode and up to 25 MV mm−1 for the nearest µPs. Given the W work function of about 4.5 eV, Murphy and Good [23] predict thermally assisted field electron emissions of 1 MV mm−1 or less for temperatures above 2000 K, corresponding to the temperatures in a hybrid target, and cold-field electron emissions from 1.1 MV mm−1 at 0 K. If the emitter surface is large and metallurgically imperfect, field electron emissions may even be experienced for fields as small as 20 kV mm−1 [24].
Therefore, field electron emission can be expected to substantially stabilize and homogenize the stream potential in the FS and reduce it to acceptable levels. Adjusting the charge state in the model layers such that the electric-field strengths at the surfaces of the µPs amount to about 1 MV mm−1 reduces the absolute electric potential to below 7 kV, which is well compatible with the requirements of medical imaging. Figure 12 illustrates the resulting potential and field strengths. Field emission may also limit charging for a free-standing P stream if the emitted electrons can escape to an adjacent auxiliary electrode. The potential and distance of the auxiliary electrode determine the steady-state voltage in the P cloud. The cathode voltage may be enhanced in such cases to adapt to the desired tube voltage.
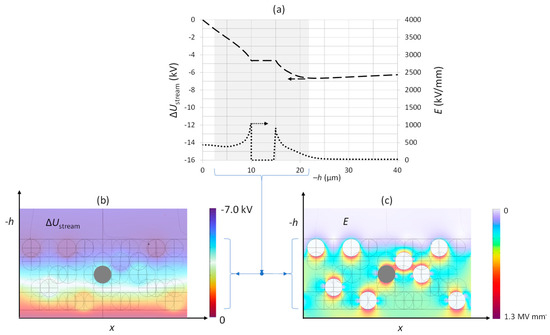
Figure 12.
Potential (∆Ustream(h)) and electric-field strength (E(h)) in field emission discharged maximally from a loaded 20 µm thick simulated P stream at a 2.5 µm distance from a planar rotating anode at the exit of the FS. (a) ∆Ustream(h) (left scale, arrow) and E(h) (right scale, arrow) as a function of the h position along the normal of the anode. (b) ∆Ustream(h) and (c) E(h) (color-coded), in a cross section comprising the normal through the center-sphere probe (dark-grey circle) that we placed in the middle layer for this chart. The electric-field strengths at the surfaces of all the µPs were adjusted to about 1 MV mm−1.
3.3.5. Other Discharge Mechanisms
It may be useful to employ smaller W µPs than modeled due to their enhanced field electron emissions, but that would deteriorate their mechanical manipulation due to enhanced sticking and agglomeration [25,26].
Other discharge mechanisms may further improve the situation. The over-the-barrier component of thermally assisted field electron emissions is significant for temperatures above 2300 K [27]. This component remains substantial for low-electrostatic fields, where it converges to standard thermionic emissions. However, this discharge mechanism requires that the electronic space charge is controlled.
Photoelectric emission discharging by the self-produced X-rays and ultraviolet radiation are not effective due to the small production yield and the inefficient photoemissions for W. External sources would have to be employed. Other actions that involve the supply of inert gas to the interaction region may be useful in special situations.
4. Discussion
While prior studies have already suggested the viability of the paradigm shift from a directly conductive energy supply of the classic anode to an indirect current fed by backscattered electrons, here, we identify the means to minimize the residual charge build-up to acceptable levels. We suggest, in addition, a technical development path employing a hybrid design that combines conventional rotating-anode technology with µPs. While minimizing the number of components, such a hybrid target already promises an unprecedented increase in the power density and, therefore, in the spatiotemporal image resolution. As disclosed in prior publications, substantial further improvement is theoretically possible. Future work will focus on the following:
- (a)
- The analysis of the rheologic aspects of µP management;
- (b)
- The use of mechanical µP accelerators;
- (c)
- The use of carbon-reinforced carbon rotors in a hybrid system to minimize the µP charging due to low backscattering (as for other low-z materials, like beryllium) and to maximize the rotor and µP velocity;
- (d)
- The use of magnetic bearings for mechanical µP accelerators that do not necessarily require current contacts;
- (e)
- The means for electrical or magnetic µP (post-) acceleration;
- (f)
- The study of the dynamics of charged µPs in the vicinity of the focal spot;
- (g)
- The introduction of auxiliary means, such as beams of electrons with low energy, to control the charge state of the μPs;
- (h)
- The implementation of mechanical electron windows to remediate the potential difficulties of the high-voltage stability in the cathode region and improve the residual-gas atmosphere in that space;
- (i)
- The usability of high-performance electron emitters by improving the residual-gas atmosphere employing cool rotor bodies, notably when using mechanical electron windows;
- (j)
- The introduction of electrical means to prevent the µPs from entering the cathode region, such as electrically biased grids or apertures to repel charged µPs, including those that may have experienced charge reversal at the electrodes;
- (k)
- The use of liquid-metal-coated surfaces as µP getters;
- (l)
- The use of stationary or rotary mechanical and electrical µP deceleration and cooling means;
- (m)
- The modulation of the µP stream density and velocity during X-ray exposure to minimize the mass flux and to keep the erosion of the hybrid target under control (such as the temperature-dependent µP flux);
- (n)
- The technology of the cooling, capturing, and recycling of the µPs in stationary and revolving X-ray sources in rotary CT gantries employing gradients of centrifugal acceleration or idle periods;
- (o)
- The possibility of hybrid µP designs, stationary anode targets, and liquid-metal jet targets;
- (p)
- The introduction of proximal auxiliary liquid or solid electrodes (such as materials with low backscattering yields) to minimize the electric potential of µP targets;
- (q)
- The realization of multi-energy X-ray sources utilizing µPs of varying sizes that employ the size-dependent backscattering characteristics;
- (r)
- The use of liquid µPs, such as droplets;
- (s)
- The generation of liquid target droplets of a small size employing electrical forces in high electric fields and / or laser or laser plasma recoil interaction;
- (t)
- The evaluation of the cost and ecological aspects (such as omitting rhenium additives or reducing the rotary anode diameter);
- (u)
- Safety aspects.
5. Conclusions
A hybrid target system comprising a rotating anode and an X-ray-generating stream of fast tungsten µPs is viable to enhance the power density in the X-ray focal spot by 85% for a monolayer equivalent of non-melting µPs and acceleration by the anode rotor itself. Further enhancements are possible with independent accelerators and denser µP streams. The charging and stream potentials can be controlled by electron backscattering, electron-field emission, and potentially by the use of other agents, such as ultraviolet radiation or enhancing the background of inert gas.
6. Patents
Particle-based X-ray sources: US11882642B2; US2023209693A1; WO2023128856A1.
Author Contributions
Conceptualization, methodology, investigation, writing—original draft preparation, R.B.; writing—review and editing, C.H., G.P. and P.T.; supervision, M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available upon request from the authors.
Conflicts of Interest
Mats Danielsson is the owner of Innovicum, Sweden. The company is the assignee of a relevant patent application. Rolf Behling is the owner of XtraininX, Technical Consulting (www.XtraininX.com), and is named as the inventor for a relevant patent application. All other authors declare that they have no competing interests.
References
- Winter, J.; Dimroth, A.; Roetzer, S.; Zhang, Y.; Krämer, K.; Petrich, C.; Matejcek, C.; Aulenbacher, K.; Zimmermann, M.; Combs, S.E.; et al. Heat management of a compact x-ray source for microbeam radiotherapy and FLASH treatments. Med. Phys. 2022, 49, 3375–3388. [Google Scholar] [CrossRef]
- Bouwers, A.P. An X-ray tube with rotating anode. Physica 10, 125 1930. In X-Ray Research and Development. A Selection of the Publications of the Philips X-Ray Research Laboratory from 1923–1933; Philips: Amsterdam, The Netherlands, 1933; pp. 110–119. [Google Scholar]
- Bouwers, A.P.E.N. X-Ray Tube Having a Rotary Anode. U.S. Patent 2081789, 25 May 1937. [Google Scholar]
- Steidel, J.; Maier, J.; Sawall, S.; Kachelrieß, M. Dose reduction potential in diagnostic single energy CT through patient-specific prefilters and a wider range of tube voltages. Med. Phys. 2022, 49, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Baek, J.; Pineda, A.R.; Pelc, N.J. To bin or not to bin? The effect of CT system limiting resolution on noise and detectability. Phys. Med. Biol. 2013, 58, 1433–1446. [Google Scholar] [CrossRef] [PubMed]
- Eggl, E.; Dierolf, M.; Achterhold, K.; Jud, C.; Günther, B.; Braig, E.; Gleich, B.; Pfeiffer, F. The Munich compact light source: Initial performance measures. J. Synchrotron Radiat. 2016, 23, 1137–1142. [Google Scholar] [CrossRef] [PubMed]
- Behling, R.; Grüner, F. Diagnostic X-ray sources—Present and future. Nucl. Instrum. Methods Phys. Res. A 2018, 878, 50–57. [Google Scholar] [CrossRef]
- Nam, I.; Min, C.-K.; Oh, B.; Kim, G.; Na, D.; Suh, Y.J.; Yang, H.; Cho, M.H.; Kim, C.; Kim, M.-J.; et al. High-brightness self-seeded X-ray free-electron laser covering the 3.5 keV to 14.6 keV range. Nat. Photonics 2021, 15, 435–441. [Google Scholar] [CrossRef]
- Macchi, A.; Pegoraro, F. Lighting up a nest for X-ray emission. Nat. Photonics 2023, 17, 129–130. [Google Scholar] [CrossRef]
- Shou, Y.; Wang, P.; Lee, S.G.; Rhee, Y.J.; Lee, H.W.; Yoon, J.W.; Sung, J.H.; Pan, Z.; Kong, D.; Mei, Z.; et al. Brilliant femtosecond-laser-driven hard X-ray flashes from carbon nanotube plasma. Nat. Photonics 2023, 17, 137–142. [Google Scholar] [CrossRef]
- Hertz, H.; Hemberg, O. Method and Apparatus for Generating X-Ray Radiation. Patent EP1305984B1, 24 November 2010. [Google Scholar]
- Espes, E.; Andersson, T.; Björnsson, F.; Gratorp, C.; Hansson, B.A.M.; Hemberg, O.; Johansson, G.; Kronstedt, J.; Otendal, M.; Tuohimaa, T.; et al. Liquid-metal-jet x-ray tube technology and tomography applications. SPIE Opt. Eng. Appl. 2014, 9212, 92120J. [Google Scholar] [CrossRef]
- Behling, R.; Danielsson, M. Particle Based X-Ray Source. U.S. Patent US11882642B2, 23 January 2024. [Google Scholar]
- Whitaker, S. Thermal Analysis of Solid, Rotating, X-Ray Tube Anodes: New Results And A Comparison with Prior Studies; Dwyer, S.J., III, Schneider, R.H., Eds.; SPIE: Bellingham, WA, USA, 1984; pp. 285–293. [Google Scholar] [CrossRef]
- Demers, H.; Poirier-Demers, N.; Couture, A.R.; Joly, D.; Guilmain, M.; de Jonge, N.; Drouin, D. Three-dimensional electron microscopy simulation with the CASINO Monte Carlo software. Scanning 2011, 33, 135–146. [Google Scholar] [CrossRef] [PubMed]
- Behling, R. Modern Diagnostic X-ray Sources, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Comsol, A.B. COMSOL Multiphysics® v. 6.2. Stockholm, Sweden. Available online: www.comsol.com (accessed on 4 July 2023).
- Tolias, P. Analytical expressions for thermophysical properties of solid and liquid tungsten relevant for fusion applications. Nucl. Mater. Energy 2017, 13, 42–57. [Google Scholar] [CrossRef]
- Muller, A. A spinning target X-ray generator and its input limit. Proc. R. Soc. Lond. A 1929, 125, 507–516. [Google Scholar] [CrossRef]
- Oosterkamp, W.J. The heat dissipation in the anode of an X-ray tube—Part II—Loads of short duration applied to rotating anodes. Philips Res. Rep. 1948, 3, 161–173. [Google Scholar]
- Tolias, P. On electron backscattering from dust grains in fusion plasmas. Plasma Phys. Control. Fusion 2014, 56, 045003. [Google Scholar] [CrossRef]
- Stronge, W.J. Impact Mechanics, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Murphy, E.L.; Good, R.H. Thermionic Emission, Field Emission, and the Transition Region. Phys. Rev. 1956, 102, 1464–1473. [Google Scholar] [CrossRef]
- Latham, R. (Ed.) High Voltage Vacuum Insulation; Academic Press: New York, NY, USA, 1995. [Google Scholar]
- Ratynskaia, S.; Tolias, P.; Shalpegin, A.; Vignitchouk, L.; De Angeli, M.; Bykov, I.; Bystrov, K.; Bardin, S.; Brochard, F.; Ripamonti, D.; et al. Elastic–plastic adhesive impacts of tungsten dust with metal surfaces in plasma environments. J. Nucl. Mater. 2015, 463, 877–880. [Google Scholar] [CrossRef]
- Riva, G.; Tolias, P.; Ratynskaia, S.; Daminelli, G.; Donde, R.; De Angeli, M.; Vassallo, E.; Pedroni, M. Adhesion measurements for tungsten dust deposited on tungsten surfaces. Nucl. Mater. Energy 2017, 12, 593–598. [Google Scholar] [CrossRef]
- Modinos, A. Field, Thermionic, and Secondary Electron Emission Spectroscopy, 1st ed.; Springer Science + Business Media: New York, NY, USA, 1984. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).