Analytical Scaling Laws for Radiofrequency-Based Pulse Compression in Ultrafast Electron Diffraction Beamlines
Abstract
1. Introduction
2. Longitudinal Envelope Equation
2.1. Envelope Equation
2.2. Solution in a Drift
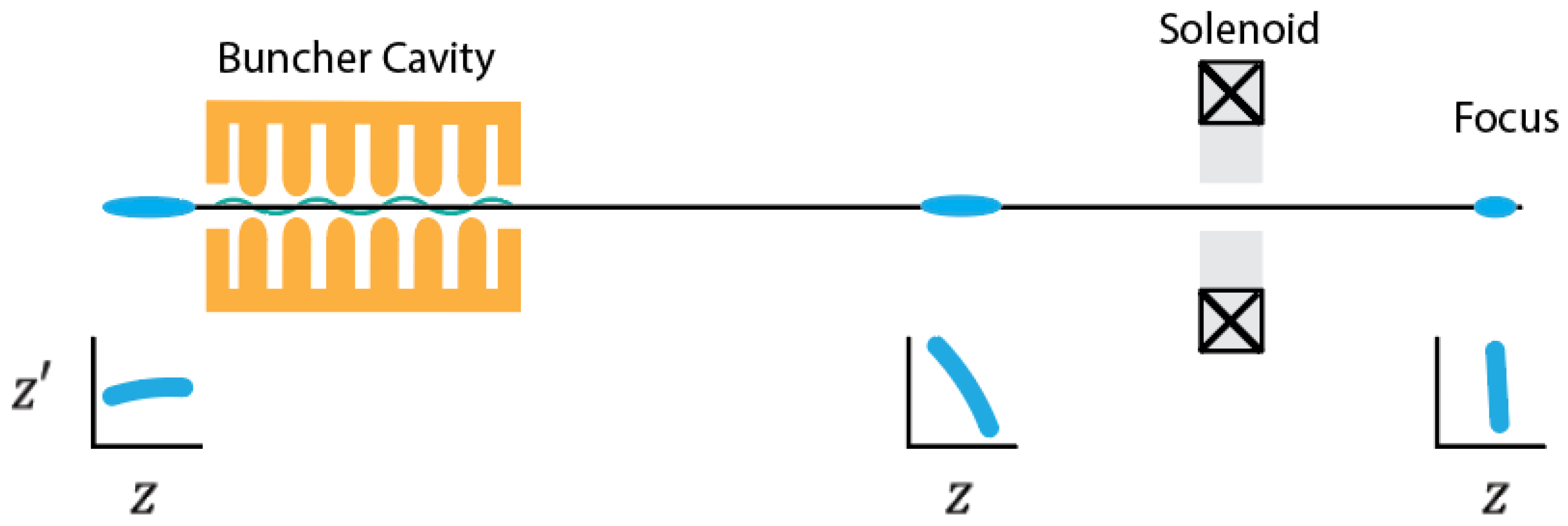
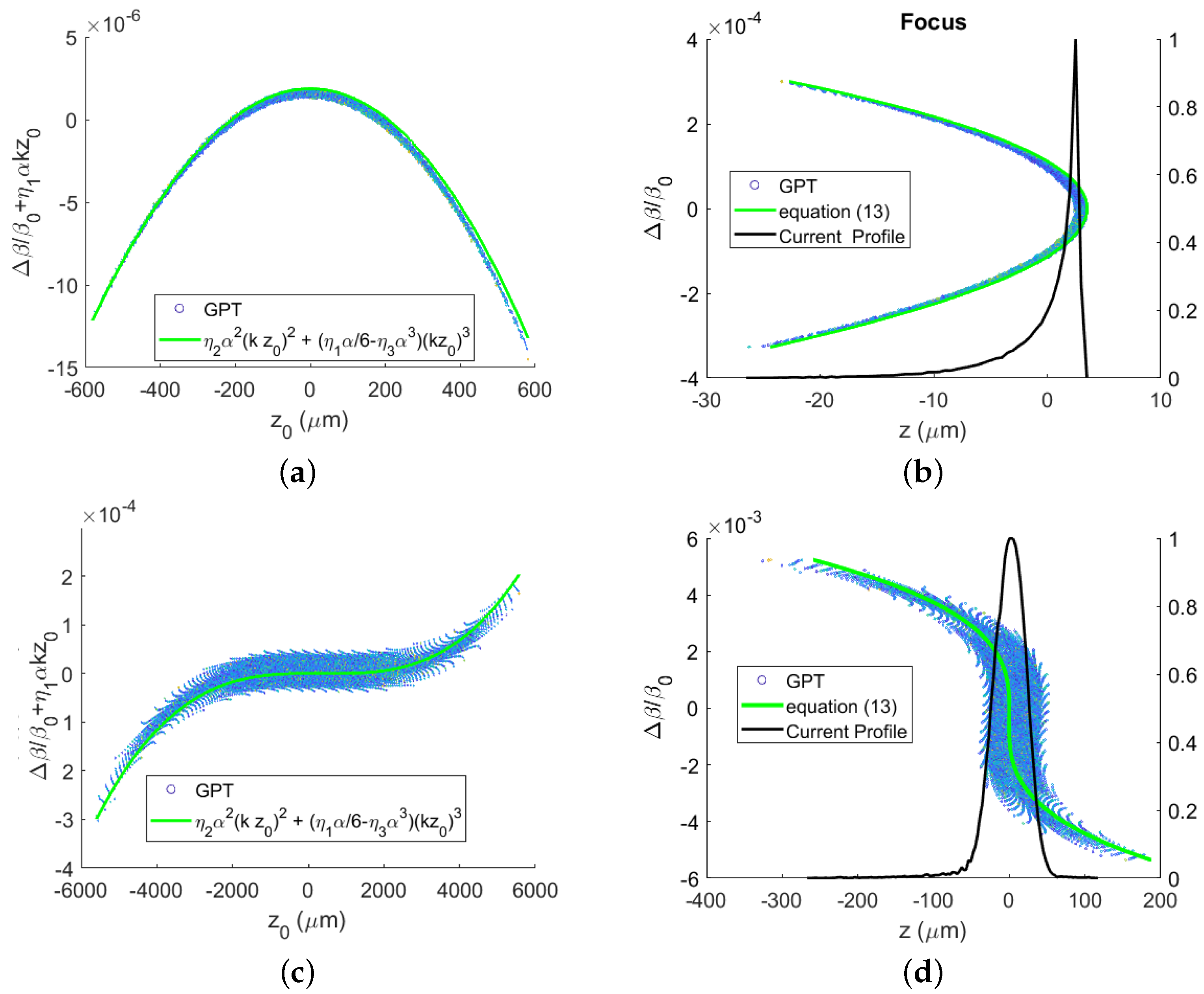
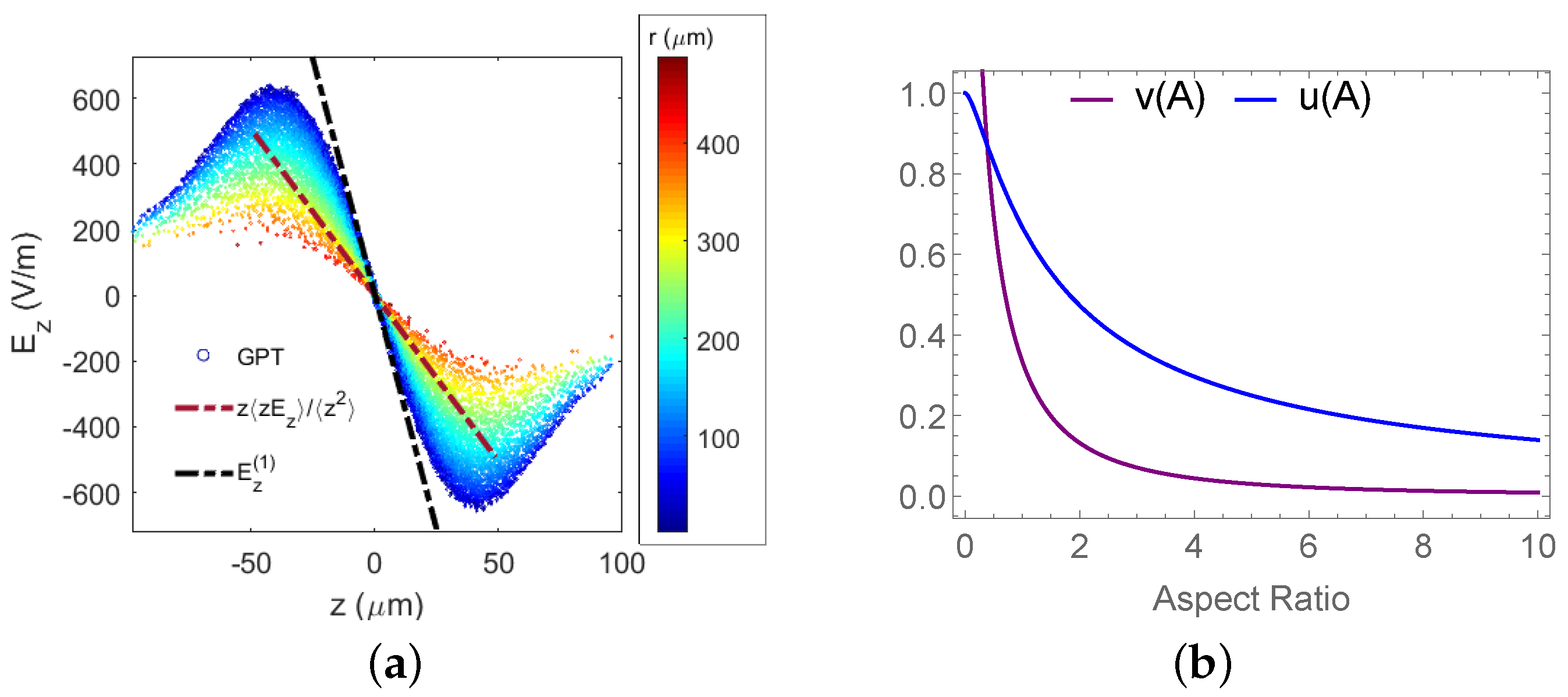
2.3. Single Particle Dynamics and Non-Linear Phase-Space Correlations in the RF Buncher
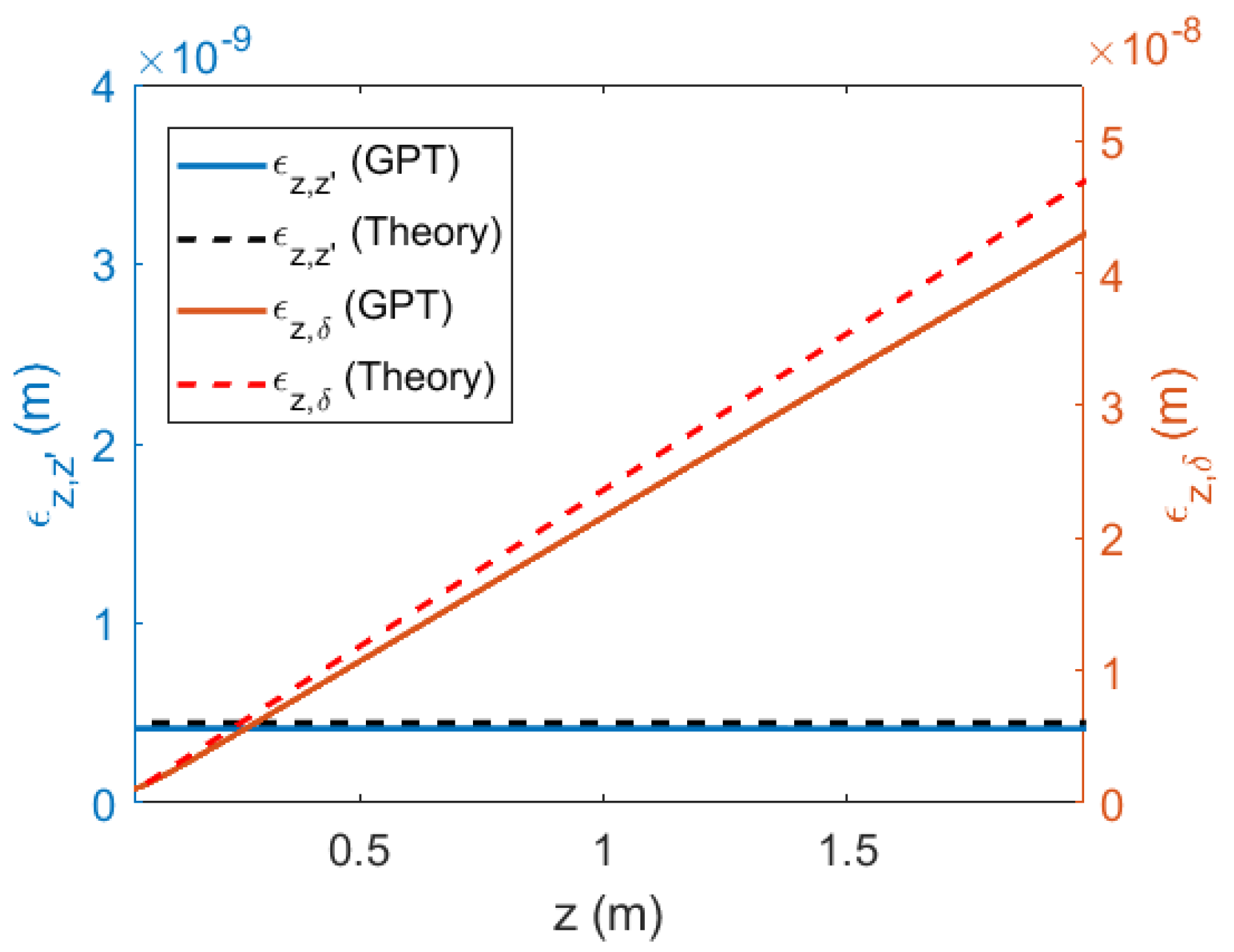
2.4. Emittance Growth Mechanisms and the Relationship between Different Longitudinal Phase Space Definitions
2.4.1. Trace Space Emittance
2.4.2. Phase Space
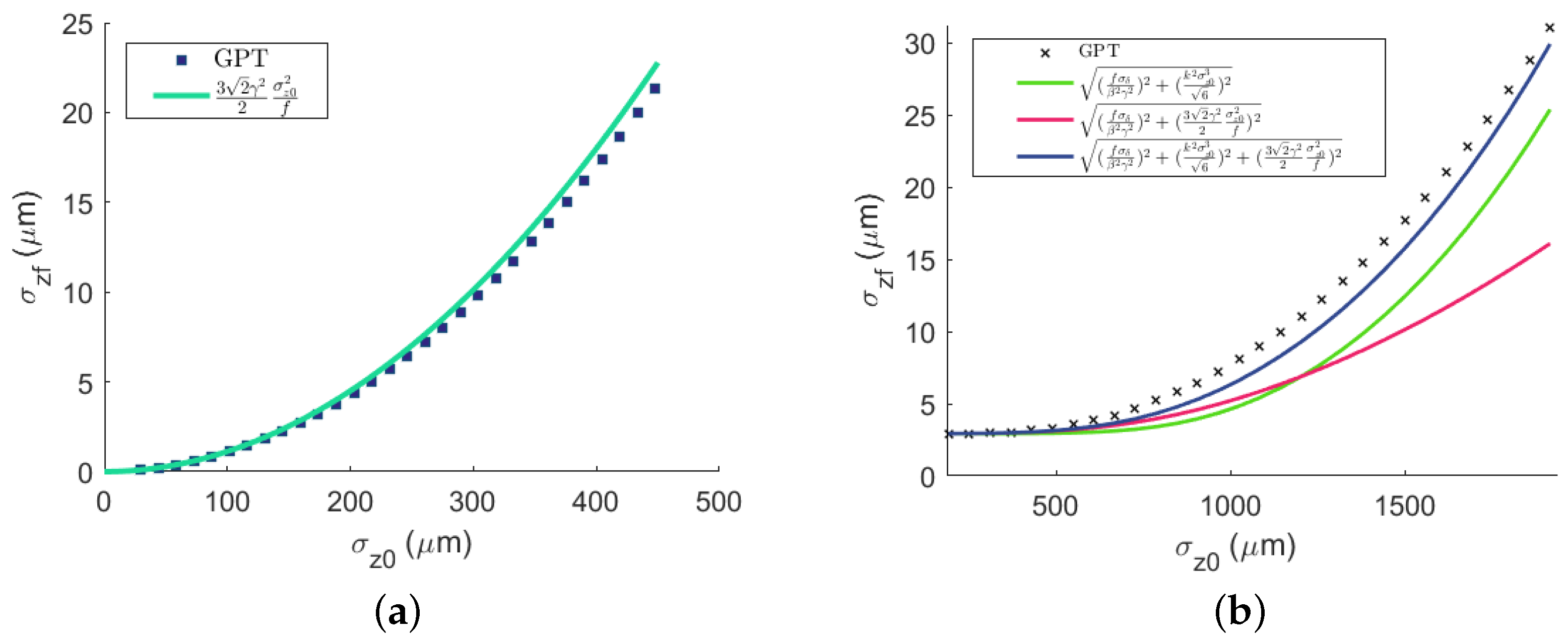
2.5. Bunch Length Limit in Absence of Space-Charge Effects
3. Space-Charge Limits to Compression
3.1. An Example of Geometry Factor Calculation: Gaussian Distribution Case
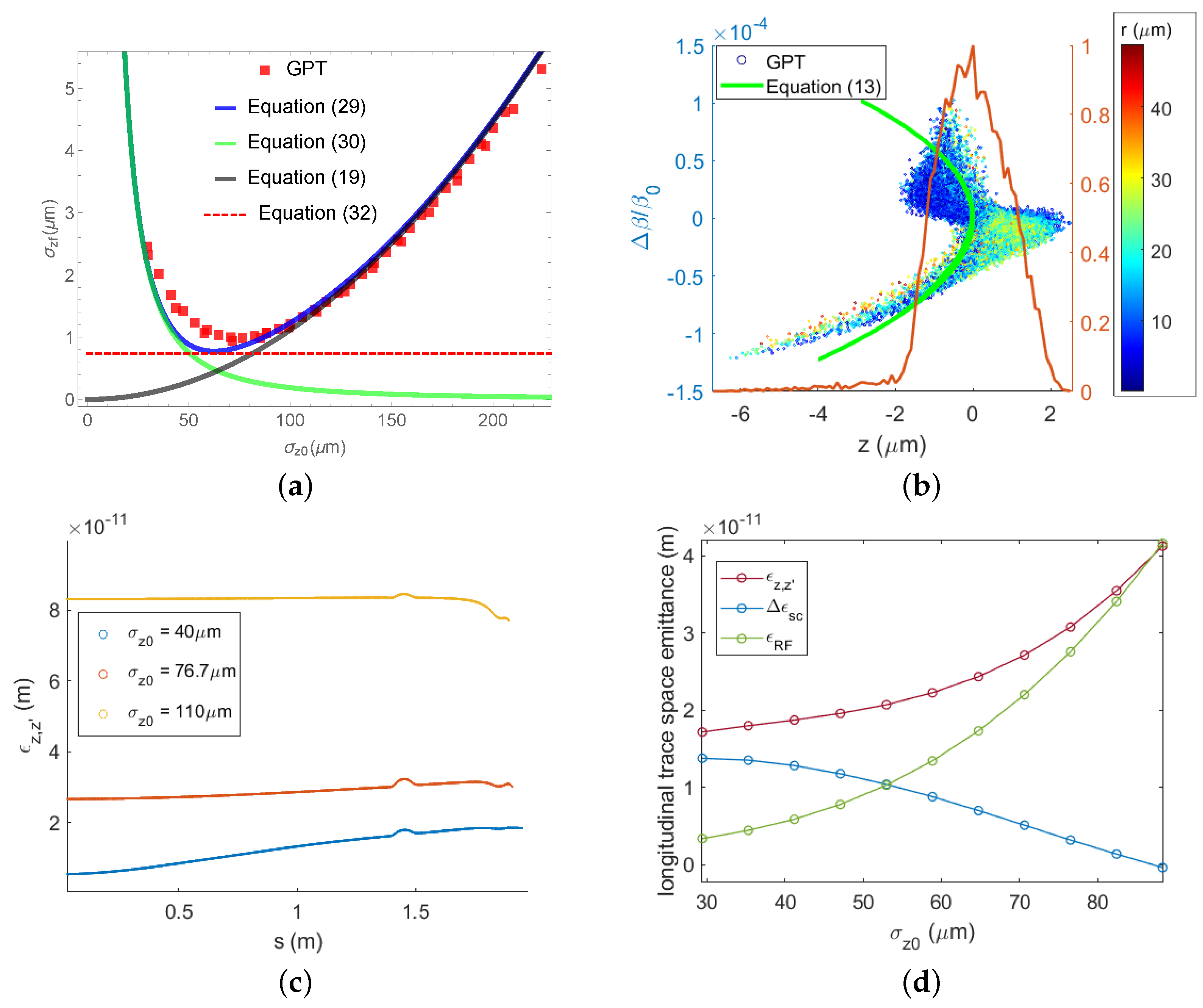
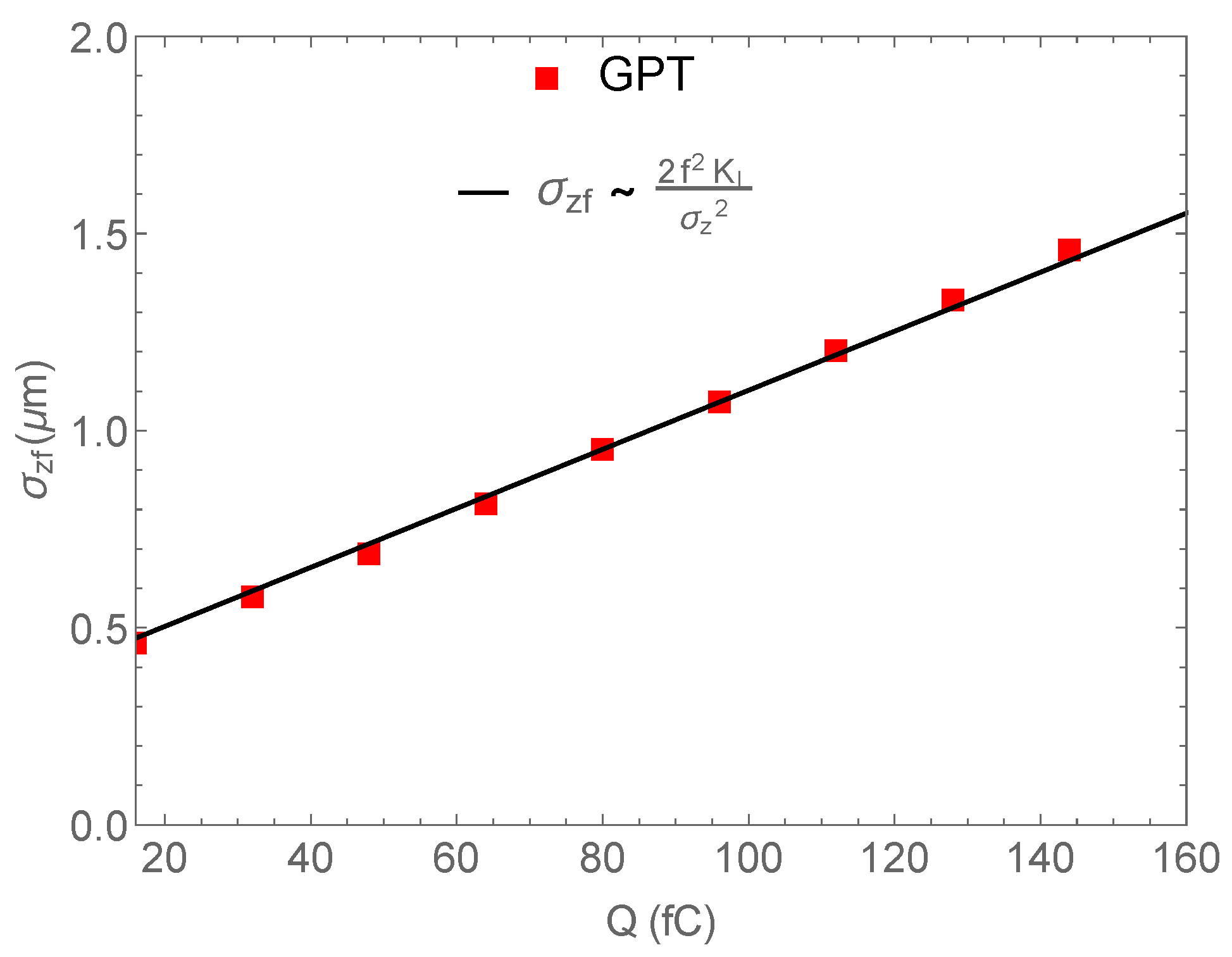
3.2. Effect of the Longitudinal Space-Charge Force on the Minimum Bunch Length
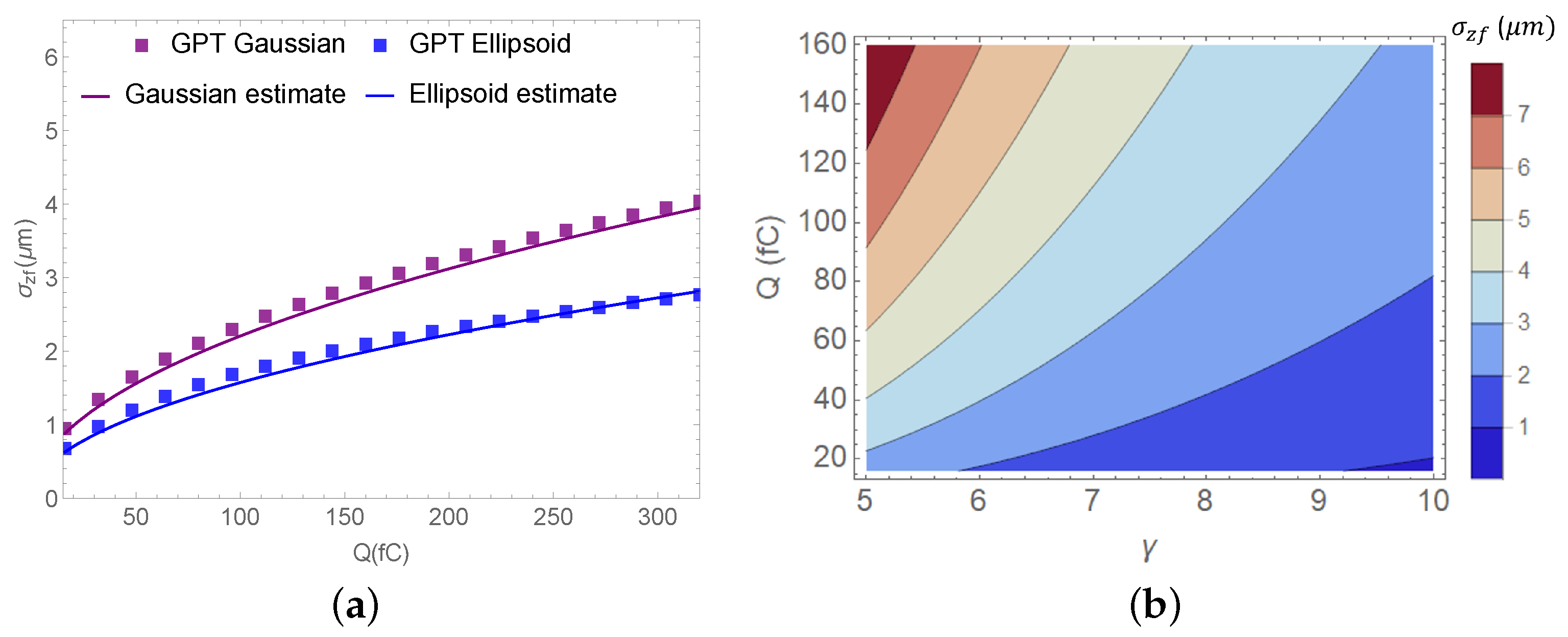
4. Bunch Compression Limits for Different Charge Distributions
5. X-Band Cavity Compensation
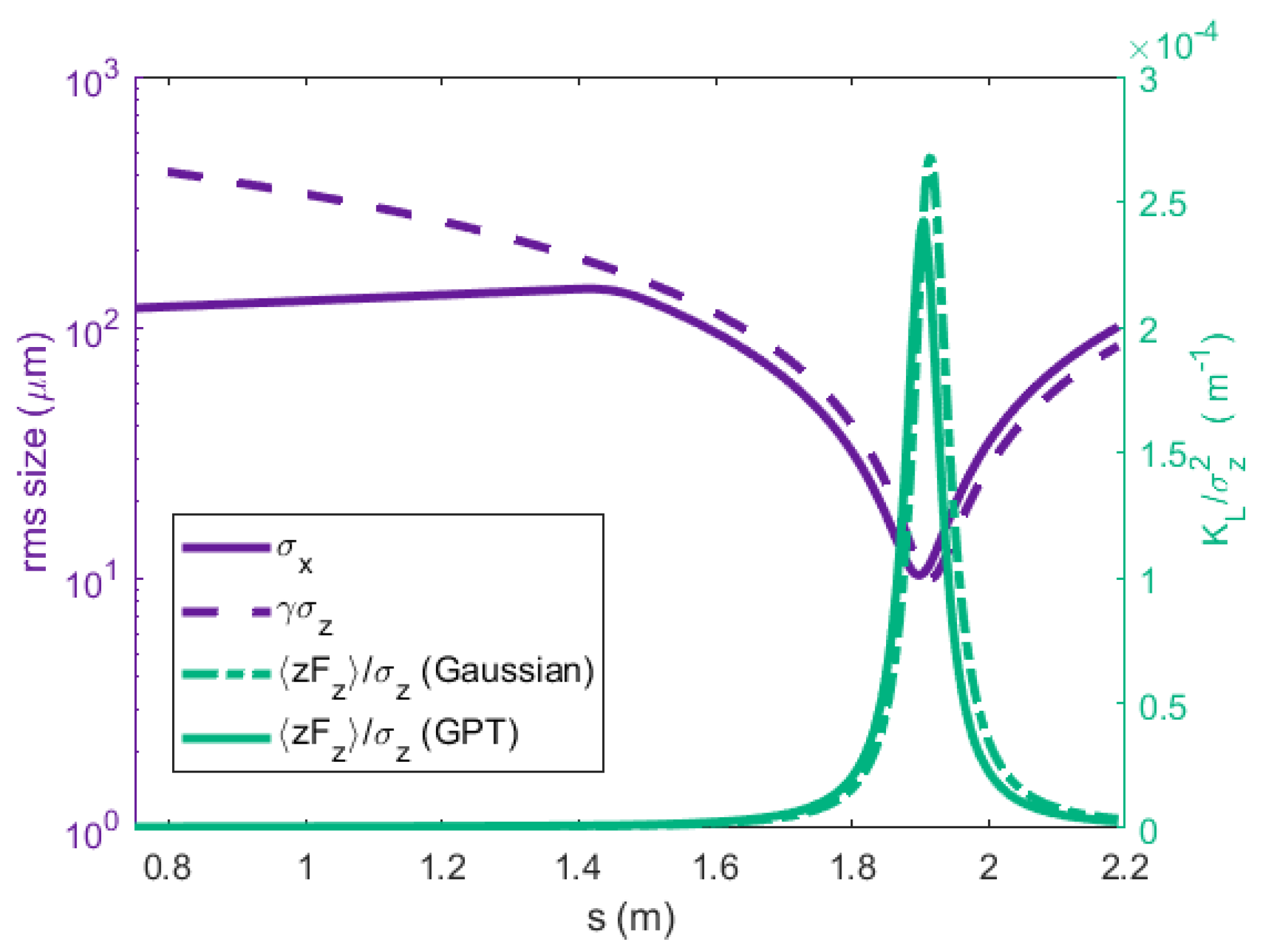
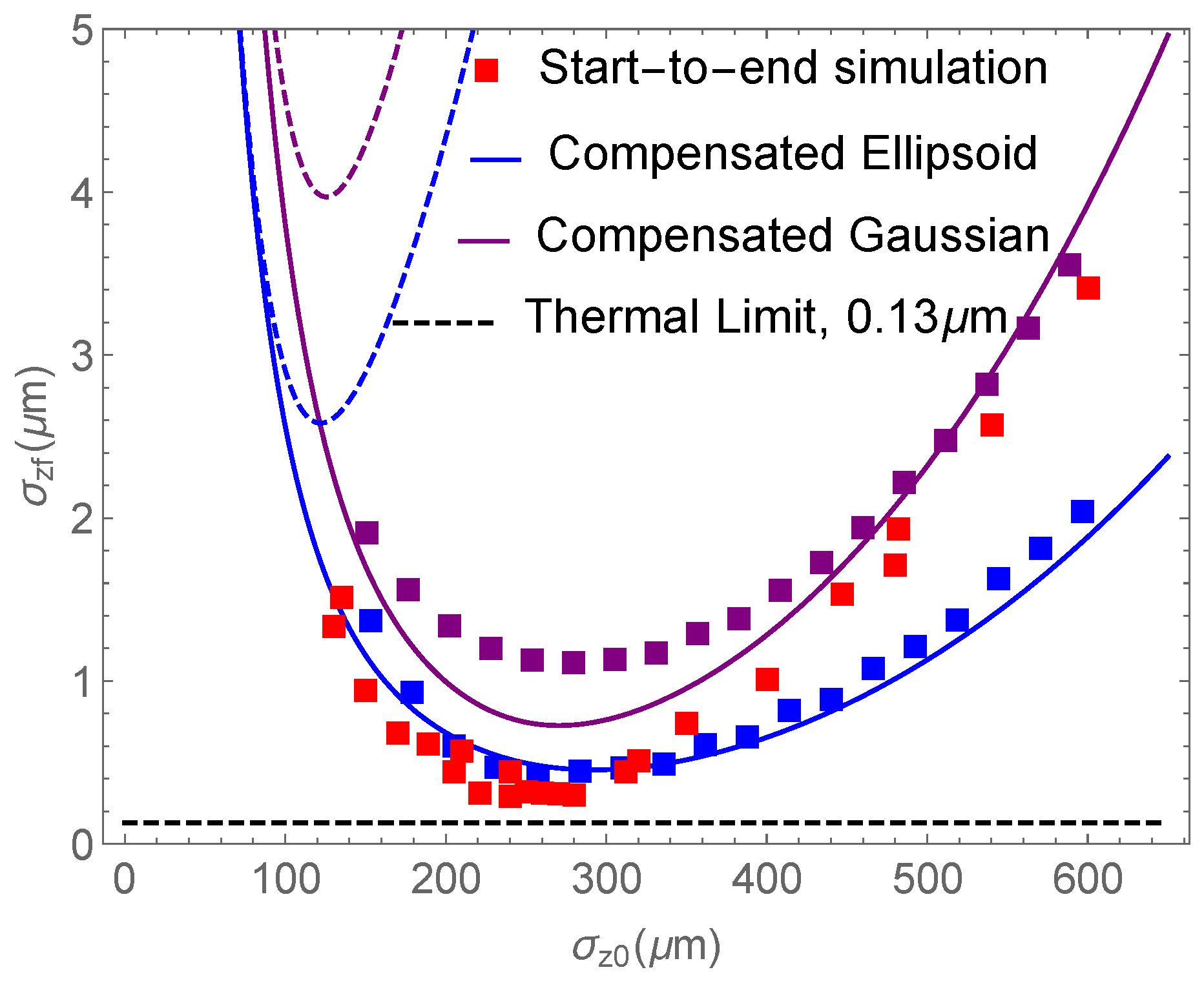
5.1. Analytical Estimates
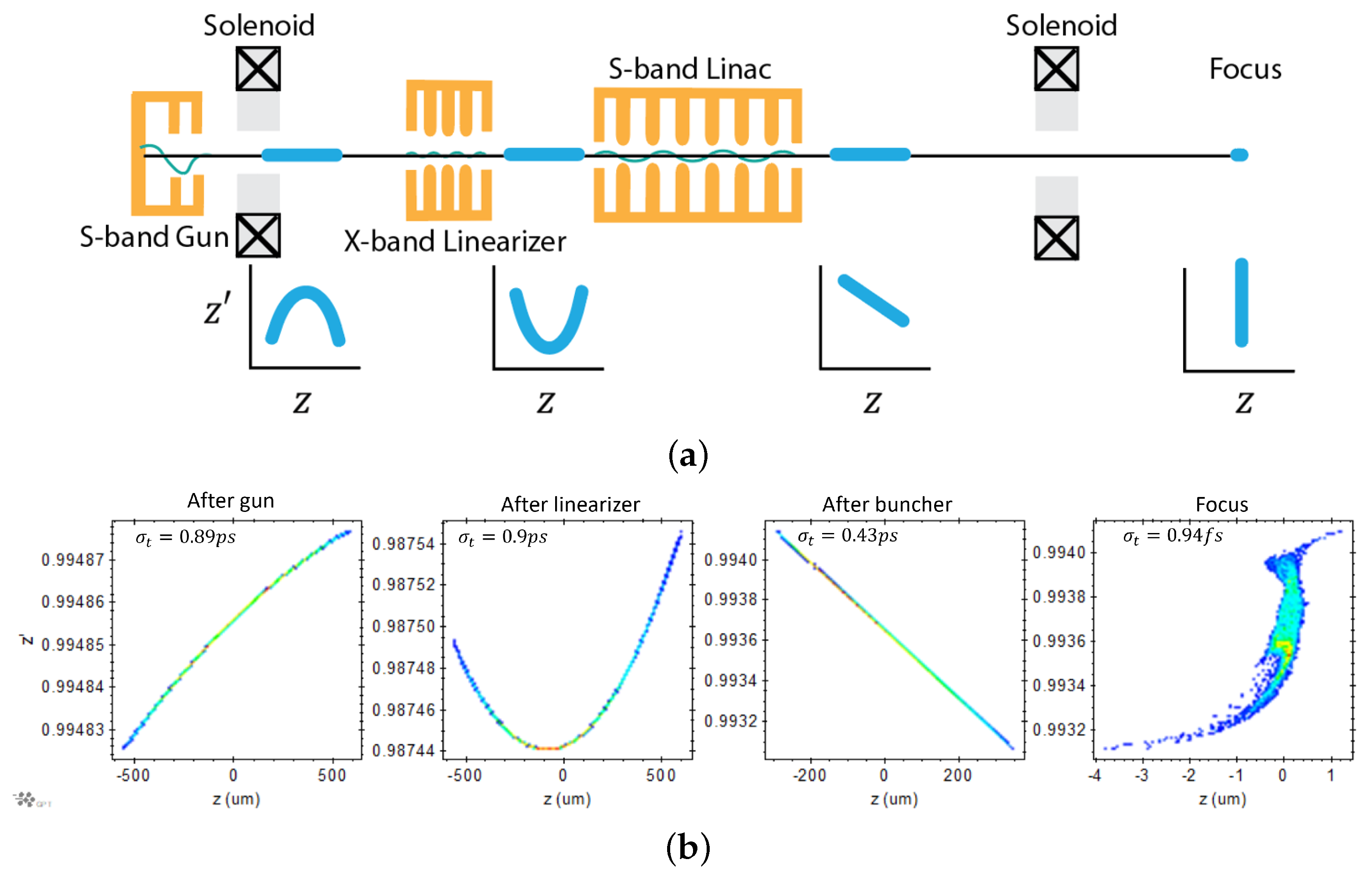
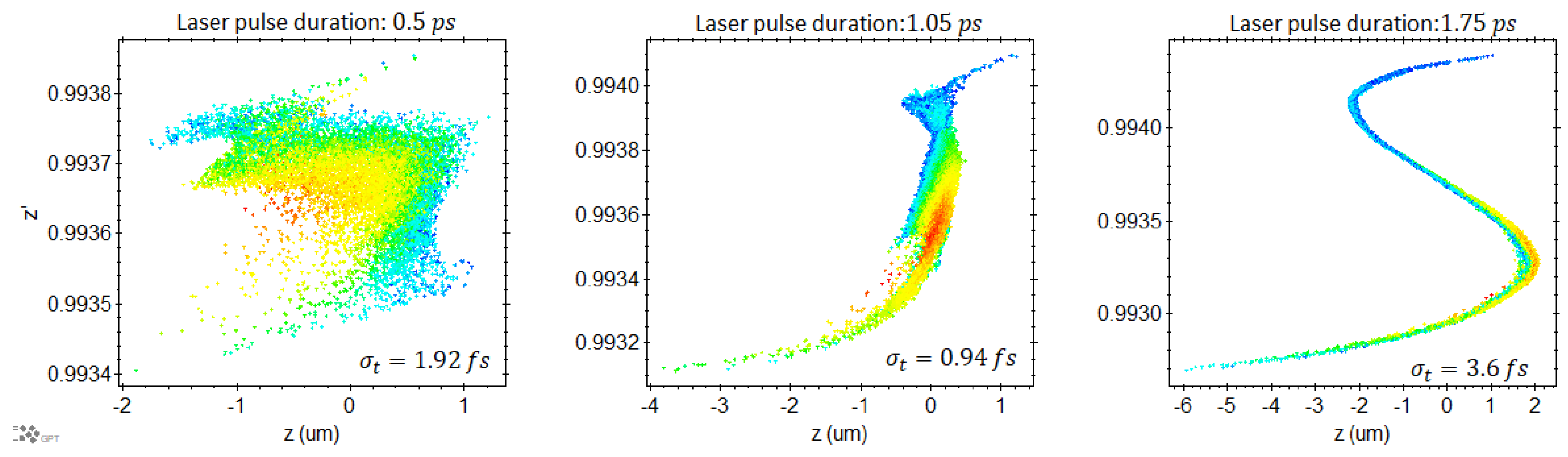
5.2. Start-to-End Simulations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zewail, A.H. 4D Ultrafast Electron Diffraction, Crystallography, and Microscopy. Annu. Rev. Phys. Chem. 2006, 57, 65–103. [Google Scholar] [CrossRef] [PubMed]
- Sciaini, G.; Miller, R.D. Femtosecond electron diffraction: Heralding the era of atomically resolved dynamics. Rep. Prog. Phys. 2011, 74, 096101. [Google Scholar] [CrossRef]
- Siwick, B.J.; Dwyer, J.R.; Jordan, R.E.; Miller, R.D. An atomic-level view of melting using femtosecond electron diffraction. Science 2003, 302, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Weathersby, S.; Brown, G.; Centurion, M.; Chase, T.; Coffee, R.; Corbett, J.; Eichner, J.; Frisch, J.; Fry, A.; Gühr, M.; et al. Mega-electron-volt ultrafast electron diffraction at SLAC National Accelerator Laboratory. Rev. Sci. Instrum. 2015, 86, 073702. [Google Scholar] [CrossRef] [PubMed]
- Zhu, P.; Zhu, Y.; Hidaka, Y.; Wu, L.; Cao, J.; Berger, H.; Geck, J.; Kraus, R.; Pjerov, S.; Shen, Y.; et al. Femtosecond time-resolved MeV electron diffraction. New J. Phys. 2015, 17, 063004. [Google Scholar] [CrossRef]
- Manz, S.; Casandruc, A.; Zhang, D.; Zhong, Y.; Loch, R.A.; Marx, A.; Hasegawa, T.; Liu, L.C.; Bayesteh, S.; Delsim-Hashemi, H.; et al. Mapping atomic motions with ultrabright electrons: Towards fundamental limits in space-time resolution. Faraday Discuss. 2015, 177, 467–491. [Google Scholar] [CrossRef] [PubMed]
- Filippetto, D.; Qian, H. Design of a high-flux instrument for ultrafast electron diffraction and microscopy. J. Phys. At. Mol. Opt. Phys. 2016, 49, 104003. [Google Scholar] [CrossRef]
- Van Oudheusden, T.; De Jong, E.; Van der Geer, S.; ’t Root, W.O.; Luiten, O.; Siwick, B. Electron source concept for single-shot sub-100 fs electron diffraction in the 100 keV range. J. Appl. Phys. 2007, 102, 093501. [Google Scholar] [CrossRef]
- Van Oudheusden, T.; Pasmans, P.; Van Der Geer, S.; De Loos, M.; Van Der Wiel, M.; Luiten, O. Compression of subrelativistic space-charge-dominated electron bunches for single-shot femtosecond electron diffraction. Phys. Rev. Lett. 2010, 105, 264801. [Google Scholar] [CrossRef] [PubMed]
- Maxson, J.; Cesar, D.; Calmasini, G.; Ody, A.; Musumeci, P.; Alesini, D. Direct measurement of sub-10 fs relativistic electron beams with ultralow emittance. Phys. Rev. Lett. 2017, 118, 154802. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Wang, Z.; Lu, C.; Wang, R.; Hu, C.; Wang, P.; Qi, J.; Jiang, T.; Liu, S.; Ma, Z.; et al. Terahertz streaking of few-femtosecond relativistic electron beams. Phys. Rev. X 2018, 8, 021061. [Google Scholar] [CrossRef]
- Snively, E.; Othman, M.; Kozina, M.; Ofori-Okai, B.; Weathersby, S.; Park, S.; Shen, X.; Wang, X.; Hoffmann, M.; Li, R.; et al. Femtosecond compression dynamics and timing jitter suppression in a THz-driven electron bunch compressor. Phys. Rev. Lett. 2020, 124, 054801. [Google Scholar] [CrossRef] [PubMed]
- Kealhofer, C.; Schneider, W.; Ehberger, D.; Ryabov, A.; Krausz, F.; Baum, P. All-optical control and metrology of electron pulses. Science 2016, 352, 429–433. [Google Scholar] [CrossRef]
- De Loos, M.; Van der Geer, S. General Particle Tracer: A new 3D code for accelerator and beamline design. In Proceedings of the 5th European Particle Accelerator Conference, Sitges, Barcelona, 10–14 June 1996; p. 1241. [Google Scholar]
- Floettmann, K. Generation of sub-fs electron beams at few-MeV energies. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2014, 740, 34–38. [Google Scholar] [CrossRef]
- Zeitler, B.; Floettmann, K.; Grüner, F. Linearization of the longitudinal phase space without higher harmonic field. Phys. Rev. Spec. Top.-Accel. Beams 2015, 18, 120102. [Google Scholar] [CrossRef]
- Bacci, A.; Rossi, A.R. Ultra-short electron bunches by Velocity Bunching as required for plasma wave accelerations. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2014, 740, 42–47. [Google Scholar] [CrossRef]
- Reiser, M.; O’Shea, P. Theory and Design of Charged Particle Beams; Wiley Online Library: Hoboken, NJ, USA, 1994; Volume 312. [Google Scholar] [CrossRef]
- Wiedemann, H. Particle Accelerator Physics; Springer Nature: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Zhao, L.; Tang, H.; Lu, C.; Jiang, T.; Zhu, P.; Hu, L.; Song, W.; Wang, H.; Qiu, J.; Jing, C.; et al. Femtosecond relativistic electron beam with reduced timing jitter from THz driven beam compression. Phys. Rev. Lett. 2020, 124, 054802. [Google Scholar] [CrossRef] [PubMed]
- Emma, P. X-Band RF Harmonic Compensation for Linear Bunch Compression in the LCLS; Rep. ILCLS-TN-01-1; SLAC: Stanford, CA, USA, 2001. [Google Scholar] [CrossRef][Green Version]
- Bartnik, A.; Gulliford, C.; Hoffstaetter, G.H.; Maxson, J. Ultimate bunch length and emittance performance of an MeV ultrafast electron diffraction apparatus with a dc gun and a multicavity superconducting rf linac. Phys. Rev. Accel. Beams 2022, 25, 093401. [Google Scholar] [CrossRef]
- Nanni, E.A.; Huang, W.R.; Hong, K.H.; Ravi, K.; Fallahi, A.; Moriena, G.; Miller, R.D.; Kärtner, F.X. Terahertz-driven linear electron acceleration. Nat. Commun. 2015, 6, 8486. [Google Scholar] [CrossRef] [PubMed]
- Cesar, D.; Maxson, J.; Shen, X.; Wootton, K.; Tan, S.; England, R.; Musumeci, P. Enhanced energy gain in a dielectric laser accelerator using a tilted pulse front laser. Opt. Express 2018, 26, 29216–29224. [Google Scholar] [CrossRef] [PubMed]
| Parameter | High Energy | Low Energy |
|---|---|---|
| Focal length | 1.88 m | 1 m |
| Beam kinetic energy | 4.6 MeV | 150 keV |
| Norm. transverse emittance | 100 nm | 8.3 nm |
| RMS transverse beam size | 100 μm | 100 μm |
| Cavity Frequency | 2.856 GHz | 2.856 GHz |
| Relative energy spread |
| Parameter | Value |
|---|---|
| Charge | |
| Laser Spot Size | 10 μm |
| Cathode MTE | 0.5 eV |
| Optimal laser pulse length | 0.95 ps (rms) |
| Gun Accelerating Gradient | 94.7 MV/m |
| Gun Phase | 35.5° |
| Linearizer accelerating voltage | 1.8 MV |
| Linearizer phase | 173.5° |
| Buncher accelerating voltage | 6.75 MV |
| Buncher phase | 101° |
| Final kinetic energy | 4.5 MeV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denham, P.; Musumeci, P. Analytical Scaling Laws for Radiofrequency-Based Pulse Compression in Ultrafast Electron Diffraction Beamlines. Instruments 2023, 7, 49. https://doi.org/10.3390/instruments7040049
Denham P, Musumeci P. Analytical Scaling Laws for Radiofrequency-Based Pulse Compression in Ultrafast Electron Diffraction Beamlines. Instruments. 2023; 7(4):49. https://doi.org/10.3390/instruments7040049
Chicago/Turabian StyleDenham, Paul, and Pietro Musumeci. 2023. "Analytical Scaling Laws for Radiofrequency-Based Pulse Compression in Ultrafast Electron Diffraction Beamlines" Instruments 7, no. 4: 49. https://doi.org/10.3390/instruments7040049
APA StyleDenham, P., & Musumeci, P. (2023). Analytical Scaling Laws for Radiofrequency-Based Pulse Compression in Ultrafast Electron Diffraction Beamlines. Instruments, 7(4), 49. https://doi.org/10.3390/instruments7040049







