Inkjet-Printed Interdigitated Capacitors for Sensing Applications: Temperature-Dependent Electrical Characterization at Cryogenic Temperatures down to 20 K
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Characterization
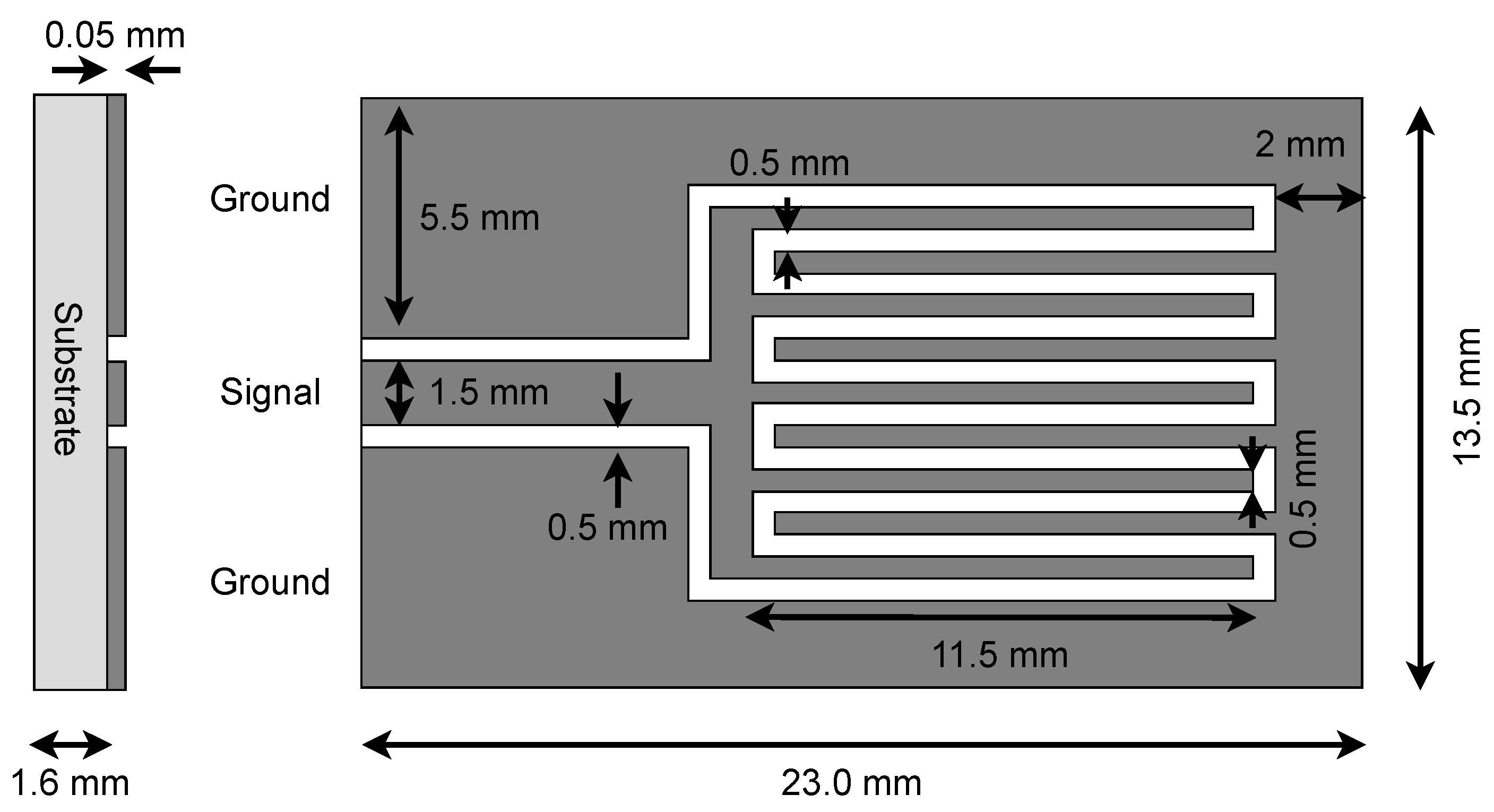
2.2. Inkjet Printed Interdigitated Capacitor: Design and Fabrication
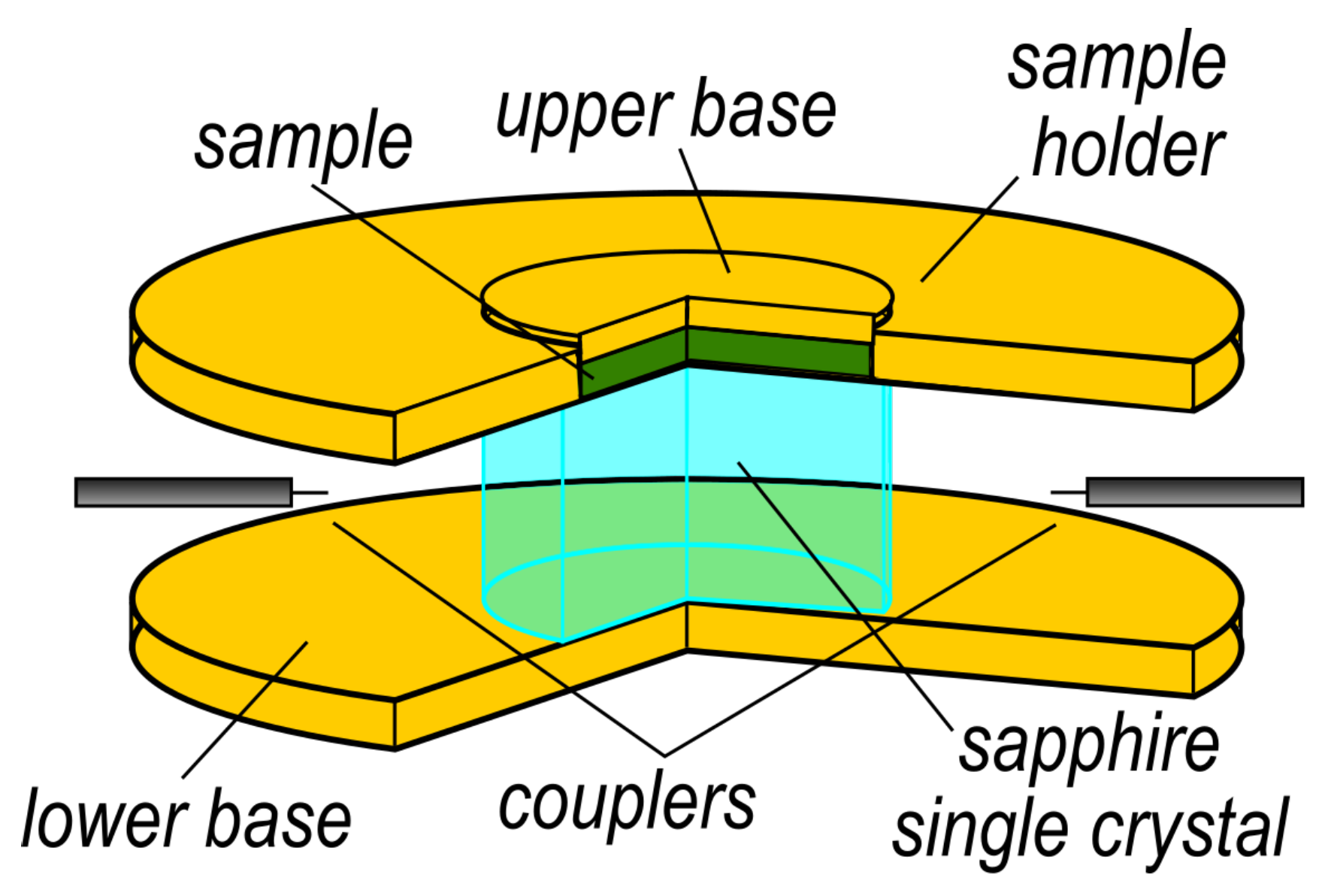
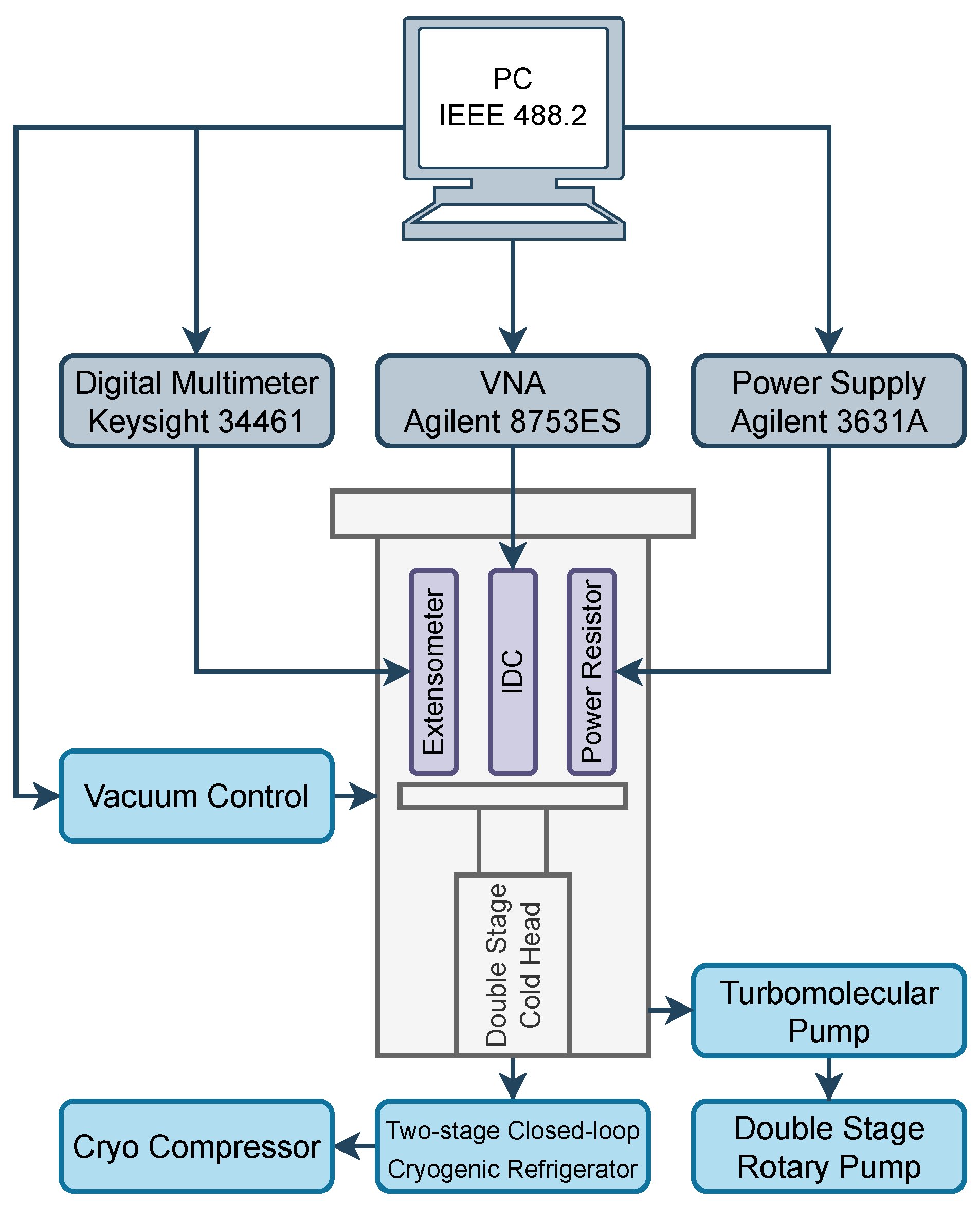
2.3. Experimental Setup
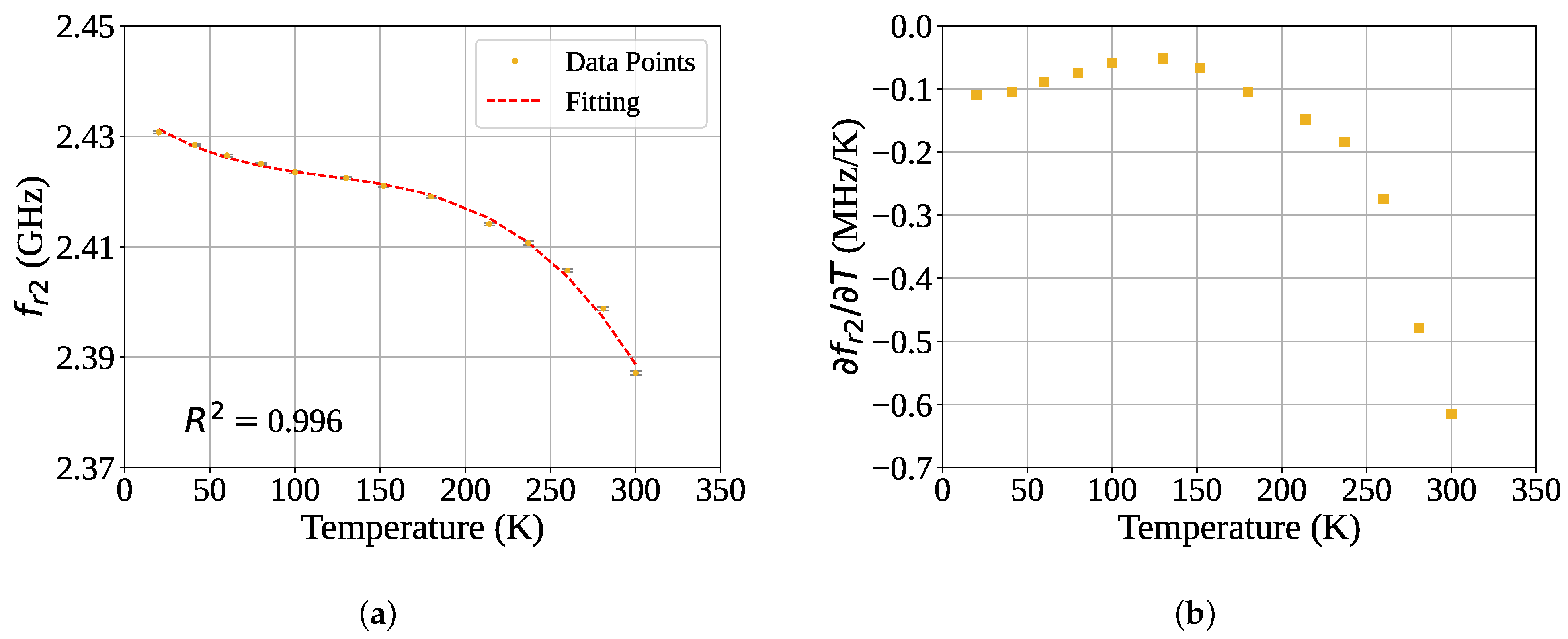
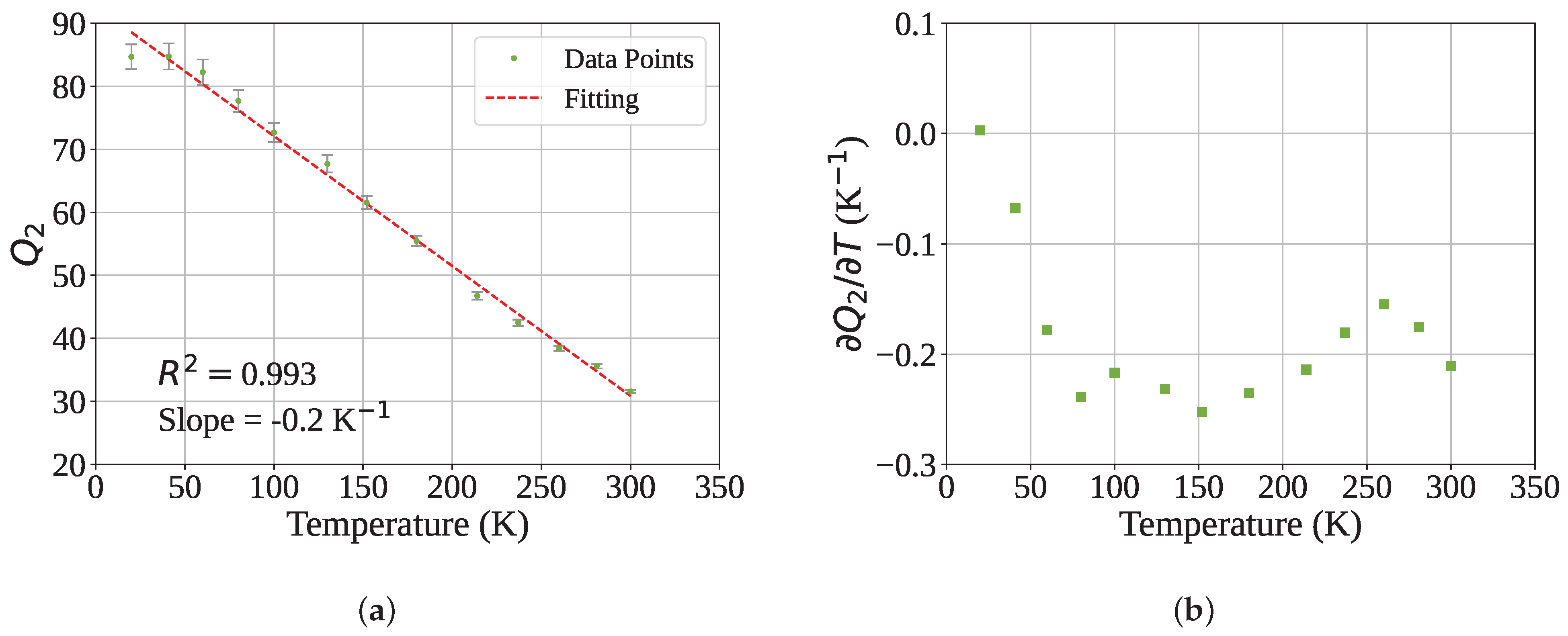
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bailly, G.; Harrabi, A.; Rossignol, J.; Michel, M.; Stuerga, D.; Pribetich, P. Microstrip spiral resonator for microwave-based gas sensing. IEEE Sens. Lett. 2017, 1, 4500404. [Google Scholar] [CrossRef]
- Gugliandolo, G.; Aloisio, D.; Campobello, G.; Crupi, G.; Donato, N. On the design and characterisation of a microwave microstrip resonator for gas sensing applications. Acta Imeko 2021, 10, 54–61. [Google Scholar] [CrossRef]
- Gugliandolo, G.; Naishadham, K.; Crupi, G.; Donato, N. Design and characterization of a microwave transducer for gas sensing applications. Chemosensors 2022, 10, 127. [Google Scholar] [CrossRef]
- Alimenti, A.; Torokhtii, K.; Pompeo, N.; Silva, E. High precision and contactless dielectric loaded resonator for room temperature surface resistance measurements at microwave frequencies. In Proceedings of the 2022 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 16–19 May 2022; pp. 1–6. [Google Scholar]
- Alimenti, A.; Torokhtii, K.; Vidal García, P.; Pompeo, N.; Silva, E. Design and Test of a New Dielectric-Loaded Resonator for the Accurate Characterization of Conductive and Dielectric Materials. Sensors 2023, 23, 518. [Google Scholar] [CrossRef] [PubMed]
- Alimenti, A.; Pittella, E.; Torokhtii, K.; Pompeo, N.; Piuzzi, E.; Silva, E. A dielectric loaded resonator for the measurement of the complex permittivity of dielectric substrates. IEEE Trans. Instrum. Meas. 2023, 72, 6001009. [Google Scholar] [CrossRef]
- Bao, X.; Ocket, I.; Crupi, G.; Schreurs, D.; Bao, J.; Kil, D.; Puers, B.; Nauwelaers, B. A planar one-port microwave microfluidic sensor for microliter liquids characterization. IEEE J. Electromagn. RF Microw. Med. Biol. 2018, 2, 10–17. [Google Scholar] [CrossRef]
- Bao, X.; Ocket, I.; Bao, J.; Liu, Z.; Puers, B.; Schreurs, D.M.P.; Nauwelaers, B. Modeling of coplanar interdigital capacitor for microwave microfluidic application. IEEE Trans. Microw. Theory Tech. 2019, 67, 2674–2683. [Google Scholar] [CrossRef]
- Crupi, G.; Bao, X.; Babarinde, O.J.; Schreurs, D.M.P.; Nauwelaers, B. Biosensor using a one-port interdigital capacitor: A resonance-based investigation of the permittivity sensitivity for microfluidic broadband bioelectronics applications. Electronics 2020, 9, 340. [Google Scholar] [CrossRef]
- Cuccaro, R.; Gavioso, R.; Benedetto, G.; Madonna Ripa, D.; Fernicola, V.; Guianvarc’h, C. Microwave determination of water mole fraction in humid gas mixtures. Int. J. Thermophys. 2012, 33, 1352–1362. [Google Scholar] [CrossRef]
- Corbellini, S.; Ramella, C.; Yu, L.; Pirola, M.; Fernicola, V. Whispering gallery mode thermometry. Sensors 2016, 16, 1814. [Google Scholar] [CrossRef]
- Gugliandolo, G.; Tabandeh, S.; Rosso, L.; Smorgon, D.; Fernicola, V. Whispering gallery mode resonators for precision temperature metrology applications. Sensors 2021, 21, 2844. [Google Scholar] [CrossRef] [PubMed]
- Gugliandolo, G.; Naishadham, K.; Crupi, G.; Campobello, G.; Donato, N. Microwave transducers for gas sensing: A challenging and promising new frontier. IEEE Instrum. Meas. Mag. 2022, 25, 42–51. [Google Scholar] [CrossRef]
- Gocen, C.; Palandoken, M. Machine Learning Assisted Novel Microwave Sensor Design for Dielectric Parameter Characterization of Water–Ethanol Mixture. IEEE Sens. J. 2021, 22, 2119–2127. [Google Scholar] [CrossRef]
- Carnerero-Cano, J.; Galindo-Romera, G.; Martínez-Martínez, J.J.; Herraiz-Martínez, F.J. A contactless dielectric constant sensing system based on a split-ring resonator-loaded monopole. IEEE Sens. J. 2018, 18, 4491–4502. [Google Scholar] [CrossRef]
- Javed, A.; Arif, A.; Zubair, M.; Mehmood, M.Q.; Riaz, K. A low-cost multiple complementary split-ring resonator-based microwave sensor for contactless dielectric characterization of liquids. IEEE Sens. J. 2020, 20, 11326–11334. [Google Scholar] [CrossRef]
- Aloisio, D.; Donato, N. Development of gas sensors on microstrip disk resonators. Procedia Eng. 2014, 87, 1083–1086. [Google Scholar] [CrossRef]
- Bogner, A.; Steiner, C.; Walter, S.; Kita, J.; Hagen, G.; Moos, R. Planar microstrip ring resonators for microwave-based gas sensing: Design aspects and initial transducers for humidity and ammonia sensing. Sensors 2017, 17, 2422. [Google Scholar] [CrossRef]
- Pittella, E.; Schiavoni, R.; Monti, G.; Masciullo, A.; Scarpetta, M.; Cataldo, A.; Piuzzi, E. Split Ring Resonator Network and Diffused Sensing Element Embedded in a Concrete Beam for Structural Health Monitoring. Sensors 2022, 22, 6398. [Google Scholar] [CrossRef]
- Tchafa, F.M.; Huang, H. Microstrip patch antenna for simultaneous strain and temperature sensing. Smart Mater. Struct. 2018, 27, 065019. [Google Scholar] [CrossRef]
- Bao, X.; Ocket, I.; Kil, D.; Bao, J.; Puers, R.; Nauwelaers, B. Liquid measurements at microliter volumes using 1-port coplanar interdigital capacitor. In Proceedings of the 2017 First IEEE MTT-S International Microwave Bio Conference (IMBIOC), Gothenburg, Sweden, 15–17 May 2017; pp. 1–4. [Google Scholar]
- Bao, X.; Ocket, I.; Bao, J.; Doijen, J.; Zheng, J.; Kil, D.; Liu, Z.; Puers, B.; Schreurs, D.; Nauwelaers, B. Broadband dielectric spectroscopy of cell cultures. IEEE Trans. Microw. Theory Tech. 2018, 66, 5750–5759. [Google Scholar] [CrossRef]
- Chehelcheraghi, M.; Franssens, V.; Ocket, I.; Nauwelaers, B. Real-Time kHz to GHz Monitoring of Incubated Yeast Cell Growth Using Interdigitated Capacitors. In Proceedings of the 2018 IEEE/MTT-S International Microwave Symposium-IMS, Philadelphia, PA, USA, 10–15 June 2018; pp. 1144–1147. [Google Scholar]
- Tesla, N. Electrical Condenser. U.S. Patent US567818A, 15 September 1896. [Google Scholar]
- Mamishev, A.V.; Sundara-Rajan, K.; Yang, F.; Du, Y.; Zahn, M. Interdigital sensors and transducers. Proc. IEEE 2004, 92, 808–845. [Google Scholar] [CrossRef]
- Love, A.E.H. Some electrostatic distributions in two dimensions. Proc. Lond. Math. Soc. 1924, 2, 337–369. [Google Scholar] [CrossRef]
- Bao, X.; Wang, Z.; Bao, J.; Gugliandolo, G.; Yuan, H.; Zhao, Z.; Li, J.; Donato, N.; Crupi, G.; Nauwelaers, B.; et al. Salt Content Detection Using a Microwave Sensor. In Proceedings of the 2022 IEEE International Workshop on Metrology for the Sea; Learning to Measure Sea Health Parameters (MetroSea), Milazzo, Italy, 3–5 October 2022; pp. 479–483. [Google Scholar]
- Bao, X.; Crupi, G.; Ocket, I.; Bao, J.; Ceyssens, F.; Kraft, M.; Nauwelaers, B.; Schreurs, D. Numerical modeling of two microwave sensors for biomedical applications. Int. J. Numer. Model. Electron. Netw. Devices Fields 2021, 34, e2810. [Google Scholar] [CrossRef]
- Wang, R.; Sun, H.; Jing, S.z.; Fan, Y. A Conformal Microwave Biosensor for Detecting Blood Viscosity. In Proceedings of the 2021 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Chongqing, China, 15–17 November 2021; pp. 25–27. [Google Scholar]
- Bailly, G.; Harrabi, A.; Rossignol, J.; Stuerga, D.; Pribetich, P. Microwave gas sensing with a microstrip interDigital capacitor: Detection of NH3 with TiO2 nanoparticles. Sens. Actuators B Chem. 2016, 236, 554–564. [Google Scholar] [CrossRef]
- Chen, W.; Stewart, K.; Mansour, R.; Penlidis, A. Novel undercoupled radio-frequency (RF) resonant sensor for gaseous ethanol and interferents detection. Sens. Actuators A Phys. 2015, 230, 63–73. [Google Scholar] [CrossRef]
- Yan, K.; Li, J.; Pan, L.; Shi, Y. Inkjet printing for flexible and wearable electronics. APL Mater. 2020, 8, 120705. [Google Scholar] [CrossRef]
- Gugliandolo, G.; Alimenti, A.; Torokhtii, K.; Pompeo, N.; Campobello, G.; Crupi, G.; Silva, E.; Donato, N. Design and test of an inkjet-printed microwave interdigital capacitor on flexible Kapton substrate. In Proceedings of the 2022 IMEKO TC4 Symposium, Brescia, Italy, 12–14 September 2022. [Google Scholar]
- Lee, H.; Shaker, G.; Naishadham, K.; Song, X.; McKinley, M.; Wagner, B.; Tentzeris, M. Carbon-nanotube loaded antenna-based ammonia gas sensor. IEEE Trans. Microw. Theory Tech. 2011, 59, 2665–2673. [Google Scholar] [CrossRef]
- Gugliandolo, G.; Vermiglio, G.; Cutroneo, G.; Campobello, G.; Crupi, G.; Donato, N. Inkjet-printed capacitive coupled ring resonators aimed at the characterization of cell cultures. In Proceedings of the 2022 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Messina, Italy, 22–24 June 2022; pp. 1–5. [Google Scholar]
- Merilampi, S.L.; Virkki, J.; Ukkonen, L.; Sydänheimo, L. Testing the effects of temperature and humidity on printed passive UHF RFID tags on paper substrate. Int. J. Electron. 2014, 101, 711–730. [Google Scholar] [CrossRef]
- Voltera. Voltera Conductor 2 (1000388); Datasheet: Waterloo, ON, Canada, 2020. [Google Scholar]
- Koledintseva, M.Y.; Drewniak, J.L.; Hinaga, S. Effect of anisotropy on extracted dielectric properties of PCB laminate dielectrics. In Proceedings of the 2011 IEEE International Symposium on Electromagnetic Compatibility, Long Beach, CA, USA, 14–19 August 2011; pp. 514–517. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; American Association of Physics Teachers: Hoboken, NJ, USA, 1999. [Google Scholar]
- Chen, L.F.; Ong, C.; Neo, C.; Varadan, V.; Varadan, V.K. Microwave Electronics: Measurement and Materials Characterization; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Hsu, Y.W.; Shen, S.J.; Chen, C.A.; Qiu, S.H.; Chen, H.H. Broadband Measurement of Dielectric Constant on FR-4 PCB by Using Discontinuous Microstrip Lines. In Proceedings of the 2021 International Symposium on Antennas and Propagation (ISAP), Taipei, Taiwan, 19–22 October 2021; pp. 1–2. [Google Scholar]
- Alimenti, A.; Torokhtii, K.; Pompeo, N.; Piuzzi, E.; Silva, E. Characterisation of dielectric 3D-printing materials at microwave frequencies. Acta Imeko 2020, 9, 26–32. [Google Scholar] [CrossRef]
- Torokhtii, K.; Pompeo, N.; Silva, E.; Alimenti, A. Optimization of Q-factor and resonance frequency measurements in partially calibrated resonant systems. Meas. Sens. 2021, 18, 100314. [Google Scholar] [CrossRef]
- Djordjevic, A.R.; Biljié, R.M.; Likar-Smiljanic, V.D.; Sarkar, T.K. Wideband frequency-domain characterization of FR-4 and time-domain causality. IEEE Trans. Electromagn. Compat. 2001, 43, 662–667. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology. JCGM 101: Evaluation of Measurement Data—Supplement 1 to the Guide to the Expression of Uncertainty in Measurement—Propagation of Distributions Using a Monte Carlo Method; Technical Report; JCGM: Sèvres, France, 2008. [Google Scholar]
- Joint Committee for Guides in Metrology. JCGM 100: Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; Technical Report; JCGM: Sèvres, France, 2008. [Google Scholar]
- Wang, C.; Ali, L.; Meng, F.Y.; Adhikari, K.K.; Zhou, Z.L.; Wei, Y.C.; Zou, D.Q.; Yu, H. High-accuracy complex permittivity characterization of solid materials using parallel interdigital capacitor-based planar microwave sensor. IEEE Sens. J. 2020, 21, 6083–6093. [Google Scholar] [CrossRef]
- Voltera. Questions about Our Products? 2022. Available online: https://www.voltera.io/faq (accessed on 4 May 2023).
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Pompeo, N.; Torokhtii, K.; Leccese, F.; Scorza, A.; Sciuto, S.; Silva, E. Fitting strategy of resonance curves from microwave resonators with non-idealities. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Torino, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar]
- Yan, D.; Yang, Y.; Hong, Y.; Liang, T.; Yao, Z.; Chen, X.; Xiong, J. Low-cost wireless temperature measurement: Design, manufacture, and testing of a PCB-based wireless passive temperature sensor. Sensors 2018, 18, 532. [Google Scholar] [CrossRef] [PubMed]
- Mekimah, B.; Messai, A.; Belhedri, A. Analysis of the effect of dielectric losses on the bandwidth of microstrip patch antenna in stacked geometry and modelling. SN Appl. Sci. 2020, 2, 767. [Google Scholar] [CrossRef]







| Property | Value |
|---|---|
| Sheet Resistance (50 µm film thickness) | 2.05 mΩ/sq |
| Resistivity (4-point-probe) | Ω·m |
| Typical cured film thickness | 50 µm |
| Density | 3.35 g/mL |
| Trace spread after print | <20% |
| Recommended Nozzle ID | 150–225 µm |
| Typical Line Width | 150–100 µm |
| Typical Print height | 50–100 µm |
| Typical Feedrate | 300–500 mm/min |
| Typical Kick | 0.35 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gugliandolo, G.; Alimenti, A.; Latino, M.; Crupi, G.; Torokhtii, K.; Silva, E.; Donato, N. Inkjet-Printed Interdigitated Capacitors for Sensing Applications: Temperature-Dependent Electrical Characterization at Cryogenic Temperatures down to 20 K. Instruments 2023, 7, 20. https://doi.org/10.3390/instruments7030020
Gugliandolo G, Alimenti A, Latino M, Crupi G, Torokhtii K, Silva E, Donato N. Inkjet-Printed Interdigitated Capacitors for Sensing Applications: Temperature-Dependent Electrical Characterization at Cryogenic Temperatures down to 20 K. Instruments. 2023; 7(3):20. https://doi.org/10.3390/instruments7030020
Chicago/Turabian StyleGugliandolo, Giovanni, Andrea Alimenti, Mariangela Latino, Giovanni Crupi, Kostiantyn Torokhtii, Enrico Silva, and Nicola Donato. 2023. "Inkjet-Printed Interdigitated Capacitors for Sensing Applications: Temperature-Dependent Electrical Characterization at Cryogenic Temperatures down to 20 K" Instruments 7, no. 3: 20. https://doi.org/10.3390/instruments7030020
APA StyleGugliandolo, G., Alimenti, A., Latino, M., Crupi, G., Torokhtii, K., Silva, E., & Donato, N. (2023). Inkjet-Printed Interdigitated Capacitors for Sensing Applications: Temperature-Dependent Electrical Characterization at Cryogenic Temperatures down to 20 K. Instruments, 7(3), 20. https://doi.org/10.3390/instruments7030020









