Polarimetry for 3He Ion Beams from Laser–Plasma Interactions
Abstract
1. Introduction
2. Polarimeter Design
2.1. Properties of Laser-Driven He Beams
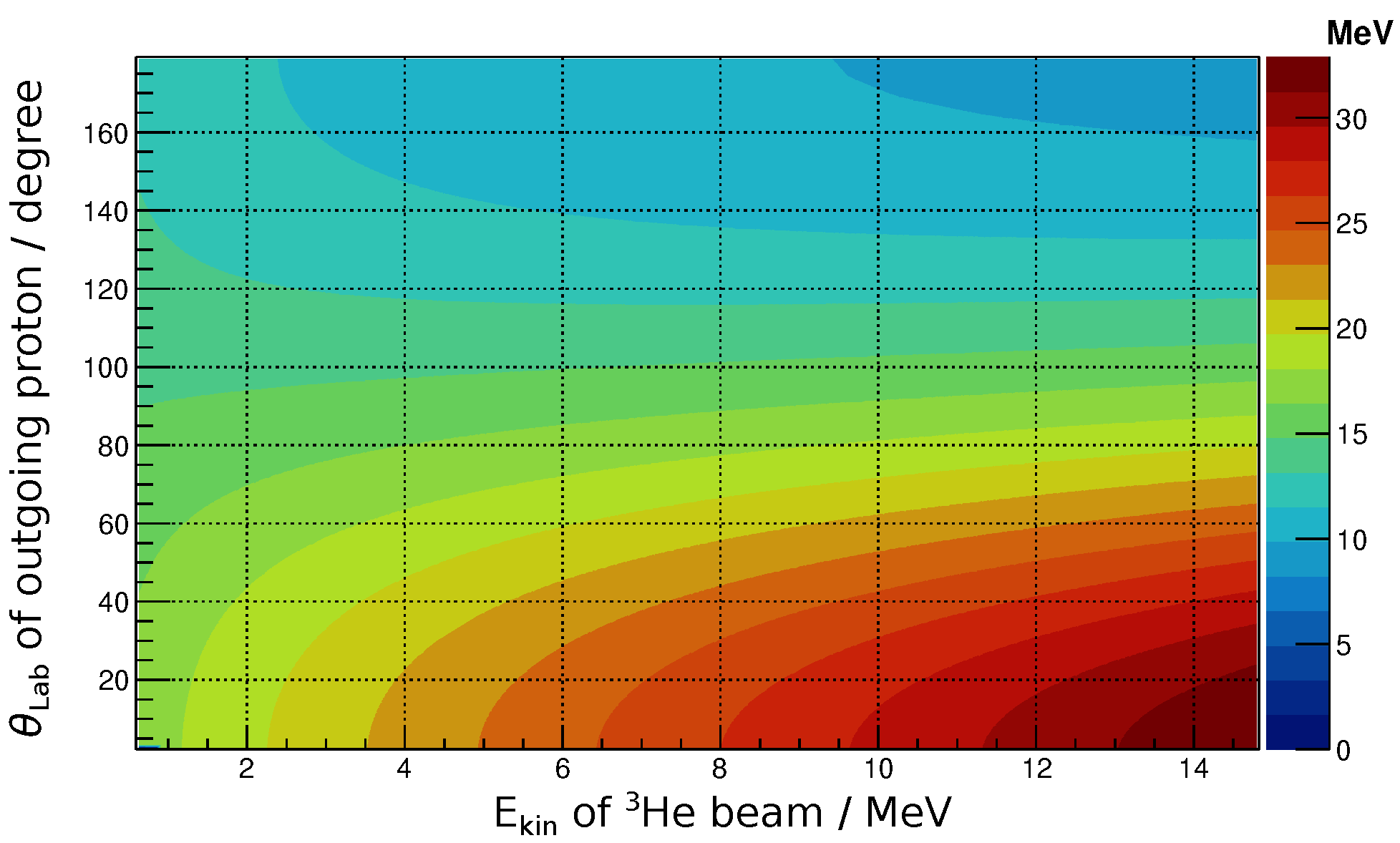
2.2. Analyzing Power of the d-He Fusion Reaction
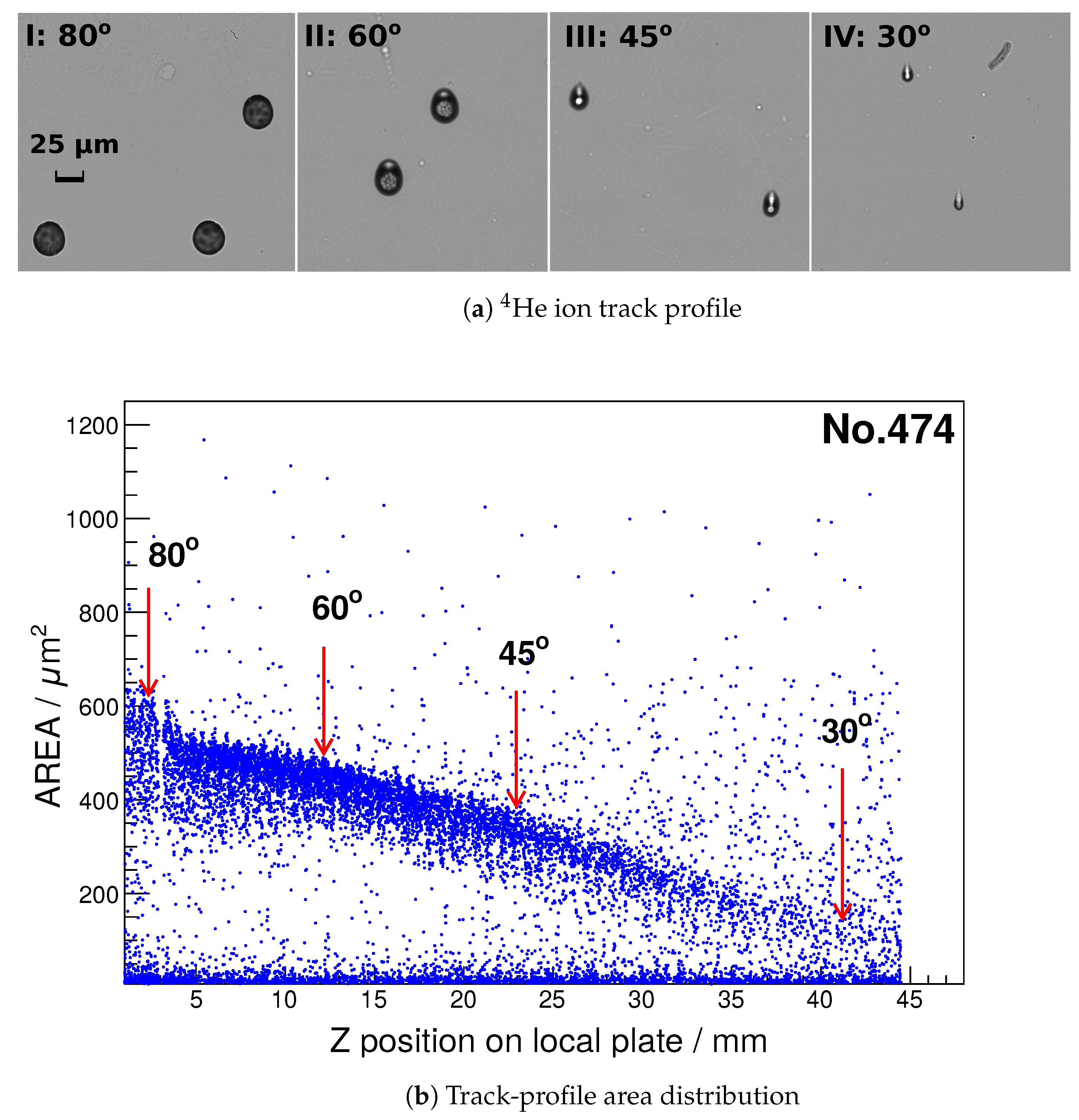
2.3. Particle Identification: Proton or Particle
2.4. Deuterated Foil-Target Production
3. Beam Test at a Tandetron
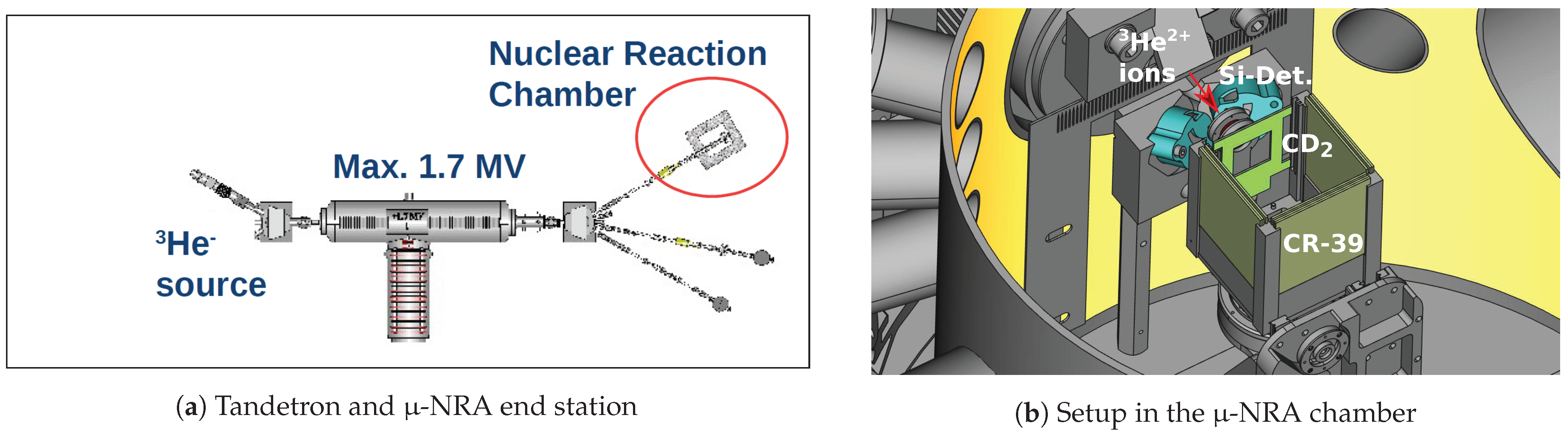
3.1. Experimental Setup
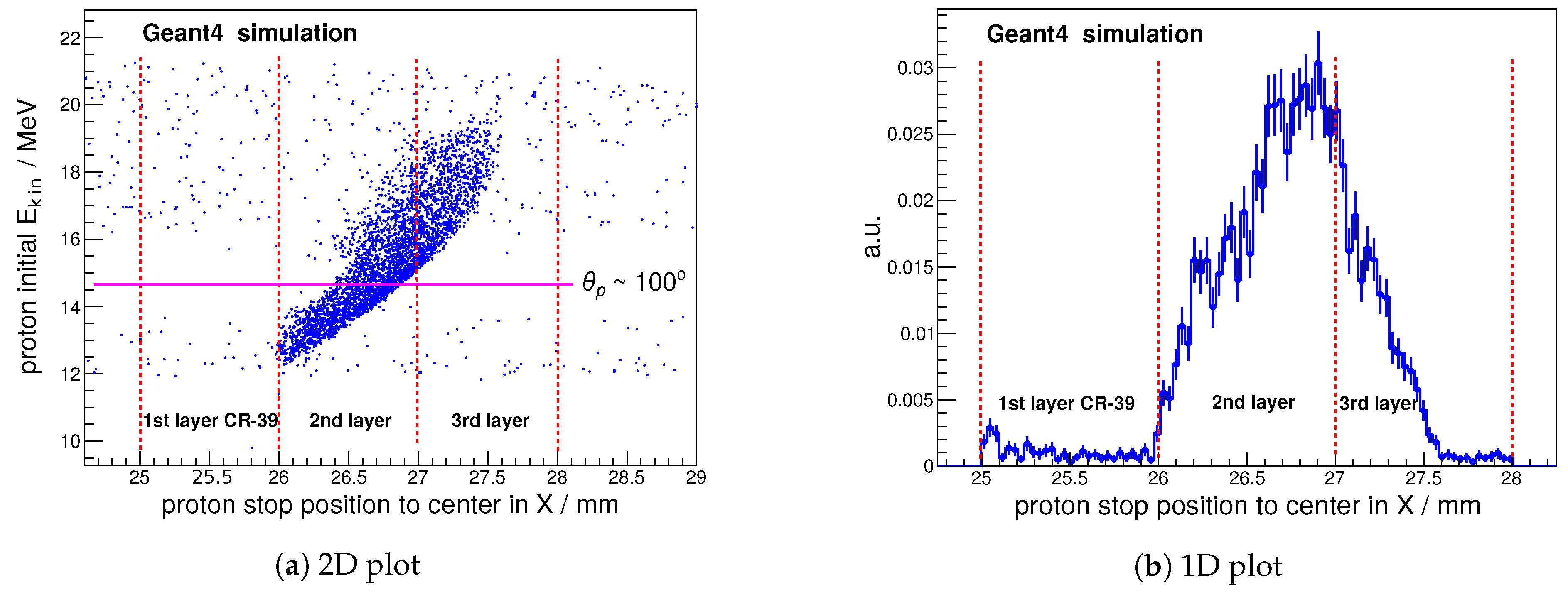
3.2. Track Profiles and Background Suppression
3.3. Left-Right Comparison and Asymmetry Criterion
3.4. Beam Monitor in Forward Direction
4. Discussion
4.1. Precision of Polarimetry and Statistics Requirement
4.2. Figure of Merit (FOM): Evaluation of Polarimetry
4.3. Accuracy Estimates
5. Conclusions & Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Assmann, R.W.; Weikum, M.K.; Akhter, T.; Alesini, D.; Alexandrova, A.S.; Anania, M.P.; Andreev, N.E.; Andriyash, I.; Artioli, M.; Aschikhin, A.; et al. EuPRAXIA conceptual design report. Eur. Phys. J. ST 2020, 229, 3675. [Google Scholar] [CrossRef]
- Mounet, N. (Ed.) European Strategy for Particle Physics—Accelerator R&D Roadmap; CERN Yellow Reports: Monographs, CERN-2022-001; CERN: Geneva, Switzerland, 2022. [Google Scholar]
- Fuchs, M.; Shadwick, B.A.; Vafaei-Najafabadi, N.; Thomas, A.G.R.; Andonian, G.; Büscher, M.; Lehrach, A.; Apsimon, O.; Xia, G.; Filippetto, D.; et al. Snowmass Whitepaper AF6: Plasma-Based Particle Sources. arXiv 2022, arXiv:2203.08379. [Google Scholar]
- Anderle, D.P.; Bertone, V.; Cao, X.; Chang, L.; Chang, N.; Chen, G.; Chen, X.; Chen, Z.; Cui, Z.; Dai, L.; et al. Electron-Ion Collider in China. Front. Phys. 2021, 16, 64701. [Google Scholar] [CrossRef]
- Ciullo, G.; Engels, R.; Büscher, M.; Vasilyev, A. (Eds.) Nuclear Fusion with Polarized Fuel; Springer Proceedings in Physics; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; Volume 187. [Google Scholar]
- Bruhaug, G.; Kish, A. The Benefits of Spin Polarization for Fusion Propulsion. arXiv 2021, arXiv:2108.01211. [Google Scholar]
- Büscher, M.; Hützen, A.; Ji, L.; Lehrach, A. Generation of polarized particle beams at relativistic laser intensities. High Power Laser Sci. Eng. 2020, 8, e36. [Google Scholar] [CrossRef]
- Jin, L.; Wen, M.; Zhang, X.; Hützen, A.; Thomas, J.; Büscher, M.; Shen, B. Spin-polarized proton beam generation from gas-jet targets by intense laser pulses. Phys. Rev. E 2020, 102, 011201. [Google Scholar] [CrossRef]
- Yan, X.; Wu, Y.; Geng, X.; Zhang, H.; Shen, B.; Ji, L. Generation of polarized proton beams with gaseous targets from CO2-laser-driven collisionless shock acceleration. Phys. Plasmas 2022, 29, 053101. [Google Scholar] [CrossRef]
- Raab, N.; Büscher, M.; Cerchez, M.; Engels, R.; Engin, L.; Gibbon, P.; Greven, P.; Holler, A.; Karmakar, A.; Lehrach, A.; et al. Polarization measurement of laser-accelerated protons. Phys. Plasmas 2014, 21, 023104. [Google Scholar] [CrossRef]
- Engin, I.; Chitgar, Z.M.; Deppert, O.; Di Lucchio, L.; Engels, R.; Fedorets, P.; Frydrych, S.; Gibbon, P.; Kleinschmidt, A.; Lehrach, A.; et al. Laser-induced acceleration of Helium ions from unpolarized gas jets. Plasma Phys. Control. Fusion 2019, 61, 115012. [Google Scholar] [CrossRef]
- Gentile, T.R.; Nacher, P.J.; Saam, B.; Walker, T.G. Optically polarized 3He. Rev. Mod. Phys. 2017, 89, 045004. [Google Scholar] [CrossRef]
- Batz, M.; Baeßler, S.; Heil, W.; Otten, E.W.; Rudersdorf, D.; Schmiedeskamp, J.; Sobolev, Y.; Wolf, M. 3He Spin Filter for Neutrons. J. Res. Natl. Inst. Stand. Technol. 2005, 110, 293–298. [Google Scholar] [CrossRef] [PubMed]
- Fedorets, P.; Zheng, C.; Engels, R.; Engin, I.; Feilbach, H.; Giesen, U.; Glückler, H.; Kannis, C.; Klehr, F.; Lennartz, M.; et al. A High-Density Polarized 3He Gas–Jet Target for Laser–Plasma Applications. Instruments 2022, 6, 18. [Google Scholar] [CrossRef]
- Bagnoud, V.; Aurand, B.; Blazevic, A.; Borneis, S.; Bruske, C.; Ecker, B.; Eisenbarth, U.; Fils, J.; Frank, A.; Gaul, E.; et al. Commissioning and early experiments of the PHELIX facility. Appl. Phys. B 2010, 100, 137–150. [Google Scholar] [CrossRef]
- Blyth, C.O.; Karban, O.; Powell, W.B.; Roman, S. Scattering of 31.5 MeV polarized 3He by protons. Nucl. Phys. A 1975, 247, 1–6. [Google Scholar] [CrossRef]
- Okumus̨oǧlu, N.T.; Blyth, C.O. A study of the 2H(3He, 4He)1H reaction with a polarized 3He beam at 27 and 33 MeV. Nucl. Phys. A 1979, 325, 45–62. [Google Scholar] [CrossRef]
- Karban, O.; Blyth, C.O.; Lui, Y.W.; Roman, S. Recoil deuteron polarimeter for a polarized 3He beam. Nucl. Instr. Meth. 1977, 141, 387–389. [Google Scholar] [CrossRef]
- McEver, W.S.; Clegg, T.B.; Joyce, J.M.; Ludwig, E.J.; Walter, R.L. An analyzer for the polarization of 3He particles. Phys. Lett. B 1970, 31, 560–562. [Google Scholar] [CrossRef]
- Hardy, D.M.; Spiger, R.J.; Baker, S.D.; Chen, Y.S.; Tombrello, T.A. Polarization in 3He + 4He elastic scattering. Phys. Lett. B 1970, 31, 355–357. [Google Scholar] [CrossRef]
- Boykin, W.R.; Baker, S.D.; Hardy, D.M. Scattering of 3He and 4He from polarized 3He between 4 and 10 MeV. Nucl. Phys. A 1972, 195, 241–249. [Google Scholar] [CrossRef]
- Atoian, G.; Zelenski, A.; Poblaguev, A.A. Precision absolute polarimeter development for the 3He++ ion beam at 5.0-6.0 MeV energy. Proc. Sci. (PoS) 2020, PSTP2019, 45. [Google Scholar]
- Bolton, P.R.; Borghesi, M.; Brenner, C.; Carroll, D.C.; De Martinis, C.; Fiorini, F.; Flacco, A.; Floquet, V.; Fuchs, J.; Gallegos, P.; et al. Instrumentation for diagnostics and control of laser-accelerated proton (ion) beams. Phys. Med. 2014, 30, 255–270. [Google Scholar] [CrossRef]
- Nurushev, S.B.; Runtso, M.F.; Strikhanov, M.N. Introduction to Polarization Physics, Chapter 8 Beam Polarimetry; Lecture Notes in Physics; Moskovski Inzhenerno-Fisitscheski Institute: Moscow, Russia, 2013; Volume 859. [Google Scholar]
- Holler, A. Machbarkeitsstudie einer polarisierten 3He-Ionenquelle mit Hilfe laserinduzierter Teichenbeschleunigung. Ph.D. Thesis, Universität zu Köln, Köln, Germany, 2014. [Google Scholar]
- Brun, R.; Rademakers, F. ROOT—An object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res. A 1997, 389, 81–86. [Google Scholar] [CrossRef]
- Rohrer, U.; Huber, P.; Leemann, C. Das Analysatorvermögen der (d,p)4He-Reaktion für Targetpolarisation im Energiegebiet von 300 keV bis 2,5 MeV. Helv. Phys. Acta 1971, 44, 846–865. [Google Scholar]
- Watt, B.E.; Leland, W.T. 3He(d, p)4He reaction proton asymmetry using a polarized 3He gas target. Phys. Rev. C 1971, 2, 1680–1681. [Google Scholar] [CrossRef]
- Guo, S.; Chen, B.; Durrani, S.A. Chapter 4 Solid-State Nuclear Track Detectors. In Handbook of Radioactivity Analysis; Elsevier Science: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Fleischer, R.L.; Price, P.B.; Walker, R.M. Nuclear Tracks in Solids: Principles and Applications; University of California Press: Berkeley, CA, USA, 1975. [Google Scholar]
- Gaillard, S.; Fuchs, J.; Renard-Le Galloudec, N.; Cowan, T.E. Study of saturation of CR39 nuclear track detectors at high ion fluence and of associated artifact patterns. Rev. Sci. Instrum. 2007, 78, 013304. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D. CR-39 Plastic Nuclear Track Detectors in Physics Research; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2012. [Google Scholar]
- Price, P.B.; Fleischer, R.L. Identification of energetic heavy nuclei with solid dielectric track detectors: Application to astrophysical and planetary studies. Annu. Rev. Nucl. Sci. 1971, 21, 295–334. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.J.N.I.; et al. Recent developments in GEANT4. Nucl. Instrum. Methods Phys. Res. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Mendenhall, M.H.; Weller, R.A. A probability-conserving cross-section biasing mechanism for variance reduction in Monte Carlo particle transport calculations. Nucl. Instrum. Methods Phys. Res. A 2012, 667, 38–43. [Google Scholar] [CrossRef]
- SIGMA-ALDRICH. Product Name: Poly(ethylene-d4)—98% Atom D, Product Number: 487007. 2021. Available online: www.sigmaaldrich.com (accessed on 10 August 2022).
- Bartle, C.M.; Meyer, H.O. Improved technique for the preparation of thin deuterated-polyethylene targets. Nucl. Instr. Meth. 1973, 112, 615. [Google Scholar] [CrossRef]
- Bartle, C.M. Improved technique for the preparation of deuterated-polyethylene targets. Nucl. Instr. Meth. 1977, 144, 599. [Google Scholar] [CrossRef]
- Braski, D.N. A study of various parting agents for producing self-supporting thin films. Nucl. Instr. Meth. 1972, 102, 553–566. [Google Scholar] [CrossRef]
- Yang, Y.Z.; (Department of Macromolecular Science, Fudan University, Shanghai, China). Private communication, 2020.
- Berger, S.; Dworschak, F. Status report of a 1.7 MV Tandem accelerator for solid state research. Nucl. Instrum. Methods Phys. Res. A 1986, 244, 48–49. [Google Scholar] [CrossRef]
- Mayer, M.; Möller, S.; Rubel, M.; Widdowson, A.; Charisopoulos, S.; Ahlgren, T.; Alves, E.; Apostolopoulos, G.; Barradas, N.P.; Donnelly, S.; et al. Ion beam analysis of fusion plasma-facing materials and components: Facilities and research challenges. Nucl. Fusion 2020, 60, 025001. [Google Scholar] [CrossRef]
- Aachen Ion Beam Technology. Available online: https://aachen-ion-beams.com/END-STATIONS/ (accessed on 10 August 2022).
- Brune, C.R.; Geist, W.H.; Karwowski, H.J.; Ludwig, E.J. Measurements of the 3He(d, p)4He reaction at low energies. Triangle Univ. Nuclear Lab. (TUNL) Annu. Rep. 1997, 36, 49. [Google Scholar]
- Fews, A.P. Flexible analysis of etched nuclear particle tracks. Nucl. Instrum. Methods Phys. Res. B 1992, 72, 91–103. [Google Scholar] [CrossRef]
- Fews, A.P. Fully automated image analysis of etched tracks in CR-39. Nucl. Instrum. Methods Phys. Res. B 1992, 71, 465–478. [Google Scholar] [CrossRef]
- Fews, A.P.; Norreys, P.A.; Beg, F.N.; Bell, A.R.; Dangor, A.E.; Danson, C.N.; Lee, P.; Rose, S.J. Plasma ion emission from high intensity picosecond laser pulse interactions with solid targets. Phys. Rev. Lett. 1994, 26, 1801–1804. [Google Scholar] [CrossRef]
- Track Analysis Systems Ltd (TASL). Available online: https://www.tasl.co.uk (accessed on 10 August 2022).
- Russ, J.C.; Neal, F.B. Chapter 10 Feature Measurements and Chapter 11 Characterizing Shape. In The Image Processing Handbook, 7th ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Büscher, M.; Adam, R.; Tusche, C.; Hützen, A.; Wiemann, C.; Chen, Y.-J.; Schneider, C.M. JuSPARC—The Jülich Short-Pulsed Particle and Radiation Center. J. Large Scale Res. Fac. 2020, 6, A138. [Google Scholar] [CrossRef]









| Reaction | FOM | ||
|---|---|---|---|
| (mb/sr) | (mb/sr) | ||
| d-He fusion reaction | |||
| E(He) at 0.64 MeV | 3.9% | 60 | 0.1 |
| at 55 | |||
| d-He fusion reaction | |||
| E(He) at 12 MeV | 50% | 5 | 1.3 |
| at 55 | |||
| He-He elastic scattering | |||
| E(He) at 5.4 MeV | 97% | 80 | 75 |
| at 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, C.; Fedorets, P.; Engels, R.; Kannis, C.; Engin, I.; Möller, S.; Swaczyna, R.; Feilbach, H.; Glückler, H.; Lennartz, M.; et al. Polarimetry for 3He Ion Beams from Laser–Plasma Interactions. Instruments 2022, 6, 61. https://doi.org/10.3390/instruments6040061
Zheng C, Fedorets P, Engels R, Kannis C, Engin I, Möller S, Swaczyna R, Feilbach H, Glückler H, Lennartz M, et al. Polarimetry for 3He Ion Beams from Laser–Plasma Interactions. Instruments. 2022; 6(4):61. https://doi.org/10.3390/instruments6040061
Chicago/Turabian StyleZheng, Chuan, Pavel Fedorets, Ralf Engels, Chrysovalantis Kannis, Ilhan Engin, Sören Möller, Robert Swaczyna, Herbert Feilbach, Harald Glückler, Manfred Lennartz, and et al. 2022. "Polarimetry for 3He Ion Beams from Laser–Plasma Interactions" Instruments 6, no. 4: 61. https://doi.org/10.3390/instruments6040061
APA StyleZheng, C., Fedorets, P., Engels, R., Kannis, C., Engin, I., Möller, S., Swaczyna, R., Feilbach, H., Glückler, H., Lennartz, M., Pfeifer, H., Pfennings, J., Schneider, C. M., Schnitzler, N., Soltner, H., & Büscher, M. (2022). Polarimetry for 3He Ion Beams from Laser–Plasma Interactions. Instruments, 6(4), 61. https://doi.org/10.3390/instruments6040061








