Electron Diagnostics for Extreme High Brightness Nano-Blade Field Emission Cathodes
Abstract
1. Introduction
2. Materials and Methods
2.1. Detectors
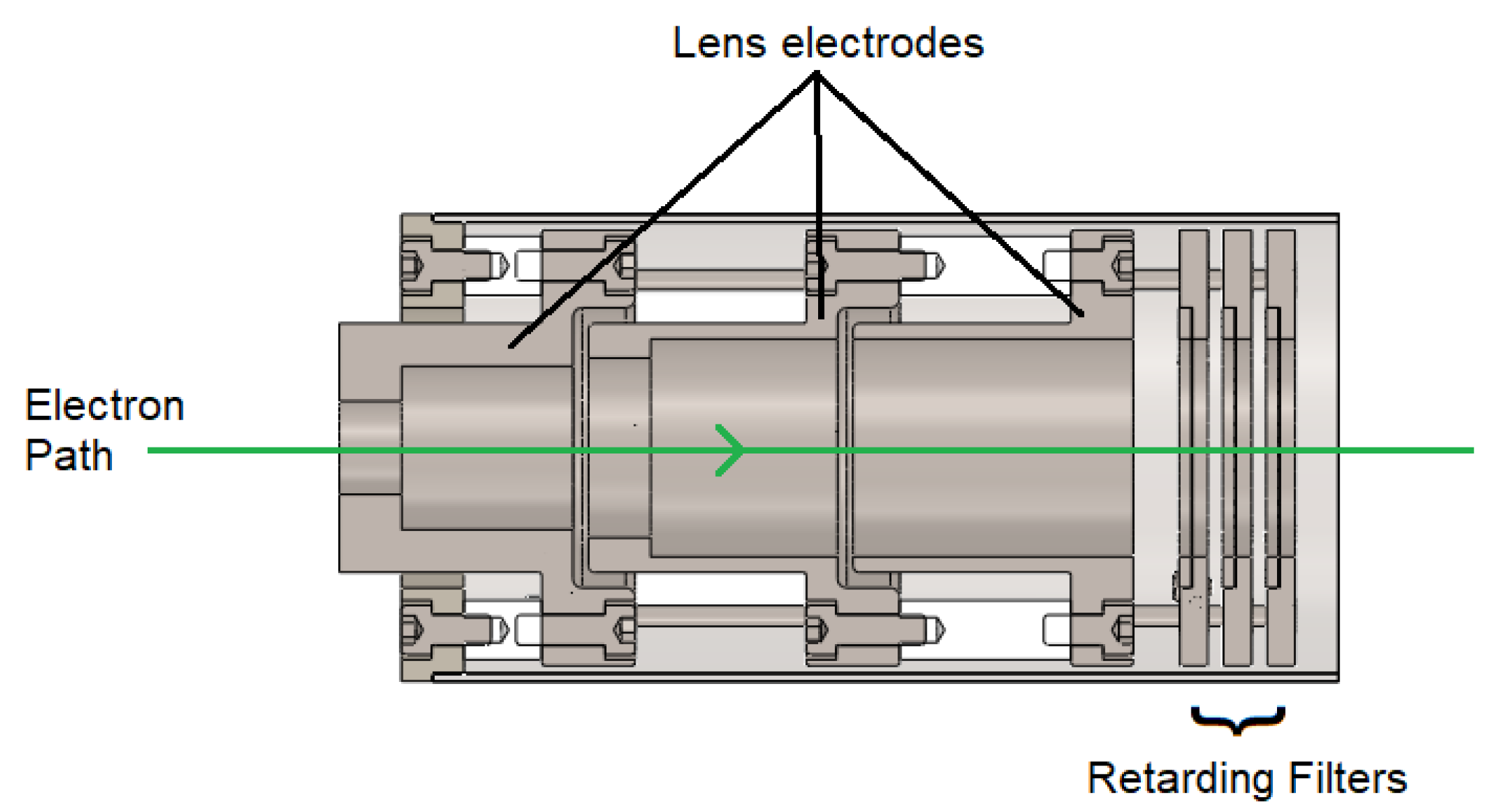
2.2. Einzel Lens
Filtering Apparatus
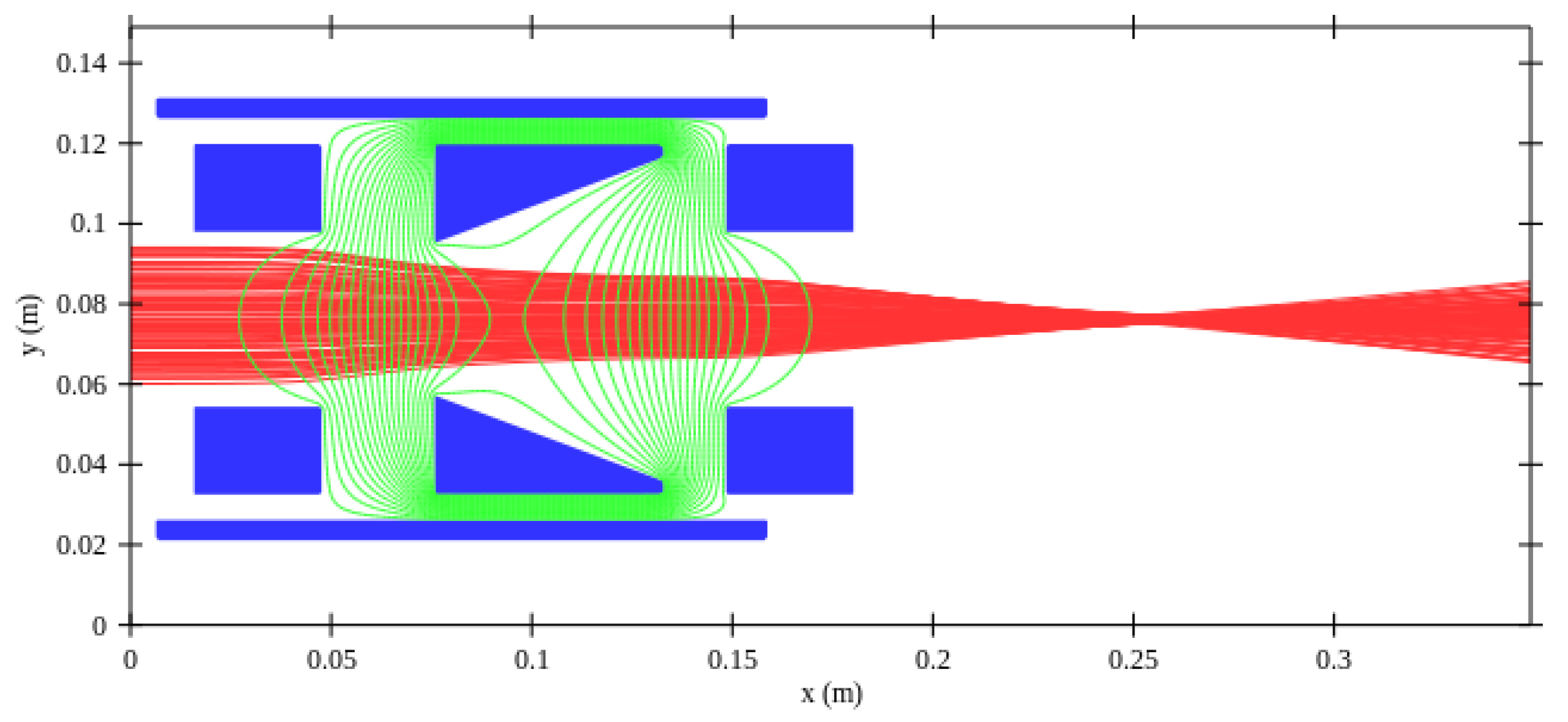
2.3. Hemispherical Deflection Analyzer
2.4. Simulation
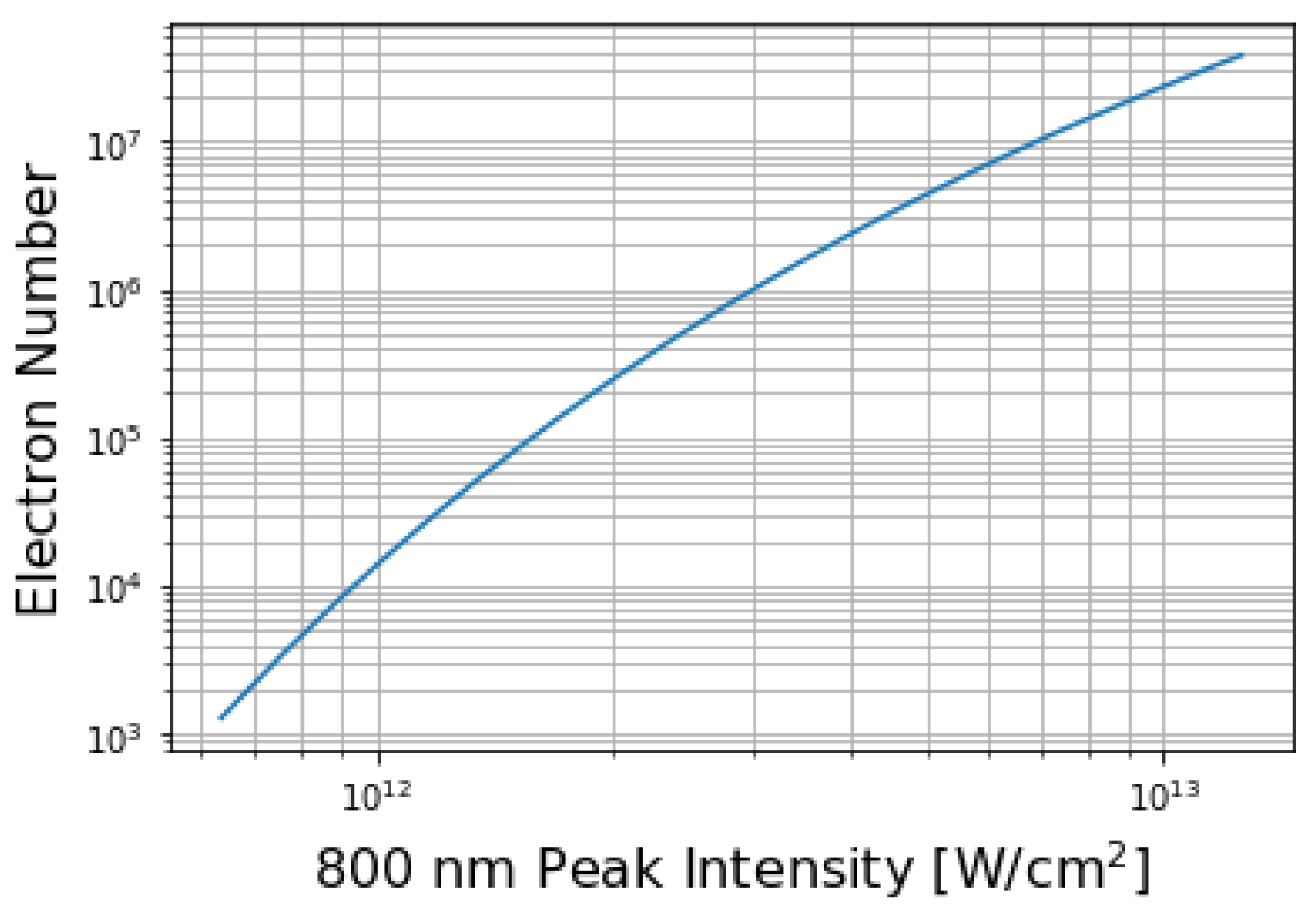
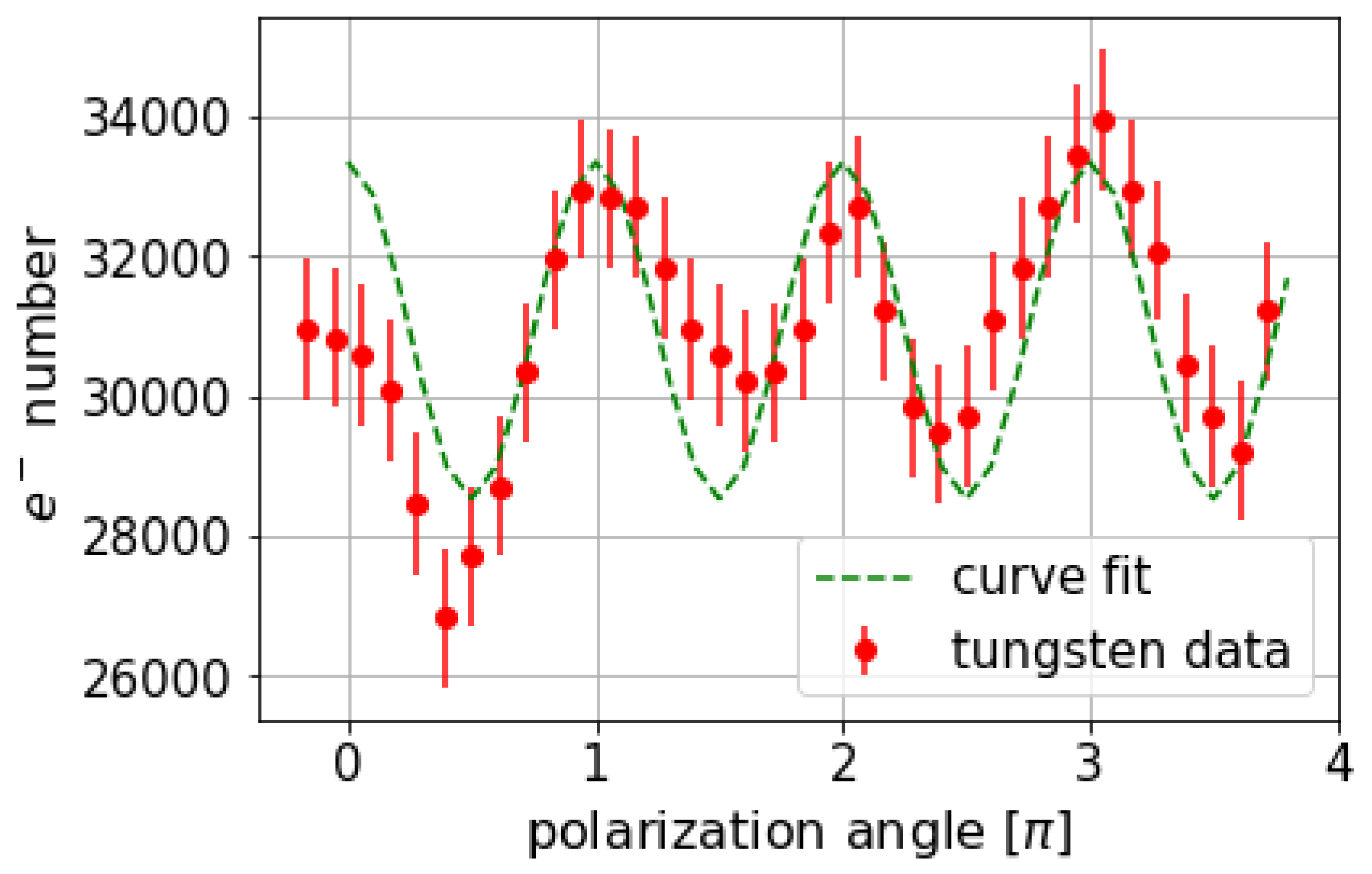
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Polman, A.; Kociak, M.; Javier García de Abajo, F. Electron-beam spectroscopy for nanophotonics. Nat. Mater. 2019. [Google Scholar] [CrossRef] [PubMed]
- McCord, M.A.; Rooks, M.J. SPIE Handbook of Microlithography, Micromachining and Microfabrication; SPIE: Bellingham, WA, USA, 2000. [Google Scholar]
- Couprie, M.E. New generation of light sources: Present and future. J. Electron Spectrosc. Relat. Phenom. 2014, 196, 3–13. [Google Scholar] [CrossRef]
- Cultrera, L.; Gulliford, C.; Bartnik, A.; Lee, H.; Bazarov, I. Ultra low emittance electron beams from multi-alkali antimonide photocathode operated with infrared light. Appl. Phys. Lett. 2016, 108, 134105. [Google Scholar] [CrossRef]
- Matsuba, S.; Honda, Y.; Jin, X.; Miyajima, T.; Yamamoto, M.; Uchiyama, T.; Kuwahara, M.; Takeda, Y. Mean Transverse Energy Measurement of Negative Electron Affinity GaAs-Based Photocathode. Jpn. J. Appl. Phys. 2012, 51, 046402. [Google Scholar] [CrossRef]
- Rao, A.V.N.; Swarnalatha, V.; Pal, P. Etching characteristics of Si110 in 20 wt% KOH with addition of hydroxylamine for the fabrication of bulk micromachined MEMS. Micro Nano Syst. Lett. 2017, 5, 23. [Google Scholar] [CrossRef]
- Ciappina, M.F.; Pérez-Hernández, J.A.; Shaaran, T.; Lewenstein, M.; Krüger, M.; Hommelhoff, P. High-order-harmonic generation driven by metal nanotip photoemission: Theory and simulations. Phys. Rev. A 2014, 89, 013409. [Google Scholar] [CrossRef]
- Pal, P.; Singh, S. A New Model for the Etching Characteristics of Corners Formed by Si111 Planes on Si110 Wafer Surface. Engineering 2013, 5, 1–8. [Google Scholar] [CrossRef]
- Wu, A.C.; Mes, K.H.; Tigner, M.; Zimmermann, F. Contemporary Physics. In Handbook of Accelerator Physics and Engineering, 2nd ed.; World Scientific Publishing: Singapore, 1980; pp. 394–395. [Google Scholar]
- Lucier, A.S. Preparation and Characterization of Tungsten Tips Suitable for Molecular Electronics Studies. Master’s Thesis, McGill University, Montreal, QC, USA, 2004. [Google Scholar]
- Wang, J.W. RF Properties of Periodic Accelerating Structures for Linear Colliders. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1989. [Google Scholar]
- Herr, W. CERN-2014-009. In Proceedings of the CAS-CERN Accelerator School: Advanced Accelerator Physics, Trondheim, Norway, 19–29 August 2013. [Google Scholar]
- Wachter, G. Simulation of Condensed Matter Dynamics in Strong Femtosecond Laser Pulses. Ph.D. Thesis, Technical University of Vienna, Wien, Austria, 2012. [Google Scholar]
- Wiza, J.L. Microchannel Plate Detectors. Nuclear Instrum. Methods 1979, 162, 587–601. [Google Scholar] [CrossRef]
- Roy, D.; Tremblay, D. Design of electron spectrometers. Rep. Prog. Phys. 1990, 53, 1621. [Google Scholar] [CrossRef]
- Paschen, T.; Roussel, R.; Heide, C.; Dienstbier, P.; Mann, J.; Seiffert, L.; Fennel, T.; Rosenzweig, J.; Hommelhoff, P. Strong-field photoemission from a nanometric blade structure. Phys. Rev. X 2019. under review. [Google Scholar]
- Nishigaki, S.; Kanai, S. Optimization of the Herzog correction in the hemispherical deflector analyzer. Rev. Sci. Instrum. 1968, 57, 225. [Google Scholar] [CrossRef]
- Jost, K. Fringing field correction for 127 degrees and 180 degrees electron spectrometers. J. Phys. E Sci. Instrum. 1979, 12, 1001. [Google Scholar] [CrossRef]
- Sise, O.; Zouros, T.J.M.; Ulu, M.; Dogan, M. Novel and traditional fringing field correction schemes for the hemispherical analyser: comparison of first-order focusing and energy resolution. Meas. Sci. Technol. 2007, 18, 1853. [Google Scholar] [CrossRef]
- Kalvas, T.; Tarvainen, O.; Ropponen, T.; Steczkiewicz, O.; Arje, J.; Clark, H. IBSIMU: A three-dimensional simulation software for charged particle optics. Rev. Sci. Instrum. 2010, 81, 02B703. [Google Scholar] [CrossRef] [PubMed]
- Der Geer, B.; De Loos, M. The general particle tracer code: Design, implementation and application. J. Bus Commun. 2001. [Google Scholar] [CrossRef]
- Riddle, G.H.N. Electrostatic einzel lenses with reduced spherical aberration for use in field emission guns. J. Vacuum Sci. Technol. 1978, 15, 857. [Google Scholar] [CrossRef]







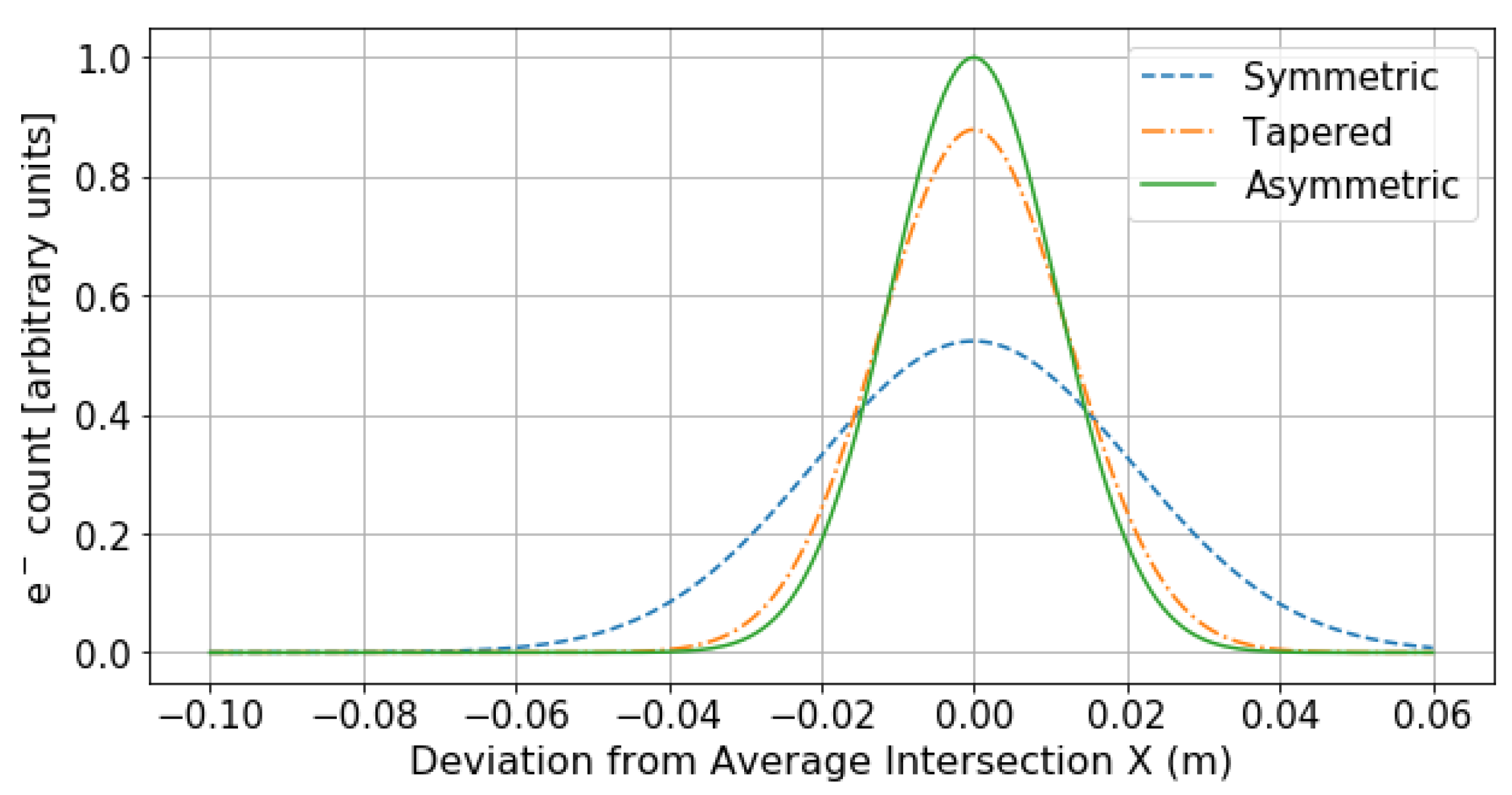
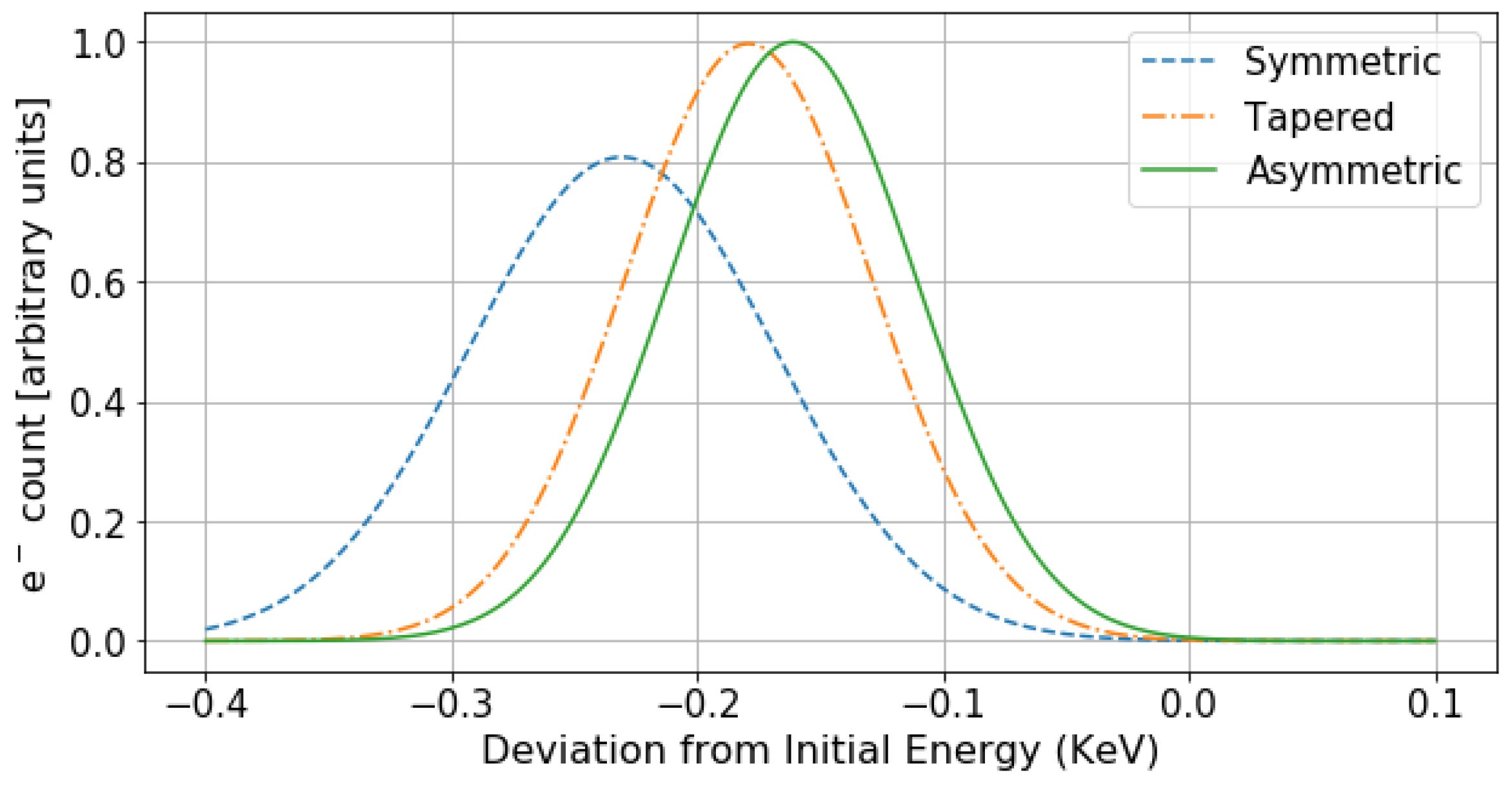
| HDA Property | Ideal | Simulated |
|---|---|---|
| Calibration factor | ≈1.59 | ≈1.25 |
| Magnification | 1 | ≈0.80 |
| Acceptance angle | 0 | 13.75 |
| Transmission efficiency | 100% | 80.9% ± 3.7% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lawler, G.; Sanwalka, K.; Zhuang, Y.; Yu, V.; Paschen, T.; Robles, R.; Williams, O.; Sakai, Y.; Naranjo, B.; Rosenzweig, J. Electron Diagnostics for Extreme High Brightness Nano-Blade Field Emission Cathodes. Instruments 2019, 3, 57. https://doi.org/10.3390/instruments3040057
Lawler G, Sanwalka K, Zhuang Y, Yu V, Paschen T, Robles R, Williams O, Sakai Y, Naranjo B, Rosenzweig J. Electron Diagnostics for Extreme High Brightness Nano-Blade Field Emission Cathodes. Instruments. 2019; 3(4):57. https://doi.org/10.3390/instruments3040057
Chicago/Turabian StyleLawler, Gerard, Kunal Sanwalka, Yumeng Zhuang, Victor Yu, Timo Paschen, River Robles, Oliver Williams, Yusuke Sakai, Brian Naranjo, and James Rosenzweig. 2019. "Electron Diagnostics for Extreme High Brightness Nano-Blade Field Emission Cathodes" Instruments 3, no. 4: 57. https://doi.org/10.3390/instruments3040057
APA StyleLawler, G., Sanwalka, K., Zhuang, Y., Yu, V., Paschen, T., Robles, R., Williams, O., Sakai, Y., Naranjo, B., & Rosenzweig, J. (2019). Electron Diagnostics for Extreme High Brightness Nano-Blade Field Emission Cathodes. Instruments, 3(4), 57. https://doi.org/10.3390/instruments3040057






