Permanent Magnet-Based Quadrupoles for Plasma Acceleration Sources

Abstract

The laser plasma accelerator has shown a great promise where it uses plasma wakefields achieving gradients as high as GeV/cm. With such properties, one would be able to build much more compact accelerators, compared to the conventional RF ones, that could be used for a wide range of fundamental research and applied applications. However, the electron beam properties are quite different, in particular, the high divergence, leading to a significant growth of the emittance along the transport line. It is, thus, essential to mitigate it via a strong focusing of the electron beam to enable beam transport. High-gradient quadrupoles achieving a gradient greater than 100 T/m are key components for handling laser plasma accelerator beams. Permanent magnet technology can be used to build very compact quadrupoles capable of providing a very large gradient up to 500 T/m. We present different designs, modeled with a 3D magnetostatic code, of fixed and variable systems. We also review different quadrupoles that have already been built and one design is compared to measurements.

1. Introduction

Ever since the discovery of the electron using a cathode-ray tube at the end of the 19th century, particle accelerators have seen tremendous progress where they became widely used tools for basic research, industry, medicine, material science etc. For the past decades, innovative and compact accelerators have been developed that address the increasing requirements in different fields. Laser Plasma Acceleration (LPA) was proposed in 1979 [1], where ultra-high accelerating fields can be produced to generate electron beams up to several GeV energy, short beam size (fs), very small transverse sizes ($\mathsf{\mu }$m) and high peak current (1–10 kA) [2,3]. The concept of LPA is based on focusing an intense laser pulse onto a gas to drive large-amplitude plasma waves that then act as accelerating structures for particles. The LPA accelerator surpasses the conventional RF one in terms of energy gradient and compactness. However the characteristics of the beam phase space are very different. In the longitudinal phase space, where the conventional accelerators typically operate at ultra-low energy spread (~0.01–0.1%) and small bunch duration (few picoseconds), the LPA exhibits ultra-short electron bunch (few femtoseconds) but with large energy spread (few %). As for the transverse phase space, the LPA appears as a diverging (few mrads) point source of few $\mathsf{\mu }$m size, whereas the conventional accelerator operates with typically tens of $\mathsf{\mu }$m divergence and tens to hundreds of $\mathsf{\mu }$m size. Consequently, the chromatic effects associated with the divergence and the energy spread, that are generally negligible on conventional accelerators, appear to play a major role and complicate the transport [4,5,6,7,8]. Thus, it is of great importance to mitigate these effects, transport and control the beam to enable the utilization of such accelerator for applications such as Free Electron Laser (FEL) [9,10,11] that allows for time-resolved atomic scale imaging.

Undulator radiation has been successively observed using LPA source [12,13,14], while FEL based applications remain very challenging due to the large energy spread and divergence. In the high gain FEL [15,16], the high density electron beam interacts with the radiation and gets micro-bunched where a longitudinal coherence is achieved and then the radiation is exponentially amplified until saturation. Large energy spread deteriorates the micro-bunching efficiency and smears out the electron bunch, which prevents the transfer of energy from the electron beam to the resonant mode of wavelength ${\lambda }_r$ [17]. The energy spread rms (${\sigma }_{\gamma }$) has to satisfy the following relation: ${\sigma }_{\gamma }<\gamma \rho$, where $\gamma$ is the relativistic factor and $\rho$ the Pierce parameter $\propto {(I/{\sigma }_x{\sigma }_z)}^{1/3}$ with I the peak current and ${\sigma }_{x,z}$ the transverse beam sizes rms. $\rho$ is normally of the orders of 10${}^{-3}$, so this condition is not acomplished by typical LPA beams since energy spreads have been measured to be ~10${}^{-2}$ for MeV-GeV [18]. In order to use these beams for FEL, the energy spread should be reduced, for example, by cutting a part of the initial distribution using a demixing chicane to select a smaller range of energies [19] or take advantage of the energy spread by opting for a different approach with the use of transverse gradient undulators (TGUs) [20,21]. The FEL amplification highly depends on the overlapping of the electron beam and the wave. Electrons tend to oscillate around the undulator axis with a period larger than the undulator period (betatron oscillations) that reduces the overlapping efficiency. So another FEL condition, the well known Pellegrini criterion [22], has to be satisfied: ${ϵ}_n<\frac{\gamma {\lambda }_r}{4\pi }$, where ${ϵ}_n$ is the normalized emittance. Even though the beam at the plasma-vacuum interface has a quite low normalized emittance (1 mm·mrad), a problem arises regarding the transport where the chromatic emittance increases quadratically with the divergence along a distance s [5]: ${ϵ}_n\left(s\right)\propto {\sigma }_{\gamma }{\sigma }_x^{{}^{\prime }2}s$, making the beam transport a big issue if not quickly mitigated.

After the emergence of the concept of magnetically self-focusing electron beam of density $n_e$ by ions from a residual gas [23] or more generally by a plasma of density $n_p$, two regimes of plasma lens can be considered. In the over-dense regime ($n_e<<n_p$); the electron beam moves away due to the plasma and self generates an azimuthal magnetic field, of focusing strength $K=2\pi r_e{n}_e/\gamma$ with $r_e$ the classical radius of the electron [24]. In the under-dense regime ($n_e>>n_p$), the electron beam pass induces a strong wave in the plasma background and can be focused by the ions uniformly distributed, with a strength given by $K=2\pi r_e{n}_p/\gamma$. Afterwards, Passive Plasma Lens (PPL) have been proposed and developed [25], which can provide high gradients, but the focusing properties depend on the electron beam itself and can present aberrations. PPL is further developed theoretically [26] and used for an LPA experiment [27]. Active Plasma Lens (APL), where the azimuthal magnetic field is controlled by a discharge in the plasma, has been proposed [28,29]. APL has been applied to ion beams [28,30] and to LPA applications [31,32,33,34,35]. APL provide high gradient of the order of kT/m, tunability and radially symmetric focusing, but are subjected to emittance degradation and charge reduction due to highly non-linear focusing arising from current discharge nonuniformity. Furthermore, their use in experiments that run for couple of weeks adds an additional level of risk. Plasma lenses are still under development and the use of conventional magnet can still appear to be more robust.

A FODO high gradient quadrupoles lattice placed very close to the plasma-vacuum interface allows for handling and controling the LPA beam divergence. However, their focusing is not symmetric, unlike APL, and at least three systems are required to provide a round beam. Conventional accelerators, operating at an intermediate energy, use electro-magnet technology for quadrupoles to transport the beam where the rigidity is limited to few tens of T·m. High energy accelerators require larger gradient quadrupoles to transport the beam, where the electro-magnet technology reaches a limit it cannot surpass. Superconducting magnets come in handy for such applications but they are much more expensive than the conventional electro-magnets due to the the cryogenic cost (installation and operation) and the possibility of a quench due to synchrotron radiation and image charges. Thus, permanent magnet advantages come into play with the absence of power supplies and cables, and in addition eliminating a large element of infrastructure for the water cooling system. Permanent magnet based quadrupoles can be reduced in size without losing the magnetic field strength making them suitable for future compact accelerators including LPA.

In this paper, we review compact designs of PMQs suitable for different applications. Whereas present synchrotron radiation sources operate with gradients of 10–20 T/m, future diffraction limited light sources at an intermediate energy will require compact quadrupoles of gradients around 100 T/m. In colliders, the beam energy is much larger and strong quadrupoles of gradients 100–300 T/m are needed for the final focusing. Regarding plasma wakefield accelerators, where the electron beam is generated with initial large divergence, quadrupoles of gradient 100–500 T/m and above are required with low multipole contents to ensure a good handling of the beam transport. We present here solutions offered by permanent magnet quadrupoles and compare the performance of different designs of fixed and variable gradient with numerical simulations using Radia code [36]. We then review the quadrupoles that are designed for the mentioned applications. Measurements using a stretched wire conducted for one design are compared to simulations.

2. Quadrupole Characteristics

Quadrupoles consist mainly of four magnets with magnetization vectors directed as shown Figure 1, in which the dipole terms at the core of the system are canceled and the field magnitude increases with the radial distance, so particles that are farther from the center experience a larger force. In the scheme, the electron experiences an inward force towards the center in the horizontal plane and outwards in the vertical plane, Thus, a quadrupole focuses in one plane and defocuses in the other.

2.1. Gradient

In the case of permanent magnets, the current density is zero, so starting with Maxwell equations:

$$\left\{\begin{array}{c}\overrightarrow{\nabla }\times \overrightarrow{B}=0\hfill \\ \overrightarrow{\nabla }.\overrightarrow{B}=0\hfill \end{array}\right.$$

where B is the magnetic field. Considering that the field along the longitudinal direction is zero ($B_s$ = 0) and does not vary ($\frac{\partial B}{\partial s}$ = 0), and neglecting higher order multipoles for small transverse displacement:

$$\overrightarrow{B}=B_x\widehat{x}+B_z\widehat{z}=G(z\widehat{x}+x\widehat{z})$$

(1)

where $G=\frac{\partial B_z}{\partial x}=\frac{\partial B_x}{\partial z}$ is the field gradient along the horizontal axis x and vertical axis z. Equation (1) is represented in Figure 1 where the field increases for larger distance from the center.

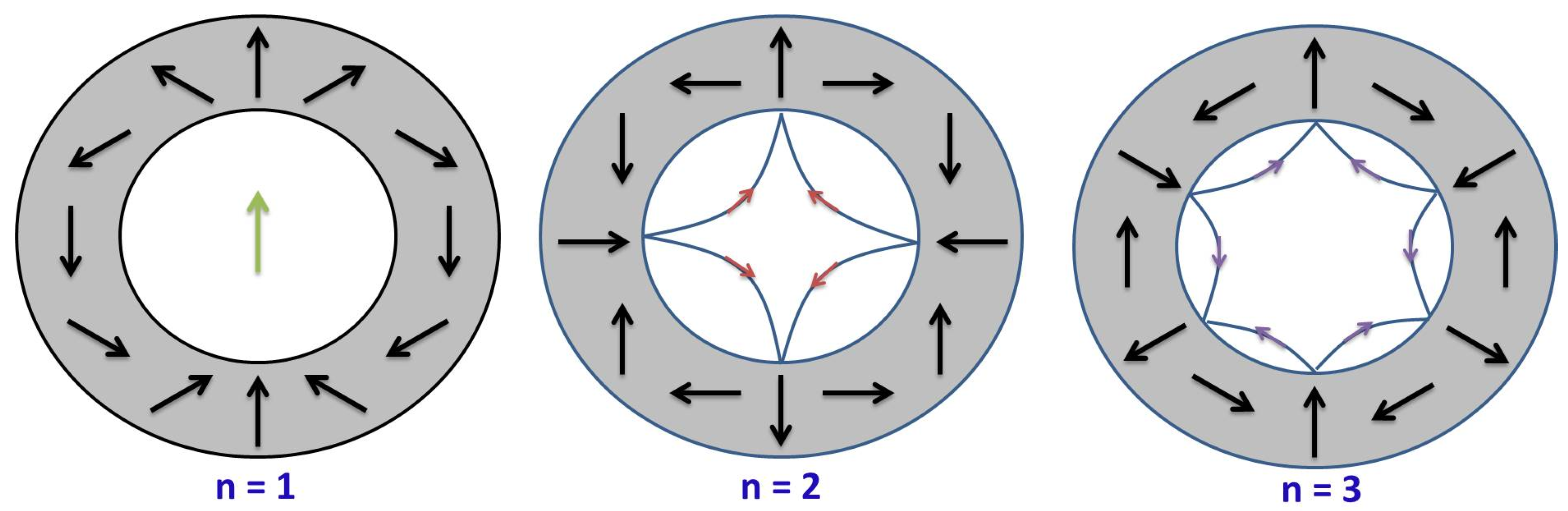
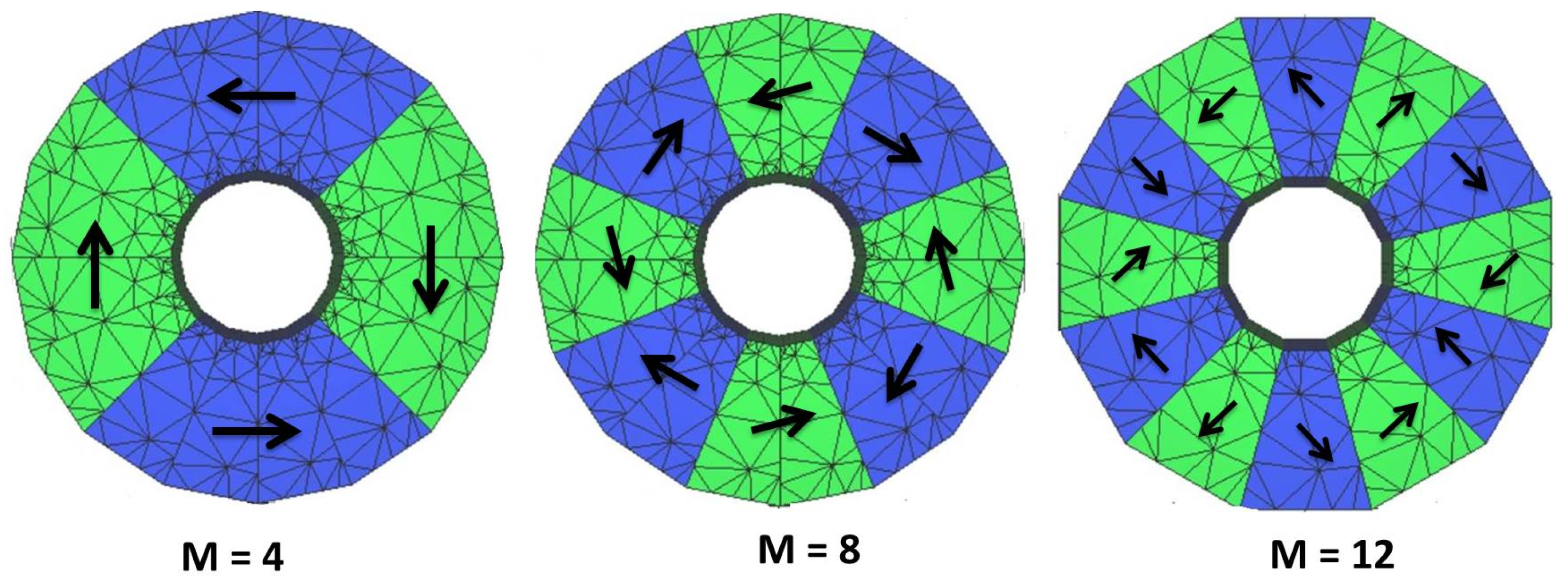
2.2. Multipoles

The magnetic field of realistic quadrupoles, even though designed to generate only one multipolar order, contains higher order multipoles called harmonics resulting from the structure and magnetic or mechanical assembly imperfections. In case of an infinitely long magnet, the local field B inside a quadrupole can be expressed as:

$$B=B_z+i{B}_x=\sum _{n=1}^{\infty }(B_n+i{A}_n)·{\left[\frac{x+iz}{r}\right]}^{n-1}$$

(2)

where n is the multipolar order, $B_n$ and $A_n$ the normal and skew multipolar coefficients respectively and r the radius for which multipolar coefficients are computed or measured. A perfect quadrupolar field consists only of $B_2$ term, as for the field generated by a ideal quadrupole contains systematic multipole terms ($B_6$, $B_{10}$, $B_{14}$, …) due to the device geometry. Mechanical and magnetic impurities give rise to the non-systematic terms including the skew components.

The vertical field component is negative for $x<$ 0, positive for $x>$ 0, and null on the axis. This evolution is the same for the horizontal field along the z. In a 3D model, the following components $a_n$ and $b_n$ defined as $a_n=\int A_n.ds$ and $b_n=\int B_n.ds$ are introduced. The quadrupole field gradient (2D and 3D) can be expressed as:

$$G_{2D}=\frac{B_2}{r}\mathbf{and}{G}_{3D}=\frac{\int B_2.ds}{rL}=\frac{b_2}{rL}$$

(3)

3. Fixed Gradient Permanent Magnet Quadrupoles

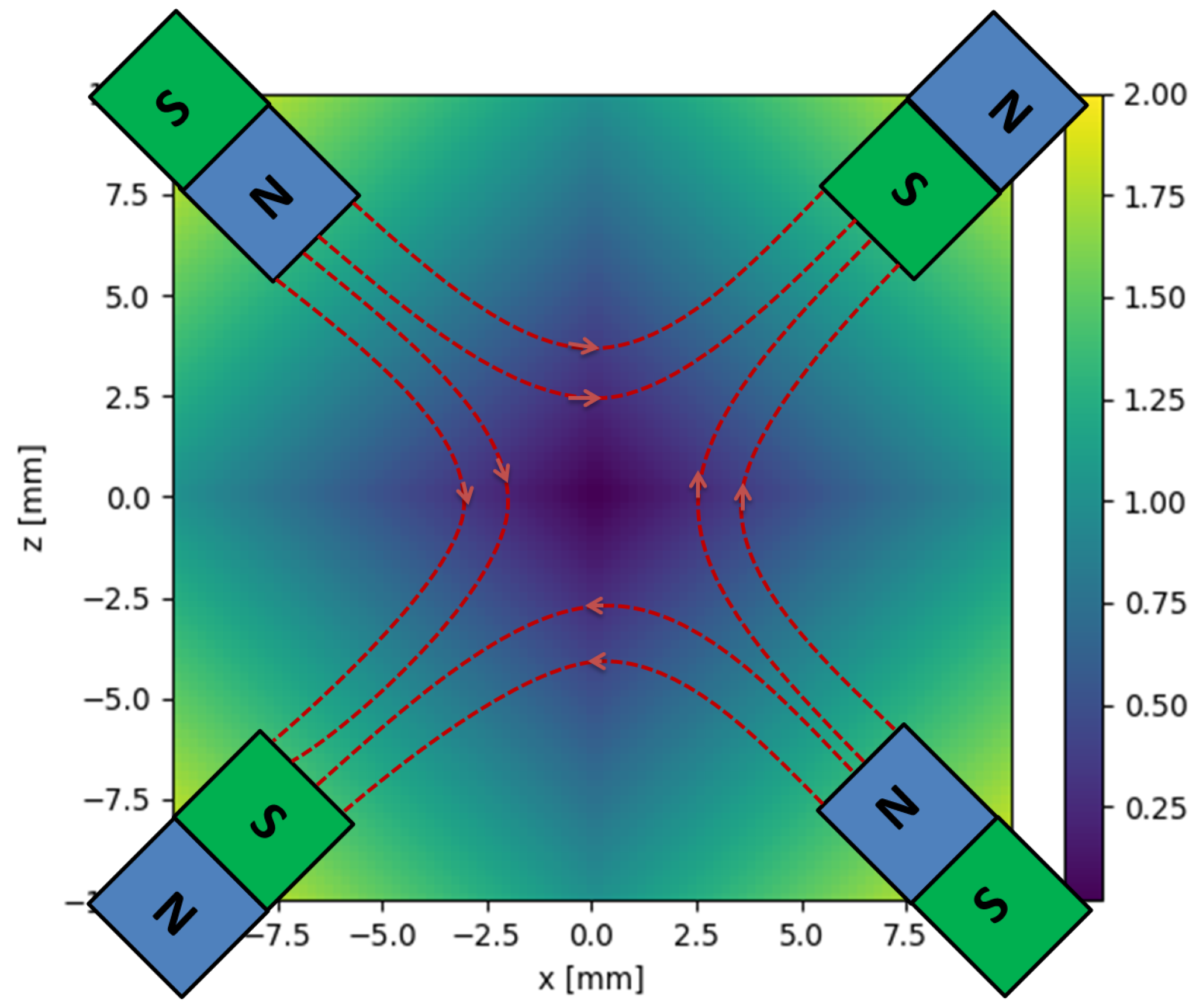
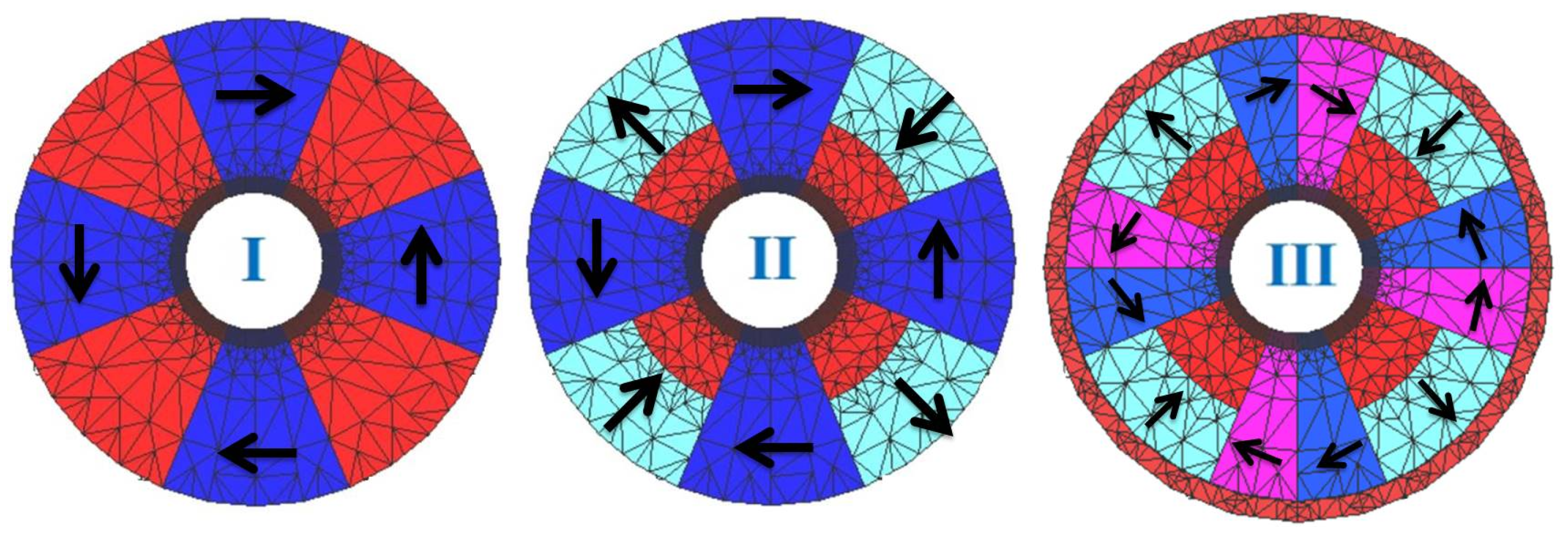
3.1. Halbach Structure

A Halbach structure is an array of magnets with specific arrangements generating a concentrated strong magnetic field on one side whilst creating a weak stray field on the opposite side [37]. Different multipole systems can be build using such structure as displayed in Figure 2 where 12 segmented magnets are used to design a dipole, quadrupole and a sextupole.

Concerning the quadrupole, and considering a long magnetic length (L) the gradient can be expressed as follows [37]:

$$\left\{\begin{array}{c}G=2B_{r}K(\frac{1}{R_i}-\frac{1}{R_o})\hfill \\ K=\frac{M}{2\pi }co{s}^2\left(\frac{\pi }{M}\right)sin\left(\frac{2\pi }{M}\right)\hfill \end{array}\right.$$

(4)

where $B_r$ is the remanence field, M the number of segments, $R_i$ the inner radius and $R_o$ the outer radius. As M tends to infinity K = 1, implying that the quadrupole gradient is enhanced for larger number of segments, but the magnet gets more complicated and expensive to manufacture.

The quadrupoles are characterized using Radia magnetostatic code based on boundary integral method. $N{d}_{2}F{e}_{14}B$ magnets are most commonly used due to their high remanent field and coercivity at room temperature [38,39,40]. The materials and quadrupole parameters are presented in

Table 1. Materials with their charateristics and geometric parameters of the reference Halbach ring used for modeling.

	Parameter	Value	Unit
	Magnet	Nd${}_2$Fe${}_{14}$B
	$B_r$	1.26	T
Materials	Coercivity	1830	kA/m
	Pole	Vanadium Permendur
	Saturation	2.35	T
	$R_i$	6	mm
Geometry	$R_o$	17	mm
	L	100	mm

.

Figure 3 shows the Halbach rings for different number of segments designed by Radia. The magnetization vectors of the magnets depends on the number of segments of the Halbach structure: ${\theta }_i$ = ($i-1$)6*$\pi$/M, where i is an integer, for example the angle between the magnetization vectors of two consecutive magnets is 270° for M = 4, 135° for M = 8 and 90° for M = 12 etc.…

Figure 4a presents the computed gradient versus magnetic length where Equation (4) is valid for large values ~50 mm. The gradient is computed for different numbers of segments and are compared to Equation (4) (see Figure 4b), where the gradient increases for higher numbers of segments. Figure 4c,d presents the computed gradient for different $R_0$, $R_i$ and shows good agreement with Equation (4).

3.2. Hybrid Quadrupole

This section presents different quadrupole designs following a Halbach structure with the addition of poles to enhance the gradient. Figure 5 shows three designs: Type (I) composed of four magnets and four poles, Type (II) composed of eight magnets and four half magnets half poles, Type (III) using 12 segmented structure in which four of them are half poles half magnets and the rest are magnets surrounded by pole ring shaped to divert the magnetic field lines back into the core of the system.

Figure 6 shows the gradient computed for the three designs of Figure 5 and are compared to the Halbach rings. Type (I) achieves a gradient higher by a factor of ~2 compared to the four segmented Halbach ring. Indeed, the addition of poles achieve a higher gradient and a less costly system. Type (II) design has the same gradient as the 8 segments Halbach ring with a slight 2% increase. The gradient achieved with the 12 segmented Halbach ring is quite remarkable as compared to type (III) with a much more complex design to generate a similar gradient.

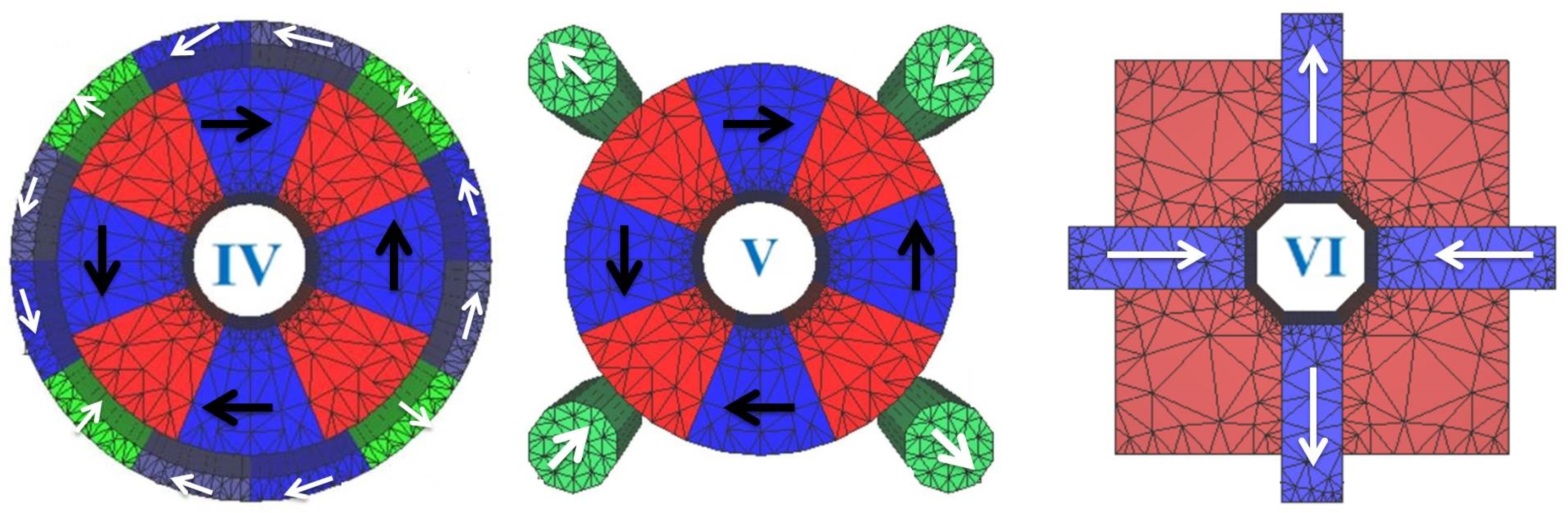
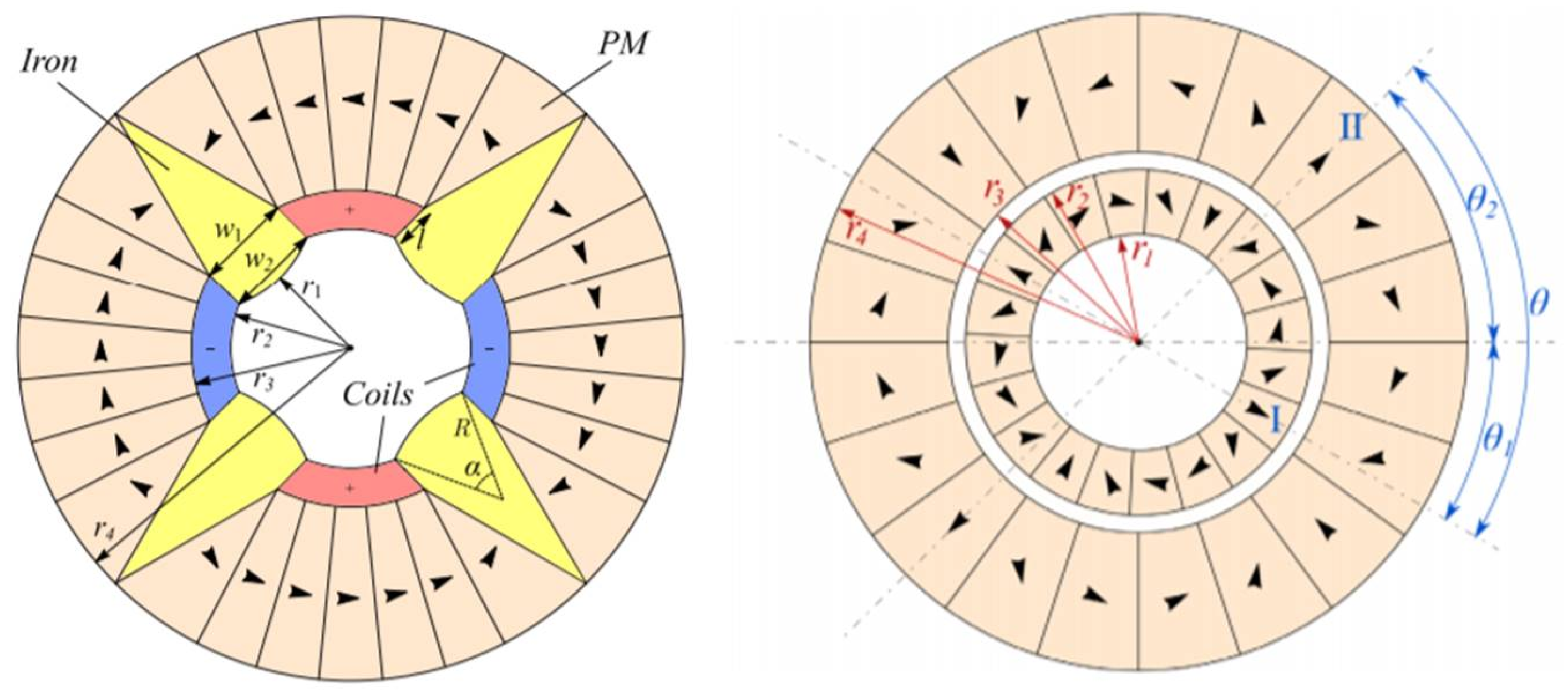
4. Variable Permanent Magnet Quadrupoles

In conventional electro magnets, the field, and so the gradient can be changed by varying the electric current. As for permanent magnets, it becomes much more challenging due to the requirement of mechanical motion to adjust the positions of the magnets taking into account the large magnetic forces induced by the system. Figure 7 shows examples of permanent magnet based quadrupoles with variable gradient: Type (IV) is composed of a Halbach hybrid ring at the center surrounded by a Halbach ring of 12 sections, and by rotating the ring the gradient is varied. Type (V) also constitutes of a Halbach hybrid ring at the center with cylindrical magnets capable of rotating around the longitudinal axis to provide gradient tunability. Type (VI) uses four magnetic rods built into a structure that can be moved to vary the gradient.

Figure 8 presents the gradient tunability as a function of the angle. Type IV design achieves a maximum gradient of 201 T/m and tunability of ~70 T/m by rotating the outer ring from −45° to 45°. Type V design provides a maximum gradient of 185 T/m and tunability of 35 T/m by rotating the cylindrical magnets from −90° to 90°. Type VI is composed of magnetic rods and by displacing them the gradient is varied from a maximum value of 100 T/m down to very low values depending how far the rods can be placed away from the center.

5. Built Quadrupoles

5.1. Fixed Gradient

Several Permanent Magnet based Quadrupoles (PMQs) with fixed gradient were built for particular applications:

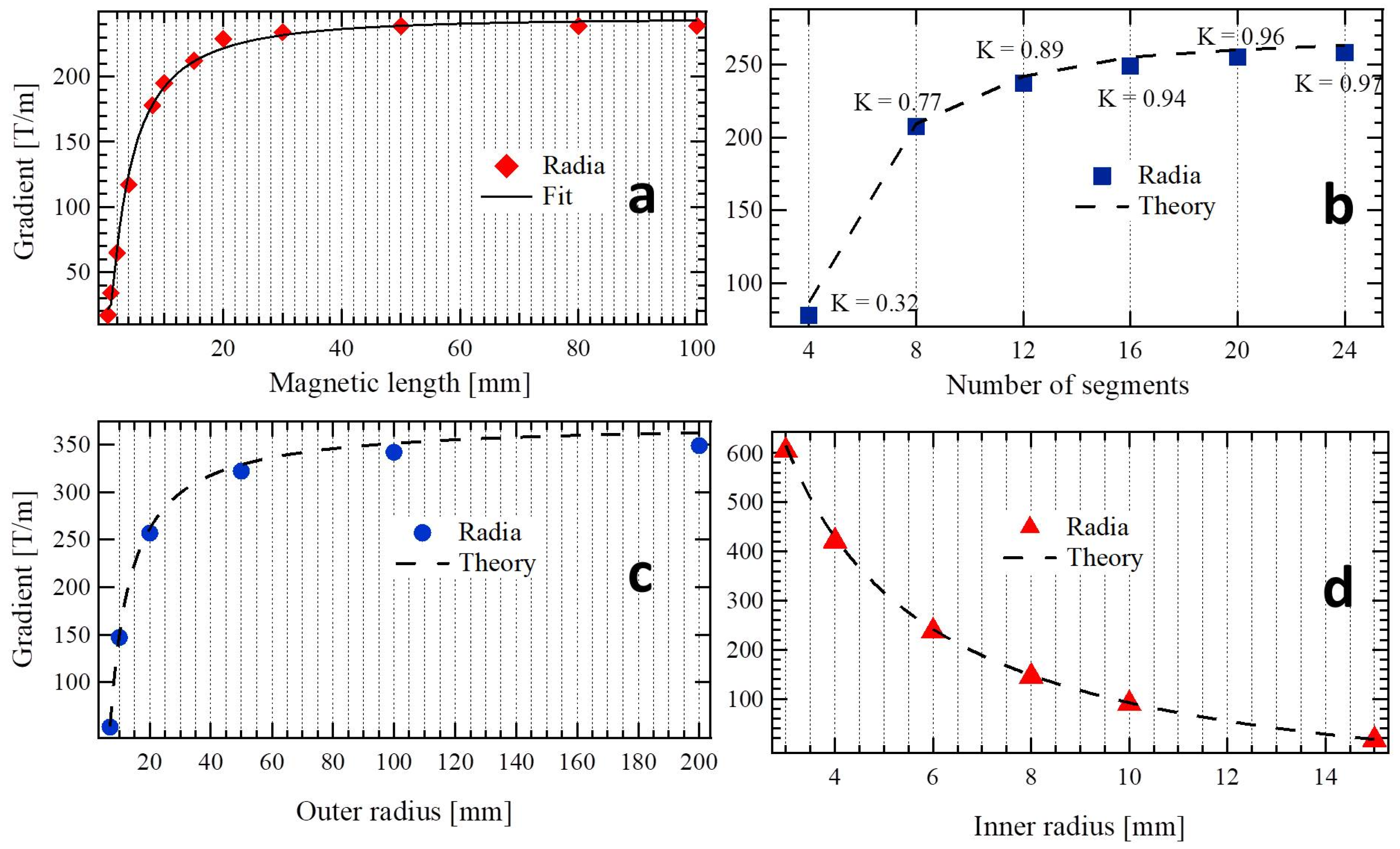
• A 12-modified PM Halbach ring system in which four of them are half permanent magnet and half iron poles (II) is proposed at Kyoto University in collaboration with SLAC as a final focus lens for a positron-electron linear collider accelerator [41]. The system has a bore radius of 7 mm with a magnetic length of 100 mm generating a maximum gradient of 289 T/m. At the department für Physik, in München for a Table-Top FEL application, two 12 PM sector Halbach ring system of 17 mm (15 mm) magnetic length and 3 mm bore radius achieve a gradient of 500 T/m a [42].
• A 16-sector PM Halbach structure with a 33.5 mm bore radius, 92 mm magnetic length, 27.1 T/m gradient and 2.5 T integrated gradient have been built at CESR [43]. Three PMQs of the same design, each made up of a Halbach ring of 16 segments, have been installed in the PLEIADES ICS experiment as a final focus system [4]. The bore radius is very small (2.5 mm) with a magnetic length of 10.4 mm providing the largest gradient recorded using PM technology that is around 560 T/m alongside a focusing tunability through longitudinal movement of the magnets.
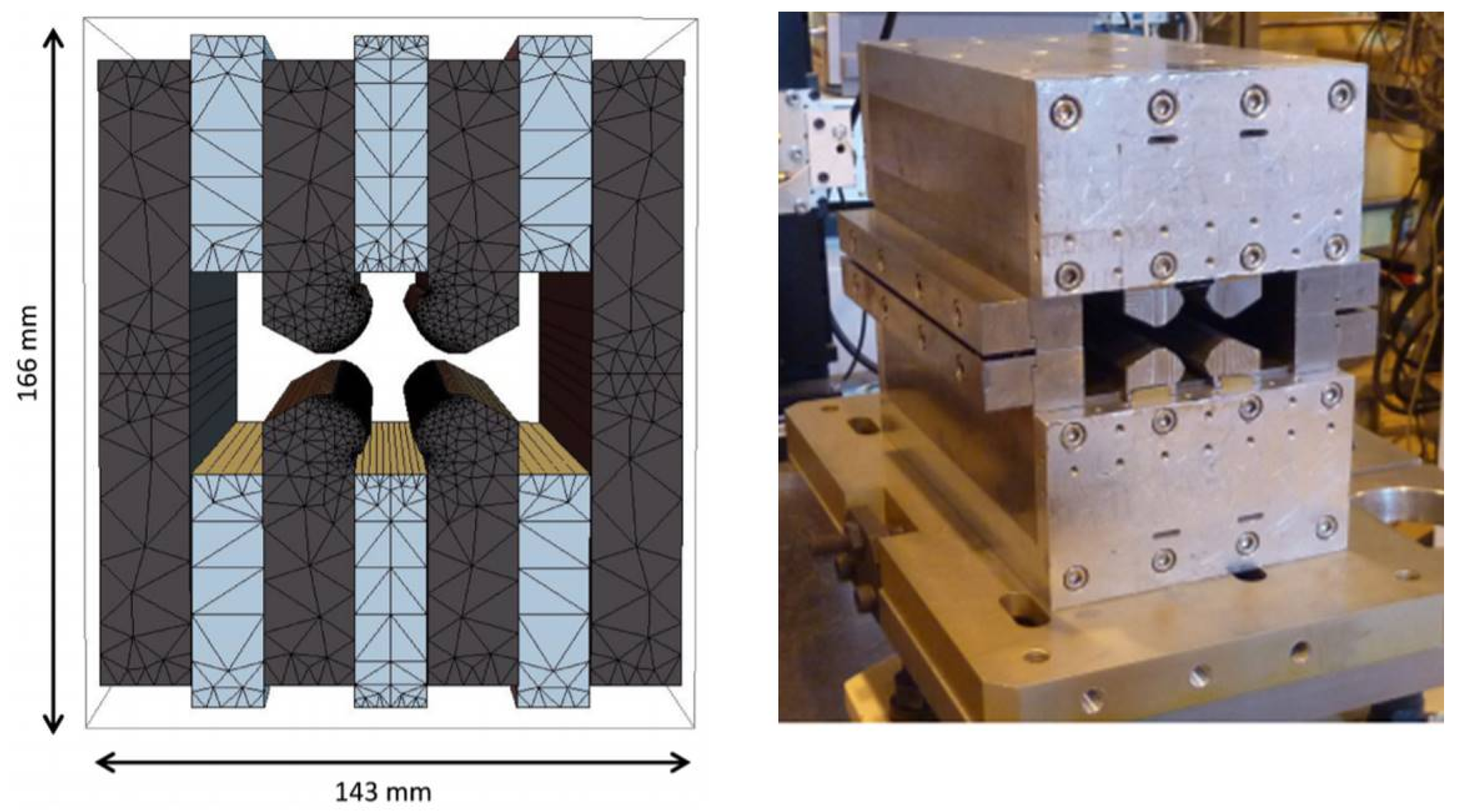
• A compact PMQ with a hybrid type design of interest for ultimate storage rings has been designed at ESRF [44]. The magnetic structure includes rectangular PM blocks and soft iron poles. A prototype with a bore radius of 12 mm and a magnetic length of 226 mm has been built (see Figure 9) provides a gradient of 85 T/m.

5.2. Variable Gradient

Various original designs were proposed and developed for the permanent magnet quadrupole to provide a variable gradient:

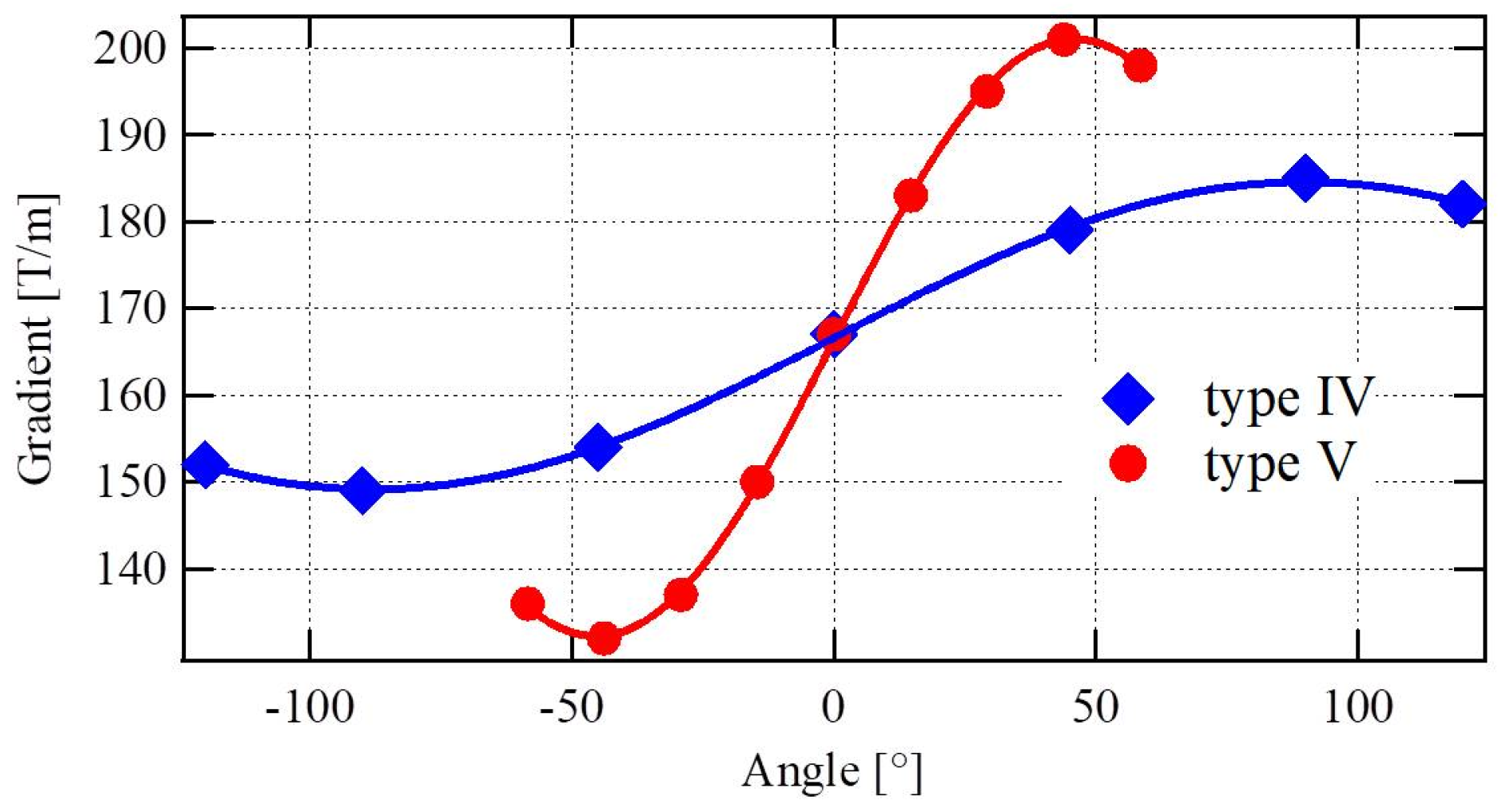
• A double Halbach ring structure of type (IV) was fabricated at Kyoto U. / SLAC collaboration for a final focus in a linear collider. The system consists of an inner hybrid ring with 8 sectors Halbach system and the outer ring being a pure 12-magnet Halbach structure rotating around the first one resulting in gradient variation from 17 T/m up to 120 T/m for a 230 mm magnetic length and 10 mm bore radius [45].
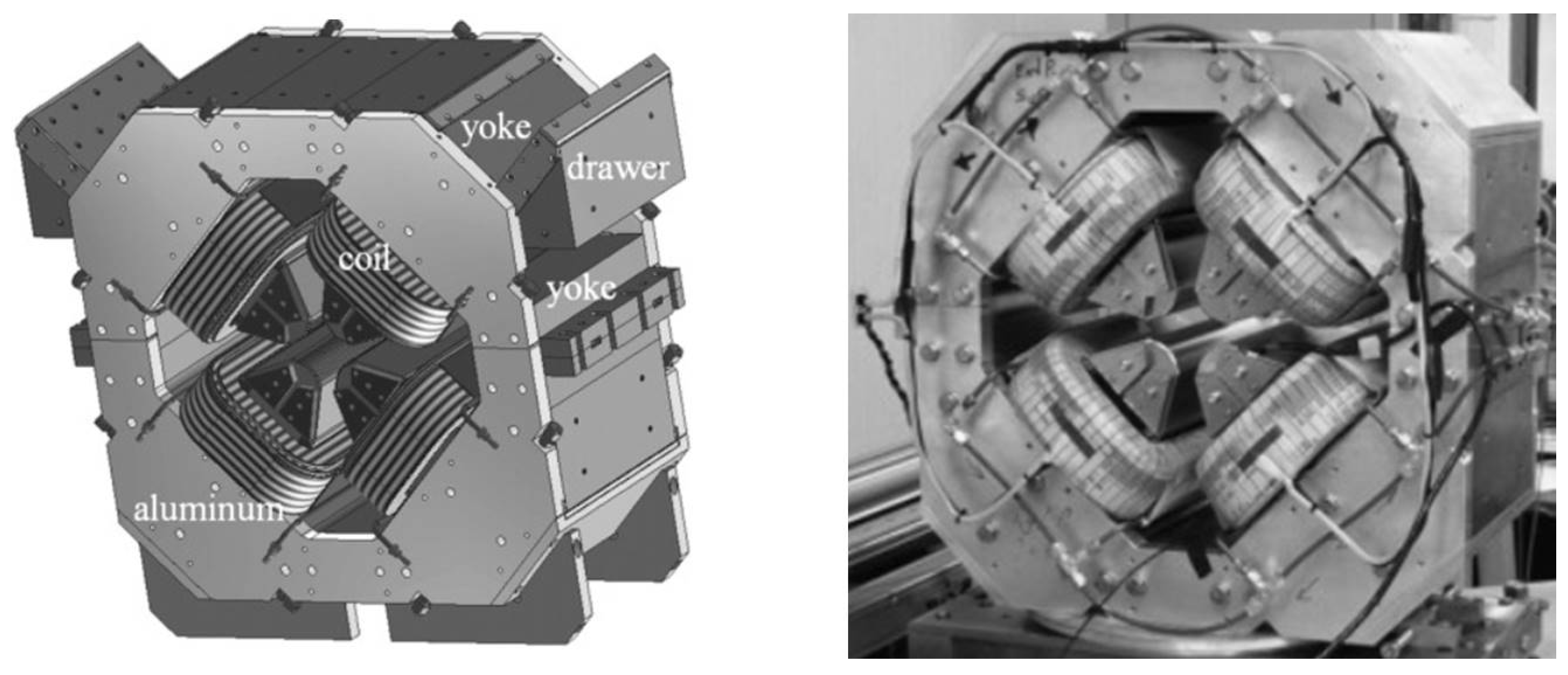
• A super hybrid quadrupole combining permanent magnetic material, coils and soft magnetic material has been built (see Figure 10) and tested for the new Brazilian Synchrotron Light Source (Sirius) [46]. The system has a bore radius of 27.5 mm and a magnetic length of 288 mm providing a maximum gradient of 28 T/m with a 30% tunability.
• An adjustable strength PM system has been built and tested, in collaboration between SLAC and Fermilab, for the Next Linear Collider. The system is based on four PM blocks and four soft iron poles of type (VI), with the possibility to retract linearly the permanent magnet blocks enabling an integrated gradient variation between 7 T and 68.7 T (gradient between 13 T/m and 115 T/m) for a 6.5 mm bore radius [47].
• A modified the 12-sector Halbach design composed of eight magnets and four poles surrounded by air-cooled electromagnetic coils as presented in Figure 11 has been proposed in the framework of CLIC/CERN collaboration [48]. The bore radius is 4.125 mm with a magnetic length of 300 mm achieving a maximum gradient of 610 T/m with 20% tunability.
• Two variable systems have been built in a collaboration of STFC Daresbury Laboratory and CERN for the Compact LInear Collider (CLIC) project [49,50] with an objective to collide electron-positron at an energy of 3 TeV. The first design, shown in Figure 12-left, provides a gradient from 15 to 60.4 T/m with a magnetic length of 241 mm. The second design, shown in Figure 12-right, provides a gradient from 2.9 to 43.8 T/m with a magnetic length of 194 mm length. The strength is adjusted by moving the PMs vertically away from the center, and by creating an air gap the gradient is reduced.
• Two variable quadrupoles are proposed for an interdigital H-mode drift tube linear accelerator using KONUS beam dynamics [51]: The first using an external adjustable electromagnets as shown in Figure 13-(left), with a bore radius of 12.5 mm providing a gradient from 50 to 100 T/m. The second using internal adjustable permanent magnets as shown in Figure 13-(right) that is similar to type (IV) but with additional number of segmented magnets. For a bore radius of 12.5 mm, the achieved gradient can be varied from 50 to 102 T/m.
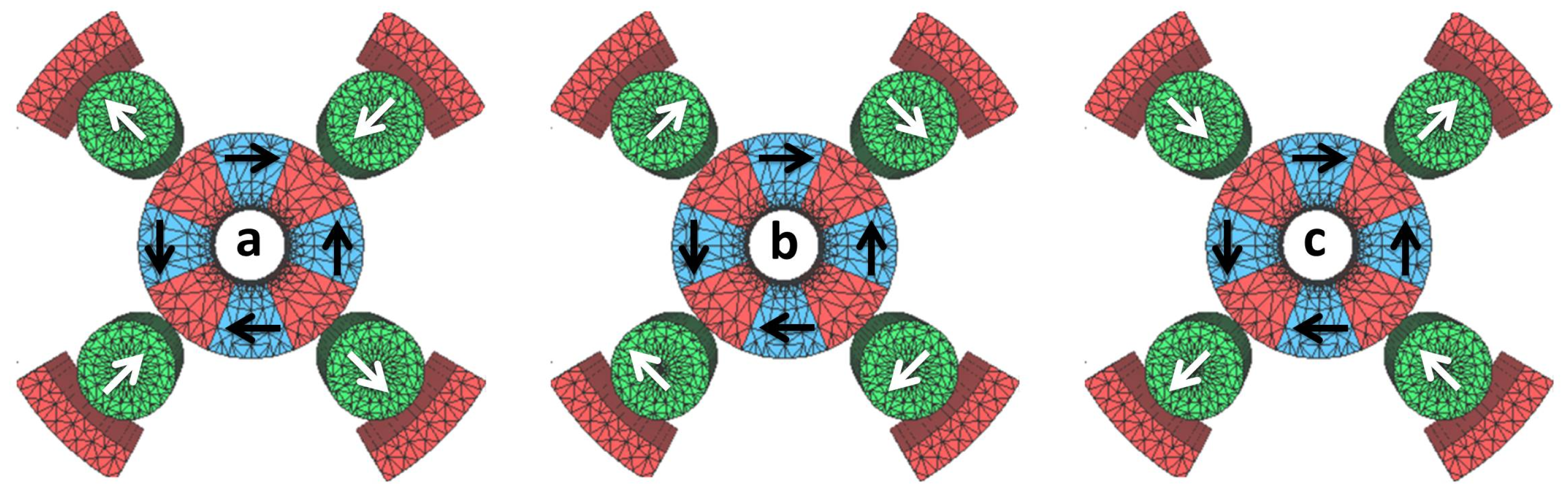
• Seven systems (QUAPEVA) of type (V) have been built in collaboration between SOLEIL and SigmaPhi [52,53] for the COXINEL project with an objective of FEL amplification using an LPA source. The QUAPEVA cosists of Nd${}_2$Fe${}_{14}$B magnets and permendur poles achieving a maximum gradient of 202 T/m and 45% tunability. The systems have a bore radius of 6 mm but with different magnetic lengths. Figure 14 presents the three particular configurations of the tuning magnets. The maximum and minimum gradient are obtained by orienting the tuning magnets easy axis towards the central magnetic poles. In these cases, the magnetic flux is either added (Figure 14a) or removed (Figure 14c) from the central poles. The average gradient is achieved when the tuning magnets are in the reference position, i.e. their easy axis is perpendicular to the central magnetic poles (Figure 14b). The QUAPEVAs are supported by translation tables (horizontal and vertical displacement) used to compensate any residual magnetic axis shift when varying the gradient, to perform electron beam based alignment [54,55]. The resulting mechanical design is shown in Figure 15 (left), also an assembled QUAPEVA on the translation table in Figure 15 (right).

5.3. Measurement

The QUAPEVAs are characterized using the stretched wire measurement, in which the multipoles are determined at a radius of 4 mm that corresponds to the good field region. The stretched-wire bench [56] has been used for magnetic field integral measurements.

Table 2. Maximum gradient measured (Equation (1)) with the stretched wire for the seven systems at a radius of 4 mm, and ${\Delta }_{sim}$ the deviation with respect to the simulated one.

QUAPEVAs	Magnetic Length [mm]	Gradient [T/m]	${\mathsf{\Delta }}_{\mathit{sim}}$ [%]
Q1	26	196	−5.1
Q2	40.7	202	−4
Q3	44.7	203	−3.5
Q4	47.1	204	−3.3
Q5	66	208	−1.8
Q6	81	209	−1.3
Q7	100	211	−0.28

presents the maximum gradient for the seven systems (QUAPEVAs) measured with the stretched wire. The difference with respect to the simulations reduces for longer magnetic length due to an insufficient number of mesh in the longitudinal axis that is time consuming.

Table 3. Multipoles computed and measured for the QUAPEVA of magnetic length of 100 mm at the maximum gradient with r = 4 mm. ${\Delta }_{sim}$ the deviation of the measured multipole with respect to the simulated one.

Multipole	Radia [T·mm]	Measurement [T·mm]	${\mathsf{\Delta }}_{\mathit{sim}}$ [%]
b${}_1$	0.021	0.039	48
b${}_2$	84.68	84.45	−0.28
b${}_6$	1.93	1.86	−3.6
b${}_{10}$	−1.46	−1.02	30

compares the measured and simulated multipoles for the QUAPEVA of magnetic length 100 mm. The dipolar term (b${}_1$) in the simulation is not equal to zero due to computational errors, and the one measured is probably due to a slight orientation of one of the cylindrical magnets or the precision of the bench. The discrepancy with respect to simulations increases for multipoles with weaker signal.

6. Summary

The models presented previously are summarized in

Table 4. PMQs modeled using Radia. The “halves” stands for half magnet or half pole. $\Delta$G/G = (G${}_{max}$ − G${}_{min}$) /G${}_{max}$.

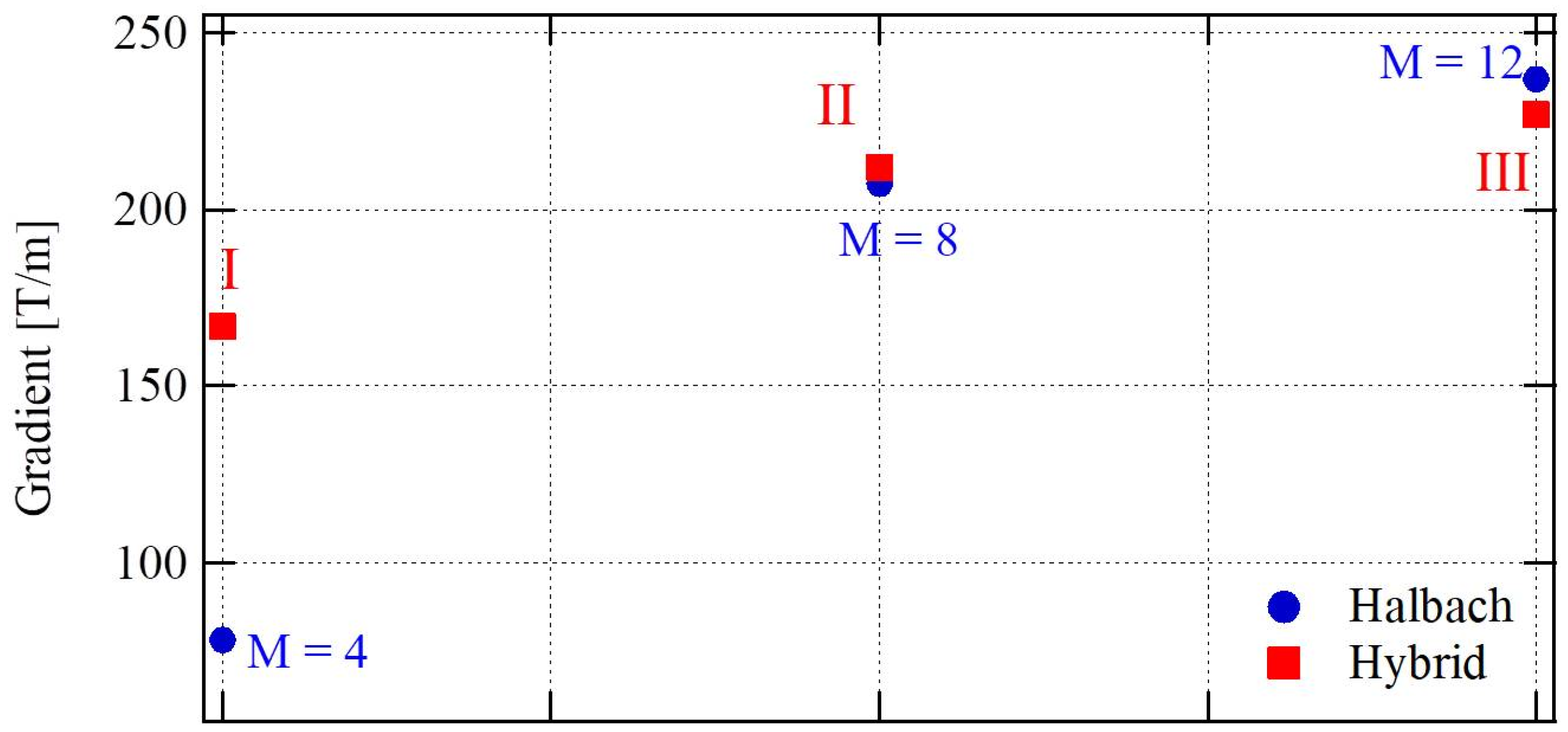
Type	n° Magnets	n° Poles	Max G	Integ G	$\mathsf{\Delta }$G/G
Halbach	4	-	78 T/m	7.8 T	-
Halbach	8	-	207 T/m	20.7 T	-
Halbach	12	-	237 T/m	23.7 T	-
Hybrid-I	4	4	166 T/m	16.6 T	-
Hybrid-II	4 + 4 halves	4 halves	211 T/m	21.1 T	-
Hybrid-III	12	4 halves + ring	227 T/m	22.7 T	-
Hybrid-IV	4 + ring	4	201 T/m	20.1 T	34%
Hybrid-V	4 + 4 cylinders	4	185 T/m	18.5 T	20%
Hybrid-VI	4	Bulk	100 T/m	10 T	90%

with their acheivable gradient and tunability. Other characterizations of a quadrupole are the systematic multipoles (b${}_6$, b${}_{10}$, b${}_{14}$, …) that derive from the structure geometry and the non-systematic multipoles that emerge from magnets/poles impurities or mechanical errors. The beam quality can quickly deteriorate if these terms are not kept low; however their effect highly depends on the beam size in the quadrupole aperture and the gradient homogeneity also known as good field region. In the case of the LPA, the specifications in terms of multipoles are less stringent than a recirculating acclerator, typically by one order of magnitude. On the other hand, the gradient tuneability should be larger.

Table 5. Fixed and variable gradient PMQs. $\Delta$G/G = (G${}_{max}$− G${}_{min}$) /G${}_{max}$.

Project	Lab	Radius	L	Max G	integ G	$\mathsf{\Delta }$G/G	References
Storage ring	CESR	33.5 mm	92 mm	27 T/m	2.5 T	-	[43]
PLEIADES ICS	Lawrence Livermore	2.5 mm	10.4 mm	560 T/m	5.8 T	-	[4]
LINEAR COLLIDER	Kyoto University	7 mm	100 mm	300 T/m	28.5 T	-	[41,57,58]
SPTEM	UCLA	3.5 mm	6.16 mm	600 T/m	3.3 T	-	[59]
Radiography	Tsinghua University	5 mm	20 mm	287 T/m	5.74 T	-	[60]
Storage Ring	ESRF	12 mm	226 mm	82 T/m	18.6 T	-	[44]
Table-Top FEL	LMU Munich	3 mm	17 mm	500 T/m	8.5 T	-	[42]
LPA	SPARC LAB	3 mm	20.2	519	10.5 T	-	[61]
LINEAR COLLIDER	Kyoto/NIRS	10 mm	200 mm	120 T/m	24.2 T	85%	[45,62]
CLIC	CERN	4.125 mm	273 mm	610 T/m	172.5	20%	[48]
CLIC	CERN/STFC	13.6 mm	214 mm	60.4 T/m	14.6 T	75%	[49]
CLIC	CERN/STFC	13.6 mm	194 mm	43.8 T/m	8.5 T	93%	[49]
Next Linear Collider	STI/SLAC	6.5 mm	420 mm	163 T/m	68.7 T	90%	[47]
COXINEL	SOLEIL	6 mm	100 mm	210 T/m	21 T	44%	[52,53]
linear accelerator	Peking University	12.5 mm	-	100 T/m	-	50%	[51]

presents a summary of the PMQs already built that are presented in the previous section.

7. Conclusions

A permanent magnet-based quadrupole is quite a compact device achieving a very high gradient of the orders of hundreds of T/m making it essential for future compact linear accelerators including laser plasma accelerators. Conventional electromagnet technology, with copper conductors wrapped around soft iron poles, enables to tune the gradient by simply changing the current but with significant continuous power consumption to maintain the magnetic field. Furthermore, superconducting magnets produce very large magnetic field but requires an expensive Helium infrastructure to keep the magnets in superconducting state. Thus, with zero power consumption, permanent magnet-based systems pave the way towards a green society and with new innovative designs. Also the challenges of wide tunability and high field homogeneity are presentely mitigated with the various examples of built systems.

So far, PMQs are intalled and commissioned for storage rings, LPA and collider applications, but the high multipole contents set a drawback for some applications like diffraction limited light sources. A proposed design to cross that barrier is to design hyperbolic-shaped magnets and poles to reduce the multipole contents in compromising on the gradient variability.

8. Patents

The QUAPEVA design has been patented (QUAPEVA program-Triangle de la Physique, SOLEIL/Sigmaphi collaboration) in Europe [63,64].