1. Introduction
Analog silicon photomultipliers (SiPMs) are arrays of many (hundreds, thousands) Single-Photon Avalanche Diodes (SPADs), each one with its integrated passive-quenching resistor, referred to as microcells. All microcells are connected in parallel to a common anode and cathode. Like single SPADs, each SiPM cell works in Geiger mode and the output current of the SiPM is the sum of all the cells, giving a signal proportional to the number of detected photons.
The SiPM has obtained growing attention in the last years as an alternative to the traditional photomultiplier tube in the detection of low photon fluxes, thanks to a number of advantages typical of solid-state detectors, such as compactness, ruggedness, ease of use, low operational voltage (tens of volts) and insensitivity to magnetic fields [
1]. They also have easier scalability, for both the microcell (pixel) size and the overall active area dimension (between less than 1 mm
2 and 100 mm
2), as shown in this paper. These properties have led to a significant development and a noticeable improvement of SiPM performance by manufactures.
SiPMs have been used for years in X-ray and gamma-ray detection, combined with scintillator crystals (see for example in
Figure 1), as a replacement of photomultiplier tubes, in medical applications [
2,
3,
4], like in positron emission tomography (PET), where their good time resolution is important for time-of-flight (TOF) information, and in high-energy nuclear physics [
5,
6]. This transition was mainly driven by the insensitivity of SiPMs to magnetic field. Many experiments and machines like PET combined with MRI (magnetic resonance imaging) require detection of gamma-rays in a strong magnetic field environment. PMT typically cannot work properly in such situations.
Thanks to progress in SiPMs technology, there has been growing interest for these detectors in several big scientific experiments, wherein they are used for the readout of liquid noble gases scintillators, such as liquid Xenon (LXe) and liquid Argon (LAr), as a replacement for photomultiplier tubes [
7,
8]. In such applications, SiPMs must be operated at cryogenic temperatures, which constitutes a technological challenge for both the detector and its packaging. Moreover, very large sensitive areas are required: there has been important studies and developments to reduce the primary dark count rate (DCR) at such very low temperatures, where tunneling generation is generally the dominant contribution [
9]. In some experiments with liquid noble gases, high sensitivity in vacuum-UV (VUV) is also needed; for example, for direct detection of LXe scintillation light, avoiding using wavelength shifters [
8]. This optimization required important research activity to bring the sensitivity in the VUV down to 175 nm. Another example of an experiment that will use SiPMs is the Cherenkov Telescope Array (CTA) in which the detectors are used to observe the Cherenkov light emitted in air showers initiated by high-energy to very-high-energy gamma-rays from both Galactic and Extragalactic sources [
10]. In this case, SiPMs are operated in the presence of a significant amount of light generated by the sky background, and minimization of optical crosstalk probability is very important to reduce the rate of random triggers and improve energy resolution.
SiPMs have recently also emerged as a promising solution for several other low-light applications, like for example, Light Detection and Ranging (LIDAR) [
11,
12], optical spectroscopy [
13,
14], fluorescence detection [
15] and Cherenkov-light detection for physics experiments or from scintillation crystals [
16,
17]. The main reason is the capability to combine single-photon sensitivity, good photon detection efficiency (PDE) and good time resolution (like SPADs) with the high dynamic range and large sensitive area. For example, in LIDAR, highly sensitive detectors, with large dynamic range are particularly of interest. As described in [
12], signals from a SiPM can have a better signal-to-noise ratio (SNR) than a PMT, but a short recovery time of the cells is necessary to not degrade the detection performance at short distances. Therefore, generally speaking, SiPMs with a large number of small pixels and short dead time could be very useful.
Among the different progresses reported in the literature, at FBK (Trento, Italy), we developed several SiPM technologies over the last years, with different characteristics. Starting from original “more planar” technologies, we developed the so-called high cell density (HD) technologies. In detail: (i) RGB-HD [
18] (RGB stands for “red/green/blue”), with PDE peaked in the green part of the visible spectrum, (ii) NUV-HD [
19] (NUV stands for “near ultraviolet”) with PDE peaked around 400 nm, (iii) VUV-HD technology [
20,
21], with detection efficiency extended in the vacuum ultraviolet, (iv) NIR-HD [
22] with PDE extended towards the red and near-infrared wavelength region. The main characteristics of the HD technologies is the deep trench isolation between the microcells. This allows for small cell size (and pitch) with a high fill-factor (FF). This was an important achievement, since lowering of the former usually means a reduction of the latter (given a certain fixed “dead border” around each cell).
In this work, we describe the basic structure and features of analog silicon photomultipliers. We describe the main issue related to their characterization and the techniques used. Finally, we describe different SiPM technologies developed at FBK and customization for different applications, outlining the most important technological and design challenges: RGB-HD SiPMs technology, NUV-HD, VUV sensitive and NIR sensitive technologies. Each technology is tailored for specific applications, having different spectral sensitivities, internal structures, and target operating conditions.
2. SiPM Structure
In an analog SiPM, the microcells (or cell) are made by SPADs with a passive quenching resistor integrated on the top. Current resistor technology includes: (i) standard polysilicon resistor, (ii) thin-metal-film, (iii) bulk epitaxial resistor and (iv) silicon resistor (so called “SiR-SiPM”). The most used approach is polysilicon resistor: a properly doped polysilicon layer is deposited and lithographically defined at the edges of the SPAD area, not losing FF, and having either direct silicon-polysilicon contact or using metal. A more recent approach is the thin-film-metal resistor [
23], which has a reduced temperature dependence (an important advantage in some applications) and the thin-film is almost transparent (>80% transmissivity), down to about 400 nm. Another approach is the resistor made in the epitaxial layer, exploiting the lateral depletion by the electric field [
24]: it extends from the junction downwards, but at the edges is not limited by the enrichment implant and creates a virtual guard ring. Using small cells and proper epi-doping, the region not depleted in the center of the cell is small enough to create a resistive path to quench the avalanche in the cell. The last one and most recent is the “silicon-resistor” (SiR): a region of silicon is isolated from the central SPAD region thanks to deep trenches, and properly doped (shallow doping) to form an inverted junction where the top (non-depleted) part is the quenching resistor for the SPAD and is directly connected to it at the end (silicon-to-silicon, no contacts needed). This last approach also showed very small temperature dependence of the resistivity value and can reduces the fabrication complexity of about 30% with respect to the polysilicon resistor.
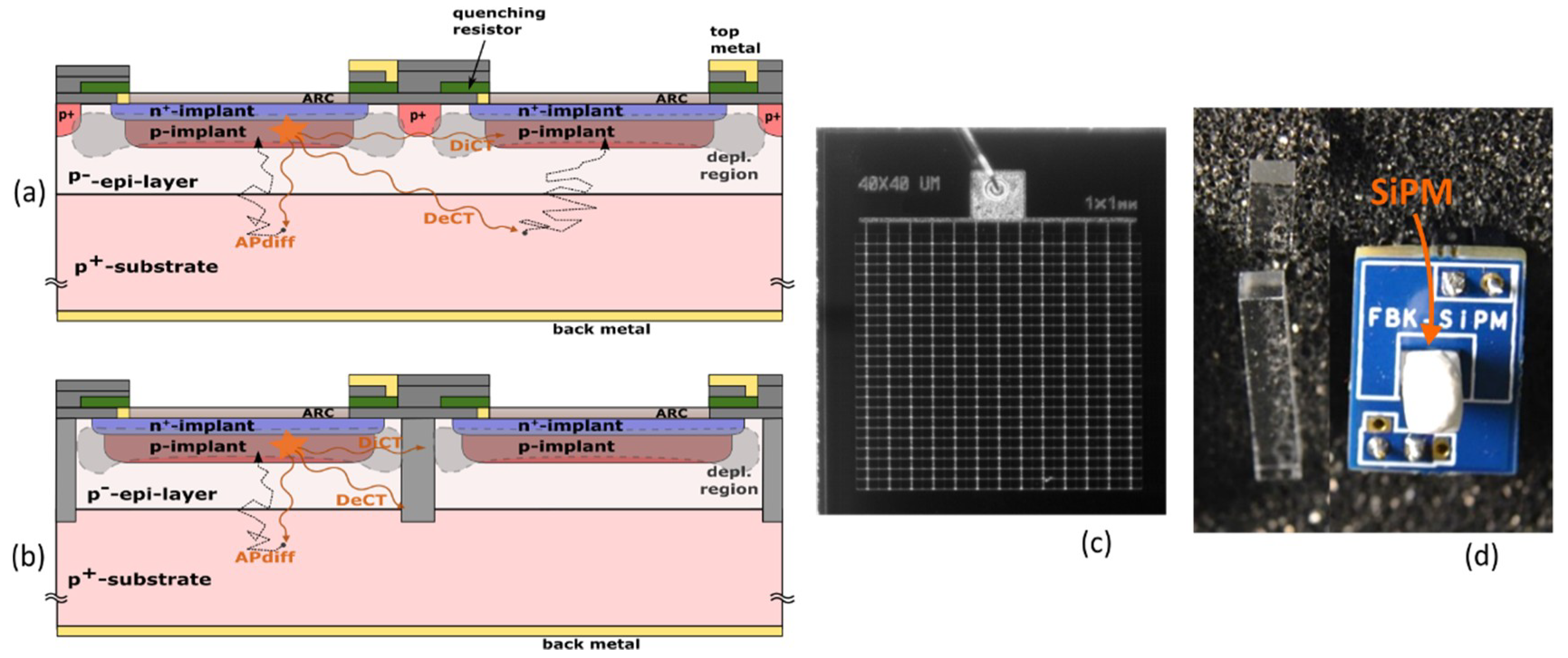
For SiPM made in custom technologies, the substrate is typically a common anode or cathode (depending on the polarity of the junction: n-on-p or p-on-n), whereas the quenching resistors are all connected to a metal grid, thus to a common pad (as shown in
Figure 1a). The layout of the metal grid proved to be very important in the extraction of the signal at high frequencies, thus affecting the overall single-photon time resolution of the SiPMs (particularly for big areas SiPMs) [
25,
26]. An example of comb-shaped metal grid is shown in
Figure 1c. The cells are placed close to each other and electrically-isolated by means of depletion-stop implants (e.g.,
Figure 1a) orwith deep-trenches (e.g.,
Figure 1b).
3. Detection Efficiency and Noise
In SiPMs, the FF is very important. The photon detection efficiency (PDE), in case of no saturation effects (thus more properly “PDE
0”, as explained above) is defined as:
where QE is the external quantum efficiency, i.e., the probability that a photon enters the device (not being reflected at the interface) and is absorbed in the “effective useful region”, i.e., in the depleted region or where it has a certain probability to reach the depleted region without being re-absorbed. This includes the transmittance of the anti-reflection coating (ARC).
Ptrig is the triggering probability of the avalanche, which depends on the position of the photon absorption and e/h pair generation [
27], and the FF is the ratio of the effective active area and the cell overall area. The effective FF can be different from the nominal one (by layout) due to the “border effect”, which is relevant in small and very-small cells, like for example the FBK “ultra-high density” technology with cell pitch down to 5 µm [
28]. Between adjacent cells, there has to be a dead region, which acts as electrical (and possibly optical) isolation between the high-fields regions, where avalanche multiplication takes place. The extension of the dead region, however, limits the FF, thus the PDE.
One possible choice to minimize the effect of the dead border (typically few micrometers) is using a large cell-pitch, e.g., between 50 µm and 100 µm. However, the saturation and another important aspect has to be considered for SiPM: the correlated noise, which depends on the cell dimensions. The larger the cell, the large is the diode capacitance and the higher the amount of charge flowing per each avalanche (so called “gain” of the cell). In single SPADs externally quenched, the amount of avalanche charge can usually be very high (i.e., >108) and dependent on the quenching circuit, whereas in analog SiPMs, the integrated quenching resistor give a more defined and lower (i.e., 105–106) gain. Generally, higher cell gains results in higher correlated noise.
In an SiPM, the noise source can be divided as: (i) primary noise and (ii) correlated noise [
29,
30]. The former is due to thermal generation from the bulk of the cell (possibly field enhanced) or tunneling in the high field region. The correlated noise instead identifies all the spurious avalanches happening subsequently to the primary one (signal or noise generated). Afterpulsing (AP) and optical crosstalk (CT) between cells are the main source of correlated noise. Indeed, as for single SPADs, due to the large amount of carrier flowing per each avalanche, some carriers can be trapped in deep-levels (in the energy-gap) inside the high field region (afterpulsing), and secondary photons can be produced and emitted isotopically. Some of them can reach neighboring cells, be absorbed, and create e/h pairs, triggering a spurious avalanche, i.e., optical crosstalk (as shown in
Figure 1). Optical crosstalk can be called “direct” (DiCT) or “prompt” (pCT), in case the secondary photon is absorbed in the depleted region, or called “delayed” (DeCT) when it is absorbed in the neutral region, and the generated carriers, drifting randomly, reach the depleted region, triggering a secondary avalanche pulse with a certain delay (typically few nanoseconds to tens of nanoseconds). Secondary photons can also be absorbed and generate e/h pairs in the same cell. This can create a spurious secondary avalanche pulse, as well as afterpulsing. This effect is called “optically induced” afterpulsing. Finally, secondary photons can also be emitted outside the cell, but then reflected back by the interface between the protective resin and the air, or by the glass of the package, or by the scintillator crystal surface, when the scintillator crystal is mounted on top of the SiPM, as in
Figure 1d. This is called “external crosstalk” and has proven to significantly increase the optical crosstalk probability [
31]. Electrical crosstalk is typically considered negligible in analog SiPMs: it can refer to signal coupling between metal tracks, which can be important in monolithic SiPM arrays, or charge sharing (or leakage) between adjacent SPADs. The latter is important typically in digital SiPMs or CMOS SPAD arrays, where deep implants need to be used [
32].
Recent SiPM Improvements
In recent years, large effort has been made to improve SiPM performance. Primary DCR has been reduced by more than one order of magnitude, nowadays being around 50 ÷ 100 kcps/mm
2 (kilo counts per second in 1 mm
2 area) [
19,
33]. Photon detection efficiency has been improved significantly, especially in the blue and near-ultraviolet range, reaching values around 60% (FF included) [
27,
33] In such a scenario, an important aspect is the correlated noise, which can be a limiting issue in some applications.
The main important improvements to reduce the correlated noise in the last few years have been: (i) reduction of afterpulsing and delayed crosstalk, thanks to a modified silicon substrate; (ii) reduction of cell size, with proper electrical isolation with trenches; (iii) the filling of the trenches with non-transparent material; and (iv) (recently) crosstalk reduction at the package level [
34]. As already introduced, optically-induced afterpulsing and delayed crosstalk probabilities depend on the photogenerated carrier lifetime in the non-depleted region and particularly in the substrate. Using a lower lifetime material, it was possible to significantly reduce the delayed correlated noise, as reported in [
29]. Another aspect is the cell size. Indeed, there are several advantages in using small cells in a SiPM: (i) reduction of afterpulsing and crosstalk, thanks to the reduction of the gain of the cell, (ii) increased granularity, which gives the SiPM a higher dynamic range and linearity to a higher photon flux [
35], and (iii) higher radiation hardness. The latter is important for example in large physics experiments, where SiPMs are used to build calorimeters. The smaller the single cell is, the higher is the number of cells in the same area, thus minor is the effect of having one cell damaged due to radiation in the overall PDE of the device and the lower is the increment in power consumption for the system. All these aspects are advantageous if the PDE is good, and not worsened because of small cell pitch. Based on these considerations, at FBK, we developed high-density (HD) technologies. For example, RGB-HD technology (cross-section represented in
Figure 1b, and detailed in [
18]), or NUV-HD SiPM technology [
19]. Microcells are separated by deep trenches, with a high aspect ratio: depth of few micrometers and a width of less than one micrometer. Thanks to these trenches, the dead border region can be reduced to less than 2 µm, preserving the electrical isolation between cells. In this case, trenches are filled with silicon dioxide: because of the different refractive index of silicon, they also provide “partial” optical isolation, due to reflections at the interface (which depends on the incident angle). An analysis of the different cell isolation technique in SiPM can be found in [
36]. The active area is defined by high energy ion implantation (enrichment implant), which increases the electric field only in the active area, to reach the avalanche condition. The space between enrichment implant and trench creates a so-called virtual guard ring (VGR), which prevents edge breakdown. In this region, the cell is not sensitive to light. For RGB-HD and NUV-HD technologies, the breakdown voltage at 20 °C is around 28 V and 26 V, respectively, the same as the previous non-HD versions.
4. Measurement Setups and Procedures
The functional characterization of the SiPM performance includes measurement of the photon detection efficiency (PDE), the primary noise, i.e., the primary dark count rate (DCR) and the probabilities of the different correlated noise components. Other quantities can be measured or derived from these, which are useful from the application point-of-view, like for example the excess noise factor (ENF) and the excess charge factor (ECF). The precise estimation of the different noise components is not straightforward, especially with large area SiPMs or generally SiPMs with a high dark count rate. On the other hand, the extremely low dark count rate at cryogenic temperatures can be a problem for noise characterization, since primary pulses are very rare, i.e., distant from each other in time, but each one can have a much closer afterpulsing or delayed crosstalk pulse. In this case, it is necessary to modify the acquisition method in a segmented acquisition mode [
9].
Different methods have been used over the past years by different authors [
29,
30,
37,
38], with pros and cons. Most of them are based on pulse counting mode, i.e., discriminating, thresholding the single pulses (with or without shape filtering or modification) and counting their frequency or extracting their inter-time distribution. This technique requires the possibility to separate single pulses, which might not be possible when the pulse tail is very long and when their frequency is very high, e.g., greater than 10 Mcps (mega counts per second). As described in [
37], a train of pulses is recorded by an oscilloscope or by a digitizer (e.g., 1 ms long output signal traces) and then processed online. In our example, we amplified the SiPM signal with 5000 V/A trans-impedance amplified and used an oscilloscope with 20 GS/s and 1 GHz bandwidth. The signal is filtered with the DLED method (“differential leading edge discriminator”) [
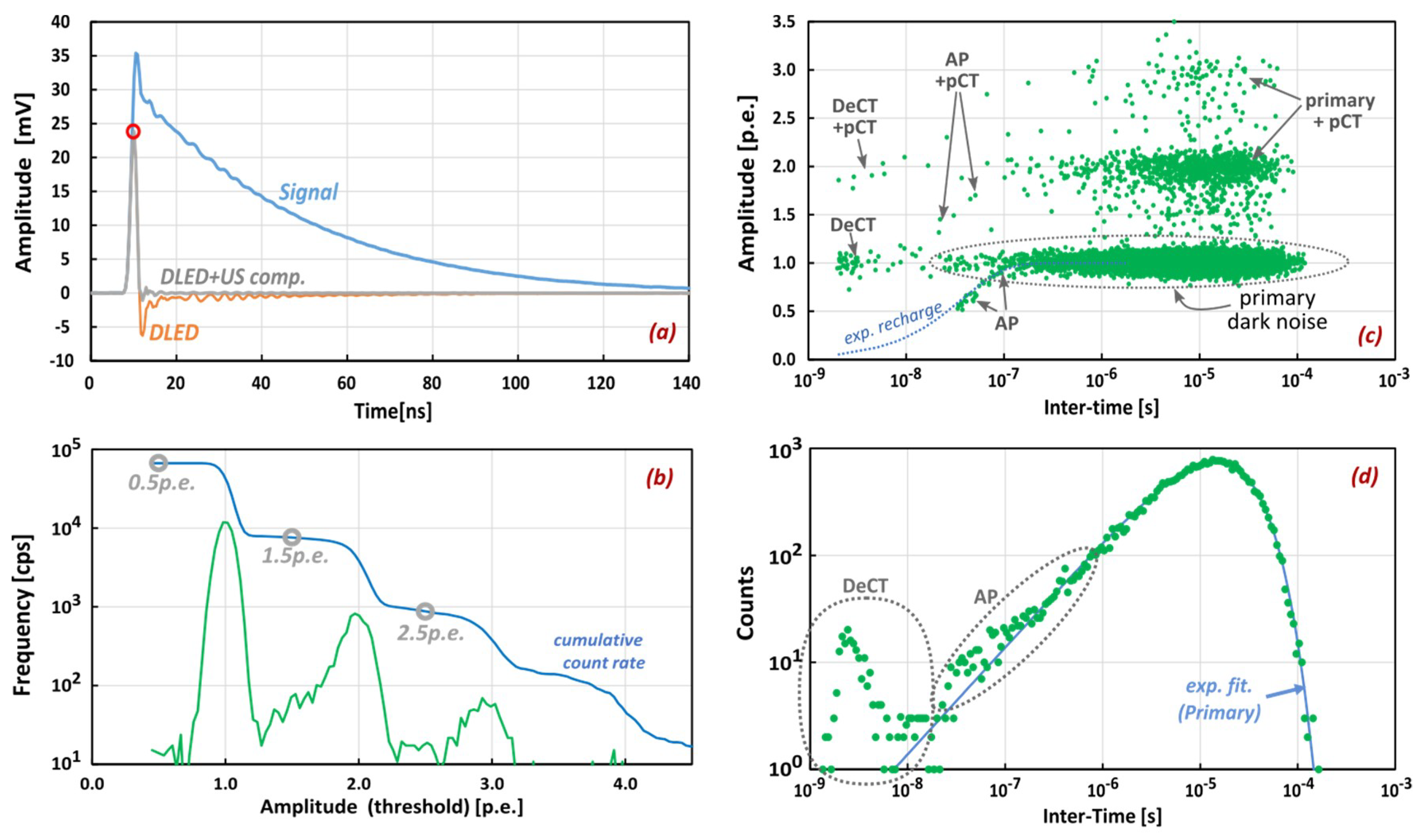
39] (or similar methods), i.e., a delayed copy of the signal is inverted and subtracted to the original signal, creating a sort of high-pass filtering. After that, the resulting undershot is re-summed to the signal, to remove it from the DLED one (see
Figure 2a). The typical undershoot has been previously pre-acquired and then for each acquired pulse it has to be scaled for the amplitude of the pulse and summed to cancel the undershoot in the final filtered signal. In doing so, the long recharge tail of the pulses from the SiPM is avoided and it is easy to identify the peaks’ amplitudes, without the typical pile-up of the pulses. The original signal is also considered to extract the average signal and for average cell gain estimation.
For each identified pulse, amplitude and inter-time (with respect to the previous one) are recoded. Plotting the amplitude versus inter-time, on a logarithmic scale with logarithmic binning, allows to clearly distinguish the events: primary, prompt CT, delayed CT, etc. as in
Figure 2c. To measure the primary dark count rate and the delayed correlated noise probabilities, it is necessary to plot the histogram of the inter-times, like in
Figure 2d. The primary dark count rate follows a Poisson distribution, thus the inter-times have an exponential distribution. To extract the primary DCR, it is possible to fit the inter-time histogram with an exponential function, but considering only the high inter-time part, where no afterpulsing or correlated noise is present. The exponential constant is the dark count rate (DCR). It can also be noted that, in such logarithmic time scale, the peak position of the curve is at 1/DCR. In the plot of
Figure 2c, the cases DeCT+pCT and AP+pCT refers to the cases where, for example, a delayed-CT or an AP is generated and then they create a prompt-CT event.
The exponential fit can be extended (at a first approximation) to the lower inter-time region of the histogram and the difference between the data points and the fit can be used to calculate the afterpulsing and delayed crosstalk probabilities. In particular, in the example, the difference integrated between 20 ns and 2 µs, divided by the total number of acquired events, give the afterpulsing probability; and the difference integrated between 1 ns and 20 ns, divided by the total number of events give the calculated delayed crosstalk probability [
37]. In the inter-time histogram, the amplitude of the pulses is not considered. As a better estimation, the AP and DeCT probabilities should be divided by the average amplitude of pulses: this is to consider, for example, that one pCT event produces just one entry in the inter-time histogram but avalanches in different cells and the subsequent correlated pulses are generated not just by one but by several avalanches. Moreover, despite the described inter-time analysis being relatively simple and effective, it does not consider the correlated effects of dark-counts and correlated pulses, as it is done in [
40]. For example, at short inter-times, primary and correlated noise are both present and there can be lesser events due to DCR than in the absence of delayed crosstalk. If DCR is not high, this issue can be considered negligible.
The amplitude of pulses, instead, is plotted in another histogram, like for example the one in
Figure 2b. In this plot, the amplitude probability density function, highlighting the one photon peak, the two photons peak, etc. as well as the cumulative distribution can be seen. The latter representation is the same of the “popular” DCR vs. threshold plot, where the dark count rate (total, not primary in this case) is plotted as a function of the discrimination threshold used on the output signal. Thus, we plotted in the vertical axis the frequency of the events, whereas the horizontal axis is the amplitude normalized to the single-cell signal amplitude, i.e., equivalent photo-electrons (p.e.). Generally, in the cumulative plot, the direct crosstalk probability can be calculated as the frequency of 2 p.e. events, measured at 1.5 p.e. threshold level, over the probability of having 1 p.e. events, measured at the 0.5 p.e. threshold level.
Finally, to measure the PDE of a SiPM, special care has to be taken to avoid the influence of crosstalk, afterpulsing, and primary dark count rate. One possible measurement method is using a pulsed light source (e.g., pulsed LED, since it does not require very short light pulses) [
27,
41] and the acquisition is synchronous with a light pulse. As in [
27], the light source is mounted on one port of an integrating sphere and a reference diode is mounted on another port to continuously measure the source intensity variations. Another port of the integrating sphere serves to illuminate the SiPM under test, placed at ~10 cm from the sphere, to ensure uniform illumination. The system was previously calibrated obtaining the light intensity ratio between the reference diode on the sphere and at the SiPM location; thus, it is possible to obtain the number of photon at the SiPM by measuring the reference diode current [
27]. By measuring the charge or amplitude spectrum, synchronous with the light pulse, the zero peak (no photons detected) can be identified and via Poisson statistics, knowing the total event number, the number of photons detected is calculated. The number of impinging photons on the detector area can be determined from the reference diode current and knowing the calibration factor, previously determined. As such, the amplitude of the pulses (i.e., 1, 2 or 3 due to crosstalk) is not important and the crosstalk is ruled out. Moreover, the repetition rate of the pulses is relatively low (e.g., 20 kHz) and the effect of afterpulsing inside the acquisition frame or between successive frames is also avoided.
Other methods can be used for the PDE measurements, like applying the inter-time discrimination method described above with and without light, extracting the primary count rate and dark count rate [
27].
Other quantities can be useful, for example, the excess charge factor (ECF) is a number that identifies the extra charge produced by each primary event, because of the correlated noise. It is higher than one, and for example if it equal to two, it means that on average each primary generation event creates one primary pulse and another one. The reverse current at the given bias above breakdown is:
where
q is the elementary electron charge. Thus, ECF is basically the ratio between measured charge (
Qout) and the charge that would have been produced in absence of correlated noise (
Qprim). The excess noise factor instead quantifies the enlargement of the charge (or amplitude) distribution with respect to the pure primary Poisson statistics because of the correlated noise:
5. High-Density SiPMs for Visible and NUV Spectral Range
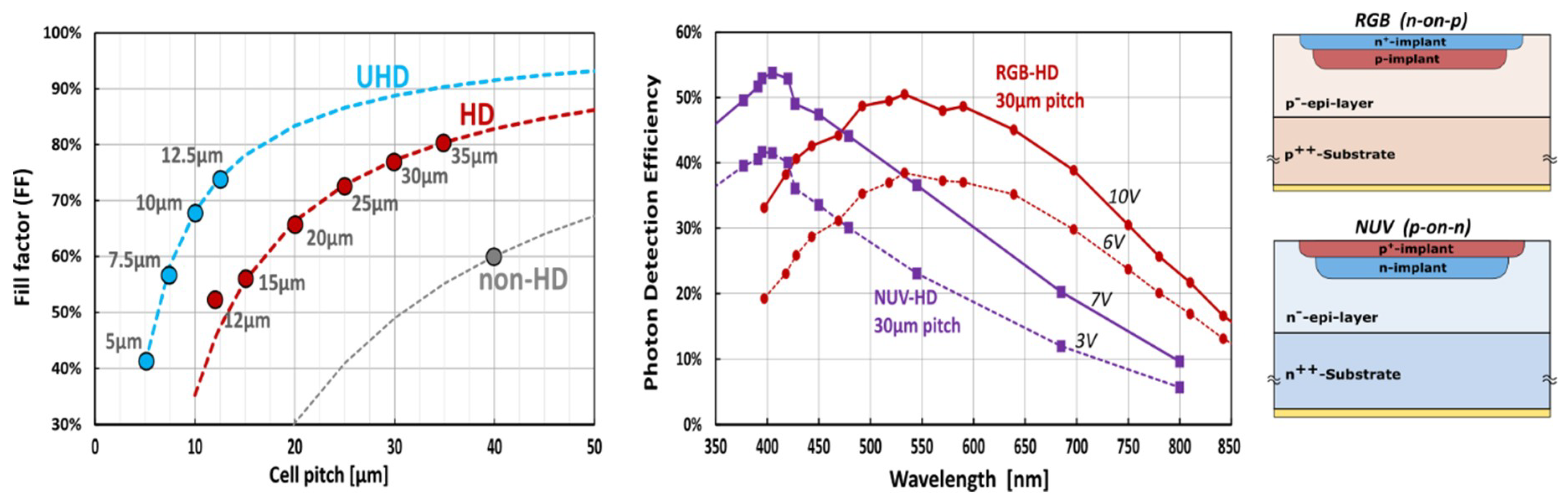
FBK RGB-HD technology identifies the SiPMs and SPADs produced with p-type substrate and with n-on-p junction type, as represented in
Figure 1. Electrons trigger the avalanche when they come from below the high electric-field region, i.e., below the junction, whereas holes trigger the avalanche coming from above the junction. Because of the different ionization coefficients, electrons have typically higher probability to trigger the avalanche, and the triggering probability for electrons saturates earlier (with lower overvoltage) than for holes. Indeed, green and red wavelength photons are absorbed mostly (but not all) beneath the p-n junction, having an absorption depth of a few micrometers. Among the photo-generated electron-hole pair, the electron is drifted towards the high field region and can trigger the self-sustaining avalanche. Instead, blue-wavelength photons are absorbed above the high-field region, where the hole will drift towards the high field region and can trigger the avalanche, with a lower triggering probability. This difference produces the different spectral PDEs shown in
Figure 3 (NUV and RGB ones), where the peak for RGB-HD is at about 500 ÷ 550 nm. In this technology, the distance from high-field region and the trenches, as well as the trench width are critical dimensions of the technology and have been minimized as much as possible, to increase the fill factor, thus PDE. There are technological limits in the trench width and the distance with the high-field region cannot be reduced too much to avoid having a high electric field at the silicon/trench interface, which has a high defect concentration.
Several cell sizes have been fabricated, each one featuring a different trade-off between PDE, correlated noise, and linearity. Indeed, linearity is strongly affected by cell density and cell recovery time [
35]. The plot of the FF as a function of the cell pitch (CP) is reported in
Figure 3, comparing HD technology to the previous non-HD, thus with a higher dead border region. The total dead border region was about 3.5 µm in old technology (per side) and now it is less than 2 µm (including half of trench width). In this plot, the new “ultra high density” (UHD) technology is also represented, featuring very small cell pitches for the state-of-the-art SiPM, between 5 µm and 12.5 µm [
28].
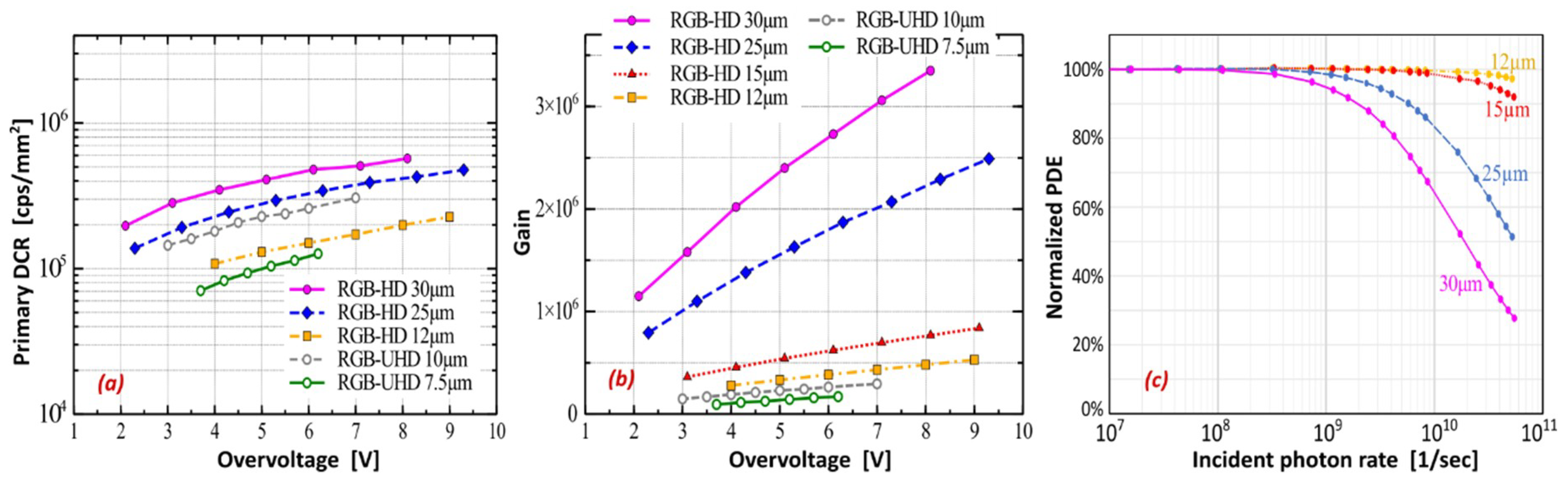
In all these technologies, care has been taken to avoid high electric field enhancement in the regions with high defect concentration and generally, to have noise as low as possible. The typical DCR per 1 mm
2 active area is reported in
Figure 4, being 100 ÷ 400 kcps/mm
2 at 5 V of overvoltage, at 20 °C. The values reported vary because of the FF and due to the variability over the production runs. The gain of the cells is approximately proportional to the cell area, thus increasing with cell pitch, being ~2.4 × 10
6 at 5 V overvoltage for 30 µm cell pitch and reducing to ~0.5 × 10
6 for 15 µm cell pitch and even smaller for UHD SiPMs with cell pitch down to 7.5 µm. The optimal cell pitch depends on the application requirements: small cells have typically smaller PDE at single (or few) photon level (PDE
0) but higher linearity up to high photon flux and lower correlated noise at a given overvoltage. Vice versa for big cells, the PDE
0 is higher, but effective PDE saturates earlier, as represented in
Figure 4c.
For detection in the blue and near ultraviolet region, NUV technology is more appropriate. FBK NUV-HD SiPM technology [
19] features deep-trench isolation, cell-layout and FF values similar to the RGB-HD technology, despite the completely complementary fabrication process, but it is based on a p-on-n junction type, on a n-type epi/substrate silicon material. In such configuration, electrons photo-generated above the junction, i.e., close to the surface, can trigger the avalanche, whereas on the contrary when photon absorption happens below the junction, holes are drifted towards the high field region, and have a certain probability of triggering the avalanche. Conversely to RGB-HD, because of the higher triggering probability of electrons, the spectral PDE is peaked at 400 nm (as shown in
Figure 3) and decreases at higher wavelengths. Blue-wavelength photons are absorbed above the junctions and photo-generated electrons (not holes) can initiate the avalanche multiplication. Avalanche triggering probability would increase faster and saturate with a few volts of overvoltage. As shown in
Figure 3, PDE is already higher than 40% with 3 V of overvoltage. NUV-HD have been improved in the last years, as well as other state-of-the-art SiPMs technologies available in the market. They feature a dark count rate level, lower than 100 kcps/mm
2 [
19]. Thanks to the reduced lifetime n-type substrate [
29] combined with trench isolation between cells, the delayed correlated noise probability is just few percent [
19].
Optimizations of NUV-HD Technology
In applications like Cherenkov Telescopes, SiPMs are used in the presence of a significant night sky background light and the reduction of the random events trigger is important. In the standard NUV-HD technology, trenches are filled with silicon dioxide (SiO2), providing electrical and partially optical isolation. To further reduce crosstalk probability, we redesigned the trench structure, adding a layer of highly doped polysilicon as light absorber inside trenches, realizing a multi-stack of SiO2 and Poly-Si. Unfortunately, it is not possible to use thick layers of polysilicon, which would absorb many of the produced secondary photons, because the trench width has to be minimized, to have a high FF. We measured a reduction of the crosstalk probability of ~35% for NUV-HD-lowCT with respect to the standard NUV-HD. The lower crosstalk probability also offers another advantage to the SiPM: the maximum operating bias voltage is increased, i.e., where the correlated noise become too high and the detector is no more usable.
Another optimization is the SiPMs DCR and afterpulsing reduction for their use in cryogenic applications. Experiments employing SiPMs for the readout of liquid noble-gas scintillators usually require the detectors to be operated at cryogenic temperatures and cover very large sensitive areas. For example, for the development of the “DarkSide 20k” experiments, using LAr, emitting at 128 nm, SiPMs will be coated with TPB (Tetraphenyl butadiene) wavelength shifter, re-emitting at 420 nm. NUV-HD technology has been significantly improved and optimized to work at cryogenic temperatures [
9], through: (i) a decrease of the primary noise generation (DCR), (ii) a reduction of the quenching-resistor value variation with temperature, and (iii) reduction of the afterpulsing probability at very low temperatures. These important developments required several studies of SiPMs behavior in a large temperature range. They also require a microcell structural modification and variation in the manufacturing process to reduce the afterpulsing at very low temperatures.
DCR dependence on temperature have been measured down to 40 K. At very low temperatures, the pulse rate in dark becomes very small and the measurement of the DCR can be very sensitive to any electric interference and noise from the front-end amplifier, which has to be properly designed to work at cryogenic temperatures [
42].
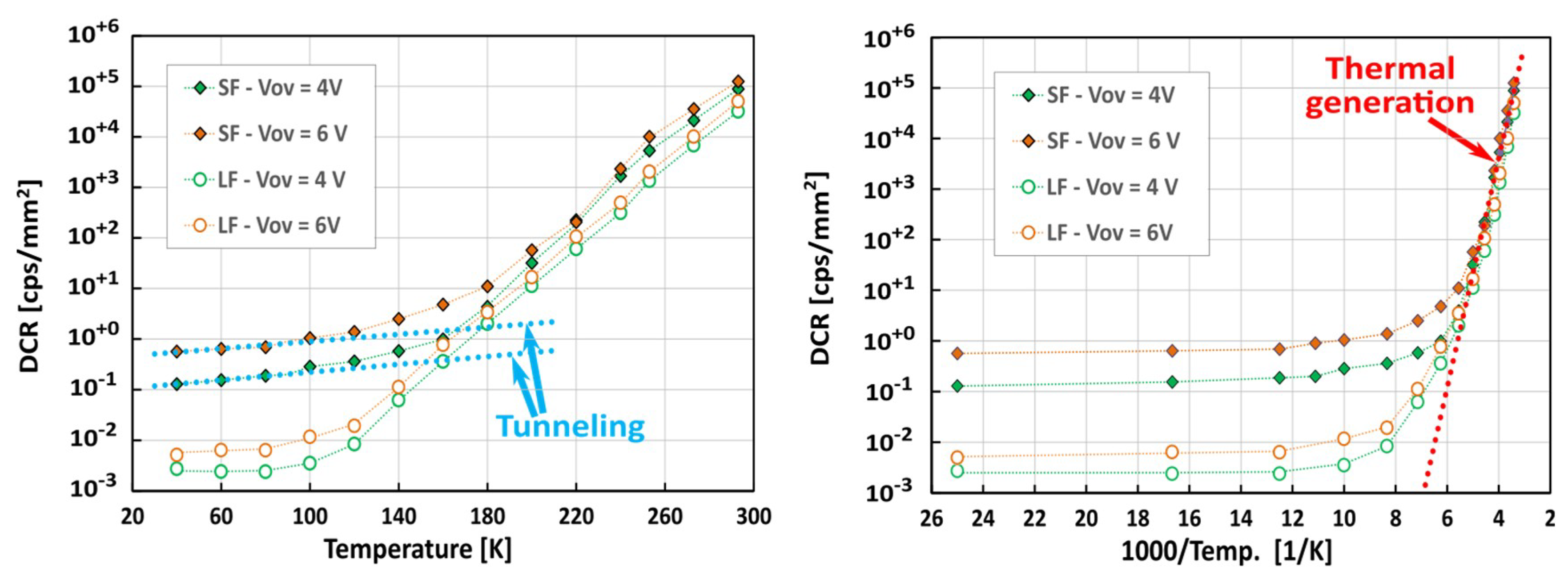
Figure 5 shows the measured primary DCR of SiPMs with 25 µm cell pitch, from two NUV-HD versions: standard electric field (SF) and low electric field (LF) [
9]. DCR reduces significantly in such big temperature range, of more than five order of magnitude and more than seven order of magnitude for the two versions, respectively. The effect of the lower electric field in the LF version is evident in reducing the tunneling generation component [
43]. Breakdown voltage increased to 32.5 V (at 20 °C) in NUV-HD-LF with respect to 26 V of the SF. At temperatures higher than 200 K, thermal generation dominates with field enhancement. At temperatures lower than 100 K, the tunneling generation is dominant and the dependence on the overvoltage is much higher: DCR rises exponentially with the overvoltage. At 80 K, we measured a DCR of a few 10
−3 cps/mm
2.
6. VUV-Sensitive SiPMs
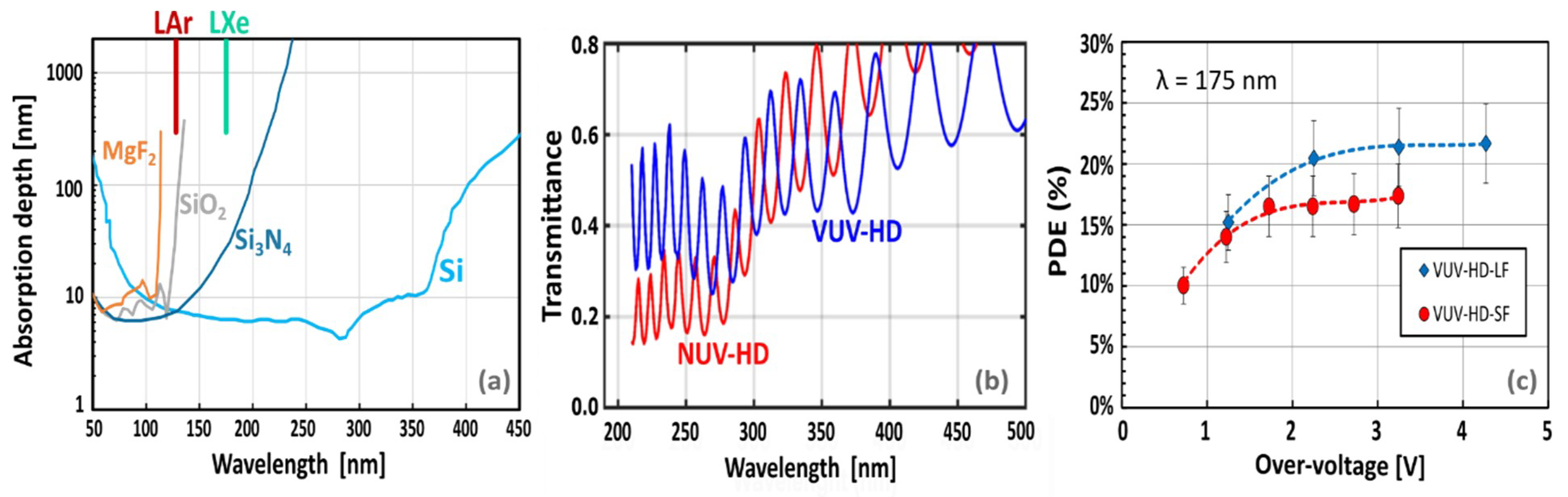
For scientific experiments using liquid Xenon as a scintillator, it is necessary to develop SiPMs with good photon detection efficiency in the vacuum ultraviolet (VUV), particularly at 175 nm (LXe scintillation wavelength). Starting from the NUV SiPMs, we noticed two main limiting factors: (i) presence of Anti-Reflective Coating (ARC) not optimized for VUV light detection and (ii) low penetration depth of VUV photons in silicon. Indeed, photons are absorbed in the first few nanometers from the surface, where typically there is a neutral region. ARC is generally made by SiO
2 and Si
3N
4 layers, but these materials, transparent to the visible light, start to absorb significantly at wavelength < 250 nm and < 150 nm, for Si
3N
4 and SiO
2 (
Figure 6a) [
44].
We began development of VUV-sensitive devices, particularly for the nEXO experiment [
8]. In the first version of VUV-HD, we modified the ARC, removing some of the dielectric layers on top of the silicon that absorbs VUV photons, but preserving a good passivation quality.
Figure 6b shows the simulated total transmittance in the silicon of VUV-HD ARC, compared to the standard NUV-HD. Simulations were carried out assuming normal light incidence and considering air as a surrounding medium. NUV-HD has higher transmittance at wavelength >300 nm, but it rapidly decreases at shorter wavelengths, mainly due to the Si
3N
4 absorption. On the other hand, the VUV-HD ARC transmittance remains in the range of 30–50% at wavelength < 200 nm, despite the small values in the visible range. The oscillations in the spectrum are due to light interferences in the multi-layers stack.
Figure 6c shows the measured PDE vs. overvoltage measured at 169 K in LXe at Stanford for both Low-Field and Standard-Filed technologies, as described in [
20]. Absolute measurement are not straightforward in this wavelength range, and typically two methods are employed: (i) relative spectrum measurement up to the visible range and then calibration in the visible range of the whole spectrum, or (ii) absolute measurement at the wavelength of interest through calibrated detectors (like PMT), in place of the SiPM. We observed a PDE value of more than 20% at 175 nm. For the experiment, another important optimization point is the reflectivity of the SiPM surface. Its high reflectivity (about 50%) is due to the large differences of the indices of refraction between silicon (nSi = ~0.682 at 175 nm [
45]), silicon dioxide (nSiO
2 = 1.61) and LXe (~1.66). R&D is still ongoing. Different materials (MgF, Al
2O
3) are considered for the ARC, or multi-layers stacks.
7. NIR-Sensitive SiPMs
The last optimization done in FBK increases the PDE towards the red and NIR wavelength region. New applications like LIDAR strongly push for highly sensitive single-photon detectors like SiPMs at wavelengths between 850 nm and 950 nm. At 850 nm, for example, the absorption length of silicon is about 18 µm. It is necessary to increase the epitaxial layer thickness to increase the internal QE of the device. In the first production runs of NIR-HD SiPM technology, based on n-on-p junction type, we used 8-µm (nominal) thick epitaxial layers [
22]. However, this also means increasing the trench depth, without changing the width, thus requiring a higher aspect ratio.
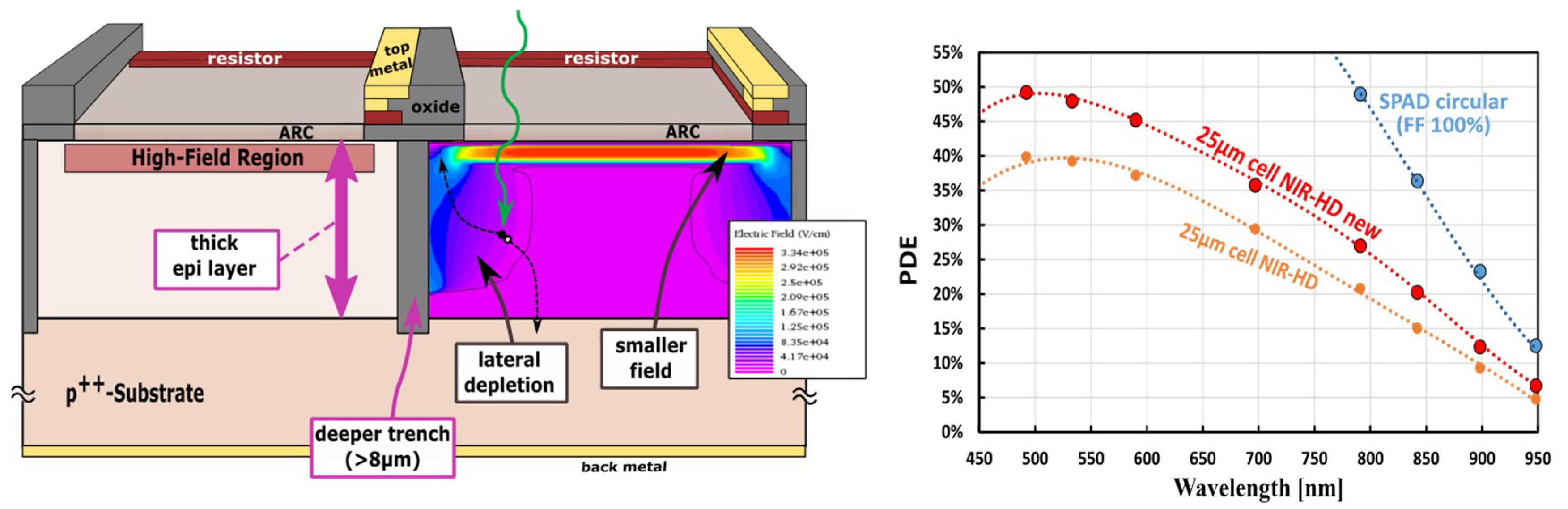
There are other structural intrinsic issues as well, related to the border effect. As described in [
22], because of the virtual guard ring approach in the cell, the effective high-electric-field region is smaller than the nominal one (defined by layout), as shown in
Figure 7. Moreover, there is also a significant lateral depletion at the edges of the SPAD, beneath the junction, where photo-generated carriers (electrons in this case) are drifted laterally instead of vertically towards the top, thus not being able to trigger the avalanche and being undetected. These border effects are more important for thicker epi-layers than for thin-epi. In particular, the lateral depletion is much higher.
One possible approach to overcome these problems is using relatively big cells, e.g., 50 µm pitch or more. In such a way, the central area with a high electric field is bigger compared to the edge. However, applications like LIDAR would benefit from SiPMs with small cells, thus having lower crosstalk, lower afterpulsing, and faster cell recharge, to have less “blinding effect” due to background light or light flashes. However, small cells with a thick epi-layer suffer more from the border effect. The benefit of thick epitaxial layers in terms of the QE in the center of the SPAD can be counterbalanced by the smaller effective FF because of the bigger borders.
In the first production of NIR-HD devices, we manufactured SiPMs and SPADs. The same layouts have been implemented on the thin epi-layer and thick epi-layer silicon wafers, to have a direct comparison of the performance. Particular care have been taken to have the same breakdown voltage for both the thin-epi and the thick-epi devices, with the same low temperature dependence. This feature can be very important in industrial and automotive applications where it is important to avoid big bias correction during system operation: smaller breakdown voltage variation leads to smaller performance deviation with temperature. We measured for both versions a breakdown voltage at 20 °C between 27.5 V and 27.9 V (variations over the produced 6” wafers) with a temperature variation coefficient of ~27 mV/°C.
We also measured and compared the other functional performance of NIR-HD SiPMs: primary dark count rate is between 600 kcps and 1 Mcps per millimeter square of active area, at 5 V of overvoltage. This is slightly higher than the thin epi SiPMs (being around 300 kcps per 1 mm2) and is likely due to the bigger depleted volume, thus higher bulk thermal generation. The direct crosstalk is another important parameter, like in LIDAR, to avoid spurious triggering due to background light random-photons, which might reach the settled threshold level. In such applications, DCR vs. PDE and CT probability vs. PDE could be considered as a figure of merit plots. In NIR-HD SiPM, the direct crosstalk is about 24% and about 12%, at 5 V of overvoltage, for 35 µm cell pitch and 25 µm cell pitch respectively. The relative values of the gain are 2.6 × 106 and 1.25 × 106.
Concerning PDE, the results obtained with first NIR-HD SiPMs were promising, but to overcome the border effect issue, we developed an improved version. This required further analysis and TCAD simulation. The results was a modification of the internal structure of the microcell, to limit the border depletion. The effective electric field part is now wider but preserves a lower field value at the silicon/trench interface. Moreover, according to TCAD simulation, the lateral depletion has been also reduced. The measured PDE of 25 µm cell-pitch NIR-HD SiPM and of the 25 µm cell-pitch NIR-HD improved-version are shown in
Figure 7. PDE has been increased from ~15% to ~20% at 850 nm, at 8 V overvoltage (FF included). In the same plot is also reported the PDE of a circular SPAD (from same production wafer) with a metal ring shielding the active area edges, thus indicating the effective maximum PDE that would be reached with 100% FF.
8. Conclusions
We presented a general description of the analog silicon photomultipliers (SiPMs) and of the main structural improvements made by the manufacturer over the last years. Applications like PET, big-energy physics experiments and LIDAR are pushing strong improvements in this field. At FBK (Trento, Italy), we differentiated and developed SiPM technologies to fit different application requirements, especially in terms of spectral sensitivity. Indeed, SiPMs are promising solutions for experiments and industrial products operating in the VUV, NUV, visible and NIR spectral range.
Performance characterization is not straightforward, due to the presence of primary noise pulses together with optical crosstalk, delayed optical crosstalk, and afterpulsing. Most promising methods are based on the analysis of the amplitude and the inter-times between pulses to distinguish their nature. This typically requires an online high resolution sampling instrument (e.g., oscilloscope) and an online analysis tool, able to filter the signals, eliminate the slow recharge tails of the pulses, identify the peaks, and plot pulse information. However, there are different methods used in the literature and they all have some limitations; for example, when the count rate is high or when operating at cryogenic temperature and the rate is extremely low.
Despite being diffused in many applications, technological optimization is still a hot topic for SiPM. For example, VUV sensitive technologies require a study and modification of the anti-reflection coating and possibly the use of completely new materials to improve photon transmission and reduce reflectivity in liquid noble gasses. As another example, different manufacturers are now intensively developing NIR-sensitive SiPMs, particularly for automotive and industrial LIDAR. The QE of the SPADs composing the SIPM have to be improved through a deeper epitaxial layer, but the FF is also very important and has to be kept high. Border effects start to become important and the structure of the microcell has to be re-designed to reduce this effects, thus increasing the effective FF.