2.1. Theoretical Derivation
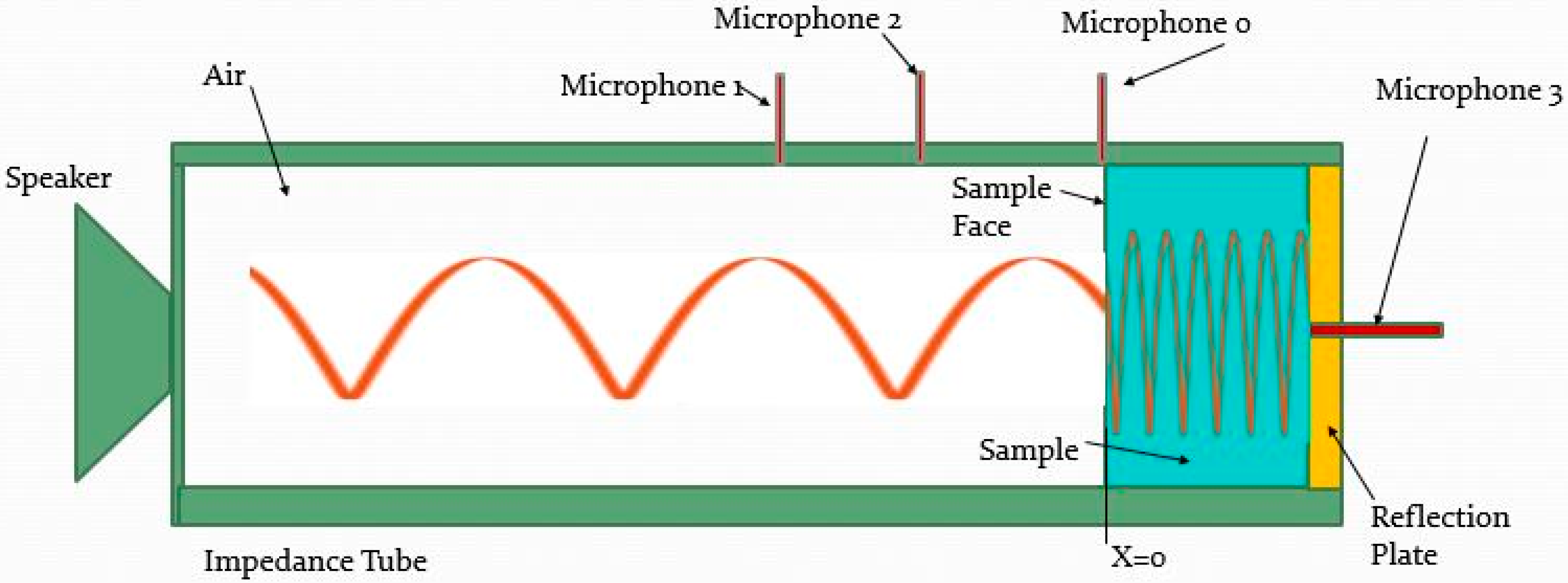
The acoustic testing apparatus for this research utilizes the impedance tube, otherwise known as Kundt's tube. The tube is a resonant structure whereby sound is inserted into one end and is reflected at the other end, yielding standing waves inside the tube that are then analyzed to extract the acoustic properties of the material under evaluation. This type of acoustic testing has a rich history for evaluating open-cell porous media for the prediction of performance properties of various materials used in noise-abatement applications [
1,
3,
4,
7,
12,
13].
Sound radiation inside an impedance tube can be modeled as an incident plane wave “Pi” traveling in one direction that is combined with a second reflected wave “Pr” traveling in the opposite direction [the “P” denotes the pressure of the wave] [
9,
12]. This simple model performs admirably in the prediction of the standing wave phenomena that occurs inside the impedance tube. Augmentation of the model allows for predicting the influence of an inserted material on the propagating waves. In the time domain, the two waves are typically modeled utilizing the following complex-valued equations (where complex vectors are constructed from phase and magnitude values of the pressure waves, known also as phasors):
where P
i(x,t) is the incident wave as a function of x and t, P
r(x,t) is the reflected wave as a function of x and t, |P
i| is the magnitude of the incident wave, |P
r| is the magnitude of the reflected wave, t is time (s), j is complex value where j = sqrt(−1), and x is position with respect to the sample surface (m). The propagation wave number of the acoustic wave in air (rad·m
−1) is given by k
o, and ω is the frequency of the sound wave (rad·s
−1).
Equations (1) and (2) are then translated to the frequency domain and combined into Equation (3):
where P(x) is the pressure at location x, k is the propagation wave number of the acoustic wave inside the material (rad·m
−1).
For use in the development of the model,
Figure 1 shows the schematic outline, which also indicates key microphone locations along with the x-position definition.
Utilizing this map, Iwase et al. [
14] provided the following derivation to develop the three-microphone method (using microphones 0, 2 and 3 positions as detailed in
Figure 1). As the derivation of interest for this article will be taking this model in a different direction, we will reproduce the initial derivation here so that it becomes clear where we deviate and branch off to the new proposed alternative technique, hereafter known as the “simplified Iwase method” (SIM). Of note is that the modern variant of the three-microphone method omits microphone 3 and practices the two-microphone method to obtain the reflection coefficient utilizing microphones 1 and 2. Thus, in essence, this derivation also extends the standard two-microphone methods [
5,
6], whereby microphone positions 1 and 2 are located as in the standard methods. As such, it begins utilizing the same approach that was used in the two- and three-microphone methods’ development. Equation (4) details the pressure wave as measured by a microphone located at position 1, where the measured pressure is due to both the incident and reflected waves (P
i and P
r, respectively):
Equation (5) details response for the microphone at position 2:
Iwase, in his report, added an additional microphone, at the face of the sample, labeled microphone 0 (
Figure 1). The response for microphone 0, at x = 0, provides Equation (6):
where P
M0 is the pressure at the location corresponding to microphone 0.
From wave theory, a plane wave in a source-less region propagating along a one-dimensional path can be used to model the effect of the material on this wave by utilizing the complex propagation coefficient for the material: γ = α + jβ [
6,
12], where α is the material propagation attenuation constant and β is the material propagation phase-delay constant. Including the propagation constant for the material allows for characterizing P
r in terms of P
i, as modified by transport through the material twice (forward and back). Of importance to note here is that for many materials, reports have been provided for which α is not constant across the frequency spectrum and is, for some materials, a function of the frequency [
15,
16,
17]. Prime examples of materials that exhibit this behavior are water, metals and other crystalline objects [
18]. The literature reports, noted above, report success in utilizing a simple power-law model that describes how α changes with frequency, and is shown here for convenience in Equation (7):
where η is the exponential correction term, α
o is a very low frequency value for the propagation attenuation constant α, and f is the frequency (Hz).
The advantage of utilizing the propagation constant of the material is that it allows for modeling how the wave is modified as it propagates through the material under test, which can then be used to provide an estimate of absorption characteristics as the sample size changes. In the analysis, α is brought in via a transition from Equations (6) and (7) to provide Equation (8):
where R is the reflection coefficient (dimensionless).
Combining P
i and P
r yields the pressure P
f at the sample surface (location of microphone 0), which is shown in Equation (9); noting P
r = P
i e
(−2γd) provides
Also of interest to the derivation is the pressure that occurs after the sound propagates through the material to arrive at the rear of the sample, at the location of microphone 3, which is written as Equation (10):
The rear of the sample is backed by a near-perfect reflector; thus, in addition to the incoming wave P
bi, there is also the reflected pressure wave, P
br, at the microphone 3 location and shown as Equation (11):
As the incident and reflecting pressure waves are co-located at location 3, the microphone measures
The next step utilizes the ratio of measurements taken at the microphone face (location 0), with respect to the microphone on the backside of the sample, at the hard reflector (location 3). This yields the transfer function between locations 0 and 3. At this point we deviate slightly from the Iwase approach and simplify the ratio utilizing hyperbolic trigonometric identities:
Then, utilizing a hyperbolic identity leads to
This can then be inverted to provide the acoustic propagation constant as shown in Equation (13), which provides the basis for our proposed two-microphone variant of the three-microphone method, hereafter termed the CSMM method, Complex-Single-Microphone-Method, which could also be performed with two microphones at locations 0 and 3; as opposed to the ASTM E1050 two-microphone method that utilizes two microphones at locations 1 and 2.
For the computation of the reflection coefficient, we note that it is not necessary to utilize two internal microphones, as per the applied method in the normal application of the three-microphone method (Salisslou). In lieu of this, we note that R can be computed directly from the propagation coefficient γ per Equation (14), which is a re-statement of Equation (8):
Of importance to note here is that Equation (13) requires the use of the complex quantity H30; as such, the measurement must measure the phase as well as the magnitude.
For a simpler experimental variant of the CSMM method, we examine the potential for the removal of the phase measurement from H
30. Starting with the definition of H
30,
We then break out the attenuation from the phase, yielding
In the time-domain, this becomes
which unfortunately is not readily transformed to a simpler form that can utilize only the magnitude. It is instructive to note, however, that the results suggest that errors will result if phase information is ignored. Hence, this derivation will now pivot to an alternative approach.
From this point we extend beyond the Iwase solution to create an equivalent single-microphone method (SSMM, Simplified-Single-Microphone-Method) that provides the benefits of a near-equivalent measurement with the benefits of providing a lower cost and easier method to put into practice, with much flexibility in the final form of the apparatus.
In moving forward to the new proposed SSMM, we propose a formulation basis for a method that only requires a single microphone or sound meter installed into the end of the tube. Use of a sound-level meter is particularly advantageous, as then no other instrumentation will be required, and results can be easily calculated from a few readings on the sound-level meter. The drawback to the sound-level meter is that as it is integrating over the spectrum, two samples could provide the same reading, yet yield very different responses across the spectrum. Hence, we recommend this approach is only used for screening purposes, and for all others, it is better to collect the data with a microphone and oscilloscope or audio data-acquisition system. The different versions of this new SMM, {SSMM or CSMM} protocol will be discussed in detail in a later section. For this section, the theory showing the equivalence for using a single microphone to obtain equivalent readings will be detailed next.
The basis for the proposed new SMM formulation is to take two measurements at the microphone 3 location (at the back of the material against the hard reflection plate;
Figure 1). The first measurement is performed with the material inserted into the sample holder, and the second measurement, an air reference, is performed without the material under test. The following derivation follows the two-microphone and Iwase theoretical derivations. The derivation for this approach looks to establish a simpler formation of a transfer function between the air reference reading, that is then taken with respect to the measurement with the material in place, yielding a new transfer function H
33 as shown in Equation (15), using Equation (12) as the expression for P
M3:
Given that over the short distance of d, α
air = 0, then converting into the time domain leads to Equation (16):
Then, a simplification of Equation 16 leads to Equation (17):
where θ = d(β − β
air) is the relative phase between the sampled signal to the air reference reading.
Of importance from this relation is that in the time domain, the cosine term of Equation (16) is only relevant to the phase of the signal, as the peak-to-peak signal is solely controlled by the attenuation term e
(−αd). Hence the attenuation of the signal, as induced by the presence of the sample, is readily obtained by measuring the time-averaged signal strength with and again without a sample in the test cell, and then taking the ratio of the two measurements. In practice, the measurement of the sound pressure level utilizes a measurement of the root-mean-squared (rms) value of the signal, which in the discrete form of a time-averaged version of the magnitude of H
33 is provided by Equation (18):
where |H
33|
RMS is the rms estimate of the magnitude of H
33, and n is the number of readings to perform the sum of squares over.
Noting further that the rms value of a sinusoid is equal to the amplitude of the signal divided by the square-root of two allows for further reduction, which leads to the result from the time-averaged reading of Equation (18) to be simplified to the form of Equation (19). This application can be performed by replacing the sinusoidal oscillator with a measurement of the peak-to-peak or rms voltage, as shown in Equations (17) and (18), for the sample and air reference readings, which in the ratio, drops the input signal out to yield the magnitude ratio |H
33|
RMS that provides Equation (19).
From Equation (19), a simple inversion provides the acoustic material propagation attenuation constant α of Equation (20) that is the final form of the SSMM method.
For the determination of the normal incident acoustic absorption coefficient ρ, this can be computed using the reflection coefficient, by using α as determined from Equation (20) to compute |R|, as detailed in Equation (8), to provide ρ, as shown in Equation (21).
where |R| = e
(−2dα) (Equations (8) and (14) re-stated for clarity), and ρ is the acoustic attenuation constant (dimensionless; range of 0–1).
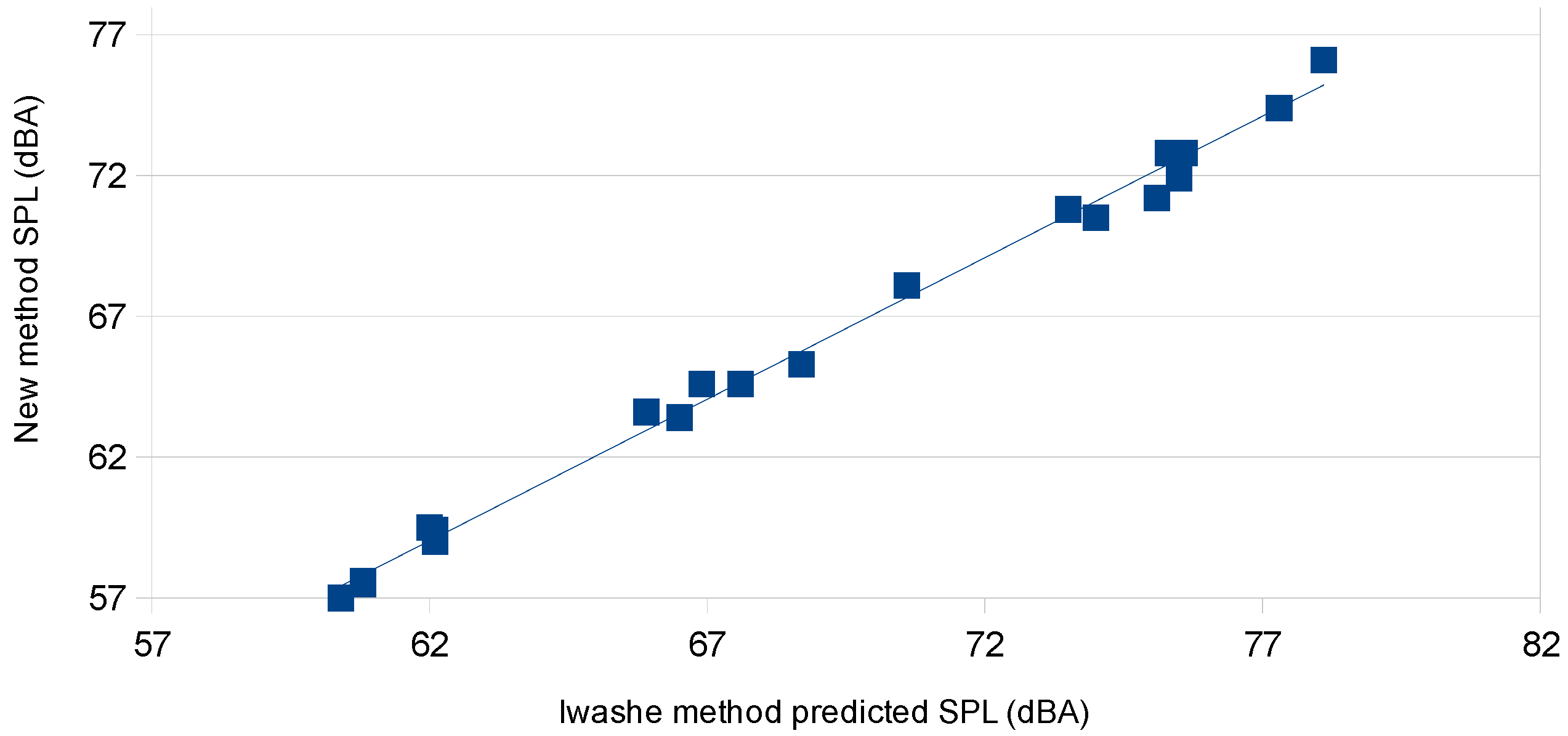
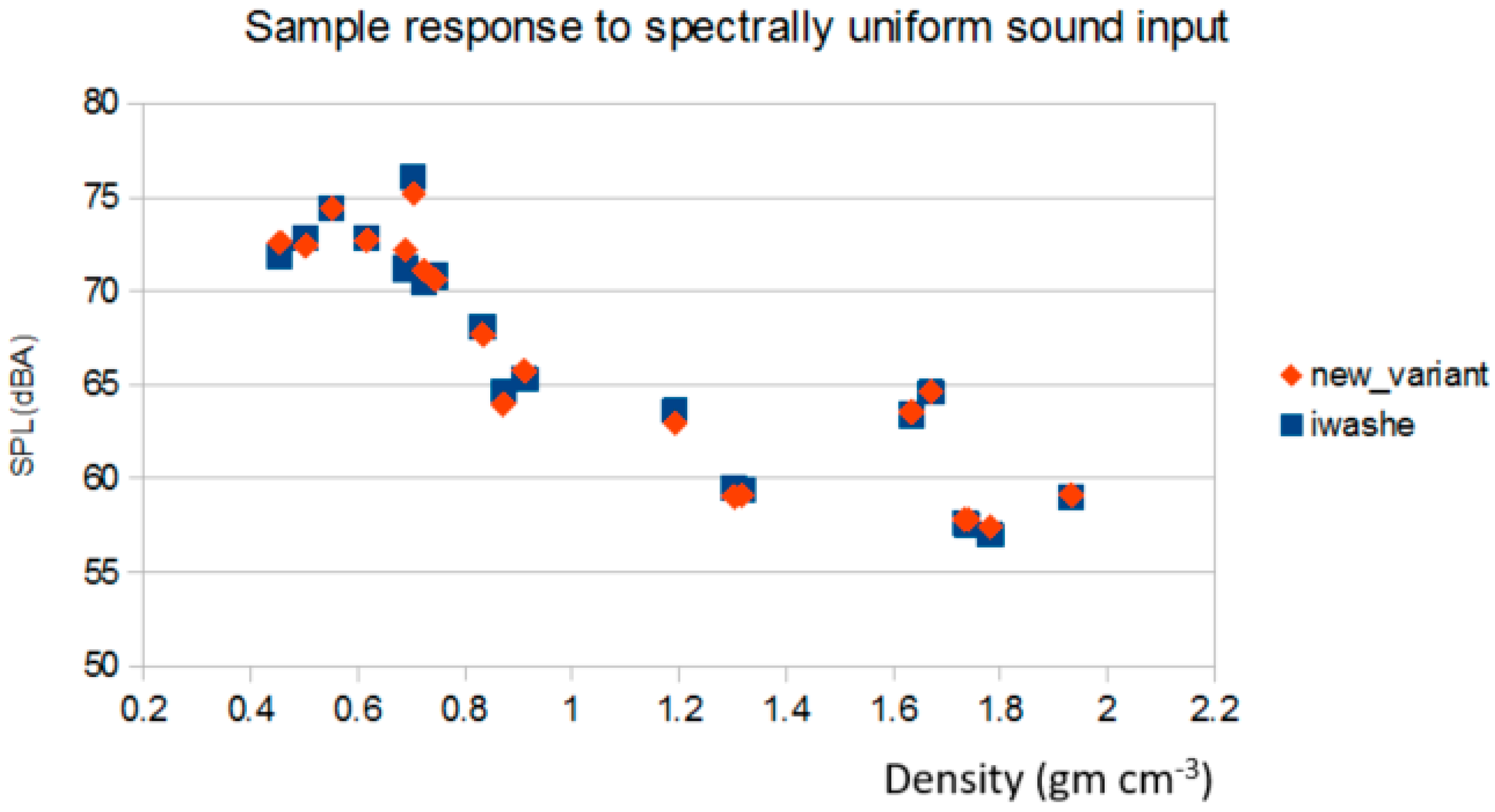
In summary, the equivalence derivation shown above provides the basis for two variants to obtain the acoustic reflection coefficient and the material’s propagation absorption coefficient. The first method, CSMM, provides a mathematically equivalent (identity) method to that obtained by the two-microphone method of ASTM E1050. Of particular interest is that the CSMM method not only provides R, but also provides a true measurement of the through-transmission propagation coefficient γ = α + j β, which is not available from the two-microphone approach. CSMM does this by capturing the single-microphone relative amplitude and relative-phase information. As such, it provides the primary information that is currently only obtainable utilizing the three- or four-microphone methods; which results in considerable savings in equipment and complexity, as it only requires two microphones, pre-amplifiers and data-acquisition channels. The next variant this analysis provides is the SSMM method, which is a low-cost means for the determination of the primary material acoustic of the propagation attenuation coefficient α. Where the SSMM method only captures the single-microphone relative amplitude information. In addition, this can be achieved from a greatly simplified acoustic test apparatus that can be as simple as a single microphone or a sound meter mounted onto the end of the tube. As with any new proposed method, of primary interest is the expected accuracy.
2.2. Accuracy
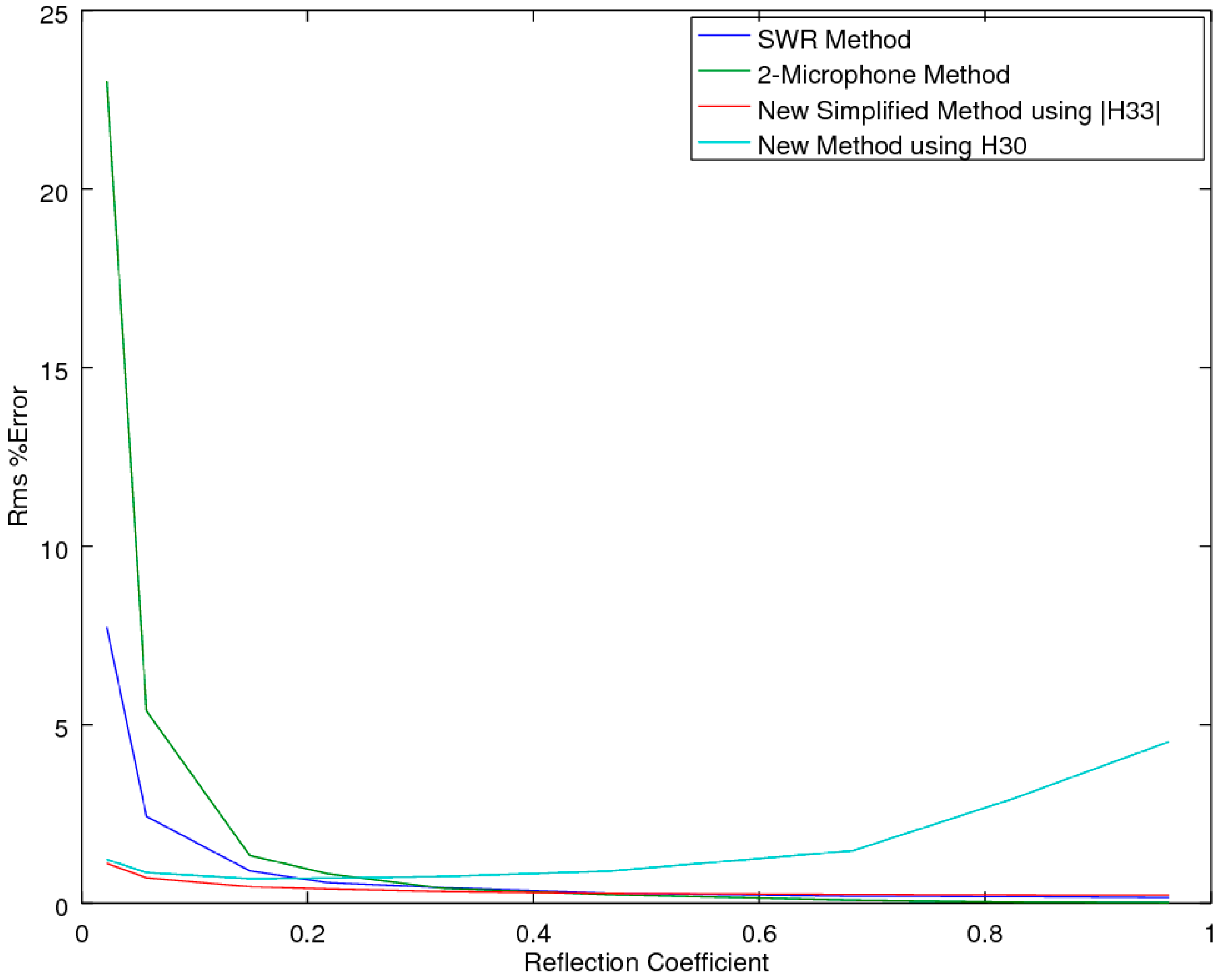
In light of the fact that there are several different methods for obtaining the same results, of interest are the trade-offs in cost and accuracy between the various methods. As was shown in the previous section, for the computation of the reflection coefficient R, the full SMM method utilizing the complex measure of H30 is a mathematical identity to the other standard methods; as such, theoretically they should all provide exactly the same value. Hence, of primary interest is how the standard methods compare to:
The simplified variant of the SMM method, SSMM (|H33|; pressure magnitudes only).
The complex SMM variant the CSMM (H30; pressure and phase).
The simplified variant of CSMM (|H30|; pressure magnitudes only).
Of note is that method 3, CSMM (|H30|), was not derived from first principles; as such, the simulation study did not include noise, but instead examined how large the error was when the full complex values with phase information were not captured in the measurements. Of potential interest for this variant is in the application for online systems, where it is inconvenient or impossible to obtain an air-reference, periodically throughout the day, that would preclude the use of the SSMM (|H33|) method, while still preserving the ease and simplicity of a magnitude-only version.
All of these issues will be explored utilizing the Monte-Carlo simulation that studied the performance of the afore-mentioned methods with respect to the standard methods [
2,
5,
6]. As the three-microphone method, in practice, [
7,
8,
9,
14] utilizes the two-microphone method for the computation of R, only the two-microphone comparison is reported on herein, as this also implicitly includes how well the three-microphone method would perform in the prediction of the reflection coefficient R. Thus, the performance comparisons will be made for the following techniques, in the presence of noise: SWR, Standing-Wave-Ratio [
2], and the two-microphone method [
5,
6].
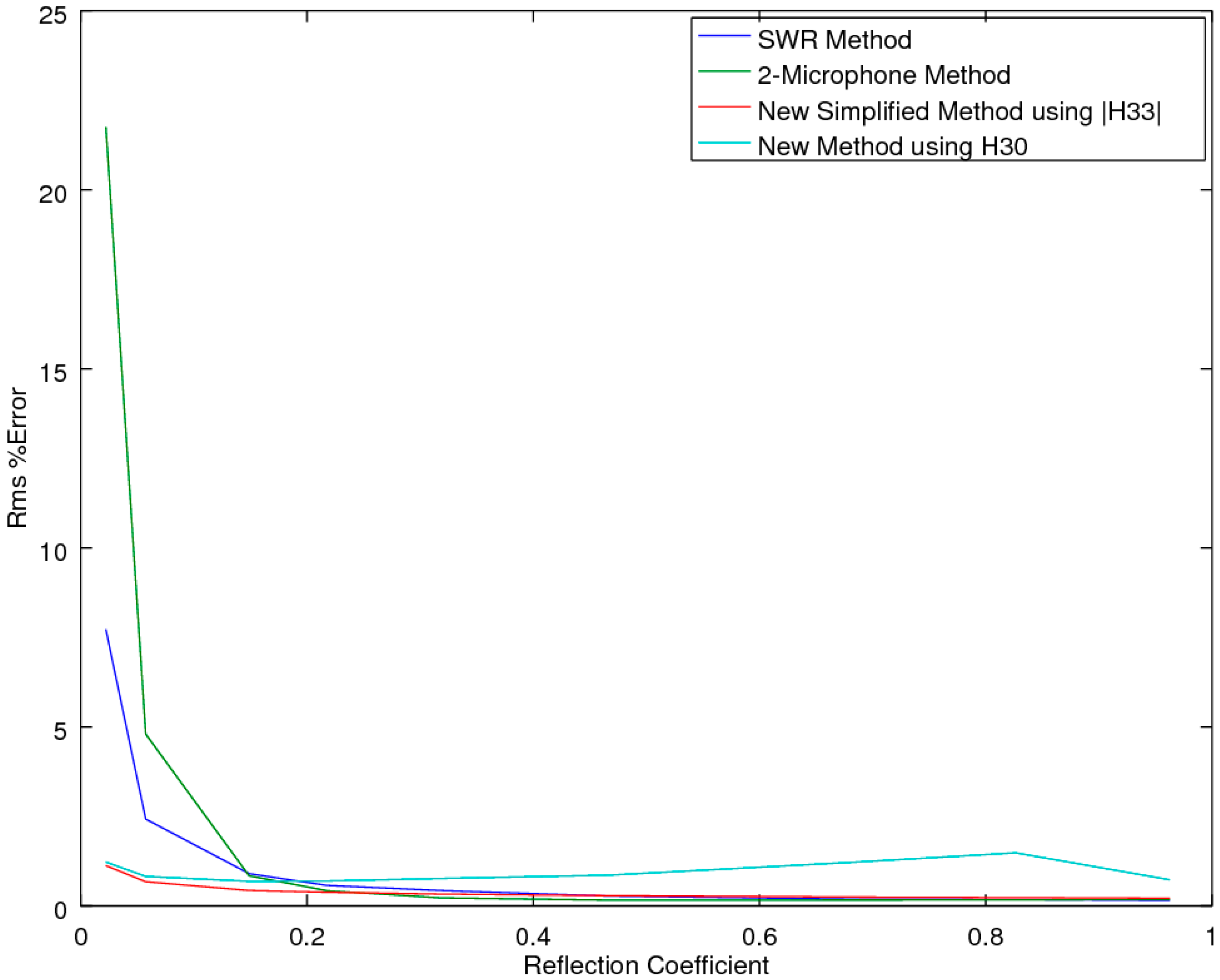
2.2.1. Accuracy Comparison in the Presence of Noise
As both of the SMM methods provide mathematical identities to the two-microphone method, for the prediction of the reflection coefficient R, of primary interest is how the CSMM and SSMM methods compare to the standard SWR [
2] and two-microphone methods (ASTM E1050 and ISO 10534-2) [
5,
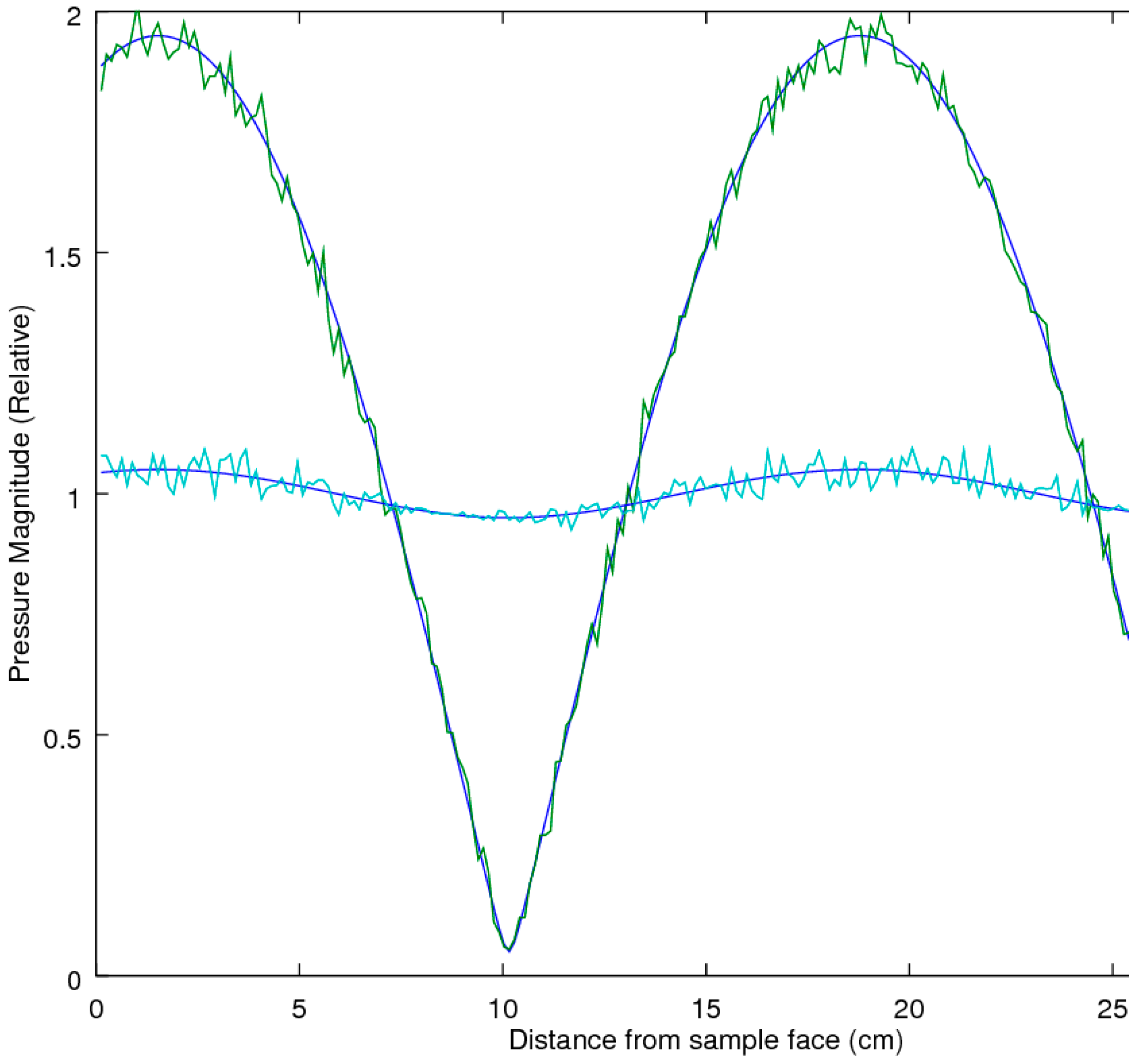
6] when the measurements are subjected to experimental noise. Of note is that the three-microphone method utilizes the two-microphone method in the measurement of R. To explore each of the methods’ ability to extract the correct estimate of R in the presence of noise, an accuracy comparison was performed, utilizing a simulation study to examine the performance of the prediction equations in an idealized theoretical solution that allowed for a full exploration across all the variables of interest, with the two main variables of interest being the attenuation and phase-delay terms in the material propagation constants. As the prediction of R implicitly utilizes a measure of the material propagation constant α, this study effectively tested this performance metric as well. The analysis was performed utilizing a Monte-Carlo simulation to predict the pressures inside the impedance tube for any given sample thickness and material properties, with and without added Gaussian white noise, at a relative signal-to-noise level of 0.005, for a typical sample thickness of 19.05 mm at a temperature of 23 °C. The locations of microphones 1 and 2 were placed at 0.07 and 0.03 m, respectively.
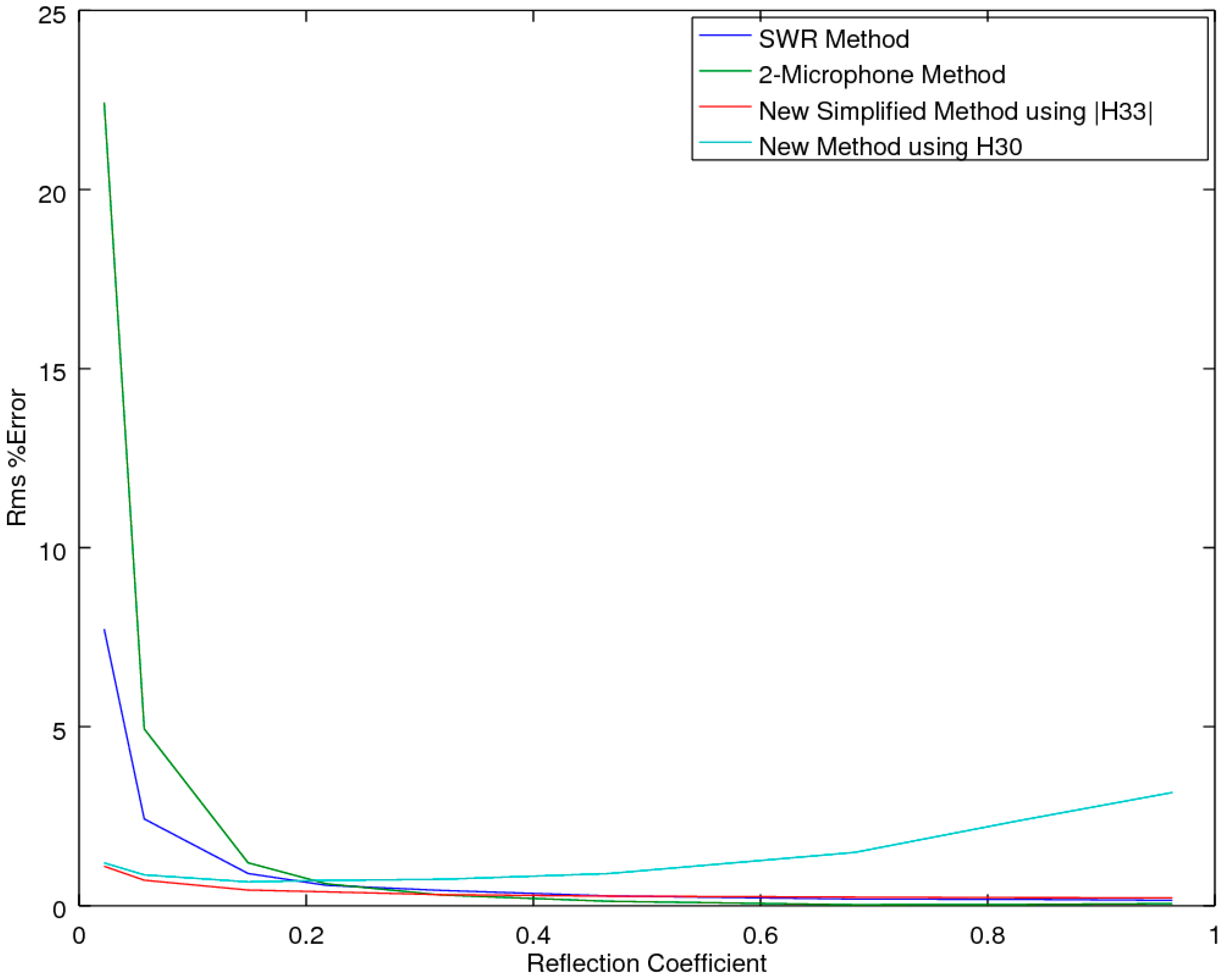
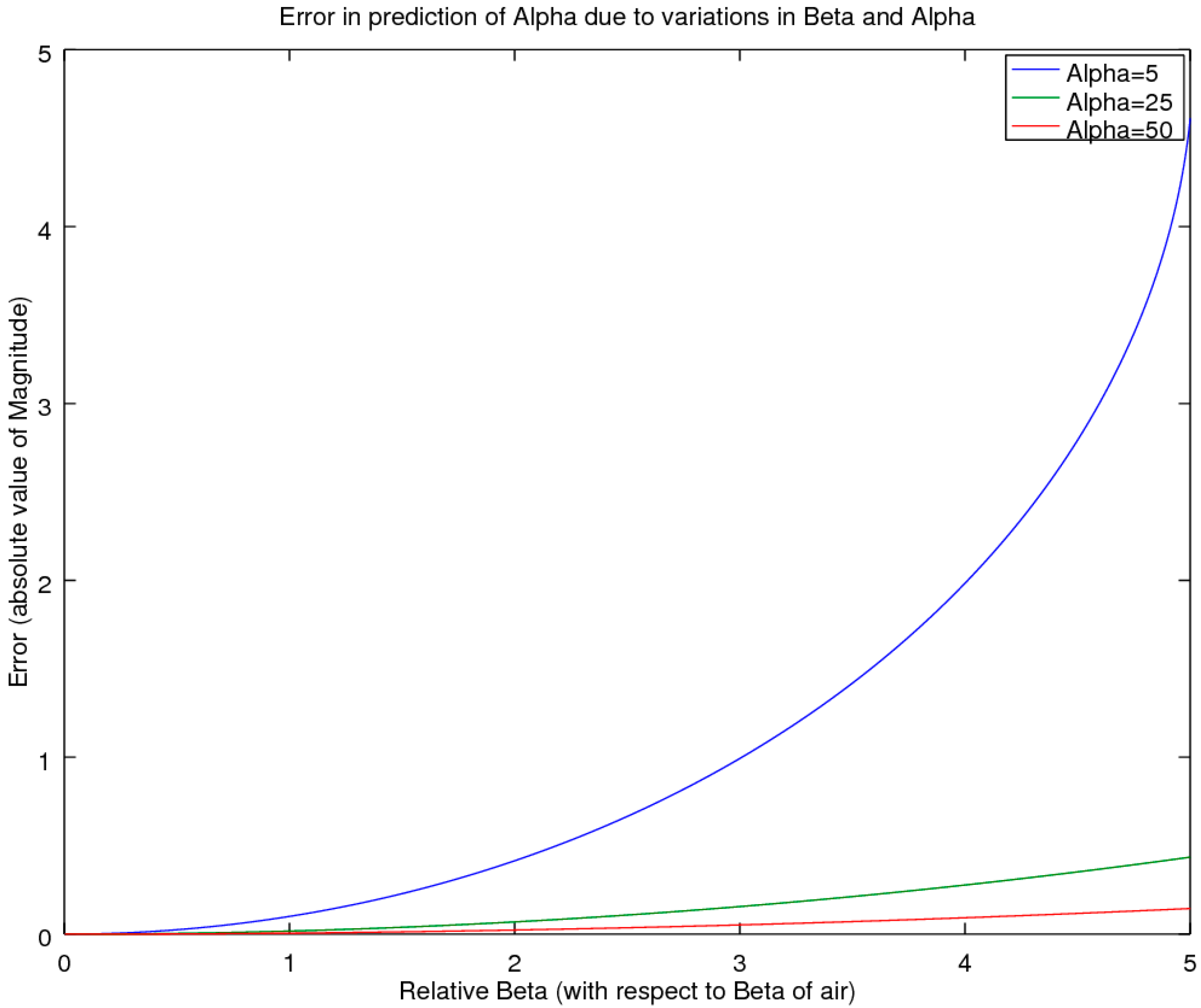
2.2.2. Accuracy Comparison for the Online Pressure Only
For start-up companies, the expenditure of acoustic equipment can represent a substantial outlay and as such, is a significant impediment for considering the setting up of an acoustic laboratory. For these situations, of interest is a screening method that could be utilized to find the acoustic test specimens that are the high performers of a batch, which could be sent out to a testing laboratory for a more accurate estimate. In the previous section, we outlined a minimal equipment variant of the CSMM method (the SSMM method), in which measurements are taken of the pressure amplitudes at microphone location 3 only, with and without a sample (air-reference) to allow for computation of H
33. This yields the lowest-cost approach that can be performed with a simple tube, a sample holder and an inexpensive sound meter. This raises the question as to the accuracy of such a simple and low-cost system. To examine this, a simulation comparison was performed, whereby the material properties of the sample were allowed to vary across the full range expected, for typical materials such as air, water, metals, wood, rubber cork and others, as reported in Beis and Hansen [
19]. For most of these materials, the propagation velocity is higher than that of air, yielding a wave-number of β < 1; in the exception to these typical materials are a few unique materials such as cork and rubber, for which the maximum β is at most equal to 5. Of note is that the authors were unable to find materials in the literature for which the velocity was slower than one-fifth that of air (β > 5). Hence, the presented range should be representative of nearly all materials of interest, with the bulk of the materials of interest having β < 1 [
19]. Also of note is that light, fibrous materials that are full of air can be expected to exhibit β’s near 1. Noting all these factors then provided the bounds for the simulation study, whereby the values of α were allowed to range from very small, α = 5, to large, α > 200. Across this two-parameter variational boundary, the error was tracked and is presented in the results section as the deviation for the measured α and its associated reflectance, R. Again, the study utilized a sample thickness of 19.05 mm at a temperature of 23 °C.
2.2.3. External Accuracy Factors
Of importance to note is that the derivation, provided in the previous section, does not make any approximations, with the exception of the magnitude only CSMM method. The derivation provides an analysis that is compatible with the methodology that provides the basis for all of the two-, three- and four-microphone methods listed in the literature, as were referenced in the earlier background section. Furthermore, as the equations are equivalent restatements or new reformulations of the other approaches, theoretically, each method should produce the same results, as they all follow the same methodology. For simulations comparing the three different methods, as noted earlier, all provided the same answers, as they were mathematical identities. As such, any inaccuracies should affect all three style measurement protocols in similar fashion, as well as the new CSMM proposed method described herein. As all of the standard methods have rich literature covering experimental sources of errors, these types of errors will not be covered again here; for more details, the interested reader is referred to [
5,
6] and Niresh et al. [
20].
Other accuracy issues, such as the influence of measurement microphone linearity and phase error in microphones are detailed in the ASTM E105 and ISO 10534-2 standards, and relevant literature is discussed previously in the background section. Of unique importance however, is to note that when utilizing a single microphone, as proposed herein, the errors due to phase differences between microphones are irrelevant, as all measurements are performed with a single microphone. As such, the single microphone method proposed herein yields yet another advantage, as it is free from this between-microphone phase error that is typically only partially corrected with the calibration procedure provided in the ASTM E105 standard method.