Topological Gauge Theory of Josephson Junction Arrays: The Discovery of Superinsulation

Abstract

We review the topological gauge theory description of Josephson junction arrays (JJA), fabricated systems which exhibit the superconductor-to-insulator transition (SIT). This description revealed the topological nature of the phases around the SIT and led to the discovery of a new state of matter, the superinsulator, characterized by infinite resistance, even at finite temperatures, due to linear confinement of electric charges. This discovery is particularly relevant for the physics of superconducting films with emergent granularity, which are modeled with JJAs and share the same phase diagram.

1. Introduction

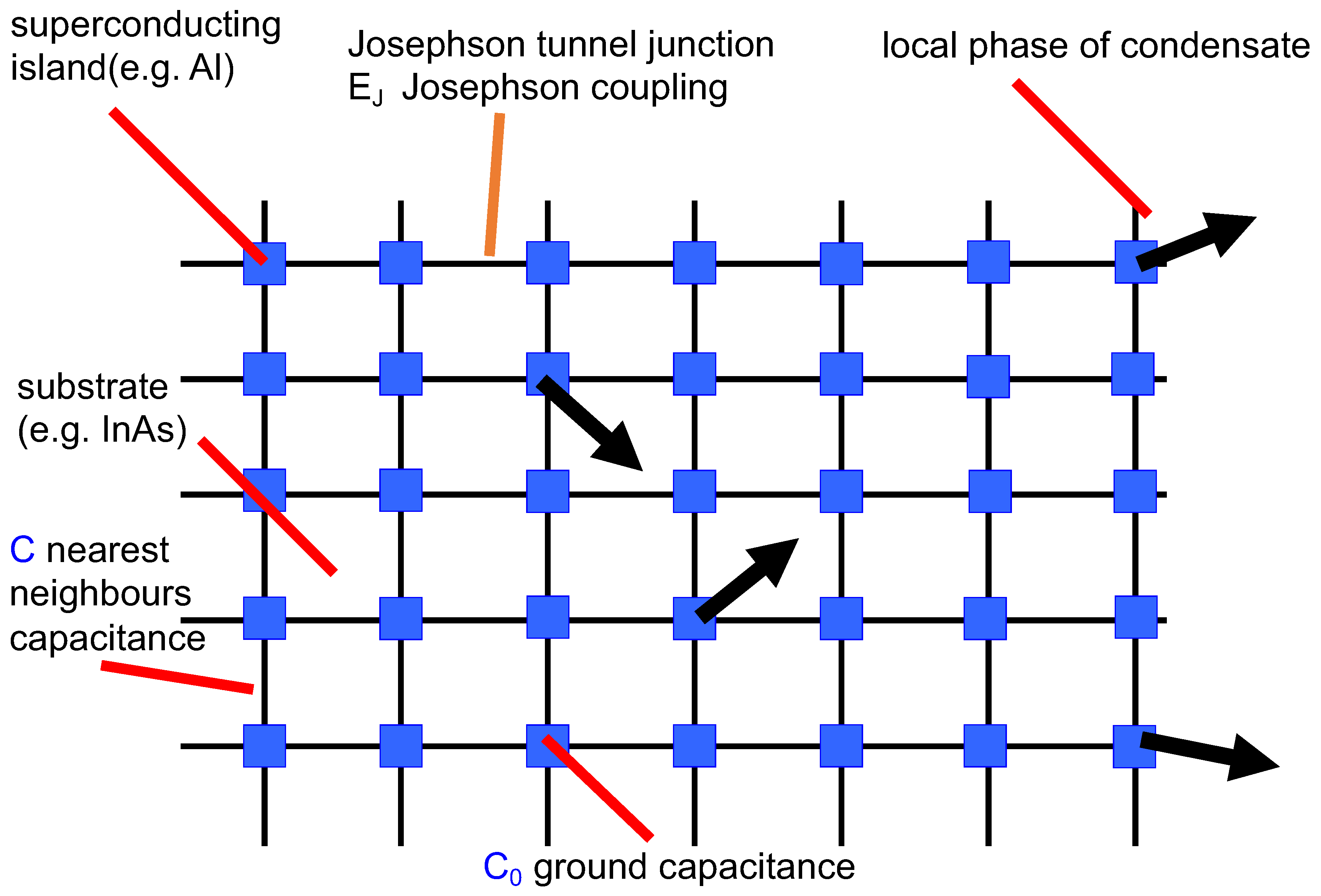
Josephson junction arrays (JJAs) [1] are fabricated materials which exhibit the superconductor-to-insulator transition (SIT) [2,3], a paradigmatic example of a quantum phase transition. Planar, quadratic JJAs are square lattices formed by superconducting islands (typical size O($\mu$m)), deposited on a substrate, with lattice spacing l (O(100 nm)), Josephson coupling $E_J$ and capacitances C between nearest-neighbor islands. An elementary square on the lattice is called a plaquette. Each island is also characterized by the phase of its local-order parameter and by a ground capacitance $C_0$. The circulation over a plaquette of the local phase represents the vortex degrees of freedom. When $C\gg C_0$, JJAs have only two relevant energy scales, $E_J$, the energy scale associated with the tunneling of Cooper pairs between the islands, and $E_C=e^2/2C$, the charging energy, with e representing the electron charge. A schematic description of such an array is presented in Figure 1.

The parameters $E_J$ and $E_C$ can be traded for a massive parameter ${\omega }_P=\sqrt{2E_C{E}_J}$, which represents the plasma frequency of the array, and a dimensionless parameter $g=\sqrt{\frac{{\pi }^2{E}_J}{2E_C}}$, which, as shown, drives the phase structure of the theory. In experimental realizations of JJA, the transition between the different phases is achieved by varying $E_J$ with $E_C$ essentially fixed. Varying $E_C$ is much more difficult.

In the classical limit $E_J\gg E_C$, global phase coherence is realized, and the array behaves as a superconductor. Above a critical temperature, the array undergoes a Berezinskii–Kosterlitz–Thouless (BKT) transition [4], and superconductivity is destroyed. When, instead, $E_c\gg E_J$, the tunneling between islands is suppressed, and the array becomes insulating. As shown in [5,6], however, this is not a usual Mott insulator but a new state of matter, called the superinsulator.

Superinsulators are emergent condensed matter states dual to superconductors: they exhibit infinite resistance even at finite temperatures. They were first theoretically predicted in [5], while the final form of the theory describing this new state of matter was established in [7]. Superinsulators have been experimentally detected [8,9,10,11,12,13,14] in thin superconducting films, which, close to the SIT, have an emergent granularity and behave as a self-organized JJA.

The infinite resistance which characterizes superinsulators is due to linear charge confinement [7] of both Cooper pairs and electrons in a magnetic monopole plasma. This squeezes electric field lines into electric flux tubes connecting charge–anticharge pairs, in analogy to the Meissner effect in superconductors [13]. Superinsulators realize, thus, an Abelian version of the dual superconductivity mechanism advocated by ‘t Hooft to explain quark confinement [15]. In his picture, mesons are chromo-electric strings with quarks at their ends. When quarks are separated, it is energetically favorable to pull out of the vacuum additional quark–antiquark pairs and to form several short strings. Free color charges can never be observed at distances larger than $1/{\Lambda }_{\mathrm{QCD}}$, and quarks are, thus, confined.

In [5], we derived a topological gauge theory description of JJAs. For planar JJAs, the relevant term dominant at large distances is the mixed Chern–Simons term [16]. This is the (2+1)-dimensional version of the BF term [17], which is the relevant term at long distances in higher dimensions. This description has made it possible to derive the quantum phase diagram of a JJA and to understand the nature of the various phases. This result is particularly important since, as we pointed out before, JJAs are a model for thin superconducting films near the SIT. Correspondingly, the gauge theory of JJAs is also an effective theory for these materials near the SIT. Interesting topological phenomena in JJAs have also be found in [18], where they arise due to a network structure forming tree-like graphs, with singular behavior of the temperature and magnetic field dependence of the Josephson current.

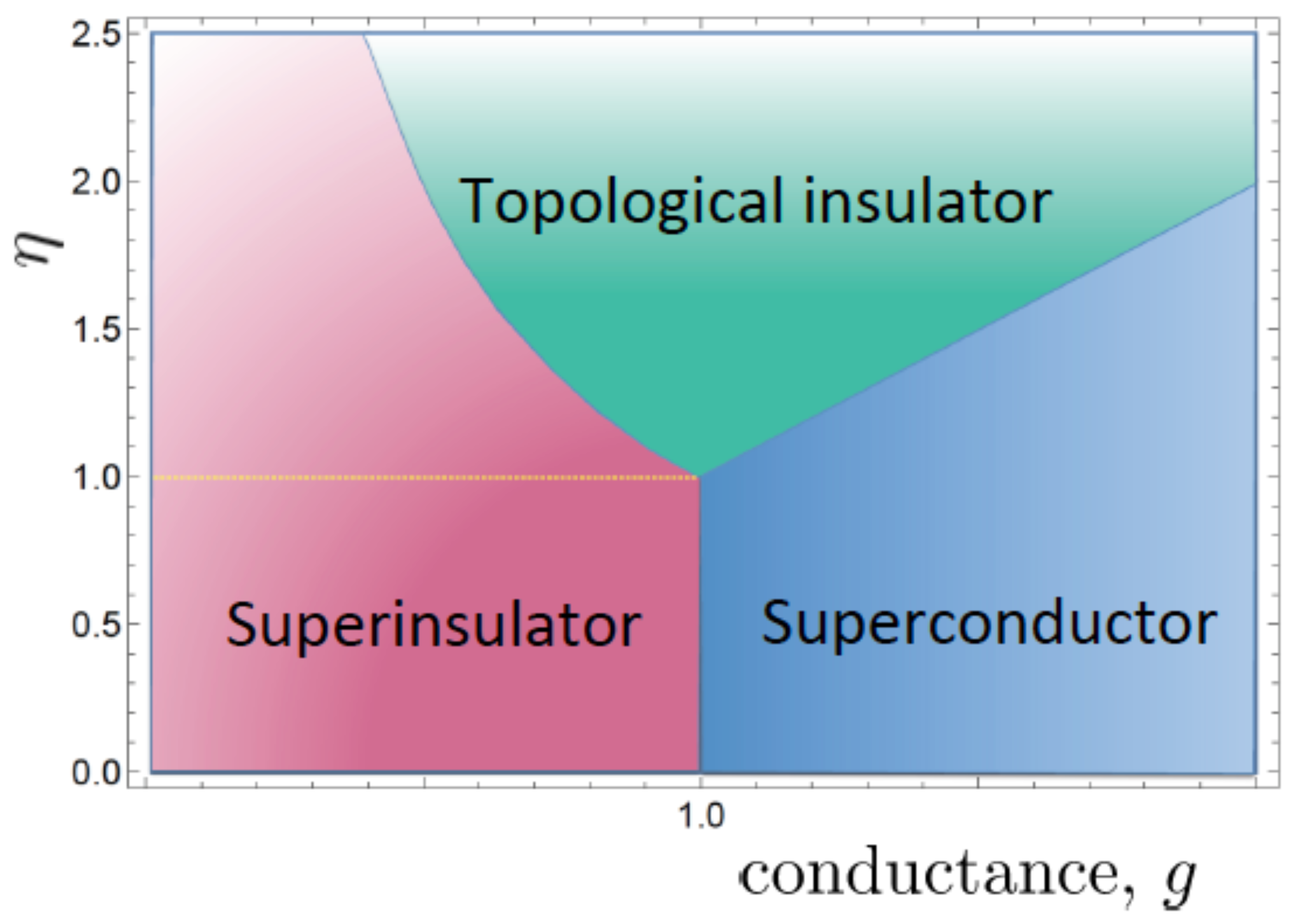
We have identified three possible phases depending on the value of a parameter $\eta$ encoding details of the array. When $\eta <1$, there is a direct transition between the superconducting and the superinsulating phases. The superconducting phase actually realizes a new type of superconductivity, which we call type-III superconductivity [19], in which the gap is opened by a topological mechanism and not by the usual Anderson–Higgs mechanism and which is not described by the standard Ginzburg–Landau theory. Superconductivity is not destroyed by the breaking of Cooper pairs but by a proliferation of vortices, implying a BKT transition in two dimensions and a Vogel–Fulcher–Tamman transition in three dimensions [19,20]. This superconductivity model may be relevant for high-$T_C$ superconductivity [21]. When $\eta >1$, an intermediate metallic phase opens up between the superconducting and the superinsulating phases [22,23]. This is called Bose metal (BM), since charge carriers are Cooper pairs, and has been experimentally confirmed in superconducting films [24,25,26,27,28,29]. This phase has long challenged the understanding of electronic fluids [30,31], since it is believed that a metallic phase in two dimensions cannot exist due to localization. Moreover, it was puzzling that certain films realized this phase and others not. In [22], we were able to identify this phase as a bosonic topological insulator and to explain, through the $\eta$-dependence, why this phase appears or not.

In Section 2, we will review the topological gauge theory formulation of JJAs. We shall focus, in particular, on the role of the kinetic term for vortices. In Section 3, we will derive the quantum phase structure of JJAs, and, in Section 4, we will then describe the properties of the new phases of matter, predicted thanks to the gauge theory formulation.

2. Topological Gauge Theory of JJAs

We consider the dynamics of a JJA on a square lattice with sites denoted by $\left\{x\right\}$ and directions indicated by Greek letters, from 0 to 2. The lattice spacing is $l_0$ in the 0 direction (time) and l in the 1 and 2 directions (space). We denote these different spacing compactly by $l_{\mu }$. The forward and backward finite-difference and shift operators are defined as

$$\begin{array}{c}\hfill {\Delta }_{\mu }f\left(x\right)=f(x+l_{\mu }\widehat{\mu })-f\left(x\right),S_{\mu }f\left(x\right)=f(x+l_{\mu }\widehat{\mu }),\\ \hfill {\widehat{\Delta }}_{\mu }f\left(x\right)=f\left(x\right)-f(x-l_{\mu }\widehat{\mu }),{\widehat{S}}_{\mu }f\left(x\right)=f(x-l_{\mu }\widehat{\mu }),\end{array}$$

(1)

where $\widehat{\mu }$ denotes a unit vector in direction $\mu$. Summation by parts on the lattice interchanges both the two finite differences (with a minus sign) and the two shift operators. Using these definition we introduce the operators:

$$K_{\mu \nu }=S_{\mu }{ϵ}_{\mu \alpha \nu }{\Delta }_{\alpha },{\widehat{K}}_{\mu \nu }={ϵ}_{\mu \alpha \nu }{\widehat{\Delta }}_{\alpha }{\widehat{S}}_{\nu },$$

(2)

where no summation is implied over the equal indices $\mu$ and $\nu$. These two operators are interchanged by summation by parts with no minus sign. They allow us to define a gauge invariant version of the Chern–Simons operator ${ϵ}_{\mu \alpha \nu }{\partial }_{\alpha }$ on the lattice [5]. Their products gives the lattice Maxwell operator:

$$K_{\mu \alpha }{\widehat{K}}_{\alpha \nu }={\widehat{K}}_{\mu \alpha }{K}_{\alpha \nu }=-{\delta }_{\mu \nu }\Delta +{\Delta }_{\mu }{\widehat{\Delta }}_{\nu },$$

(3)

where $\Delta ={\widehat{\Delta }}_{\mu }{\Delta }_{\mu }$ is the 3D Laplace operator.

Our starting point is the Hamiltonian for a JJA on the above lattice, with nearest-neighbor Josephson couplings $E_J$, ground capacitances $C_0$ and nearest-neighbor capacitances C [1,32]:

$$\begin{array}{c}H=\sum _{\mathbf{x}}\frac{C_0}{2}{V}_{\mathbf{x}}^2+\sum _{<\mathbf{x}\mathbf{y}>}\frac{C}{2}{\left(V_{\mathbf{y}}-V_{\mathbf{x}}\right)}^2+E_{\mathrm{J}}\left(1-\cos \left({\phi }_{\mathbf{y}}-{\phi }_{\mathbf{x}}\right)\right),\hfill \\ H=\sum _{\mathbf{x}}\frac{1}{2}{V}_{\mathbf{x}}\left(C_0-C\Delta \right)V_{\mathbf{x}}+\sum _{\mathbf{x},i}{E}_{\mathrm{J}}\left(1-\cos \left({\Delta }_i{\phi }_{\mathbf{x}}\right)\right),\hfill \end{array}$$

(4)

where $<\mathbf{x}\mathbf{y}>$ indicates nearest neighbors and $\Delta \equiv {\widehat{\Delta }}_i{\Delta }_i$ is the two-dimensional finite difference Laplacian. In what follows, we will use natural units $c=1$, $\hslash =1$, ${\epsilon }_0=1$.

Each island is characterized by an electric potential $V_{\mathbf{x}}$ and by the phase of the local-order parameter ${\phi }_{\mathbf{x}}$, which is quantum-mechanically conjugated to the charge ${\mathcal{E}}_{\mathbf{x}}$ on the island. Charges are quantized in integer multiples of 2e (Cooper pairs), ${\mathcal{E}}_{\mathbf{x}}=2e{q}_{\mathbf{x}},q_{\mathbf{x}}\in Z$.

Using the discrete version of Poisson’s equation:

$$\left(C_0-C\Delta \right)V_{\mathbf{x}}={\mathcal{E}}_{\mathbf{x}},$$

(5)

and introducing the charging energy $E_{\mathrm{C}}\equiv e^2/2C$, we can rewrite the Hamiltonian Equation (4) as:

$$H=\sum _{\mathbf{x}}4E_{\mathrm{C}}{q}_{\mathbf{x}}\frac{1}{C_0/C-\Delta }{q}_{\mathbf{x}}+\sum _{\mathbf{x},i}{E}_{\mathrm{J}}\left(1-\cos \left({\Delta }_i{\phi }_{\mathbf{x}}\right)\right).$$

(6)

The integer charges $q_{\mathbf{x}}$ in Equation (6) interact via a two-dimensional Yukawa potential with mass $\sqrt{C_0/C}/\ell$, which, in the limit $C\gg C_0$, becomes a two-dimensional Coulomb potential.

The next step in our derivation of the gauge theory description is the construction of the phase-space path-integral representation [5] of the JJA. To this end, we introduce a fictitious temperature $\beta =1/T$ and write the partition function of the JJA as:

$$\begin{array}{c}\hfill Z=\sum _{\left\{q\right\}}{\int }_{-\pi }^{+\pi }\mathcal{D}\phi \exp (-S),\\ \hfill S={\int }_0^{\beta }dt\sum _{\mathbf{x}}i{q}_{\mathbf{x}}{\dot{\phi }}_{\mathbf{x}}+4E_C{q}_{\mathbf{x}}\frac{1}{C_0/C-\Delta }{q}_{\mathbf{x}}+\sum _{\mathbf{x},i}{E}_J\left(1-\cos \left({\Delta }_i{\phi }_{\mathbf{x}}\right)\right),\end{array}$$

(7)

In the experimentally accessible limit $C_0\gg C$, this becomes

$$\begin{array}{c}\hfill Z=\sum _{\left\{q\right\}}{\int }_{-\pi }^{+\pi }\mathcal{D}\phi \exp (-S),\\ \hfill S={\int }_0^{\beta }dt\sum _{\mathbf{x}}i{q}_{\mathbf{x}}{\dot{\phi }}_{\mathbf{x}}+4E_C{q}_{\mathbf{x}}\frac{1}{-\Delta }{q}_{\mathbf{x}}\\ \hfill +\sum _{\mathbf{x},i}{E}_J\left(1-\cos \left({\Delta }_i{\phi }_{\mathbf{x}}\right)\right).\end{array}$$

(8)

Since charges are integers, continuous time must be traded for a discrete time with intervals $l_0$. We thus also introduce forward and backward finite time differences ${\Delta }_0$ and ${\widehat{\Delta }}_0$. Using the Villain representation [33], we can remove the cosine at the price of introducing a set of integer link variables $a_i$. By introducing real charge currents $j_i$, we can express the quadratic term ${\left({\Delta }_i\phi +2\pi a_i\right)}^2$, originating from the Villain approximation, as a Gaussian integrals over these variables,

$$\begin{array}{c}\hfill Z=\sum _{\left\{a_i\right\},\left\{j_0\right\}}\int \mathcal{D}{j}_i{\int }_{-\pi }^{+\pi }\mathcal{D}\phi \exp (-S),\\ \hfill S=\sum _{x}i{j}_0{\Delta }_0\phi +i{j}_i\left({\Delta }_i\phi +2\pi a_i\right)+4{\ell }_0{E}_{\mathrm{C}}{j}_0\frac{1}{-\Delta }{j}_0+\frac{1}{2{\ell }_0{E}_{\mathrm{J}}}{j_i}^2,\end{array}$$

(9)

where we renamed $j_0$ the integer charges $q_{\mathbf{x}}$ for reasons outlined below.

The longitudinal part of $a_i$ is not physical and can be reabsorbed in a redefinition of $\phi$. As shown, the transverse degrees of freedom encode the vortices of the model. In fact, it is important to notice that Equation (9) contains a kinetic term only for the charges but not for vortices. While this omission has no consequences for overdamped junctions, in the general case this is not correct. As shown in [32], the kinetic term for vortices is generated by integration over charge fluctuations and must thus be already included at the tree level. Moreover, in our case, the Coulomb interaction is long-range, and the dissipation is reduced [34], making the vortex kinetic term relevant. The kinetic term for the vortices represents tunneling events between adjacent plaquettes of the lattice. These events are the generalizations to two dimensions of quantum phase slips, which play a crucial role in Josephson junction chains [35]. They can be thought of as half-lines of simultaneous phase slips of opposite chirality, which end on the island between the two adjacent plaquettes. Ballistic vortex motion corresponding to vortex tunneling from one plaquette to the other has actually been experimentally observed in [36]. The kinetic term for vortices involves the time derivative of $a_i$, ${\left({\Delta }_0{a}_i\right)}^2$. To introduce it properly, let us start by introducing a fictitious electric field ${\phi }_i=K_{i\mu }{a}_{\mu }$ and a real Lagrange multiplier $a_0$. Taking the coefficient of the kinetic term as ${\pi }^2/4{\ell }_0{E}_C$, we write the vortex kinetic term and the charge Coulomb interaction as:

$$\begin{array}{c}\hfill Z=\sum _{\left\{a_i\right\},\left\{j_0\right\}}\int \mathcal{D}{a}_0\mathcal{D}{j}_i{\int }_{-\pi }^{+\pi }\mathcal{D}\phi \exp (-S),\\ \hfill S=\sum _{x}i{j}_0\left({\Delta }_0\phi +2\pi a_0\right)+i{j}_i\left({\Delta }_i\phi +2\pi a_i\right)+\frac{1}{2{\ell }_0{E}_{\mathrm{J}}}{j_i}^2+\frac{{\pi }^2}{4{\ell }_0{E}_C}{\phi }_i^2,\end{array}$$

(10)

where now the Coulomb interaction between the charges follows from the Gauss law constraint associated with the Lagrange multiplier $a_0$. In this case, we have chosen a particular value of the vortex mass for which the JJA is dual with interchanges of charges and vortices and of ${\pi }^2{E}_J\leftrightarrow 2E_C$, or, alternatively, $g\leftrightarrow 1/g$. This is the self-dual approximation introduced in [5]. It is important to notice, however, that a different vortex mass will, in general, renormalize the value of $E_C$ and, as consequence, change the quantum parameter g. A larger or smaller vortex mobility will, thus, influence the phase structure.

The integration over $\phi$ in Equation (10) gives the constraint ${\Delta }_{\mu }{j}_{\mu }=0$. The current $j_{\mu }$ is thus conserved and can be represented in terms of a fictitious gauge field $b_{\mu }$.

$$j_0=K_{0i}{b}_i,j_i=K_{i0}{b}_0+K_{ij}{b}_j,$$

(11)

In Equation (11), $b_0$ is a real variable, while $b_i$ and $a_i$ are integers. These can be turned into real variables using Poisson’s formula,

$$\sum _{n_{\mu }}f\left(n_{\mu }\right)=\sum _{k_{\mu }}\int d{n}_{\mu }f\left(n_{\mu }\right){\mathrm{e}}^{i2\pi n_{\mu }{k}_{\mu }},$$

(12)

so that all components of the gauge fields $a_{\mu }$ and $b_{\mu }$ become real at the price of introducing integer link variables $Q_i$ and $M_i$:

$$\begin{array}{c}\hfill Z=\sum _{\left\{Q_i\right\}}\sum _{\left\{M_i\right\}}\int \mathcal{D}{a}_{\mu }\mathcal{D}{b}_{\mu }{\int }_{-\pi }^{+\pi }\mathcal{D}\phi \exp (-S),\\ \hfill S=\sum _{x}i2\pi a_{\mu }{K}_{\mu \nu }{b}_{\nu }+\frac{1}{2{\ell }_0{E}_{\mathrm{J}}}{j_i}^2+\frac{{\pi }^2}{4{\ell }_0{E}_C}{\varphi }_i^2+i2\pi a_i{Q}_i+i2\pi b_i{M}_i\\ \hfill +b_i\left({\widehat{K}}_{i0}{\Delta }_0\phi +{\widehat{K}}_{ij}{\Delta }_j\phi \right)+b_0{\widehat{K}}_{0i}{\Delta }_i\phi .\end{array}$$

(13)

The last step of our derivation consists of reabsorbing the quantity $\left({\widehat{K}}_{i0}{\Delta }_0\phi +{\widehat{K}}_{ij}{\Delta }_j\phi \right)$ in a redefinition of the integers $M_i$ and introducing a set of integers $M_0$ trough the definition ${\widehat{K}}_{0i}{\Delta }_i\phi =2\pi M_0$. This step is justified given that ${\widehat{K}}_{\mu \nu }{\Delta }_{\nu }\phi$ are the circulations of the array phases around the plaquettes orthogonal to the direction $\mu$ in 3D Euclidean space-time and are thus quantized as $2\pi \mathrm{integers}$. At this point, again using Poisson’s formula, we can express the integral over $\phi$ as a sum over the integer $M_0$, giving the final expression for the topological gauge theory describing the JJA:

$$\begin{array}{c}\hfill Z=\sum _{\left\{Q_i\right\}}\sum _{\left\{M_{\mu }\right\}}\int \mathcal{D}{a}_{\mu }\mathcal{D}{b}_{\mu }\exp (-S),\\ \hfill S=\sum _{x}i2\pi a_{\mu }{K}_{\mu \nu }{b}_{\nu }+\frac{1}{2{\ell }_0{E}_{\mathrm{J}}}{j_i}^2+\frac{{\pi }^2}{4{\ell }_0{E}_C}{\varphi }_i^2+i2\pi a_i{Q}_i+i2\pi b_{\mu }{M}_{\mu }.\\ \hfill \end{array}$$

(14)

The first term in the action is the lattice version of the mixed Chern–Simons term, which, being linear in derivatives, is dominant at large distances. The second and third terms are the electric fields for the fictitious gauge fields $a_{\mu }$ and $b_{\mu }$, respectively. The effect of the CS term is to give a mass to these gauge fields without the Anderson–Higgs mechanism [16]. This mass is nothing other than the plasma frequency of the array: $m_{top}={\omega }_p=\sqrt{8E_C{E}_J}$. The two kinetic terms have a coupling constant with dimensions of mass and are thus naively irrelevant. However, they cannot be neglected, since the correct topological limit $m_{top}\to \infty$ has to be derived from the full theory, including the kinetic terms, in order to describe physical systems; otherwise, states will not be normalizable. The topological limit $E_J\to \infty ,E_C\to \infty$ is not well defined without specifying the value of the ratio g in this limit, and, as we will show, the phase diagram depends crucially on this.

The dual field strengths of the fictitious gauge fields, $j_{\mu }=K_{\mu \nu }{b}_{\nu }$ and ${\phi }_{\mu }=K_{\mu \nu }{a}_{\nu }$ represent charge and vortex fluctuations, respectively. The integer fields $Q_i$ and $M_i$ are the electric and magnetic topological excitations, respectively. Together with the vortex number $M_0$, the latter forms a three-current $M_{\mu }$, which is conserved due to gauge invariance in the $b_{\mu }$ gauge sector, ${\widehat{\Delta }}_{\mu }{M}_{\mu }=0$. Perfect duality is broken by the absence of the integer variable $Q_0$, which can be explained as follows. In contrast to electric Noether charges, magnetic vortices are topological excitations, characterized by a topological quantum number. The configuration space of the theory of vortices decomposes into so-called superselection sectors, characterized by the integer total vortex number. These sectors are connected via instantons, non-perturbative configurations representing quantum tunneling events between topological vacua [37]. As a consequence, electric charges are conserved, but vortices are not and can “appear” and“disappear” via quantum tunneling events represented by the instantons.

By rescaling the emergent gauge fields, expressed with their canonical dimensions, by $1/2\pi$, and using lattice derivatives instead of finite differences, we can rewrite the action in Equation (14) as

$$S=\sum _{x}i\frac{l_0{l}^2}{2\pi }{a}_{\mu }{K}_{\mu \nu }{b}_{\nu }+\frac{l_0{l}^2}{8{\pi }^2{E}_{\mathrm{J}}}{j_i}^2+\frac{l_0{l}^2}{16E_C}{\varphi }_i^2+il{a}_i{Q}_i+i{l}_0{b}_0{M}_0+l{b}_i{M}_i.$$

(15)

This equation is the limit for $ϵ=1,\mu \to \infty$ and $v=1/\sqrt{ϵ\mu }=1/\sqrt{\mu }\ll 1$ of the action:

$$\begin{array}{ccc}\hfill S=\sum _x& & i\frac{{\ell }^2{l}_0}{2\pi }{a}_{\mu }{k}_{\mu \nu }{b}_{\nu }+\frac{{\ell }^2{l}_0{v}^2}{8{\pi }^2{E}_J}{j}_0{j}_0+\frac{l_0{l}^2}{8{\pi }^2{E}_{\mathrm{J}}}{j_i}^2+\hfill \\ & & \frac{{\ell }^2{l}_0{v}^2}{16E_C}{\phi }_0{\phi }_0++\frac{l_0{l}^2}{16E_C}{\varphi }_i^2+il{a}_i{Q}_i+i{l}_0{b}_0{M}_0+l{b}_i{M}_i.\hfill \end{array}$$

(16)

We can now compute the induced action for the $Q_i$ and $M_{\mu }$, obtained by integrating over the emergent gauge fields. To this end, we add the term $i{l}_0{a}_0{Q}_0$ and the sum over $Q_0$ in the partition function. This term renders the action completely self-dual with respect to electric and magnetic degrees of freedom, which allows us to rewrite Equation (16) as:

$$\begin{array}{ccc}\hfill S=\sum _x& & i\frac{{\ell }^2{l}_{0}v}{2\pi }{a}_{\mu }{k}_{\mu \nu }{b}_{\nu }+\frac{{\ell }^2{l}_{0}v}{8{\pi }^2{E}_J}{j}_{\mu }{j}_{\mu }+\frac{{\ell }^2{l}_{0}v}{16E_C}{\phi }_{\mu }{\phi }_{\mu }+\hfill \\ & & +il{a}_{\mu }{Q}_{\mu }+il{b}_{\mu }{M}_{\mu },\hfill \end{array}$$

(17)

where we rescaled to $l_0=l/v,d_0\to d_0,j_i\left({\phi }_i\right)\to \frac{1}{v}{j}_i\left({\phi }_i\right)$. In Equation (17), gauge invariance imposes the constraint $\widehat{d_{\mu }}{Q}_{\mu }=\widehat{d_{\mu }}{M}_{\mu }=0$. Since $\widehat{d_i}{Q}_i=0$, we also have $\widehat{d_0}{Q}_0$, implying that there are no “electric instantons”. To recover the exact result for the JJA, we should set $Q_0=0$ at the end of the calculation. Making the theory perfectly self-dual, however, will not change the nature of the possible phases, which justifies using this approximation.

Integrating out the emergent gauge fields, we obtain [5,6]:

$$\begin{array}{ccc}\hfill S_{\mathrm{TOP}}& & =\sum _{x}v\frac{8E_C}{\ell }{Q}_{\mu }\frac{1}{v^4{m}^2-d_0{\widehat{d}}_0-v^2{\nabla }_2^2}{Q}_{\mu }+\hfill \\ & & +v\frac{4{\pi }^2{E}_J}{\ell }{M}_{\mu }\frac{1}{v^4{\tilde{m}}^2-d_0{\widehat{d}}_0-v^2{\nabla }_2^2}{M}_{\mu }+\hfill \\ & & +i\frac{2\pi v^6{m}^2}{\ell }{Q}_{\mu }\frac{K_{\mu \nu }}{(d_0{\widehat{d}}_0+v^2{\nabla }_2^2)(v^4{m}^2-d_0{\widehat{d}}_0-v^2{\nabla }_2^2)}{M}_{\nu }.\hfill \end{array}$$

(18)

The last, imaginary term in the action is a lattice version of the topological linking of electric and magnetic strings, which, due to the Dirac condition, becomes an integer in the limit $vm\to \infty$. This term is also an integer if we set $Q_0=0$. We can, thus, drop it [5].

3. Quantum Phase Structure

The $T=0$ quantum phase structure of a JJA is determined by the behavior of the integer fields $Q_{\mu }$ and $M_{\mu }$. These can be decomposed into a transverse component, ${\widehat{d}}_{\mu }{Q}_{\mu }^T=0$, ${\widehat{d}}_{\mu }{M}_{\mu }^T=0$, representing closed electric and magnetic loops or infinitely long strings, and a longitudinal component, ${\widehat{k}}_{\mu \nu }{Q}_{\nu }^L=0$, ${\widehat{k}}_{\mu \nu }{M}_{\nu }^L=0$, representing open electric and magnetic strings ending on electric and magnetic monopoles $q={\widehat{d}}_{\mu }{Q}_{\mu }^L$ and $m={\widehat{d}}_{\mu }{M}_{\mu }^L$. Notice, however, that, in Equation (15), only the integers $Q_i$ appear, implying that ${\widehat{d}}_i{Q}_i=0$.

To determine when infinitely long electric or magnetic strings proliferate, one has to consider the energy–entropy balance determined by the parameters of the model. Let us start from Equation (18), where we ignore the imaginary term, as explained above. Near the transition, we expect to have very long strings and large loops. These configurations are, in general, very random, and we expect that forces between links in the same loop and in other ones cancel out. Thus, we retain only the self-interaction terms in Equation (18) [38]. We assign an energy (equivalent to Euclidean action in statistical field theory) to a closed string made of N links with integer quantum numbers Q and M on all the lattice links forming the string (and zero elsewhere)

$$S_{\mathrm{top}}=\pi m\ell G\left(m\ell \right)\left[\frac{2E_C}{{\pi }^2{E}_J}{Q}^2+\frac{{\pi }^2{E}_J}{2E_C}{M}^2\right]N,$$

(19)

where $G\left(m\ell \right)$ is the diagonal element of the lattice kernel $G(m\ell ,x-y)$ representing the inverse of the operator ${\ell }^2(m^2-{\nabla }^2)$. The kernel $G(m\ell ,x-y)$ is defined by the equation

$${\ell }^2\left(m^2-{\nabla }^2\right)G(ml,x-y)={\delta }_{x-y,0}.$$

(20)

Defining the Fourier transform $G(m\ell ,x-y)={\int }_{-\pi }^{\pi }{d}^{3}kG(m\ell ,k)\exp (ik·x)$, we obtain

$${\int }_{-\pi }^{\pi }{d}^{3}kG(m\ell ,k){\ell }^2\left(m^2-{\nabla }^2\right){\mathrm{e}}^{ik·x}=\frac{1}{{\left(2\pi \right)}^3}{\int }_{-\pi }^{\pi }{d}^{3}k{\mathrm{e}}^{ik·x}.$$

(21)

Finally, applying the finite difference operator ${\ell }^2\left(m^2-{\nabla }^2\right)$ to the exponential in the Fourier transform gives the final result

$$G\left(ml\right)\equiv G(ml,0)=\frac{1}{{\left(2\pi \right)}^3}{\int }_{-\pi }^{\pi }{d}^{3}k\frac{1}{{\left(m\ell \right)}^2+{\sum }_{i=0}^{2}4\sin {\left(\frac{k^i}{2}\right)}^2}.$$

(22)

The string entropy, however, is also proportional to the length. It is given by $\mu N$ with $\mu \approx ln\left(5\right)$, since at each step the non-backtracking strings can choose among five possible directions on which to continue. One can thus assign the free energy

$$F=\pi m\ell G\left(m\ell \right)\left[\frac{1}{g}{Q}^2+g{M}^2-\frac{1}{\eta }\right]N,$$

(23)

to a string of length $L=\ell N$ carrying electric and magnetic quantum numbers Q and M, respectively. Here, we have introduced the dimensionless parameter

$$\eta =\frac{\pi m\ell G\left(m\ell \right)}{\mu },$$

(24)

which, together with the ratio $g=\sqrt{\frac{{\pi }^2{E}_J}{2E_C}}$, fully determines the quantum phase structure, as we now show.

The ground state of the quantum model is found by minimizing its free energy as a function of N. When the energy term in Equation (23) dominates, the free energy is positive and consequently minimized by short closed-loop configurations. When, instead, the entropy dominates, the free energy is negative and minimized by large strings, long closed loops, and instantons that break the original $\mathbb{R}$ gauge symmetry down to $\mathbb{Z}$. The condition for condensation of long strings with integer quantum numbers Q and M is thus given by

$$\eta \frac{1}{g}{Q}^2+\eta g{M}^2<1.$$

(25)

If two or more condensations are allowed, one has to choose the one with the lowest free energy.

This condition describes the interior of an ellipse with semiaxes

$$\begin{array}{c}\hfill r_Q=\sqrt{g\frac{1}{\eta }},\\ \hfill r_M=\sqrt{\frac{1}{g}\frac{1}{\eta }},\end{array}$$

(26)

on a square lattice of integer electric and magnetic charges. The phase diagram is consequently found by simply recording which integer charges lie within the ellipse when the semi-axes are varied,

$$\begin{array}{ccc}\hfill \eta & & <1\to \left\{\begin{array}{c}\sqrt{\frac{2E_C}{{\pi }^2{E}_J}}<1,\mathrm{electric}\mathrm{condensation}=\mathrm{type}\mathrm{III}\mathrm{superconductor},\hfill \\ \sqrt{\frac{2E_C}{{\pi }^2{E}_J}}>1,\mathrm{magnetic}\mathrm{condensation}=\mathrm{superinsulator},\hfill \end{array}\right.\hfill \\ \hfill \eta & & >1\to \left\{\begin{array}{c}\sqrt{\frac{2E_C}{{\pi }^2{E}_J}}<\frac{1}{\eta },\mathrm{electric}\mathrm{condensation}=\mathrm{type}\mathrm{III}\mathrm{superconductor},\hfill \\ \frac{1}{\eta }<\sqrt{\frac{2E_C}{{\pi }^2{E}_J}}<\eta ,\mathrm{no}\mathrm{condensation}=\mathrm{bosonic}\mathrm{topological}\mathrm{insulator}/\mathrm{Bose}\mathrm{metal},\hfill \\ \sqrt{\frac{2E_C}{{\pi }^2{E}_J}}>\eta ,\mathrm{magnetic}\mathrm{condensation}=\mathrm{superinsulator}.\hfill \end{array}\right.\hfill \end{array}$$

The phase diagram is shown in Figure 2.

For $\eta >1$, the SIT in a JJA occurs via an intermediate phase in which both $Q_{\mu }$ and $M_{\mu }$ are dilute. In this phase, the action for the JJA reduces to the action of a bosonic topological insulator [39]:

$$S=\sum _{x}i2\pi a_{\mu }{K}_{\mu \nu }{b}_{\nu }.$$

(27)

The existence of this phase was first predicted in [5]. The SIT point [40] is known to be a universal quantum phase transition point with resistance R equal to the quantum of resistance $R_Q$. This topological state is often referred to as a Bose metal because it hosts symmetry-protected metallic edge states [30]. It forms due to the same competition of quantum orders, charge condensate, and vortex condensate that leads to the universal SIT point. This intermediate phase is separated by two quantum BKT transitions from the superinsulating phase for $g<1$ and from the superconducting phase for $g>1$ [22]. For $g\ge 1$, $R\le R_Q$, the saturation of the sheet resistance and the vortex BKT transition has been experimentally observed in [41] in an Al/InAs JJA using a gate voltage to suppress charge tunneling and drive the transition, thereby confirming the validity of our model. In terms of the array parameters, this means varying $E_J$, keeping $E_C$ fixed to increase the value of g. An analogue result for $g\le 1$, showing the saturation of the resistance and the charge BKT transition in JJA, confirms that superinsulation, already measured in NbTin films in [42], is not associated with disorder.

In the superconducting phase, electric topological defects proliferate. It is this new type of superconductivity that we call type-III [19]. It is characterized by a topological gap, and superconductivity is lost through a BKT transition, both at $T=0$ and at finite T, as discussed in the introduction.

For $\eta <1$, instead, when $\sqrt{2E_C/{\pi }^2{E}_J}$ lies between $\eta$ and $1/\eta$, electric and magnetic excitations coexist, indicating a direct first-order phase transition between the superinsulator and the superconductor.

4. Superinsulators

In the superinsulating phase, it is the magnetic monopole defects $M_{\mu }$ which are condensed. To understand the nature of this phase, we compute the induced effective action for the electromagnetic gauge potential $A_{\mu }$ minimally coupled to the electric current,

$$S\to S+i\sum _{\mathbf{x}}{l}_0{l}^2{A}_{\mu }{j}_{\mu }=S+i\sum _{\mathbf{x},\mathbf{i}}\left(l^2{b}_0{F}_0+l_{0}l{b}_i{F}_i\right),$$

(28)

where $F_{\mu }={\widehat{k}}_{\mu \nu }{A}_{\nu }$. The induced action is:

$${\mathrm{e}}^{-S_{\mathrm{eff}}\left(A_{\mu }\right)}=\sum _{Q_{\mu },M_{\mu }}{\int }_{a_{\mu },b_{\mu }}\mathcal{D}{a}_{\mu }\mathcal{D}{b}_{\mu }{\mathrm{e}}^{-S\left(a_{\mu },b_{\mu },Q_{\mu },M_{\mu },A_{\mu }\right)},$$

(29)

and the corresponding induced current is:

$$j^{\mu }=\frac{1}{{\ell }^3}\frac{\delta }{\delta A_{\mu }}{S}_{\mathrm{eff}}\left(A_{\mu }\right).$$

(30)

The coupling with the external electromagnetic field can be taken into account by shifting $M_0$ and $M_i$ in ${\sum }_{\mathbf{x}}(l_0{b}_0{M}_0+i{b}_i{M}_i)$ to:

$$M_0\to M_0^{\prime }=M_0+\frac{l^2}{2\pi }{F}_0,M_i\to M_i^{\prime }=M_i+\frac{l{l}_0}{2\pi }{F}_i,$$

(31)

we obtain, from Equation (18),

$$\begin{array}{ccc}\hfill S_{\mathrm{top}}\left(Q_{\mu },M_{\mu },A_{\mu }\right)& & =\sum _{x,i}{\ell }_0{\ell }^{2}g\frac{\mu \eta \ell }{4{\pi }^2}\left[v{\left(F_0+\frac{2\pi }{{\ell }^2}{M}_0\right)}^2+\frac{1}{v}{\left(F_i+\frac{2\pi }{{\ell }_0\ell }{M}_i\right)}^2\right]\hfill \\ & & +\sum _x\frac{1}{g}\mu \eta Q_{\mu }{Q}_{\mu }+\sum _{x,i}i\frac{\mu \eta mv\ell }{2\pi }\left({\ell }_0{A}_0{Q}_0+\ell A_i{Q}_i\right),\hfill \end{array}$$

(32)

where, also in this case, we retained only self-interactions. This corresponds to the limit ${\ell }_0{\omega }_P=l_{0}m\gg 1$.

In the superinsulating phase, the electric topological excitations $Q_i$ are suppressed because of their large energy, so that $Q_i=0$, and we restore $Q_0=0$. By Equation (32) we thus obtain,

$$\begin{array}{ccc}& & \sum _{\left\{M_i\right\}}{\int }_{-\pi }^{+\pi }\mathcal{D}{A}_{\mu }{\mathrm{e}}^{S\left(A_{\mu },M_i\right)},\hfill \\ & & S\left(A_{\mu },M_i\right)=\frac{g}{4\pi {\ell }_0{\omega }_P}\sum _x{\left(F_i-2\pi M_i\right)}^2,\hfill \end{array}$$

(33)

where we used $m={\omega }_P$ and finite lattice differences. In Equation (33), the gauge fields $F_i$ are periodic with the shifts $F_i\to F_i+2\pi M_i$, showing that they are angular variables defined on the interval $[-\pi ,+\pi ]$. What we obtained is the deep non-relativistic limit of Polyakov’s compact QED action [43,44], in which only electric fields survive. It is the compactness of the gauge fields that allows the presence of magnetic monopoles (instantons). As we will show, also in the non-relativistic case, the presence of monopoles induces linear confinement of probe charges, which become bound by electric flux tubes. There is, however, one crucial difference with the relativistic case. To see this, we decompose $M_i$ into its transverse and longitudinal components [43,44]:

$$\begin{array}{ccc}& & M_i={M^{\mathrm{T}}}_i+{M^{\mathrm{L}}}_i,{M^{\mathrm{T}}}_i={ϵ}_{ij}{\Delta }_{j}n+{ϵ}_{ij}{\Delta }_j\xi ,n\in Z\hfill \\ & & {M^{\mathrm{L}}}_i={\Delta }_i\lambda ,\Delta \lambda ={\widehat{\Delta }}_i{\Delta }_i\lambda =m,\hfill \end{array}$$

(34)

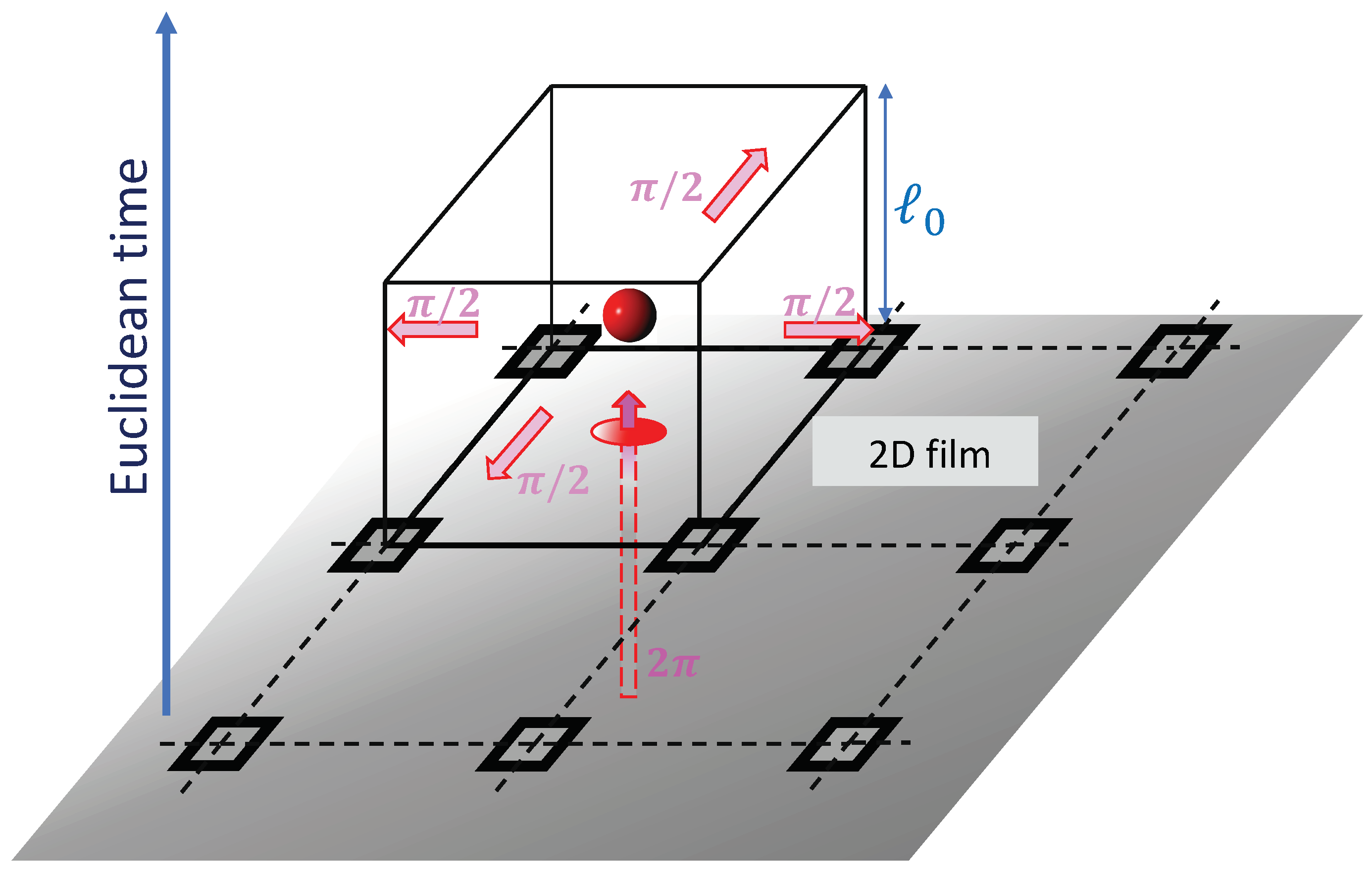
where m is integer magnetic monopoles (see Figure 3).

The sum over $\left\{M_i\right\}$ can be traded for the sum over $\left\{n\right\}$ and $\left\{q\right\}$. The integers $\left\{n\right\}$ are used to shift the integration domain for the gauge field $A_{\mu }$ to $[-\infty ,+\infty ]$, and the real variables $\left\{\xi \right\}$ can be absorbed into the gauge field, giving an integral over the non-compact gauge field $A_{\mu }$ and a sum over the monopole degrees of freedom in the partition function:

$$Z=Z_0{Z}_{\mathrm{inst}}=Z_0\sum _{\left\{m\right\}}{e}^{-\frac{\pi g}{{\ell }_0{\omega }_P}{\sum }_x{m}_x\frac{1}{-\Delta }{m}_x}$$

(35)

where $Z_0$ is the Gaussian integral over $A_{\mu }$. While, in the relativistic case, monopoles interact with a potential $\propto 1/x$ and are, thus, always in a confining plasma phase, in the non-relativistic case realized in JJA, they interact with the inverse of the spatial Laplacian, which gives a $(e_{\mathrm{eff}}^2/2\pi )\log \left|\mathbf{x}\right|$ potential in 2d with $e_{\mathrm{eff}}^2={\pi }^2{l}_0{\omega }_P/g$. Monopoles thus undergo a quantum BKT transition with g playing the role of an inverse temperature. For low values of g, instantons are free and confine probe charges; at the SIT, instead, instantons become confined, and probe charges are liberated.

To see how instantons modify the Coulomb potential and cause linear confinement, we compute the expectation value of the Wilson loop operator $W\left(C\right)$, where C is a closed loop in 3D Euclidean space-time restricted to the plane formed by the Euclidean time and one of the space coordinates. This gives the interaction potential between two external probe charges of strength $\pm q_{\mathrm{ext}}$:

$$\langle W\left(C\right)\rangle =\frac{1}{Z_{A_{\mu },M_i}}\sum _{\left\{M_i\right\}}{\int }_{-\pi }^{+\pi }\mathcal{D}{A}_{\mu }{\mathrm{e}}^{-\frac{g}{4\pi {\ell }_0{\omega }_P}{\sum }_x{\left(F_i-2\pi M_i\right)}^2}{\mathrm{e}}^{i{q}_{\mathrm{ext}}{\sum }_C{A}_{\mu }},$$

(36)

where we absorbed a factor l in $A_{\mu }$. A linear interaction between the probe charges will give rise to an area law [37,43]:

$$\langle W\left(C\right)\rangle =e^{-\sigma A},$$

(37)

where A is the area of the surface S enclosed by the loop C and $\sigma$ is called the string tension [37,43].

Using the lattice Stoke theorem, one rewrites Equation (36) as

$$\langle W\left(C\right)\rangle =\frac{1}{Z_{A_{\mu },M_i}}\sum _{\left\{M_i\right\}}{\int }_{-\pi }^{+\pi }\mathcal{D}{A}_{\mu }{\mathrm{e}}^{-\frac{g}{4\pi {\ell }_0{\omega }_P}{\sum }_x{\left(F_i-2\pi M_i\right)}^2}{\mathrm{e}}^{i{q}_{\mathrm{ext}}{\sum }_S{S}_i(F_i-2\pi M_i)},$$

(38)

where the quantities $S_i$ are unit vectors perpendicular to the plaquettes forming the surface S encircled by the loop C and vanish on all other plaquettes. We have also multiplied the Wilson loop operator by 1 in the form $\exp (-i2\pi q_{\mathrm{ext}}{M}_i)$ on all plaquettes forming S. Repeating the steps that lead to Equation (35), we obtain,

$$\langle W\left(C\right)\rangle =\frac{1}{Z_{\mathrm{m}}}\sum _{\left\{m\right\}}{e}^{-\frac{\pi g}{{\ell }_0{\omega }_P}{\sum }_x{m}_x\frac{1}{-\Delta }{m}_x}{e}^{i2\pi q_{\mathrm{ext}}{\sum }_S{\widehat{\Delta }}_i{S}_i\frac{1}{-\Delta }{m}_x},$$

(39)

where we neglected $Z_0$, which is not relevant for what follows [6].

We now perform the sum over the instantons. To this end, we introduce an auxiliary scalar field $\chi$ and write the quadratic term in the instantons in Equation (39) as a Gaussian integral. At low g, in the deep superinsulating regime, we use the dilute instanton approximation, summing only over the single-monopole configuration $m=\pm 1$. This gives [43],

$$\langle W\left(C\right)\rangle =\frac{1}{Z_{Ø}}\int \mathcal{D}\chi e^{-\frac{{\ell }_0{\omega }_P}{4\pi g}{\sum }_x{\Delta }_i\chi {\Delta }_i\chi +\frac{8\pi g}{{\ell }_0{\omega }_P}z(1-\cos (\chi +q_{\mathrm{ext}}\eta ))},$$

(40)

where the angle $\eta =2\pi {\widehat{\Delta }}_i{S}_i/(-{\Delta }_2)$ represents a dipole sheet on the Wilson surface S, and the monopole fugacity z is determined by the self-interaction as

$$z=e^{-\frac{\pi g}{{\ell }_0{\omega }_P}G\left(0\right)},$$

(41)

with $G\left(0\right)$ being the inverse of the 2D Laplacian at coinciding arguments. Equation (40) can be rewritten as:

$$\langle W\left(C\right)\rangle =\frac{1}{Z_{Ø}}\int \mathcal{D}\chi e^{-\frac{{\ell }_0{\omega }_P}{2\pi g}{\sum }_x\frac{1}{2}{\Delta }_i(\chi -q_{\mathrm{ext}}\eta ){\Delta }_i(\chi -q_{\mathrm{ext}}\eta )+{\mu }^2(1-\cos \left(\chi \right))},$$

(42)

where we define ${\mu }^2=4\pi gz/{\ell }_0{\omega }_P$ and we shift $\chi \to \chi -q_{\mathrm{ext}}$.

To compute the string tension $\sigma$, we have to evaluate the integral Equation (42) for both Cooper pairs, with $q_{\mathrm{ext}}=1$ and single electrons, corresponding to $q_{\mathrm{ext}}=1/2$ in our case. To evaluate Equation (42) we use the saddle point approximation,

$${\Delta }_2{\chi }_{\mathrm{cl}}=q_{\mathrm{ext}}{\Delta }_2\eta +{\mu }^2\sin {\chi }_{\mathrm{cl}},$$

(43)

valid for small g where the integral is dominated by the classical solution to the equation of motion. This reduces the problem to a one-dimensional equation when we consider time and one spatial coordinate, e.g., in the $(t,x_2)$ plane far from the boundaries of S:

$${\widehat{\Delta }}_{x1}{\Delta }_{x1}{\chi }_{\mathrm{cl}}=-2\pi q_{\mathrm{ext}}{\widehat{\Delta }}_{x1}{S}_1+{\mu }^2\sin {\chi }_{\mathrm{cl}}.$$

(44)

To solve this equation, we use the continuum limit [43] with boundary conditions ${\chi }_{\mathrm{cl}}\to 0$ for $|x_1|\to \infty$. For Cooper pairs ($q_{\mathrm{ext}}=1$), we obtain:

$${\chi }_{\mathrm{cl}}=\mathrm{sign}\left(x_1\right)4\arctan {\mathrm{e}}^{-\mu |x_1|},$$

(45)

which gives Equation (37) with $\sigma$:

$$\sigma =\frac{\hslash {\omega }_P}{\ell }\sqrt{\frac{16}{\pi g{\ell }_0{\omega }_P}}\sqrt{z}=\frac{\hslash {\omega }_P}{\ell }\sqrt{\frac{16}{\pi g{\ell }_0{\omega }_P}}{\mathrm{e}}^{-\frac{\pi g}{2{\ell }_0{\omega }_P}G\left(0\right)}.$$

(46)

The string binds together charges, prevents charge transport on arrays of a sufficient size and is the origin of the infinite resistance characterizing superinsulation. If we consider, instead, a single-electron probe, $q_{\mathrm{ext}}=1/2$, with the same boundary conditions, we obtain the string tension

$${\sigma }_{\mathrm{electrons}}=\frac{1}{2}\sigma ,$$

(47)

which implies that single electrons are also confined. This explains why charge transport mediated by thermally excited normal quasiparticles is not present in superinsulators.

From Equation (46), we can estimate the typical string size ${\ell }_{\mathrm{string}}=\sqrt{c\hslash /\sigma }$. Taking the following typical values for the experimental JJA, $\ell =100$ nm and ${\omega }_{\mathrm{P}}=10$ GHz, and taking for ${\ell }_0{\omega }_{\mathrm{P}}=\mathcal{O}\left(1000\right)$, we arrive at ${\ell }_{\mathrm{string}}/\ell \approx 150$ lattice spacing, which represents the distance between the superconducting islands. This sets a minimum dimension for the arrays to be able to accommodate an electric pion and to show superinsulation. To be able to see superinsulation in JJA, moreover, it is necessary to lower the value of g, which, in terms of the array parameters, implies increasing the vortex tunneling parameter $E_C$. While making $g>1$ has been experimentally achieved in [41], the opposite limit seems to be more difficult. It will require a “more insulating” substrate to be able to increase vortex mobility and govern $E_C$. Taking as an example the experiment realized in [41] in Al/InAs JJA, we can imagine an exposed substrate which forms a “dual lattice” with a mechanism that can control the vortex tunneling and, thus, $E_C$. In a system like this, it will be possible to independently vary $E_J$ and $E_C$, the key features to explore the phase diagram of the model. We predict that, in this case, it will also be possible to observe superinsulation in JJAs.