Abstract
Muonic Atom X-ray Emission spectroscopy (µ-XES) is a novel elemental technique that exploits the high-energy X-rays emitted from the muonic atom cascade process to characterize materials. At the ISIS Neutron and Muon Source, the technique is performed at Port4 of the RIKEN-RAL facility, with a user demand that is increasing every year. To cope with this demand, it is necessary to continue to improve the method, either for the hardware (detectors, acquisition, etc.) or software (data analysis and interpretation). In both cases, Monte Carlo codes play an important role: with a simulation, it is possible to reproduce the experimental setup and provide a reliable quantitative analysis. In this work, we investigate the capabilities of GEANT4 for such applications. From the results, we observed that the generation of X-rays, especially the kα and kβ transition for high Z atoms, are not in agreement with the experimental ones. A solution to this issue, other than an attempt with a small modification of the GEANT4 cascade class, could be provided by a database of transition energy calculated by a Dirac equation software called MuDirac. The software, developed by the UKRI scientific computing department and the ISIS muon group, can compute all the transition energy for a given nuclide. Here, preliminary results of the implementation of the MuDirac database in GEANT4 are reported.
1. Introduction
Monte Carlo simulation software are invaluable tools for the progress and development of many projects in the scientific community. Especially in particle physics, where the complexity and scale of experiments are increasing, having simulation software that precisely implement all the phenomena and hardware involved in an investigation is of key importance. GEANT4, FLUKA and MCNP are among the most used tools to handle the transportation of particles and all the related physical processes [1,2,3]. The first is developed via international collaboration and provides users with all the instruments necessary to run applications that describe the geometry (experimental setup and detectors), the particles and the physical processes of a given experiment. As with other software, the GEANT4 code is open source and can be handled by users and developers to best suit their requirements. At the Milano Bicocca section of the National Institute of Nuclear Physics (INFN), the weak interaction group utilises GEANT4 through a user-friendly software called “Arby” [4,5]. Arby employs GEANT4 physics processes and classes with high flexibility and ease of use. Differently from GEANT4, however, the user is not required to write an application to run a simulation in Arby but just a configuration file that stores all the information about the experimental setup (detectors and samples). The code and physics implementation are managed by Arby developers [6]. Particle type, direction, number of events, etc. are accessed via simple instructions on the command line, from which the simulation is launched. Finally, the output of a simulation (either text or root file) is processed with dedicated software to obtain a detector response function. The Arby tool and all other related software are continuously developed by INFN staff and have been used in several physics of rare events experiments [7,8]. More recently, in the framework of a collaboration between the INFN, the University of Milano Bicocca and the ISIS Neutron and Muon Source, Arby has been used as a tool for the development of the Muonic Atom X-ray Emission spectroscopy (µ-XES) [9]. µ-XES is a novel technique developed in the past decades at several facilities around the world like PSI, JPARC and ISIS, and it uses negative muons to investigate matter [10,11,12]. Indeed, when negative muons are implanted in matter, they form the so-called Muonic atom, a bound state in which the muon rapidly cascades down from the capture level to the nucleus. The process, after initial muon-induced Auger emission, becomes radiative, with the emission of high-energy X-rays (an extensive description of muon capture and muonic atoms can be found here [13]). With a particular interest in Cultural Heritage studies, the technique has many fields of applications, from the characterization of lithium batteries to meteorites to material engineering [14,15,16,17,18,19,20,21,22]. Given its novelty, the technique has room for improvement, especially as it is now performed at the ISIS facility in terms of detector, electronics and data interpretation. Arby has been already used to perform preliminary characterizations of a new detector set-up and to perform thin layer characterization by comparing simulation results with output from SRIM/TRIM and real data sets [23,24]. In addition, the software is being used to provide improvement of a more reliable quantitative analysis: as it is performed now, it requires measurements of Standard Reference Materials to produce reliable calibration curves. With Arby or other Monte Carlo (MC) software, it could be possible to reproduce the experiment and compare the simulated one with the measured one, similarly to what is already done with XRF [25,26]. To do so, it is important to precisely implement all the involved physical processes: in GEANT4, however, the muonic cascade process is not yet reliable for this kind of application. Indeed, it has been found that, especially for high Z atoms and high-energy transitions, there is a large deviation from simulated and measured values, as explained in the next paragraphs. Here, we propose a new approach that involves the creation of a new database of transition energies produced by an open-source Dirac equation Solver called MuDirac, developed by the UKRI scientific computing department and the ISIS Muon group [27].
2. Methods
2.1. GEANT4/Arby Characterization
The GEANT4 class currently responsible for the muon cascade process is the G4EmCaptureCascade, available since GEANT4 version 9.6. This class, as stated in the code, “calculates the energy of a K mesoatom level using the energy of the hydrogen atom by taking into account the finite size of the nucleus” [28]. The class includes a list of 28 atoms and their 1s energy. Some issues in the calculations were found from preliminary simulations; therefore, to further characterize the software, an extensive set of simulations was performed. The simulations covered a large part of the periodic table, with 21 elements ranging from lithium to bismuth (GEANT4 version used: 10.04.p03). In this first part of the project, interest was mainly devoted to the detection of all the X-rays emitted; therefore, very simple geometry was used. A small rod of the selected element was placed in a cylinder made of germanium to simulate a nearly 100% efficient detector (Figure 1). Then, an interaction with a 30 MeV/c muon beam was simulated (with an average of 107 events simulated). The simulation output (.root or .txt file) was processed in a dedicated software that reproduced the detector response, with the final product in the form of an energy spectrum.

Figure 1.
The basic setup of the simulations: the negative muon beam (in red) is generated from a point-like source and hits a target placed inside the germanium active area (blue). The interaction produces a radiative emission (green lines). With this configuration, most of all the generated radiations are collected by the crystal.
The results of the K, L and M lines for some of the simulated elements (that cover the low and high Z region) are reported in Table 1. For the lower energy emissions corresponding to the L and M lines, the agreement with the literature is good, with energy differences generally lower than 2 keV (except for gold and silver, where the delta is higher). It has to be stated that even in the literature, there is some deviation in the listed values; therefore, an energy delta within 2 keV is acceptable [29,30]. The main differences are in the high-energy region of each atom, corresponding to the Kα and Kβ lines. For these lines, the delta is always above 10 keV, increasing with Z but without a well-defined pattern (this deviation was observed in all the simulated atoms). If not missing, some Kβ transitions are present with a very low peak intensity. For example, in copper, one would expect a double peak around 1500 keV. However, as shown in Figure 2b (red spectra), the Kβ 1502.2 keV transition, which should have a higher intensity than the corresponding Kα at 1491.3 keV, is a small peak just above the baseline level. Therefore, from this first set of simulations, it was evident that the main problem of the cascade calculations resides in the calculations of the K shell transition.

Table 1.
Corresponding peak values for the principal transitions in the literature and from GEANT4 simulations (unit: keV). Literature data were taken from [29,30].
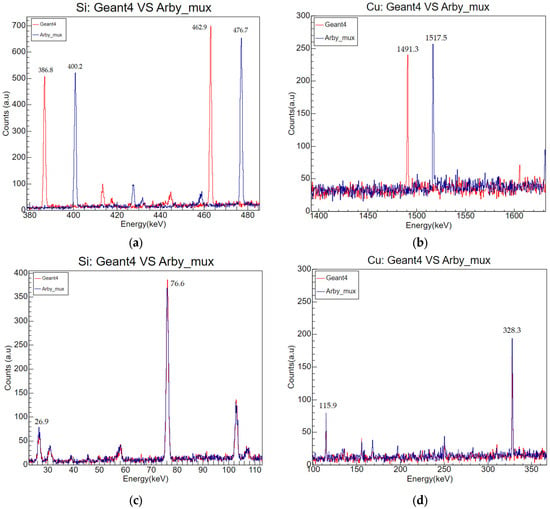
Figure 2.
K transitions energy range: (a) silicon; (b) copper. As stated in the text, for low Z atoms like silicon, the kα and kβ transition are simulated, whereas for elements with higher atomic numbers, just one transition is simulated or the second one is present at a very low intensity, just above background. Instead, for the low-energy transition, the two Arby versions provide the same output: (c) silicon and (d) copper.
2.2. Modification of the GEANT4 Class (Arby_Mux)
The issue described above was also identified during the simulation work for the FAMU experiment by the INFN group of Trieste. FAMU is an international collaboration whose goal is to measure the proton Zemach radius with the measurement of the hyperfine splitting of the muonic hydrogen ground state [31]. To tackle the problem, the group implemented the GEANT4 class by increasing the listed number of atoms from 28 to 57 and by adding a small correction to the calculation of the K shell transitions. For the FAMU experiment, however, interest was mainly in low Z atoms; therefore, implementation was not evaluated for the high Z part of the periodic table. Thus, to test the modified class, an extensive set of simulations was performed. To distinguish the results from the previous ones, Arby/GEANT4 is called Arby_Mux here. The results of the K, L and M lines are reported in Table 2. As for the Arby/GEANT4, the L and M lines agree with the literature—except for silver and gold—all within a 2 keV delta. Concerning the K transition, the correction produced good agreement with the literature for the low Z atoms like aluminium and silicon, with a very small difference in literature data. However, for high Z atoms, the situation was not improved. In the modified class, Kα are completely missing, while Kβ are present but with delta energy that increases with Z. Figure 2 reports the simulated spectra from each of the two Arby versions to better visualize the differences in the high-energy transitions. Figure 2a shows that, with Arby_Mux, the peaks are shifted to higher energies to match the expected values, whereas for the low-energy peak, there is no difference between Arby/Geant and Arby_Mux (Figure 2c,d). If Z increases, as shown in Figure 2b, peaks are shifted, but the signature double peak of copper is still missing. Therefore, even with the updated class, GEANT4 is still not able to properly reproduce the K shell transition.

Table 2.
Comparison between literature and Arby_Mux simulations. Literature data were taken from [29,30].
2.3. The MuDirac Database (Arby_MuDirac)
A solution to improve the reliability of the simulation could be provided by a data-driven library. The implementation of a new database in GEANT4 has already been employed in some processes, like for the Low Energy Electromagnetic package, responsible for the simulation of atomic relaxation [32]. Recently, the generation of the X-ray and Auger emission from the process has been implemented by a data-driven database (called ANSTO, both for ionisation cross sections and transition probabilities) to be used along with the default one [33]. The implementation of a database, moreover, requires less manpower than the editing or development of an entire class. The idea proposed here is to use a third-party software, MuDirac, to create the database. MuDirac calculates the transition energies of the cascade and produces an output in which the transition energy is associated with the transition rate (in s−1). In addition, the software provides a simulated spectrum with the calculated transitions. MuDirac works from the terminal, and the calculation parameters are stored in an input file. The user can select the transitions to calculate for a given atom, the model used to describe the nucleus, the electronic configuration, etc. (for a detailed description and the code, see [34]). To create the database, calculations for the most abundant isotopes—from hydrogen to bismuth—were performed. For each simulation, the starting level for the cascade calculation was selected as n = 6. It is well known that the radiative emission after negative muon capture becomes dominant at the end of the cascade when the muon approaches lower muonic orbitals; therefore, there was no interest in increasing the starting level [35]. Nevertheless, this setting can be modified based on interests. The output of the MuDirac calculation selected for the database was the “.dat” file containing the simulated spectrum data, a two-column file with energy and intensity. To make the database available in GEANT4/Arby, the Arby setup file was edited with an environment variable pointing to the folder containing all the calculated outputs. When a simulation was launched, the energy corresponding to the transition was extracted and used by GEANT4 if a Mudirac file of the given specimen was found. If the file was missing, a warning was generated, and the program continued the simulation with the standard cascade generation. A preliminary test with this edited Arby version, called “Arby_MuDirac”, was performed to evaluate the feasibility of the approach (dedicated GEANT4 version: 11.1.1). With this approach, having a MuDirac output that is as complete as possible is of key importance. That is because, by using the database, the information coming from the cascade calculation made by GEANT4 is lost with the MuDirac; indeed, a single deexcitation is generated instead of the entire cascade. The process of capture is maintained, and gamma rays are generated. The results of the simulations are reported in Table 3; here, the K transition columns have agreement between simulations and literature, with a delta lower than 2 keV. In addition, with the MuDirac database, some low-energy peaks are adjusted in position. This happens not only for the lines in the table but also for some other peaks in the spectrum. For instance, copper K and L lines are reported in Figure 3. Copper is easily distinguished by a double peak at 330 and 336 keV, other than the one at 1.5 Mev. This double peak, as shown in Figure 3a, is not present in the Arby_Mux version, while it appears in the MuDirac version of Arby. This means that, by setting a precise parameter of the Mudirac calculation, it is possible to have an overall correction along the spectrum, especially in critical points like the one used for element identification.

Table 3.
Comparison between literature and Arby_MuDirac simulations (unit: keV). Here, delta energy is lower than two keV with the only exception of lead Kβ, which is slightly larger. This is due to the fact that the literature value is for natural lead, whereas the simulated one is from 208 Pb. Literature data were taken from [29,30].
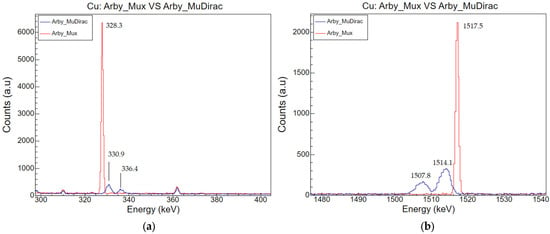
Figure 3.
Comparison between Arby_Mux (red) and Arby_MuDirac (blue) for copper. In the Arby version with the database, the two fingerprint double peaks of copper are visible both in the low energy (a) and high energy (b) part of the spectrum.
3. Discussion
To finally evaluate the capabilities of the Arby_MuDirac version, simulations were compared to a standard measurement performed at ISIS. The instrument setup of a negative muon experiment, consisting of four HPGe detectors placed at 15 cm from the sample position with a 30° angle was modelled in Arby [17]. The sample consisted of a thin foil of a given material, placed 10 cm from the beam exit. Testing was done for a set of elements, and the results for silicon are reported here. As shown in Figure 4a, intensities of the simulated spectra (red) are not well reproduced. Here, even though the patterns are similar between the two spectra, silicon K-line intensities are much higher than the M-lines in the simulated spectrum—a relationship inverted in the measured spectra. This is due to the fact that MuDirac assumes that all states can be starting points of a transition, without considering their differences in the probability of being populated. Therefore, since the intensity is related to the population of the starting decay level, the computed intensities are not properly correct. For now, they are just based on the probability of a transition to take place. In addition, the simulations do not consider the efficiency of the detection system. MuDirac developers are working towards a solution to the issue, and a MuDirac 2.0 version is expected soon. For the moment, to try to tackle the problem, a solution could be provided by scaling the calculated intensities using a measured spectrum. A normalization factor for each peak was obtained by dividing the normalised peak area of the measured spectrum by the normalised peak area of the simulated spectrum. The MuDirac intensities, in particular, were scaled with a constraint: the maximum value, instead of being the 400 keV peak, was set to be the 76 keV peak, which is the most intense peak in the measured spectrum. The results of the scaled data are reported in Figure 4b: with this approach, peaks are better modelled, especially in the high-energy range.
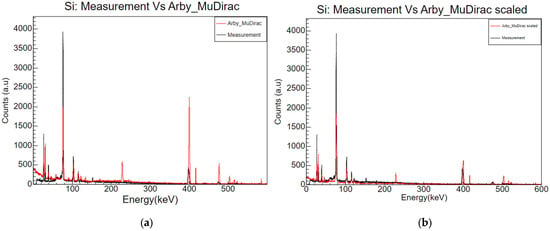
Figure 4.
Comparison between real measured data of Silicon (black) and the simulations with Arby_MuDirac (a) and Arby_MuDirac with scaled peak intensities (b). Differences are evident in the 76 keV peak at the beginning of the spectra and the 400 keV peak. In the real measurement, the first is more intense than the second, which is the most intense peak in the Arby_MuDirac simulation instead. After scaling, the intensities are better reproduced. The extra peaks present in the simulated spectrum could be due to the other material present in the modelled environment (230 keV) or to an error in the simulation process (at 416 keV, for example, the peak is too sharp and narrow to be considered part of the cascade).
4. Conclusions
A preliminary approach to the development of a new database for GEANT4 was performed. With MuDirac, a database of transition energies was created and implemented in the Arby toolkit. The results are promising and show that a better agreement with the literature data is reached when using the Arby_MuDirac version. Still, the software presents some drawbacks, especially in cases of calculated intensities that are not well reproduced. However, MuDirac is an open-source software and is in continuous development, and a new and implemented software is also in development. This means that the database can be kept updated as the software improves. Finally, the solution proposed in this work, as done with other databases, could be directly implemented into GEANT4. This would require adding an alternative class to the G4EmCaptureCascade class, as well as other extra classes to handle the database.
Author Contributions
Conceptualization, M.C. (Massimiliano Clemenza) and M.C. (Matteo Cataldo); writing—original draft preparation, M.C. (Matteo Cataldo); writing—review and editing, M.C. (Matteo Cataldo), A.D.H., O.C., E.M. and M.C. (Massimiliano Clemenza), software, O.C., S.P., E.M. and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
The author (Matteo Cataldo) PhD is co-founded by ISIS and UNIMIB under the studentship agreement No. S2 2021 002 CN8647, INFN via Commission V and Cultural Heritage Net of INFN.
Data Availability Statement
Not applicable. However, GEANT4 and MuDirac are opens source software and the results reported here can be easily reproduced.
Acknowledgments
The authors acknowledge the ISIS Neutron and Muon Source, the University of Milano Bicocca and the INFN for funding and collaborating to the research and development of the Muon spectroscopy techniques at the RIKEN-RAL facility.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Ferrari, A.; Sala, P.R.; Fasso, A.; Ranft, J. FLUKA: A Multi-Particle Transport Code; Program Version 2005; CERN: Geneva, Switzerland, 2005. [Google Scholar]
- Werner, C.J. MCNP User Manual; Code Versione 6.2; Los Alamos National Laboratory: Los Alamos, NM, USA, 2017. [Google Scholar]
- Pavan, M.; Callegaro, C.; Capelli, S.; Carrettoni, M.; Clemenza, M.; Gironi, L.; Gorla, P.; Maiano, C.; Nones, C.; Pedretti, M. Control of bulk and surface radioactivity in bolometric searches for double-beta decay. Eur. Phys. J. A 2008, 36, 159–166. [Google Scholar] [CrossRef]
- Alduino, C.; Alfonso, K.; Artusa, D.R.; Avignone, F.T.; Azzolini, O.; Banks, T.I.; Bari, G.; Beeman, J.W.; Bellini, F.; Benato, G.; et al. The projected background for the CUORE experiment. Eur. Phys. J. C 2017, 77, 543. [Google Scholar] [CrossRef]
- Abusleme, A.; Adam, T.; Ahmad, S.; Ahmed, R.; Aiello, S.; Akram, M.; An, F.; An, Q.; Andronico, G.; Anfimov, N.; et al. Radioactivity control strategy for the JUNO detector. J. High Energy Phys. 2021, 2021, 102. [Google Scholar] [CrossRef]
- The CUORE Collaboration. Search for Majorana neutrinos exploiting millikelvin cryogenics with CUORE. Nature 2022, 604, 53–58. [Google Scholar] [CrossRef] [PubMed]
- Alduino, C.; Alfonso, K.; Artusa, D.R.; Avignone, F.T.; Azzolini, O.; Banks, T.I.; Bari, G.; Beeman, J.W.; Bellini, F.; Bersani, A.; et al. Measurement of the two-neutrino double-beta decay half-life of 130 Te with the CUORE-0 experiment. Eur. Phys. J. C 2017, 77, 13. [Google Scholar] [CrossRef]
- Giuntini, L.; Castelli, L.; Massi, M.; Fedi, M.; Czelusniak, C.; Gelli, N.; Liccioli, L.; Giambi, F.; Ruberto, C.; Mazzinghi, A.; et al. Detectors and Cultural Heritage: The INFN-CHNet Experience. Appl. Sci. 2021, 11, 3462. [Google Scholar] [CrossRef]
- Hillier, A.D.; Lord, J.S.; Ishida, K.; Rogers, C. Muons at ISIS. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2019, 377, 20180064. [Google Scholar] [CrossRef]
- Biswas, S.; Gerchow, L.; Luetkens, H.; Prokscha, T.; Antognini, A.; Berger, N.; Cocolios, T.E.; Dressler, R.; Indelicato, P.; Jungmann, K.; et al. Characterization of a Continuous Muon Source for the Non-Destructive and Depth-Selective Elemental Composition Analysis by Muon Induced X- and Gamma-rays. Appl. Sci. 2022, 12, 2541. [Google Scholar] [CrossRef]
- Miyake, Y.; Shimomura, K.; Kawamura, N.; Strasser, P.; Makimura, S.; Koda, A.; Fujimori, H.; Nakahara, K.; Takeshita, S.; Kobayashi, Y.; et al. J-PARC muon facility, MUSE. J. Phys. Conf. Ser. 2010, 225, 012036. [Google Scholar] [CrossRef]
- Measday, D. The nuclear physics of muon capture. Phys. Rep. 2001, 354, 243–409. [Google Scholar] [CrossRef]
- Cataldo, M.; Clemenza, M.; Ishida, K.; Hillier, A.D. A Novel Non-Destructive Technique for Cultural Heritage: Depth Profiling and Elemental Analysis Underneath the Surface with Negative Muons. Appl. Sci. 2022, 12, 4237. [Google Scholar] [CrossRef]
- Clemenza, M.; Bonesini, M.; Carpinelli, M.; Cremonesi, O.; Fiorini, E.; Gorini, G.; Hillier, A.; Ishida, K.; Menegolli, A.; Mocchiutti, E.; et al. Muonic atom X-ray spectroscopy for non-destructive analysis of archeological samples. J. Radioanal. Nucl. Chem. 2019, 322, 1357–1363. [Google Scholar] [CrossRef]
- Hillier, A.D.; Hampshire, B.; Ishida, K. Depth-Dependent Bulk Elemental Analysis Using Negative Muons. In Handbook of Cultural Heritage Analysis; D’Amico, S., Venuti, V., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 23–43. [Google Scholar] [CrossRef]
- Kubo, M.K.; Moriyama, H.; Tsuruoka, Y.; Sakamoto, S.; Koseto, E.; Saito, T.; Nishiyama, K. Non-destructive elemental depth-profiling with muonic X-rays. J. Radioanal. Nucl. Chem. 2008, 278, 777–781. [Google Scholar] [CrossRef]
- Umegaki, I.; Kondo, Y.; Tampo, M.; Nishimura, S.; Takeshita, S.; Higuchi, Y.; Kondo, H.; Sasaki, T.; Shimomura, K.; Miyake, Y. Non-destructive operando measurements of muonic X-rays on Li-ion battery. J. Phys. Conf. Ser. 2023, 2462, 012018. [Google Scholar] [CrossRef]
- Terada, K.; Ninomiya, K.; Osawa, T.; Tachibana, S.; Miyake, Y.; Kubo, M.K.; Kawamura, N.; Higemoto, W.; Tsuchiyama, A.; Ebihara, M.; et al. A new X-ray fluorescence spectroscopy for extraterrestrial materials using a muon beam. Sci. Rep. 2014, 4, 5072. [Google Scholar] [CrossRef]
- Biswas, S.; Megatli-Niebel, I.; Raselli, L.; Simke, R.; Cocolios, T.E.; Deokar, N.; Elender, M.; Gerchow, L.; Hess, H.; Khasanov, R.; et al. The non-destructive investigation of a late antique knob bow fibula (Bügelknopffibel) from Kaiseraugst/CH using Muon Induced X-ray Emission (MIXE). Heritage Sci. 2023, 11, 43. [Google Scholar] [CrossRef]
- Shimada-Takaura, K.; Ninomiya, K.; Sato, A.; Ueda, N.; Tampo, M.; Takeshita, S.; Umegaki, I.; Miyake, Y.; Takahashi, K. A novel challenge of nondestructive analysis on OGATA Koan’s sealed medicine by muonic X-ray analysis. J. Nat. Med. 2021, 75, 532–539. [Google Scholar] [CrossRef]
- Ninomiya, K. Non-destructive, position-selective, and multi-elemental analysis method involving negative muons. J. Nucl. Radiochem. Sci. 2019, 19, 8–13. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter (2010). Nucl. Instrum. Methods B 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Cataldo, M.; Hillier, A.D.; Porcinai, S.; Ishida, K.; Grazzi, F.; Clemenza, M. Negative muons for the characterization of thin layers in Cultural Heritage artefacts. J. Phys. Conf. Ser. 2023, 2462, 012003. [Google Scholar] [CrossRef]
- Helsen, J.; Vrebos, B. Monte Carlo simulations of XRF intensities in non-homogeneous matrices. Spectrochim. Acta Part B At. Spectrosc. 1984, 39, 751–759. [Google Scholar] [CrossRef]
- Giurlani, W.; Berretti, E.; Lavacchi, A.; Innocenti, M. Thickness determination of metal multilayers by ED-XRF multivariate analysis using Monte Carlo simulated standards. Anal. Chim. Acta 2020, 1130, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Sturniolo, S.; Hillier, A. Mudirac: A Dirac equation solver for elemental analysis with muonic X-rays. X-Ray Spectrom. 2020, 50, 180–196. [Google Scholar] [CrossRef]
- Ivanchenko, V. Geant4. Available online: https://geant4.kek.jp/lxr/source/processes/hadronic/stopping/src/G4EmCaptureCascade.cc (accessed on 18 July 2023).
- Engfer, R.; Schneuwly, H.; Vuilleumer, J.L.; Walter, H.K.; Zehnder, A. Charge-distribution parameters, isotope shifts, isomer shifts and magnetic hyperfine constants from muonic atoms. Data Nucl. Data Tables 1974, 14, 509–597. [Google Scholar] [CrossRef]
- Zinatulina, D.; Briançon, C.; Brudanin, V.; Egorov, V.; Perevoshchikov, L.; Shirchenko, M.; Yutlandov, I.; Petitjean, C. Electronic catalogue of muonic X-rays. EPJ Web Conf. 2018, 177, 03006. [Google Scholar] [CrossRef]
- Pizzolotto, C.; Adamczak, A.; Bakalov, D.; Baldazzi, G.; Baruzzo, M.; Benocci, R.; Bertoni, R.; Bonesini, M.; Bonvicini, V.; Cabrera, H.; et al. The FAMU experiment: Muonic hydrogen high precision spectroscopy studies. Eur. Phys. J. A 2020, 56, 185. [Google Scholar] [CrossRef]
- Guatelli, S.; Mantero, A.; Mascialino, B.; Nieminen, P.; Pia, M.G. Geant4 Atomic Relaxation. IEEE Trans. Nucl. Sci. 2007, 54, 585–593. [Google Scholar] [CrossRef]
- Bakr, S.; Cohen, D.D.; Siegele, R.; Archer, J.W.; Incerti, S.; Ivanchenko, V.; Mantero, A.; Rosenfeld, A.; Guatelli, S. Geant4 X-ray fluorescence with updated libraries. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2021, 507, 11–19. [Google Scholar] [CrossRef]
- Mudirac. Available online: https://github.com/muon-spectroscopy-computational-project/mudirac (accessed on 25 July 2023).
- Okumura, T.; Azuma, T.; Bennett, D.A.; Caradonna, P.; Chiu, I.; Doriese, W.B.; Durkin, M.S.; Fowler, J.W.; Gard, J.D.; Hashimoto, T.; et al. Deexcitation Dynamics of Muonic Atoms Revealed by High-Precision Spectroscopy of Electronic X-rays. Phys. Rev. Lett. 2021, 127, 053001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).