Abstract
We explore the dynamics and interactions of multiple bright droplets and bubbles, as well as the interactions of kinks with droplets and with antikinks, in the extended one-dimensional Gross–Pitaevskii model including the Lee–Huang–Yang correction. Existence regions are identified for the one-dimensional droplets and bubbles in terms of their chemical potential, verifying the stability of the droplets and exposing the instability of the bubbles. The limiting case of the droplet family is a stable kink. The interactions between droplets demonstrate in-phase (out-of-phase) attraction (repulsion), with the so-called Manton’s method explicating the observed dynamical response, and mixed behavior for intermediate values of the phase shift. Droplets bearing different chemical potentials experience mass-exchange phenomena. Individual bubbles exhibit core expansion and mutual attraction prior to their destabilization. Droplets interacting with kinks are absorbed by them, a process accompanied by the emission of dispersive shock waves and gray solitons. Kink–antikink interactions are repulsive, generating counter-propagating shock waves. Our findings reveal dynamical features of droplets and kinks that can be detected in current experiments.
1. Introduction
Quantum droplets are self-bound many-body states emanating from the competition between mean-field and quantum-fluctuation energy contributions [1], which crucially depend on the system’s dimensionality [2]. Droplets have been first observed in dipolar atomic condensates [3,4] and then in bosonic mixtures with contact interactions, under the action of external confinement [5,6,7] and in free space [8]. Quantum fluctuations are commonly modeled by the Lee–Huang–Yang (LHY) term [9] added to the mean-field Gross–Pitaevskii Equations (GPEs) [1,10]. The accordingly amended GPEs have been successfully applied for the description of droplet structures and dynamics [11,12,13], including their collective response [14,15,16,17], thermal [18,19] and modulational [20,21,22] instabilities, as well as the capability to maintain robust self-trapping in the soliton [23,24,25] and vortex [26,27] states. Droplets are filled by an extremely dilute quantum fluid. Because the density is limited by a maximum value admitted by the competition between the mean-field attraction and LHY repulsion, the increase of the number of atoms bound in the droplets leads to the formation of their flat-top shapes [1]. This is in sharp contrast to other quantum self-bound states, such as liquid-helium drops [28,29], which feature densities at least six orders of magnitude higher than quantum droplets.
More recently, it was found that, besides the droplets, similar states exist at relatively low chemical potentials. While their density profiles resemble dark solitons, they typically feature a substantially larger width and no phase jump. Those states are dubbed bubbles [23] hereafter in the present work. These structures are represented by homoclinic solutions attached to potential maxima in the corresponding phase space, as is shown in the discussion below. In contrast to self-confined (“bright”) droplets, the excitation spectra and dynamical response of bubbles are largely unexplored, which is one of the foci of the present work. Notice that exploring the excitation spectrum for the bright droplets [14] reveals that, under specific conditions, upon tuning the interactions the droplets tend to “cool down”, i.e., it is not energetically favorable for the droplet to be in an excited state.
An important open question concerns the interaction among droplets and that between bubbles, as well as the fate of droplets colliding with other structures, such as kinks [26]. An interesting prospect here is to develop an effective particle-like dynamical picture, similar to what was achieved previously for solitary waves [30,31,32,33], aiming to capture the quantitative aspects of interactions between the droplets. Collisions of 3D droplets in K [34] have been experimentally monitored. It was demonstrated that two slowly colliding droplets merge into a single one, while fast collisions are quasi-elastic. A theoretical analysis argued that these outcomes may be attributed to effective range interactions and selective three-body recombination processes in the condensate [35]. The same categorization of collisions has also been demonstrated theoretically in 2D [36], although the latter can feature more than two droplets as a dynamical outcome. The work of Ref. [37] argued that tuning the relative velocity, phase shift and atom number allows the colliding droplets to merge or even fragment. Similar effects, i.e., elastic or inelastic collisions, take place in the presence of spin–orbit coupling [38]. The scattering of effectively 1D bright droplets on a potential barrier or well leads to splitting into transmitted, reflected, and trapped fractions, depending on the initial velocity and atom number of the droplet [39]. It is also of particular importance to understand if, similarly to what is well known for usual 1D solitons, interacting droplets attract or repel each other, depending on their relative phase difference.
In the present work, we start by revisiting the stability properties of 1D droplets [14]. Here, we benchmark the stability of droplets throughout their interval of existence in terms of the chemical potential. By analyzing the relevant dynamical system, well-defined boundaries between the existence of droplets and bubbles are identified, varying the chemical potential. The linear spectrum of small perturbations is computed for bubbles, demonstrating their instability, which dynamically manifests itself via expansion of their core.
Turning to interactions between droplets, we conclude that they are pairwise-attractive (-repulsive) when the droplets are in-phase (out-of-phase). For well-separated in- and out-of-phase droplets, we develop the so-called Manton’s method [31] that quantifies their interaction force. Very good agreement of this particle-like picture with the amended GPE predictions is showcased. One can observe accordingly an initial attraction for the case of phase differences between 0 and , while, on the other hand, repulsion is prevalent for relative phases between and . Moreover, in the case of different chemical potentials, the interactions appear to be more complex and lead to mass exchange. Interactions between bubbles are sensitive to their relative distance. They can either lead to a merger, i.e., a heavier bubble, while emitting counter-propagating shock waves, or to individual core expansion of each bubble, creating a bright droplet in-between. On the other hand, droplets are attracted to and subsequently “absorbed” by kinks, a process followed by the nucleation of dispersive shock waves and the downstream emission of gray solitons. Kink–antikink interactions are found to be repulsive. This interaction is accompanied by the spontaneous emission of counter-propagating shock waves. The above constitute the prototypical interaction features identified in the present manuscript.
This work is organized as follows. Section 2 introduces the theoretical framework in terms of the LHY-amended GPEs, the linearized (Bogoliubov–de Gennes) equations for small perturbations and the effective interaction potential for droplets and bubbles. We elaborate on the stability of bright droplets and bubbles in Section 3 and Section 4, respectively. The droplet–droplet, bubble–bubble, droplet–kink, and kink–antikink interactions and their dependence on the relative distance, phase shift and chemical potential of the interacting modes are addressed in Section 5. We provide a summary and discuss future research directions in Section 6.
2. Droplet and Bubble Settings
2.1. The Extended Gross–Pitaevskii Equation
In what follows, we assume a homonuclear mass-balanced () mixture of bosonic atoms in two different hyperfine states, experiencing equal intracomponent repulsion () and intercomponent attraction, . As argued in Refs. [23,40], this setting naturally supports self-confined (“bright”) droplet and bubble modes at different values of the chemical potential. Experimentally, such a mixture can be realized in free space by employing, in particular, the hyperfine states, and , of K, as demonstrated in Ref. [8] for the respective 3D setting. Under the above-described symmetry arguments, the two-component system coalesces into a single GPE [1,10] supplemented by the LHY term, reduced to the 1D quadratic form. The latter term represents the attractive interaction in this limit [13] and the respective 1D amended GPE is given by:
where represents the wave function of both components and describes the balance of mean-field intracomponent repulsion and intercomponent attraction [1,13]. The effective interaction strengths are experimentally tunable by dint of the Fano-Feshbach [41] or confinement-induced resonances [42]; see also Ref. [8] for the magnetic-field dependence of the scattering lengths in K. The energy of the system is measured in units of , where is the healing length. Rescaling time, length and wave function as , and , respectively, Equation (1) can be cast in the following dimensionless form:
In the following, we focus on the stability and interactions of both droplets and bubbles. It is the balance between the residual mean-field repulsion, LHY attraction and the kinetic energy which allows the self-trapping of stable droplets in free space; see also Ref. [14]. We have checked that numerous of our findings reported below persist in the presence of weak external traps, yet, for our present purposes, we restrict the discussion to the most fundamental setting that does not include an external potential. Typical evolution times of in the scaled units, which we consider here, translate, in a typical experimental setup [43], with the perpendicular trap Hz, into 600 ms in physical units.
2.2. The Effective-Potential Picture and Existence Regions of Droplets and Bubbles
When seeking for stationary-state solutions of Equation (2), the usual ansatz is employed, leading to the second-order ordinary differential Equation (ODE) —or 2D (Hamiltonian) dynamical system—
where x plays the role of the independent variable [23]. Without loss of generality for our 1D problem, we may assume that the stationary solutions are real, reducing Equation (3) to the Newtonian equation of motion for a unit-mass particle with coordinate u experiencing the effective potential:
Characteristic profiles of are shown in Figure 1 for two chemical potentials. The fixed points of this potential correspond to:
The homogeneous state associated with is modulationally unstable [20], and therefore, we do not consider it here. On the other hand, both (for ) and the homogeneous state are modulationally stable, with the latter arising at through a saddle-center bifurcation (together with ), as seen in Equation (5). Then, the shape of the effective potential defined by Equation (4) determines the nature of the solitonic states that can exist in this setting. Specifically, local maxima of located at and have equal heights at .
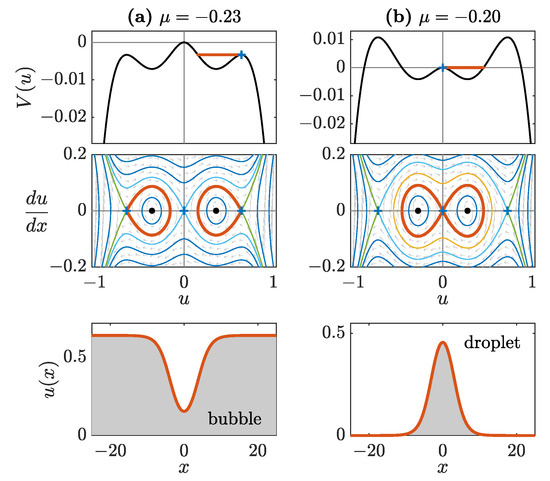
Figure 1.
Self-localized nonlinear structures (see thick red curves) supported by the LHY correction. Typical (a) bubble and (b) droplet solutions (bottom panels) corresponding to two types of homoclinic connections (middle panels) stemming from the Newtonian effective potential reduction (top panels). The bubble refers to a homoclinic connection anchored at the non-zero constant background, while the droplet represents a homoclinic connection of the zero () background.
Turning to the case of , when the maximum of at is higher than that at [top panel of Figure 1a], Equation (3) produces a bubble (or its negative) homoclinic [i.e., tending asymptotically to the same steady state from the Greek “” (to tend) and “” (same)] to , see red curves in the middle and bottom panels of Figure 1a. For chemical potentials in the interval , where the maxima at are higher than the one at [top panel in Figure 1b], there exists a bright droplet (in addition to a heteroclinic dark-soliton state that has been examined elsewhere [40]; heteroclinic stems from “” and “” (different), i.e., tending asymptotically to different steady states, see the red curves in the middle and bottom panels in Figure 1b. For , the homogeneous states and collide through a subcritical pitchfork bifurcation [23] and, finally, at , the equilibrium point at becomes a local minimum of the potential. In the latter case, the situation is similar to that known for the cubic nonlinear Schrödinger (NLS) equation and it is not considered further herein. As elaborated below, the states of interest, namely bubbles and “bright” droplets, exist, respectively, for and . These chemical potential intervals will be our main focus, in addition to the separatrix value of , where kinks and antikinks exist.
2.3. The Bogoliubov–De Gennes Linearized Equations
To address the stability of droplets and bubbles, Equation (2) is linearized for small perturbations () around the respective stationary solution . This is achieved via the ansatz:
yielding the following Bogoliubov–de Gennes (BdG) equations:
where . and are the self-adjoint linearization operators with domain , while the adopted notation was previously introduced, e.g., in Refs. [44,45]. Using a separation of variables of the eigenfunctions (where denotes transposition), and a temporal part proportional to , leads to an eigenvalue problem whose solution enables the consideration of the spectral stability of the obtained solutions, as we will discuss in further detail below.
3. Stability Analysis for Droplets
The droplet solution of Equation (3):
with , exists in the interval of [14]. In the limit of , the droplet turns into a kink solution, which connects the asymptotically constant values, and , fixed at [14,23]:
The scaled number of atoms in the droplet, , is:
The latter is provided in Figure 2a as a function of the chemical potential. Evidently, it diverges as and decays to zero as .
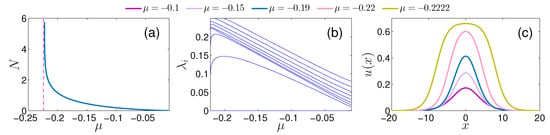
Figure 2.
(a) Numerically obtained scaled atom number for the droplet solution as a function of the chemical potential. An increase of N occurs when tending to the transition point, below which only bubbles exist. This behavior is in accordance to the analytical prediction of Equation (9). (b) The imaginary part of the linearization eigenvalues, , is depicted with respect to . Spectral stability, where , can be inferred independently of lying within the bright droplet regime. (c) Bright droplet waveforms for different values of (see legend) deforming from a quasi-Gaussian profile as to a flat-top configuration as . These shapes and overall trend are in excellent agreement, as they should, with the exact solution of Equation (7).
The BdG spectrum assuming the above-mentioned separation of variables, namely and in Equation (6) with eigenvalues is presented in Figure 2b. Notice that all eigenvalues remain imaginary confirming the spectral stability of the bright droplet throughout its region of existence. We do not dwell on the relevant result and the bifurcation of internal modes of the bright droplet stemming from the band edge of the continuous spectrum at , since the relevant features have been analyzed in Ref. [14]. Characteristic profiles of the bright droplet solution for varying values of are shown in Figure 2c. The bright droplet changes its shape from a Gaussian () to a flat-top () configuration for decreasing .
4. Stationary Bubbles
We subsequently investigate bubbles appearing for , see also Figure 1a. Utilizing the first integral formulation of the relevant quadrature problem of Equations (3)–(5), the relevant solution can be obtained via:
The bubble is represented by the homoclinic orbit attached to , with mechanical energy (see Equation (4)), which can be obtained through the substitution . A direct calculation, as expected, shows that the quantity under the radical in Equation (10) can be rewritten in a quadratic form with respect to w:
where and . The evaluation of the integral, see Ref. [46], leads to the exact analytical expression for a bubble centered at :
where . The complementary mass of the bubble,
is shown as a function of in Figure 3a. As can be seen, as , since the relevant bubble profile becomes nearly homogeneous (see Figure 3c for just before the branch disappearance), while it diverges in the limit of , where the bubble core is the deepest. The progressive modification of this solution towards a homogeneous (flat) one as increases is also presented in Figure 3c. The above-described trend of is reminiscent of the one found for bright droplets but in terms of N (Figure 2a).
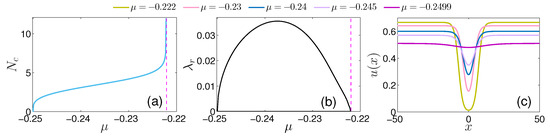
Figure 3.
(a) Complementary scaled atom number, , see also Equation (12), for a bubble stationary state in terms of . (b) The real part of the BdG spectrum upon chemical potential variation demonstrating the unstable nature of bubbles throughout their domain of existence. Dashed magenta lines in both (a) and (b) mark the boundary above which bubbles cease to exist. (c) The wave function of bubbles for distinct values (see legend). As can be seen, for smaller , the bubble’s core becomes deeper, tending to be infinitely broad in the limit of .
The underlying stability properties of a single bubble upon chemical potential variations are depicted in Figure 3b. Specifically, only the real eigenvalues, , versus are illustrated demonstrating the spectral instability of this configuration throughout its interval of existence. For instance, the unstable eigenvalues for the limit bubble solutions, i.e., for and are and , respectively. We remark that the time at which the instability dynamically manifests itself is inversly proportional to the magnitude of the ensuing eigenvalue. Our findings are supported by the results of Refs. [44,45] arguing that in NLS settings bearing multi-stability, bubble-like states when they exist are always unstable.
Applying the arguments of Refs. [44,45] to the present case, we note the following. The stationary wave function satisfies ; however, , given the asymptotics of the bubble. Accordingly, 0 is not an eigenvalue of , and hence, the range of is dense in and we can define the inverse operator as an unbounded one with a dense domain in [44,45]. Indeed, Ref. [45] proves in Lemma 3.2 that is a positive operator, i.e., holds for all . On the other hand, it is straightforward to use the Sturm–Liouville theory to prove that has a negative eigenvalue. This is because the derivative of the bubble, , is an odd function in with a single node satisfying . Hence, the Sturm comparison theorem for this self-adjoint operator establishes the existence of a nodeless negative eigenfunction. The combination of the two statements leads to Theorem 3.1 in Ref. [45], which suggests that in that case the eigenvalue problem represented by Equation (6) can be written as:
Furthermore, one can establish an upper bound of the relevant eigenvalue as , where [45]. The corresponding existence of an eigenvector such that the fraction in Equation (13) is negative confirms the existence of an associated eigenvalue pair with , which, in turn, renders the bubble generically unstable. It is interesting to contra-distinct the present case with the solitary waves vanishing at , in which case 0 is an eigenvalue of [47]. This point explains the difference between the instability of the bubbles and the stability of the droplets. An interpretation of such instability provided, e.g., in the work of Ref. [44], has to do with the metastability of the relevant configuration, in comparison with the global minimum of the energy, involving the homogeneous state with vanishing amplitude. This is also reflected in the unstable dynamics of the state to which we will return in the next section. However, the difference between that and the stable dark soliton configuration lies in the effective topological protection of the latter (due to its phase jump) that precludes its destabilization, contrary to what we will see below for the bubbles.
5. Dynamics and Interactions of Droplets
5.1. Droplet Collisions and Manton’s Method
Next, we explore the dynamics of multiple droplets with phase differences ranging from (in-phase) to (out-of-phase) in analogy with what has been experimentally probed for bright solitons [48]. To examine the interactions between identical in- and out-of-phase droplets, we develop the Manton’s method [31] following the analysis reported in Ref. [30] for the NLS model. This method deploys the conservation laws for the scaled atom number, N, as well as the linear momentum:
The basic idea is that, given the conservation laws associated with N and P, the calculation of their rates of change will result in contributions stemming purely from the surface terms produced by the corresponding fluxes within the respective conservation laws. Therefore, evaluating in a spatial domain between points a and b, and using the equation of motion, leads to:
On the other hand, amounts to a force. Then, if one assumes the presence of two droplets centered at and and considering , with sufficiently large and b, the expression in Equation (15) mostly garners a contribution from the right boundary, since the left one, at , is exponentially weaker. As such, the only “force” at stems from the interaction of the droplet at with that at . Utilizing the asymptotic form of the two droplets, namely and , for the region near , and using the ansatz (where is the phase shift between the two droplets and ), one arrives at the effective force:
Subsequently, following the arguments of Ref. [30], it is possible to derive the following evolution equation for the relative position between the droplets:
where the separation, s, between the two droplets has been taken into account, as well as the fact that the mass of each droplet is given by Equation (9), while the force takes the form of Equation (16). Notice that the relative phase appears to play a similar role as in the case of regular bright solitary waves [30,48], namely, in-phase interaction leads to attraction, while an out-of-phase one leads to repulsion. A similar approximation for the interaction between 2D and 3D solitons was elaborated in Ref. [49].
Commenting more generally on the applicability of the method, we note the following. In principle, Manton’s method can be applied when the model possesses an invariance with respect to translation that leads to the existence of a momentum conservation law. In addition, the model needs to possess solitary waves that feature an exponential tail and effective particle dynamics, as is the case with numerous 1D models that bear solitons or solitary waves or even (exponentially decaying in space) breather solutions. At the moment, we are not familiar with applications of the (standard Manton) method in models that are not translationally invariant or ones in which the waves feature power law tails. For the latter, recently, a far more elaborate method was introduced for capturing their interactions in Ref. [50], yet to the best of our knowledge, this has not been systematized including in higher-dimensional settings. The latter clearly constitutes an interesting direction for further explorations.
The dynamical prediction of Equation (17) has been tested for the case of in-phase bright droplet attraction (Figure 4a), as well as in that of out-of-phase droplet repulsion (Figure 4b). Here, droplets are originally () placed at a relative distance . The overall phenomenology is essentially the same for different . It is evident that the time-evolved density, , as captured by the amended GPE model of Equation (2), is in excellent agreement with the analytical estimate of the particle picture as concerns the droplet motion. This analytical estimate is obtained upon integrating Equation (17) and is directly compared with the attractive and the repulsive case, see the dashed black lines in Figure 4a and b, respectively. It is also relevant to point out that in the case where the droplets attract, Equation (17) is utilized up to the point where the droplets lose their individual character by approaching each other at distances comparable to their individual widths. In that regime, our assumption put forth for the Manton method (in terms of ) is no longer valid and we cannot aspire to describe the relevant dynamics accurately. Nevertheless, it is observed that in-phase droplets upon collision attempt to separate, yet cannot escape each other’s attraction and collide anew for sufficiently long times, a pattern that recurs throughout the evolution. On the other hand, the repulsion of out-of-phase droplets leads them to indefinite separation.
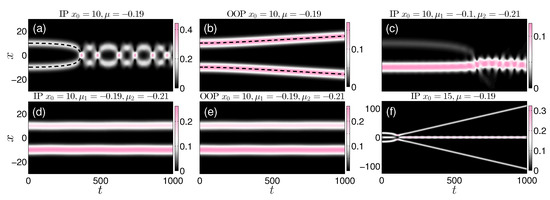
Figure 4.
(a–e) The spatiotemporal evolution of the density of two bright droplets, initially at rest, placed symmetrically with respect to at , with different relative phases ( or ), and chemical potentials , (see legends). It is evident that (a) in-phase (IP) bright droplets bearing the same feature attraction, while (b) out-of-phase (OOP) ones repel. Dashed black lines indicate the prediction of the respective Manton’s method which is in excellent agreement with the simulations of Equation (2). In contrast, particle-imbalanced droplets either being (d) IP or (e) OOP remain nearly intact for small chemical potential differences. (c) Highly imbalanced IP droplets experience enhanced particle transfer. (f) Density dynamics of three identical IP bright droplets leading to a central, heavier and excited droplet and two lighter counter-propagating ones.
To gain an overview of the droplet dynamical response and interactions, situations where the two bright droplets pertain to unequal chemical potentials, i.e., are also explored. This scenario is shown in Figure 4c–e. Focusing on relatively small chemical potential differences depicted in Figure 4d,e, e.g., and , it is found that irrespectively of the relative phase (), a quasi-stationary state occurs persisting for all evolution times (). For instance, it can be seen that even for in-phase interactions with the two droplets initialized at the same distance as before, the relevant force is much weaker, not allowing to infer its definitive nature. Further increase of the chemical potential imbalance, which is effectively related to the number-of-atoms, i.e., mass imbalance between the droplets, results in a drastically altered dynamics, see Figure 4c. Particularly, the in-phase droplet collision entails a significant transfer of mass from the lighter to the heavier one. Transfer of mass has been also reported in droplet collisions with finite relative velocity [37]. Moreover, it turns out from the amended GPE predictions that imbalanced droplets experience weaker attraction than balanced ones as can be inferred from the later occurrence of the relevant collision event (compare Figure 4a,c). This inelastic process leads to the merger of the colliding objects into a single droplet in an excited state. Recall that droplet mergers can also be observed in a different context during the process of the so-called modulation instability mechanism [20,21].
As a next step, we investigate situations with a larger number of droplets. A scenario of this sort is illustrated in Figure 4f, consisting of a three droplet pair-wise in-phase initialization. It is found that the collision of the three identical (particle-balanced) droplets appears to occur significantly faster compared to the two droplet case (Figure 4a), even though they are initially placed at larger distances. This is natural to expect on the basis of the enhanced attraction arising in the present case. Partial transfer of mass from the side droplets to the central one takes place producing two lighter and, thus, faster counter-propagating ones and a heavier central droplet in an excited state, which then exhibits breathing evolution. These findings motivate further studies and possible future work on the collisional dynamics of multi-droplet lattices, as such scenarios have been experimentally implemented in the realm of, e.g., dark solitons in the work of Ref. [51].
To further understand the role that the phase difference plays on droplet interactions, we additionally explored the dynamics for different values of the phase shift between the two droplets (see Figure 5). Phase differences between 0 and manifest an initial attraction as predicted by the effective force of Equation (16) within the particle picture. Interestingly, it is observed that the droplets experience a slow mass exchange during their interaction. Note that the mass transfer among initially identical droplets implies symmetry breaking between them. An explanation for this effect in soliton–soliton collisions, which can also be conceptually considered relevant to the present setting, was proposed in Ref. [52]. This involves the mismatch in the profiles’ density centers and the mismatch in their phase centers, leading, in turn, to the dynamical manifestation of symmetry breaking. In our setting, this mass exchange is responsible for the modification of the chemical potential of the individual droplets. Specifically, the droplet with the largest will advance its phase faster than the other one, see for instance Figure 5e,h. As a result, in the course of the evolution, , becomes larger than and eventually reaches . Therefore, the droplets will experience repulsion. A characteristic example where two droplets with an initial phase difference , corresponding to a zero mutual force according to the particle picture, start exchanging mass and, around , their phase difference gets closer to , which leads to the droplets repelling each other is showcased in Figure 5b,c. The inter-droplet mass exchange is quantified by defining the mass imbalance parameter as follows:
where corresponds to a mass-balanced scenario and () to the right (left) droplet being more massive. Exploring other cases with (not shown for brevity), an initial attraction was indeed observed for droplets initialized with the same chemical potentials in accordance with the particle picture. However, the mass imbalance generally led to an eventual repulsion of the droplets. This phenomenology is absent for , where attraction is prevalent inducing droplet collisions similarly to the recurrent collisional events observed for in-phase () identical (mass balanced) droplets presented in Figure 4a. Additionally, for repulsion dominates the dynamics (not shown here).
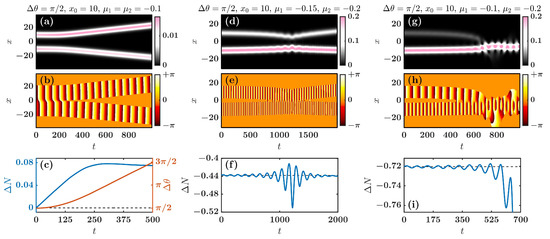
Figure 5.
Temporal evolution of two interacting droplets possessing a phase difference and initial separation . Panels (a,b) depict, respectively, the spatio-temporal evolution of the density, , and phase of two identical droplets with , while panel (c) presents the corresponding time-evolution of the mass imbalance (see Equation (18)) and the relative phase, , between the two droplets. (d–f) The same as (a–c) but for the case where the initially seeded droplets have different chemical potentials, i.e., and . (g–i) Similar to (d–f) but for larger chemical potential differences, namely and . In all cases, transfer of mass among the droplets takes place.
Paradigmatic droplet interactions where the droplets are initialized bearing different masses (i.e., distinct chemical potentials) are illustrated in Figure 5d–f for , and Figure 5g–i with , . In both cases, oscillation of the mass imbalance (Figure 5f,i) is accompanied by a weak attraction between the droplets (Figure 5d,g) until their collision, where both processes are enhanced. Particularly, for increasing chemical potential imbalances, a definitive collision point can be inferred, leading to a perfect mass transfer and the generation of a merger, i.e., a heavier and excited single droplet as shown in Figure 5g. However, in the case of smaller initial chemical potential imbalance, the droplets do not experience a clear collision point (i.e., they reach a minimum distance) before separating, see Figure 5d. According to the above discussion, the interaction dynamics between droplets with intrinsically involves mass exchange and strongly depends on the initial separation, relative phases and chemical potentials. It is important to mention that the particle picture that was presented above is only valid under the assumption of equal chemical potentials between the two droplets. Therefore, if one is to cast a particle picture for non-mass-balanced droplets, a different approach is necessary and, indeed, worth developing. Efforts to better understand more general droplet interactions, together with their corresponding particle picture, fall outside of the scope of the present work and will be reported elsewhere.
5.2. Dynamics of Bubbles and Their Interactions
Having established the instability of the bubbles in their entire existence interval (see Figure 3b), we proceed to explore their instability-driven dynamics. To this end, we monitor the evolution of these configurations in the framework of the amended GPE of Equation (2), as presented in Figure 6a for the single bubble and Figure 6b,c for two bubbles. Note that, when addressing configurations including two or more bubbles, the necessity to match the backgrounds makes it possible to consider solely bubbles with equal chemical potentials, so that they asymptote to the same background value, [see Equation (11)]. In this case, a natural ansatz is , where is half the separation between the bubbles, and is given by the single-bubble analytical solution, as described by Equation (11).
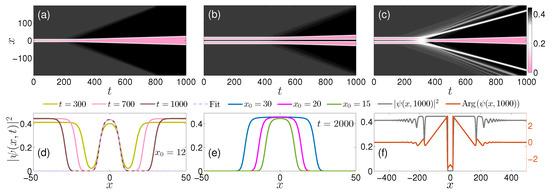
Figure 6.
(a) Density evolution of a single bubble for . The unstable dynamics of the bubble manifests through the expansion of its core. Dynamics of the density of two in-phase bubbles placed at a relative distance (b) and (c) exposing the crucial role of . Namely, for relatively small , the bubbles attract before destabilizing, generating a heavier central bubble while emitting counter-propagating shock waves leaving behind gray solitons, see in panel (f) the corresponding profile and phase at . Slightly larger distances lead to non-interacting bubbles whose cores expand in the course of the evolution trapping in between a droplet, as illustrated in panel (d) at distinct time-instants for and in (e) at a specific time-instant and varying initial separation (see legends). The dashed line in panel (d) refers to a fit of the numerically obtained waveform to the analytical droplet solution given by Equation (7).
The dynamics depicted in Figure 6a suggest that, in line with the analysis of the general bubble dynamics provided in Refs. [44,45], the inherent instability experienced by a single bubble causes it to modify its width, eventually leading it to a continuous expansion. Naturally, to maintain the total-mass conservation, the evolution leads to a slight increase of the height of the background supporting the bubble. It is interesting to note that this dynamical response is inherently related to the used Neumann or periodic boundary conditions, while it is naturally expected to be modified in the presence of hard-wall boundaries due to the fixed background.
On the other hand, in the case of two bubbles, it is observed that the ensuing interaction depends crucially on their relative distance. Placing the bubbles sufficiently far apart, their individual instability arises before they have the opportunity to interact with each other (Figure 6b). The individual core expansion persists for evolution times . However, it is not a symmetric expansion with respect to the center of each bubble’s core. Rather, the outer part of each bubble extends as before, while in the region in between the two bubbles, a density hump is developed and trapped. We were able, upon fitting, to identify the latter as a bright droplet, see in particular Figure 6d. The chemical potential of the fitted droplet is . Thus, the background density self-adjusts to the value corresponding to the droplet. The same dynamical bright droplet formation occurs upon further increase of the initial bubble separation, as depicted in Figure 6e. To shed further light on the bubble interactions, we then bring them in sufficient proximity that enables their interaction to commence early enough so that they merge, prior to the manifestation of their individual instability; see (Figure 6c). Evidently, an apparent attraction occurs between the two bubbles leading to a corresponding central merger and counter-propagating dispersive shock wave (DSW) structures with a downstream emission of a gray soliton train; see Figure 6f [53]. This central bubble is in turn subjected to the previously discussed instability. It is also worthwhile to point out that the aforementioned emitted entities have nearly constant speed, as manifested by their nearly constant slope in the spatiotemporal density evolution shown in Figure 6. This behavior can be inferred from their trajectories (see the white regions in Figure 6c).
5.3. Droplet–Kink Interactions
Next, we address hybrid interactions between droplets and the kink, i.e., the exact stable state given by Equation (7) with that of Equation (8). The droplet is initially placed at distance from the central point () of the kink. Figure 7 displays examples of the ensuing interaction. In particular, the top row of panels corresponds to an initial separation and zero initial velocity of the droplet. The latter initially features attraction that leads to its eventual collision and “absorption” ( of the droplet’s norm is carried away by a reflected wave). by the kink occurring around ; see the details below. Figure 7b offers a visualization of such collision and subsequent events imprinted in the instantaneous density profiles. The collision entails intrinsic excitation of the kink. In particular, we observe spontaneous emission of a DSW traveling through the kink background and leaving behind a slower gray soliton that remains intact, despite its interaction with the former DSW while propagating. A characteristic signature of the gray soliton is produced by the evolution of the phase, , displayed in Figure 7c, which features a clear and constant phase jump. The faint ripples in , taking place ahead of the gray soliton signature, are shock-wave imprints. In general, the droplet gets “absorbed” by the kink, subsequently leading to the emission of the above structures (DSW and gray soliton) independently of the droplets’ chemical potential (quantifying its mass) and original position . Naturally, the phenomenology happens faster for heavier droplets and smaller distances (results not shown here).
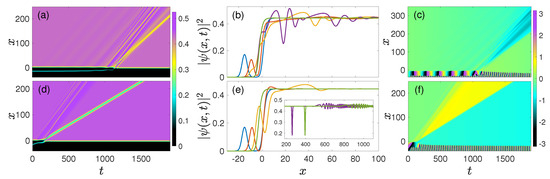
Figure 7.
(a) Density evolution for the interaction of a kink placed at with a bright droplet placed at while having (a) zero and (d) finite velocity . (b) [(e)] Corresponding instantaneous profiles of (a) [(d)] at (blue line), (orange line), (yellow line), (purple line) and (green line) [ (blue line), (orange line), (yellow line), (purple line) and (green line)]. (c) [(f)] Dynamics of the wave function’s phase, , for case (a) [(d)]. The collision leads to the “absorption” of the droplet by the kink accompanied by the excitation of the latter and the spontaneous emission of dispersive shock waves (see also the inset in panel (e)) leaving behind a robustly propagating gray soliton (captured by the characteristic phase jump in panel (f)).
This phenomenology can be generalized for droplets with initial velocity . In this case, the collision is, as expected, accelerated, as seen from the comparison of Figure 7a,d, as well as of the corresponding snapshots in Figure 7b,e. This conclusion is also supported by monitoring the phase of the wave function, in the course of the evolution, where signatures of both the shock wave (ripples) and the gray soliton (phase jump being a fraction of ) can be distinguished. In this case, the emission of the DSW and the nucleation of the gray soliton become more conspicuous; see the inset of Figure 7e, where both entities are clearly captured. A more detailed study of collisions of traveling droplets with kinks or other effective scattering potentials is a relevant direction for studies beyond the scope of the present work. In this context, it will be relevant to consider related transmission and reflection phenomena, as was recently done in Ref. [39] for a droplet colliding with a square well.
5.4. The Kink–Antikink Interaction
In addition to the kink waveform of Equation (8), Equation (3) gives rise to the antikink solution, . As such, for reasons of completeness, we also examine kink–antikink interactions. The overlap in the kink–antikink pair exponentially decays with the separation between them, and therefore, the interaction is appreciable only for a relatively small separation (i.e., of a few times the width of the individual kink). In fact, this condition is favorable to a potential experimental realization, as a relatively small spatial domain and short timescales are required. An example, when the kink and antikink are brought in close proximity, with initial separation , is presented in Figure 8a. Apparently, the kink–antikink interaction is repulsive, in line with a similar result known for the cubic-quintic NLS model [54]; we note here in passing the similarly repulsive interaction of the (kink-like) dark solitons of the standard NLS model. Specifically, repulsion (Figure 8b) is accompanied by the spontaneous emission of two counter-propagating DSWs, as can be identified by inspecting the density snapshots shown in Figure 8c. Note that, in contrast to the genuinely repulsive out-of-phase droplet–droplet interaction (Figure 4b), here, we deal with heteroclinic waveforms, and thus, the definition of the associated mass is an intriguing problem in its own right; for a recent discussion of the simpler, standard GPE problem and its dark soliton heteroclinic solutions, see, e.g., Ref. [55] and, in particular, Appendix C therein. Nevertheless, we still observe a repulsive interaction in Figure 8a, and the accompanying DSW emission leads the kinks into a slowdown that eventually halts them in line with the expectation that no such solutions exist in the model under consideration.
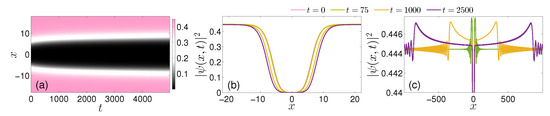
Figure 8.
(a) Spatiotemporal evolution of the density, , in the course of the apparently repulsive kink–antikink interaction with initial separation . (b) Snapshots of (a) at different time-instants (see legend). (c) Magnification of (b) for visualizing the counter-propagating shock-wave emission.
6. Conclusions and Perspectives
We have studied the static properties of droplets and bubbles within the one-dimen-sional amended GPE model relevant to the inclusion of the LHY term in homonuclear, mass-balanced, bosonic mixtures. In this context, we systematically explored the interactions among different types of nonlinear excitations. Particularly, our investigation involved multiple droplets and bubbles, but also droplet–kink and kink–antikink ones. The stability of droplets and bubbles upon chemical potential variations has been explored, expanding upon related earlier work. The parametric regions of existence of each solution were identified with droplets transitioning from Gaussian to flat-top ones for decreasing chemical potential while bubbles becoming wider, deeper, and flatter. Moreover, the stability of the droplets and instability of bubbles has been demonstrated by extracting the corresponding Bogoliubov–de Gennes excitation spectrum. The destabilization of bubbles manifests through expansion of their core in the course of the evolution.
Turning to the dynamics, interactions between droplets were found, similarly to bright solitons, to depend on their relative phase and chemical potential difference. Importantly, the particle picture for droplets is constructed revealing their in-phase attraction and out-of-phase repulsion. This outcome is subsequently tested by monitoring the interactions of these entities through the amended GPE model. Additionally, we showcase that for intermediate phase differences, droplets initially experience attraction followed by repulsion. The interaction between droplets with different chemical potentials leads to mass exchange between them and the formation of heavier droplets in an excited state.
On the other hand, bubble interactions, given the bubbles’ individual and unstable nature, are highly susceptible to different outcomes depending on their initial separation. Particularly, if placed in close proximity, they merge into a single bubble due to their mutual attraction followed by the emission of counter-propagating shock waves and the subsequent formation of gray soliton trains. However, for suitably increased separation, they show individual core expansion, trapping in between them a droplet. Examining interactions among kinks and droplets reveals the transformation of the latter by the former accompanied by the spontaneous generation of a dispersive shock wave, leaving behind a gray soliton. These dynamical features are enhanced for traveling or lighter droplets. We have also explored kink–antikink interactions, which generically result in mutual repulsion and emission of weak counter-propagating shock waves.
Our findings suggest pathways for further work. A direct extension is to consider a quasi-1D geometry, aiming to reveal the role of transversal excitations in colliding droplets and bubbles. In our view, this would be particularly useful for connecting with experimental settings (including in the presence of external confinement). Furthermore, a detailed analysis of the emitted shock-wave structures following the droplet–kink collision is an issue of substantial interest. The generalization of the “two-body” particle-like dynamical picture developed herein for droplets and bubbles to 1D chains of such structures is a promising prospect, producing potentially effective dynamical lattice equations similar to the ones for dark and bright NLS solitons described in Ref. [56]. Other relevant directions are to further quantify the analytical characterization of inter-soliton interactions (of different type), as well as to study interactions and collisions between solitons and/or vortical droplets in the 2D setting combining the mean-field and LHY terms and, on the other hand, in full quantum states (beyond the limits of the LHY description) [57,58,59].
Author Contributions
Conceptualization, S.I.M., B.A.M. and P.G.K..; methodology, G.C.K., S.I.M., D.J.F., R.C.-G. and P.G.K.; software, G.C.K., S.I.M., R.C.-G. and P.G.K.; validation, G.C.K., S.I.M. and R.C.-G.; formal analysis, G.C.K., S.I.M., R.C.-G., B.A.M., D.J.F. and P.G.K.; resources, S.I.M., B.A.M., R.C.-G. and P.G.K.; writing—original draft preparation, G.C.K., S.I.M., B.A.M., D.J.F., R.C.-G. and P.G.K.; visualization, G.C.K., S.I.M. and R.C.-G.; project administration, S.I.M., R.C.-G. and P.G.K.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by U.S. National Science Foundation grant numbers PHY-2110038, PHY-2110030, and DMS-2204702 and by the Israel Science Foundation through grant number 1695/22.
Data Availability Statement
Data available upon request.
Acknowledgments
S.I.M. acknowledges support from the NSF through a grant for ITAMP at Harvard University. This material is based upon work supported by the U.S. National Science Foundation under awards PHY-2110038 (R.C.G.) and PHY-2110030 and DMS-2204702 (P.G.K.). The work of B.A.M. was supported, in part, by the Israel Science Foundation through grant No. 1695/22.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Petrov, D.S. Quantum mechanical stabilization of a collapsing Bose-Bose mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef]
- Khan, A.; Debnath, A. Quantum Droplet in Lower Dimensions. Front. Phys. 2022, 10, 887338. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Böttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef]
- Chomaz, L.; Ferrier-Barbut, I.; Ferlaino, F.; Laburthe-Tolra, B.; Lev, B.L.; Pfau, T. Dipolar physics: A review of experiments with magnetic quantum gases. Rep. Progr. Phys. 2022, 86, 026401. [Google Scholar]
- Cabrera, C.R.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose-Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright Soliton to Quantum Droplet Transition in a Mixture of Bose-Einstein Condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Res. 2019, 1, 033155. [Google Scholar] [CrossRef]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-bound quantum droplets of atomic mixtures in free space. Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low-temperature properties. Phys. Rev. 1957, 106, 1135. [Google Scholar] [CrossRef]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute Low-Dimensional Liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef]
- Ferioli, G.; Semeghini, G.; Terradas-Briansó, S.; Masi, L.; Fattori, M.; Modugno, M. Dynamical formation of quantum droplets in a 39K mixture. Phys. Rev. Res. 2020, 2, 013269. [Google Scholar] [CrossRef]
- Fort, C.; Modugno, M. Self-Evaporation Dynamics of Quantum Droplets in a 41K-87Rb Mixture. Appl. Sci. 2021, 11, 866. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Volosniev, A.G.; Barfknecht, R.E.; Fogarty, T.; Busch, T.; Foerster, A.; Schmelcher, P.; Zinner, N.T. Cold atoms in low dimensions–a laboratory for quantum dynamics. arXiv 2022, arXiv:2202.11071. [Google Scholar]
- Tylutki, M.; Astrakharchik, G.E.; Malomed, B.A.; Petrov, D.S. Collective excitations of a one-dimensional quantum droplet. Phys. Rev. A 2020, 101, 051601. [Google Scholar] [CrossRef]
- Englezos, I.A.; Mistakidis, S.I.; Schmelcher, P. Correlated dynamics of collective droplet excitations in a one-dimensional harmonic trap. Phys. Rev. A 2023, 107, 023320. [Google Scholar] [CrossRef]
- Stürmer, P.; Tengstrand, M.N.; Sachdeva, R.; Reimann, S.M. Breathing mode in two-dimensional binary self-bound Bose-gas droplets. Phys. Rev. A 2021, 103, 053302. [Google Scholar] [CrossRef]
- Cappellaro, A.; Macrì, T.; Salasnich, L. Collective modes across the soliton-droplet crossover in binary Bose mixtures. Phys. Rev. A 2018, 97, 053623. [Google Scholar] [CrossRef]
- De Rosi, G.; Astrakharchik, G.E.; Massignan, P. Thermal instability, evaporation, and thermodynamics of one-dimensional liquids in weakly interacting Bose-Bose mixtures. Phys. Rev. A 2021, 103, 043316. [Google Scholar] [CrossRef]
- Wang, J.; Hu, H.; Liu, X.J. Thermal destabilization of self-bound ultradilute quantum droplets. New J. Phys. 2020, 22, 103044. [Google Scholar] [CrossRef]
- Mithun, T.; Maluckov, A.; Kasamatsu, K.; Malomed, B.A.; Khare, A. Modulational Instability, Inter-Component Asymmetry, and Formation of Quantum Droplets in One-Dimensional Binary Bose Gases. Symmetry 2020, 12, 174. [Google Scholar] [CrossRef]
- Mithun, T.; Mistakidis, S.I.; Schmelcher, P.; Kevrekidis, P.G. Statistical mechanics of one-dimensional quantum droplets. Phys. Rev. A 2021, 104, 033316. [Google Scholar] [CrossRef]
- Otajonov, S.R.; Tsoy, E.N.; Abdullaev, F.K. Modulational instability and quantum droplets in a two-dimensional Bose-Einstein condensate. Phys. Rev. A 2022, 106, 033309. [Google Scholar] [CrossRef]
- Katsimiga, G.C.; Mistakidis, S.I.; Koutsokostas, G.N.; Frantzeskakis, D.J.; Carretero-González, R.; Kevrekidis, P.G. Solitary waves in a quantum droplet-bearing system. Phys. Rev. A 2023, 107, 063308. [Google Scholar] [CrossRef]
- Saqlain, S.; Mithun, T.; Carretero-González, R.; Kevrekidis, P.G. Dragging a defect in a droplet Bose-Einstein condensate. Phys. Rev. A 2023, 107, 033310. [Google Scholar] [CrossRef]
- Gangwar, S.; Ravisankar, R.; Muruganandam, P.; Mishra, P.K. Dynamics of quantum solitons in Lee-Huang-Yang spin–orbit-coupled Bose-Einstein condensates. Phys. Rev. A 2022, 106, 063315. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Lashkin, V.M.; Modugno, M.; Torner, L. Spinor-induced instability of kinks, holes and quantum droplets. New J. Phys. 2022, 24, 073012. [Google Scholar] [CrossRef]
- Tengstrand, M.N.; Stürmer, P.; Karabulut, E.; Reimann, S.M. Rotating binary Bose-Einstein condensates and vortex clusters in quantum droplets. Phys. Rev. Lett. 2019, 123, 160405. [Google Scholar] [CrossRef]
- Barranco, M.; Guardiola, R.; Hernández, S.; Mayol, R.; Navarro, J.; Pi, M. Helium nanodroplets: An overview. J. Low Temp. Phys. 2006, 142, 1–81. [Google Scholar] [CrossRef]
- Toennies, J.P.; Vilesov, A.F. Superfluid helium droplets: A uniquely cold nanomatrix for molecules and molecular complexes. Angew. Chem. Int. Ed. 2004, 43, 2622–2648. [Google Scholar] [CrossRef] [PubMed]
- Kevrekidis, P.G.; Khare, A.; Saxena, A. Solitary wave interactions in dispersive equations using Manton’s approach. Phys. Rev. E 2004, 70, 057603. [Google Scholar] [CrossRef]
- Manton, N.S. An effective Lagrangian for solitons. Nucl. Phys. B 1979, 150, 397–412. [Google Scholar] [CrossRef]
- Zhao, W.; Bourkoff, E. Interactions between dark solitons. Opt. Lett. 1989, 14, 1371–1373. [Google Scholar] [CrossRef]
- Katsimiga, G.C.; Koutentakis, G.M.; Mistakidis, S.I.; Kevrekidis, P.G.; Schmelcher, P. Dark—Bright soliton dynamics beyond the mean-field approximation. New J. Phys. 2017, 19, 073004. [Google Scholar] [CrossRef]
- Ferioli, G.; Semeghini, G.; Masi, L.; Giusti, G.; Modugno, G.; Inguscio, M.; Gallemí, A.; Recati, A.; Fattori, M. Collisions of Self-Bound Quantum Droplets. Phys. Rev. Lett. 2019, 122, 090401. [Google Scholar] [CrossRef]
- Cikojević, V.; Markić, L.V.; Pi, M.; Barranco, M.; Ancilotto, F.; Boronat, J. Dynamics of equilibration and collisions in ultradilute quantum droplets. Phys. Rev. Res. 2021, 3, 043139. [Google Scholar] [CrossRef]
- Hu, Y.; Fei, Y.; Chen, X.L.; Zhang, Y. Collisional dynamics of symmetric two-dimensional quantum droplets. Front. Phys. 2022, 17, 61505. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Malomed, B.A. Dynamics of one-dimensional quantum droplets. Phys. Rev. A 2018, 98, 013631. [Google Scholar] [CrossRef]
- Gangwar, S.; Ravisankar, R.; Muruganandam, P.; Mishra, P.K. Effect of beyond mean-field interaction on the structure and dynamics of the one-dimensional quantum droplet. arXiv 2023, arXiv:2303.01216. [Google Scholar]
- Debnath, A.; Khan, A.; Malomed, B. Interaction of One-Dimensional Quantum Droplets with Potential Wells and Barriers. arXiv 2023, arXiv:2302.13367. [Google Scholar] [CrossRef]
- Edmonds, M. Dark quantum droplets in beyond-mean-field Bose-Einstein condensate mixtures. Phys. Rev. Research 2023, 5, 023175. [Google Scholar] [CrossRef]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225. [Google Scholar] [CrossRef]
- Olshanii, M. Atomic scattering in the presence of an external confinement and a gas of impenetrable bosons. Phys. Rev. Lett. 1998, 81, 938. [Google Scholar] [CrossRef]
- Katsimiga, G.C.; Mistakidis, S.I.; Bersano, T.M.; Ome, M.K.H.; Mossman, S.M.; Mukherjee, K.; Schmelcher, P.; Engels, P.; Kevrekidis, P.G. Observation and analysis of multiple dark-antidark solitons in two-component Bose-Einstein condensates. Phys. Rev. A 2020, 102, 023301. [Google Scholar] [CrossRef]
- Barashenkov, I.; Gocheva, A.; Makhankov, V.; Puzynin, I. Stability of the soliton-like “bubbles”. Phys. D Nonlinear Phenom. 1989, 34, 240–254. [Google Scholar] [CrossRef]
- de Bouard, A. Instability of Stationary Bubbles. SIAM J. Math. Anal. 1995, 26, 566–582. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 4th ed.; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Kapitula, T.; Promislow, K. Spectral and Dynamical Stability of Nonlinear Waves; Springer: New York, NY, USA, 2013. [Google Scholar]
- Nguyen, J.H.V.; Dyke, P.; Luo, D.; Malomed, B.A.; Hulet, R.G. Collisions of matter-wave solitons. Nat. Phys. 2014, 10, 918–922. [Google Scholar] [CrossRef]
- Malomed, B. Potential of interaction between two- and three-dimensional solitons. Phys. Rev. E 1998, 58, 7928–7933. [Google Scholar] [CrossRef]
- Manton, N.S. Forces between kinks and antikinks with long-range tails. J. Phys. Math. Theor. 2019, 52, 065401. [Google Scholar] [CrossRef]
- Theocharis, G.; Weller, A.; Ronzheimer, J.P.; Gross, C.; Oberthaler, M.K.; Kevrekidis, P.G.; Frantzeskakis, D.J. Multiple atomic dark solitons in cigar-shaped Bose-Einstein condensates. Phys. Rev. A 2010, 81, 063604. [Google Scholar] [CrossRef]
- Khaykovich, L.; Malomed, B. Deviation from one dimensionality in stationary properties and collisional dynamics of matter-wave solitons. Phys. Rev. A 2006, 74, 023607. [Google Scholar] [CrossRef]
- El, G.; Hoefer, M. Dispersive shock waves and modulation theory. Phys. D Nonlinear Phenom. 2016, 333, 11–65. [Google Scholar] [CrossRef]
- Filatrella, G.; Malomed, B.A.; Salerno, M. Domain walls and bubble droplets in immiscible binary Bose gases. Phys. Rev. A 2014, 90, 043629. [Google Scholar] [CrossRef]
- Martone, G.I.; Recati, A.; Pavloff, N. Supersolidity of cnoidal waves in an ultracold Bose gas. Phys. Rev. Res. 2021, 3, 013143. [Google Scholar] [CrossRef]
- Ma, M.; Navarro, R.; Carretero-González, R. Solitons riding on solitons and the quantum Newton’s cradle. Phys. Rev. E 2016, 93, 022202. [Google Scholar] [CrossRef]
- Parisi, L.; Astrakharchik, G.E.; Giorgini, S. Liquid State of One-Dimensional Bose Mixtures: A Quantum Monte Carlo Study. Phys. Rev. Lett. 2019, 122, 105302. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Mithun, T.; Kevrekidis, P.G.; Sadeghpour, H.R.; Schmelcher, P. Formation and quench of homonuclear and heteronuclear quantum droplets in one dimension. Phys. Rev. Res. 2021, 3, 043128. [Google Scholar] [CrossRef]
- Ota, M.; Astrakharchik, G. Beyond Lee-Huang-Yang description of self-bound Bose mixtures. Sci. Phys. 2020, 9, 020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).