Influence of Frustration Effects on the Critical Current of DC SQUID
Abstract
1. Introduction
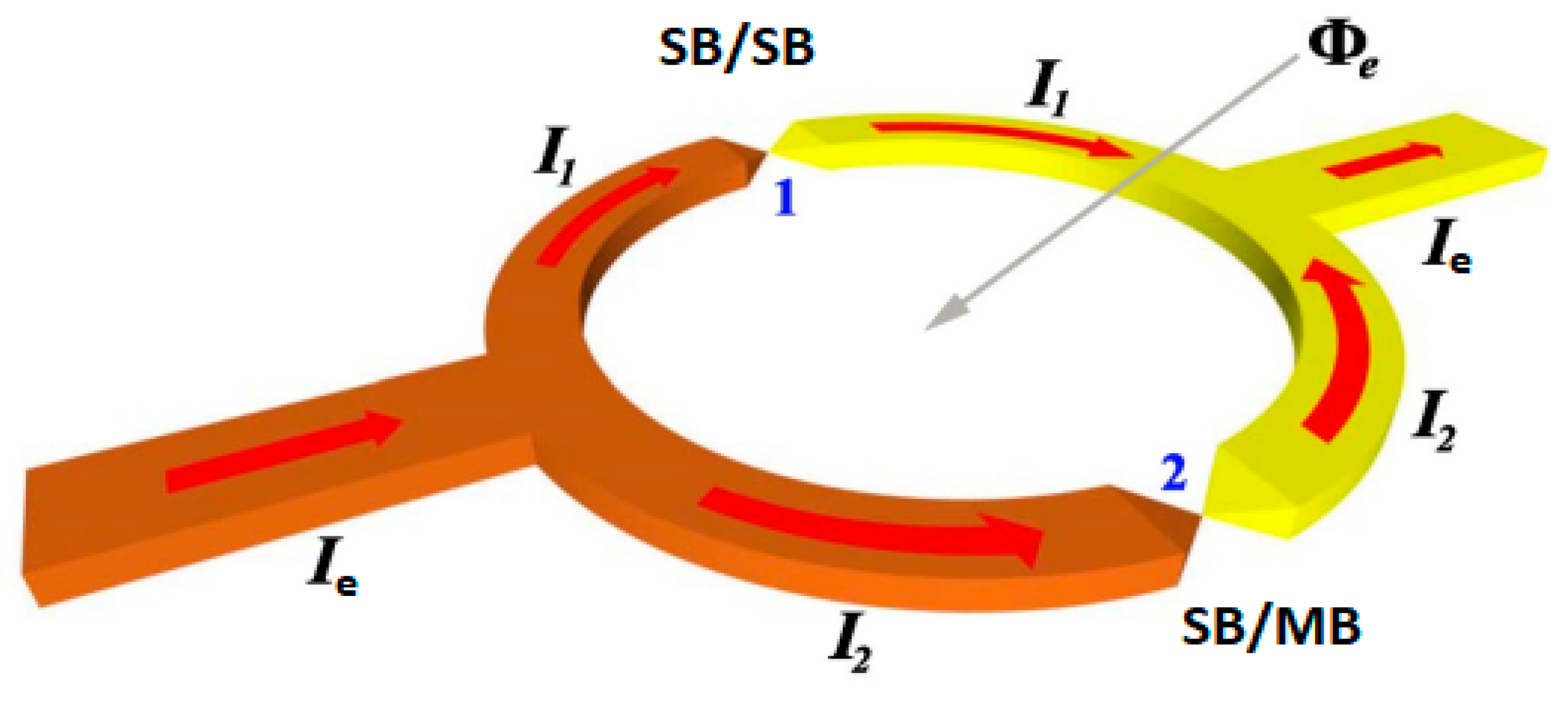
2. Basic Equations
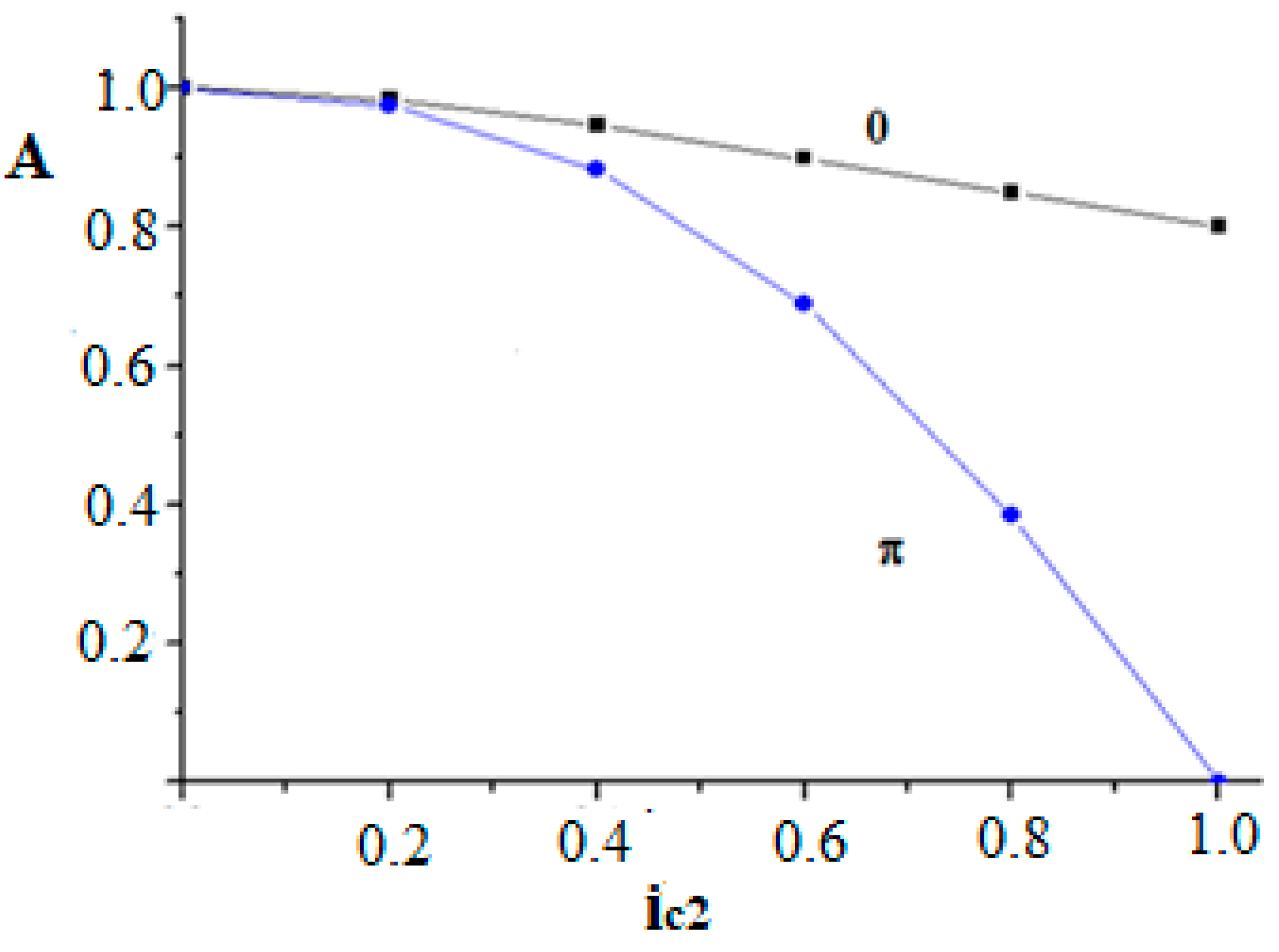
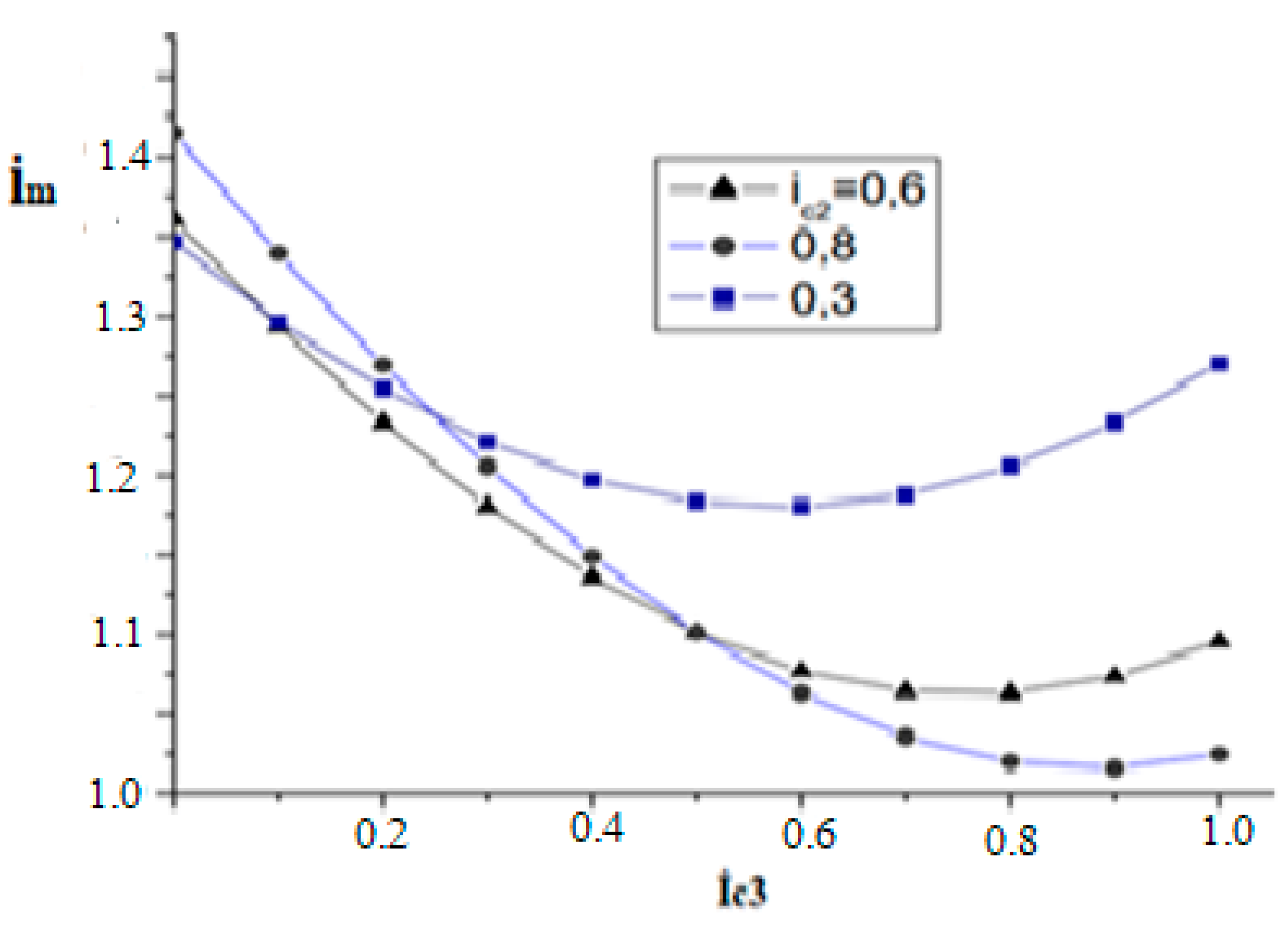
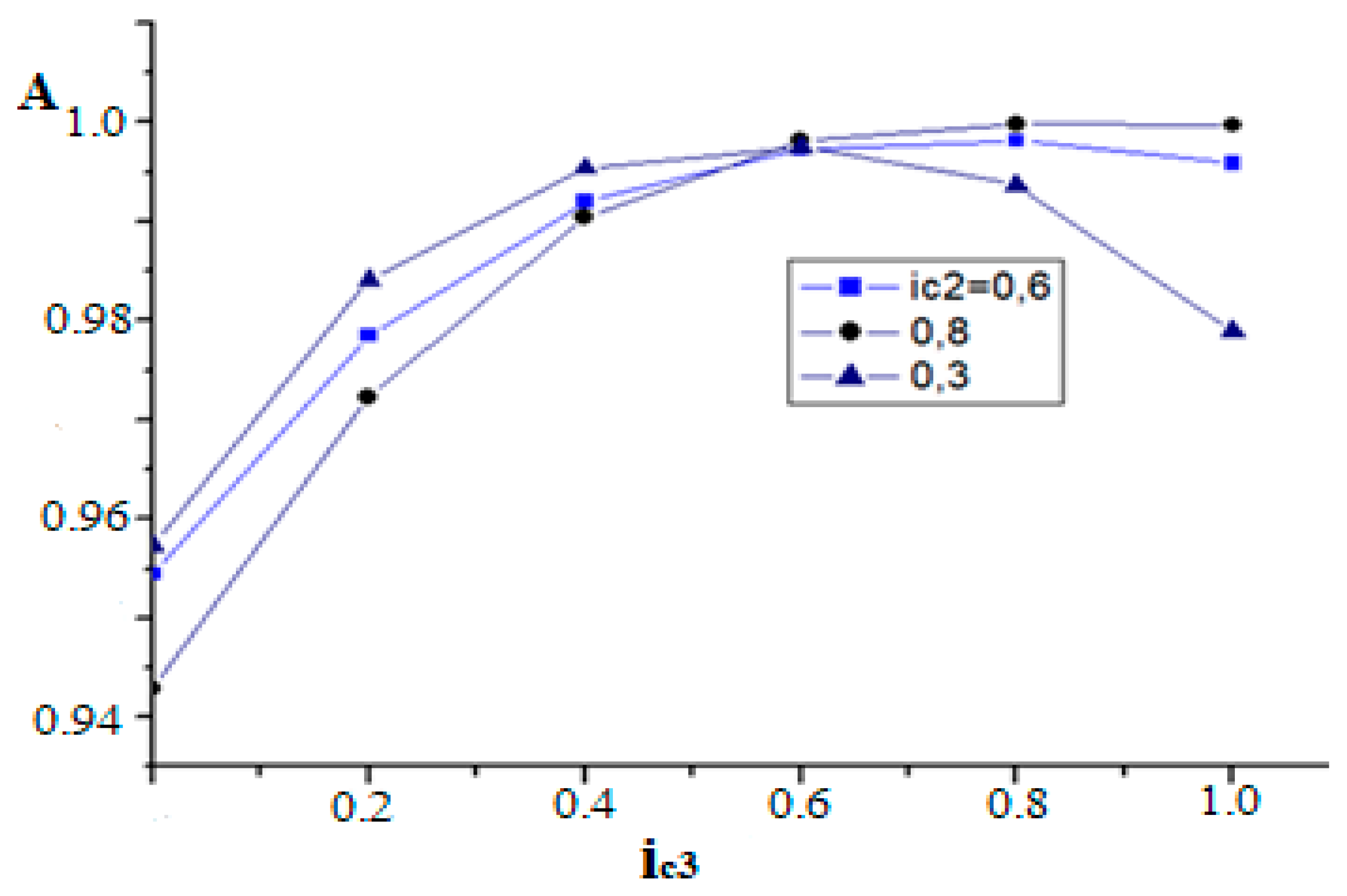
3. Results
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Likharev, K.K. Introduction into Dynamics of Josephson Junctions and Circuits; Gordon Breach: New York, NY, USA, 1986; p. 586. [Google Scholar]
- Askerzade, I.; Bozbey, A.; Canturk, M. Modern Aspects of Josephson Dynamics and Superconductivity Electronics; Springer: Berlin, Germany, 2017. [Google Scholar]
- Il’ichev, E.; Zakosarenko, V.; Fritzsch, L.; Fritzsch, R.; Hoenig, H.E.; Meyer, H.-G.; Götz, M.; Zorin, A.B.; Khanin, V.V.; Pavolotsky, A.B.; et al. Radio-frequency based monitoring of small supercurrents. Rev. Sci. Instrum. 2001, 72, 1882. [Google Scholar] [CrossRef]
- Yerin, Y.S.; Omelyanchouk, A.N. Frustration phenomena in Josephson point contacts between single-band and three-band superconductors. Low Temp. Phys. 2014, 40, 943–949. [Google Scholar] [CrossRef]
- Askerzade, I. Unconventional Superconductors: Anisotropy and Multiband Effects; Springer: Berlin, Germany, 2012; p. 177. [Google Scholar]
- Yerin, Y.S.; Omelyanchouk, A.N.; Il’ichev, E. DC SQUID based on a three-band superconductor with broken time-reversal symmetry. Supercond. Sci. Technol. 2015, 28, 095006. [Google Scholar] [CrossRef][Green Version]
- Ng, T.; Nagaosa, N. Broken time-reversal symmetry in Josephson junction involving two-band superconductors. Europhys. Lett. 2009, 87, 17003. [Google Scholar] [CrossRef]
- Stanev, V.; Tešanović, Z. Three-band superconductivity and the order parameter that breaks time-reversal symmetry. Phys. Rev. B 2010, 81, 134522. [Google Scholar] [CrossRef]
- Dias, R.; Marques, A. Frustrated multiband superconductivity. Supercond. Sci. Technol. 2011, 24, 085009. [Google Scholar] [CrossRef][Green Version]
- Lin, S.-Z. Josephson effect between a two-band superconductor with s++ or s± pairing symmetry and a conventional s-wave superconductor. Phys. Rev. B 2012, 86, 014510. [Google Scholar] [CrossRef]
- Bojesen, T.A.; Babaev, E.; Sudbø, A. Time reversal symmetry breakdown in normal and superconducting states in frustrated three-band systems. Phys. Rev. B 2013, 88, 220511(R). [Google Scholar] [CrossRef]
- Askerzade, I.N. Escape rate in Josephson junctions between single -band and two -band superconductors. Phys. C 2020, 374, 1353647. [Google Scholar] [CrossRef]
- Askerzade, I.N.; Aydın, A. Frustration effect on escape rate in Josephson junctions between single-band and three-band superconductors in the macroscopic quantum tunneling regime. Low Temp. Phys. 2021, 47, 282–286. [Google Scholar] [CrossRef]
- Askerzade, I.N.; Askerbeyli, R.; Ulku, I. Effect of unconventional current-phase relation of Josephson junction on escape rate in ac SQUID. Physica C 2022, 598, 1354068. [Google Scholar] [CrossRef]
- Askerzade, I.N. Influence of Anharmonic and Frustration Effects on Josephson Phase Qubit Characteristics. Condens. Matter 2023, 8, 20. [Google Scholar] [CrossRef]
- Grigorishin, K. Effective Ginzburg–Landau free energy functional for multi-band isotropic superconductors. Phys. Lett. A 2016, 380, 1781. [Google Scholar] [CrossRef]
- Tongkhonburi, P.; Udomsamuthirun, P. The study on penetration depth of anisotropic two-band superconductors by Ginzburg–Landau approach. Physica C 2019, 561, 45. [Google Scholar] [CrossRef]
- Grigorishin, K. Collective Excitations in Two-Band Superconductors. J. Low Temp. Phys. 2022, 206, 360. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askerzade, I.N. Influence of Frustration Effects on the Critical Current of DC SQUID. Condens. Matter 2023, 8, 65. https://doi.org/10.3390/condmat8030065
Askerzade IN. Influence of Frustration Effects on the Critical Current of DC SQUID. Condensed Matter. 2023; 8(3):65. https://doi.org/10.3390/condmat8030065
Chicago/Turabian StyleAskerzade, Iman N. 2023. "Influence of Frustration Effects on the Critical Current of DC SQUID" Condensed Matter 8, no. 3: 65. https://doi.org/10.3390/condmat8030065
APA StyleAskerzade, I. N. (2023). Influence of Frustration Effects on the Critical Current of DC SQUID. Condensed Matter, 8(3), 65. https://doi.org/10.3390/condmat8030065









