Dispersion in Single-Wall Carbon Nanotube Film: An Application of Bogoliubov–Valatin Transformation for Hamiltonian Diagonalization
Abstract
1. Introduction
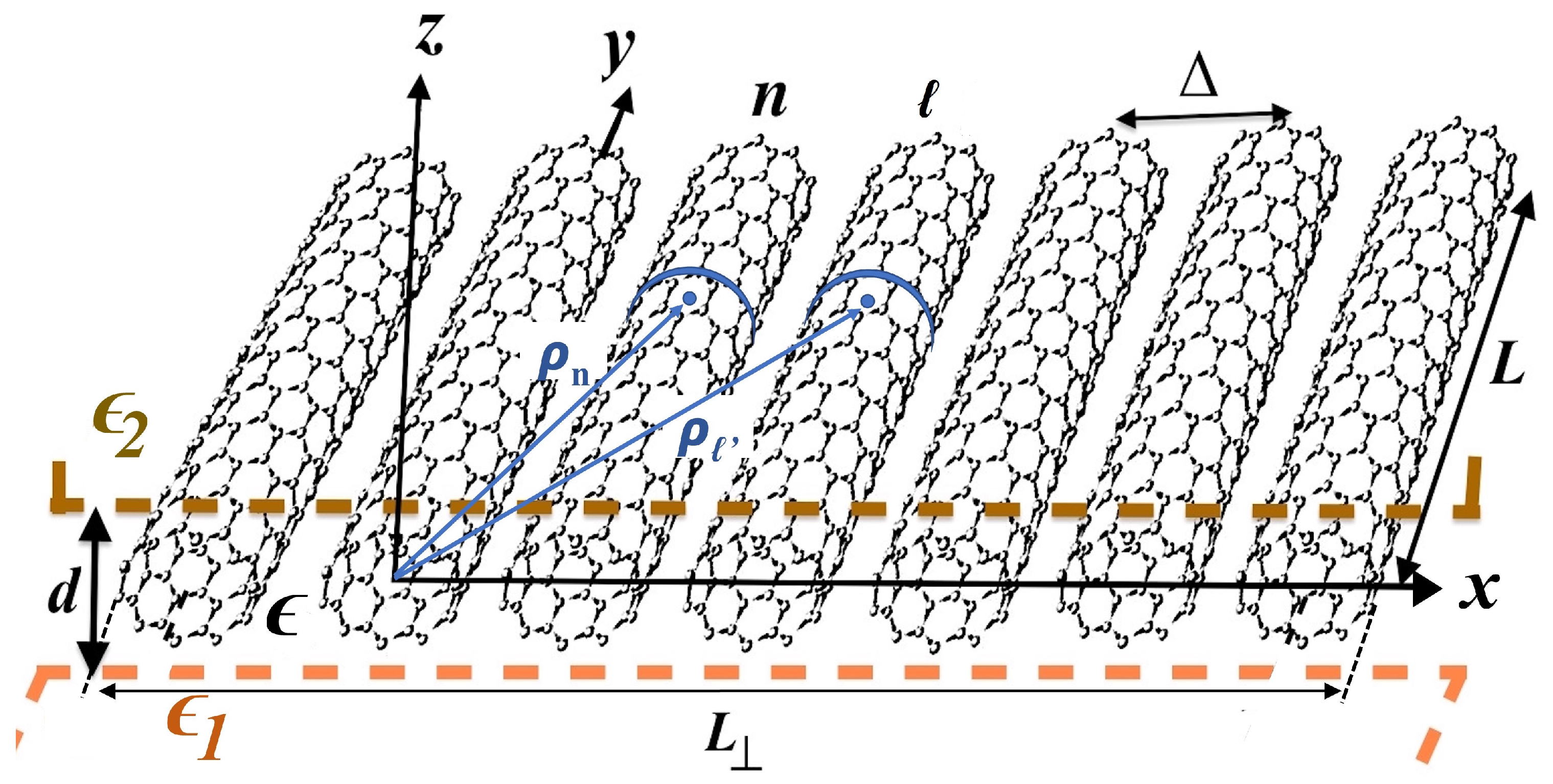
2. Mathematical Formulation
3. Bogoliubov–Valatin Transformation Technique of Hamiltonian Diagonalization
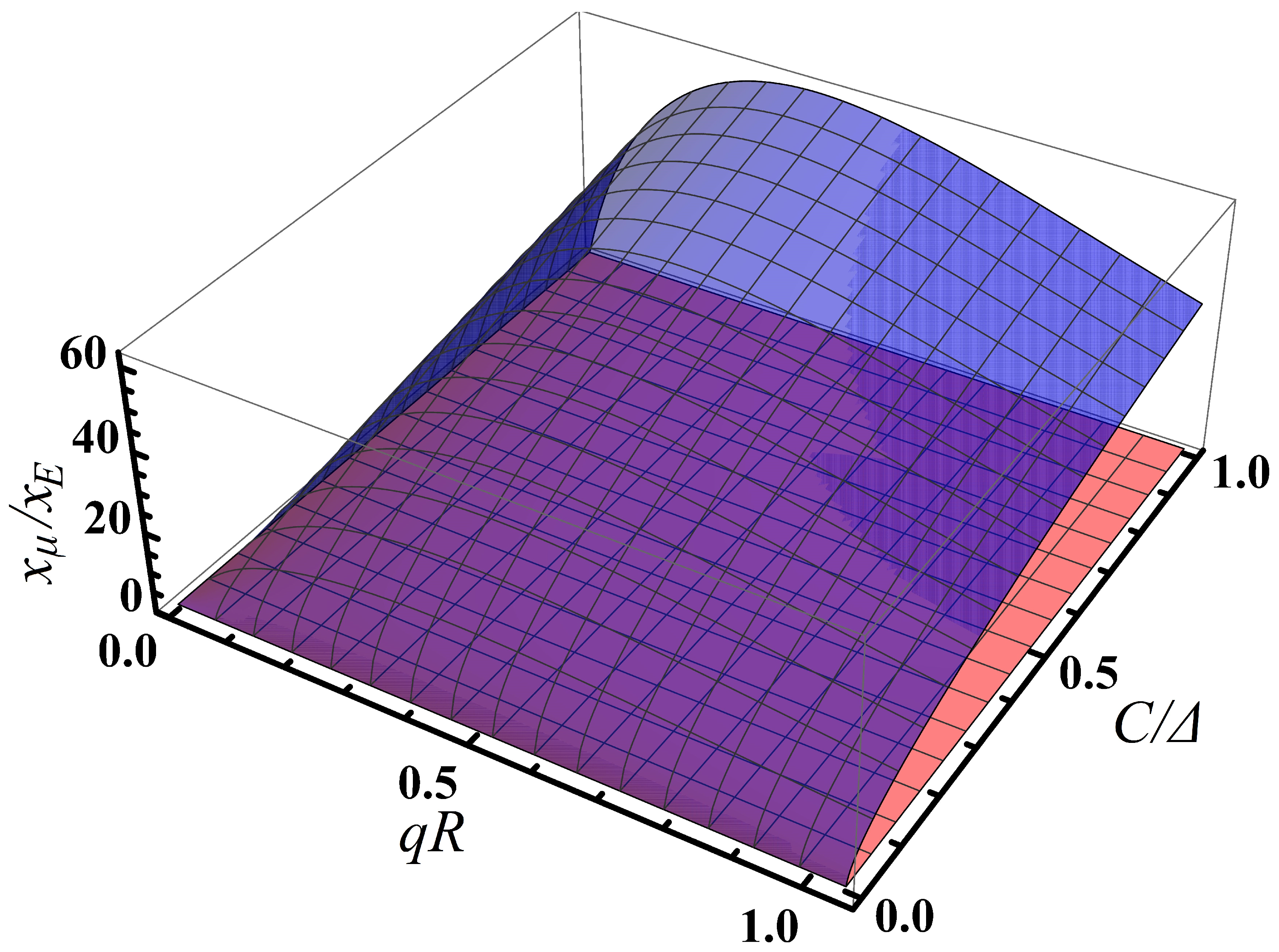
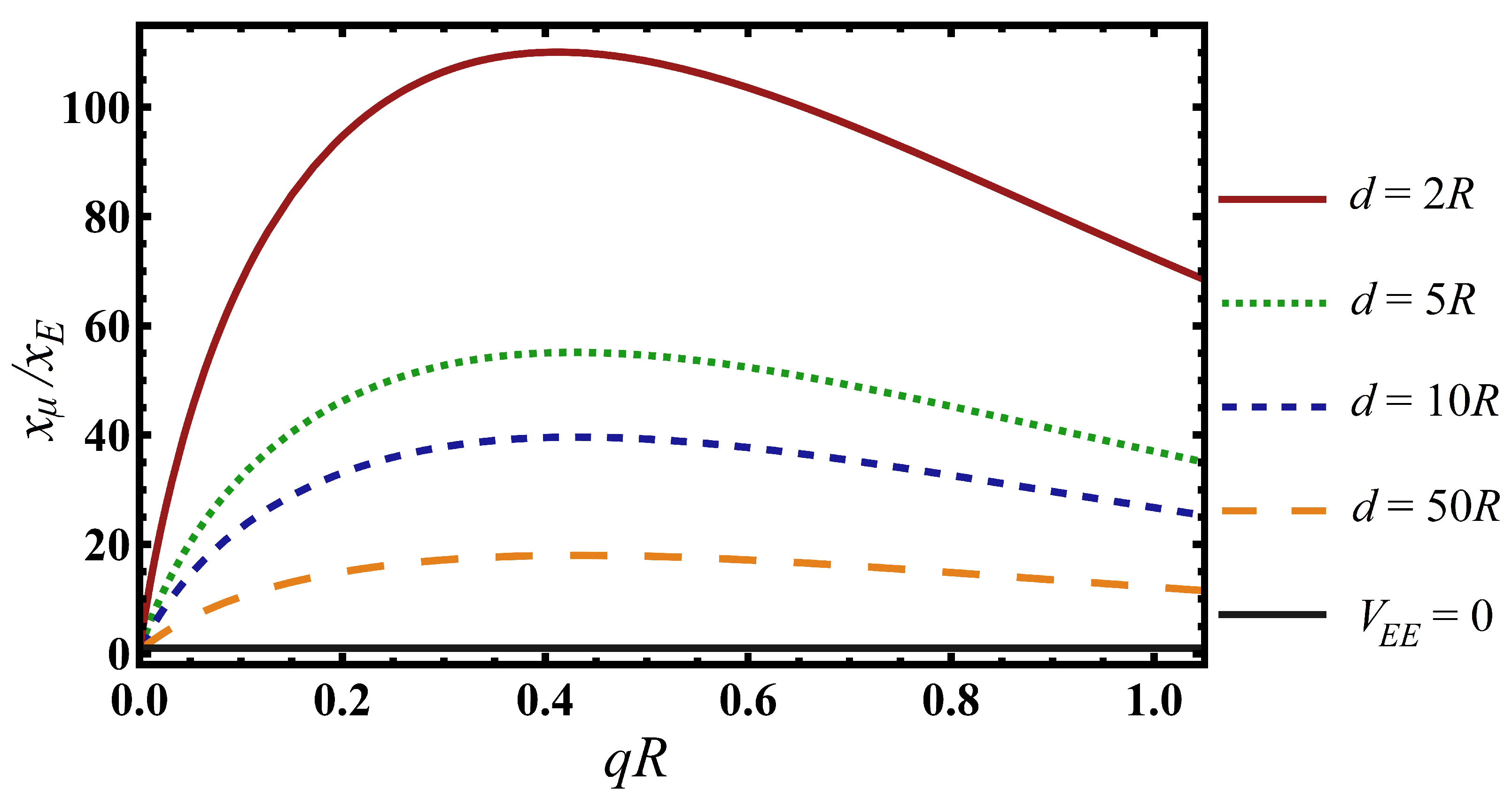
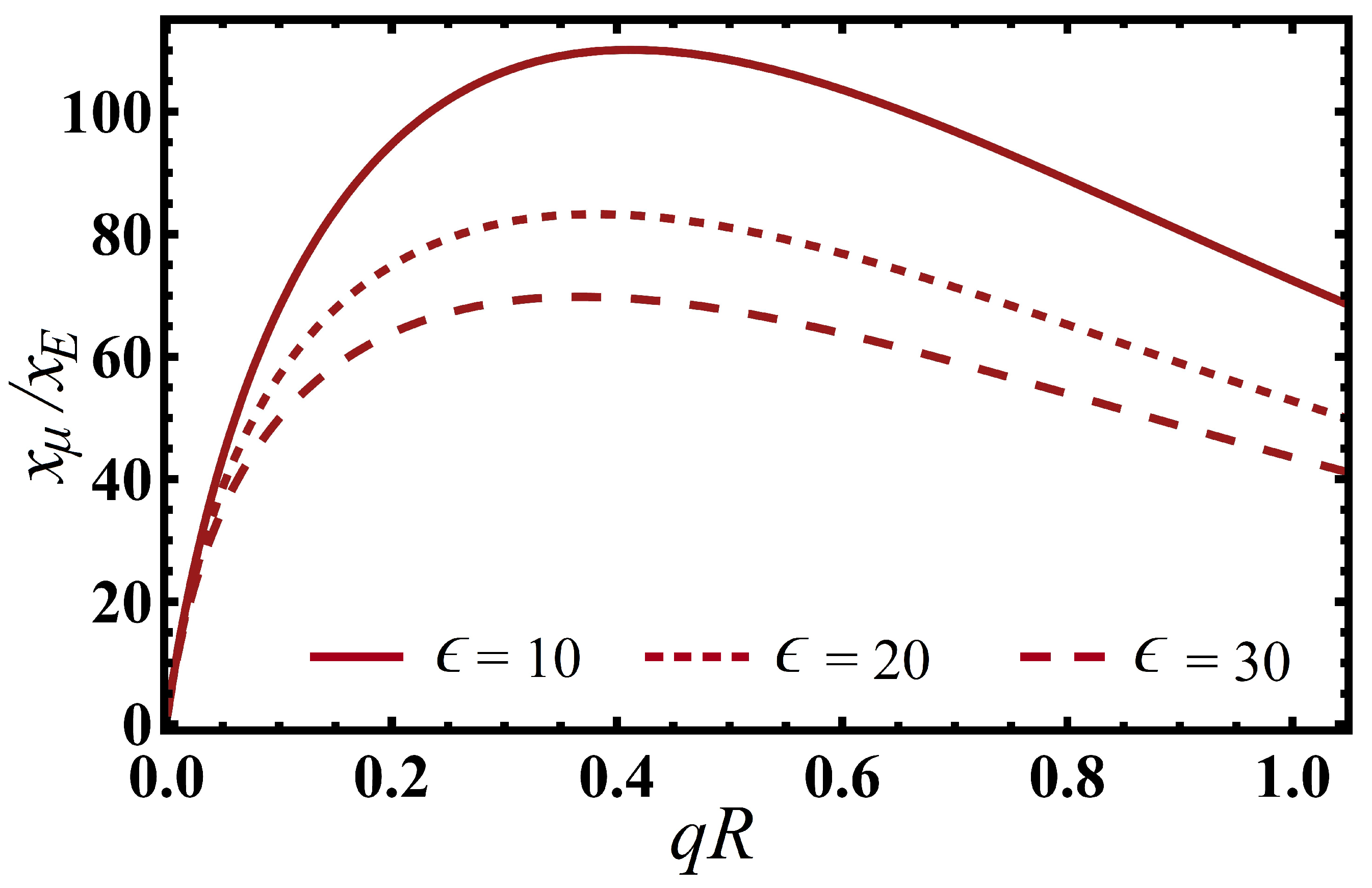
4. Numerical Example: Energy Dispersion of (11,0) SWCNT Film
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Collins, P.G.; Avouris, P. Nanotubes for electronics. Sci. Am. 2000, 62, 283. [Google Scholar] [CrossRef]
- Zhang, A.Y. Research on the Properties and Defects of Carbon Nanotubes. In Advanced Materials Research; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2014; Volume 157, p. 971. [Google Scholar]
- Hong, S.; Myung, S. Nanotube electronics: A flexible approach to mobility. Nat. Nanotechnol. 2007, 2, 207. [Google Scholar] [CrossRef]
- Mintmire, J.W.; Dunlap, B.I.; White, C.T. Are fullerene tubules metallic? Phys. Rev. Lett. 1992, 68, 631. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Chen, Z. Curved pi-conjugation, aromaticity, and the related chemistry of small fullerenes (<C60) and single-walled carbon nanotubes. Chem. Rev. 2005, 105, 3643. [Google Scholar]
- Pop, E.; Mann, D.; Wang, Q.; Goodson, K.; Dai, H. Thermal conductance of an individual single-wall carbon nanotube above room temperature. Nano Lett. 2006, 6, 96. [Google Scholar] [CrossRef]
- Ashiba, H.; Iizumi, Y.; Okazaki, T.; Wang, X.; Fujimaki, M. Carbon Nanotubes as Fluorescent Labels for Surface Plasmon Resonance-Assisted Fluoroimmunoassay. Sensors 2017, 17, 2569. [Google Scholar] [CrossRef]
- Roberts, J.A.; Yu, S.J.; Ho, P.H.; Schoeche, S.; Falk, A.L.; Fan, J.A. Tunable hyperbolic metamaterials based on self-assembled carbon nanotubes. Nano Lett. 2019, 19, 3131. [Google Scholar] [CrossRef] [PubMed]
- Bati, A.S.R.; Yu, L.P.; Tawfik, S.A.; Spencer, M.J.S.; Shaw, P.E.; Batmunkh, M.; Shapter, J.G. Electrically Sorted Single-Walled Carbon Nanotubes-Based Electron Transporting Layers for Perovskite Solar Cells. iScience 2019, 14, 100. [Google Scholar] [CrossRef]
- Bondarev, I.V.; Adhikari, C.M. Collective Excitations and Optical Response of Ultrathin Carbon-Nanotube Films. Phys. Rev. Appl. 2021, 15, 034001. [Google Scholar] [CrossRef]
- Adhikari, C.M.; Bondarev, I.V. Optical response of ultrathin periodically aligned single-wall carbon nanotube films. Mrs Adv. 2020, 5, 2685. [Google Scholar] [CrossRef]
- Keldysh, L.V. Coulomb interaction in thin semiconductor and semimetal films. Engl. Transl. JETP Lett. 1980, 29, 658. [Google Scholar]
- Shah, D.; Kudyshev, Z.A.; Saha, S.; Shalaev, V.M.; Boltasseva, A. Transdimensional material platforms for tunable metasurface design. MRS Bull. 2020, 45, 188. [Google Scholar] [CrossRef]
- Boltasseva, A.; Shalaev, V.M. Transdimensional Photonics. ACS Photonics 2019, 6, 1. [Google Scholar] [CrossRef]
- Mahan, G.D. Many-Particle Physics, 3rd ed.; Kluwer Academic: New York, NY, USA, 2000. [Google Scholar]
- Tyablikov, S.V. Method in Quantum Theory of Magnetism; Springer: New York, NY, USA, 1967. [Google Scholar]
- Agranivich, V.M. Dispersion of electromagnetic waves in crys tals. J. Exptl. Theoret. Phys. 1959, 37, 430. [Google Scholar]
- Philpott, M.R. Diagonalization of a Molecular-Exciton Hamiltonian for an Impure Crystal, Absorption Spectroscopy of Individual Single-Walled Carbon Nanotubes. J. Chem. Phys. 1968, 49, 4537. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Oswald, W.; Wu, Z. Energy gaps in graphene nanomeshes. Phys. Rev. B 2012, 85, 115431. [Google Scholar] [CrossRef]
- Goodaire, E.G. Linear Algebra: Pure & Applied; World Scientific Publishing Company: Singapore, 2013. [Google Scholar]
- Jentschura, U.D.; Debierre, V.; Adhikari, C.M.; Matveev, A.; Kolachevsky, N. Long-range interactions of hydrogen atoms in excited states. II. Hyperfine-resolved 2S-2S systems. Phys. Rev. A 2017, 95, 022704. [Google Scholar] [CrossRef]
- Adhikari, C.M.; Debierre, V.; Jentschura, U.D. Adjacency graphs and long-range interactions of atoms in quasi-degenerate states: Applied graph theory. Appl. Phys. B 2017, 123, 13. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Adhikari, C.M. Long-Range Interactions for Hydrogen: 6P-1S and 6P-2S Systems. Atoms 2017, 5, 48. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Adhikari, C.M.; Dawes, C.M.; Matveev, A.; Kolachevsky, N. Pressure shifts in high-precision hydrogen spectroscopy. I. Long-range atom-atom and atom-molecule interactions. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 075005. [Google Scholar] [CrossRef]
- Adhikari, C.M.; Jentschura, U.D. Long-Range Interactions for Hydrogen Atoms in Excited D States. Atoms 2022, 10, 6. [Google Scholar] [CrossRef]
- Amori, A.R.; Hou, Z.; Krauss, T.D. Excitons in Single-Walled Carbon Nanotubes and Their Dynamics. Annu. Rev. Phys. Chem. 2018, 69, 81. [Google Scholar] [CrossRef]
- Umari, P.; Petrenko, O.; Taioli, S.; De Souza, M.M. Communication: Electronic band gaps of semiconducting zig-zag carbon nanotubes from many-body perturbation theory calculations. J. Chem. Phys. 2012, 136, 181101. [Google Scholar] [CrossRef]
- Kilina, S.; Badaeva, E.; Piryatinski, A.; Tretiak, S.; Saxena, A.; Bishop, A.R. Bright and dark excitons in semiconductor carbon nanotubes: Insights from electronic structure calculations. Phys. Chem. Chem. Phys. 2009, 11, 4113. [Google Scholar] [CrossRef]
- Weisman, R.B.; Bachilo, S.M. Dependence of Optical Transition Energies on Structure for Single-Walled Carbon Nanotubes in Aqueous Suspension: An Empirical Kataura Plot. Nano Lett. 2003, 3, 1235. [Google Scholar] [CrossRef]
- Cubukcua, E.; Degirmencia, F.; Kocabasb, C.; Zimmlera, M.A.; Rogersc, J.A.; Capasso, F. Aligned carbon nanotubes as polarization-sensitive, molecular near-field detectors. Proc. Natl. Acad. Sci. USA 2009, 106, 2495. [Google Scholar] [CrossRef]
- Benedict, L.X.; Louie, S.G.; Cohen, M.L. Static polarizabilities of single-wall carbon nanotubes. Phys. Rev. B 1995, 52, 8541. [Google Scholar] [CrossRef]
- Kozinsky, B.; Marzari, N. Static dielectric properties of carbon nanotubes from first principles. Phys. Rev. Lett. 2006, 96, 166801. [Google Scholar] [CrossRef]
- Sasaki, K.-I.; Riichiro Saito, R. Pseudospin and Deformation-Induced Gauge Field in Graphene. Prog. Theor. Phys. Suppl. 2008, 176, 253. [Google Scholar] [CrossRef]
- Marconcini, P.; Macucci, M. The k · p method and its application to graphene, carbon nanotubes andgraphene nanoribbons: The Dirac equation. Riv. Nuovo Cim. 2011, 34, 489. [Google Scholar]
- Karlheinz, S. Microwave dielectric constants of silicon, gallium arsenide, and quartz. J. Appl. Phys. 1988, 63, 5439. [Google Scholar]
- Kazimierczuk, M.K. Pulse-Width Modulated DC-DC Power Converters; Wiley: Weinheim, Germany, 2015. [Google Scholar]
- Adhikari, C.M.; Bondarev, I.V. Controlled exciton–plasmon coupling in a mixture of ultrathin periodically aligned single-wall carbon nanotube arrays. J. Appl. Phys. 2021, 129, 015301. [Google Scholar] [CrossRef]
- Bondarev, I.V.; Woods, L.M.; Tatur, K. Strong exciton-plasmon coupling in semiconducting carbon nanotubes. Phys. Rev. B 2009, 80, 085407. [Google Scholar] [CrossRef]
- Spataru, C.D.; Ismail-Beigi, S.; Capaz, R.B.; Louie, S.G. Theory and Ab Initio Calculation of Radiative Lifetime of Excitons in Semiconducting Carbon Nanotubes. Phys. Rev. Lett. 2005, 95, 247402. [Google Scholar] [CrossRef]
- Dong, S.; Zhang, Q.; Cao, G.; Ni, J.; Shi, T.; Li, S.; Duan, J.; Wang, J.; Li, Y.; Sun, S.; et al. On-chip trans-dimensional plasmonic router. Nanophotonics 2020, 9, 3357. [Google Scholar] [CrossRef]
- Ando, T. Theory of Electronic States and Transport in Carbon Nanotubes. J. Phys. Soc. Jpn. 2005, 74, 777. [Google Scholar] [CrossRef]
- Saad, Y. Numerical Methods for Large Eigenvalues Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adhikari, C.M.; Morris, D.M.; Noonan, T.W.; Neupane, T.; Lamichhane, B.R.; Gautam, B.R. Dispersion in Single-Wall Carbon Nanotube Film: An Application of Bogoliubov–Valatin Transformation for Hamiltonian Diagonalization. Condens. Matter 2023, 8, 53. https://doi.org/10.3390/condmat8020053
Adhikari CM, Morris DM, Noonan TW, Neupane T, Lamichhane BR, Gautam BR. Dispersion in Single-Wall Carbon Nanotube Film: An Application of Bogoliubov–Valatin Transformation for Hamiltonian Diagonalization. Condensed Matter. 2023; 8(2):53. https://doi.org/10.3390/condmat8020053
Chicago/Turabian StyleAdhikari, Chandra M., Da’Shawn M. Morris, Thomas W. Noonan, Tikaram Neupane, Basu R. Lamichhane, and Bhoj R. Gautam. 2023. "Dispersion in Single-Wall Carbon Nanotube Film: An Application of Bogoliubov–Valatin Transformation for Hamiltonian Diagonalization" Condensed Matter 8, no. 2: 53. https://doi.org/10.3390/condmat8020053
APA StyleAdhikari, C. M., Morris, D. M., Noonan, T. W., Neupane, T., Lamichhane, B. R., & Gautam, B. R. (2023). Dispersion in Single-Wall Carbon Nanotube Film: An Application of Bogoliubov–Valatin Transformation for Hamiltonian Diagonalization. Condensed Matter, 8(2), 53. https://doi.org/10.3390/condmat8020053








