Abstract
The experimental critical temperature of the systems of superconducting () and normal (, and ) nanoparticles, with a random distribution and sizes less than their respective coherence lengths, is governed by the proximity effect, as shown by the experimental data. At first glance, the behavior of the variation in the critical temperature in function of the ratio of volume fractions of the superconducting and the normal metal components seems to suggest a weak coupling behavior for the superconductor. In reality, upon a more careful analysis, using Eliashberg’s theory for the proximity effect, the system instead shows a strong coupling nature. The most interesting thing is that the theory has no free parameters and perfectly explains the behavior of the experimental data just with the assumption in the case of the nanoparticles and , that the value of the density of states at the Fermi level of silver and copper is equal to the value of lead.
1. Introduction
The superconductive proximity effect consists of the modification of the superconducting and normal properties of a superconductor in contact with a metal [1,2,3,4]. In the more general case, the metal can be superconductive (with a lower critical temperature with respect to the first superconductor), which is normal or magnetic. The superconducting coherence length is the characteristic length scale of the proximity effect in the superconductor, while in the metal, the coherence length of normal electrons is , where is the superconductive gap, is the Fermi speed of the superconductor and the normal metal, respectively, l is the mean free path and T is the temperature. When the superconducting and normal layer thicknesses (, ) are smaller than the respective coherence lengths and , the system is the Cooper limit [5] (S and N indicate “superconductor” and “normal”, respectively). It is possible to demonstrate through experimental measurements and simple but accurate models, reproducing the aforementioned measurements, that just depends on the thickness ratio . With the original theory of the proximity effect, introduced into the framework before the BCS theory in [6] and after Eliashberg’s theory in [2,7,8,9,10,11,12], one usually presupposes a plain sample geometry, i.e., the theory was born for describing the proximity effect between a slab of superconductor of thickness separated by a potential barrier from a slab of normal metal of thickness . A profound analogy exists between the proximity system and the two-gap model. If we assume that there is no intrinsic pairing in the second band as in the normal film (for example, as has happened in magnesium diboride [13,14]), then we induce superconductivity, i.e., an induced energy gap appears. The substantial difference between these two situations is that, in the two-band model, the bands are separated in momentum space and the second band acquires an order parameter due to phonon exchange, while in the proximity effect, the systems are spatially separated and superconductivity is induced by the tunneling of Cooper pairs. In the first case, the coupling is in k-space, while in the second, the coupling is in the real space but the mathematical formalism is the same. Furthermore, the effect of a static electric field on the critical temperature of a superconductor can also be explained in the framework of proximity introduced in Eliashberg’s theory [15,16,17,18]. Finally, the role of Andreev reflection [19] is fundamental in the understanding of the microscopic mechanism at the origin of the proximity effect [20]. It happens that single-electron states from normal metal are converted into Cooper pairs in the superconductor. The proximity effect can be seen as the result of interplay between the long-range order inside the normal metal and Andreev reflection at the normal metal–superconductor interface [21]. The link between Andreev reflection and the proximity effect exists because the Andreev reflection of an electron or a hole is equivalent to the transfer of a Cooper pair in or out of the superconductor, i.e., to presence of Cooper pairs inside the normal metal.
Subsequently, it was understood that this theory could also include the more general situation wherein only the ratio of the volume fraction of superconducting metal component to the ratio of normal metal component was known, as happens in a two-component system consisting of a random distribution of superconducting and normal nanoparticles, with sizes which are inferior to their respective coherence lengths [5,22,23]. In this case, as in [5], one may replace the ratio of the thickness of the superconductor metal layer to the thickness of the normal metal layer in the de Gennes–Werthamer theory [24,25] by the ratio of the volume fraction . This fact allows us to use Eliashberg’s theory with the proximity effect [12], without free parameters, to also explain the experimental data, as has been successfully achieved, for example, with experimental data relative to the heterostructure [26] grown on Si(111) using molecular-beam epitaxy. We will examine the cases where the superconducting nanoparticles are of lead while the normal ones are of silver, copper and aluminum. According to the interpretation proposed by the authors of the measures [22], the lead behaves as a weak-coupling superconductor in the random lead–silver () nanocomposites. The same situation occurred in [23] for the lead–copper () nanocomposites. This interpretation is based on the use of analytical formulas obtained with numerous simplifications from the BCS theory and leading to the non-physical values of some parameters. The problem is that the lead is a strong coupling superconductor and there is no reason why it should behave differently. In the last case [5] which will be analyzed, namely that of lead–aluminum () nanocomposites, the strong coupling behavior will be immediately evident. In principle, one should also consider the way in which the electron–phonon interaction interplays with the quantum-size effects [27,28]. Here, we are not dealing with individual grains but rather nanocrystalline films where these effects, which on the critical temperature can be of the opposite sign, on average, probably cancel each other out. This paper is organized as follows. In Section 2, the model used herein for the computation of the superconductive critical temperature of these proximity systems is shown, i.e., the one-band s-wave Eliashberg equations with the proximity effect. In Section 3, the results obtained herein are discussed in comparison with experimental data. Finally, conclusions are given in Section 4.
2. Model: Proximity Eliashberg Equations
By solving the one-band s-wave Eliashberg equations [29,30], generalized to the case wherein the proximity effect is present, it is possible to calculate the critical temperature of this superconducting–normal system. Four coupled equations have to be solved, namely two for the gaps and two for the renormalization functions . If the Migdal theorem is valid [31], the Eliashberg equations with a proximity effect on the imaginary axis [7,8,9,10,11,12,15] (where denotes the Matsubara frequencies), for the gaps , read:
while those for the renormalization functions are
where is the Heaviside function, is a cutoff energy and are the Coulomb pseudopotentials in the superconductive and normal layer, respectively. The coupling terms between the normal and superconductive layers are
where is the transmission matrix, A is the junction cross-sectional area, are the superconductive and normal layer thicknesses, respectively, are the densities of states at the Fermi level for the superconductive and normal materials, respectively, and the rate of the coupling terms is . Finally, the terms relative to quasiparticles and the Cooper pair density of states are:
The phononic glue is inside the following term:
where are the electron–phonon spectral functions and the electron–phonon coupling constants are defined as
A lot of input parameters appear in this set of coupled equations; however, fortunately, these are all known because these materials are phononic. In particular, these input parameters are: two electron–phonon spectral functions ; two Coulomb pseudopotentials ; two values of the normal density of states at the Fermi level ; and the thickness of the superconductive layer and normal layer (these last ones are experimental inputs). In principle, the product between the junction cross-sectional area A and the transmission matrix are also present, but we have verified, as it should be, that the final result does not depend on the value of A, and therefore, not even on the value of the product .
All inputs parameters are known and will be specified below. The letter S is for and the letter N is for , and . The electron–phonon spectral functions of lead () [29], aluminum () [32], silver () [33] and copper () [33] are present in the literature (they are shown in the insert of the figures) as the values of the normal density of states at the Fermi level [15,34] eV for the unit cell; eV for the unit cell; eV for the unit cell; and eV for the unit cell. The value of the Coulomb pseudopotential is fixed for obtaining K in a system without a proximity effect for lead and K for aluminum: we find and by using a cutoff energy meV and a maximum energy meV. The Coulomb pseudopotential for copper and silver is the same [33] . The values of and are experimental data. By specifying these inputs parameters, this calculation has no free parameters.
3. Results and Discussion
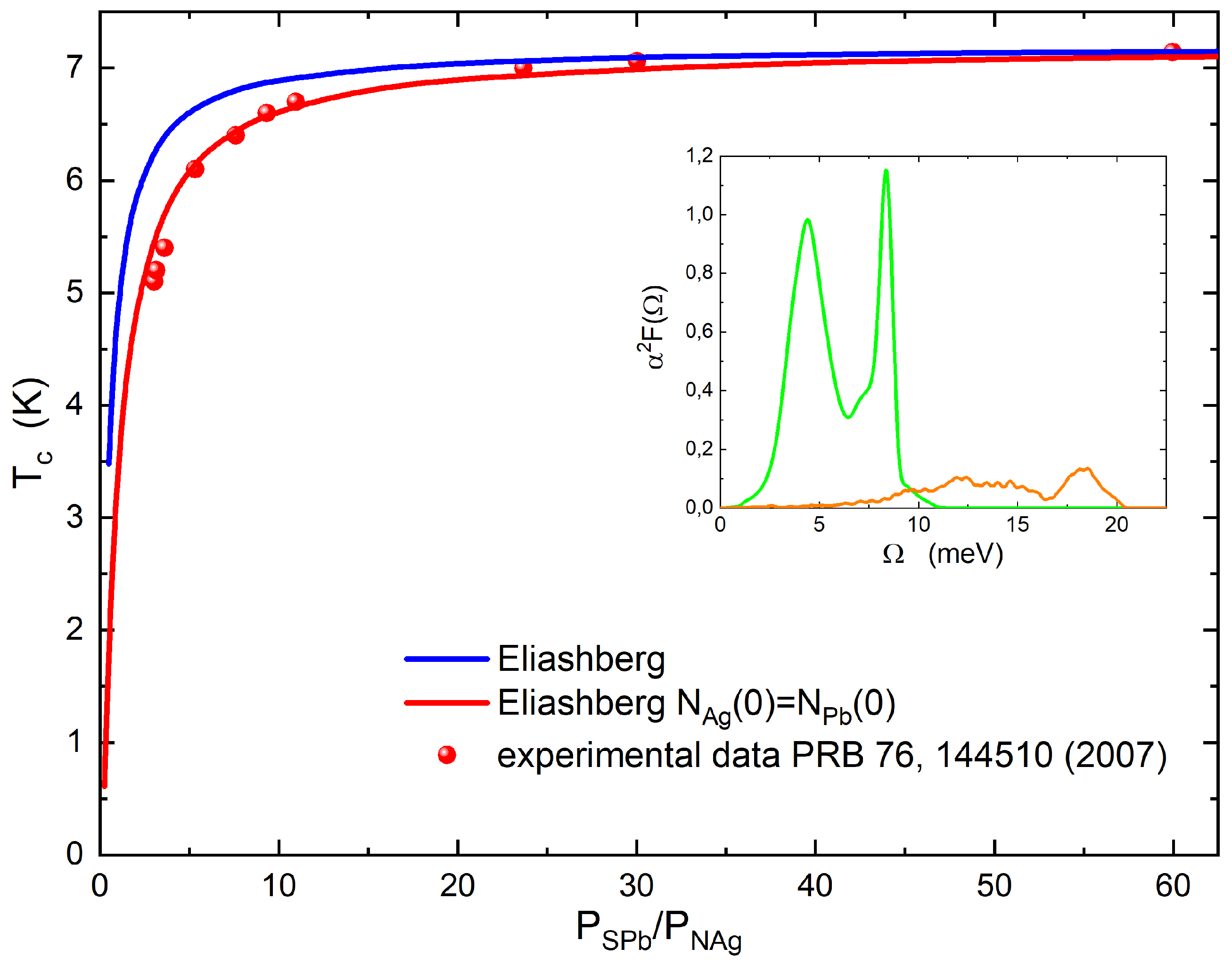
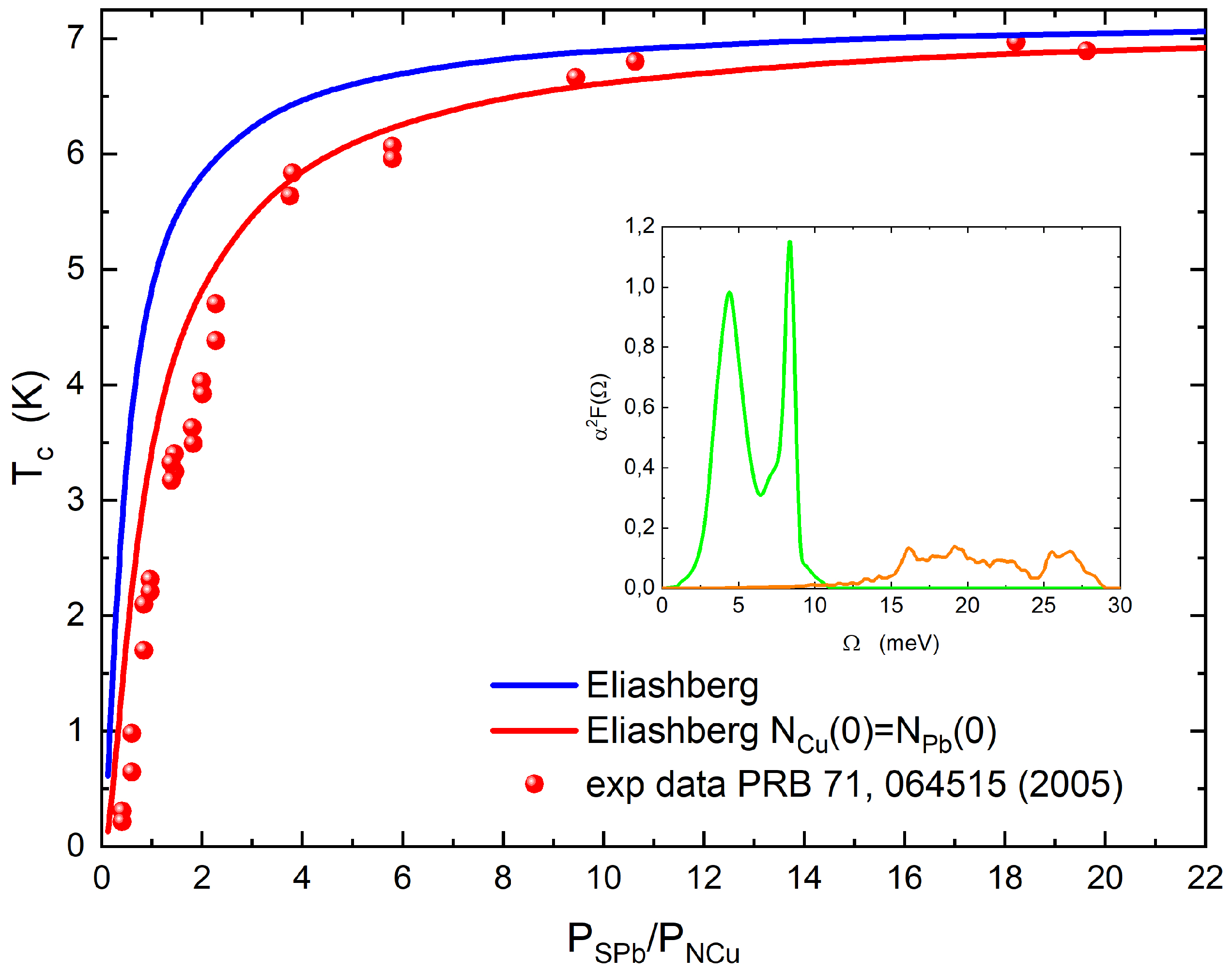
The Eliashberg equations are solved numerically in a recursive way. This is a standard method that works very well because the solution is quickly reached [29]. From the solution of Eliashberg equations, it is possible to determine the critical temperature as a function of the ratio of the volume fraction of the superconducting and the normal metal components . However, the comparison with experimental data is not so good, as seen in Figure 1 and Figure 2 (dark blue solid line). Thus, it is necessary to formulate specifically one new hypothesis to solve this problem. We assume that, to explain the experimental data, it is necessary that the density of the states at the Fermi level of the normal metal nanoparticles is substituted, in the equations, by the value of the superconductor density of states, but only when the size of normal metal nanoparticles is less than the superconductor coherence length. The characteristic length of the proximity effect is the coherence length, that is, the typical size of the Cooper pairs and the proximity effect is connected with the Cooper pairs inside the normal metal. If the dimensions of the nanoparticles are only smaller than the coherence length of the superconductor (i.e., the dimensions of the Cooper pairs), it is possible that the electronic properties of the nanoparticles are replaced by those of the superconductor. The coherence length of lead [35] is 96 nm, so the silver and copper nanoparticle size is always less than this distance. As such, we just change the value of : now , but all other input parameters remain the same and we solve the Eliashberg equations. The result is the solid red line in Figure 1 and Figure 2 that shows very good agreement with the experimental data. The author found the same behavior in the superconductor/normal metal heterostructure epitaxially grown [26]. Furthermore, in this case, we made the same hypothesis and perfectly reproduced the experimental data [12]. One could say that, within a thickness less than the superconducting coherence length, the superconductor “wins” over the metal and this is observable because the has a large coherence length. Since the same phenomenon—namely a decrease in the critical temperature of these systems which was faster than expected—occurred both in the nanocomposites and in the high-quality superconductor/normal metal heterostructure, the fact that this phenomenon will be of a general nature will probably not affect the quality or the particular characteristics of the samples. Thus, this assumption that () allows us to very effectively explain the experimental data, and could lead to investigating the nature of these systems using first-principles calculus. If Eliashberg’s theory is assumed to be valid, and we see no reason to doubt it, the only way to reproduce the experimental data is by this assumption. The only other input parameters which, in theory, could be changed, are the Coulomb pseudopotential and the electron–phonon coupling constants; however, in this case, we should admit that these input parameters are a function of , because for high values of , we have to regain the lead bulk critical temperature. Furthermore, even by varying the Coulomb pseudopotential, it is not possible to reproduce the experimental data in any way, as we have been able to verify.
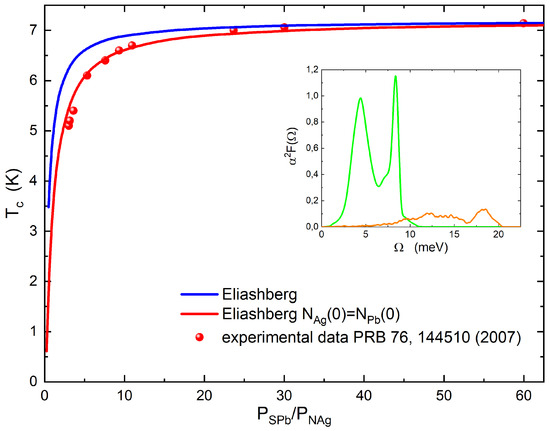
Figure 1.
(Color online) Case . Theoretical critical temperature calculated by solving the Eliashberg equations with (dark blue solid line) and with (red solid line) is shown in function of the rate . The experimental data (full red circles) are from ref [22]. In the insert, the electron–phonon spectral functions of lead (green solid line) and silver (orange solid line) are shown.
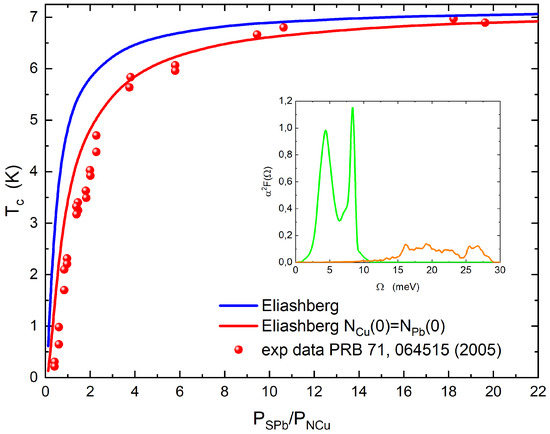
Figure 2.
(Color online) Case . Theoretical critical temperature calculated by solving the Eliashberg equations with (dark blue solid line) and with (red solid line) is shown in function of the rate . The experimental data (full red circles) are from ref [23]. In the inset, the electron–phonon spectral functions of lead (green solid line) and copper (orange solid line) are shown.
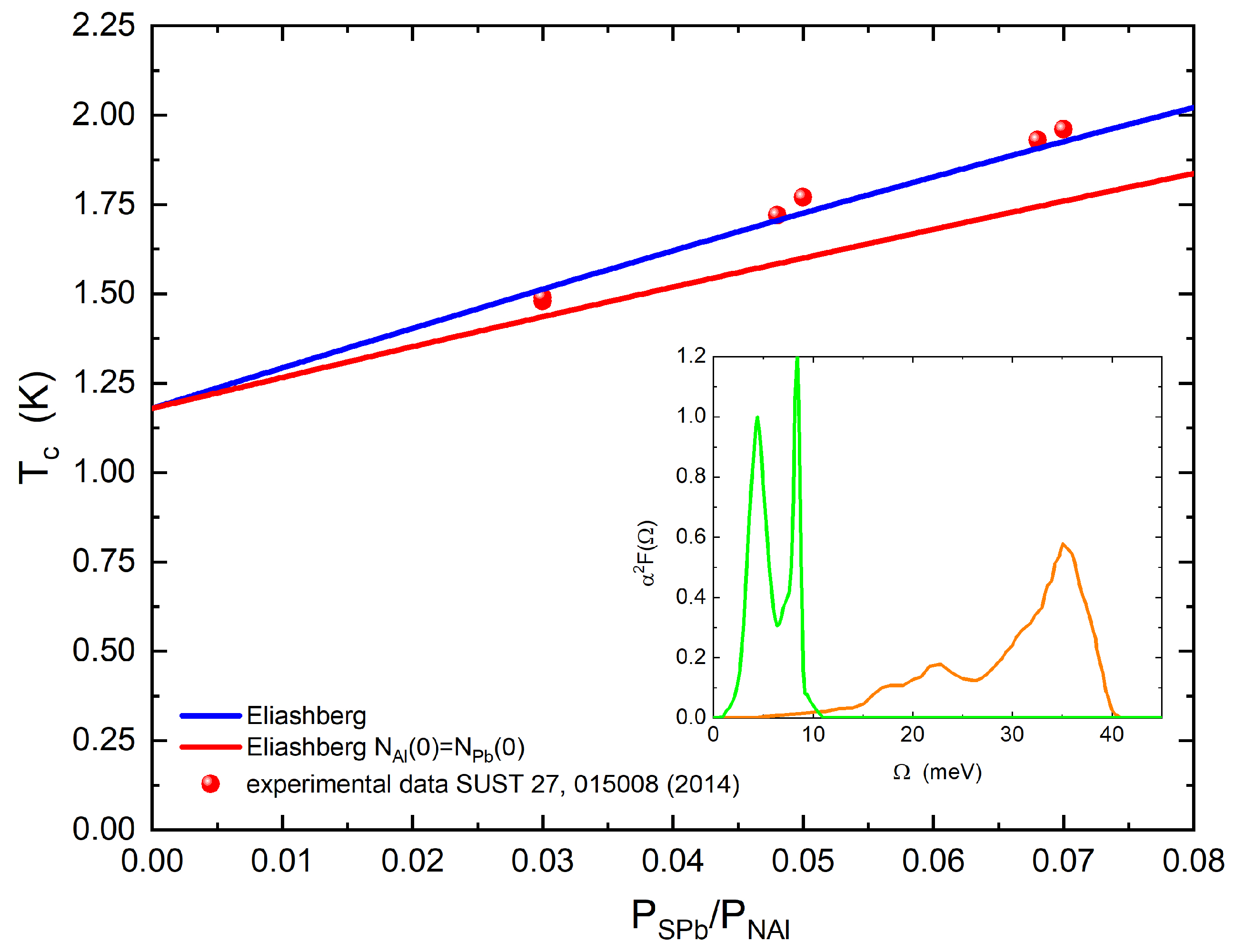
In the last case (aluminum), the standard theory without free parameters reproduces the experimental data very well, as shown in Figure 3. In the latter case, the aluminum which is a superconductor, but also a normal metal if under the temperature conditions in the range studied herein, perfectly follows the standard theory. For completeness, the calculation is also shown in the figure with the replacement of the density of the normal states with the superconducting one as in the previous cases. Here, it is very clear that this method does not work. The reason is simple: in this case, the standard theory works because the layer size is greater and the starting assumption is therefore no longer valid.
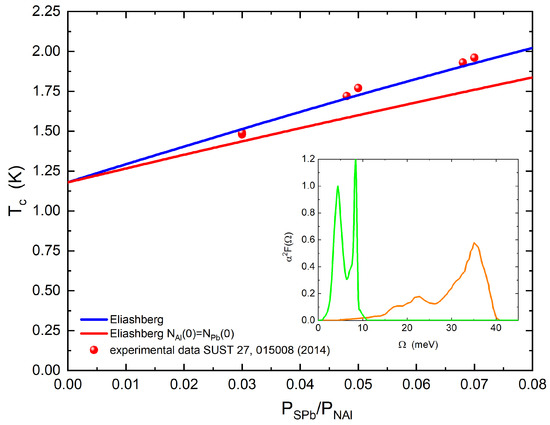
Figure 3.
(Color online) Case . Theoretical critical temperature calculated by solving the Eliashberg equations with (dark blue solid line) and with (red solid line) is shown in function of the rate . The experimental data (full red circles) are from ref [5]. In the inset, the electron–phonon spectral functions of lead (green solid line) and aluminum (orange solid line) are shown.
4. Conclusions
The experimental critical temperature of systems of superconducting () and normal (, ) nanoparticles with a random distribution can be very effectively reproduced in the framework of Eliashberg’s theory by assuming that the density of the states at the Fermi level of the superconductor is replaced by the value present in the normal material in the proximity systems and . In the last case (), the standard theory perfectly explains the experimental data without an additional hypothesis, and of course, free parameters. We emphasize that, to justify this assumption, it would be necessary to resort to calculations from the first principles, which are not present in the literature. In general, it is possible to state that all the experimental data are accurately described by Eliashberg’s theory of proximity effect with no free parameters and without any “strange weak coupling behavior”, as had been hypothesized by the authors of the measurements on the proximity system [22].
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
G.A. Ummarino thanks for the support received from the MEPhI Academic Excellence Project (Contract No. 02.a03.21.0005).
Conflicts of Interest
The author declares no conflict of interest.
References
- Deutscher, G.; de Gennes, P.G. Superconductivity; Marcel Dekker, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Wolf, E.L. Principles of Electron Tunneling Spectroscopy; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]
- Daghero, D.; Ummarino, G.A.; Gonnelli, R.S. The Oxford Handbook of Small Superconductors; Narlikar, A.V., Ed.; Oxford University Press: Oxford, UK, 2017; pp. 144–182. ISBN 978-0-19-873816-9. [Google Scholar]
- Bose, S.; Ayyub, P. A review of finite size effects in quasi-zero dimensional superconductors. Rep. Prog. Phys. 2014, 77, 116503. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Picot, T.; Houben, K.; Moorkens, T.; Grigg, J.; Haesendonck, C.V.; Biermans, E.; Bals, S.; Brown, S.A.; Vantomme, A.; et al. The superconducting proximity effect in epitaxial Al/Pb nanocomposites. Supercond. Sci. Technol. 2014, 27, 015008. [Google Scholar] [CrossRef]
- McMillan, W.L. Tunneling Model of the Superconducting Proximity Effect. Phys. Rev. 1968, 175, 537. [Google Scholar] [CrossRef]
- Schachinger, E.; Carbotte, J.P. Critical temperature of a proximity junction using Eliashberg theory. J. Low Temp. Phys. 1984, 54, 129. [Google Scholar] [CrossRef]
- Zarate, H.G.; Carbotte, J.P. Effects of paramagnons in a proximity sandwich. Phys. Rev. B 1987, 35, 3256. [Google Scholar] [CrossRef]
- Zarate, H.G.; Carbotte, J.P. Tunneling in proximity junctions with paramagnons. Physica B+ C 1985, 135, 203. [Google Scholar] [CrossRef]
- Stephan, W.; Carbotte, J.P. Properties of proximity systems including magnetic impurities. J. Low Temp. Phys. 1991, 82, 145. [Google Scholar] [CrossRef]
- Kresin, V.Z.; Morawitz, H.; Wolf, S.A. Mechanisms of Conventional and High Tc Superconductivity; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Ummarino, G.A. Superconductive critical temperature of Pb/Ag heterostructures. Physica C 2020, 568, 1353566. [Google Scholar] [CrossRef]
- Daghero, D.; Gonnelli, R.S.; Ummarino, G.A.; Stepanov, V.A.; Jun, J.; Kazakov, S.M.; Karpinski, J. Point-contact spectroscopy in MgB2 single crystals in magnetic field. Physica C 2003, 385, 255. [Google Scholar] [CrossRef]
- Daghero, D.; Calzolari, A.; Ummarino, G.A.; Tortello, M.; Gonnelli, R.S.; Stepanov, V.A.; Tarantini, C.; Manfrinetti, P.; Lehmann, E. Point-contact spectroscopy in neutron-irradiated. Phys. Rev. B 2006, 74, 174519. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Piatti, E.; Daghero, D.; Gonnelli, R.S.; Sklyadneva, I.Y.; Chulkov, E.V.; Heid, R. Proximity Eliashberg theory of electrostatic field-effect doping in superconducting films. Phys. Rev. B 2017, 96, 064509. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Romanin, D. Theoretical Explanation of Electric Field-Induced Superconductive Critical Temperature Shifts in Indium Thin Films. Phys. Status Solidi B 2020, 257, 1900651. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Romanin, D. Proximity two bands Eliashberg theory of electrostatic field-effect doping in a superconducting film of MgB2. J. Phys. Condens. Matter 2019, 31, 024001. [Google Scholar] [CrossRef] [PubMed]
- Romanin, D.; Ummarino, G.A.; Piatti, E. Migdal-Eliashberg theory of multi-band high-temperature superconductivity in field-effect-doped hydrogenated (111) diamond. Appl. Surf. Sci. 2021, 536, 147723. [Google Scholar] [CrossRef]
- Gonnelli, R.S.; Calzolari, A.; Daghero, D.; Natale, L.; Ummarino, G.A.; Stepanov, V.A.; Ferretti, M. Evidence for pseudogap and phase-coherence gap separation by Andreev reflection experiments in Au/La2-x Sr x CuO4 point-contact junctions. Eur. Phys. J. B 2001, 22, 411. [Google Scholar]
- Klapwijk, T.M. Proximity effect from an Andreev perspective. J. Supercond. 2004, 17, 593. [Google Scholar] [CrossRef]
- Pannetier, B.; Courtois, H. Andreev reflection and proximity effect. J. Low Temp. Phys. 2000, 118, 599. [Google Scholar] [CrossRef]
- Bose, S.; Ayyub, P. Superconducting proximity effect in nanocomposites. Phys. Rev. B 2007, 76, 144510. [Google Scholar] [CrossRef]
- Sternfeld, I.; Shelukhin, V.; Tsukernik, A.; Karpovski, M.; Gerber, A.; Palevski, A. Proximity effect in granular superconductor–normal metal structures. Phys. Rev. B 2005, 71, 064515. [Google Scholar] [CrossRef]
- De Gennes, P.G. Boundary Effects in Superconductors. Rev. Mod. Phys. 1964, 36, 225. [Google Scholar] [CrossRef]
- Werthamer, N.R. Theory of the superconducting transition temperature and energy gap function of superposed metal films. Phys. Rev. 1963, 132, 2440. [Google Scholar] [CrossRef]
- Nam, H.; Zhang, C.; Lee, W.; Zhu, S.; Gao, H.; Niu, Q.; Fiete, G.A.; Shih, C. Behavior of superconductivity in a Pb/Ag heterostructure. Phys. Rev. B 2019, 100, 094512. [Google Scholar] [CrossRef]
- Croitoru, M.D.; Shanenko, A.A.; Vagov, A.; Milosevic, M.V.; Axt, V.M.; Peeters, F.M. Phonon limited superconducting correlations in metallic nanograins. Sci. Rep. 2015, 5, 16515. [Google Scholar] [CrossRef] [PubMed]
- Croitoru, M.D.; Shanenko, A.A.; Vagov, A.; Vasenko, A.S.; Milosevic, M.V.; Axt, ·.M.; Peeters, F.M. Influence of disorder on superconducting correlations in nanoparticles. J. Supercond. Nov. Magn. 2016, 29, 605. [Google Scholar] [CrossRef]
- Carbotte, J.P. Properties of boson-exchange superconductors. Rev. Mod. Phys. 1990, 62, 1027. [Google Scholar] [CrossRef]
- Ummarino, G.A. Eliashberg Theory. In Emergent Phenomena in Correlated Matter; Pavarini, E., Koch, E., Schollwöck, U., Eds.; Forschungszentrum Jülich GmbH and Institute for Advanced Simulations: Jülich, Germany, 2013; pp. 13.1–13.36. ISBN 978-3-89336-884-6. [Google Scholar]
- Ummarino, G.A.; Gonnelli, R.S. Breakdown of Migdal’s theorem and intensity of electron-phonon coupling in high-Tc superconductors. Phys. Rev. B 1997, 56, 14279. [Google Scholar] [CrossRef]
- Bauer, R.; Schmid, A.; Pavone, P.; Strauch, D. Electron-phonon coupling in the metallic elements Al, Au, Na, and Nb: A first-principles study. Phys. Rev. B 1998, 57, 11276. [Google Scholar] [CrossRef]
- Giri, A.; Tokina, M.V.; Prezhdo, O.V.; Hopkins, P.E. Electronephonon coupling and related transport properties of metals and intermetallic alloys from first principles. Mater. Today Phys. 2020, 12, 100175. [Google Scholar] [CrossRef]
- Butler, W.H.; Williams, R.K. Electron-phonon interaction and lattice thermal conductivity. Phys. Rev. B 1978, 18, 6483. [Google Scholar] [CrossRef]
- Gasparovic, R.F.; McLean, W.L. Superconducting Penetration Depth of Lead. Phys. Rev. B 1970, 2, 2519. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).