Thermal and Quantum Fluctuation Effects on Non-Spherical Nuclei: The Case of Spin-1 System
Abstract
1. Introduction
2. The Model
3. Time Evolution of the Model under Static and Rotating Magnetic Fields
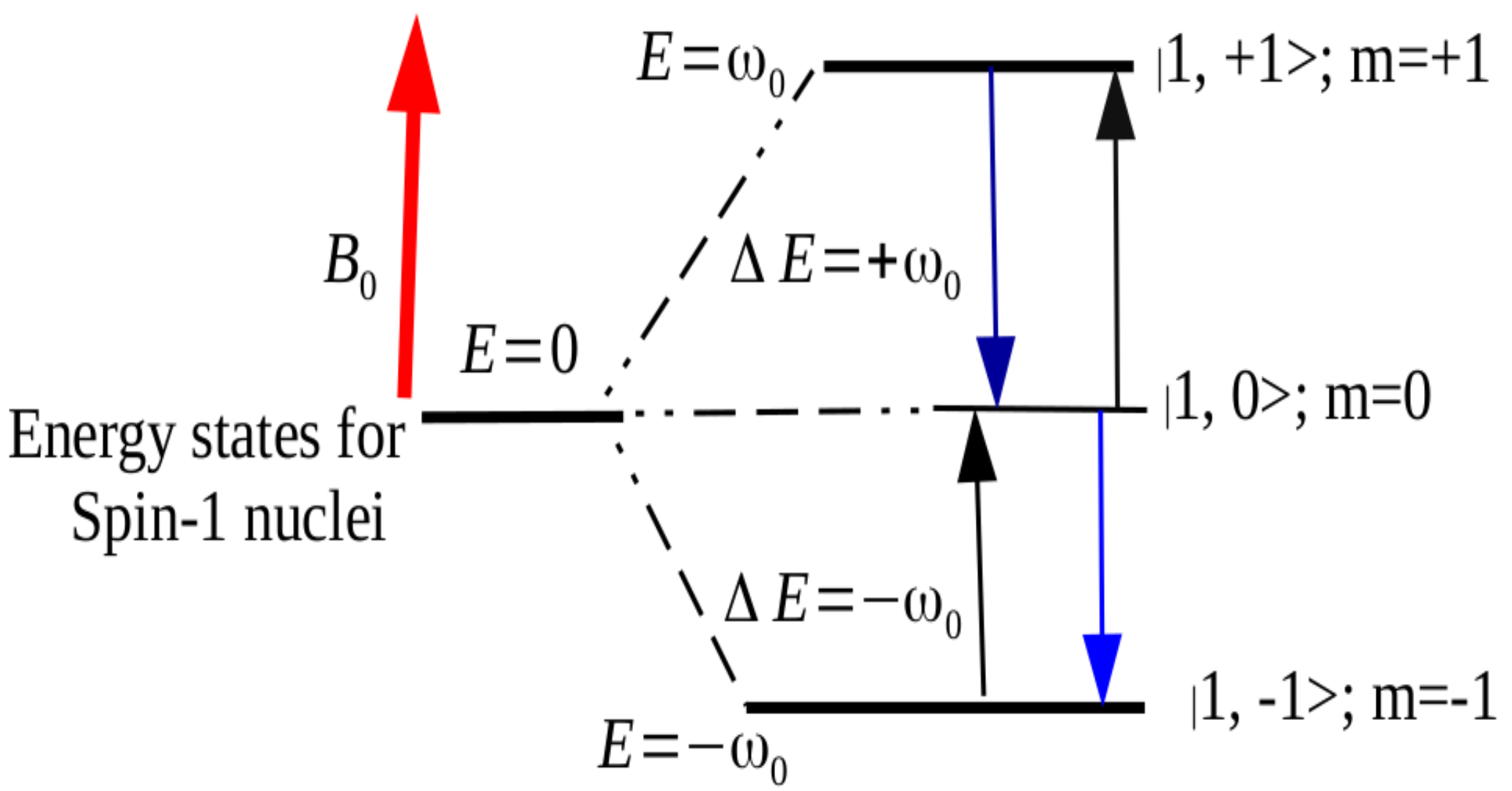
3.1. Spin-1 in a Static Magnetic Field
3.2. Spin in a Rotating Magnetic Field
4. Dynamics of the Spin-One System
5. Properties of Work Distribution
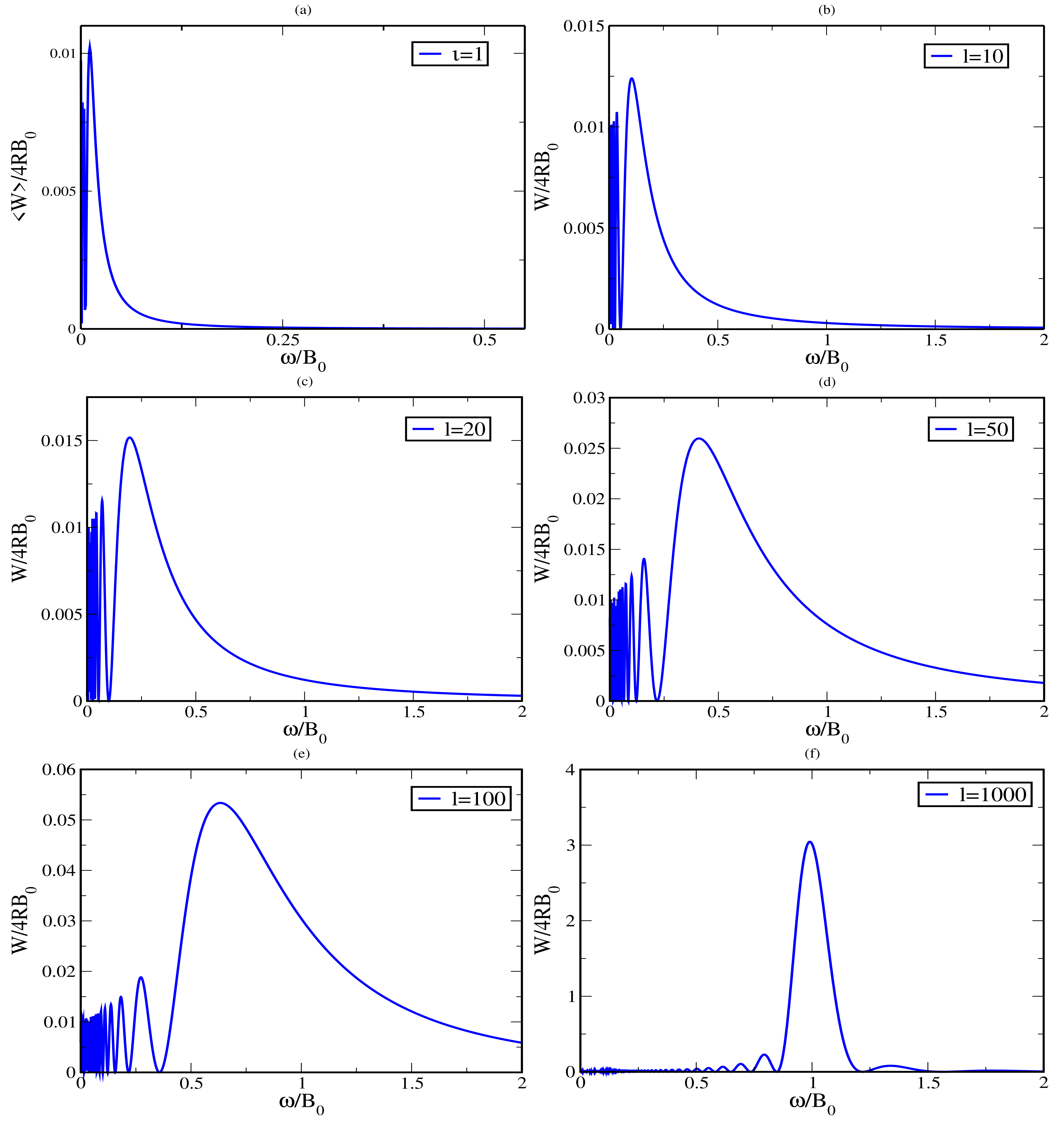
5.1. The Work Distribution
5.2. The Average Work
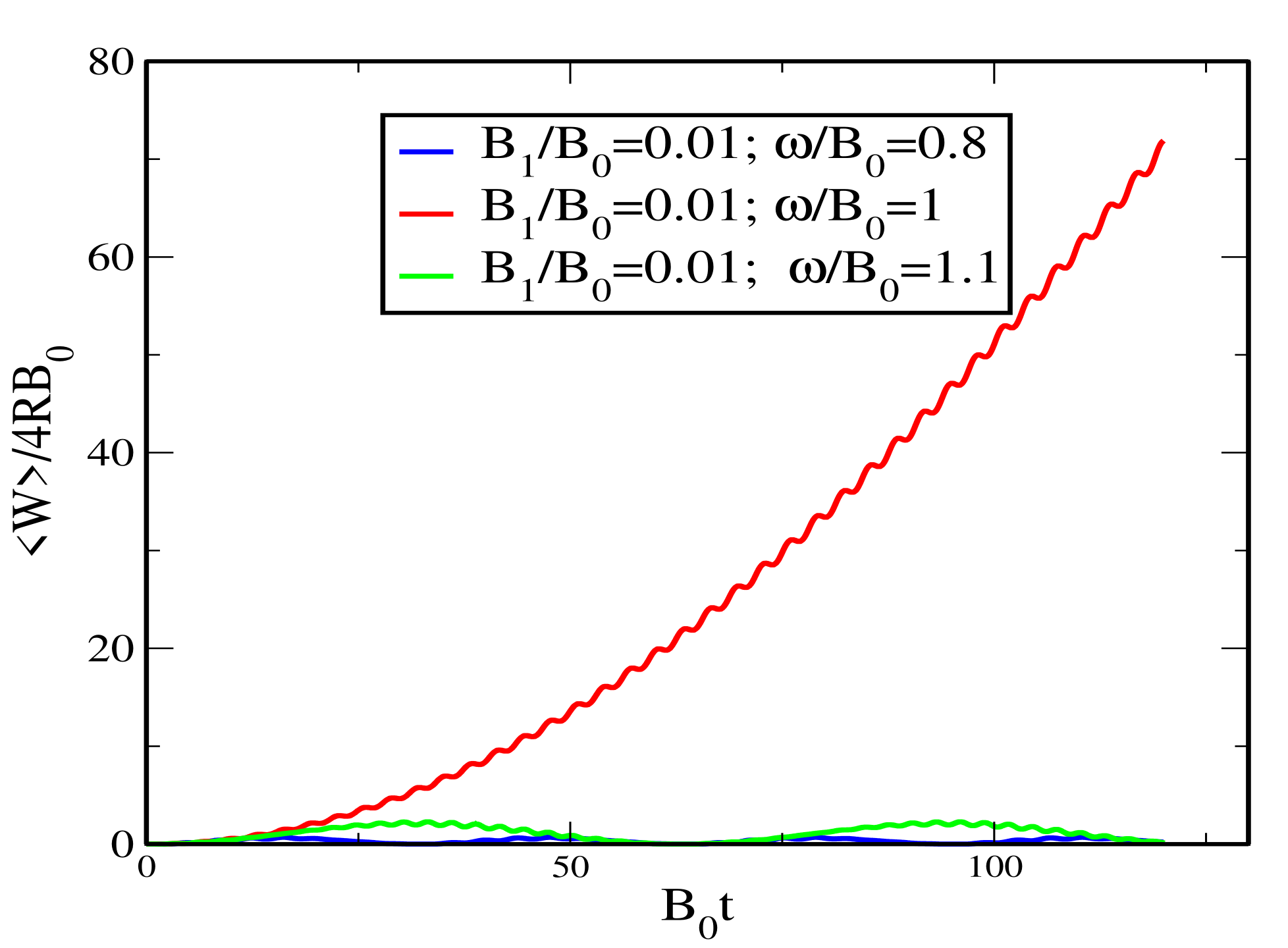
5.3. The Average Work as a Function of Time
6. Characteristic Function and Distribution of Work
7. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Majewski, W.A. On quantum statistical mechanics: A study guide. Adv. Math. Phys. 2017, 2017, 9343717. [Google Scholar] [CrossRef]
- Trotzky, S.; Chen, Y.A.; Flesch, A.; McCulloch, I.P.; Schollwöck, U.; Eisert, J.; Bloch, I. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 2012, 8, 325–330. [Google Scholar] [CrossRef]
- Rousseau, R.; Marx, D. The role of quantum and thermal fluctuations upon properties of lithium clusters. J. Chem. Phys. 1999, 111, 5091–5101. [Google Scholar] [CrossRef]
- Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. [Google Scholar] [CrossRef]
- Miller, H.J.; Anders, J. Time-reversal symmetric work distributions for closed quantum dynamics in the histories framework. New J. Phys. 2017, 19, 062001. [Google Scholar] [CrossRef]
- Gemmer, J.; Michel, M.; Mahler, G. Quantum Thermodynamics: Emergence of Thermodynamic Behavior within Composite Quantum Systems; Springer: Berlin/Heidelberg, Germany, 2009; Volume 784. [Google Scholar]
- Hubisz, J.L. Books on Thermodynamics: Reviews by the Book Review Editor. Phys. Teach. 2011, 49, 192. [Google Scholar] [CrossRef]
- Chou, T.; Mallick, K.; Zia, R. Non-equilibrium statistical mechanics: From a paradigmatic model to biological transport. Rep. Prog. Phys. 2011, 74, 116601. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics. Am. J. Phys. 1998, 66, 164–167. [Google Scholar] [CrossRef]
- Demirel, Y. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665. [Google Scholar] [CrossRef]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- An, S.; Zhang, J.N.; Um, M.; Lv, D.; Lu, Y.; Zhang, J.; Yin, Z.Q.; Quan, H.; Kim, K. Experimental test of the quantum Jarzynski equality with a trapped-ion system. Nat. Phys. 2015, 11, 193–199. [Google Scholar] [CrossRef]
- Soare, A.; Ball, H.; Hayes, D.; Sastrawan, J.; Jarratt, M.; McLoughlin, J.; Zhen, X.; Green, T.; Biercuk, M. Experimental noise filtering by quantum control. Nat. Phys. 2014, 10, 825–829. [Google Scholar] [CrossRef]
- Talkner, P.; Lutz, E.; Hänggi, P. Fluctuation theorems: Work is not an observable. Phys. Rev. E 2007, 75, 050102. [Google Scholar] [CrossRef]
- Kirkpatrick, T.; Dorfman, J.; Sengers, J. Work, work fluctuations, and the work distribution in a thermal nonequilibrium steady state. Phys. Rev. E 2016, 94, 052128. [Google Scholar] [CrossRef]
- Ribeiro, W.L.; Landi, G.T.; Semião, F.L. Quantum thermodynamics and work fluctuations with applications to magnetic resonance. Am. J. Phys. 2016, 84, 948–957. [Google Scholar] [CrossRef]
- Jarzynski, C. Equilibrium free-energy differences from nonequilibrium measurements: A master-equation approach. Phys. Rev. E 1997, 56, 5018. [Google Scholar] [CrossRef]
- Bryan, G. Elementary principles in statistical mechanics. Nature 1902, 66, 291–292. [Google Scholar] [CrossRef]
- Ross, S.M. A First Course in Probability; Technical report; Pearson: New York, NY, USA, 1976. [Google Scholar]
- Levitt, M.H. Spin Dynamics: Basics of Nuclear Magnetic Resonance; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wexler, A.D.; Woisetschläger, J.; Reiter, U.; Reiter, G.; Fuchsjäger, M.; Fuchs, E.C.; Brecker, L. Nuclear Magnetic Relaxation Mapping of Spin Relaxation in Electrically Stressed Glycerol. ACS Omega 2020, 5, 22057–22070. [Google Scholar] [CrossRef]
- Bradt, H.; Peters, B. Abundance of lithium, beryllium, boron, and other light nuclei in the primary cosmic radiation and the problem of cosmic-ray origin. Phys. Rev. 1950, 80, 943. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmud, M.; Bekele, M.; Bassie, Y. Thermal and Quantum Fluctuation Effects on Non-Spherical Nuclei: The Case of Spin-1 System. Condens. Matter 2022, 7, 62. https://doi.org/10.3390/condmat7040062
Mahmud M, Bekele M, Bassie Y. Thermal and Quantum Fluctuation Effects on Non-Spherical Nuclei: The Case of Spin-1 System. Condensed Matter. 2022; 7(4):62. https://doi.org/10.3390/condmat7040062
Chicago/Turabian StyleMahmud, Mohammed, Mulugeta Bekele, and Yigermal Bassie. 2022. "Thermal and Quantum Fluctuation Effects on Non-Spherical Nuclei: The Case of Spin-1 System" Condensed Matter 7, no. 4: 62. https://doi.org/10.3390/condmat7040062
APA StyleMahmud, M., Bekele, M., & Bassie, Y. (2022). Thermal and Quantum Fluctuation Effects on Non-Spherical Nuclei: The Case of Spin-1 System. Condensed Matter, 7(4), 62. https://doi.org/10.3390/condmat7040062






