Possible Benefits from Phonon/Spin-Wave Induced Gaps below or above EF for Superconductivity in High-TC Cuprates
Abstract
1. Introduction
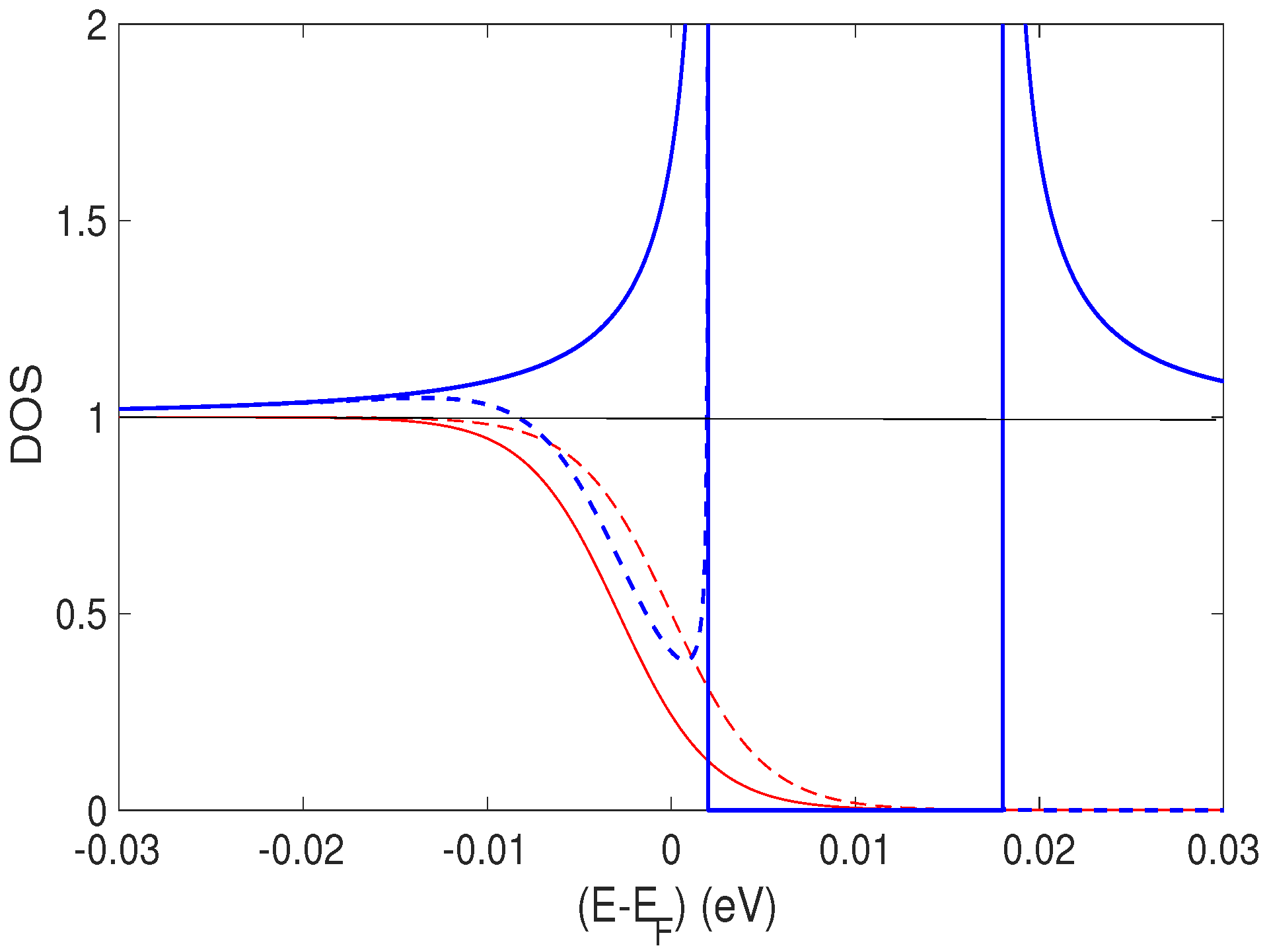
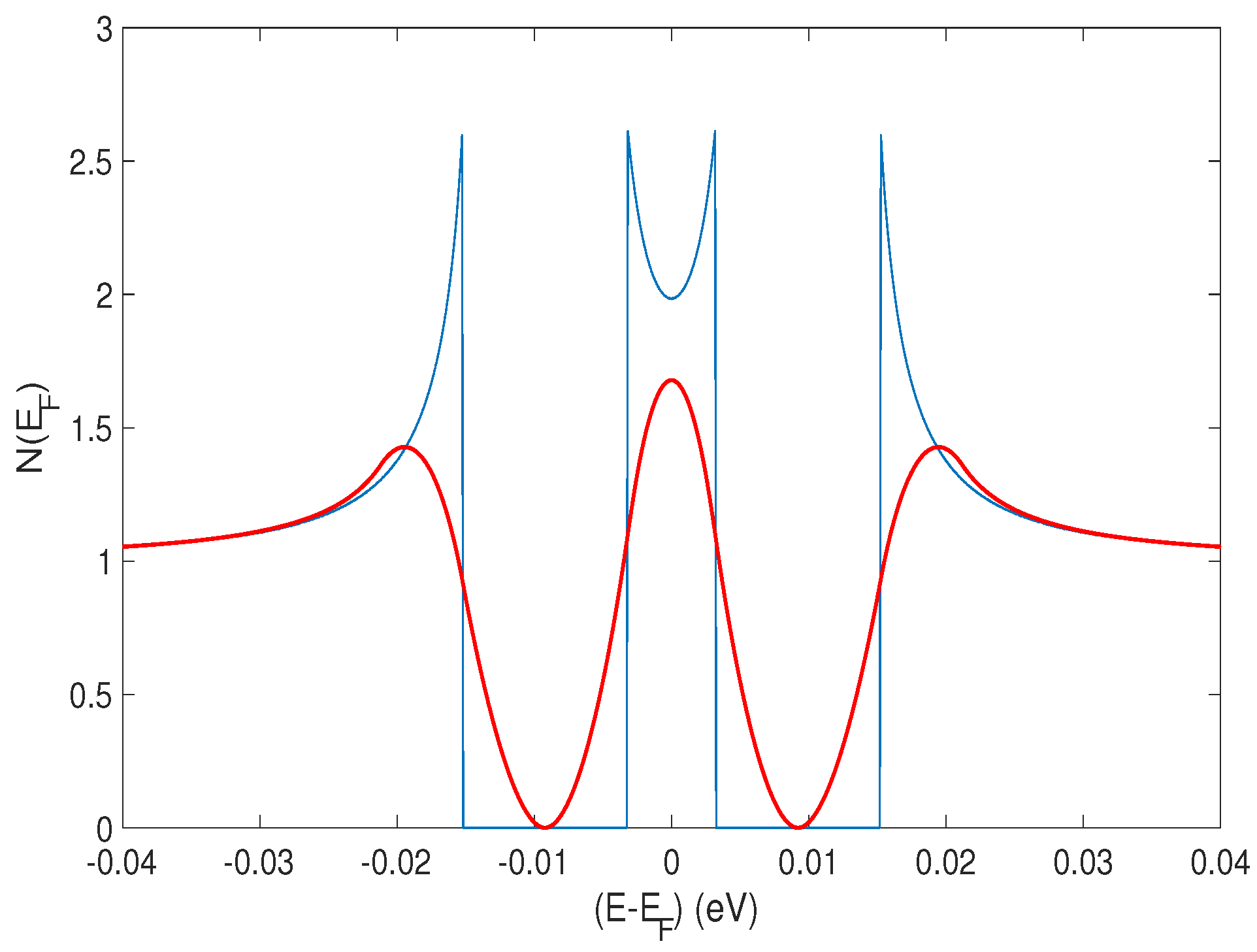
2. Theory
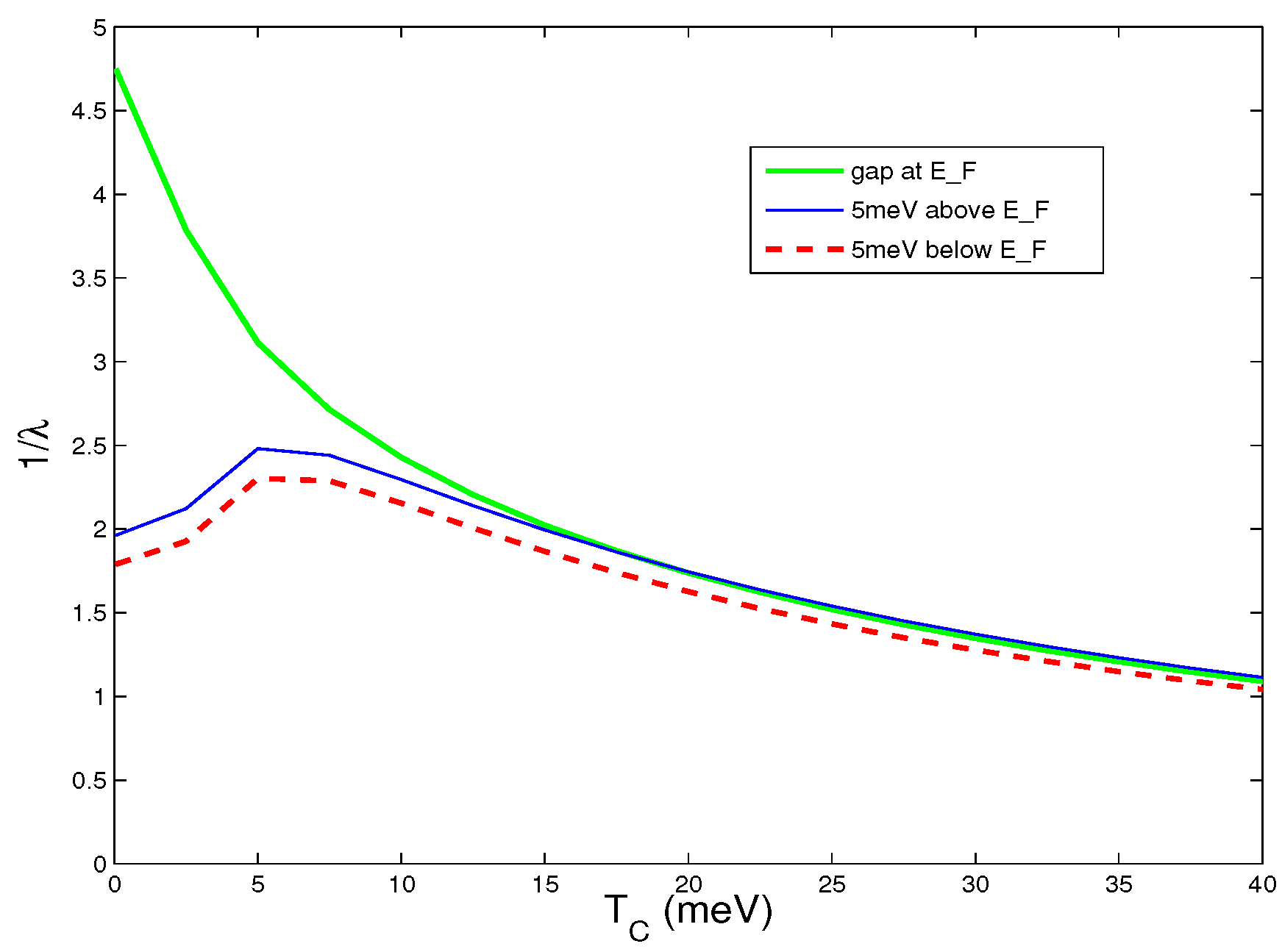
3. Results
4. Possible Spin-Waves
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- McMillan, W.L. Transition Temperature of Strong-Coupled Superconductors. Phys. Rev. 1968, 167, 331. [Google Scholar] [CrossRef]
- Gaspari, G.D.; Gyorffy, B.L. Electron-Phonon Interactions, d Resonances, and Superconductivity in Transition Metals. Phys. Rev. Lett. 1972, 28, 801. [Google Scholar] [CrossRef]
- Papaconstantopoulos, D.A.; Boyer, L.L.; Klein, B.M.; Williams, A.R.; Moruzzi, V.L.; Janak, J.F. Calculations of the superconducting properties of 32 metals with Z ≤ 49. Phys. Rev. B 1977, 15, 4221. [Google Scholar] [CrossRef]
- Klein, B.M.; Papaconstantopoulos, D.A. Electron-Phonon Interaction and Superconductivity in Transition Metals and Transition-Metal Carbides. Phys. Rev. Lett. 1974, 32, 1193. [Google Scholar] [CrossRef]
- Arbman, G.; Jarlborg, T. Trend studies of A15 compounds by self-consistent band calculations. Solid State Commun. 1978, 26, 857. [Google Scholar] [CrossRef]
- Jarlborg, T.; Manuel, A.A.; Peter, M. Experimental and theoretical determination of the Fermi surface of V3Si. Phys. Rev. B 1983, 27, 4210. [Google Scholar] [CrossRef]
- Li, Y.; Hao, J.; Liu, H.; Li, Y.; Ma, Y. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 2014, 140, 174712. [Google Scholar] [CrossRef]
- Drozov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73. [Google Scholar] [CrossRef]
- Pickett, W.E. Electronic structure of the high-temperature oxide superconductors. Rev. Mod. Phys. B 1989, 61, 433. [Google Scholar] [CrossRef]
- Ekimov, E.A.; Sidorov, V.A.; Bauer, E.D.; Mel’nik, N.N.; Curro, N.J.; Thompson, J.D.; Stishov, S.M. Superconductivity in diamond. Nature 2004, 428, 542. [Google Scholar] [CrossRef]
- Jarlborg, T. Theoretical aspects of simple and nested Fermi surfaces for superconductivity in doped semiconductors and high-TC cuprates. Solid State Commun. 2014, 181, 15–19. [Google Scholar] [CrossRef][Green Version]
- Jarlborg, T. Effects of spin-phonon interaction within the CuO plane of high-TC superconductors. Physica C 2007, 454, 5–14. [Google Scholar] [CrossRef]
- Perali, A.; Bianconi, A.; Lanzara, A.; Saini, N.L. The gap amplification at a shape resonance in a superlattice of quantum stripes: A mechanism for high Tc. Solid State Commun. 1996, 100, 181–186. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of a striped phase at the atomic limit. Phys. C Supercond. 1998, 296, 269–280. [Google Scholar] [CrossRef]
- Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes. Supercond. Sci. Technol. 2012, 25, 124002. [Google Scholar] [CrossRef]
- Kittel, C. Schematic figures of phonon displacements on individual atoms can be found in C. Kittel. In Introduction to Solid State Physics, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 1971. [Google Scholar]
- Ziman, J.M. Principles of the Theory of Solids; Cambridge University Press: New York, NY, USA, 1971. [Google Scholar]
- Jarlborg, T. A model of the T-dependent pseudogap and its competition with superconductivity in copper oxides. Solid State Commun. 2011, 151, 639. [Google Scholar] [CrossRef][Green Version]
- Berk, N.F.; Schrieffer, J.R. Effect of Ferromagnetic Spin Correlations on Superconductivity. Phys. Rev. Lett. 1966, 17, 433. [Google Scholar] [CrossRef]
- Fay, D.; Appel, J. Coexistence of p-state superconductivity and itinerant ferromagnetism. Phys. Rev. B 1980, 22, 3173. [Google Scholar] [CrossRef]
- Jarlborg, T. Q-dependent stoner factors and reformulated spin-fluctuation enhancements: V and Pd. Solid State Commun. 1986, 57, 683. [Google Scholar] [CrossRef]
- Monthoux, P.; Pines, D.; Lonzarich, G. Superconductivity without phonons. Nature 2007, 450, 1177. [Google Scholar] [CrossRef] [PubMed]
- Jarlborg, T. Ferromagnetic and antiferromagnetic spin fluctuations and superconductivity in the hcp-phase of Fe. Phys. Lett. A 2002, 300, 518–523. [Google Scholar] [CrossRef]
- Balseiro, C.A.; Falicov, L.M. Superconductivity and charge-density waves. Phys. Rev. B 1979, 20, 4457. [Google Scholar] [CrossRef]
- Markiewicz, R.S.; Kusco, C.; Kidambi, V. Pinned Balseiro-Falicov Model of Tunneling and Photoemission in the Cuprates. Phys. Rev. B 1999, 60, 627. [Google Scholar] [CrossRef]
- Damascelli, A.; Shen, Z.-X.; Hussain, Z. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 2003, 75, 473. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Jarlborg, T.; Bianconi, A.; Valletta, A. Room temperature superconductivity dome at a Fano resonance in superlattices of wires. Europhys. Lett. 2021, 134, 17001. [Google Scholar] [CrossRef]
- Jarlborg, T. Mechanisms for higher TC in copper oxide superconductors: Ideas from band calculations. Appl. Phys. Lett. 2009, 94, 212503. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates. Condens. Matter 2019, 4, 15. [Google Scholar] [CrossRef]
- McKenzie, R.H.; Wilkins, J.W. Effect of Lattice Zero-Point Motion on Electronic Properties of the Peierls-Frohlich State. Phys. Rev. Lett. 1992, 69, 1085. [Google Scholar] [CrossRef]
- Hedin, L.; Rosengren, A. On temperature broadening in X-ray spectra of metals. J. Phys. F Metal Phys. 1977, 7, 1339. [Google Scholar] [CrossRef]
- Dugdale, S.; Jarlborg, T. Thermal disorder versus correlation in Compton profiles from alkali metals. Solid State Commun. 1998, 105, 283. [Google Scholar] [CrossRef]
- Jarlborg, T. ϵ-FeSi: A material sensitive to thermal disorder. Phys. Lett. A 1997, 236, 143. [Google Scholar] [CrossRef]
- Jarlborg, T. Role of thermal disorder for magnetism and the α-γ transition in cerium: Results from density-functional theory. Phys. Rev. B 2014, 89, 184426. [Google Scholar] [CrossRef]
- Jarlborg, T.; Chudzinski, P.; Giamarchi, T. Effects of thermal and spin fluctuations on the band structure of purple bronze Li2Mo12O34. Phys. Rev. B 2012, 85, 235108. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Breakdown of the Migdal approximation at Lifshitz transitions with giant zero-point motion in the H3S superconductor. Sci. Rep. 2016, 6, 24816. [Google Scholar] [CrossRef]
- Fischer, Ø.; Kugler, M.; Maggio-Aprile, I.; Berthod, C.; Renner, C. Scanning tunneling spectroscopy of high-temperature superconductors. Rev. Mod. Phys. 2007, 79, 353. [Google Scholar] [CrossRef]
- Stoner, E.C. Ferromagnetism. Rep. Prog. Phys. 1948, 11, 43. [Google Scholar]
- Janak, J.F. Uniform susceptibilities of metallic elements. Phys. Rev. B 1977, 16, 255. [Google Scholar] [CrossRef]
- Jarlborg, T.; Freeman, A.J. Magnetism and superconductivity in C15 compounds from self-consistent band calculations. Phys. Rev. B 1980, 22, 2232. [Google Scholar] [CrossRef]
- Barbiellini, B.; Jarlborg, T. Importance of Local Band Effects for Ferromagnetism in Hole-Doped La2CuO4 Cuprate Superconductors. Phys. Rev. Lett. 2008, 101, 157002. [Google Scholar] [CrossRef]
- Sonier, J.E. High-field muSR studies of superconducting and magnetic correlations in cuprates above Tc. J. Phys. Cond. Matt. 2010, 22, 203202. [Google Scholar] [CrossRef]
- Jarlborg, T. Supercell Band Calculations and Correlation for High-TC Copper Oxide Superconductors. Adv. Condens. Matter Phys. 2009, 2010, 912067. [Google Scholar]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Nokelainen, J.; Lane, C.; Markiewicz, R.S.; Barbiellini, B.; Pulkkinen, A.; Singh, B.; Sun, J.; Pussi, K.; Bansil, A. Ab initio description of the Bi2Sr2CaCu2O8+δ electronic structure. Phys. Rev. B 2020, 101, 214523. [Google Scholar] [CrossRef]
- Tranquada, J.M.; Woo, H.; Perring, T.G.; Goka, H.; Gu, G.D.; Xu, G.; Fujita, M.; Yamada, K. Quantum magnetic excitations from stripes in copper oxide superconductors. Nature 2004, 429, 534. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarlborg, T. Possible Benefits from Phonon/Spin-Wave Induced Gaps below or above EF for Superconductivity in High-TC Cuprates. Condens. Matter 2022, 7, 41. https://doi.org/10.3390/condmat7020041
Jarlborg T. Possible Benefits from Phonon/Spin-Wave Induced Gaps below or above EF for Superconductivity in High-TC Cuprates. Condensed Matter. 2022; 7(2):41. https://doi.org/10.3390/condmat7020041
Chicago/Turabian StyleJarlborg, Thomas. 2022. "Possible Benefits from Phonon/Spin-Wave Induced Gaps below or above EF for Superconductivity in High-TC Cuprates" Condensed Matter 7, no. 2: 41. https://doi.org/10.3390/condmat7020041
APA StyleJarlborg, T. (2022). Possible Benefits from Phonon/Spin-Wave Induced Gaps below or above EF for Superconductivity in High-TC Cuprates. Condensed Matter, 7(2), 41. https://doi.org/10.3390/condmat7020041





