Absence of Spin Frustration in the Kagomé Layers of Cu²⁺ Ions in Volborthite Cu₃V₂O₇(OH)₂·2H₂O and Observation of the Suppression and Re-Entrance of Specific Heat Anomalies in Volborthite under an External Magnetic Field

Abstract

We determined the spin exchanges between the Cu²⁺ ions in the kagomé layers of volborthite, Cu₃V₂O₇(OH)₂·2H₂O, by performing the energy-mapping analysis based on DFT+U calculations, to find that the kagomé layers of Cu²⁺ ions are hardly spin-frustrated, and the magnetic properties of volborthite below ~75 K should be described by very weakly interacting antiferromagnetic uniform chains made up of effective S = 1/2 pseudospin units. This conclusion was verified by synthesizing single crystals of not only Cu₃V₂O₇(OH)₂·2H₂O but also its deuterated analogue Cu₃V₂O₇(OD)₂·2D₂O and then by investigating their magnetic susceptibilities and specific heats. Each kagomé layer consists of intertwined two-leg spin ladders with rungs of linear spin trimers. With the latter acting as S = 1/2 pseudospin units, each two-leg spin ladder behaves as a chain of S = 1/2 pseudospins. Adjacent two-leg spin ladders in each kagomé layer interact very weakly, so it is required that all nearest-neighbor spin exchange paths of every two-leg spin ladder remain antiferromagnetically coupled in all spin ladder arrangements of a kagomé layer. This constraint imposes three sets of entropy spectra with which each kagomé layer can exchange energy with the surrounding on lowering the temperature below ~1.5 K and on raising the external magnetic field B. We discovered that the specific heat anomalies of volborthite observed below ~1.5 K at B = 0 are suppressed by raising the magnetic field B to ~4.2 T, that a new specific heat anomaly occurs when B is increased above ~5.5 T, and that the imposed three sets of entropy spectra are responsible for the field-dependence of the specific heat anomalies.

1. Introduction

Properties of a magnetic material are described by a spin Hamiltonian, defined in terms of a few spin exchange paths between magnetic ions. The repeat pattern of strong spin exchange paths forms a spin lattice, with which the spin Hamiltonian generates the energy spectrum to be utitilized in describing the magnetic properties. Consequently, the use of a correct spin lattice is paramount because the nature of the energy spectrum generated by a spin Hamiltonian depends on the nature of the spin lattice chosen. Antiferromagnets possessing a kagomé arrangement of transition-metal magnetic ions M are often believed to be spin-frustrated, hence suppressing a long-range magnetic order, so they are prime candidates that can give rise to exotic magnetic ground states [1,2]. However, spin frustration is not guaranteed per se by, for example, a trigonal, a kagomé or a pyrochlore structural arrangement of magnetic transition-metal ions M. This is so because they interact strongly with the surrounding main-group ligands L to form ML_n polyhedra, thereby splitting its d-states. What is crucial for geometrical spin frustration is not the geometrical pattern imposed by the arrangement of magnetic ions M, but rather that of the spin exchanges these ions generate with their neighboring ions. The direction-dependence of spin exchanges between magnetic ions M is determined by their magnetic orbitals, namely, the singly occupied d-states of their ML_n polyhedra [3,4]. The d-states have the d-orbitals of M combined out of phase with the p-orbitals of the ligands L, so they are highly anisotropic in shape. Consequently, even if the magnetic ions form a kagomé arrangement, the spin exchanges between magnetic ions do not necessarily generate the same pattern. The anisotropy of spin exchange is most strongly manifested for a magnetic ion possessing only one magnetic orbital (e.g., S = 1/2 ions Cu²⁺ and Ti³⁺), and least strongly for a magnetic ion with five magnetic orbitals (e.g., S = 5/2 ions Mn²⁺ and Fe³⁺).

Volborthite, Cu₃V₂O₇(OH)₂·2H₂O, consisting of Cu²⁺ (d⁹, S = 1/2) ions in kagomé arrangement, has received much attention over the past decade [5,6,7,8,9,10,11], largely because it is believed to be spin-frustrated [5,11] The kagomé layers of Cu²⁺ ions (see Figure 1) are slightly distorted from an ideal kagomé shape with two different crystallographic sites for Cu²⁺ in a ratio 2:1. Below room temperature, each Cu²⁺ ion forms an axially elongated CuO₆ octahedron, so that, with the local z-axis taken along the elongated Cu-O bonds, the magnetic orbital of each CuO₆ octahedron is the x²−y² state contained in the CuO₄ equatorial plane, which is quite anisotropic in shape. In volborthite, the kagomé layers of composition Cu₃O₆(OH)₂ parallel to the ab-plane are pillared by pyrovanadates V₂O₇. The voids between the layers provide space for crystal water molecules. Below room temperature, volborthite undergoes two structural phase transitions, one at ~292 K from a C2/c phase to a I2/a phase, and the other at about ~155 K from the I2/a phase to a P2₁/c phase [6]. The latter structural phase transition generates two slightly different kagomé layers, which are slightly different in structure. Below 1.5 K, volborthite exhibits magnetic order, indicated by two anomalies in the magnetic specific heat [10].

On the basis of their DFT+U calculations, Janson et al. [11] described the magnetic properties of volborthite using a trigonal spin lattice made up of pseudo S = 1/2 units, i.e., linear spin trimers in which adjacent Cu²⁺ ions are strongly coupled antiferromagnetically. However, with this spin lattice model, it is difficult to explain why volborthite undergoes a magnetic ordering below 1.5 K [10]. Furthermore, the magnetic susceptibility Janson et al. calculated for volborthite by their exact diagonalization method for the spin Hamiltonian of the trigonal lattice show a spin gap below the susceptibility maximum at ~17 K. The latter is in sharp contrast to the experimental observation [5], which reveals that the magnetic susceptibility remains rather high as the temperature is decreased toward 0 K [5]. Thus, results of Janson et al.’s exact diagonalization based on their trigonal spin lattice model are inappropriate for understanding the physics of volborthite below ~17 K. The magnetic entropy removed by the long-range order is small compared to Rln2, as is typically found for low-dimensional short-range ordered (SRO) magnetic systems, e.g., for S = 1/2 antiferromagnetic uniform Heisenberg (AUH) chains. Then, one might speculate if the magnetic ordering of volborthite observed below 1.5 K is associated with a magnetic ordering of such S = 1/2 AUH chains, although it has been believed that volborthite is spin-frustrated [5,11].

To explore the magnetic order below 1.5 K, especially its dependence on the magnetic field, as well as the origin of the apparent finite susceptibility as T→0 K, we re-analyzed the spin lattice of volborthite by performing an energy-mapping analysis based on DFT+U calculations [3,4] to find that the magnetic properties of volborthite below ~75 K should be described by two-leg spin ladders with rungs of S = 1/2 pseudospin units rather than by a trigonal lattice of S = 1/2 pseudospin units, as proposed by Janson et al. [11]. We verified this conclusion by acquiring new magnetic susceptibility data and re-analyzing reported magnetization data of volborthite to show that the kagomé layer of Cu²⁺ ions is hardly spin-frustrated, and the low-temperature magnetic properties of volborthite should be described by an AUH chain composed of S = 1/2 pseudospin units. We characterized the magnetic phase transitions below 1.5 K by carrying out specific heat measurements for Cu₃V₂O₇(OH)₂·2H₂O and its deuterated analogue, Cu₃V₂O₇(OD)₂·2D₂O, under a magnetic field B = 0–9 T. Our work shows that the magnetic ordering of volborthite below 1.5 K is suppressed by field B > ~4.5 T, while a new magnetic ordering takes place when B > ~5.5 T, and that these field-dependent behaviors of the magnetic ordering originate from the three sets of magnetic entropy spectra of each kagomé layer of Cu²⁺ ions, created by constrained interactions between adjacent two-leg spin ladders.

2. Experimental and Calculations

To determine the spin exchanges of the I2/a and P21/c phases of volborthite, we carried out DFT+U calculations, employing the Vienna ab Initio Simulation Package (VASP) [12,13] using the projector augmented wave (PAW) [14,15] method and the PBE [16] exchange-correlation functional. The electron correlation associated with the 3d states of Cu was taken into consideration by DFT+U calculations, i.e., by performing DFT calculation with an effective on-site repulsion U_eff = U − J = 4 and 5 eV added on the magnetic ions Cu²⁺ [17].

Single crystals of volborthite were grown using hydrothermal techniques, as described in the literature [6]. Deuterated samples of volborthite were prepared by replacing light by heavy water (isotope enrichment 99.5%). The magnetic susceptibilities were measured at constant field as a function of the temperature in a Magnetic Property Measurement System SQUID magnetometer (MPMS-XL7, Quantum Design, San Diego, CA, USA). The specific heats of a collection of oriented crystals were determined using the relaxation method of a 3-He Physical Property Measurement System (PPMS, Quantum Design, San Diego, CA, USA). In order to construct a lattice reference needed to evaluate the magnetic contribution to the specific heat of volborthite, we prepared a polycrystalline sample of the diamagnetic mineral martyite with composition Zn₃V₂O₇(OH)₂·2H₂O from an aqueous solution of NH₄VO₃ and zinc acetate, Zn(CH₃CO₂)₂, following a recipe reported in the literature [18].

3. Results

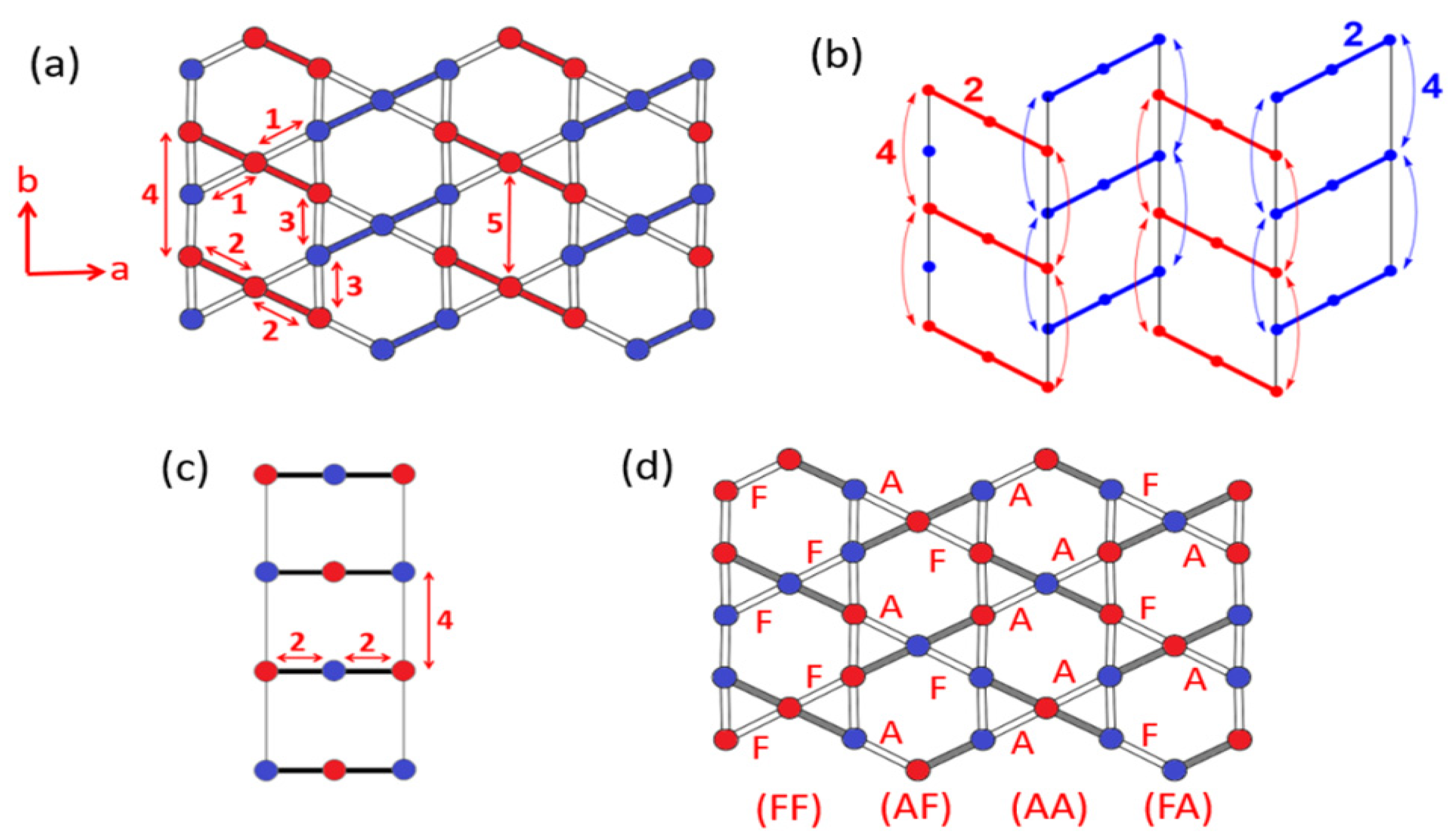
3.1. Spin Exchanges and Spin Lattice of Volborthite

We determine the spin exchanges J₁–J₅ defined in Figure 1a by performing the energy-mapping analyses [3,4] based on DFT+U calculations (for details of calculations, see the Supplemental Material). Below room temperature down to ~155 K, volborthite has a crystal structure with two equivalent kagomé layers in the unit cell (space group I2/a) and below 155 K a structure with two slightly non-equivalent kagomé layers of Cu²⁺ ions (space group P2₁/a) [5,8]. The spin exchanges of the two phases are very similar, as summarized in

Table 1. Values (in K) of the spin exchanges J₁–J₅ calculated for the I2/a and P2₁/a phases of volborthite obtained by DFT+U calculations.

I2/a Phase a		P21/a Phase a		P21/a Phase b
		Layer 1	Layer 2	Layer 1	Layer 2
J1/J2	0.010	−0.001	−0.025	−0.15	−0.11
J3/J2	0.025	0.031	0.031	−0.34	−0.32
J4/J2	0.145	0.141	0.135	0.17	0.15
J5/J2	0.014	0.014	0.013	-	-
J2	542 K	550 K	582 K	193 K	205 K

^a Present work with U_eff = 4 eV, ^b Janson et al. (ref. [11]) with U_eff = 8.5 eV.

, where only the values obtained with U_eff = 4 eV are listed. Those calculated with U_eff = 5 eV are given in the Supplemental Material. Janson et al. [11] carried out DFT+U calculations using U_eff = 8.5, 9.5 and 10.5 eV to determine the spin exchanges of the P2₁/a structure by fitting the electronic band structure in terms of a tight binding approximation. In the following, we first discuss the spin lattice of volborthite suggested by the spin exchanges we obtained. Subsequently, we show that the same picture is obtained from those of Janson et al., despite that their spin exchanges are considerably smaller than ours in the strengths of AFM character due to their use of very large U_eff values.

As can be seen from Table 1, the strongest exchange J₂ is AFM and forms isolated linear trimers (Figure 1a). The second strongest spin exchange J₄ is also AFM but is weaker than J₂ by nearly an order of magnitude. All other spin exchanges are weaker than J₂ by more than an order of magnitude. Since J₂ is much stronger than other spin exchanges, each linear trimer at T << J₂ constitutes a pseudospin S = 1/2 unit and such units form a triangular lattice, as already pointed out by Janson et al. [11] However, we note that the linear trimers interact through the AFM exchange J₄ to form two-leg spin ladders with the linear trimers as rungs (Figure 1b). This feature is hidden in a kagomé layer because nearest-neighbor spin ladders are geometrically entangled with their superposed legs.

The two-leg spin ladder model as the spin lattice of volborthite described above is also supported by Janson et al.’s spin exchanges (Table 1), although their spin exchanges differ considerably from ours in magnitude. In general, a spin exchange J between two magnetic ions located at sites i and j can be written as the sum of the FM and AFM components (J_F and J_AF, respectively), namely, J = J_F + J_AF [3,4,19]. With the magnetic orbitals describing the spin sites i and j as ψ_i and ψ_j, respectively, the overlap density ρ_ij = ψ_iψ_j gives rise to the exchange repulsion K_ij, while the overlap integral <ψ_i|ψ_j> leads to an energy split Δe between the two states described by the magnetic orbitals. Then, J_F and J_AF are written as

$${\mathrm{J}}_{\mathrm{F}}=-{\mathrm{K}}_{\mathrm{i}\mathrm{j}}, \mathrm{and} {\mathrm{J}}_{\mathrm{AF}}=\frac{{(\Delta \mathrm{e})}^2}{{\mathrm{U}}_{\mathrm{eff}}}$$

(1)

Since the AFM component J_AF is inversely proportional to U_eff, using a large U_eff value in DFT+U calculations should make J value less AFM or even shift it to a FM spin exchange. This explains why the J₂ and J₄ values of Janson et al. are less strongly AFM than ours, and why their J₁ and J₃ values are more strongly FM than ours.

We now examine the interactions between adjacent two-leg spin ladders, under the constraint that the spin exchanges J₂ and J₄ forming the two-leg spin ladders are much stronger than J₃ and J₁, which provide interactions between spin ladders. The latter requires that, in all possible spin ladder arrangements, all J₂ and J₄ exchange paths of each two-leg spin ladder must remain antiferromagnetically coupled (Figure 1d). In every intertwined leg, each J₂ leg has two consecutive J₃ paths. Since each J₂ leg is antiferromagnetically coupled, J₃ has no effect on the interaction between adjacent two-leg spin ladders, regardless of whether it is AFM or FM. Thus, adjacent two-leg spin ladders interact only through the very weak exchanges J₁ (Figure 1a). Note that J₁ is weakly AFM for the I2/a phase but is weakly FM for the P2₁/a phase in our calculations. This difference does not influence how the ordering between spin ladders in a kagomé layer is affected by J₁ (see below). Since J₁ is more than an order of magnitude weaker than J₄, the magnetic property of each kagomé layer at low temperatures (|J₁| < T << J₂) is primarily determined by those of the two-leg spin ladders with each linear trimer acting as an effective S = 1/2 pseudospin rung (Figure 1c). At sufficiently low temperatures where excitations within the rungs are negligible, the dominant AFM spin exchanges form two-leg spin ladders predicting that volborthite should be regarded primarily as a system of very weakly coupled S = 1/2 AUH chains. In the following, we first demonstrate that the magnetic properties of volborthite below ~75 K are well explained by the model of very weakly interacting S = 1/2 AUH chains.

3.2. Experimental Evidence for the Spin-Half AFM Uniform Heisenberg Chain Character

Figure 2 displays the magnetic susceptibilities of volborthite, which exhibits a broad peak at ~17 K and a finite susceptibility as T→0 K, characteristic of low-dimensional AFM SRO behavior. As implied by the results of the DFT+U calculations, the magnetic susceptibilities of volborthite between 3 and 75 K can indeed be very well fitted by those theoretically predicted for a S = 1/2 AUH chain according to

χ_mol(T) = χ_spin(J_C, g, T) + χ₀

(2)

where χ_spin(J_C, g, T) represents the magnetic susceptibility of the S = 1/2 AUH chain with nearest-neighbor (NN) spin exchange J_C (Figure 2a). For χ_spin(J_C, g, T), we used the Padé approximant of Quantum Monte Carlo (QMC) results for the S = 1/2 AUH chain [20]. The second term refers to the temperature-independent susceptibility χ₀ arising from the diamagnetism of the electrons in the closed shells (−175 × 10⁻⁶ cm³/mol per formula unit, FU) [21,22] and also from the van Vleck paramagnetic susceptibility due to excitations to the excited states of each Cu²⁺ ion (~100 × 10⁻⁶ cm³/mol per Cu atom) [23], leading to χ₀ = +125 × 10⁻⁶ cm³/mol per FU. Up to ~75 K, the experimental susceptibility is well reproduced by the susceptibility calculated for a S = 1/2 AUH chain with J_C = 27.8(5) K and g = 2.33 (the solid blue curve in Figure 2a). The fitted g-factor is found to be 2.33, which is at the higher end of the g-factor expected for Cu²⁺ ions [24]. The S = 1/2 AUH chain model readily explains the susceptibility maximum at T_max = 17 K as well as the finite susceptibility below T_max. The exchange J_C = 27.8(5) K agrees very well with the expected value J_C = T_max/0.64085 = 26 K. In addition, the ratio χ_spinT_max/g² = 0.0346 cm³K/mol concurs well with the value 0.0353 expected for the S = 1/2 AUH chain [20]. The difference between the experimental data and the chain susceptibility (green solid line in Figure 1) vanishes below ~75 K and gradually increases to higher temperatures. The susceptibilities above ~75 K without any constraints matches very well with the susceptibility of an isolated linear spin S = 1/2 trimer described by the spin Hamiltonian

$$H=J_{\mathrm{trim}}({\overrightarrow{S}}_1·{\overrightarrow{S}}_2+{\overrightarrow{S}}_2·{\overrightarrow{S}}_3)$$

(3)

where ${\overrightarrow{S}}_i$ (i = 1, 2, 3) represent the three spin sites. Replacing χ_spin(J_C, g, T) in Equation (2) with the susceptibility of a spin S = 1/2 trimer given e.g., by Boukhari et al. [25], the susceptibility data above ~75 K can be well fitted without further constraints. The trimer spin exchange amounts to 197(2) K, indicating a ratio J_C/J_trim = 0.14, in good agreement with the ratio J₄/J₂ obtained from our DFT+U calculation (see Table 1), suggesting that the spin trimers should be identified as the rungs of the two-leg spin ladders running along the crystallographic b axis.

Another characteristic feature of the magnetic properties of volborthite is the low-temperature 1/3 magnetization plateau extending over a wide magnetic field range, displayed in Figure 2b [8,9]. Note that we multiplied the published literature data by a factor of three to obtain the magnetization per one FU of volborthite (3 Cu atoms); the experimental data are well reproduced by the magnetization predicted for the S = 1/2 AUH chain with J_C = 27.5 K. The theoretical magnetization was obtained by Quantum Monte Carlo Calculations (QMC), employing the path integral method of the loop code incorporated within the ALPS project [26,27]. To ensure a low statistical error, these simulations included 250 spins and 1.5 × 10⁵ Monte Carlo steps for the initial, as well as the subsequent, thermalization.

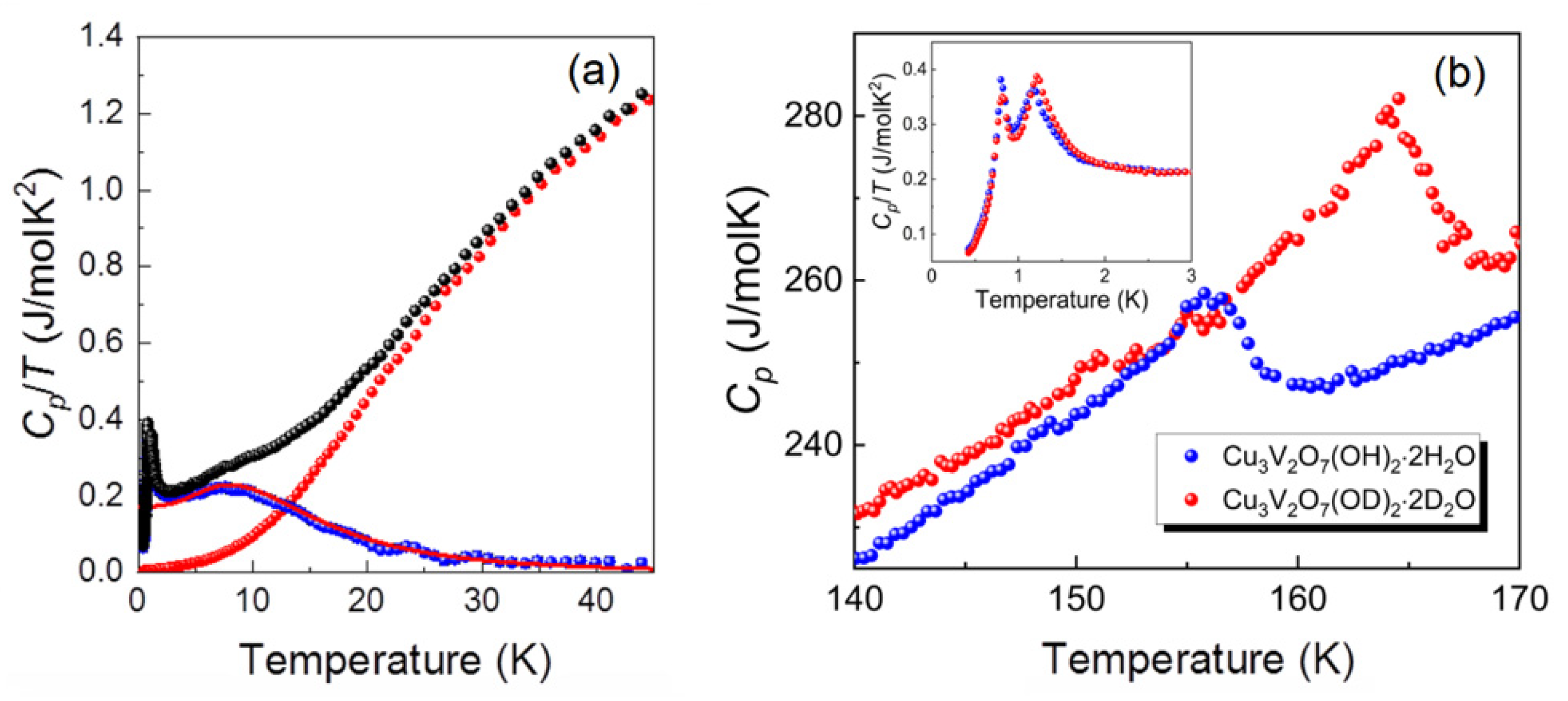
3.3. Specific Heat Anomalies of Volborthite

3.3.1. Specific Heat Anomalies of Volborthite

In Figure 3a, we show the specific heat measured for an ensemble of aligned crystal of volborthite Cu₃V₂O₇(OH)₂ 2H₂O in zero magnetic field with magnetic field applied along the b axis, the estimated lattice contribution to the heat capacity constructed from the specific heat of Zn₃V₂O₇(OH)₂·2H₂O [28] and the difference between the two representing the magnetic contribution to the specific heat of volborthite. It is difficult to obtain a proper lattice specific heat reference because the atomic masses of Cu and Zn are not the same, and because the space groups describing the crystal structures of Zn₃V₂O₇(OH)₂ 2H₂O $\left(P\overline{3}m1\right)$ and Cu₃V₂O₇(OH)₂ 2H₂O (I2/a and P2₁/a) are different. In our work, we adopt the procedure suggested by Boo and Stout [29] and stretch the temperature axis of the specific heat data for Zn₃V₂O₇(OH)₂·2H₂O with a smooth function, varying from 1.15 at 0 K to 1.05 at 50 K. The latter values were chosen such that the specific heat of Zn₃V₂O₇(OH)₂·2H₂O smoothly approaches that of volborthite as T→50 K. The magnetic specific heat of volborthite thus obtained exhibits a broad maximum consistent with the specific heat capacity expected for a S = 1/2 AUH, with a NN spin exchange of J_C = 26 K. The latter value is in good agreement with the spin exchanges derived from the analyses of the magnetic susceptibility and magnetization data. The total magnetic entropy amounts to ~80% of Rln2 expected for a S = 1/2 system, consistent with the result reported by Yamashita et al. [10].

3.3.2. Effect of Isotope Substitution

In Figure 3b, we compare the specific heats of Cu₃V₂O₇(OH)₂·2H₂O and its deuterated analogue, Cu₃V₂O₇(OD)₂·2D₂O, prepared by using 99.5% isotope enriched heavy water in the preparation. The specific heat anomalies of Cu₃V₂O₇(OH)₂·2H₂O below 1.5 K (see inset Figure 3b) are hardly affected by the deuteration. However, the structural phase transition from C2/c to I2/a near 155 K undergoes a 5% upshift for the deuterated sample. This strongly suggests that the two specific heat anomalies below 1.2 K are related to magnetic ordering. Apparently, the D→H substitution does not essentially modify the spin exchange between adjacent kagomé layers, but substantially affects the structural properties of volborthite. The latter finding reflects the fact that the pyrovanadate groups connecting neighboring kagomé layers provide large interlayer spacing. The hydrogen bond network, from an OH group of a kagomé layer to a crystal water to an O atom of the adjacent kagomé layer, is loosened by the D→H substitution, which facilitates the I2/a to P2₁/a structural transition in Cu₃V₂O₇(OD)₂·2D₂O.

3.3.3. Effect of a Magnetic Field on Magnetic Ordering

Given that the specific heat anomalies below 1.5 K are associated with magnetic ordering, it is reasonable to expect that it can be destroyed, and the specific heat anomalies disappear under the sufficiently high external magnetic field. To confirm this conjecture, we carried out specific heat measurements for volborthite under magnetic fields B = 0–9 T (Figure 4a). As B increases, the two specific heat anomalies observed at B = 0 widen but remain separated, forming two ridges until they eventually merge into one and then abruptly disappear for B > ~4.2 T (see Figure 4a). Surprisingly, however, a new specific heat anomaly occurs for fields B > ~5.5 T. This new anomaly forms a single broad ridge, widening and shifting to higher temperatures with increasing B.

To probe the cause for the field-dependence of the specific heat anomalies, it is necessary to find the magnetic energy spectra of volborthite available below 1.5 K, with which it can exchange energy with the surrounding phonon bath. At a temperature T below 1.5 K, the free energy G_i of volborthite associated with its magnetic arrangement i can be written as G_i = H_i − TS_i, where H_i and S_i are the enthalpy and entropy of the magnetic arrangement I, respectively. If volborthite has a set of different magnetic arrangements i = 1, 2, 3, …, it has the corresponding energy spectrum {G₁, G₂, G₃, …}. Then, volborthite can absorb energy from the surroundings by using this energy spectrum reflected by the specific heat anomaly. Since the magnetic specific heat anomalies are observed below 1.5 K, one might assume that the enthalpies H_i are identical for all members i = 1, 2, 3, …. Then, the free energy spectrum {G₁, G₂, G₃, …} is determined by the corresponding entropy spectrum {S₁, S₂, S₃, …}, so the specific heat anomalies below 1.5 K arise from the entropy spectrum of volborthite, which is due most likely to the magnetic ordering of each kagomé layer. The latter implies that each kagomé layer must possess at least two different sets of entropy spectra, so that one set is responsible for the specific heat anomalies below ~4.2 K, and the other for those above ~5.5 K. In the next section, we show that each kagomé layer has three different sets of entropy spectra associated with the arrangements of two-leg spin ladders in each kagomé layer. These entropy spectra are a direct consequence of the fact that interactions between adjacent two-leg spin ladders in each kagomé layer are topologically constrained (see below).

4. Entropy Spectra and Specific Heat Anomalies

4.1. Spin Ladder Arrangements

In this section we discuss the magnetic-field dependence of the magnetic ordering in volborthite below 1.5 K. Our experiments gave conclusive evidence for an effective AUH chain behavior of volborthite at low temperatures, based on the two-leg spin ladders formed by J₂ and J₄. As already mentioned, the two-leg spin ladders (thereafter, referred to as the spin ladder for short) interact with their neighboring spin ladders to establish two-dimensional correlations within each kagomé layer via the spin exchange J₁ (Section 3.1). To begin with, we examine what kinds of spin ladder arrangements are possible in a kagomé layer. As already mentioned, in all possible magnetic arrangements of each kagomé layer at temperatures below 1.5 K, all J₂ and J₄ exchange paths of every spin ladder should remain antiferromagnetically coupled (Figure 1d) because the spin exchanges J₂ and J₄ forming the spin ladders are AFM and are much stronger in magnitude than J₁. This constraint on the magnetic arrangements of a kagomé layer leads to three different groups of spin ladder arrangements. Note that each spin ladder has a set of two consecutive J₁ paths running along the leg direction, which consists of the left and right sets of J₁ paths. Then, the first topological constraint is that the left or right set of J₁ paths in each spin ladder be coupled either all antiferromagnetically or all ferromagnetically. For simplicity, we use the labels A (F) to represent the set of J₁ paths all antiferromagnetically (ferromagnetically) coupled in each spin ladder. The two sets of the J₁ paths in each spin ladder can have one of the four possible arrangements, (AA), (AF), (FA), and (FF), as illustrated in Figure 1d. Here, the (AF) arrangement, for example, means that the spin ladder indicated by a parenthesis has the J₁ paths all antiferromagnetically coupled in the left set, but all ferromagnetically coupled in the right set. Use of bold labels in the (AA) and (FF) arrangements stems from the ease of recognizing the spin ladder arrangements, as will be seen below. Figure 1d illustrates a kagomé layer in which the (FF), (AF), (AA) and (FA) spin ladders occur consecutively. It is convenient to denote this arrangement of spin ladders by (FF)(AF)(AA)(FA). As can be seen from this arrangement, the second topological constraint is that, when crossing from one spin ladder to its adjacent one, the two sets of the J₁ paths adjacent to the boundary between the two be opposite in the nature of the spin exchange coupling, e.g., “F)(A” or “A)(F”. As a consequence, the third topological constraint is that (AA) spin ladders cannot be nearest neighbors, nor can be (FF) spin ladders. This implies also that (AA) and (FF) ladders always have to alternate in any spin ladder arrangement. These three constraints imply that there occur only three different sets of spin ladder arrangements in each kagomé layer, in which the members of each set are distinguished by how many pairs of (AA) and (FF) spin ladders are present. For simplicity, we use (AF)_m to represent the occurrence of m consecutive (AF) spin ladders, and (FA)_n that of n consecutive (AF) spin ladders. Then, with the integers m, n, o, p, q and r counting the numbers of consecutive (AF) or (FA) arrangements, examples of the spin ladder arrangements in Groups I, II and III are written as follows:

Group I:

(AF)_m(AA)(FA)_n(FF)(AF)_o(AA)(FA)_p(FF)(AF)_q.

Group II:

(AF)_m(AA)(FA)_n(FF)(AF)_o(AA)(FA)_p(FF)(AF)_q(AA)(FA)_r.

Group III:

(FA)_m(FF)(AF)_n(AA)(FA)_o(FF)(AF)_p(AA)(FA)_q(FF)(AF)_r.

The example of Group I given above illustrates the case when two pairs of (AA) and (FF) spin ladders are separated by patches of consecutive (FA) and (AF) spin ladders. All possible spin ladder arrangements of Group I are obtained by changing the number of (AA) and (FF) pairs, m (=0, 1, 2, 3, …). With respect to any member of Group I, the corresponding member of Group II has one more (AA) spin ladder, while that of Group III has one more (FF) spin ladder.

4.2. Entropy Spectra

For a given (AF)_m(AA)(FA)_n arrangement, it is important to note that the (AF)_m patch represents a domain of (AF)-coupled spin ladders while the (FA)_n patch represents a domain of (FA)-coupled spin ladders, and the (AA) spin ladder is a boundary between the two domains. Similarly, in a given (FA)_m(FF)(AF)_n arrangement, the (FF) spin ladder represents a boundary between the (FA)_m and (AF)_n domains. Thus, each member of the Groups I, II and III arrangements is characterized by how many pairs of (AA) and (FF) boundaries it has, regardless of the widths (e.g., values of m, n, …) of each individual domain. This point is important in connection with the enthalpy of any given spin ladder arrangement. All members of Group I have an identical enthalpy, $H_I=J_1 {\displaystyle {\sum }_{i>j}}{\overrightarrow{S}}_i{\overrightarrow{S}}_j=0$ per kagomé layer, because each member has equal numbers of antiferromagnetically and ferromagnetically coupled J₁ paths. Similarly, all spin ladder arrangements of Group II are identical in enthalpy, H_II = H_I − 2J₁ = −2J₁ per kagomé layer, and those of Group III are identical in enthalpy, H_III = H_I + 2J₁ = +2J₁ per kagomé layer. Note that J₁ is weakly FM in the P2₁/a phase (see Table 1), and that the value of −2J₁ for Group II is the enthalpy of one (AA) spin ladder while the value of +2J₁ for Group III is the enthalpy of one (FF) spin ladder. Since J₁ is very weak and since a kagomé layer has a large number of spin ladders, one can for all practical purposes assume H_I = H_II = H_III = 0 per kagomé layer, that is, all spin ladder arrangements of Groups I, II and III are practically identical in enthalpy.

The spin ladder arrangements of Groups I, II and III give rise to entropy spectra that are characterized by the number m of (AA) and (FF) pairs. To probe the entropy spectra of Groups I, II and III, we consider that a kagomé layer has N spin ladders, where N = N_A/3 per FU of volborthite Cu₃V₂O₇(OH)₂·2H₂O with N_A as Avogadro’s number. The factor 1/3 takes into account the fact that each spin ladder has three Cu²⁺ ions per repeat unit. For the case when there are m pairs of (AA) and (FF) arrangements, the total number of different spin ladder arrangements, Ω_A(2m), in Group I, is given by

Ω_I(2m) = 2(_NC_2m) = 2(N!)/[(2m)!(N − 2m)!],

where _NC_2m is the binomial expansion coefficient, and the factor 2 arises because the m pairs of sites in each arrangement can be occupied first with a (FF) spin ladder or first with an (AA) spin ladder when m > 0. For m = 0, Ω_I(0) = 2 because one can have the (AF)_∞ = …(AF)(AF)(AF)… or the (FA)_∞ = …(FA)(FA)(FA)… arrangement. The corresponding numbers for Group II (Group III) are given by

Ω_II(2m) = Ω_III(2m) = Ω_I(2m) Ω_E(2m),

where Ω_E(2m) represents the number of possible sites available for an extra spin ladder after m pairs of (AA) and (FF) spin ladders are chosen from N spin ladders. Due to the topological constraints on the spin ladder ordering, Ω_E(2m) ≤ N − 2m. Then, the entropies S associated with the three groups of spin ladder arrangements are given by

S_I(2m) = k_B lnΩ_I(2m),

S_II(2m) = S_III(2m) = S_I(2m) + S_E(2m),

S_E(2m) = k_B lnΩ_E(2m).

Since Ω_I(2m) = Ω_I(N − 2m), Ω_I(2m) increases as 2m increases from 0 toward N/2, reaching a maximum at 2m = N/2, and decreases as 2m increases beyond N/2 toward N (Figure 4b). Consequently, S_I(2m) = S_I(N − 2m), and S_I(2m) increases as 2m increases from 0 toward at N/2 and as 2m decreases from N toward N/2.

The kagomé layers of volborthite satisfy the three conditions necessary for a crystalline solid to exhibit a purely entropy-driven phase transitions: [30,31,32] (1) It has a set of states identical in enthalpy H. (2) The members of this set are grouped into subsets i = 1, 2, 3, …, with degeneracies Ω₁, Ω₂, Ω₃, …, respectively. (3) The degeneracy Ω_i increases steadily, e.g., Ω₁ < Ω₂ < Ω₃ < …, so the associated entropy increases steadily. Thus, one may expect that already moderate magnetic fields inducing Zeeman energies comparable to J₁ are able to substantially alter the entropy balance, causing dramatic effects on the low-temperature ordering behavior. In fact, as shown Figure 4a, the specific heat anomalies observed at B = 0 indeed disappears for B > ~4.2 T, but a new anomaly occurs when B > ~5.5 T. Below ~2 K, neither electronic nor vibrational energy of volborthite is available for the energy absorption, causing the specific heat anomalies. Thus, in the following, we analyze the dependence of the specific heat anomalies on T and B in terms of the entropy spectra of Groups I, II and III (Figure 4b).

4.3. Specific Heat Anomalies and Entropy Spectra

As shown above, the entropy S_I(2m) of Group I is smaller than that of Group II or III by S_E(2m). As the magnetic field B increases from 0, a kagomé layer starts absorbing energy by exploiting the entropy spectrum of Group I, so the anomaly below ~4.2 T arises from the entropy spectrum of Group I. Since Ω_I(2m) becomes larger with increasing 2m from 0 to N/2 and also with decreasing 2m from N to N/2, more states are involved in the energy absorption from Zeeman energy. This allows one to understand why the intensity of the specific heat anomaly increases with increasing field B. The entropies S_I(2m) from the states for 2m = 0 − N/2 as well as 2m = N − N/2 are used to absorb energy, eventually reaching the highest entropy level S_I(N/2) (Figure 4b). When all entropy levels are exploited, there is no more entropy level with which a kagomé layer can absorb energy any further, even if B is increased. At this stage, the spin ladder ordering within a kagomé layer assumes a liquid-like disordered state, and the specific heat in the valley between ~4.2 T and ~5.5 T reaches that of the disordered state of the S = 1/2 AUH chains (the green plateau in Figure 4a). It is most reasonable to assign the higher-temperature specific heat ridge to a magnetic ordering within each kagomé layer, and the lower-temperature one to a three-dimensional ordering, i.e., an ordering between the magnetically ordered kagomé layers. When the magnetic field increases further, a kagomé layer can utilize the entropy spectra of Groups II and III simultaneously, leading to the single broad specific heat anomaly above ~5.5 T. However, this requires that the spin ladder arrangements of a kagomé layer must be converted from Group I to Groups II and III. Each spin ladder has two sets of J₁ exchanges, e.g., a (AF) spin ladder has one set of AFM-coupled J₁ and another set of FM-coupled J₁ exchanges. Suppose that a set of J₁ paths is switched from FM to AFM, e.g., from an (AF) to a (AA) spin ladder in one member of Ω_A(2m) of Group I to create an extra (AA) spin ladder. Such a J₁-flip, e.g., (AF)_m(AF)(AF)_n→(AF)_m(AA)(FA)_n, converts the electronic structure from Group I to Group II, raising the entropy from S_I(2m) to S_II(2m) = S_I(2m) + S_E(2m). Similarly, a J₁-flip can create an extra (FF) spin ladder, e.g., (FA)_m(FA)(FA)_n→(FA)_m(FF)(AF)_n, converting the electronic structure from Group I to Group III, raising the entropy from S_I(2m) to S_III(2m) = S_I(2m) + S_E(2m).

With a magnetic field, it is energetically more favorable to induce a J₁-flip from AFM to FM rather than that from FM to AFM. In contrast, thermally-driven J₁-flips from AFM to FM or from FM to AFM are equally likely. Thus, thermal agitation will be more effective in creating J₁-flips than Zeeman energy, approximately by a factor of 2. The positions of two ridges of the specific heat below ~4.2 T are nearly parallel to the magnetic field axis, whereas the single specific heat ridge above ~5.5 T is slanted with slope gμ_BB/k_BT ≈ 2. This reflects that, at a strong enough magnetic field, the kagomé layers of Group II spin ladder arrangements absorb energy equally, as do those of Group III spin ladder arrangements.

The entropy spectra II and III are identical in the degeneracy of each entropy level, but differ in the nature of spin ladder arrangements. Whether a given kagomé layer produces the entropy spectrum II or III has no effect on the enthalpy difference. Consequently, there is no ordering between kagomé layers, which explains the occurrence of a single specific heat anomaly at magnetic field above ~5.5 T. The latter forms a single ridge with increasing B, the shape of which suggests that not all available entropy states of the entropy spectra II and III are populated at 9 T. If it is assumed that this above-5.5 T specific heat anomaly (Figure 4a) retains a symmetric shape with respect to the temperature and magnetic field, one might expect that the magnetic order above ~5.5 T will disappear under a magnetic field higher than ~13 T.

Finally, we note that in all ordered magnetic states of Groups I, II and III, there occurs a strong gain of translational entropy with respect to those states in which there is no order between neighboring spin ladders, because the ordered states have translational symmetry along the leg direction. This provides a strong driving force for the magnetic ordering. In a sense, this situation is similar to the nematic phase transition in a system of thin rods examined by Onsager [31].

5. Concluding Remarks

The spin exchanges of volborthite show that each kagomé layer of Cu²⁺ ions is hardly spin-frustrated, but rather consists of very weakly interacting two-leg spin ladders with linear trimers as rungs. Below ~75 K, these rungs act as S = 1/2 pseudospin units, making each two-leg spin ladder behave as a S = 1/2 antiferromagnetic uniform Heisenberg chain. This conclusion was confirmed by synthesizing single crystal samples of volborthite Cu₃V₂O₇(OH)₂·2H₂O and its deuterated analogue Cu₃V₂O₇(OD)₂·2D₂O and subsequently measuring their magnetic susceptibilities and specific heat anomalies. Under a magnetic field B higher than ~4.2 T, the specific heat anomalies below 1.5 K are suppressed. However, a new specific heat anomaly appears when B is raised above ~5.5 T. The dependence of the specific heat anomalies on the magnetic field are governed by the fact that the magnetic properties of each kagomé has three sets of entropy spectra with which it can exchange energy with the surrounding. These entropy spectra arise from the topologically constrained interactions between adjacent two-leg spin ladders in each kagomé layer; that all spin exchange paths forming each two-leg spin ladder should remain antiferromagnetically coupled.

The present work makes it clear that the use of a correct spin lattice is critical in describing the properties of a magnetic material. As a criterion for finding a proper spin lattice, the geometrical pattern of magnetic ion arrangement can be grossly misleading because a spin lattice is decided by the geometrical pattern of the strong spin exchange paths [3,4,19]. If volborthite were to be treated as a spin-frustrated kagomé lattice model, the S = 1/2 antiferromagnetic uniform Heisenberg chain behaviors of its magnetic susceptibility and magnetization are exotic and novel, as are its specific heat anomalies below 1.5 K. By the same token, all other magnetic properties of volborthite not explained by a spin-frustrated kagomé lattice model would be novel and surprising. However, our work showed that each kagomé layer of Cu²⁺ ions consists of very-weakly interacting two-leg spin ladders, so the seemingly exotic magnetic properties previously attributed to magnetic frustration are simply explained by a well-studied S = 1/2 antiferromagnetic uniform Heisenberg chain model. To find a correct spin lattice for any given magnetic material, it is necessary to evaluate the relative strengths of various possible spin exchanges of a given magnetic system by using an unbiased and straightforward method such as the energy-mapping analysis, based on first principles DFT calculations [3,4,19,33].