High-Precision X-ray Total Scattering Measurements Using a High-Accuracy Detector System

Abstract

The total scattering method, which is based on measurements of both Bragg and diffuse scattering on an equal basis, has been still challenging even by means of synchrotron X-rays. This is because such measurements require a wide coverage in scattering vector Q, high Q resolution, and a wide dynamic range for X-ray detectors. There is a trade-off relationship between the coverage and resolution in Q, whereas the dynamic range is defined by differences in X-ray response between detector channels (X-ray response non-uniformity: XRNU). XRNU is one of the systematic errors for individual channels, while it appears to be a random error for different channels. In the present study, taking advantage of the randomness, the true sensitivity for each channel has been statistically estimated. Results indicate that the dynamic range of microstrip modules (MYTHEN, Dectris, Baden-Daettwil, Switzerland), which have been assembled for a total scattering measurement system (OHGI), has been successfully restored from 10⁴ to 10⁶. Furthermore, the correction algorithm has been optimized to increase time efficiencies. As a result, the correcting time has been reduced from half a day to half an hour, which enables on-demand correction for XRNU according to experimental settings. High-precision X-ray total scattering measurements, which has been achieved by a high-accuracy detector system, have demonstrated valence density studies from powder and PDF studies for atomic displacement parameters.

1. Introduction

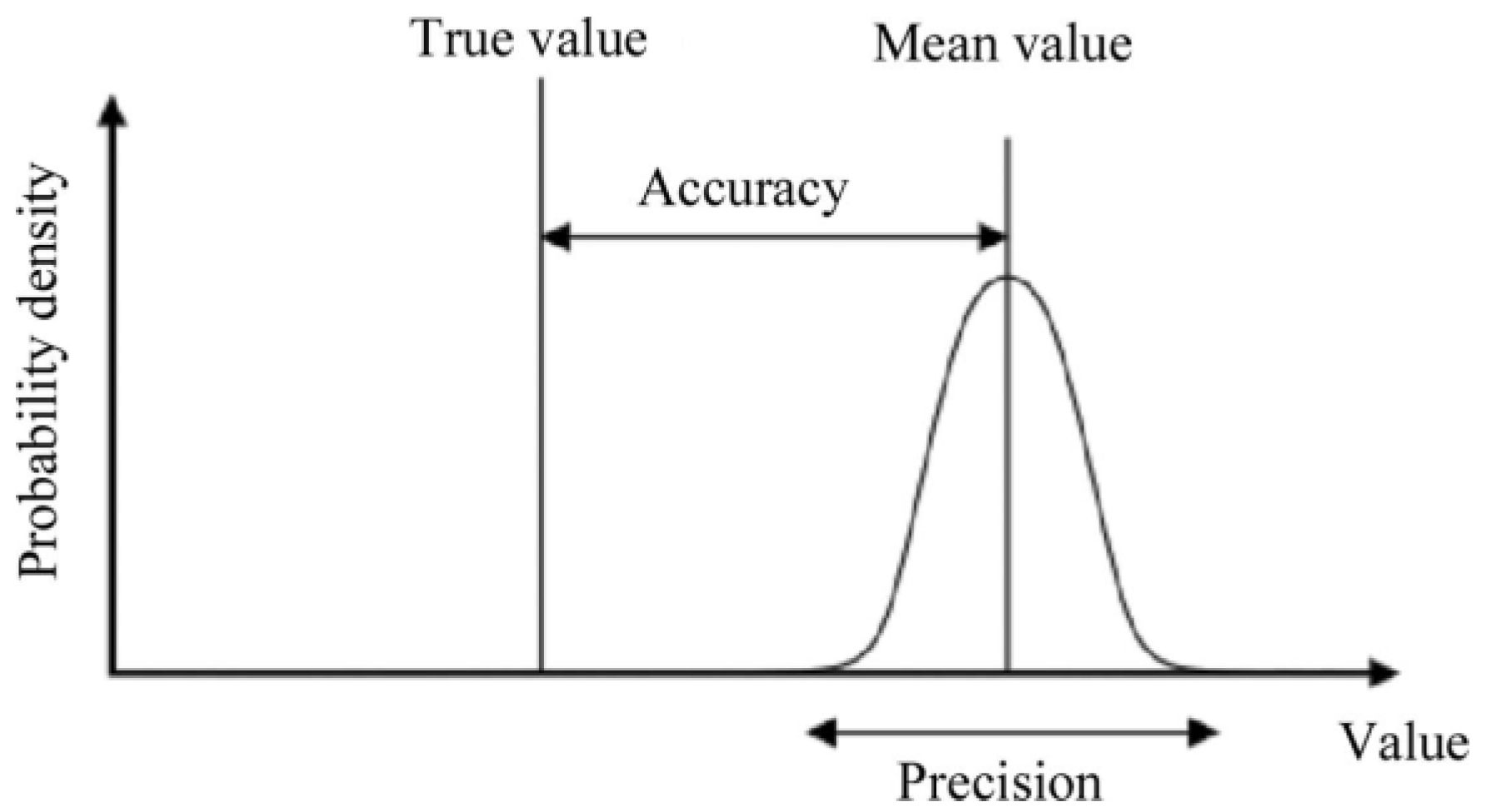
The two words for experimental uncertainties, “precision” and “accuracy”, are used with different meanings in measurement science, as shown in Figure 1 [1]. Accuracy means a bias from the true value or a systematic error, whereas precision refers to a deviation from the mean value or a random error. The present work has aimed at developing a high-“accuracy” detector system for high-“precision” X-ray total scattering measurements.

Total scattering refers to all coherent scattering such as Bragg and diffuse scattering, which originate from crystalline and amorphous materials, respectively [2]. In most materials, crystalline domains coexist with amorphous domains such as lattice defects. Therefore, Bragg and diffuse scattering should be measured on an equal basis. However, such total scattering measurements have been still challenging, even by using synchrotron X-rays. Bragg scattering, which gives rise to high and sharp peaks, has been measured with a high Q (the magnitude of scattering vector) resolution setup [3]. On the other hand, diffuse scattering, which gives rise to lower, broader peaks, has been measured with a wide Q range setup [4]. To measure both scattering simultaneously, it is necessary to meet three requirements of total scattering data collected with a single setup: the maximum Q value (Q_max) of 30 Å⁻¹, a Q step of 10⁻³ Å⁻¹, and a precision of 0.1%. Detector systems in general have a trade-off between the Q_max and Q step values. In order to solve the trade-off problem, multiple silicon microstrip modules (MYTHEN, Dectris) [5] have been assembled at BL44B2 of SPring-8, which is referred to as the overlapped high-grade intelligencer (OHGI) [6]. The arrangement of fifteen modules in a curve without gap in 2θ has made it possible to cover 150° at intervals of 0.01° in 2θ at the same time. Provided that the incident X-ray energy is set at 30 keV, it is possible to meet the two requirements for Q_max and Q step. However, it was virtually impossible to achieve a precision of 0.1% due to inaccuracy in the microstrip modules, which is caused by differences in X-ray response between microstrips (X-ray response non-uniformity: XRNU).

Here, we report on how accuracy can be improved in X-ray detectors for high-precision total scattering measurements.

2. Materials and Methods

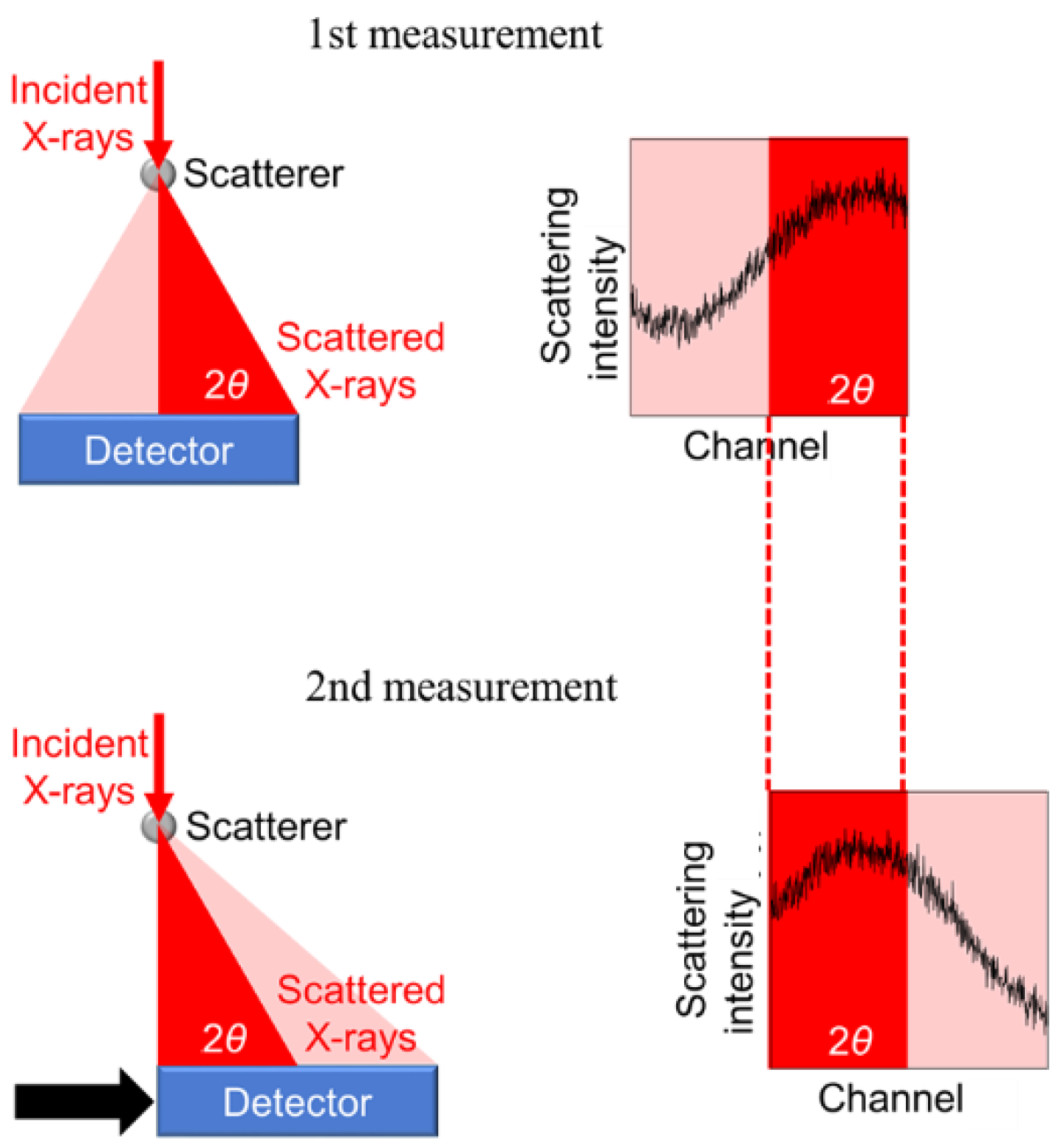
Our approach to correct scattering data for XRNU is based on the fact that XRNU appears to be a random error between microstrips [6]. Let us explain the approach using the simplest case in Figure 2. First, X-rays scattered from an object (any object can be used in principle) is measured using a detector. Next, the detector is shifted by half of its length, and then scattered X-rays are measured under the same condition. Ideally, the first scattering intensities at 2θ should be consistent with the second intensities at the same 2θ, measured with different channels within the Poisson noise. In practice, there are significant inconsistencies between the two intensities, which are caused by XRNU. Our approach takes an average between the two intensities to statistically estimate the reference intensities for the XRNU correction. From the ratio of the reference intensity to the raw intensity, the correction factor for each channel can be calculated. Accordingly, the reliability of the statistical approach is determined by the statistics of the reference intensities.

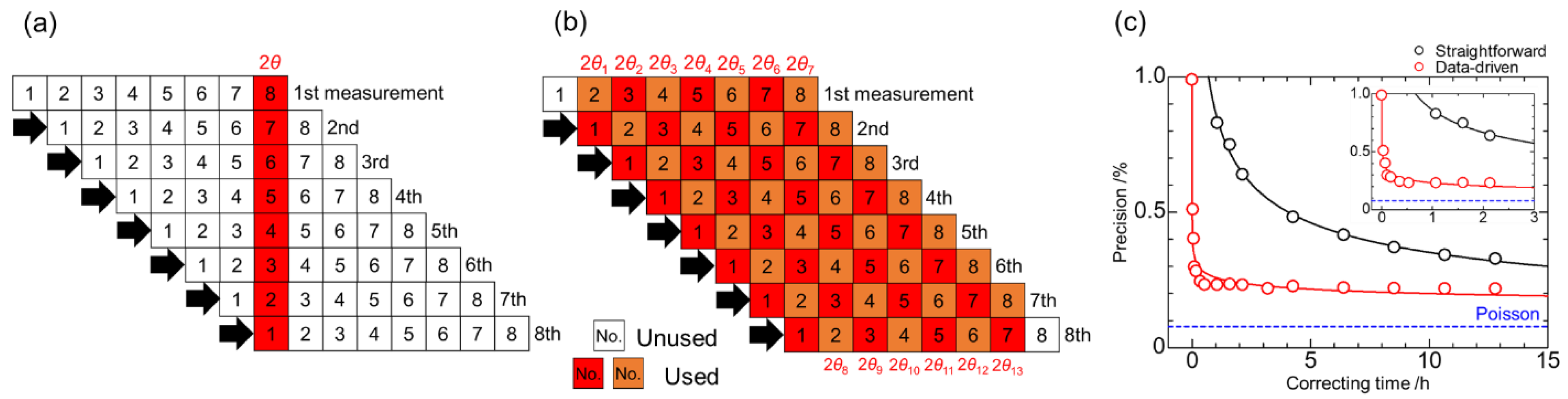
On the basis of the straightforward approach mentioned above, however, it took about half a day to achieve a precision of 0.1%. XRNU in detectors varies with experimental settings, such as X-ray energy, threshold energy, and atmospheric temperature. To overcome the time efficiency problem, the approach has been improved in terms of the algorithm for the correction factor calculations [7]. Let us explain the difference between the straightforward and improved algorithms using a one-dimensional detector with 8 microstrips in Figure 3a,b where a horizontal line corresponds to a detector. Eight scattering measurements of an object are performed, shifting the detector by one channel.

In the straightforward algorithm, only one vertical line is used to calculate the correction factor for each channel. The reference intensity, $\overline{y_{2\theta }}$, at 2θ can be estimated as the arithmetic mean of eight intensities $y_{2\theta }\left(i\right)$ measured by eight channels (i = 1–8) at 2θ, as follows:

$$\overline{y_{2\theta }}=\frac{{{\displaystyle \sum }}_{i=1}^8{y}_{2\theta }\left(i\right)}{8}$$

(1)

The correction factor c(i) for each channel i can be found as the ratio of the reference intensity, $\overline{y_{2\theta }}$, to the measured intensity, $y_{2\theta }\left(i\right)$, as follows:

$$c\left(i\right)=\frac{\overline{y_{2\theta }}}{y_{2\theta }\left(i\right)}$$

(2)

From Figure 3a, it is found that the number of blocks used for estimating reference intensity is 8, whereas the number of those that are unused is 56.

On the other hand, in the improved algorithm, all vertical lines, except for both ends, can be used for correction factors. From each vertical line, “local” correction factors can be obtained based on the straightforward algorithm. Subsequently, multiple local correction factors for each channel are averaged using the statistical weight to obtain “global” factors. In other words, the straightforward algorithm has been improved to calculate the average of correction factors. The “local” correction factor $c_k\left(i\right)$ for channel i can be estimated based on the reference intensity at 2θ_k in the same way as the straightforward algorithm, as follows:

$$c_1\left(i\right)=\frac{{{\displaystyle \sum }}_{j=1}^2{y}_{2{\theta }_1}\left(j\right)}{2}\frac{1}{y_{2{\theta }_1}\left(i\right)}, 1\le i\le 2$$

(3)

$$c_2\left(i\right)=\frac{{{\displaystyle \sum }}_{j=1}^3{y}_{2{\theta }_2}\left(j\right)}{3}\frac{1}{y_{2{\theta }_2}\left(i\right)}, 1\le i\le 3$$

(4)

$$c_3\left(i\right)=\frac{{{\displaystyle \sum }}_{j=1}^4{y}_{2{\theta }_3}\left(j\right)}{4}\frac{1}{y_{2{\theta }_3}\left(i\right)}, 1\le i\le 4$$

(5)

$$c_4\left(i\right)=\frac{{{\displaystyle \sum }}_{j=1}^5{y}_{2{\theta }_4}\left(j\right)}{5}\frac{1}{y_{2{\theta }_4}\left(i\right)}, 1\le i\le 5$$

(6)

$$c_5\left(i\right)=\frac{{{\displaystyle \sum }}_{j=1}^6{y}_{2{\theta }_5}\left(j\right)}{6}\frac{1}{y_{2{\theta }_5}\left(i\right)} 1\le i\le 6$$

(7)

$$c_6\left(i\right)=\frac{{{\displaystyle \sum }}_{j=1}^7{y}_{2{\theta }_6}\left(j\right)}{7}\frac{1}{y_{2{\theta }_6}\left(i\right)}, 1\le i\le 7$$

(8)

$$c_7\left(i\right)=\frac{{{\displaystyle \sum }}_{j=1}^8{y}_{2{\theta }_7}\left(j\right)}{8}\frac{1}{y_{2{\theta }_7}\left(i\right)}, 1\le i\le 8$$

(9)

$$c_8\left(i\right)=\frac{{{\displaystyle \sum }}_{j=2}^8{y}_{2{\theta }_8}\left(j\right)}{7}\frac{1}{y_{2{\theta }_8}\left(i\right)}, 2\le i\le 8$$

(10)

$$c_9\left(i\right)=\frac{{{\displaystyle \sum }}_{j=3}^8{y}_{2{\theta }_9}\left(j\right)}{6}\frac{1}{y_{2{\theta }_9}\left(i\right)}, 3\le i\le 8$$

(11)

$$c_{10}\left(i\right)=\frac{{{\displaystyle \sum }}_{j=4}^8{y}_{2{\theta }_{10}}\left(j\right)}{5}\frac{1}{y_{10}\left(i\right)}, 4\le i\le 8$$

(12)

$$c_{11}\left(i\right)=\frac{{{\displaystyle \sum }}_{j=5}^8{y}_{2{\theta }_{11}}\left(j\right)}{4}\frac{1}{y_{11}\left(i\right)}, 5\le i\le 8$$

(13)

$$c_{12}\left(i\right)=\frac{{{\displaystyle \sum }}_{j=6}^8{y}_{2{\theta }_{12}}\left(j\right)}{3}\frac{1}{y_{12}\left(i\right)}, 6\le i\le 8$$

(14)

$$c_{13}\left(i\right)=\frac{{{\displaystyle \sum }}_{j=7}^8{y}_{2{\theta }_{13}}\left(j\right)}{2}\frac{1}{y_{13}\left(i\right)}, 7\le i\le 8$$

(15)

The “global” correction factor, c(i), for channel i can be estimated as the weighted mean of the multiple “local” correction factors $c_k\left(i\right)$, as follows:

$$c\left(1\right)=\frac{{{\displaystyle \sum }}_{k=1}^7{w}_k\left(1\right)c_k\left(1\right)}{{{\displaystyle \sum }}_{k=1}^7{w}_k\left(1\right)}$$

(16)

$$c\left(2\right)=\frac{{{\displaystyle \sum }}_{k=1}^8{w}_k\left(2\right)c_k\left(2\right)}{{{\displaystyle \sum }}_{k=1}^8{w}_k\left(2\right)}$$

(17)

$$c\left(3\right)=\frac{{{\displaystyle \sum }}_{k=2}^9{w}_k\left(3\right)c_k\left(3\right)}{{{\displaystyle \sum }}_{k=2}^9{w}_k\left(3\right)}$$

(18)

$$c\left(4\right)=\frac{{{\displaystyle \sum }}_{k=3}^{10}{w}_k\left(4\right)c_k\left(4\right)}{{{\displaystyle \sum }}_{k=3}^{10}{w}_k\left(4\right)}$$

(19)

$$c\left(5\right)=\frac{{{\displaystyle \sum }}_{k=4}^{11}{w}_k\left(5\right)c_k\left(5\right)}{{{\displaystyle \sum }}_{k=4}^{11}{w}_k\left(5\right)}$$

(20)

$$c\left(6\right)=\frac{{{\displaystyle \sum }}_{k=5}^{12}{w}_k\left(6\right)c_k\left(6\right)}{{{\displaystyle \sum }}_{k=5}^{12}{w}_k\left(6\right)}$$

(21)

$$c\left(7\right)=\frac{{{\displaystyle \sum }}_{k=6}^{13}{w}_k\left(7\right)c_k\left(7\right)}{{{\displaystyle \sum }}_{k=6}^{13}{w}_k\left(7\right)}$$

(22)

$$c\left(8\right)=\frac{{{\displaystyle \sum }}_{k=7}^{13}{w}_k\left(8\right)c_k\left(8\right)}{{{\displaystyle \sum }}_{k=7}^{13}{w}_k\left(8\right)}$$

(23)

where $w_k\left(i\right)$ is the weight for $c_k\left(i\right)$ expressed by $1/{\sigma }_k{\left(i\right)}^2$, and σ_k(i) is the standard deviation of $c_k\left(i\right)$. From Figure 3b, it is found that the number of blocks used for estimating reference intensity is 62, whereas the number of those which are unused is 2.

The improved algorithm has been optimized for OHGI, which has 1280 × 15 microstrips. Figure 3c shows a comparison between the two algorithms in terms of time efficiency. The straightforward and improved algorithms reach a plateau in half a day and half an hour, respectively. Moreover, the precision based on the improved algorithm is better than that based on the straightforward algorithm. For that reason, the improved algorithm has been referred to as a data-driven approach to the XRNU correction.

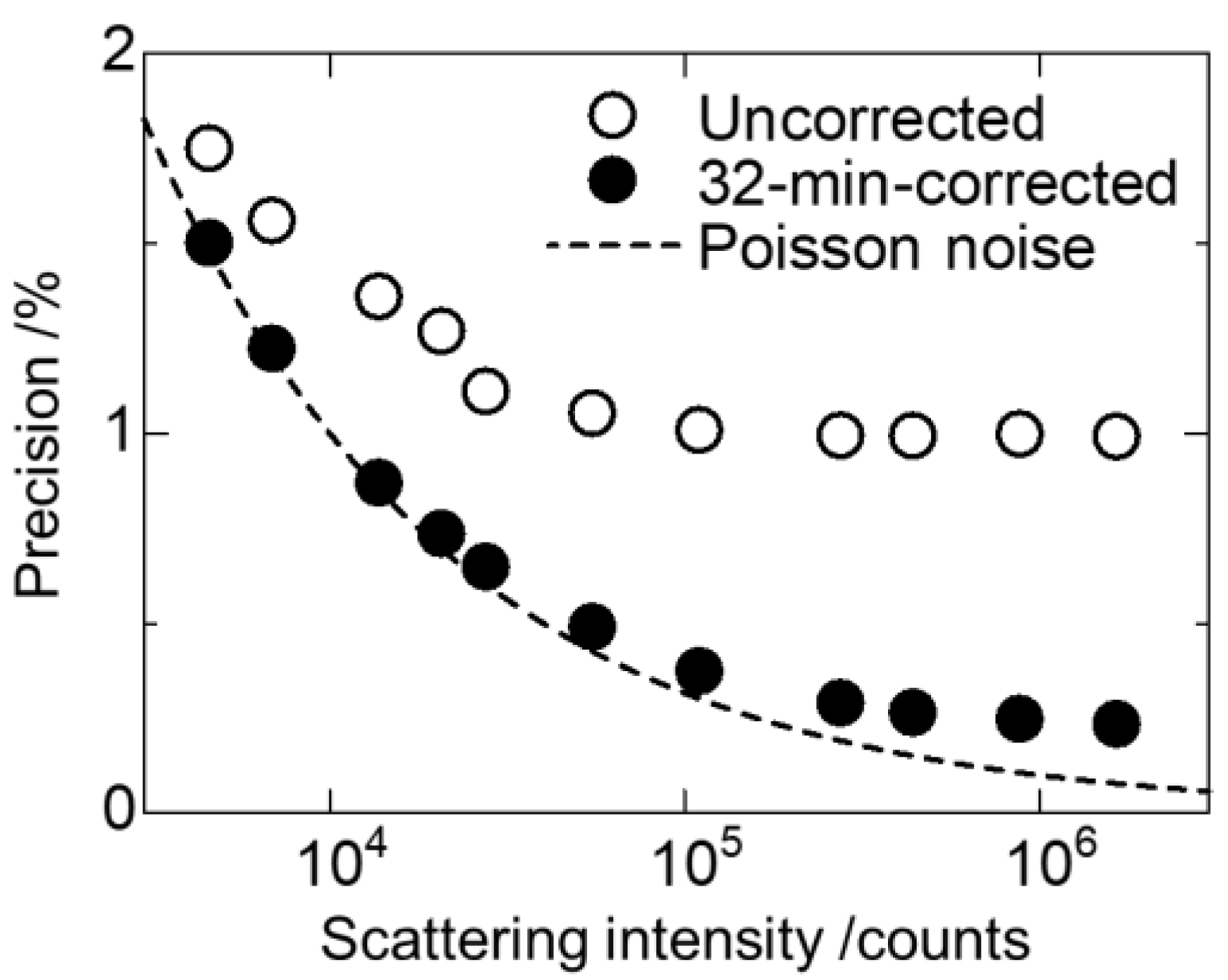
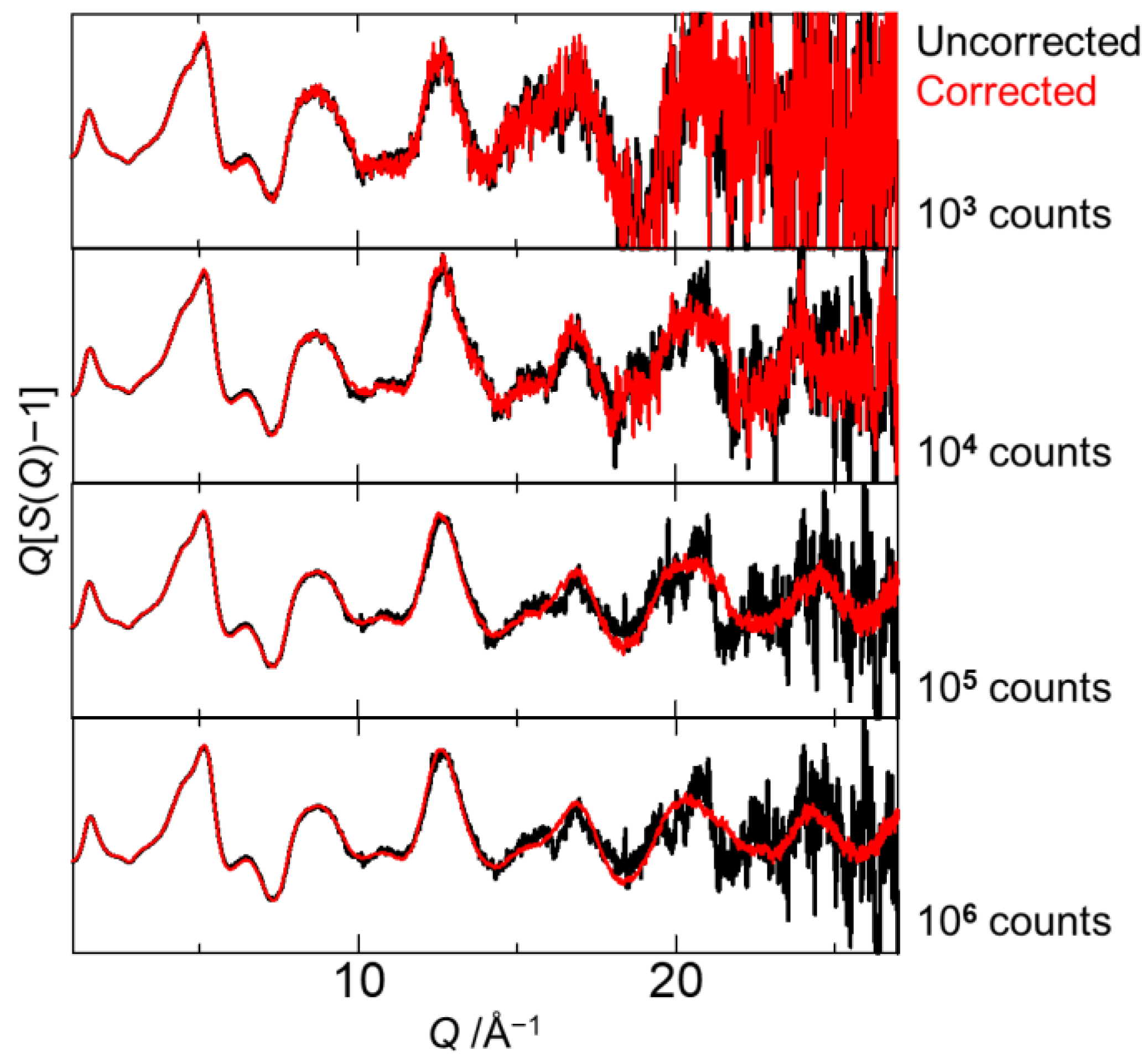
Figure 4 shows the data precision as a function of scattering intensity, which was estimated based on the standard deviation and the mean intensity from total scattering data of amorphous SiO₂. In the ideal case, the precision improves with scattering intensity in accordance with the Poisson distribution. Without our correction, however, the precision reaches a plateau at about 1%, which is equivalent to a dynamic range of 10⁴. Even though the manufacturer-supplied, flat-field correction factors were applied to the uncorrected data, the precision has not been improved. In contrast, the data-driven approach has successfully improved the precision from 1.0% to 0.1%, which is equivalent to a dynamic range of 10⁶.

3. Results and Discussion

Figure 5 shows structure functions Q[S(Q)−1] of amorphous SiO₂ measured with OHGI in different times, which were reduced from total scattering data with intensity from 10³ to 10⁶ counts at high Q. Without the XRNU correction, there seems to be no significant improvement in statistics at high Q even by increasing scattering intensity. In contrast, a systematic improvement in the corrected data has been observed in accordance with photon statistics. The results indicate that the XRNU correction has enabled us to observe diffuse scattering with lower and broader peaks.

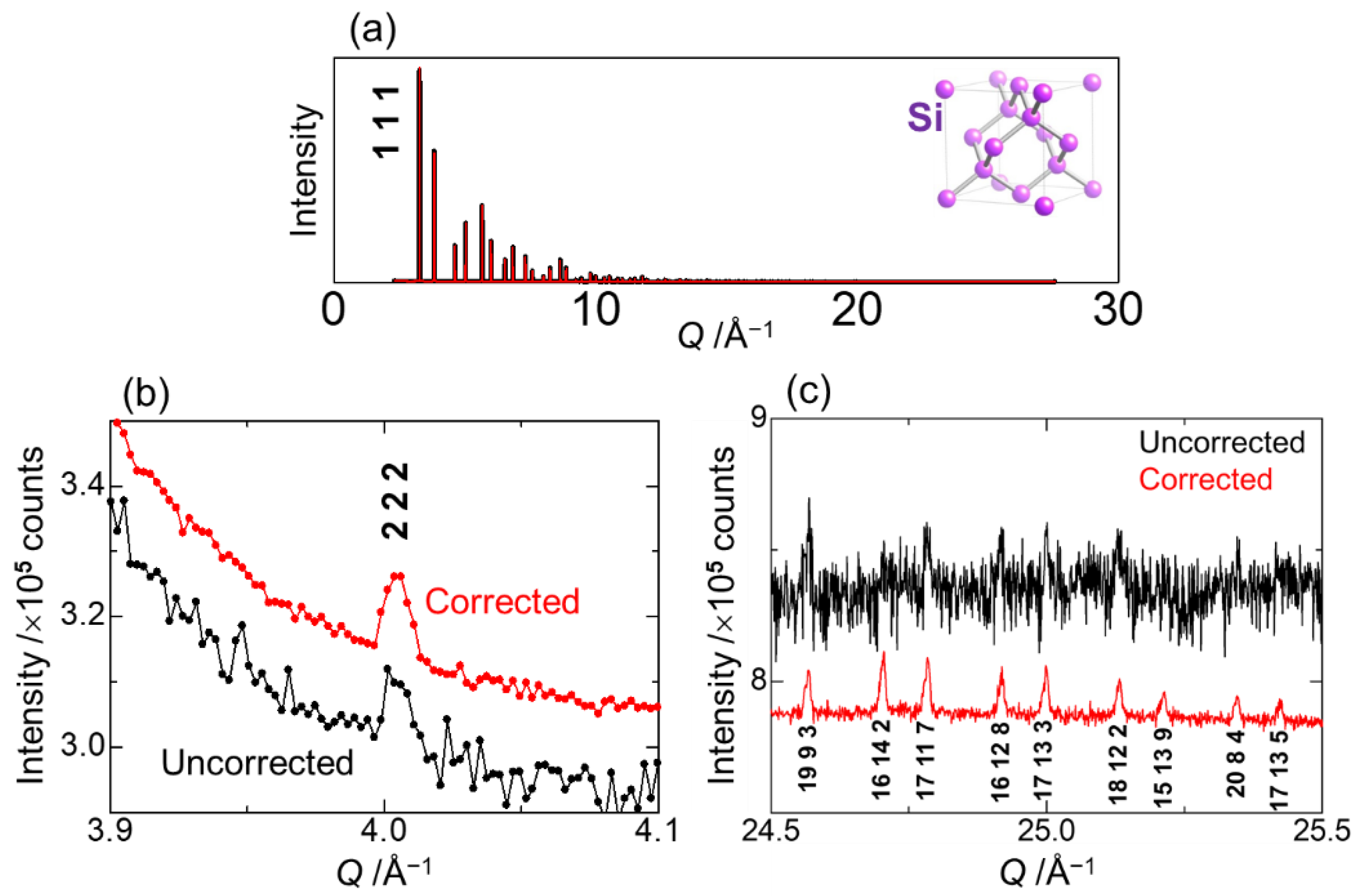
Figure 6 focuses on Bragg reflections of crystalline Si measured with OHGI. The 2 2 2 reflection from Si crystal is a forbidden reflection; nevertheless it is possible to observe the reflection due to anharmonicity of Si atoms. In fact, the reflection has been observed by using synchrotron X-ray powder diffraction [8]. However, the precision of the integrated intensity is lower than that of fundamental reflections. Figure 6b shows that the data-driven approach has considerably improved the precision. Figure 6c shows higher order reflections at high Q, which are four orders of magnitude lower than the highest reflection 1 1 1 in Figure 6a. These reflections were not observed due to the XRNU noise. The XRNU correction has successfully brought the quite weak reflections into “relief” against the background. That is why the data-driven approach has been referred to as ReLiEf (response-to-light effector) [7].

Let us discuss why the dynamic range in microstrip modules used for OHGI has been improved from 10⁴ to 10⁶ without the cost of Q resolution, resulting in observation of both Bragg and diffuse scattering. The specifications of the detector state a dynamic range of 10⁷ [5]. In the strict sense, however, this value means the dynamic range not for the system but for each microstrip. In other words, the effective dynamic range has been limited by the XRNU noise. It should be emphasized that the ReLiEf method has just restored the dynamic range of the microstrip module, which enables total scattering measurements.

Atomic displacement parameters (ADP), which are estimated from Debye–Waller factors, is one of the most important parameters for structural analysis.

Table 1. Atomic displacement parameters (ADP) U obtained by different experimental techniques.

	TS-PDF 1	SXRD 2	PND 3	INS 4	CBED 5
Probe	X-rays	X-rays	Neutrons	Neutrons	Electrons
Sample	Powder	Single crystal	Powder	Single crystal	Single crystal
T/K	298	293–298	284–293	293	300
U/(10−4 Å2)	59.5(1)	58.7(1)	59(3)	59.4(2)	58.6

¹ Total-scattering pair distribution function (present study) [10]. ² Single-crystal X-ray diffraction [11]. ³ Powder neutron diffraction [12]. ⁴ Inelastic neutron scattering [9]. ⁵ Convergent-beam electron diffraction [13].

lists ADPs of Si obtained by different experimental techniques. Among others, inelastic neutron scattering is recognized to yield the most accurate and precise value (59.4(2) × 10⁻⁴ Ų) [9]. In the present study, the pair distribution function (PDF) analysis of total scattering data shows that the ADP is estimated to be 59.5(1) × 10⁻⁴ Ų [10], which is agreement with the reference value within the estimated standard deviation. The results clearly indicate that our total scattering data are both accurate and precise.

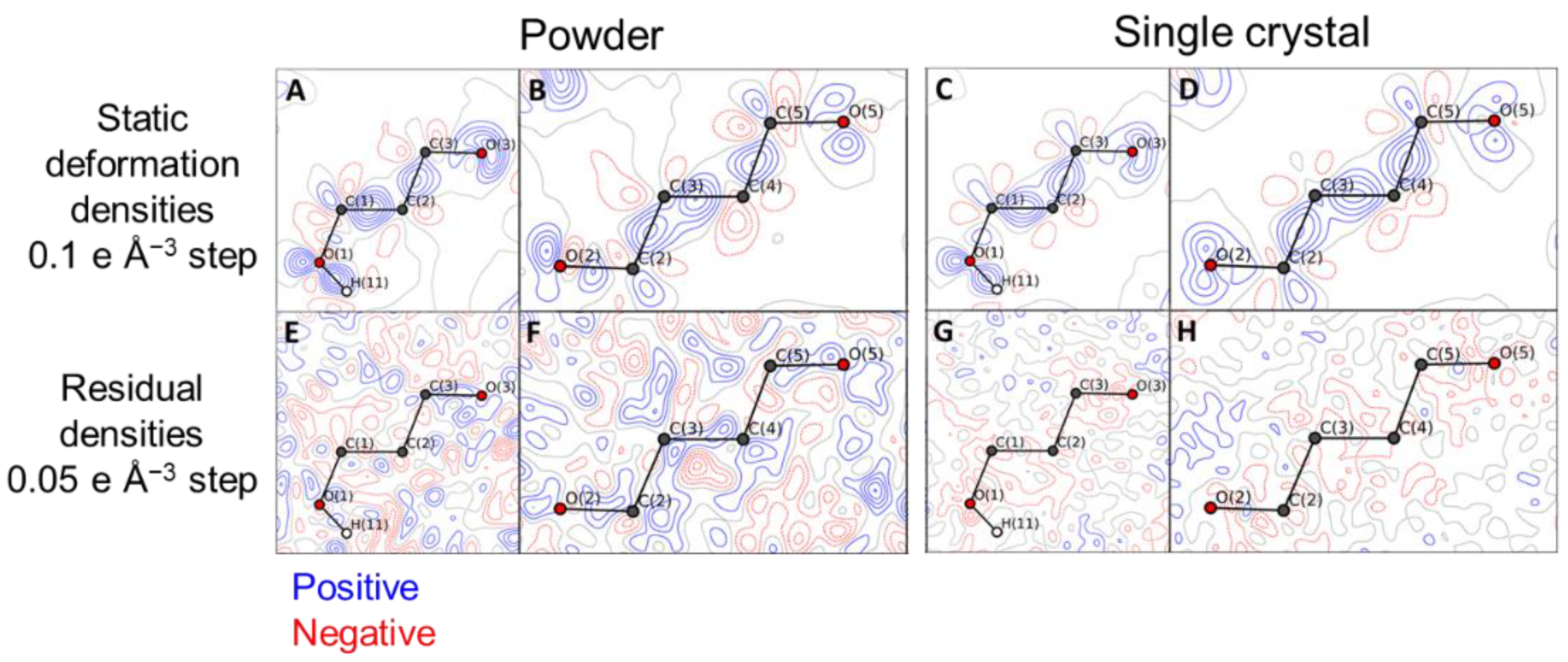
It remains challenging for powder X-ray diffraction to study valence densities of organic compounds due to lower scattering power and crystal symmetry. In fact, valence density studies have been performed using single crystals [14]. To evaluate the quality of Bragg reflections reduced from total scattering data, inorganic and organic compounds have been analyzed by the multipole refinement method [15]. Figure 7 illustrates the static deformation and the residual densities of xylitol, obtained by our powder method, which are compared to those by a reference single crystal method. The results from powders are comparable to those from single crystals. The consistency between the two results is due to the XRNU correction of the OHGI data.

4. Conclusions

In the present study, we achieved a precision of 0.1% in total scattering data by improving accuracy or XRNU in microstrip detectors, which leads to valence density studies from powders [15] and PDF studies for ADPs [10]. Consequently, the integration of hardware (OHGI) [6] into software (ReLiEf) [7] has received a positive comment, as “Nothing trumps good data” [16].