Abstract
Zirconium nitride (ZrN) is an important material for the mechanical industries due to its excellent properties such as excellent wear resistance, high hardness, etc. In practical applications, it is necessary to study how to regulate the mechanical properties of materials to meet the needs of different applications. To better understand the influence of vacancies and oxygen on the mechanical property of ZrN, we studied the tensile strength of the ZrN with oxygen atom doping and zirconium vacancy introduction by ab initio density functional theory. The mechanical property changes of modified ZrN in three crystallographic directions (<001>, <110>, and <111>) were calculated. The results show that the tensile strength of ZrN can be increased by oxygen doping at a certain concentration, while that of ZrN can be decreased by the introduction of zirconium vacancy.
1. Introduction
Transition metal nitrides indicates a class of compounds in which the nitrogen atoms are integrated into the lattice gap of the parent transition metal [1]. As a material widely used in mechanical manufacturing, transition metal nitrides have attracted the attention of many researchers due to their excellent properties, including excellent thermal conductivity, corrosion resistance, and mechanical properties. In addition, their excellent electrical properties [2] make them of great value in supercapacitors, lithium-ion batteries, catalysis, sensors, etc. [3,4,5]. In recent years, related researches on pure transition metal nitrides have gradually reached a bottleneck, prompting researchers to search for a method to improve the performance of transition metal nitrides [6]. Many different methods have been proposed as methods to modify transition metal nitrides including plasma modification [7], heterostructure building [8], oxidation [9], etc.
Zirconium nitride (ZrN) is one kind of 4-D transition metal nitride, and is a NaCl type metal crystal with a space group of . The crystal structure of ZrN is cubic symmetry in which each ion has six adjacent ions (i.e., each ion is located in the center of one octahedral gap) [10,11,12]. ZrN possesses numerous outstanding performances in the field of manufacturing, including excellent wear resistance, high hardness, and higher chemical stability at room temperature [1,11,12,13]. The excellent performance of ZrN makes it an attractive material for machine tools, which need excellent mechanical properties. Materials with different mechanical properties (i.e., tensile strength, shear strength, elasticity, and plasticity) will have completely different applications in industrial production, which demonstrates the importance to study the method to regulate the mechanical property of corresponding materials. In the past few decades, people have conducted numerous researches to modify the parent material for more excellent mechanical property. Among them, the doping process was widely reported: Wang G et al. reported the mechanical strength of silicon single crystal with the doping of nitrogen, which indicated the doped nitrogen atoms can increase the flexure strength of the single crystal silicon [14]; Wang P et al. reported an investigation about the multicrystalline silicon by germanium doping, which shows a higher fracture strength than the parent material [15]; Chen J.H et al. reported the enhancement effect of germanium doping on the mechanical property of Czochralski silicon wafers [16]. These previous studies have fully demonstrated that the doping of atoms is feasible and important for improving the mechanical properties of materials. As a kind of popular modified method, oxygen doping and vacancy introduction can significantly change the properties of materials, which has been confirmed in many previous studies [17,18]. However, studies about how the oxygen and zirconium vacancy influence the strength properties of ZrN were lacking.
Density functional theory (DFT) is a computational modelling method based on the quantum mechanical theory. In the past few decades, the DFT has been applied as an important material research method in physics, chemistry, and materials science. Compared with experiments, using DFT method to study material properties can avoid excessive time and financial costs, and provide guidance for material design in laboratory [19,20,21]. The wide application of DFT has greatly promoted the research progress of material properties. Numerous researches have implemented DFT calculations to obtain the mechanical properties of different materials, thus greatly improving the efficiency of the design of related materials [22,23]. For example, Zhang M et al. calculated the stress–strain relations of d-BC3 (i.e., highly symmetric BC3 phase in the cubic diamond structure) with DFT and demonstrated its super hard nature and excellent ductility [24]; Krenn C.R. et al. performed a series of pseudopotential DFT and obtained the ideal shear strength of aluminum and copper [25]; Zhang R.F et al. calculated the stress–strain relationship under tensile and shear load of the silicon nitrides by ab initio calculation based on DFT, which successfully demonstrated that the Si3N4 was mechanically stronger than the SiN.
In this study, we modified the ZrN with the introduction of oxygen atoms and zirconium vacancies. The ideal stress–strain relationship of the zirconium nitride under oxygen doping and vacancy introduction was obtained through a series of DFT calculations. In doped ZrN, oxygen atoms have been introduced as interstitial and substitutional defects, and their formation energies was calculated. Then, we modified the structure of Zr32N32 with oxygen doping and vacancy introduction. In order to investigate the changes in mechanical properties, we studied them from three different crystallographic directions: <001>, <110>, and <111>. The related content is discussed in next part.
2. Results and Discussions
Before the doping of oxygen atoms into the crystal structure of ZrN, it is necessary to study how the oxygen atoms will exist in the crystal structure. Therefore, the formation energy of doping oxygen atoms was calculated. As is shown in Figure 1a,b, the primitive cell of ZrN was expanded with multiple to avoid the phase transition caused by the excessively high content of oxygen atoms or VZr and the structure of (i.e., or ) was obtained. There are two possible manners of doping: substitutional doping and interstitial doping. Therefore, the structure of was firstly doped with 1, 2, and 3 oxygen atoms, respectively, in an interstitial manner, and the corresponding structures after doping were denoted as (n = 1, 2, and 3). The corresponding structures after the doping was shown in Figure S2. In this process, the formation energy of single oxygen atom () can be obtained according to the following formula [26]:
where and represent the energy of and oxygen molecule (), respectively. As the blue line in Figure 1c shows, the formation energy of one oxygen atom is −0.24 eV, −0.17 eV and −0.15 eV, respectively.
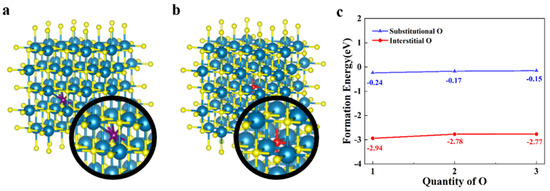
Figure 1.
(a) The structure of ZrN after doping of oxygen atoms in interstitial manner (blue atoms: Zr, yellow atoms: N, and purple atom: interstitial O). (b) The structure of ZrN after doping of oxygen atoms in substitutional manner (red atom: substitutional O). (c) The formation energy of single oxygen atom under different doping ratio.
Then, we performed the oxygen doping on in a substitutional manner, and the structure of was obtained (n = 1, 2, and 3). The corresponding crystal structures can be seen in Figure 1b. The formation energy of one substitutional oxygen atom was calculated according the following formula:
where and represent the total energy of and nitrogen molecule (), respectively. As shown in Figure 1c, in different doping ratios of substitutional oxygen were −2.94 eV, −2.78 eV, and −2.77 eV, respectively. The formation energy of substitutional oxygen atom was much lower than that of the interstitial oxygen atom (>2 eV). The lower formation energy of the substitutional oxygen atom means that it has higher stability than interstitial oxygen. In this process, we demonstrated that the oxygen atom existed in the zirconium nitride crystal structure in a substitution-doped manner. In this part of the calculation, the total energy of and can be seen in Table S1 in the Supplementary Materials. The values of and were obtained from the experimental data [27].
We first calculated the stress–strain relationship in the crystal direction of <001>, <010>, and <100>, which are shown in Figure 2. Figure 2a shows the initial structure of Zr32N32, while Figure 2b,c shows the front view and the top view of the structure after tensile strain (i.e., in the crystallographic direction of <001>). Apparently, the structure of Zr32N32 became longer after the simulation of tensile stain, but the arrangement of the atoms is still ordered. Then, different ratios of tensile distances in the lattice of Zr32N32 were applied. As is shown in Figure 2d–f, the same processes are performed on three mutually perpendicular crystallographic direction (<001>, <010>, and <100>), and the corresponding relationships between stress and strain are obtained. The maximum value in the stress–strain relationship reflects the tensile strength of the lattice in one of the crystal directions. In Figure 2d–f, the stress of Zr32N32 reaches its maximum value at a ratio strain of 0.11, indicating a corresponding ideal tensile strength of 28.2 GPa. As the strain continued to increase, there was no sudden drop in stress, indicating that the Zr32N32 did not fracture during the tensile process. In addition, it is clear that the stress–strain relationships of ZrN in the three crystallographic directions are almost identical, which is the result of the symmetry of ZrN.
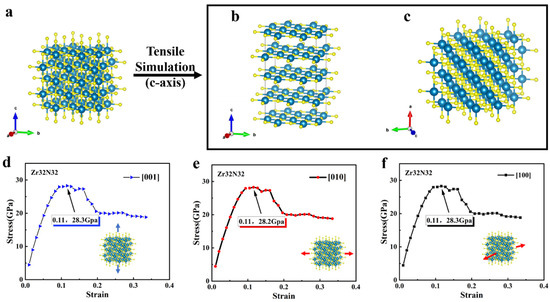
Figure 2.
(a) The structure of Zr32N32 (Blue atoms: Zr, yellow atoms: O) (b) Front view of the structure after tensile strain. (c) Top view of the structure after tensile strain (d–f) The stress–strain relationship of Zr32N32 in three different crystallographic directions (<001>, <010>, and <100>).
The mechanical properties of the relevant structures in the crystallographic direction of <001> are analyzed. The structure of Zr32N31O (i.e., Zr32N32 with doping one oxygen atom) and Zr31N32 (i.e., Zr32N32 with one Zr atom being removed) are shown in Figure 3a,c, respectively. After a similar DFT calculation, the stress–strain relationship (i.e., in the <001> crystallographic direction) of Zr32N31O are shown in Figure 3b and Figure S1a,b. Compared to Zr32N32, the ideal tensile stress of Zr32N31O was increased to 29.4 GPa. The stress–strain relationships of Zr31N32 in the <001> were shown in Figure 3d and Figure S1c,d. The ideal tensile stress of Zr31N32 was increased to 29.0GPa compared to that of Zr32N32. In addition, the mechanical properties of Zr32N31O and Zr31N32 are very similar in the three crystal directions, which further indicated that the symmetry of the crystals was well maintained. Therefore, only the mechanical properties in the <001> crystal direction will be analyzed in the following part of this paper.
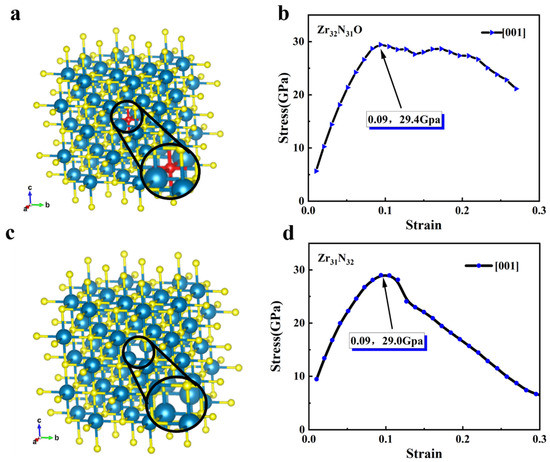
Figure 3.
(a) The structure of Zr32N31O (blue atoms: Zr, yellow atoms: N, red atom: O). (b) Stress–strain relationship of Zr32N31O in the <001> crystallographic direction. (c) The structure of Zr31N32. (d) Stress–strain relationship of Zr31N32 in the <001> crystallographic direction.
The tensile simulation tests were then performed in the <110> crystallographic direction and <111> crystallographic direction of the related structures. The stress–strain relationships of Zr32N32, Zr32N31O, and Zr31N32 in the <110> crystallographic direction were shown in Figure 4a,c,e. In the <110> crystallographic direction, the tensile strengths of Zr32N32, Zr32N31O, and Zr31N32 were 28.6 GPa, 40.2 GPa, and 31.3 GPa, respectively. The variation of the above values indicates that the doping of oxygen atoms and the introduction of zirconium vacancies both increase the ideal tensile strength of ZrN. In addition, both Zr32N31O and Zr31N32 fracture in the process of tensile simulations (i.e., a steep drop of stress), indicating a reduced plasticity (corresponding material becomes more brittle). The stress–strain relationships of Zr32N32, Zr32N31O, and Zr31N32 in the <111> crystallographic direction are shown in Figure 4b,d,f. In the <111> crystallographic direction, the doping of oxygen atoms and the introduction of zirconium vacancies also reduced the plasticity. However, the values of tensile strength of Zr32N31O (40.2 GPa) and Zr31N32 (28.3 GPa) were both reduced compared to Zr32N32 (42.8 GPa).The effect of oxygen atom doping and the introduction of vacancies on the mechanical properties of the ZrN structure varies with the crystallographic direction. In fact, the mechanical properties of polycrystalline ZrN should be isotropic. Therefore, the mechanical property variations of the three crystallographic directions should be considered comprehensively. The crystal grains of modified ZrN are randomly arranged in various directions to form a polycrystalline ZrN and grain boundaries between two grains are also connected in an arbitrary orientation, indicating that polycrystalline materials are isotropic. Therefore, the crystallographic direction with the greatest change will dominate the overall change of mechanical properties. After doping Zr32N32 with oxygen atoms, the change in tensile strength in the <110> crystallographic direction (i.e., increased by 14.5 GPa) is much larger than that in the other two directions. After introducing on zirconium vacancy into Zr32N32, the change in tensile strength in the <111> crystallographic direction (i.e., decreased by 14.5 GPa) is much larger than that in the other two directions. These results illustrated that the doping of oxygen can increase the tensile strength and the introduction of zirconium vacancy decrease the tensile strength.
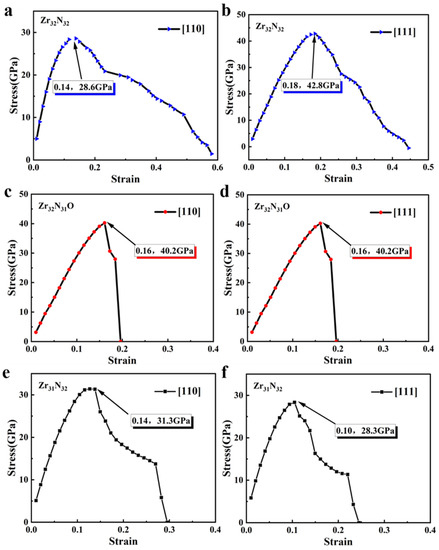
Figure 4.
(a,b) The stress–strain relationship of Zr32N32 in <110> and <111> crystallographic direction. (c,d) The stress–strain relationship of Zr32N31O in <110> and <111> crystallographic direction. (e,f) The stress–strain relationship of Zr32N31O in <110> and <111> crystallographic direction.
3. Computational Details
To obtain the mechanical properties of the ZrN under the doping of oxygen and introduction of zirconium vacancy, the Vienna ab initio simulation package (VASP) code was used for the related calculation [28]. The cutoff energy was set at 600 eV. The k-point mesh of was used for the optimization and a k-point mesh of was used for the calculation of the ideal tensile strength. In our calculation, the convergence criteria of the energy and force were and , respectively. We used the Monkhorst–Pack grid route to sample the Brillouin zone. The Perdew–Burke–Ernzerhof (PBE) exchange-correlation function within the generalized gradient approximation (GGA) was chosen for the description of interactions between ions and electrons. The stress–strain relationship was obtained through the procedure provided by Liu et al. [24,29,30], which is available on the official website of the ideal-strength-vasp.
4. Conclusions
In summary, a series of DFT calculations on mechanical properties and energies were implemented to obtain stress–strain relationships for ZrN under oxygen doping and zirconium vacancy introduction. In this paper, the most probable manner of oxygen atom doping is first investigated. By comparing the formation energies, it is demonstrated that the substitutional oxygen atoms are more stable than the interstitial oxygen atoms. Thereafter, we modified the structure of Zr32N32 with two methods, including the doping of oxygen atoms and the introduction of zirconium vacancies. In order to investigate the changes in mechanical properties, we studied them from three different crystallographic directions: <001>, <110>, and <111>.
After doping Zr32N32 with oxygen atom, the ideal tensile strength in the <001> direction increases by 1.4 GPa; the ideal tensile strength in the <110> direction increased by 11.6 GPa; and the ideal tensile strength in the <111> direction decreased by 2.6 GPa. In addition, the fracture of Zr32N31O in the <110> and <111> directions proves that its plasticity is lower than that of Zr32N32. Therefore, the doping of oxygen atoms can increase the tensile strength and decrease the plasticity of ZrN.
After the introduction of vacancies into the Zr32N32 lattice, the tensile strength changed less in the <001> and <110> crystal directions (less than 3 GPa). In the <111> crystal direction, the tensile strength decreased by 14.5 GPa. The above changes indicate that the introduction of zirconium vacancies decreases the tensile strength of ZrN. In addition, the introduction of vacancies also leads to the fracture of the related structures, indicating that the plasticity of ZrN becomes lower.
In this work, the mechanical property of ZrN under doping of oxygen and introduction of zirconium vacancies was analyzed by theoretical calculations. Therefore, experimental synthesis of corresponding materials and verification of related properties by tensile test will be necessary, which will be considered in our future research. In addition, the effect of higher concentration of oxygen atoms and vacancy defects on the performance of ZrN will also be the focus of future work.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/condmat6030032/s1, Figure S1. Stress-strain relationship of Zr32N31O; Figure S2. The location of the oxygen atoms during the calculation of formation energy; Table S1. The total energies in the calculation of the formation energy. The procedure used to obtain the stress–strain relationship in this study (i.e., provided by Dr. Liu et al.) is available at: https://sourceforge.net/projects/ideal-strength-vasp/files/.
Author Contributions
J.C.: Conceptualization, Methodology, Visualization, Data curation, and Writing—Original draft. S.W.: Methodology and Visualization. J.L.: Conceptualization, Methodology, Supervision, Resources, and Writing—Review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by the National Key Laboratory of Science and Technology on Micro/Nano Fabrication, China.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Zhao, S.; Ma, J.; Xu, R.; Lin, X.; Cheng, X.; Hao, S.; Zhao, X.; Deng, C.; Liu, B. Synthesis and Characterization of Zirconium Nitride Nanopowders by Internal Gelation and Carbothermic Nitridation. Sci. Rep. 2019, 9, 19199. [Google Scholar] [CrossRef]
- Kobayashi, K. First-principles study of the electronic properties of transition metal nitride surfaces. Surf. Sci. 2001, 493, 665–670. [Google Scholar] [CrossRef]
- Idrees, M.; Mukhtar, A.; Ata-ur-Rehman; Abbas, S.M.; Zhang, Q.; Li, X. Transition metal nitride electrodes as future energy storage devices: A review. Mater. Today Commun. 2021, 27, 102363. [Google Scholar] [CrossRef]
- Cheng, Z.; Qi, W.; Pang, C.H.; Thomas, T.; Wu, T.; Liu, S.; Yang, M. Recent Advances in Transition Metal Nitride-Based Materials for Photocatalytic Applications. Adv. Funct. Mater. 2021, 31, 2100553. [Google Scholar] [CrossRef]
- Park, S.H.; Jo, T.H.; Lee, M.H.; Kawashima, K.; Mullins, C.B.; Lim, H.-K.; Youn, D.H. Highly active and stable nickel–molybdenum nitride (Ni2Mo3N) electrocatalyst for hydrogen evolution. J. Mater. Chem. A 2021, 9, 4945–4951. [Google Scholar] [CrossRef]
- Kang, B.K.; Choi, Y.J.; Choi, H.W.; Kwon, S.B.; Kim, S.; Kim, Y.J.; Park, J.S.; Yang, W.S.; Yoon, D.H.; Ryu, W.-H. Rational design and in-situ formation of nickel–cobalt nitride multi-core/hollow N-doped carbon shell anode for Li-ion batteries. Chem. Eng. J. 2021, 420, 129630. [Google Scholar] [CrossRef]
- Osonkie, A.; Lee, V.; Chukwunenye, P.; Cundari, T.; Kelber, J. Plasma modification of vanadium oxynitride surfaces: Characterization by in situ XPS experiments and DFT calculations. J. Chem. Phys. 2020, 153, 144709. [Google Scholar] [CrossRef] [PubMed]
- Pham, K.D.; Nguyen, C.Q.; Nguyen, C.V.; Cuong, P.V.; Hieu, N.V. Two-dimensional van der Waals graphene/transition metal nitride heterostructures as promising high-performance nanodevices. New J. Chem. 2021, 45, 5509–5516. [Google Scholar] [CrossRef]
- Baturina, O.A.; Epshteyn, A.; Leff, A.C.; Purdy, A.P.; Brintlinger, T.; Simpkins, B.S.; Santiago, E.Y.; Govorov, A.O. Photoelectrochemical Methanol Oxidation Under Visible and UV Excitation of TiO2-Supported TiN and ZrN Plasmonic Nanoparticles. J. Electrochem. Soc. 2021, 168, 016503. [Google Scholar] [CrossRef]
- Patsalas, P.; Kalfagiannis, N.; Kassavetis, S.; Abadias, G.; Bellas, D.V.; Lekka, C.; Lidorikis, E. Conductive Nitrides: Growth Principles, Optical and Eectronic Properties, and Their Perspectives in Photonics and Plasmonics. Mater. Sci. Eng. R Rep. 2018, 123, 1. [Google Scholar] [CrossRef]
- Hao, Y.-J.; Ren, H.-S.; Zhu, B.; Zhu, J.; Qu, J.-Y.; Chen, L.-Q. Theoretical study of the structural phase transformation and elastic properties of the zirconium nitride under high pressure. Solid State Sci. 2013, 17, 1–5. [Google Scholar] [CrossRef]
- Patsalas, P. Zirconium Nitride: A Viable Candidate for Photonics and Plasmonics? Thin Solid Film. 2019, 688, 137438. [Google Scholar] [CrossRef]
- Courts, S.S.; Swinehart, P.R. Review of CernoxTM (Zirconium Oxy-Nitride) Thin-Film Resistance Temperature Sensors. AIP Conf. Proc. 2003, 684, 393–398. [Google Scholar]
- Wang, G.; Yang, D.; Li, D.; Shui, Q.; Yang, J.; Que, D. Mechanical strength of nitrogen-doped silicon single crystal investigated by three-point bending method. Phys. B Condens. Matter 2001, 308–310, 450–453. [Google Scholar] [CrossRef]
- Wang, P.; Yu, X.; Li, Z.; Yang, D. Improved fracture strength of multicrystalline silicon by germanium doping. J. Cryst. Growth 2011, 318, 230–233. [Google Scholar] [CrossRef]
- Chen, J.; Yang, D.; Ma, X.; Zeng, Z.; Tian, D.; Li, L.; Que, D.; Gong, L. Influence of germanium doping on the mechanical strength of Czochralski silicon wafers. J. Appl. Phys. 2008, 103, 123521. [Google Scholar] [CrossRef]
- Jung, J.; Bae, D.; Kim, S.; Kim, H.-D. Reduced Operation Current of Oxygen-Doped ZrN Based Resistive Switching Memory Devices Fabricated by the Radio Frequency Sputtering Method. Coatings 2021, 11, 197. [Google Scholar] [CrossRef]
- Liu, Q.; Li, Y.; Xiao, W. Oxygen impurity effects on the mechanical properties of SiC studied by first principles calculations. Mater. Today Commun. 2019, 19, 360–365. [Google Scholar] [CrossRef]
- Jain, A.; Hautier, G.; Moore, C.J.; Ping Ong, S.; Fischer, C.C.; Mueller, T.; Persson, K.A.; Ceder, G. A high-throughput infrastructure for density functional theory calculations. Comput. Mater. Sci. 2011, 50, 2295–2310. [Google Scholar] [CrossRef]
- Armiento, R.; Kozinsky, B.; Fornari, M.; Ceder, G. Screening for high-performance piezoelectrics using high-throughput density functional theory. Phys. Rev. B 2011, 84, 014103. [Google Scholar] [CrossRef]
- Curtarolo, S.; Hart, G.L.W.; Nardelli, M.B.; Mingo, N.; Sanvito, S.; Levy, O. The High-throughput Highway to Computational Materials Design. Nat. Mater. 2013, 12, 191–201. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef]
- Emery, A.A.; Saal, J.E.; Kirklin, S.; Hegde, V.I.; Wolverton, C. High-Throughput Computational Screening of Perovskites for Thermochemical Water Splitting Applications. Chem. Mater. 2016, 28, 5621–5634. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, H.; Li, Q.; Gao, B.; Wang, Y.; Li, H.; Chen, C.; Ma, Y. Superhard BC3 in Cubic Diamond Structure. Phys. Rev. Lett. 2015, 114, 015502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krenn, C.R.; Roundy, D.; Morris, J.W.; Cohen, M.L. The non-linear elastic behavior and ideal shear strength of Al and Cu. Mater. Sci. Eng. A 2001, 317, 44–48. [Google Scholar] [CrossRef]
- Huang, H.H.; Fan, X.; Hu, C.Q.; Singh, D.J.; Jiang, Q.; Zheng, W.T. Transformation of Electronic Properties and Structural Phase Transition from HfN to Hf3N4. J. Phys. Condens. Matter 2015, 27, 225501. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-energy Calculations Using A Plane-wave Basis Set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Hao, J.; Liu, H.; Lu, S.; Tse, J.S. High-Energy Density and Superhard Nitrogen-Rich B-N Compounds. Phys. Rev. Lett. 2015, 115, 105502. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Lu, M.; Du, Y.; Gao, L.; Lu, C.; Liu, H. Hardness of FeB4: Density functional theory investigation. J. Chem. Phys. 2014, 140, 174505. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).