Abstract
Using fingerprints used mainly in machine learning schemes of the potential energy surface, we detect in a fully algorithmic way long range effects on local physical properties in a simple covalent system of carbon atoms. The fact that these long range effects exist for many configurations implies that atomistic simulation methods, such as force fields or modern machine learning schemes, that are based on locality assumptions, are limited in accuracy. We show that the basic driving mechanism for the long range effects is charge transfer. If the charge transfer is known, locality can be recovered for certain quantities such as the band structure energy.
1. Introduction
Most approximate chemical simulation schemes are based on a locality assumption. A local property, such as a local charge distribution, an atomic spin polarization or atomic energy as well as bond lengths are assumed to depend only on a nearby local environment, but not features far away. The locality assumption is very well satisfied in many covalently bonded systems. As an example let us consider the total energy of the alkanes polymers, . Each monomer is energetically virtually an independent unit. As one adds an additional monomer, the energy increases by an amount that is nearly independent of the chain length. Insertion of a monomer into the smallest chain, , gives already an energy gain that agrees to within Ha with the asymptotic value of the insertion energy for very long chains [1]. This shows that the electrons belonging to this inserted sub-unit no longer “see” the end of the chain. This locality principle has therefore been dubbed “nearsightedness” by Walter Kohn [2,3,4] and he claimed it to be valid nearly universally. While charge transfer driven by electronegativity differences in multi-component systems is well established and accounted for in most simulation schemes, it is generally neglected in single-component covalent materials. In this study, we will consider pure carbon systems and show that even in such a simple covalent system, non-local effects play an important role.
All the standard force fields for this material [5], such as EDIP [6], Tersoff [7], Brenner [8] or recent versions of bond order potentials [9], are also based on this locality assumption. Modern machine learning schemes [10,11,12] are based on this locality assumption as well. The energy is given in these schemes as a sum over atomic energies which depend only on a short range environment. Long range electrostatic energies are sometimes still added [13,14,15,16], but the atomic charges giving rise to these interactions depend again only on a local environment, whereas in reality, they are strongly influenced by non-local effects.
2. Methodology
To demonstrate the existence of non-local effects, one has to show that local physical properties are different for short range environments that are virtually identical. Environment descriptors, also called atomic fingerprints, that quantify the similarity of chemical environments have recently been developed in the context of machine learning and for analysing big structural data banks [17,18,19,20]. We will use in this study mainly the fingerprints based on the eigenvalues of an atom-centered overlap matrix [21], since these descriptors have demonstrated a high reliability in detecting differences in the local environment [22]. We use a cutoff radius of 6 Å and s and p type orbitals for the overlap matrix. Denoting a fingerprint vector describing the environment of two atoms and by and , we obtain a measure of the similarity by calculating the fingerprint distance as the euclidean norm . Small values indicate that the environments are similar. In addition, we also use the SOAP fingerprint [18], which is another high resolution fingerprint [22]. For the SOAP fingerprint, we used the same cutoff radius of 6 Å together with the following parameters: , Å and Å. The SOAP fingerprint distance is calculated in the usual way as .
In this work, we will correlate fingerprint distances with differences of localized physical properties of the system, such as atomic charge densities, atomic energies, and atom-projected densities of states. These changes in the charge densities will finally also modify bond lengths of our systems in a non-local way.
To split up global quantities into atomic quantities, we use the following partitioning of the unity :
where is the number of atoms in the system and denotes the Cartesian coordinates of atom . is some smearing parameter which we take to be equal to the covalent radius of atom . The function has large values around atom , and as we move further away from atom , it becomes very small and it has the property . It can be considered as some kind of smooth Voronoi decomposition of space, since it will give the Voronoi decomposition in the limit of small . Let us also still point out the trivial but important point that this smooth Voronoi decomposition depends only on the nearest neighbor positions. So, if the local environment is not changed, the Voronoi volume will not be modified either. Hence, if some quantity that is derived from this partitioning exhibits non-local effects, it cannot be due to some change in the shape of the smooth Voronoi volume, but must be due to a change in the physical quantities. The physical quantities that will be examined are the wavefunctions and their Kohn–Sham eigenvalues.
As a first quantity, we define atomic charges
where and are eigenvalues and eigenfunctions of the Hamiltonian of the system and are obtained by solving the Schroedinger equation for the system within density functional theory (DFT) using the Perdew-Burke-Ernzerhof (PBE) functional [23] together with accurate norm conserving pseudopotentials [24]. The calculations were done with the BigDFT code [25] using a grid spacing of 0.4 Bohr and a self-consistent field (SCF) convergence threshold of . is the occupation number of the state with energy at an electronic temperature of Ha. Since, as pointed out above, the Voronoi volume will not be influenced by non-local effects, this quantity is a direct measure of the change in the charge density around the central atom. This is in contrast to some other charge decomposition schemes such as Bader [26] or Mulliken [27], where the volume associated to an atom is not determined by the geometry of the local environment, but by the charge density or the wavefunction.
As a second quantity, we define atomic energies . Since the decomposition of the total energy is highly ambiguous [28], we perform this decomposition only for the band structure energy, which can again be assigned in a unique way to the smooth Voronoi volumes by partitioning the energy density.
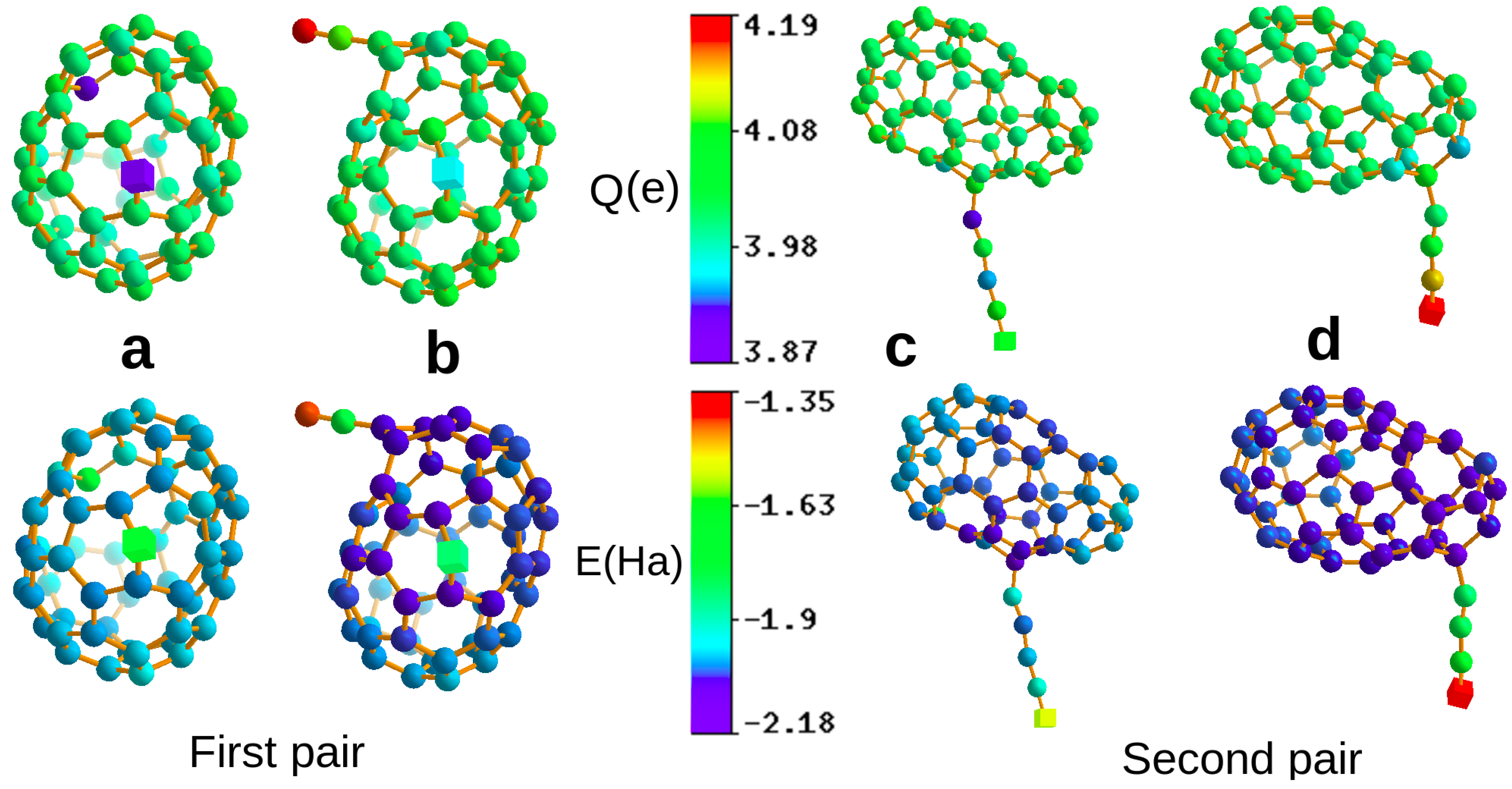
Since is a partitioning of the unity, the sum over all the atomic energies gives the band structure energy, i.e., . As is well known [29], the band structure energy term, , is the most important term to describe variations in the total energy. As shown in Figure 1, these atomic energies agree well with our basic chemical intuition, of which environment will give rise to low or high atomic energies. The atoms at the end of the chains have, for instance, the highest energies, whereas the atoms of the cage have lower energies. For these atoms, the energy is however also larger for atoms in a defective cage region.
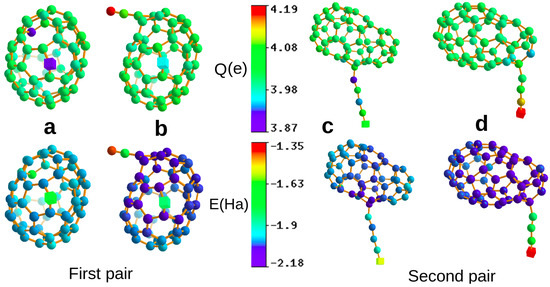
Figure 1.
Two pairs of distinct structures (a–d), where we can find central atoms (shown as cubes) that are in virtually identical short range chemical environments, with fingerprint distances of . Due to long range effects, the atomic charges and atomic energies are, however, quite different. The atoms in the first and second row are coloured according to their atomic charges and energies respectively. Ha and electrons for the pair in the left column and Ha and electrons for the pair in the right column.
As a third quantity, we study the atom projected density of states. The density of states for the system is . We define the atom-projected density of states for atom to be:
With the property . We replace for in Equation (4), where is a smearing parameter whose value is 0.05 Ha. We define the difference between the atom-projected density of states of two atoms in structure p and in structure q to be:
This quantity can be calculated analytically for the numerically obtained s.
3. Results
By a combination of minima hopping [30,31,32] (MH) and molecular dynamics (MD) coupled to density functional-based tight binding (DFTB) [33], we have generated a large number of clusters, with 60 carbon atoms. This data base of 3000 configurations contains a wide range of structural motifs, including chains, graphitic sheets and cages. In this way, 180,000 environments were created. By analysing the correlation between the fingerprint distances and the physical observables, we will show that it is possible to detect in a fully automatic way non-local effects in our structures. So, our search for non-local effects is much more comprehensive than would be possible with a search based on human intuition.
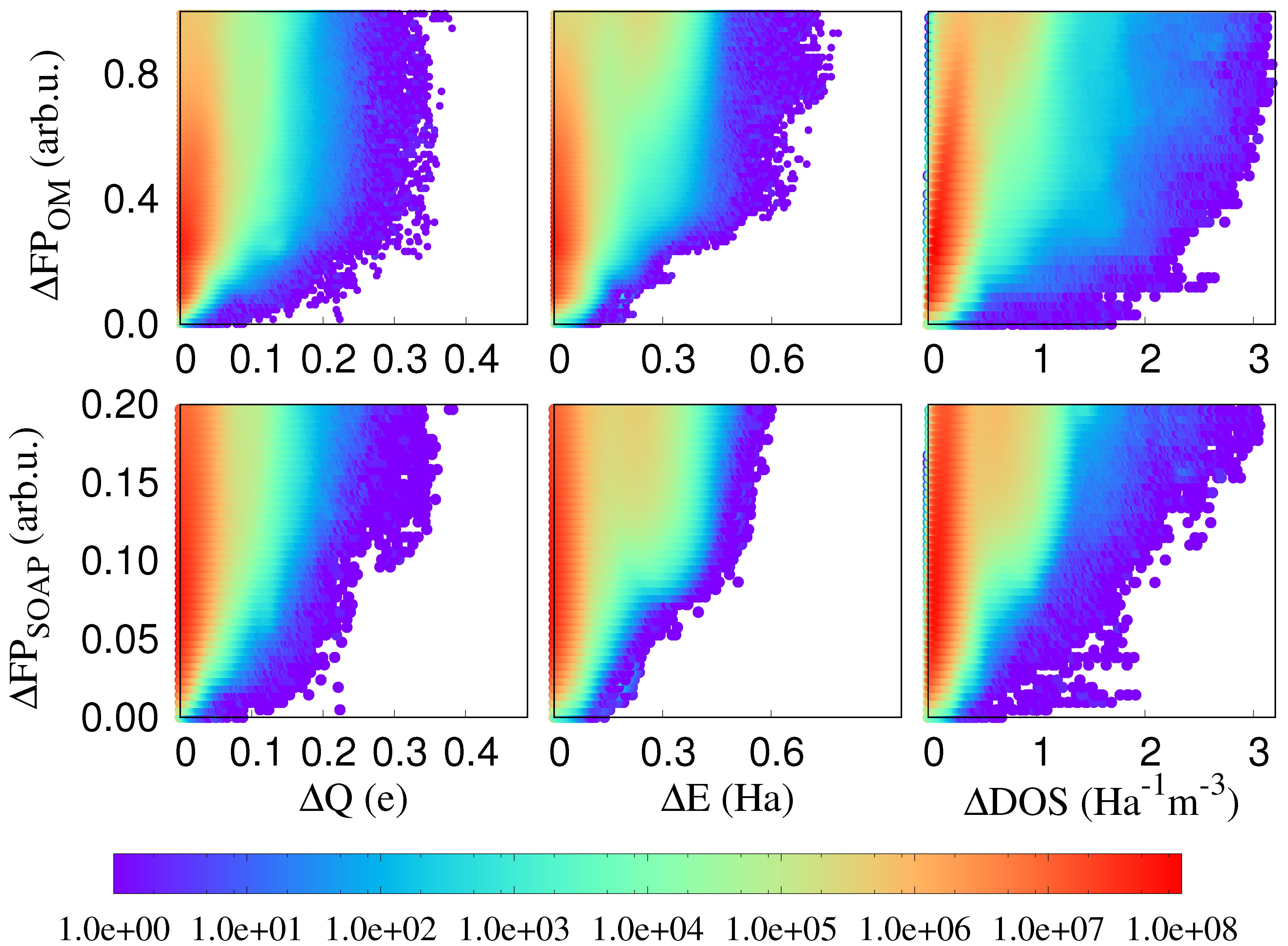
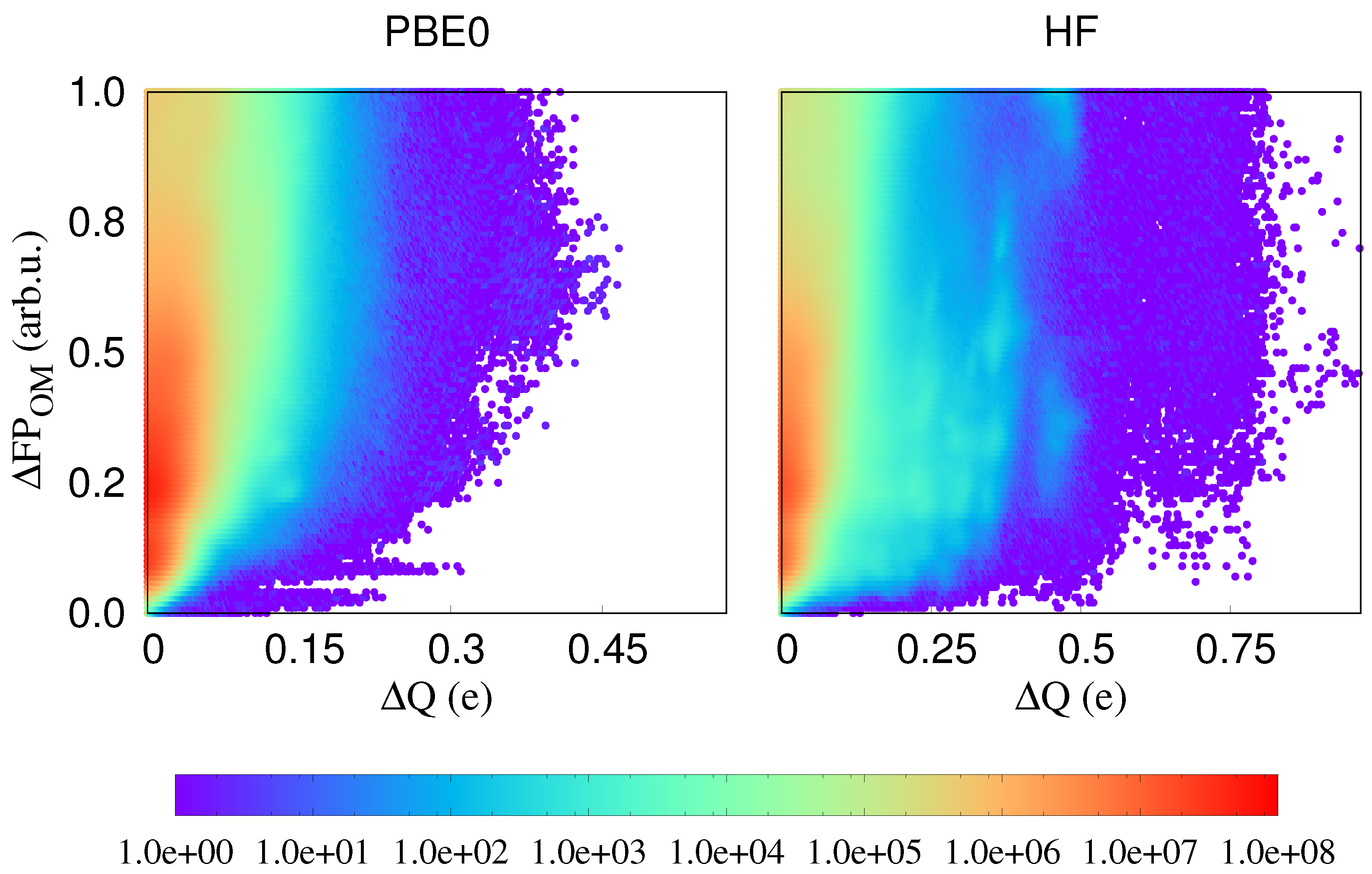
In Figure 2, we plot differences of three local physical properties, namely atomic charges, atomic energies and the atom-projected density of states, against fingerprint distances. In all these cases, it may happen that the same value of a physical property is observed for different environments. Energies might for instance be degenerate. However, if these localised physical properties differ for identical or nearly identical environments, localised physical properties are influenced by long range effects. Such cases correspond to points on or very close to the x axis in our correlation plots and we see that indeed plenty of such problematic points exist. Since in related contexts it was shown that PBE does not give a very accurate description of charge transfer [34], we have in addition performed the same calculations with the PBE0 functional [35,36] and the Hartree–Fock method. As can be seen from Figure 3, such problematic points exist in all cases and the non-local effects are clearly not an artifact of the PBE functional. Neither does the choice of the fingerprint influence the result. As can also be seen from Figure 2, virtually identical results are obtained with the SOAP fingerprint [18]. Hence, long range effects clearly exist in this single component covalent system.
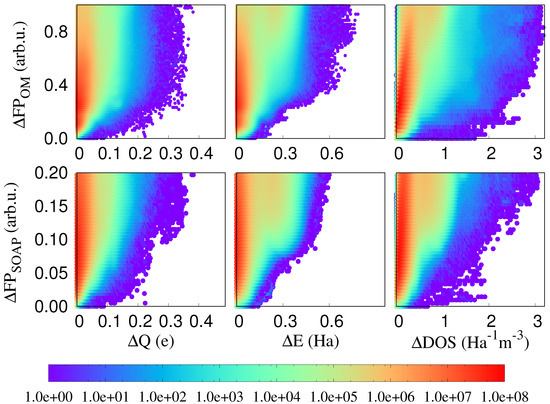
Figure 2.
The correlation plot between OM and SOAP fingerprint distances among atomic environments and the differences in atomic charge (Equation (2)), atomic energy (Equation (3)), and the atom projected DOS (Equation (4)) of the central atoms of these environments. The colour coding indicates the density of correlation pairs. Within our chosen resolution, there are about 200,000 points on the x-axis, which corresponds to about 0.001 percent of the total number of points.
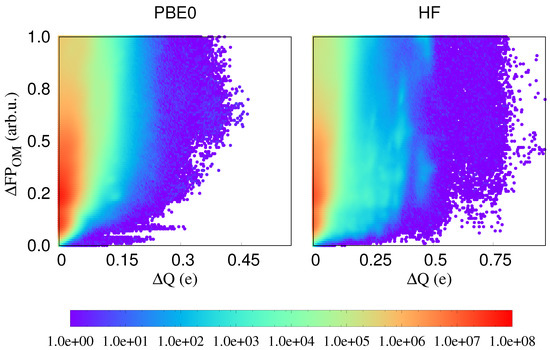
Figure 3.
The correlation between fingerprint distances and the atomic charge differences calculated in PBE0 and HF. The color coding indicates the density of correlation pairs.
Having established the existence of long range effects on local physical properties in a purely algorithmic way, it is interesting to see whether they can also be explained by traditional physical arguments. A structure that is strongly affected by non-local effects is the structure shown in Figure 1d. It consists of a cage of 56 carbon atoms and a 4 carbon atom chain attached to it. If one calculates the Kohn–Sham eigenvalues of the two isolated fragments, i.e., the 4 atom chain and the 56 atom cage one finds that the LUMO level of the chain is lower than the HOMO level of the cage. Hence, in a simple one particle picture one electron would be transferred from the cage to the chain. In a DFT calculation, such a charge transfer is always reduced by the electron-electron repulsion, and based on our analysis of the atomic charges, we find indeed only a charge transfer of about 0.34 electrons, with the PBE functional in this case. We were able to find analogous explanations for several other cases that we inspected in more detail, but not for all of them.
It is for instance probably not possible to predict by basic chemical reasoning the variation on the atomic charge on the central atoms in the pair of structures shown in Figure 1c,d. Both central atoms are the outermost ones in a chain attached to a cage and the cage structures look quite similar. Hard to explain by traditional arguments are also the differences in the charge of the two central atoms shown in Figure 1a,b, where again, the near environments are almost identical and only the bond connectivity of the cages differs slightly. One can actually even transfer an additional 0.07 electrons onto the chain by just compressing some bonds in the region of the cage furthest away from the docking point of the chain.
Varying atomic charges are supposed to lead to variations in the bond length, and this is indeed the case for this system. The bond lengths of the 4 atom chain differ depending on whether the chain is isolated or attached to the cage. The bond lengths of the PBE-relaxed free chain of 4 carbon atoms are 1.293, 1.313 (middle bond), and 1.293. If one attaches the chain with these bond lengths to a cage the forces acting on the atoms of the chain are not any more zero, because charge is transferred from the chain onto the cage. This change of the forces for identical geometries can obviously not be obtained from local fingerprints. Due to the charge transfer, the bond lengths relax then during a local geometry optimization to the new values of 1.243, 1.327 (middle bond), and 1.280 (the bond at the free end of the chain), as shown in Figure 1d). So, the bond length at the free end of the chain becomes significantly shorter due to the transferred charge. In addition, the electronic ground state of the free chain is also spin polarised. So, long range effects modify both the bond lengths and the spin moments.
Having established the ubiquitous existence of non-local effects in a standard covalent material, one has to question whether the near-sightedness postulated by Walter–Kohn holds. Actually in the publication where this notion of near-sightedness was introduced there is a caveat, namely that it is only valid if the chemical potential is constant. Since charge transfer is driven by an equalisation of initially different chemical potentials, this principle is therefore not directly applicable in real systems where, as shown in this study, such a charge transfer is quite common. Because of its central importance in the calculation of the total energy, we will, in the following, concentrate on the atomic band structure energy and show that locality can be restored for this quantity if one includes not only information about the structure in a limited environment, but also about the atomic charges. For this purpose, we modify our OM fingerprint such that it also depends on the atomic charges within the sphere with our chosen cutoff radius. The resulting charge-sensitive overlap matrix fingerprint (CSOM) is a variant of OM fingerprint, which includes information about charges in the near environment. To calculate the CSOM fingerprint of an atom k, we first proceed like for the calculation of the standard OM fingerprint. We find all the neighbors of the central atom within the sphere of some cutoff radius and then place a minimal basis set of four Gaussian type orbitals (GTOs) (i.e., radial Gaussians times spherical harmonics) on each atom i in the sphere, namely one s-type GTO (), and 3 p-type GTOs (). The width of the radial Gaussian is given by the covalent radius of the element. Then, the overlap between all atoms in the sphere is calculated as:
To obtain the charge sensitive version of the fingerprint, we add the charge variations for each atom in the sphere to the diagonal of S, i.e.,
where is defined in Equation (2), c is some constant ( in our case) and is the average valence charge of the atoms, which is 4 for carbon. The remaining steps are again identical to the case of the standard OM fingerprint. Each element of this matrix is multiplied by two amplitudes, and , where is a cutoff function which smoothly tends to zero at . Beyond , the amplitude is zero. So, the only difference between CSOM and OM fingerprints is the second term in Equation (7), where we added atomic DFT charges to move the points on the fingerprint axis of the correlation between fingerprint and atomic energy upward. The vector containing all the eigenvalues of this matrix is then the fingerprint of atom k. The fingerprint distance between two atoms is again taken to be the Euclidean distance between the two fingerprint vectors.
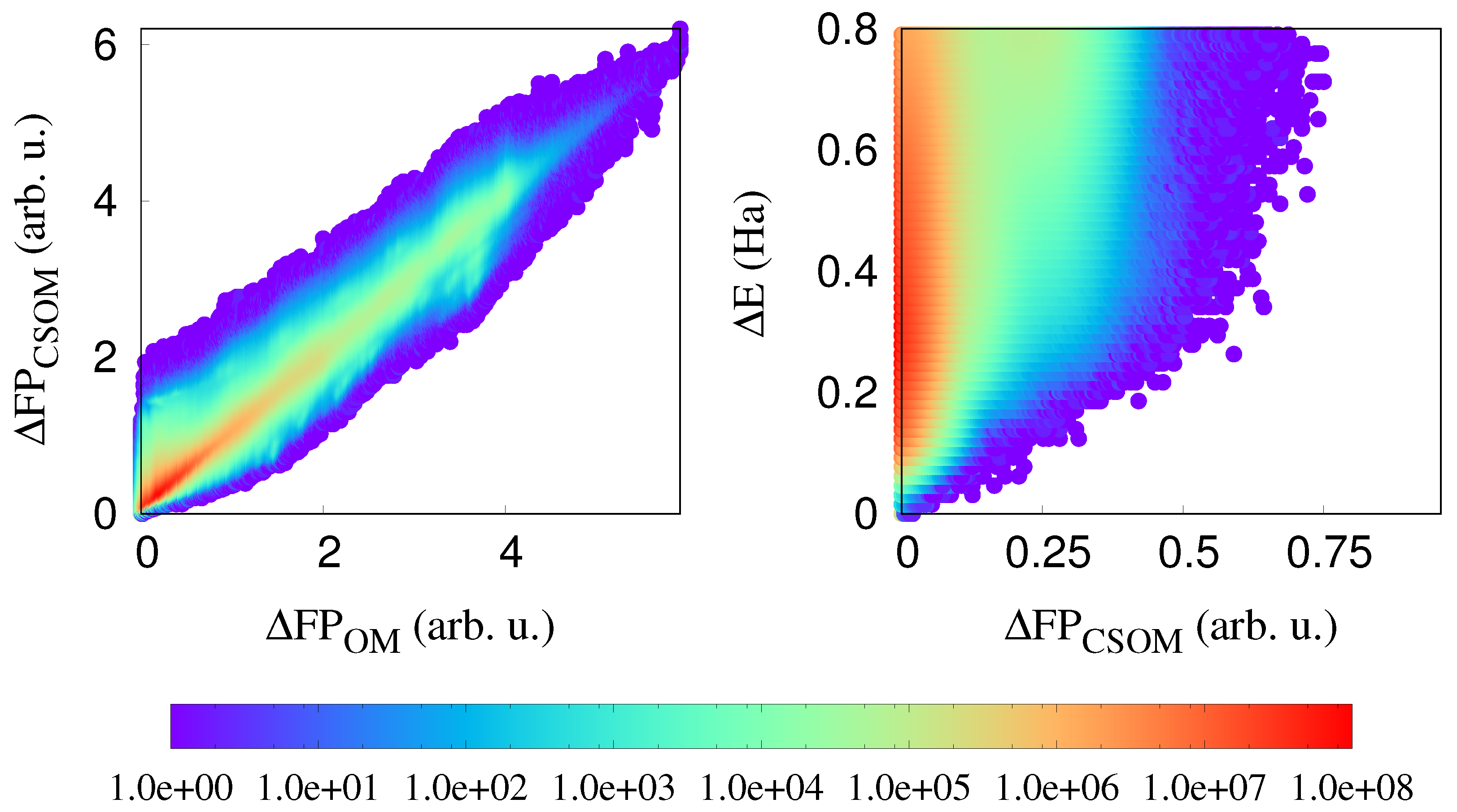
In the left panel of Figure 4, we show the correlation plot between OM and CSOM fingerprints. There are no points on the x axis (OM axis), but there are some points on the y axis (CSOM axis), which shows that the CSOM fingerprint does not loose any information, and is in addition capable of distinguishing identical structural environments that have different atomic charges. So, the CSOM fingerprint still has a strong sensitivity to the geometrical structure, but in addition, a weak sensitivity to the charges.
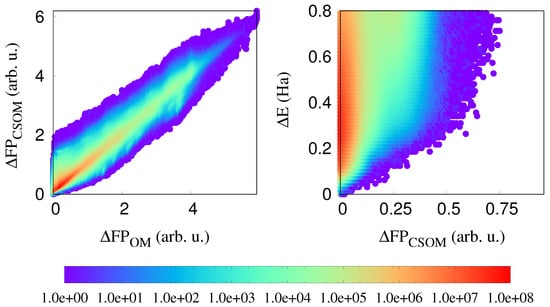
Figure 4.
(Left): The correlation between OM and CSOM fingerprints. (Right): The correlation between distances calculated with the charge-sensitive OM fingerprint (CSOM) and the atomic energy differences.
As can be seen from the right panel of the same Figure 4, all the points which were in Figure 2 close to the x-axis are moved upward when the CSOM fingerprint is used. Hence, there are no more additional long range effects. This means that the charge transfer is the basic long-range effect. Once this charge transfer is known, the total energy can be obtained from purely local information.
4. Conclusions
This finding has important consequences for machine learning schemes. Charge transfer is not possible in most of these schemes. Hence, they will necessarily be limited in accuracy. For instance, the environment descriptors of the atoms at the end of the chains in Figure 1 would have in all standard machine learning schemes a cutoff range which is shorter than the length of the chain. Hence, the standard descriptor can not see whether the chain is free standing or attached to the cage. Some long range fingerprints that might cope with this deficiency have, however, also been proposed recently [14,37]. Non-local charge transfer effects in combination with standard short range fingerprints can however be described by the charge equilibration via neural network technique (CENT) [38,39], where a machine learning scheme is combined with a charge equilibration scheme. Consequently, a scheme of this type has to be an integral part of any machine learning scheme that strives to obtain very high accuracy also for systems where long range effects cannot be neglected.
Author Contributions
Data curation, D.S.D.; Software, J.A.F.; Supervision, S.G.; Writing—original draft, B.P.; Writing—review & editing, B.P., J.A.F. and S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was performed within the NCCR MARVEL, funded by the Swiss National Science Foundation.
Data Availability Statement
Data is available under request.
Acknowledgments
The calculations were performed on the computational resources of the Swiss National Supercomputer (CSCS) under project s963 and on the Scicore computing center of the University of Basel.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goedecker, S. Linear scaling electronic structure methods. Rev. Mod. Phys. 1999, 71, 1085. [Google Scholar] [CrossRef]
- Kohn, W. Density functional and density matrix method scaling linearly with the number of atoms. Phys. Rev. Lett. 1996, 76, 3168. [Google Scholar] [CrossRef]
- Prodan, E.; Kohn, W. Nearsightedness of electronic matter. Proc. Natl. Acad. Sci. USA 2005, 102, 11635–11638. [Google Scholar] [CrossRef]
- Prodan, E. Nearsightedness of electronic matter in one dimension. Phys. Rev. B 2006, 73, 085108. [Google Scholar] [CrossRef]
- Marks, N.A.; Cooper, N.; McKenzie, D.; McCulloch, D.; Bath, P.; Russo, S. Comparison of density-functional, tight-binding, and empirical methods for the simulation of amorphous carbon. Phys. Rev. B 2002, 65, 075411. [Google Scholar] [CrossRef]
- Marks, N.A. Generalizing the environment-dependent interaction potential for carbon. Phys. Rev. B 2000, 63, 035401. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991. [Google Scholar] [CrossRef]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 1990, 42, 9458. [Google Scholar] [CrossRef] [PubMed]
- Los, J.H.; Ghiringhelli, L.M.; Meijer, E.J.; Fasolino, A. Improved long-range reactive bond-order potential for carbon. I. Construction. Phys. Rev. B 2005, 72, 214102. [Google Scholar] [CrossRef]
- Deringer, V.L.; Csányi, G. Machine learning based interatomic potential for amorphous carbon. Phys. Rev. B 2017, 95, 094203. [Google Scholar] [CrossRef]
- Rupp, M.; Tkatchenko, A.; Müller, K.R.; Von Lilienfeld, O.A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 2012, 108, 058301. [Google Scholar] [CrossRef]
- Brockherde, F.; Vogt, L.; Li, L.; Tuckerman, M.E.; Burke, K.; Müller, K.R. Bypassing the Kohn-Sham equations with machine learning. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef]
- Behler, J. Constructing high-dimensional neural network potentials: A tutorial review. Int. J. Quantum Chem. 2015, 115, 1032–1050. [Google Scholar] [CrossRef]
- Grisafi, A.; Ceriotti, M. Incorporating long-range physics in atomic-scale machine learning. J. Chem. Phys. 2019, 151, 204105. [Google Scholar] [CrossRef] [PubMed]
- Bereau, T.; DiStasio, R.A., Jr.; Tkatchenko, A.; Von Lilienfeld, O.A. Non-covalent interactions across organic and biological subsets of chemical space: Physics-based potentials parametrized from machine learning. J. Chem. Phys. 2018, 148, 241706. [Google Scholar] [CrossRef]
- Yao, K.; Herr, J.E.; Toth, D.W.; Mckintyre, R.; Parkhill, J. The TensorMol-0.1 model chemistry: A neural network augmented with long-range physics. Chem. Sci. 2018, 9, 2261–2269. [Google Scholar] [CrossRef] [PubMed]
- Behler, J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 2011, 134, 074106. [Google Scholar] [CrossRef] [PubMed]
- Bartók, A.P.; Kondor, R.; Csányi, G. On representing chemical environments. Phys. Rev. B 2013, 87, 184115. [Google Scholar] [CrossRef]
- Faber, F.A.; Christensen, A.S.; Huang, B.; Von Lilienfeld, O.A. Alchemical and structural distribution based representation for universal quantum machine learning. J. Chem. Phys. 2018, 148, 241717. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, A.; Ghasemi, S.A.; Schaefer, B.; Mohr, S.; Lill, M.A.; Goedecker, S. Metrics for measuring distances in configuration spaces. J. Chem. Phys. 2013, 139, 184118. [Google Scholar] [CrossRef]
- Zhu, L.; Amsler, M.; Fuhrer, T.; Schaefer, B.; Faraji, S.; Rostami, S.; Ghasemi, S.A.; Sadeghi, A.; Grauzinyte, M.; Wolverton, C.; et al. A fingerprint based metric for measuring similarities of crystalline structures. J. Chem. Phys. 2016, 144, 034203. [Google Scholar] [CrossRef]
- Parsaeifard, B.; De, D.S.; Christensen, A.S.; Faber, F.A.; Kocer, E.; De, S.; Behler, J.; von Lilienfeld, A.; Goedecker, S. An assessment of the structural resolution of various fingerprints commonly used in machine learning. Mach. Learn. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Willand, A.; Kvashnin, Y.O.; Genovese, L.; Vázquez-Mayagoitia, Á.; Deb, A.K.; Sadeghi, A.; Deutsch, T.; Goedecker, S. Norm-conserving pseudopotentials with chemical accuracy compared to all-electron calculations. J. Chem. Phys. 2013, 138, 104109. [Google Scholar] [CrossRef]
- Genovese, L.; Neelov, A.; Goedecker, S.; Deutsch, T.; Ghasemi, S.A.; Willand, A.; Caliste, D.; Zilberberg, O.; Rayson, M.; Bergman, A.; et al. Daubechies wavelets as a basis set for density functional pseudopotential calculations. J. Chem. Phys. 2008, 129, 014109. [Google Scholar] [CrossRef]
- Bader, R.F. The quantum mechanical basis of conceptual chemistry. Monatshefte Chem. Chem. Mon. 2005, 136, 819–854. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic population analysis on LCAO–MO molecular wave functions. I. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef]
- Nakai, H. Energy density analysis with Kohn–Sham orbitals. Chem. Phys. Lett. 2002, 363, 73–79. [Google Scholar] [CrossRef]
- Harris, J. Simplified method for calculating the energy of weakly interacting fragments. Phys. Rev. B 1985, 31, 1770. [Google Scholar] [CrossRef] [PubMed]
- Goedecker, S. Minima hopping: An efficient search method for the global minimum of the potential energy surface of complex molecular systems. J. Chem. Phys. 2004, 120, 9911–9917. [Google Scholar] [CrossRef]
- Roy, S.; Goedecker, S.; Hellmann, V. Bell-Evans-Polanyi principle for molecular dynamics trajectories and its implications for global optimization. Phys. Rev. E 2008, 77, 056707. [Google Scholar] [CrossRef] [PubMed]
- Sicher, M.; Mohr, S.; Goedecker, S. Efficient moves for global geometry optimization methods and their application to binary systems. J. Chem. Phys. 2011, 134, 044106. [Google Scholar] [CrossRef]
- Aradi, B.; Hourahine, B.; Frauenheim, T. DFTB+, a sparse matrix-based implementation of the DFTB method. J. Phys. Chem. A 2007, 111, 5678–5684. [Google Scholar] [CrossRef] [PubMed]
- Moore, B.; Sun, H.; Govind, N.; Kowalski, K.; Autschbach, J. Charge-Transfer Versus Charge-Transfer-Like Excitations Revisited. J. Chem. Theory Comput. 2015, 11, 3305–3320. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Ratcliff, L.E.; Degomme, A.; Flores-Livas, J.A.; Goedecker, S.; Genovese, L. Affordable and accurate large-scale hybrid-functional calculations on GPU-accelerated supercomputers. J. Phys. Condens. Matter 2018, 30, 095901. [Google Scholar] [CrossRef] [PubMed]
- Hirn, M.; Mallat, S.; Poilvert, N. Wavelet scattering regression of quantum chemical energies. Multiscale Model. Simul. 2017, 15, 827–863. [Google Scholar] [CrossRef]
- Ghasemi, S.A.; Hofstetter, A.; Saha, S.; Goedecker, S. Interatomic potentials for ionic systems with density functional accuracy based on charge densities obtained by a neural network. Phys. Rev. B 2015, 92, 045131. [Google Scholar] [CrossRef]
- Amsler, M.; Rostami, S.; Tahmasbi, H.; Rahmatizad, E.; Faraji, S.; Rasoulkhani, R.; Ghasemi, S.A. FLAME: A library of atomistic modeling environments. Comput. Phys. Commun. 2020, 256, 107415. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).