Cross-Correlation of THz Pulses from the Electron Storage Ring BESSY II
Abstract
1. Introduction
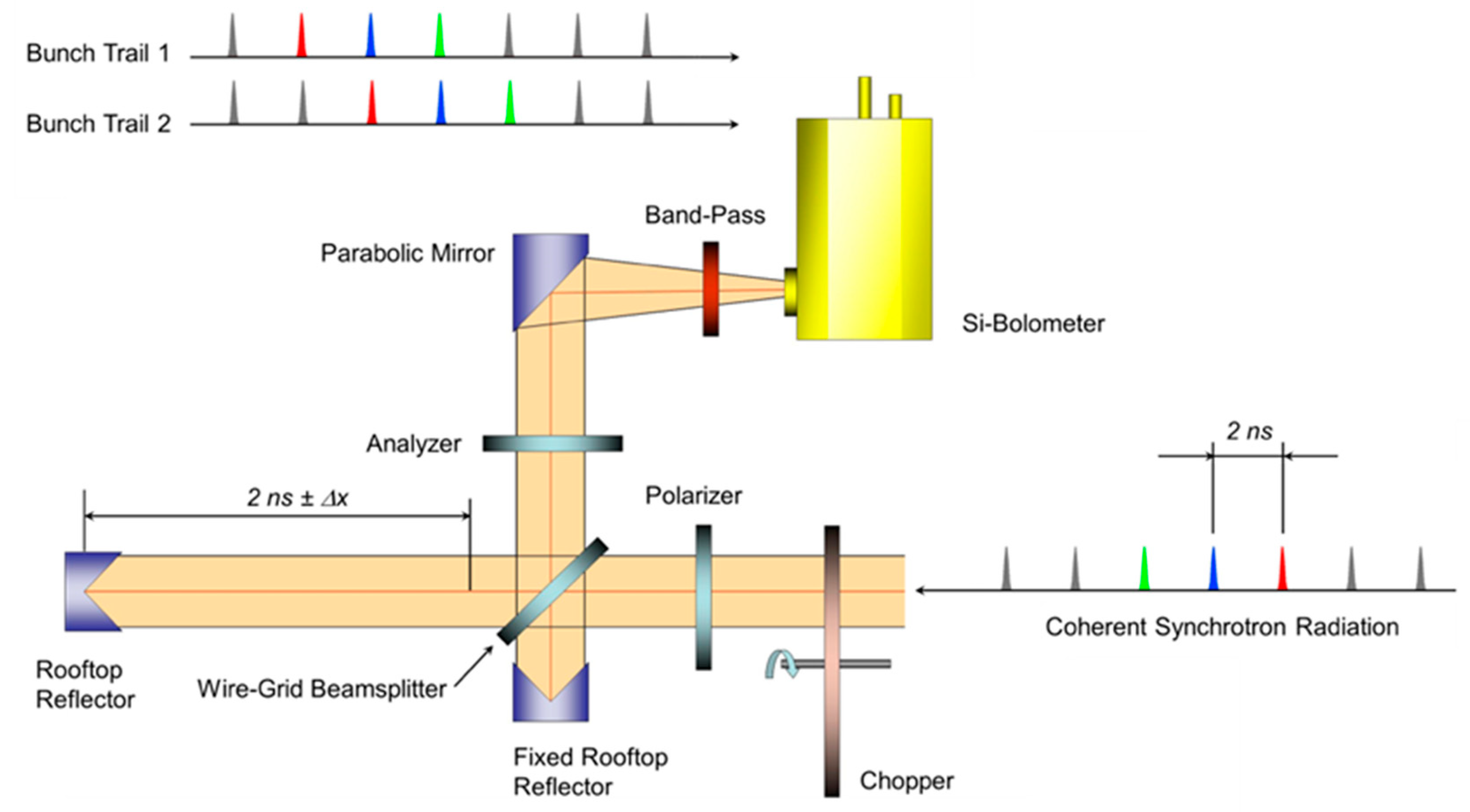
2. Experimental Section
3. Results and Discussion
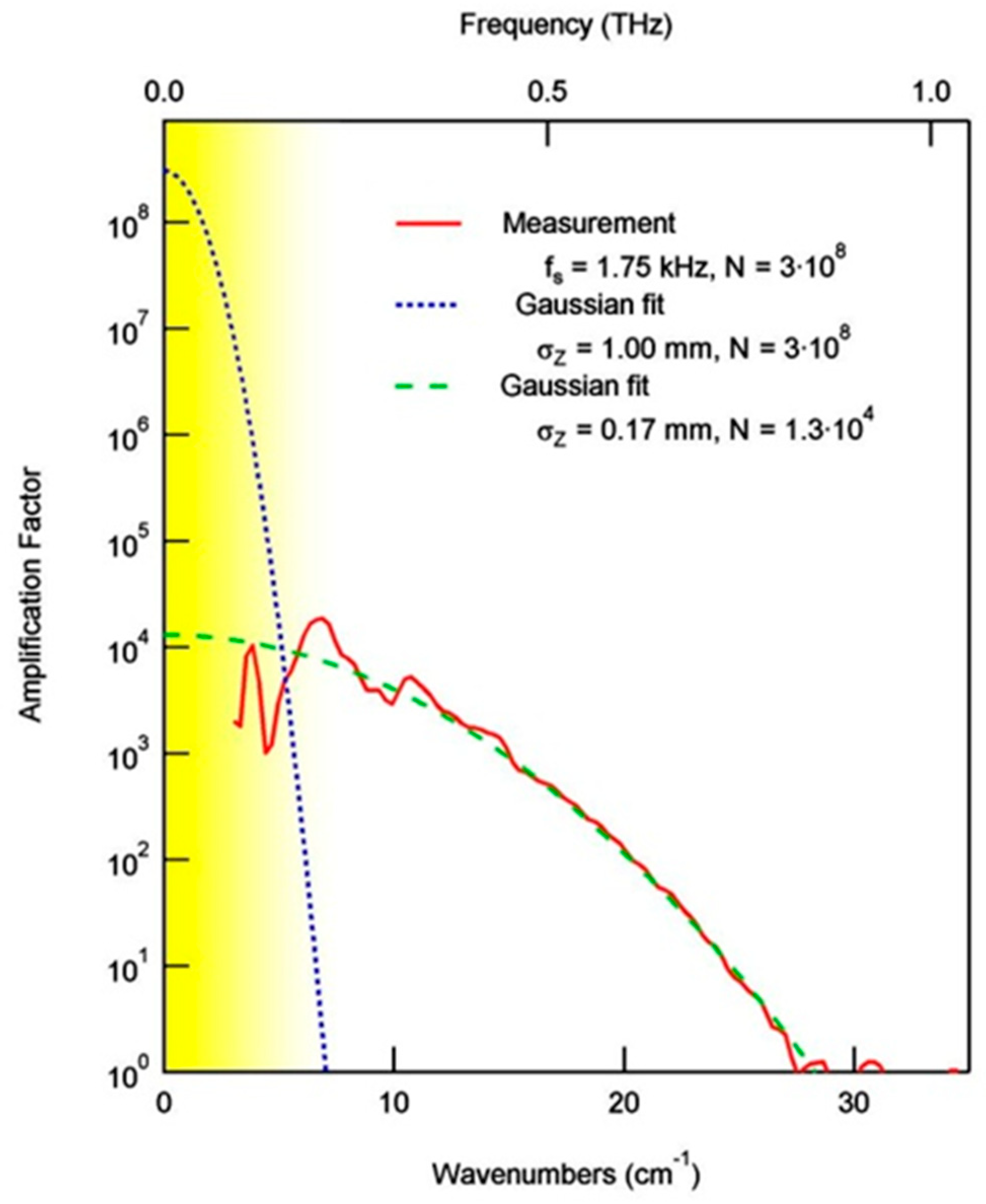
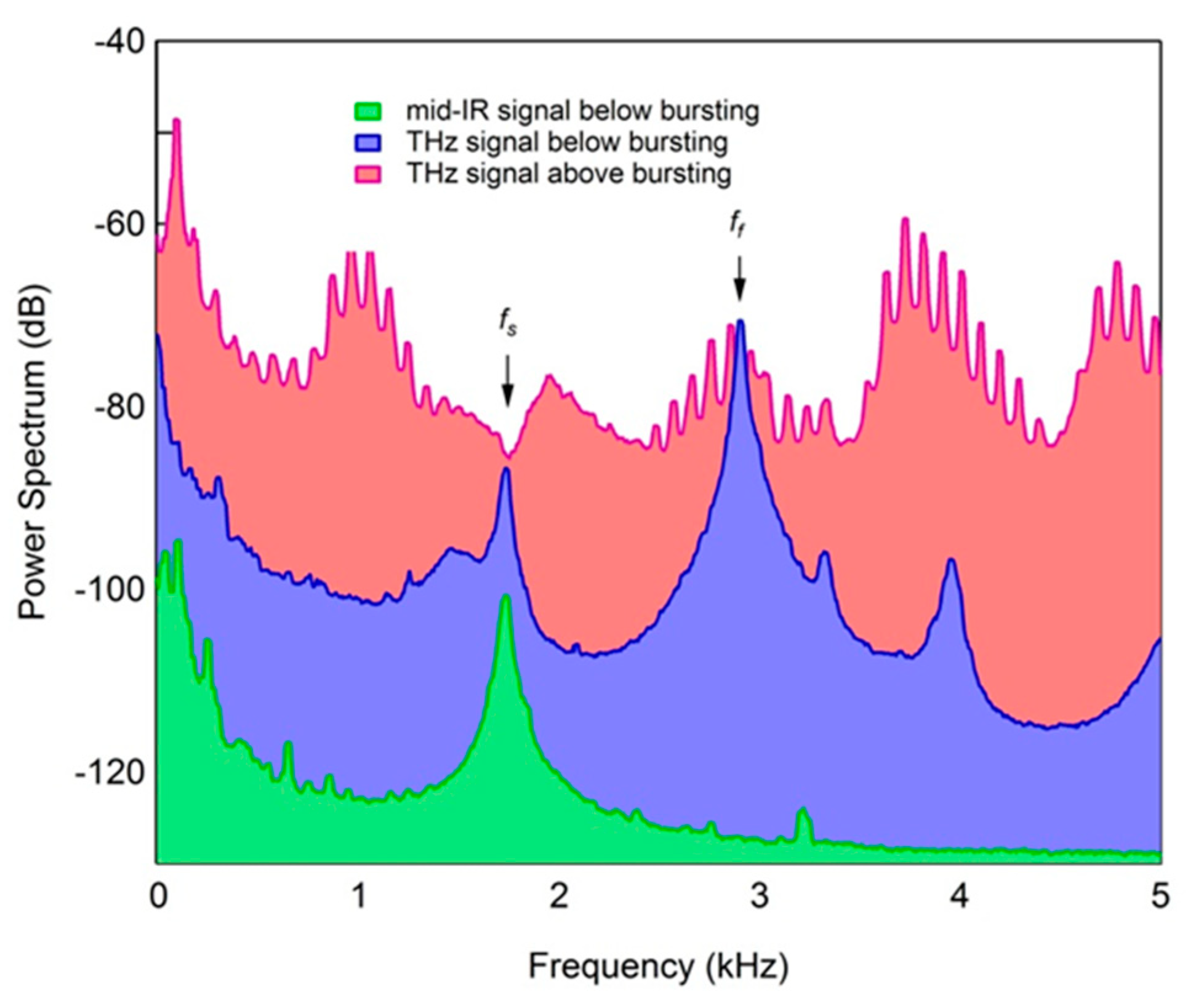
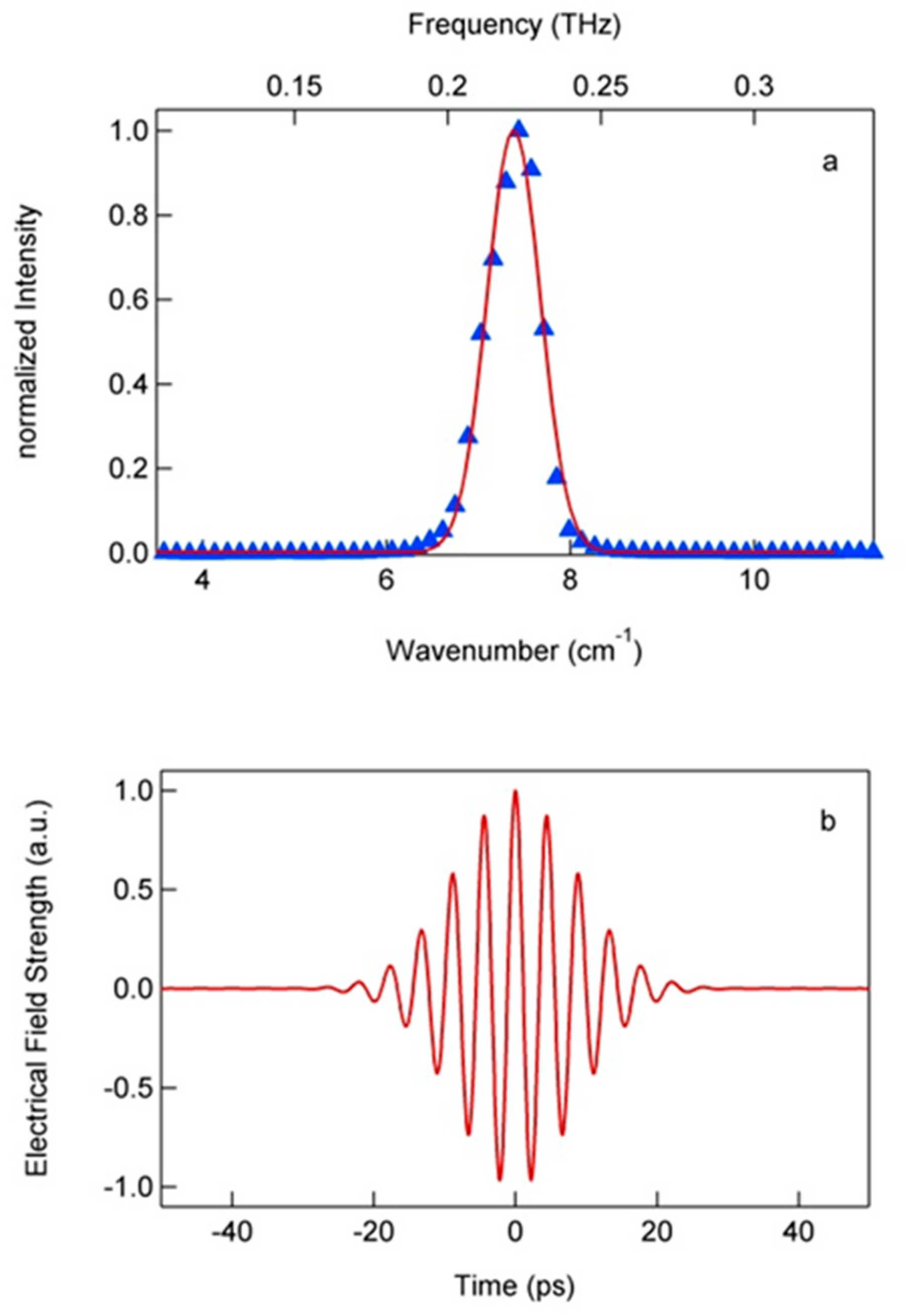
3.1. Coherent Synchrotron Emission
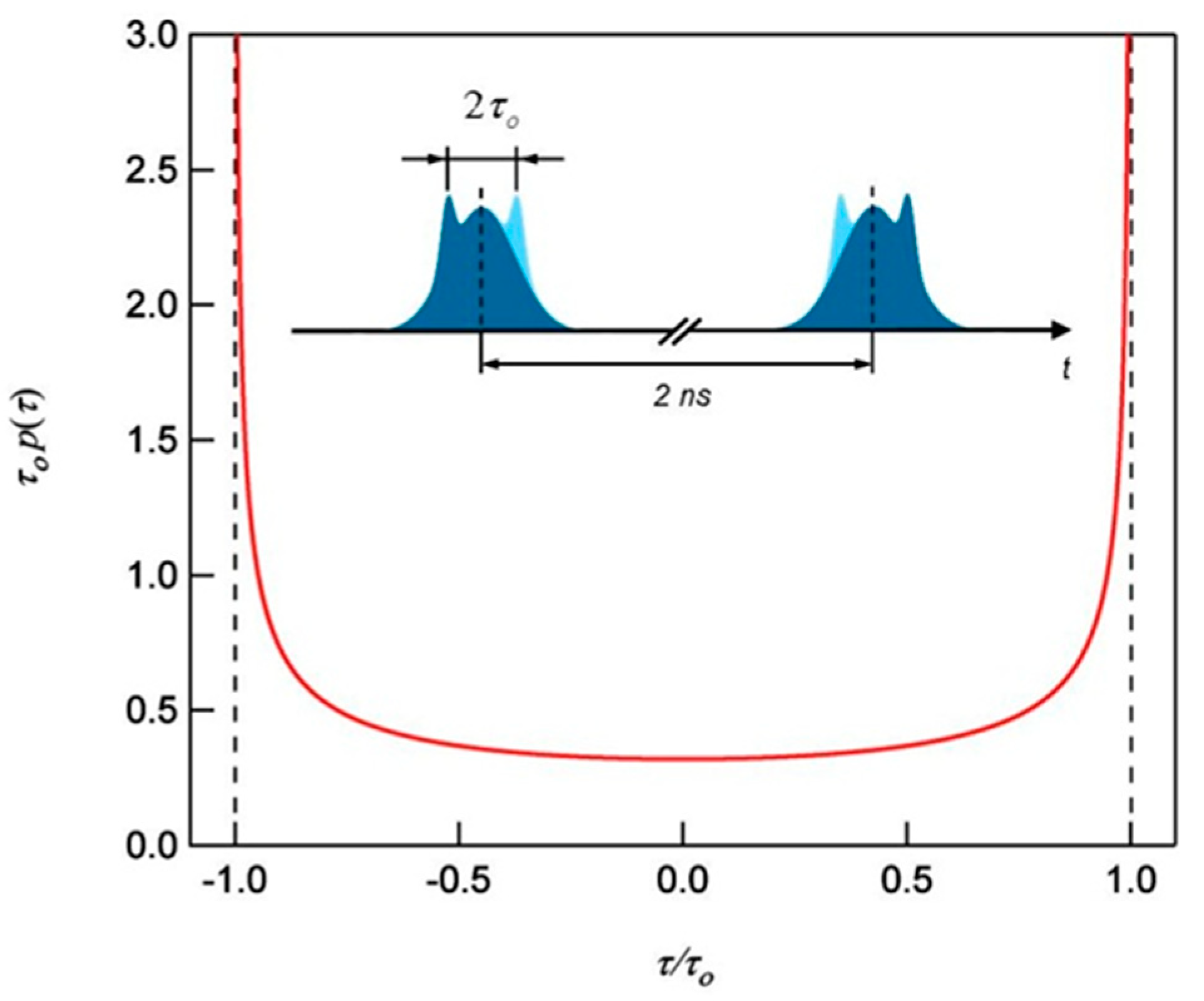
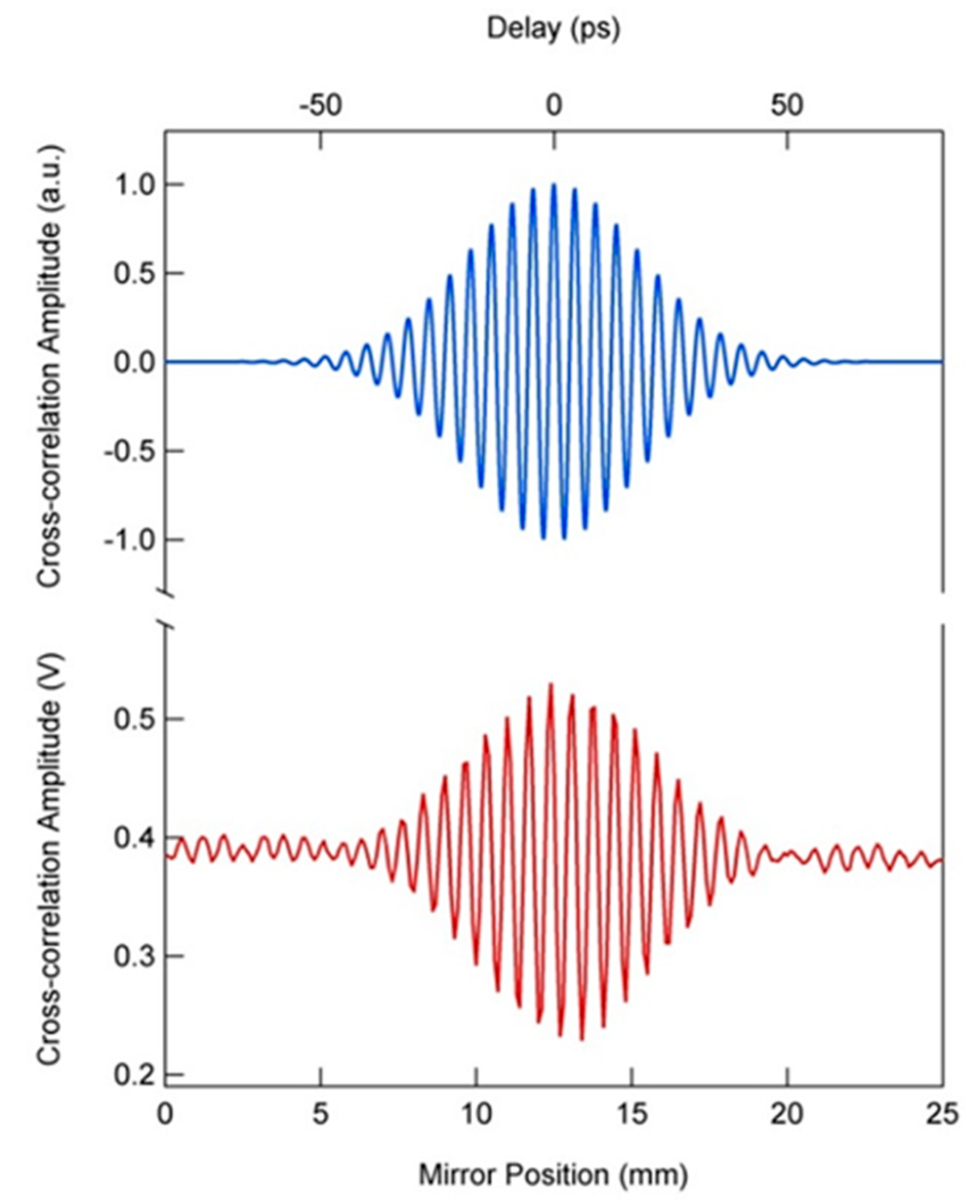
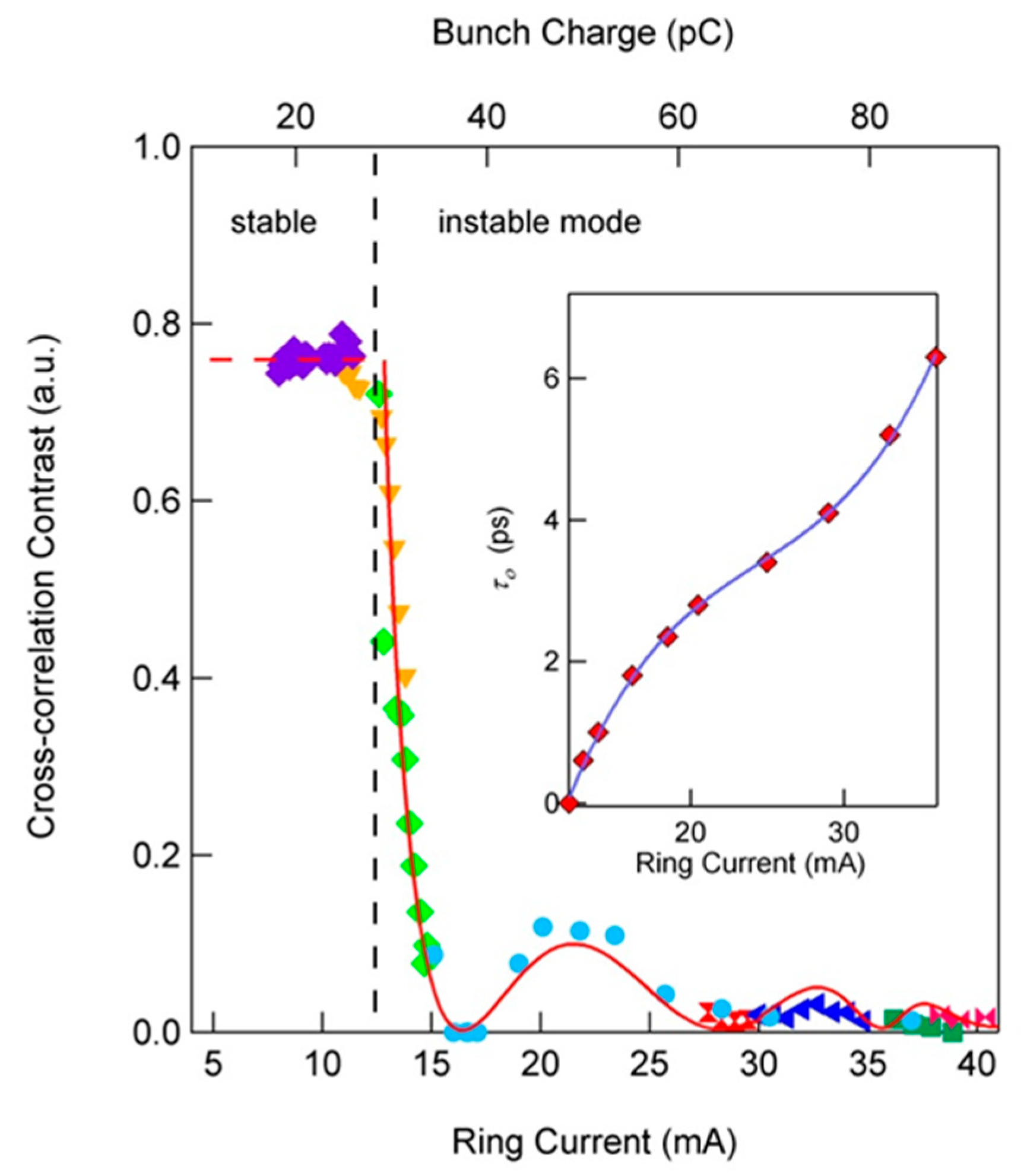
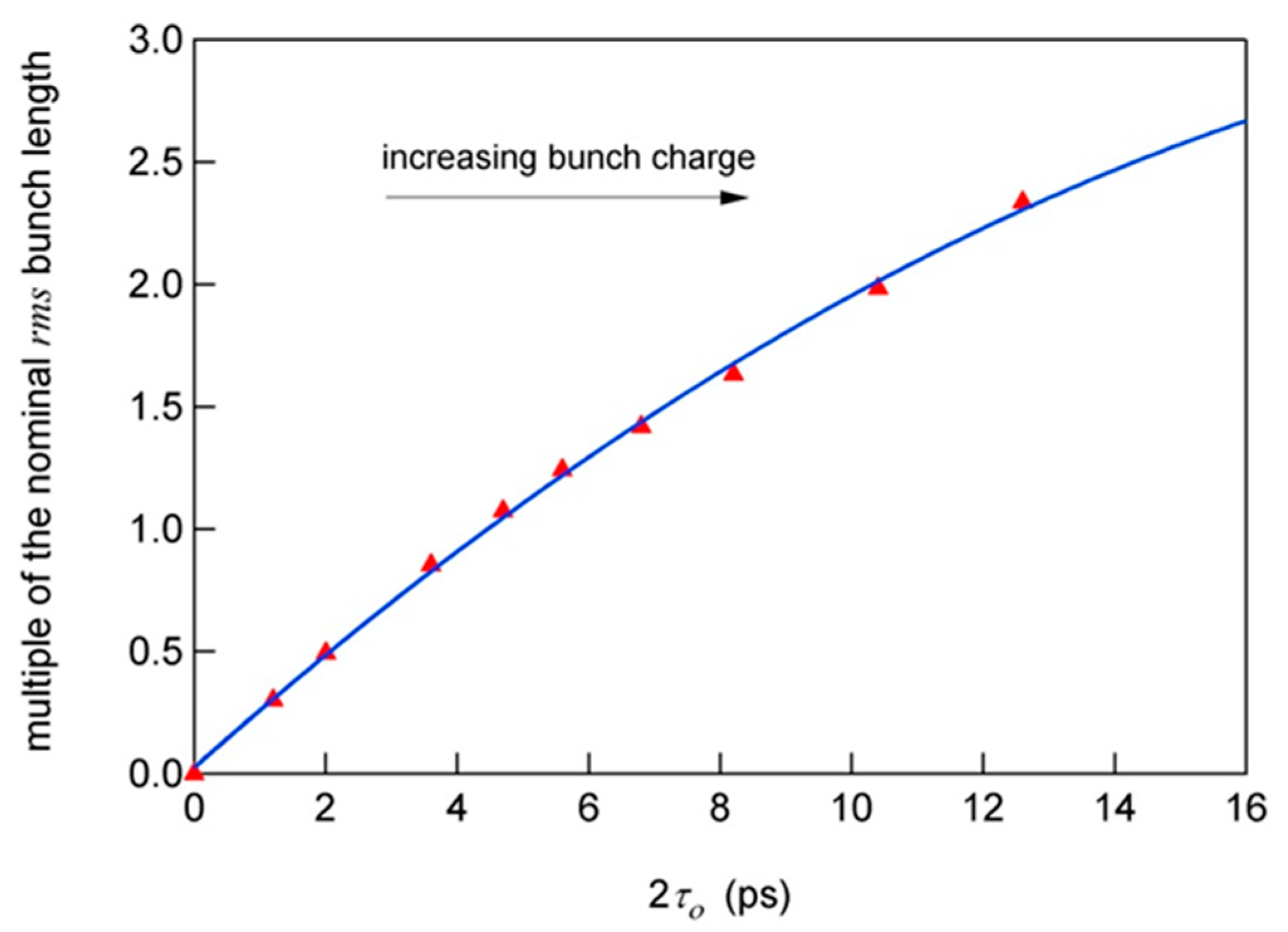
3.2. Cross-Correlation of Subsequent Bunches
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Carr, G.L.; Martin, M.C.; McKinney, W.R.; Jordan, K.; Neil, G.R.; Williams, G.P. High-Power Terahertz Radiation from Relativistic Electrons. Nature 2002, 420, 153–156. [Google Scholar] [CrossRef] [PubMed]
- Williams, G.P.; Hirschmugl, C.J.; Kneedler, E.M.; Takacs, P.Z.; Shleifer, M.; Chabal, Y.J.; Hoffmann, F.M. Coherence Effects in Long-Wavelength Infrared Synchrotron Radiation Emission. Phys. Rev. Lett. 1989, 62, 261–263. [Google Scholar] [CrossRef] [PubMed]
- Nodvick, J.S.; Saxon, D.S. Suppression of Coherent Radiation by Electrons in a Synchrotron. Phys. Rev. 1954, 96, 180–184. [Google Scholar] [CrossRef]
- Abo-Bakr, M.; Feikes, J.; Holldack, K.; Wüstefeld, G.; Hübers, H.-W. Steady-State Far-Infrared Coherent Synchrotron Radiation Detected at BESSY II. Phys. Rev. Lett. 2002, 88, 254801. [Google Scholar] [CrossRef] [PubMed]
- Sannibale, F.; Byrd, J.M.; Loftsdóttir, Á.; Venturini, M.; Abo-Bakr, M.; Feikes, J.; Holldack, K.; Kuske, P.; Wüstefeld, G.; Hübers, H.-W.; et al. A Model Describing Stable Coherent Synchrotron Radiation in Storage Rings. Phys. Rev. Lett. 2004, 93, 094801. [Google Scholar] [CrossRef] [PubMed]
- Heifets, S.; Stupakov, G.; Krinsky, S. Coherent Synchrotron Radiation Instability in a Bunch Compressor. Phys. Rev. Spec. Top. Accel. Beams 2002, 5, 064401. [Google Scholar] [CrossRef]
- Venturini, M.; Warnock, R. Bursts of Coherent Synchrotron Radiation in Electron Storage Rings: A Dynamical Model. Phys. Rev. Lett. 2002, 89, 224802. [Google Scholar] [CrossRef]
- Abo-Bakr, M.; Feikes, J.; Holldack, K.; Kuske, P.; Peatman, W.; Schade, U.; Wüstefeld, G.; Hübers, H.-W. Brilliant, Coherent Far-Infrared (THz) Synchrotron Radiation. Phys. Rev. Lett. 2003, 90. [Google Scholar] [CrossRef]
- Singley, E.; Abo-Bakr, M.; Basov, D.; Feikes, J.; Guptasarma, P.; Holldack, K.; Hübers, H.; Kuske, P.; Martin, M.; Peatman, W.; et al. Measuring the Josephson Plasma Resonance in Bi2Sr2CaCu2O8 Using Intense Coherent THz Synchrotron Radiation. Phys. Rev. B 2004, 69, 092512. [Google Scholar] [CrossRef]
- Müller, A.-S.; Birkel, I.; Gasharova, B.; Huttel, E.; Kubat, R.; Mathis, Y.-L.; Moss, D.A.; Mexner, W.; Rossmanith, R.; Wuensch, M.; et al. Far Infrared Coherent Synchrotron Edge Radiation at ANKA. In Proceedings of the 2005 Particle Accelerator Conference, Knoxville, TN, USA, 16–20 May 2005; pp. 2518–2520. [Google Scholar]
- Barros, J.; Manceron, L.; Brubach, J.B.; Creff, G.; Evain, C.; Couprie, M.E.; Loulergue, A.; Nadolski, L.; Tordeux, M.A.; Roy, P. Toward Highly Stable Terahertz Coherent Synchrotron Radiation at the Synchrotron SOLEIL. J. Phys. Conf. Ser. 2012, 359, 4–8. [Google Scholar] [CrossRef]
- Hashimoto, S.; Shoji, Y.; Ando, A.; Takahashi, T. Observation of Coherent Synchrotron Radiation at NewSUBARU. In Proceedings of the 2005 Particle Accelerator Conference, Knoxville, TN, USA, 16–20 May 2005; pp. 4188–4190. [Google Scholar]
- Mochihashi, A.; Hosaka, M.; Katoh, M.; Shimada, M.; Kimura, S. UVSOR-II Electron Storage Ring. In Proceedings of the 2006 European Particle Accelerator Conference, Edinburgh, UK, 26–30 Jun 2006; pp. 3380–3382. [Google Scholar]
- Martin, I.P.S.; Rehm, G.; Thomas, C.; Bartolini, R. Experience with Low-Alpha Lattices at the Diamond Light Source. Phys. Rev. Spec. Top. Accel. Beams 2011, 040705, 1–11. [Google Scholar] [CrossRef]
- Feikes, J.; von Hartrott, M.; Ries, M.; Schmid, P.; Wüstefeld, G.; Hoehl, A.; Klein, R.; Müller, R.; Ulm, G. Metrology Light Source: The First Electron Storage Ring Optimized for Generating Coherent THz Radiation. Phys. Rev. Spec. Top. Accel. Beams 2011, 14, 030705. [Google Scholar] [CrossRef]
- Schade, U.; Ortolani, M.; Lee, J. THz Experiments with Coherent Synchrotron Radiation from BESSY II. Synchrotron Radiat. News 2007, 20, 17–24. [Google Scholar] [CrossRef]
- Schnegg, A.; Behrends, J.; Lips, K.; Bittl, R.; Holldack, K. Frequency Domain Fourier Transform THz-EPR on Single Molecule Magnets Using Coherent Synchrotron Radiation. Phys. Chem. Chem. Phys. 2009, 11, 6820. [Google Scholar] [CrossRef] [PubMed]
- Tammaro, S.; Pirali, O.; Roy, P.; Lampin, J.F.; Ducournau, G.; Cuisset, A.; Hindle, F.; Mouret, G. High Density Terahertz Frequency Comb Produced by Coherent Synchrotron Radiation. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Wüstefeld, G.; Jankowiak, A.; Knobloch, J.; Ries, M. Simultaneous Long and Short Electron Bunches in the BESSY II Storage Ring. In Proceedings of the 2011 International Particle Accelerator Conference, San Sebastian, Spain, 4–9 September 2011; pp. 2936–2938. [Google Scholar]
- Jankowiak, A.; Wüstefeld, G. Low-α Operation of BESSY II and Future Plans for an Alternating Bunch Length Scheme BESSY VSR. Synchrotron Radiat. News 2013, 26, 22–24. [Google Scholar] [CrossRef]
- Evain, C.; Barros, J.; Loulergue, A.; Tordeux, M.A.; Nagaoka, R.; Labat, M.; Cassinari, L.; Creff, G.; Manceron, L.; Brubach, J.B.; et al. Spatio-Temporal Dynamics of Relativistic Electron Bunches during the Micro-Bunching Instability in Storage Rings. Europhys. Lett. 2012, 98, 40006. [Google Scholar] [CrossRef]
- Roussel, E.; Evain, C.; Le Parquier, M.; Szwaj, C.; Bielawski, S.; Manceron, L.; Brubach, J.-B.; Tordeux, M.-A.; Ricaud, J.-P.; Cassinari, L.; et al. Observing Microscopic Structures of a Relativistic Object Using a Time-Stretch Strategy. Sci. Rep. 2015, 5, 10330. [Google Scholar] [CrossRef]
- Evain, C.; Roussel, E.; Le Parquier, M.; Szwaj, C.; Tordeux, M.A.; Brubach, J.B.; Manceron, L.; Roy, P.; Bielawski, S. Direct Observation of Spatiotemporal Dynamics of Short Electron Bunches in Storage Rings. Phys. Rev. Lett. 2017, 118, 1–6. [Google Scholar] [CrossRef]
- Steinmann, J.L.; Boltz, T.; Brosi, M.; Bründermann, E.; Caselle, M.; Kehrer, B.; Rota, L.; Schönfeldt, P.; Schuh, M.; Siegel, M.; et al. Continuous Bunch-by-Bunch Spectroscopic Investigation of the Micro-bunching Instability. Phys. Rev. Accel. Beams 2018, 21, 110705. [Google Scholar] [CrossRef]
- Brosi, M.; Steinmann, J.L.; Blomley, E.; Boltz, T.; Bründermann, E.; Gethmann, J.; Kehrer, B.; Mathis, Y.L.; Papash, A.; Schedler, M.; et al. Systematic Studies of the Microbunching Instability at Very Low Bunch Charges. Phys. Rev. Accel. Beams 2019, 22, 20701. [Google Scholar] [CrossRef]
- Bielawski, S.; Blomley, E.; Brosi, M.; Bründermann, E.; Burkard, E.; Evain, C.; Funkner, S.; Hiller, N.; Nasse, M.J.; Niehues, G.; et al. From Self-Organization in Relativistic Electron Bunches to Coherent Synchrotron Light: Observation Using a Photonic Time-Stretch Digitizer. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Peatman, W.B.; Schade, U. A Brilliant Infrared Light Source at BESSY. Rev. Sci. Instrum. 2001, 72, 1620–1624. [Google Scholar] [CrossRef]
- Feikes, J.; Holldack, K.; Kuske, P.; Wüstefeld, G. Sub-Picosecond Electron Bunches in the BESSY Storage Ring. In Proceedings of the 2004 European Particle Accelerator Conference, Lucerne, Switzerland, 5–9 July 2004; pp. 1954–1956. [Google Scholar]
- Martin, D.H.; Puplett, E. Polarised Interferometric Spectrometry for the Millimetre and Submillimetre Spectrum. Infrared Phys. 1969, 10, 105–109. [Google Scholar] [CrossRef]
- Billinghurst, B.E.; Bergstrom, J.C.; Baribeau, C.; Batten, T.; May, T.E.; Vogt, J.M.; Wurtz, W.A. Longitudinal Bunch Dynamics Study with Coherent Synchrotron Radiation. Phys. Rev. Accel. Beams 2016, 19, 1–11. [Google Scholar] [CrossRef]
- Wüstefeld, G. Short Bunches in Electron Storage Rings and Coherent Synchrotron Radiation. In Proceedings of the 2008 European Particle Accelerator Conference, Genoa, Italy, 23–27 June 2008; pp. 26–30. [Google Scholar]
- Kuske, P. Investigation of the Temporal Structure of CSR-Bursts at BESSY II. In Proceedings of the 2009 Particle Accelerator Conference, Vancouver, BC, Canada, 4–8 May 2009; pp. 4682–4684. [Google Scholar]
- Roussel, E.; Evain, C.; Szwaj, C.; Bielawski, S. Microbunching Instability in Storage Rings: Link between Phase-Space Structure and Terahertz Coherent Synchrotron Radiation Radio-Frequency Spectra. Phys. Rev. Spec. Top. Accel. Beams 2014, 17, 1–6. [Google Scholar] [CrossRef]
- Blochinzew, D.I. Grundlagen der Quantenmechanik; Deutscher Verlag der Wissenschaften: Berlin, Germany, 1953; p. 147. [Google Scholar]
- Cohen, L. The Generalization of the Wiener-Khinchin Theorem. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, Seattle, WA, USA, 12–15 May 1998; Volume 3, pp. 1577–1580. [Google Scholar]
- The time–bandwidth product of a Fourier-transform limited Gaussian-shaped pulse is about 0.08 when the rms criterion is used for the temporal and spectral width
- Griffiths, P.R.; de Haseth, J.A. Fourier Transform Infrared Spectroscopy; John Wiley & Sons, Ltd.: New York, NY, USA, 1986; p. 3. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schade, U.; Kuske, P.; Lee, J.; Marchetti, B.; Ortolani, M. Cross-Correlation of THz Pulses from the Electron Storage Ring BESSY II. Condens. Matter 2020, 5, 24. https://doi.org/10.3390/condmat5020024
Schade U, Kuske P, Lee J, Marchetti B, Ortolani M. Cross-Correlation of THz Pulses from the Electron Storage Ring BESSY II. Condensed Matter. 2020; 5(2):24. https://doi.org/10.3390/condmat5020024
Chicago/Turabian StyleSchade, Ulrich, Peter Kuske, Jongseok Lee, Barbara Marchetti, and Michele Ortolani. 2020. "Cross-Correlation of THz Pulses from the Electron Storage Ring BESSY II" Condensed Matter 5, no. 2: 24. https://doi.org/10.3390/condmat5020024
APA StyleSchade, U., Kuske, P., Lee, J., Marchetti, B., & Ortolani, M. (2020). Cross-Correlation of THz Pulses from the Electron Storage Ring BESSY II. Condensed Matter, 5(2), 24. https://doi.org/10.3390/condmat5020024




