Structure of Manganese Oxide Nanoparticles Extracted via Pair Distribution Functions
Abstract
1. Introduction
2. Experimental Details
3. Results and Discussion
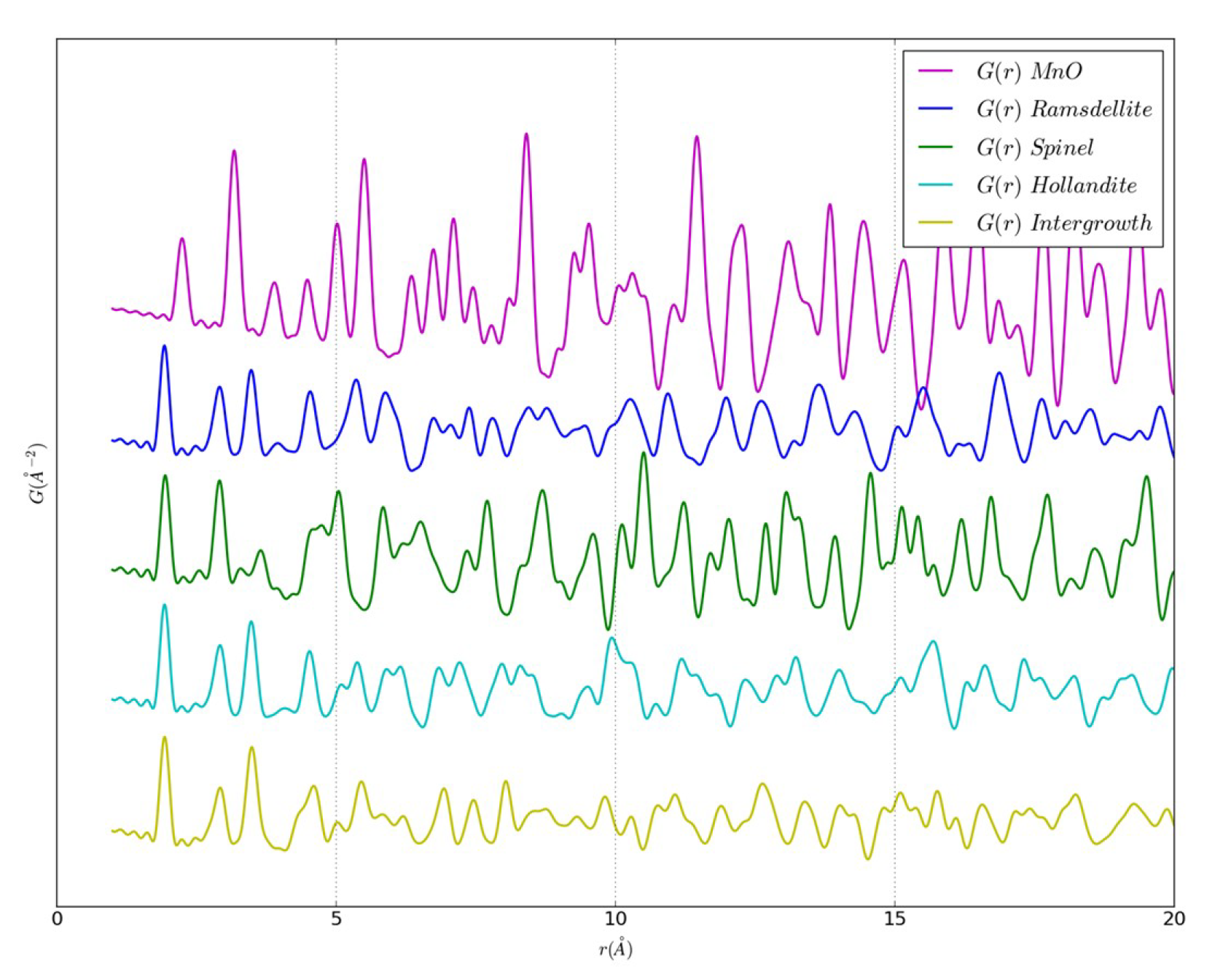
3.1. Computational Details
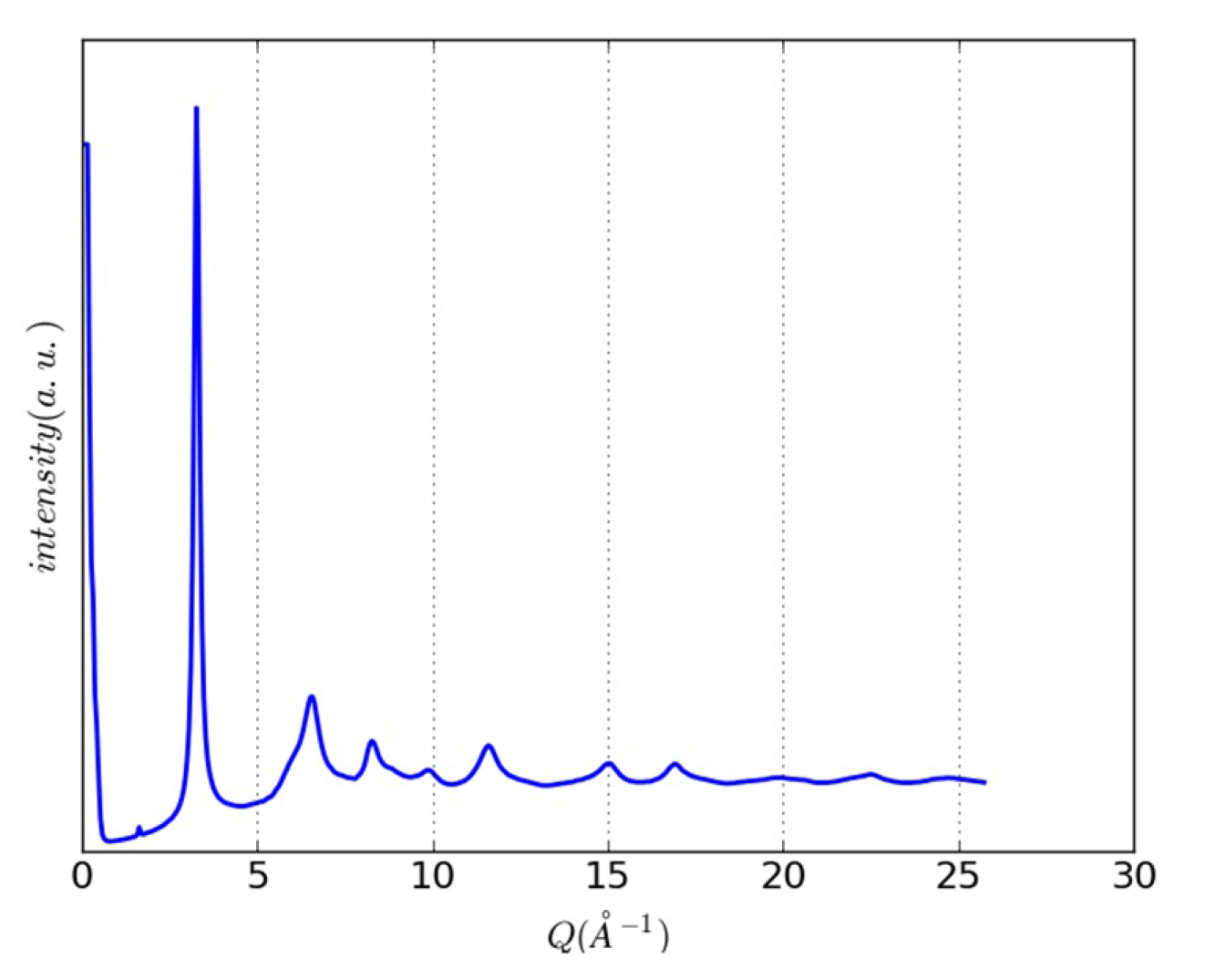
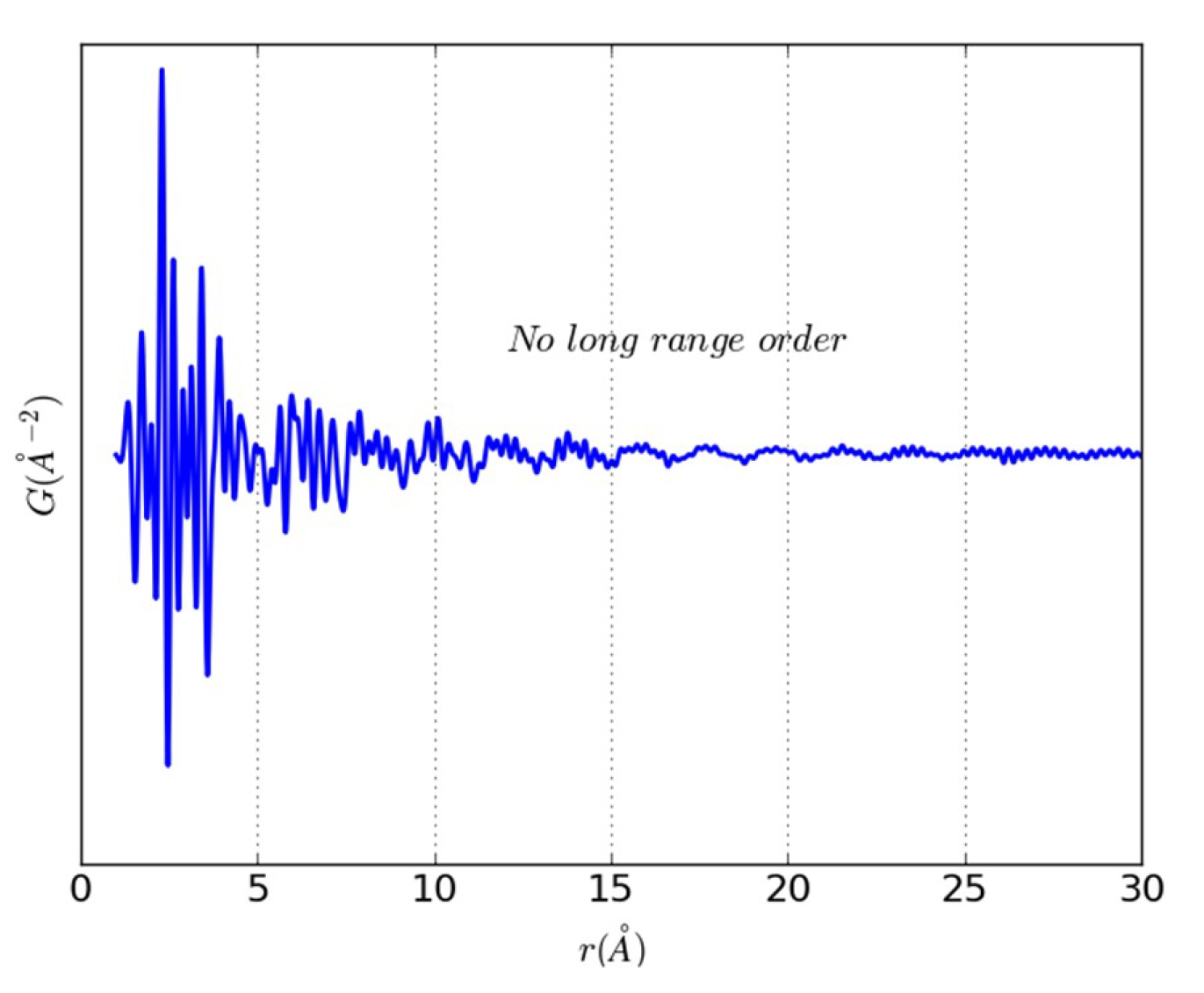
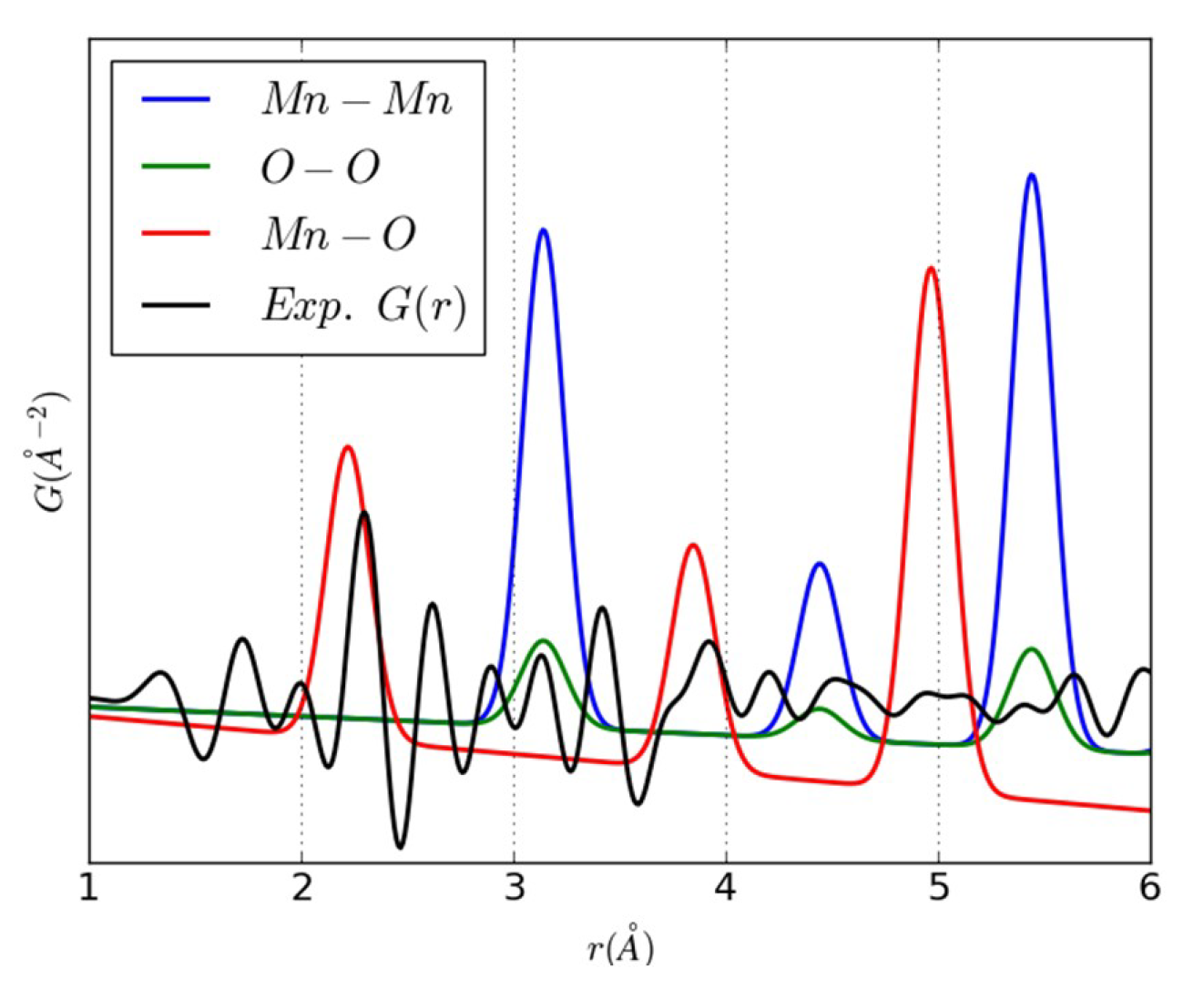
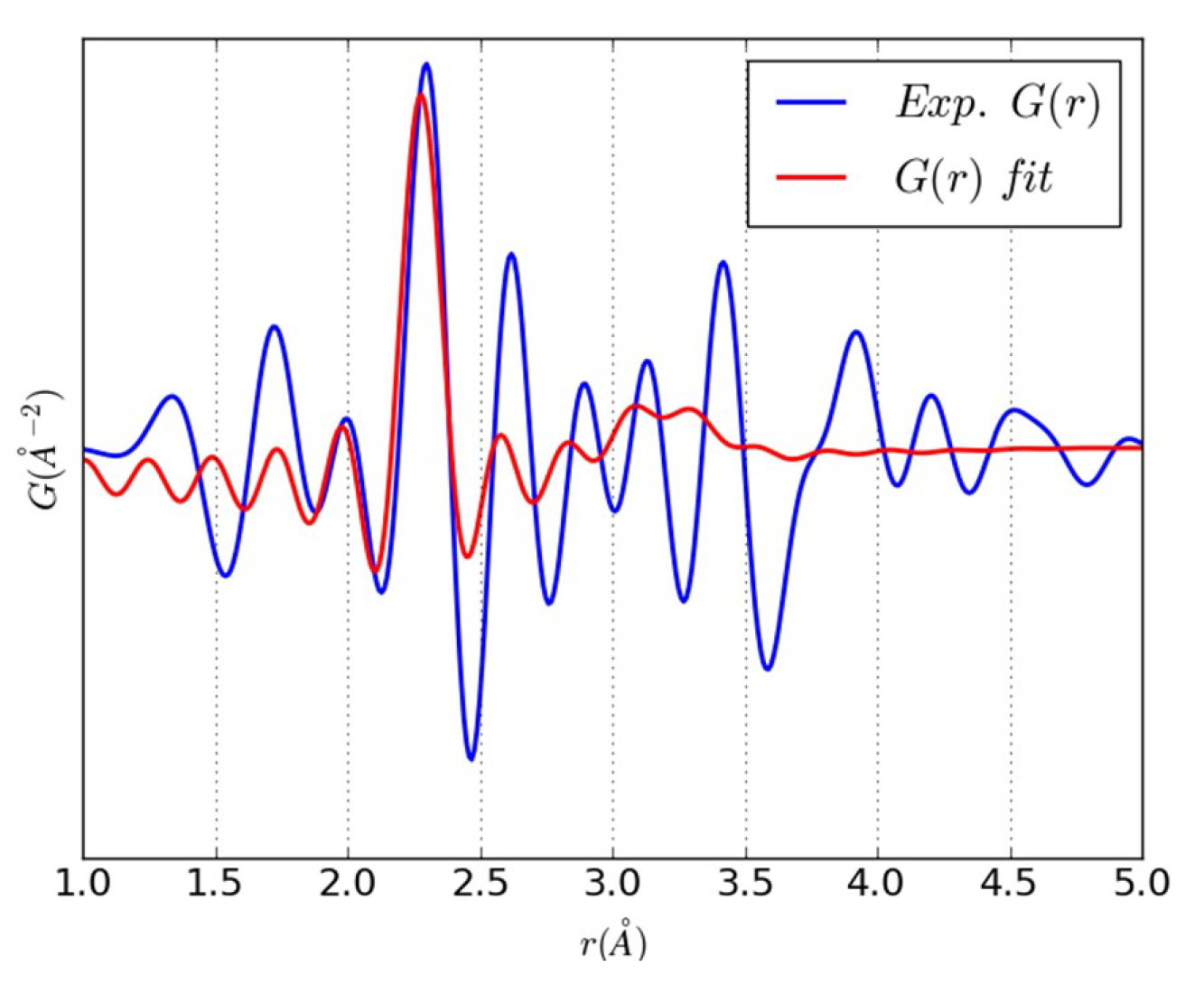
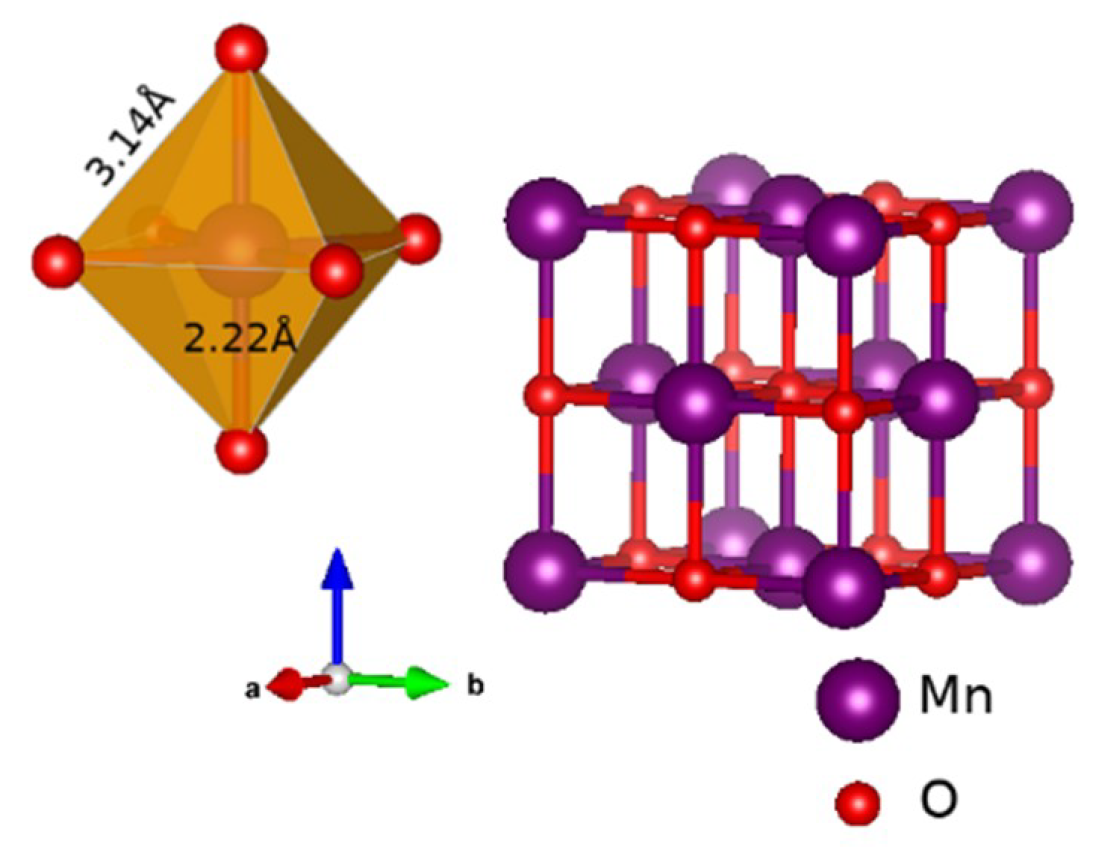
3.2. An Illustrative Analysis of the MnO Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khilari, S.; Pandit, S.; Ghangrekar, M.M.; Das, D.; Pradhan, D. Graphene supported α-MnO2 nanotubes as a cathode catalyst for improved power generation and wastewater treatment in single-chambered microbial fuel cells. RSC Adv. 2013, 3, 7902. [Google Scholar] [CrossRef]
- Post, J. Manganese oxide minerals: Crystal structures and economic and environmental significance. Proc. Natl. Acad. Sci. USA 1999, 96, 3447. [Google Scholar] [CrossRef] [PubMed]
- Jin, K.; Chu, A.; Park, J.; Jeong, D.; Jerng, S.E.; Sim, U.; Jeong, H.-Y.; Lee, C.W.; Park, Y.-S.; Yang, K.D.; et al. Partially Oxidized Sub-10 nm MnO Nanocrystals with High Activity for Water Oxidation Catalysis. Sci. Rep. 2015, 5, 10279. [Google Scholar] [CrossRef] [PubMed]
- Sinha, A.K.; Suzuki, K.; Takahara, M.; Azuma, H.; Nonaka, T.; Fukumoto, K. Mesostructured Manganese Oxide/Gold Nanoparticle Composites for Extensive Air Purification. Angew. Chem. Int. Ed. 2007, 46, 2891–2894. [Google Scholar] [CrossRef]
- Huang, M.; Li, F.; Dong, F.; Zhang, Y.X.; Zhang, L.L. MnO2-based nanostructures for high-performance supercapacitors. J. Mater. Chem. A 2015, 3, 21380–21423. [Google Scholar] [CrossRef]
- Hui, X.; Ying, S.M.; Xiaogan, L.; Guoliang, Y.; Chong, C. Porous manganese oxide generated from lithiation/delithiation with improved electrochemical oxidation for supercapacitors. J. Mater. Chem. 2011, 21, 15521–15526. [Google Scholar] [CrossRef]
- Tang, N.; Tian, X.; Yang, C.; Pi, Z.; Han, Q. Facile synthesis of α-MnO2 nanorods for high-performance alkaline batteries. J. Phys. Chem. Solids 2010, 71, 258–262. [Google Scholar] [CrossRef]
- Zhang, Y.; Steiner, J.D.; Uzodinma, J.; Walsh, J.; Zydlewski, B.; Lin, F.; Chen, Y.; Tang, J.; Pradhan, N.; Dai, Q. Thermally synthesized MnO nanoparticles for magnetic properties and lithium batteries. Mater. Res. Express 2019, 6, 25015. [Google Scholar] [CrossRef]
- Tan, Y.; Meng, L.; Peng, Q.; Li, Y. One-dimensional single-crystalline Mn3O4nanostructures with tunable length and magnetic properties of Mn3O4 nanowires. Chem. Commun. 2011, 47, 1172–1174. [Google Scholar] [CrossRef]
- Balamurugan, M.; Venkatesan, G.; Ramachandran, S.; Saravanan, S. Synthesis and Fabrication of Nanomaterials. Bloomsbury India 2015, 1, 31. [Google Scholar]
- Cheng, F.F.; Zhao, J.; Song, W.; Li, C.; Ma, H.; Chen, J.; Shen, P. Facile Controlled Synthesis of MnO2 Nanostructures of Novel Shapes and Their Application in Batteries. Inorg. Chem. 2006, 45, 2038–2044. [Google Scholar] [CrossRef] [PubMed]
- Tran, D.T.; Ozkaya, D. TEM-based Pair Distribution Function study of interatomic distances in C-supported Pt. J. Phys. Conf. Ser. 2017, 902, 12029. [Google Scholar] [CrossRef]
- Guzzinati, G.; Altantzis, T.; Batuk, M.; De Backer, A.; Lumbeeck, G.; Samaee, V.; Batuk, D.; Idrissi, H.; Hadermann, J.; Van Aert, S.; et al. Recent Advances in Transmission Electron Microscopy for Materials Science at the EMAT Lab of the University of Antwerp. Materials 2018, 11, 1304. [Google Scholar] [CrossRef] [PubMed]
- Midgley, P.A.; Weyland, M. 3D Electron Microscopy in the Physical Sciences: The Development of Z-Contrast and EFTEM Tomography. Ultramicroscopy 2003, 96, 413–431. [Google Scholar] [CrossRef]
- Midgley, P.A.; Dunin-Borkowski, R.E. Electron Tomography and Holography in Materials Science. Nat. Mater. 2009, 8, 271–280. [Google Scholar] [CrossRef]
- Ersen, O.; Florea, I.; Hirlimann, C.; Pham-Huu, C. Exploring Nanomaterials with 3D Electron Microscopy. Mater. Today 2015, 18, 395–408. [Google Scholar] [CrossRef]
- Möbus, G.; Doole, R.C.; Inkson, B.J. Spectroscopic Electron Tomography. Ultramicroscopy 2003, 96, 433–451. [Google Scholar] [CrossRef]
- Liakakos, N.; Gatel, C.; Blon, T.; Altantzis, T.; Lentijo-Mozo, S.; Garcia-Marcelot, C.; Lacroix, L.M.; Respaud, M.; Bals, S.; Van Tendeloo, G. Co-Fe Nanodumbbells: Synthesis, Structure, and Magnetic Properties. Nano Lett. 2014, 14, 2747–2754. [Google Scholar] [CrossRef]
- Goris, B.; Meledina, M.; Turner, S.; Zhong, Z.; Batenburg, K.J.; Bals, S. Three Dimensional Mapping of Fe Dopants in Ceria Nanocrystals Using Direct Spectroscopic Electron Tomography. Ultramicroscopy 2016, 171, 55–62. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray Diffraction; Dover Publications Inc.: New York, NY, USA, 1969. [Google Scholar]
- Takeshi, E.; Billinge, S.J.L. Underneath the Bragg Peaks: Structural Analysis of Complex Materials; Pergamon Press: Oxford, UK, 2003. [Google Scholar]
- Campi, G.; Cappelluti, E.; Proffen, T.; Qiu, X.; Bozin, E.S.; Billinge, S.J.L.; Agrestini, S.; Saini, N.L.; Bianconi, A. Study of temperature dependent atomic correlations in MgB2. Eur. Phys. J. B Condens. Matter Complex Syst. 2006, 52, 15–21. [Google Scholar] [CrossRef]
- Proffen, T.; Page, K.L.; Seshadri, R.; Cheetham, A. Pair Distribution Function for Nanoparticle Studies. Los Alamos Sci. 2006, 30, 161. [Google Scholar]
- Billinge, S.J.L.; Levin, I. The Problem with Determining Atomic Structure at the Nanoscale. Science 2007, 316, 561–565. [Google Scholar] [CrossRef] [PubMed]
- Petkov, V. Nanostructure by high-energy X-ray diffraction. Mater. Today 2008, 11, 28–38. [Google Scholar] [CrossRef]
- Norberg, S.T.; Tucker, M.G.; Hull, S. Bond valence sum: A new soft chemical constraint for RMC Profile. J. Appl. Cryst. 2009, 42, 179–184. [Google Scholar] [CrossRef]
- Keen, D.A.; Goodwin, A.L. The crystallography of correlated disorder. Nature 2015, 521, 303–309. [Google Scholar] [CrossRef]
- Mancini, A.; Malavasi, L. Recent advances in the application of total scattering methods to functional materials. Chem. Commun. 2015, 51, 16592. [Google Scholar] [CrossRef]
- Jensen, K.M.Ø.; Blichfeld, A.B.; Bauers, S.R.; Wood, S.R.; Dooryhée, E.; Johnson, D.C.; Iversen, B.B.; Billinge, S.J.L. Demonstration of thin film pair distributionfunction analysis (tfPDF) for the study of localstructure in amorphous and crystalline thin films. IUCrJ 2015, 2, 481–489. [Google Scholar] [CrossRef]
- Jensen, K.M.Ø.; Juhas, P.; Tofanelli, M.A.; Heinecke, C.L.; Vaughan, G.; Ackerson, C.J.; Billinge, S.J.L. Polymorphism in magic-sized Au144(SR)60 clusters. Nat. Commun. 2016, 7, 11859. [Google Scholar] [CrossRef]
- Dippel, A.-C.; Jensen, K.M.Ø.; Tyrsted, C.; Bremholm, M.; Bøjesen, E.D.; Saha, D.; Birgisson, S.; Christensen, M.; Billinge, S.J.L.; Iversen, B.B. Towards atomistic understanding of polymorphism in the solvothermal synthesis of ZrO2 nanoparticles. Acta Cryst. 2016, 72, 645–650. [Google Scholar] [CrossRef]
- Frandsen, B.A.; Brunelli, M.; Page, K.; Uemura, Y.J.; Staunton, J.B.; Billinge, S.J.L. Verification of Anderson Super exchange in MnO via Magnetic Pair Distribution Function Analysis and ab initio Theory. PRL 2016, 197204. [Google Scholar] [CrossRef]
- Diaz-Lopez, M.; Freire, M.; Joly, Y.; Colin, C.V.; Fischer, H.E.; Blanc, N.; Boudet, N.; Pralong, V.; Bordet, P. Local Structure and Lithium Diffusion Pathways in Li4Mn2O5 High Capacity Cathode Probed by Total Scattering and XANES. Chem. Mater. 2018, 30, 3060–3070. [Google Scholar] [CrossRef]
- Christiansen, T.L.; Bøjesen, E.D.; Juelsholt, M.; Etheridge, J.; Jensen, K.M.Ø. Size Induced Structural Changes in Molybdenum Oxide Nanoparticles. ACS Nano 2019, 13, 8725–8735. [Google Scholar] [CrossRef] [PubMed]
- Dippel, A.-C.; Roelsgaard, M.; Boettger, U.; Schneller, T.; Gutowskia, U.; Ruett, U. Local atomic structure of thin and ultrathin films via rapid high-energy X-ray total scattering at grazing incidence. IUCrJ 2019, 6, 290–298. [Google Scholar] [CrossRef] [PubMed]
- Mathiesen, J.K.; Väli, R.; Härmas, M.; Lust, E.; von Bülow, J.F.; Jensen, K.M.Ø.; Norby, P. Following the in-plane disorder of sodiated hard carbon through operando total scattering. J. Mater. Chem. A 2019, 7, 11709–11717. [Google Scholar] [CrossRef]
- Banerjee, S.; Liu, C.-H.; Jensen, K.M.Ø.; Juhás, P.; Lee, J.D.; Tofanelli, M.; Ackerson, C.J.; Murray, C.B.; Billinge, S.J.L. Cluster-mining: An approach for determining core structures of metallic nanoparticles from atomic pair distribution function data. Acta Cryst. 2020, 76, 24–31. [Google Scholar] [CrossRef]
- Gallo, J.; Alam, I.S.; Lavdas, I.; Wylezinska-Arridge, M.; Aboagye, E.O.; Long, N.J. RGD-targeted MnO nanoparticles as T1 contrast agents for cancer imaging—The effect of PEG length in vivo. J. Mater. Chem. B 2014, 2, 868–876. [Google Scholar] [CrossRef]
- Kohara, S.; Itou, M.; Suzuya, K.; Inamura, Y.; Sakurai, Y.; Ohishi, Y.; Takata, M. Structural studies of disordered materials using high-energy X-ray diffraction from ambient to extreme conditions. J. Phys. Condens. Matter 2007, 19, 506101. [Google Scholar] [CrossRef]
- Barbiellini, B.; Platzman, P.M. The healing mechanism for excited moleculesnear metallic surfaces. New J. Phys. 2006, 8, 20. [Google Scholar] [CrossRef][Green Version]
- Lide, D.R. Handbook of Chemistry and Physics, 72nd ed.; CRC Press: Boca Raton, FL, USA, 1991–1992.
- King, R.B. Encyclopedia of Inorganic Chemistry; Wiley: Chichester, NY, USA, 1994. [Google Scholar]
- Kuriyama, M.; Hosoya, S. X-ray Measurement of Scattering Factors of Manganese and Oxygen Atoms in Manganous Oxide. J. Phys. Soc. Jpn. 1962, 17, 1022–1029. [Google Scholar] [CrossRef]
- Juhás, P.; Davis, T.; Farrow, C.L.; Billinge, S.J.L. PDFgetX3: A rapid and highly automatable program for processing powder diffraction data into total scattering pair distribution functions. J. Appl. Cryst. 2013, 46, 560–566. [Google Scholar] [CrossRef]
- Juhás, P.; Farrow, C.L.; Yang, X.; Knox, K.R.; Billinge, S.J.L. Complex modeling: A strategy and software program for combining multiple information sources to solve ill posed structure and nanostructure inverse problems. Acta Crystallogr. A 2015, 71, 562–568. [Google Scholar] [CrossRef] [PubMed]
- Belli, M.; Scafati, A.; Bianconi, A.; Mobilio, S.; Palladino, L.; Reale, A.; Burattini, E. X-Ray Absorption Near Edge Structures (XANES) In Simple and Complex Mn Compounds. Solid State Commun. 1980, 35, 355–361. [Google Scholar] [CrossRef]
- Hafiz, H.; Suzuki, K.; Barbiellini, B.; Orikasa, Y.; Kaprzyk, S.; Tsuji, N.; Yamamoto, K.; Terasaka, A.; Hoshi, K.; Uchimoto, Y.; et al. Identification of ferrimagnetic orbitals preventing spinel degradation by charge ordering in LixMn2O4. Phys. Rev. B 2019, 100, 205104. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pussi, K.; Gallo, J.; Ohara, K.; Carbo-Argibay, E.; Kolen’ko, Y.V.; Barbiellini, B.; Bansil, A.; Kamali, S. Structure of Manganese Oxide Nanoparticles Extracted via Pair Distribution Functions. Condens. Matter 2020, 5, 19. https://doi.org/10.3390/condmat5010019
Pussi K, Gallo J, Ohara K, Carbo-Argibay E, Kolen’ko YV, Barbiellini B, Bansil A, Kamali S. Structure of Manganese Oxide Nanoparticles Extracted via Pair Distribution Functions. Condensed Matter. 2020; 5(1):19. https://doi.org/10.3390/condmat5010019
Chicago/Turabian StylePussi, Katariina, Juan Gallo, Koji Ohara, Enrique Carbo-Argibay, Yury V. Kolen’ko, Bernardo Barbiellini, Arun Bansil, and Saeed Kamali. 2020. "Structure of Manganese Oxide Nanoparticles Extracted via Pair Distribution Functions" Condensed Matter 5, no. 1: 19. https://doi.org/10.3390/condmat5010019
APA StylePussi, K., Gallo, J., Ohara, K., Carbo-Argibay, E., Kolen’ko, Y. V., Barbiellini, B., Bansil, A., & Kamali, S. (2020). Structure of Manganese Oxide Nanoparticles Extracted via Pair Distribution Functions. Condensed Matter, 5(1), 19. https://doi.org/10.3390/condmat5010019






