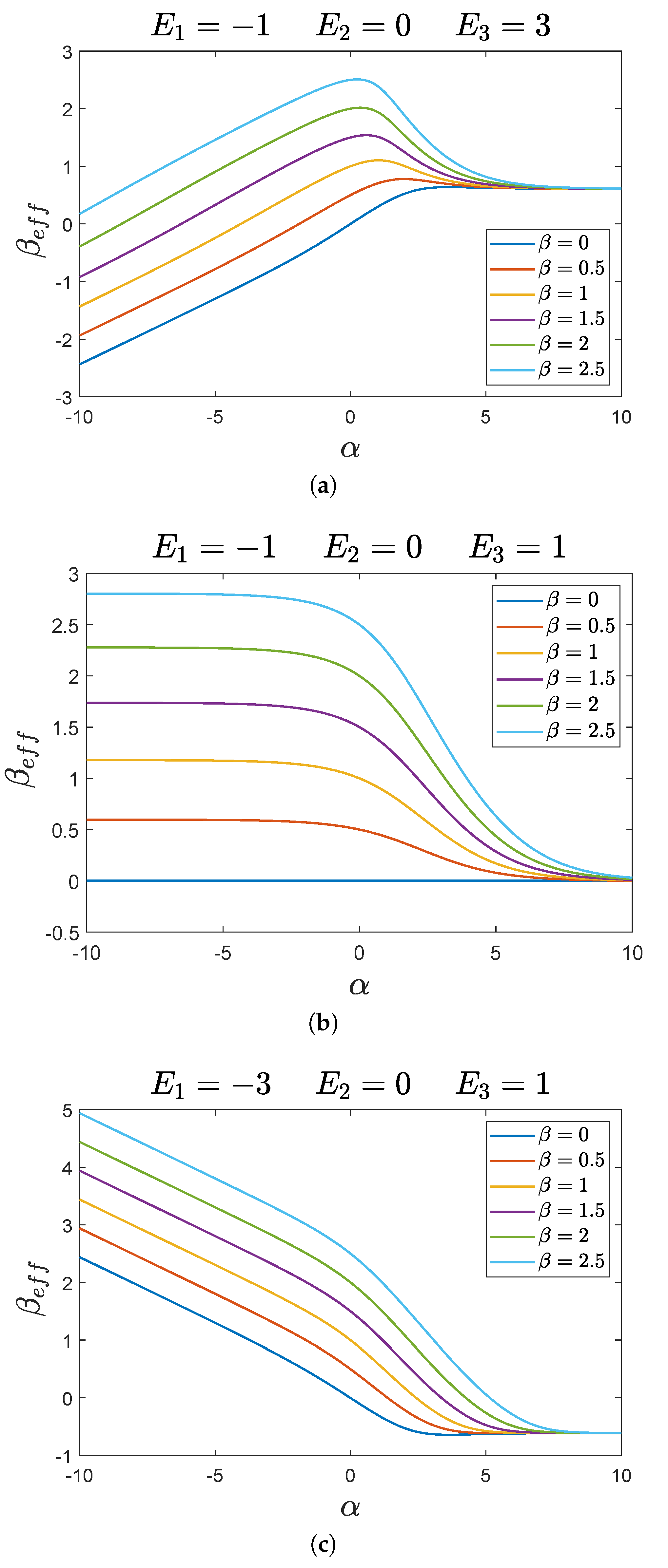1. Introduction
Fluctuation theorems relate fluctuations of thermodynamic quantities of a given system to equilibrium properties evaluated at the steady state [
1,
2,
3,
4]. This statement finds fulfillment in the Jarzynski equality, whose validity has been extensively theoretically and experimentally discussed in the last two decades for both classical and quantum systems [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17].
The evaluation of the relevant work originated by using a coherent modulation of the system Hamiltonian has been the subject of intense investigation [
18,
19,
20,
21,
22,
23,
24]. A special focus was devoted to the study of heat and entropy production, obeying of the second law of thermodynamics, the interaction with one or more external bodies, and/or the inclusion of an observer [
25,
26,
27,
28,
29,
30,
31,
32,
33,
34].
In this respect, the energy variation and the emission/absorption of heat induced—and sometimes enhanced—by the application of a sequence of quantum measurements was studied [
17,
35,
36,
37,
38,
39,
40,
41]. In such a case, the term quantum heat has been used [
41,
42]; we will employ it as well in the following to refer to the fact that the fluctuations of energy exchange are induced by quantum projective measurements performed during the time evolution of the system. As recently discussed in Ref. [
17], the information about the fluctuations of energy exchanges between a quantum system and an external environment may be enclosed in an energy scaling parameter that only depends on the initial and the asymptotic (for long times) quantum states resulting from the system dynamics.
In Ref. [
41], the effect of stochastic fluctuations on the distribution of the energy exchanged by a quantum two-level system with an external environment under sequences of quantum measurements was characterized and the corresponding quantum-heat probability density function was derived. It has been shown that, when a stochastic protocol of measurements is applied, the quantum Jarzynski equality is obeyed. In this way, the quantum-heat transfer was characterized for two-level systems subject to projective measurements. Two-level systems have the property that a density matrix in the energy basis (as the one obtained after a measurement of the Hamiltonian operator [
18]) can be always written as a thermal state and, therefore, the Jarzynski equality has a 1 on its right-hand side. Therefore, a natural issue to be investigated is the study of quantum-heat fluctuation relations for
N-level systems, e.g.,
, where this property of the initial state of a two-points measurement scheme of being thermal is no longer valid. So, it would be desirable, particularly for the case of a large number of quantum measurements, to study the properties of the characteristic function of the quantum heat when initial states cannot be written as thermal states.
With the goal of characterizing the effects of having arbitrary initial conditions, in this paper, we study quantum systems described by finite dimensional Hilbert spaces, focusing on the case of three-level systems. We observe that finite-level quantum systems may present peculiar features with respect to continuum systems. As shown in Ref. [
23], even when the quantum Jarzynski equality holds and the average of the exponential of the work equals the free energy difference, the variance of the energy difference may diverge for continuum systems, an exception being provided by finite-level quantum systems.
In this paper we analyze, using numerical simulations, (i) the distribution of the quantum heat originated by a three-level system under a sequence of M projective measurements in the limit of a large M, and (ii) the behavior of an energy parameter , such that the Jarzynski equality has 1 on its right-hand side, always in the limit of a large M. We also discuss the dependence of on the initial state, before the application of the sequence of measurements.
2. The Protocol
Let us consider a quantum system described by a finite dimensional Hilbert space. We denote with
H the time-independent Hamiltonian of the system that admits the spectral decomposition
where
N is the dimension of the Hilbert space. We assume that no degeneration occurs in the eigenstates of
H.
At time
, just before the first measurement of
H is performed, the system is supposed to be in an arbitrary quantum state described by the density matrix
s.t.
. This allows us to write
where
and
.
Then, we assume that the fluctuations of the energy variations, induced by a given transformation of the state of the system, are evaluated by means of the so-called two-point measurement (TPM) scheme [
18]. According to this scheme, a quantum projective measurement of the system hamiltonian is performed both at the initial and the final times of the transformation. This hypothesis justifies the initialization of the system in a mixed state, as given in Equation (
2). By performing a first projective energy measurement, at time
, the system is in one of the states
with probability
, while the system energy is
. Afterwards, we suppose that the system
S is subject to a number
M of consecutive projective measurements of the generic observable
where
and
denote, respectively, the outcomes and the eigenstates of
O. According to the postulates of quantum mechanics, the state of the system after one of these projective measurements is given by one of the projectors
. Between two consecutive measurements, the system evolves with the unitary dynamics generated by
H, i.e.,
, where
ℏ has been set to unity and the waiting time
is the time difference between the
and the
measurement of
O.
In general, the waiting times
can be random variables, and the sequence
is distributed according to the joint probability density function
. The last (i.e, the
) measurement of
O is immediately followed by a second projective measurement of the energy, as prescribed by the TPM scheme. By denoting with
the outcome resulting from the second energy measurement of the scheme, the final state of the system is
and the quantum heat
Q exchanged during the transformation is thus given by
As
Q is a random variable, one can define the characteristic function
where
denotes the probability of obtaining
at the end of the protocol conditioned to have measured
at the first energy measurement of the TPM scheme. If the initial state is thermal, i.e.,
, then one recovers the Jarzynski equality stating that
Let us notice that
is a convex function such that
and
, as discussed in Ref. [
17]. Hence, as long as
, one can unambiguously introduce the parameter
defined by the relation
which formally plays the role of an effective inverse temperature. Focusing on three-level systems, in the following, we will study the characteristic function
and the properties of such a parameter
. For comparison, we first pause in the next subsection to discuss what happens for two-level systems.
Intermezzo on Two-Level Quantum Systems
We pause here to remind the reader of the results for two-level systems. The state of any two-level system, diagonal on the Hamiltonian basis, is a thermal state for some value of
. Of course, if the state is thermal, the value of
trivially coincides with
. In particular, in Ref. [
41], the energy exchanged between a two-level quantum system and a measurement apparatus was analyzed, with the assumption that the repeated interaction with the measurement device can be reliably modeled by a sequence of projective measurements occurring instantly and at random times. Numerically, it has been observed that, as compared with the case of measurements occurring at fixed times, the two-level system exchanges more energy in the presence of randomness when the average time between consecutive measurements is sufficiently small in comparison with the inverse resonance frequency. However, the quantum-heat Jarzynski equality, related to the equilibrium properties of the transformation applied to the system, is still obeyed, as well as when the waiting times between consecutive measurements are randomly distributed and for each random realization. These results are theoretically supported by the fact that, in the analyzed case, the dynamical evolution of the quantum system is unital [
11,
12]. A discussion on the values of the parameter
, extracted from experimental data for nitrogen-vacancy (NV) centers in diamonds subject to projective measurements in a regime where an effective two-level approximation is valid was recently presented in Ref. [
17].
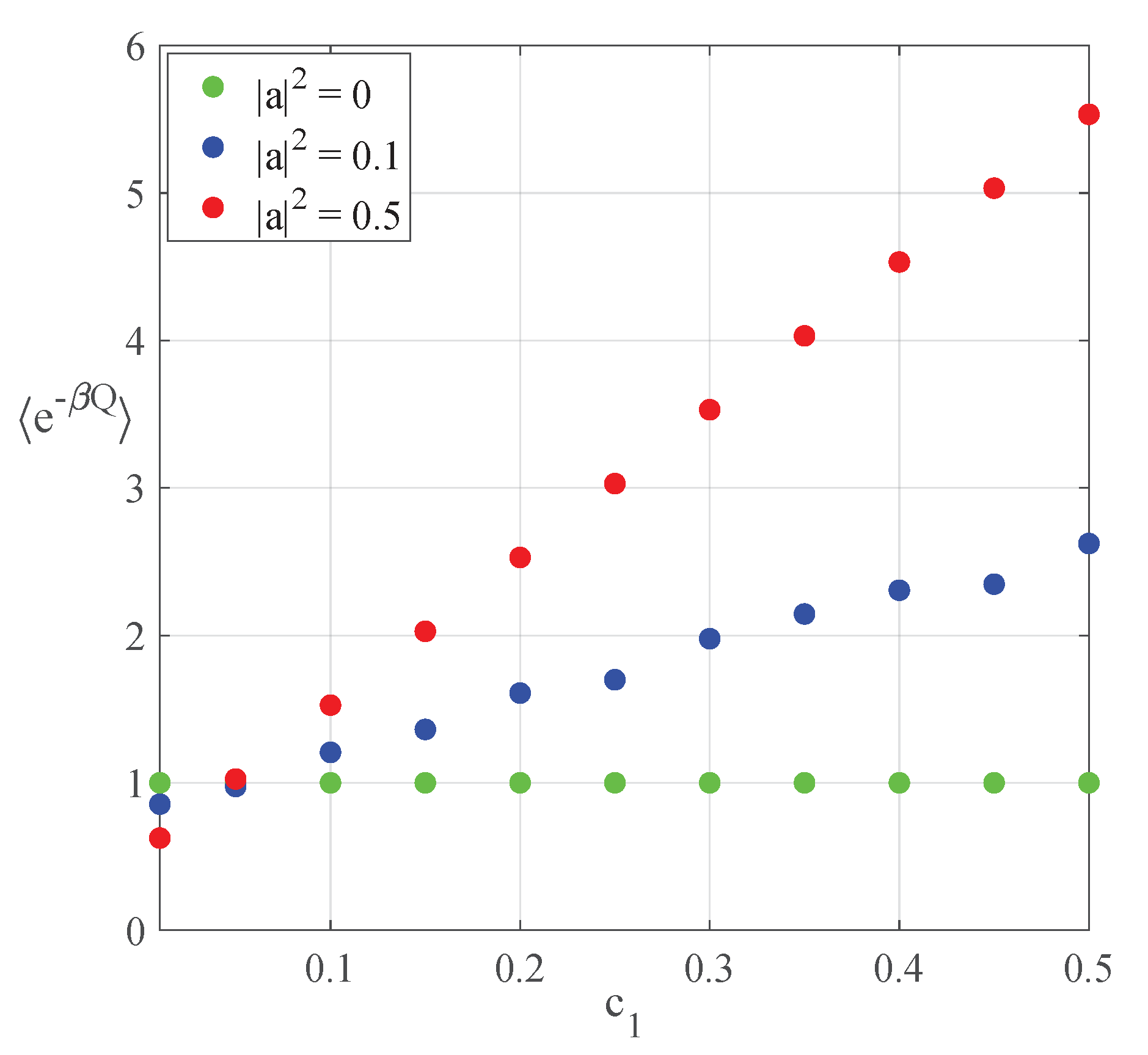
In
Figure 1, we plot the quantum-heat characteristic function
as a function of the parameter
that appears in the decomposition of the initial state
with respect to the energy eigenstates
and
where
. The function is plotted for three values of the parameter
, used to parametrize the eigenstates
of
O as a function of the energy eigenstates of the system, i.e.,
with
and
. As a result, one can observe that
for the value of
ensuring that
. Further details can be found in Ref. [
41].
The case is trickier: Since, in general, the initial state is no longer thermal, it is not trivial to determine the value of , and its dependence on the initial condition is interesting to investigate. In this regard, in the following, we will numerically address the case by providing results on the asymptotic behavior of the system in the limit . For the sake of simplicity, from here on, we assume that the values of the waiting times are fixed for any . However, our findings turn out to be the same for any choice of the marginal probability distribution functions , up to “pathological” cases such as . So, having random waiting times does not significantly alter the scenario emerging from the presented results.
3. Parametrization of the Initial State
In this paragraph, we introduce a parametrization of the initial state for the case, which will be useful for a thermodynamic analysis of the system.
As previously recounted, for a two-level quantum system in a mixed state, as given by Equation (
2), it is always formally possible to define a temperature. In particular, one can implicitly find an effective inverse temperature, making
a thermal state, by solving the following equation for
In the
case, however, we have two independent parameters in (
2) (the third parameter indeed enforces the condition
), and thus, in general, it is no longer possible to formally define a single temperature for the state. Here, we propose the following parametrization of
that generalizes the one of Equation (
10).
We denote as
partial effective temperatures the three parameters
, defined through the ratios of
,
, and
such that, for a thermal state,
,
. The three parameters are not independent, as they are constrained by the relation
which gives in turn the following equality
By introducing
,
, and
, Equation (
13) can be written as
where by definition
Thus, as expected, the thermal state is a solution of the condition (
14) for any choice of
. This has also a geometric interpretation. In the space of the
,
, Equation (
14) becomes an orthogonality condition between the
and the
vectors, while (
15) defines a plane that is orthogonal to the vector
. When
is proportional to
, the orthogonality condition is automatically satisfied and one finds a thermal state. This suggests that, in general, one can conveniently parametrize
in terms of both the components that are orthogonal and parallel to the plane
. Such terms have the physical meaning of the thermal and non-thermal components of the initial state. Formally, this means that we can parametrize each
through the fictitious inverse temperature
and a deviation
, i.e.,
where
v acts as a normalization constant
Hence, taking into account the normalization constraint, the coefficients
are given by
or, in terms of the parameters
and
,
where
is a pseudo-partition function ensuring the normalization of the
′s
Let us provide some physical intuition about the parameters and : For , we recover a thermal state, whereby if , or vice versa if . On the other hand, the non-thermal component can be used to obtain a non-monotonic behavior of the coefficients . For example, for , since is greater than both and , one finds that if .
As a final remark, it is worth noting that we can reduce the dimension of the space of the parameters. In particular, without loss of generality, one can choose the zero of the energy by taking (and then , ), or we can reduce our analysis to the cases with . As a matter of fact, the parametrization is left unchanged by the transformation , with the result that the case of can be explored by simply considering in the fictitious system with (here, the choice of guarantees that this second case can be simply obtained by substituting with ).
4. Large Limit
Here, we numerically investigate the behavior of a three-level system subject to a sequence of M projective quantum measurements with a large M (asymptotic limit) and where is not infinitesimal. From here on, we adopt the language of spin-1 systems, and we thus identify O with .
In the asymptotic limit, the behavior of the system is expected not to depend on the choice of the evolution Hamiltonian, with the exception that at least one of the eigenstates of is also an energy eigenstate. In such a case, indeed, if the energy outcome corresponding to the common eigenstate is obtained by the first measurement of the TPM scheme, then the evolution is trivially deterministic, as the system is locked in the measured eigenstate.
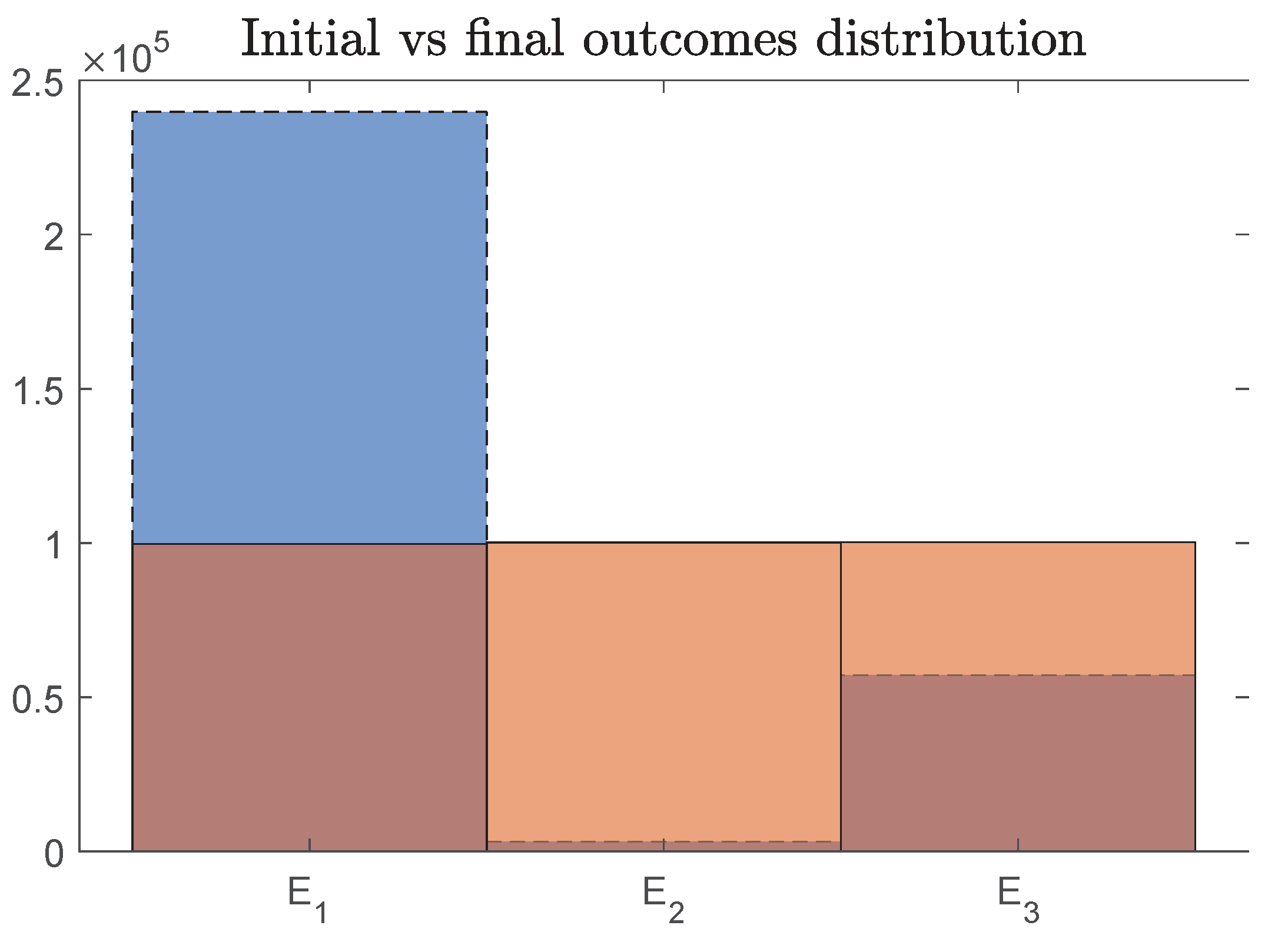
Choosing a generic observable (with no eigenstates in common with
H), numerical simulations (cf.
Figure 2) suggest that our protocol leads the system to the completely uniform state. The latter can be interpreted as a canonical state with
(notice that this result holds in the situation we are analyzing, with a finite dimensional Hilbert space). The system evolves with Hamiltonian
, where the energy units are chosen such that
and
. It is initialized in the state
with
, corresponding to
and
, and we performed
projective measurements of the observable
separated by the time
.
This numerical finding allows us to derive an analytic expression of the quantum-heat characteristic function. In this regard, as the final state is independent of the initial one for a large
M, the joint probability of obtaining
and
, after the first and the second energy measurement respectively, is equal to
As a consequence,
G can be expressed in terms of the partition function
and of the pseudo-partition function introduced in Equation (20), i.e.,
Regardless of the choice of the system parameters, the already known results are straightforwardly recovered, i.e.,
and
for
(initial thermal state). In
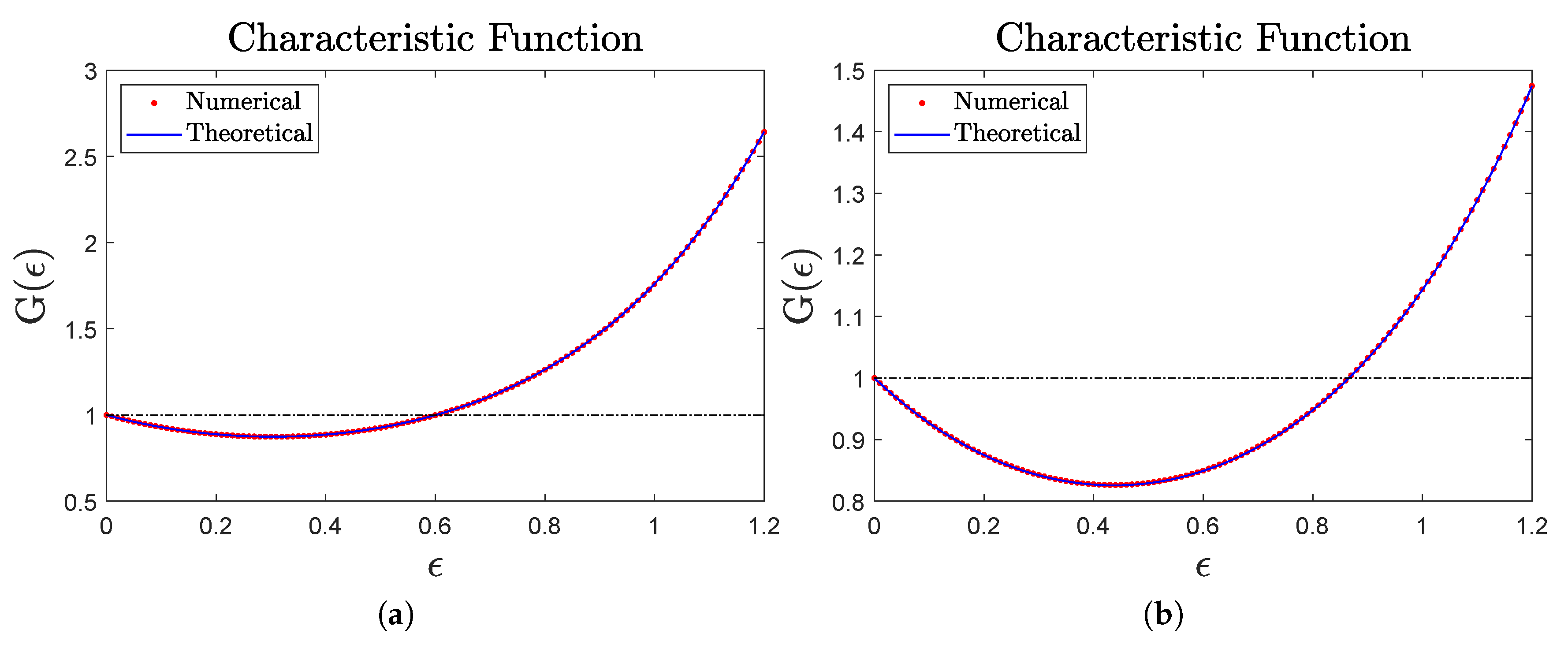
Figure 3, our analytical expression for
is compared with its numerical estimate for two different Hamiltonians, showing a very good agreement.
We remark that the distribution of
after the second energy measurement could also be obtained by simply imposing the maximization of the von Neumann entropy. This is reasonable, since the measurement device is macroscopic and can provide any amount of energy. As a final remark, notice that, in the numerical findings of
Figure 3, the statistics of the quantum-heat fluctuations originated by the system respect the same ergodic hypothesis that is satisfied whenever a sequence of quantum measurements is performed on a quantum system [
43,
44,
45]. In particular, in
Figure 3, one can observe that the analytical expression of
for a large
M (i.e., in the asymptotic regime obtained by indefinitely increasing the time duration of the implemented protocol) practically coincides with the numerical results obtained by simulating a sequence with a finite number of measurements (
) but over a quite large number (
) of realizations. This evidence is quite important, because it means that the quantum-heat statistics is homogeneous and fully take into account even phenomena occurring with very small probability in a single realization of the protocol.
5. Estimates of
In this section, we study the behavior of
, i.e., the nontrivial solution of
, as a function of the initial state (parametrized by
and
) and of the energy levels of the system. Let us first notice that, by starting from Equation (
22), obtaining an analytical expression for
in the general case appears to be a very non-trivial task. Thus, in
Figure 4, we numerically compute
as a function of
(the non-thermal component of
) for different values of
. Three representative cases for the energy levels are taken, i.e.,
,
, and
, respectively. This choice allows us to deal both with the cases
and
. The choice of the energy unit is such that the smallest energy gap between
and
is set to one. As stated above, we consider
; the corresponding negative values of the inverse temperature are obtained by taking
with
. As expected, for
, we have
, regardless of the values of the
’s.
In the next two subsections, we continue discussing in detail the findings of
Figure 4, presenting the asymptotic behaviors for large positive and negative values of
.
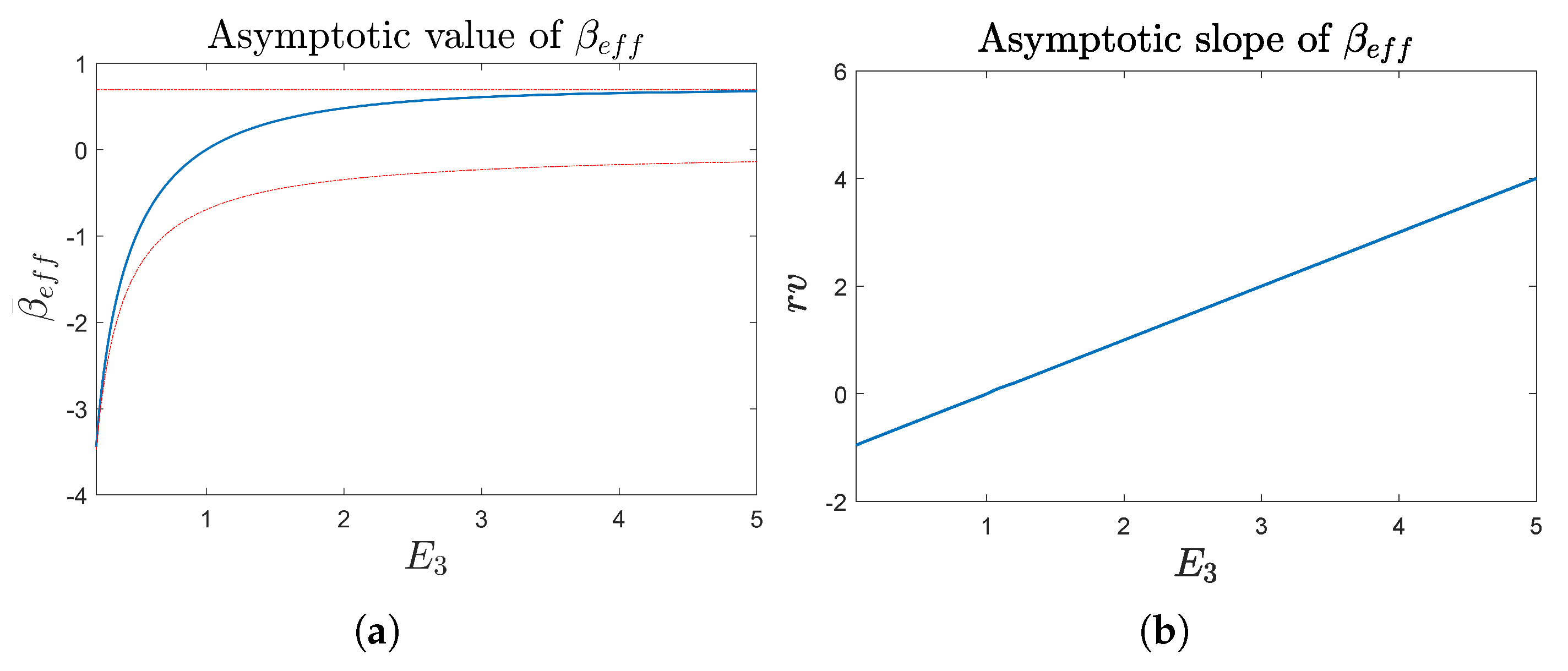
5.1. Asymptotic Behavior for a Large Positive
From
Figure 4, one can deduce that, for large positive values of
(corresponding to having as the initial density operator the pure state
),
, which only depends on
and
. This asymptotic value
is positive if
, negative if
, and zero when
. To better explain the plots in
Figure 4, let us consider the analytic expression of
. In this regard, for a large
and finite
, we can write
so that, by using Equation (
23), the condition
reads as
, or, setting
,
Notice that, if
the only solution of Equation (
25) is
, while a positive solution appears for
and a negative one if
, thus confirming what was observed in the numerical simulations. Moreover, by replacing
and
, the value of
changes its sign.
Now, without loss of generality, let us fix the energy unit so that
. The behavior of
as a function of
is shown in
Figure 5. We observe a monotonically increasing behavior of
up to a constant value for
. Once again, this value can be analytically computed from Equation (
25), which, for a large value of
, gives
. Putting together all of the above considerations and restoring the energy scales, the limits of
are the following
The lower and the upper bounds of
are also shown in
Figure 5, in which
and
.
5.2. Asymptotic Behavior for a Large Negative
From
Figure 4, one can also conclude that, for large negative values of
, the behavior of
is linear with
with
if
,
when
, and
r is negative otherwise. This divergence is easily understood: In fact, the limit
(for finite
) corresponds to the initial state
when
or
if
. On the other hand, those states (thermal states with
) are also reached in the limits
with a finite
. This simple argument does not imply the linear divergence of
as in Equation (
27), nor does it provide insights about the value of
r, which, however, can be derived from Equation (
23). Although the calculation makes a distinction on the sign of
r depending on whether
is greater or smaller than
, the result is independent of this detail. In particular, by considering the case
(
) and taking into account the divergence of
, we find in the
regime that the characteristic function
has the following form:
Hence, in order to ensure that
in the limit
, the following relation has to be satisfied
The numerical estimate of
as a function of
is shown in
Figure 5. The numerical results confirm the linear dependence of
as a function of
.
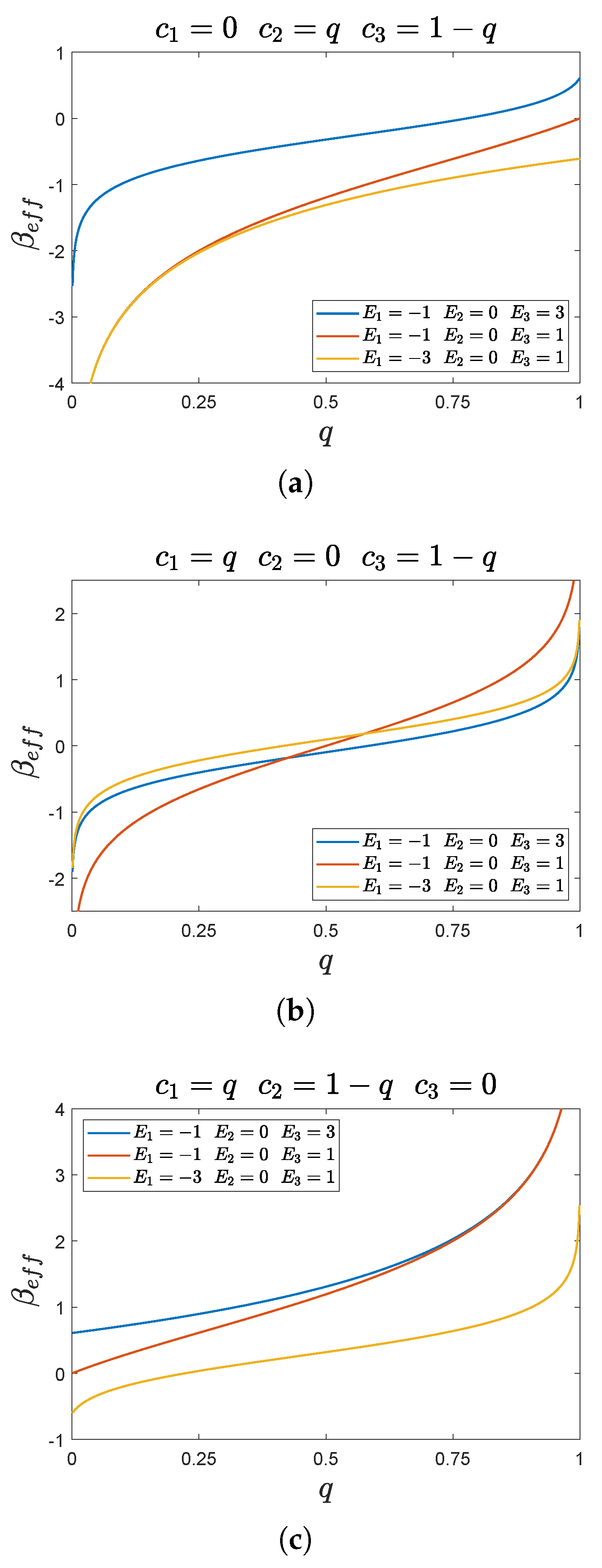
5.3. Limits of the Adopted Parametrization
The parametrization introduced in
Section 3 is singular in correspondence of the initial states
with one or more coefficients
equal to zero. In this regard, as remarked above, initial pure states can be easily obtained in the limits
,
finite (corresponding to
and
, respectively) and
,
finite (that provides
). Instead, initial states with only a coefficient
equal to zero, namely
with
, cannot be easily written in terms of
and
. In fact, the expressions in Equation (
30) correspond to the limit in which
with
for suitable
a,
b. This result can be obtained, e.g., for the first of the states in Equation (
30), considering the state
,
, and
in the limit
. Solving for
and
, we have
so that
, while the
q dependence is encoded in the next-to-leading term. For this reason, the parametrization in terms of
turns out to be the most convenient in the case of singularity. In
Figure 6, the numerical estimates of
as a function of
q are shown for the three cases in Equation (
30), respectively for
greater, equal to, and smaller than
. The symmetries
,
,
and
, due to our choice of parametrization, can be observed.
6. Conclusions
In this paper, we studied the quantum-heat distribution originating from a three-level quantum system subject to a sequence of projective quantum measurements.
As figure of merit, we analyze the characteristic function
of the quantum heat
Q by using the formalism of stochastic thermodynamics. In this regard, it is worth recalling that, as the system Hamiltonian
H is time-independent, the fluctuations of the energy variation during the protocol can be effectively referred of as quantum heat. As shown in Ref. [
17], the fluctuation relation describing all the statistical moments of
Q is simply given by the equality
, where the energy-scaling parameter
can be considered as an effective inverse temperature. The analytic expression of
has been determined only for specific cases, as, for example, two-level quantum systems.
Here, a three-level quantum system was considered and, in order to gain information on the value of , we performed specific numerical simulations. In doing this, we introduced a convenient parametrization of the initial state , such that its population values can be expressed as a function of the reference inverse temperature and the parameter , identifying the deviation of from the thermal state. Then, the behavior of the system when M, the number of projective measurements, is large is numerically analyzed. The condition of a large M leads to an asymptotic regime whereby the final state of the system tends to a completely uniform state, stationary with respect to the energy basis. This means that such a state can be equivalently described by an effective thermal state with zero inverse temperature. In this regime, the value of the energy scaling allowing for the equality (i.e., ) is evaluated. As a consequence, , which uniquely rescales energy exchange fluctuations, implicitly encloses information on the initial state . In other terms, once and the system (time-independent) Hamiltonian H are fixed, remains unchanged by varying parameters pertaining to the measurements performed during the dynamics, e.g., the time interval between the measurements.
We have also determined as a function of and for large M. Except for few singular cases, we found that, for large negative values of , is linear with respect to , while it tends to become constant and independent of for large positive values of . Such conditions can be traced back to an asymptotic equilibrium regime, because any dependence from the initial state is lost.
As a final remark, we note that, overall, the dynamics acting on the analyzed three-level system are unital [
11,
12]. As a matter of fact, this is the result of a non-trivial composition of unitary evolutions (between each couple of measurements) and projections. It would certainly also be interesting to analyze a three-level system subject to both a sequence of quantum measurements and in interaction with an external (classical or quantum) environment. In this respect, in light of the results in Refs. [
17,
46], the most promising platforms for this kind of experiment are NV centers in diamonds [
47]. Finally, also the analysis of general
N-level systems, and the study of large
M behavior deserve further investigations.
Author Contributions
Conceptualization, G.G., S.G., A.T. and S.R.; Data curation, G.G.; Formal analysis, G.G., S.G. and A.T.; Supervision, S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MISTI Global Seed Funds MIT-FVG: NV centers for the test of the Quantum Jarzynski Equality (NVQJE).
Acknowledgments
The authors gratefully acknowledge M. Campisi, P. Cappellaro, F. Caruso, F. Cataliotti, N. Fabbri, S. Hernández-Gómez, M. Müller and F. Poggiali for useful discussions. This work was financially supported by the MISTI Global Seed Funds MIT-FVG Collaboration Grant “NV centers for the test of the Quantum Jarzynski Equality (NVQJE)”. The author (SG) also acknowledges PATHOS EU H2020 FET-OPERN grant No. 828946 and UNIFI grant Q-CODYCES. The author (SR) thanks the editors of this issue for inviting him to write a paper in honour of Shmuel Fishman, whom he had the pleasure to meet several times and appreciate his broad and deep knowledge of various fields of the theory of condensed matter; besides that, Shmuel Fishman was a lovely person with whom it was a privilege to spend time in scientific and more general discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665. [Google Scholar] [CrossRef]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuations relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 1653. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems, and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Deffner, S.; Campbell, S. Quantum Thermodynamics: An Introduction to the Thermodynamics of Quantum Information; Morgan & Claypool Publishers: Williston, VT, USA, 2019. [Google Scholar]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Crooks, G. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721. [Google Scholar] [CrossRef]
- Collin, D.; Ritort, F.; Jarzynski, C.; Smith, S.B.; Tinoco, I.; Bustamante, C. Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies. Nature 2005, 437, 231–234. [Google Scholar] [CrossRef]
- Toyabe, S.; Sagawa, T.; Ueda, M.; Muneyuki, E.; Sano, M. Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality. Nat. Phys. 2010, 6, 988–992. [Google Scholar] [CrossRef]
- Kafri, D.; Deffner, S. Holevo’s bound from a general quantum fluctuation theorem. Phys. Rev. A 2012, 86, 044302. [Google Scholar] [CrossRef]
- Albash, T.; Lidar, D.A.; Marvian, M.; Zanardi, P. Fluctuation theorems for quantum process. Phys. Rev. A 2013, 88, 023146. [Google Scholar]
- Rastegin, A.E. Non-equilibrium equalities with unital quantum channels. J. Stat. Mech. 2013, 6, P06016. [Google Scholar] [CrossRef]
- Sagawa, T. Lectures on Quantum Computing, Thermodynamics and Statistical Physics; World Scientific: Singapore, 2013. [Google Scholar]
- An, S.; Zhang, J.N.; Um, M.; Lv, D.; Lu, Y.; Zhang, J.; Yin, Z.; Quan, H.T.; Kim, K. Experimental test of the quantum Jarzynski equality with a trapped-ion system. Nat. Phys. 2015, 11, 193–199. [Google Scholar] [CrossRef]
- Batalhão, T.B.; Souza, A.M.; Mazzola, L.; Auccaise, R.; Sarthour, R.S.; Oliveira, I.S.; Goold, J.; Chiara, G.D.; Paternostro, M.; Serra, R.M. Experimental Reconstruction of Work Distribution and Study of Fluctuation Relations in a Closed Quantum System. Phys. Rev. Lett. 2014, 113, 140601. [Google Scholar] [CrossRef]
- Cerisola, F.; Margalit, Y.; Machluf, S.; Roncaglia, A.J.; Paz, J.P.; Folman, R. Using a quantum work meter to test non-equilibrium fluctuation theorems. Nat. Comm. 2017, 8, 1241. [Google Scholar] [CrossRef] [PubMed]
- Bartolotta, A.; Deffner, S. Jarzynski Equality for Driven Quantum Field Theories. Phys. Rev. X 2018, 8, 011033. [Google Scholar] [CrossRef]
- Hernández-Gómez, S.; Gherardini, S.; Poggiali, F.; Cataliotti, F.S.; Trombettoni, A.; Cappellaro, P.; Fabbri, N. Experimental test of exchange fluctuation relations in an open quantum system. arXiv 2019, arXiv:1907.08240. [Google Scholar]
- Talkner, P.; Lutz, E.; Hänggi, P. Fluctuation theorems: Work is not an observable. Phys. Rev. E 2007, 75, 050102(R). [Google Scholar] [CrossRef]
- Campisi, M.; Talkner, M.; Hänggi, P. Fluctuation Theorem for Arbitrary Open Quantum Systems. Phys. Rev. Lett. 2009, 102, 210401. [Google Scholar] [CrossRef]
- Mazzola, L.; De Chiara, G.; Paternostro, M. Measuring the characteristic function of the work distribution. Phys. Rev. Lett. 2013, 110, 230602. [Google Scholar] [CrossRef]
- Allahverdyan, A.E. Nonequilibrium quantum fluctuations of work. Phys. Rev. E 2014, 90, 032137. [Google Scholar] [CrossRef]
- Talkner, P.; Hänggi, P. Aspects of quantum work. Phys. Rev. E 2016, 93, 022131. [Google Scholar] [CrossRef]
- Jaramillo, J.D.; Deng, J.; Gong, J. Quantum work fluctuations in connection with the Jarzynski equality. Phys. Rev. E 2017, 96, 042119. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Jaramillo, J.D.; Hänggi, P.; Gong, J. Deformed Jarzynski Equality. Entropy 2017, 19, 419. [Google Scholar] [CrossRef]
- Jarzynski, C.; Wojcik, D.K. Classical and Quantum Fluctuation Theorems for Heat Exchange. Phys. Rev. Lett. 2004, 92, 230602. [Google Scholar] [CrossRef] [PubMed]
- Campisi, M.; Pekola, J.; Fazio, R. Nonequilibrium fluctuations in quantum heat engines: Theory, example, and possible solid state experiments. New J. Phys. 2015, 17, 035012. [Google Scholar] [CrossRef]
- Campisi, M.; Pekola, J.; Fazio, R. Feedback-controlled heat transport in quantum devices: Theory and solid-state experimental proposal. New J. Phys. 2017, 19, 053027. [Google Scholar] [CrossRef]
- Batalhao, T.B.; Souza, A.M.; Sarthour, R.S.; Oliveira, I.S.; Paternostro, M.; Lutz, E.; Serra, R.M. Irreversibility and the arrow of time in a quenched quantum system. Phys. Rev. Lett. 2015, 115, 190601. [Google Scholar] [CrossRef]
- Gherardini, S.; Müller, M.M.; Trombettoni, A.; Ruffo, S.; Caruso, F. Reconstructing quantum entropy production to probe irreversibility and correlations. Quantum Sci. Technol. 2018, 3, 035013. [Google Scholar] [CrossRef]
- Manzano, G.; Horowitz, J.M.; Parrondo, J.M. Quantum Fluctuation Theorems for Arbitrary Environments: Adiabatic and Nonadiabatic Entropy Production. Phys. Rev. X 2018, 8, 031037. [Google Scholar] [CrossRef]
- Batalhão, T.B.; Gherardini, S.; Santos, J.P.; Landi, G.T.; Paternostro, M. Characterizing irreversibility in open quantum systems. In Thermodynamics in the Quantum Regime; Springer: Berlin/Heidelberger, Germany, 2018; pp. 395–410. [Google Scholar]
- Santos, J.P.; Céleri, L.C.; Landi, G.T.; Paternostro, M. The role of quantum coherence in non-equilibrium entropy production. npj Quant. Inf. 2019, 5, 23. [Google Scholar] [CrossRef]
- Kwon, H.; Kim, M.S. Fluctuation Theorems for a Quantum Channel. Phys. Rev. X 2019, 9, 031029. [Google Scholar] [CrossRef]
- Rodrigues, F.L.; De Chiara, G.; Paternostro, M.; Landi, G.T. Thermodynamics of Weakly Coherent Collisional Models. Phys. Rev. Lett. 2019, 123, 140601. [Google Scholar] [CrossRef]
- Campisi, M.; Talkner, P.; Hänggi, P. Fluctuation Theorems for Continuously Monitored Quantum Fluxes. Phys. Rev. Lett. 2010, 105, 140601. [Google Scholar] [CrossRef] [PubMed]
- Campisi, M.; Talkner, P.; Hänggi, P. Influence of measurements on the statistics of work performed on a quantum system. Phys. Rev. E 2011, 83, 041114. [Google Scholar] [CrossRef] [PubMed]
- Yi, J.; Kim, Y.W. Nonequilibirum work and entropy production by quantum projective measurements. Phys. Rev. E 2013, 88, 032105. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, G.; Venkatesh, B.P.; Talkner, P.; Campisi, M.; Hänggi, P. Quantum fluctuation theorems and generalized measurements during the force protocol. Phys. Rev. E 2014, 89, 032114. [Google Scholar] [CrossRef] [PubMed]
- Hekking, F.W.J.; Pekola, J.P. Quantum jump approach for work and dissipation in a two-level system. Phys. Rev. Lett. 2013, 111, 093602. [Google Scholar] [CrossRef] [PubMed]
- Alonso, J.J.; Lutz, E.; Romito, A. Thermodynamics of weakly measured quantum systems. Phys. Rev. Lett. 2016, 116, 080403. [Google Scholar] [CrossRef]
- Gherardini, S.; Buffoni, L.; Müller, M.M.; Caruso, F.; Campisi, M.; Trombettoni, A.; Ruffo, S. Nonequilibrium quantum-heat statistics under stochastic projective measurements. Phys. Rev. E 2018, 98, 032108. [Google Scholar] [CrossRef]
- Elouard, C.; Herrera-Martí, D.A.; Clusel, M.; Auffèves, A. The role of quantum measurement in stochastic thermodynamics. npj Quantum Info. 2017, 3, 9. [Google Scholar] [CrossRef]
- Gherardini, S.; Gupta, S.; Cataliotti, F.S.; Smerzi, A.; Caruso, F.; Ruffo, S. Stochastic quantum Zeno by large deviation theory. New J. Phys. 2016, 18, 013048. [Google Scholar] [CrossRef]
- Gherardini, S.; Lovecchio, C.; Müller, M.M.; Lombardi, P.; Caruso, F.; Cataliotti, F.S. Ergodicity in randomly perturbed quantum systems. Quantum Sci. Technol. 2017, 2, 015007. [Google Scholar] [CrossRef]
- Piacentini, F.; Avella, A.; Rebufello, E.; Lussana, R.; Villa, F.; Tosi, A.; Marco, G.; Giorgio, B.; Eliahu, C.; Lev, V.; et al. Determining the quantum expectation value by measuring a single photon. Nat. Phys. 2017, 13, 1191–1194. [Google Scholar] [CrossRef]
- Wolters, J.; Strauß, M.; Schoenfeld, R.S.; Benson, O. Quantum Zeno phenomenon on a single solid-state spin. Phys. Rev. A 2013, 88, 020101(R). [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).