Review: Interactions of Active Colloids with Passive Tracers
Abstract
1. Introduction
2. Spotlight on Theoretical Considerations
3. Experimental Studies
3.1. Body Deformation
3.2. Phoresis
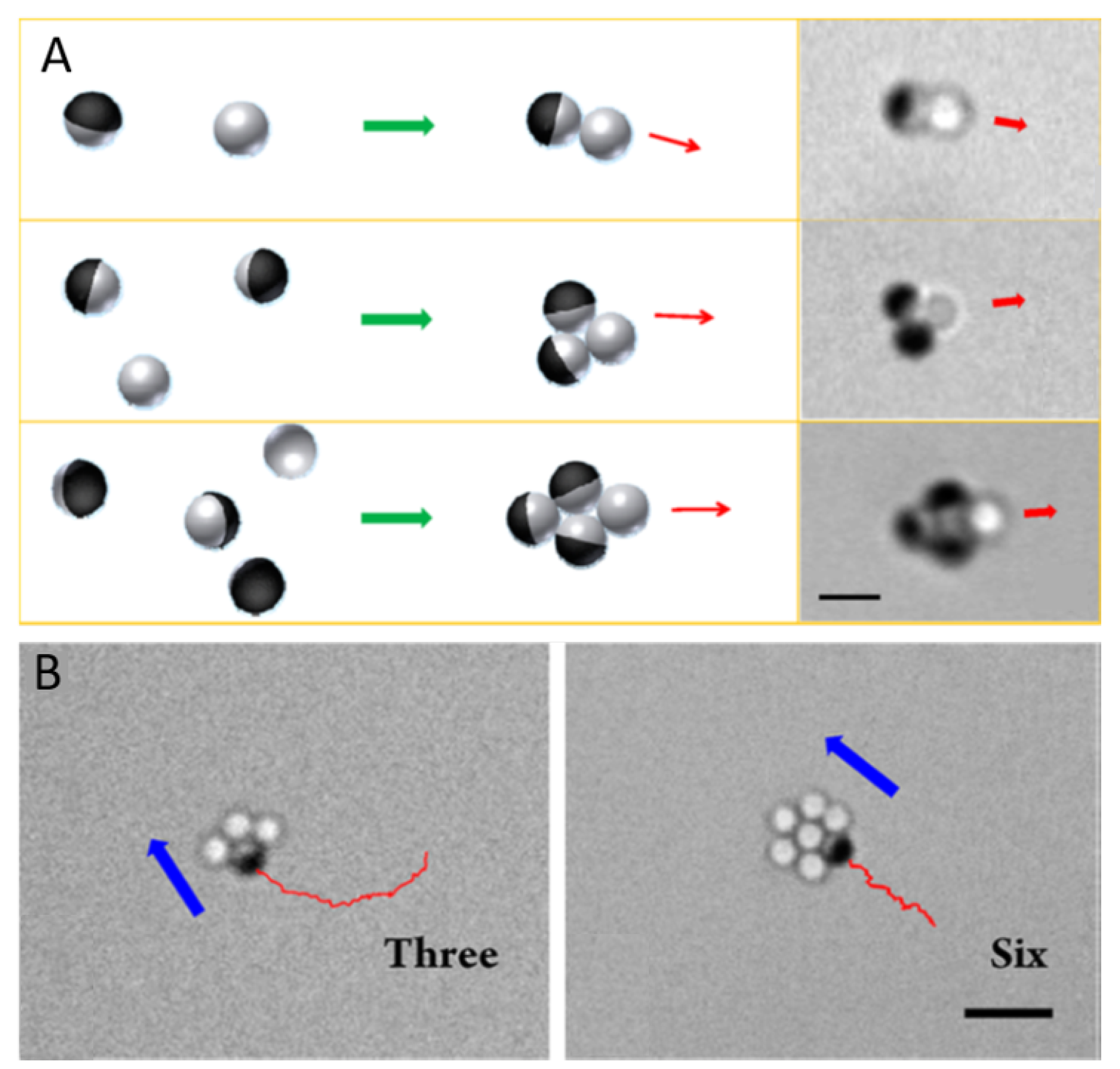
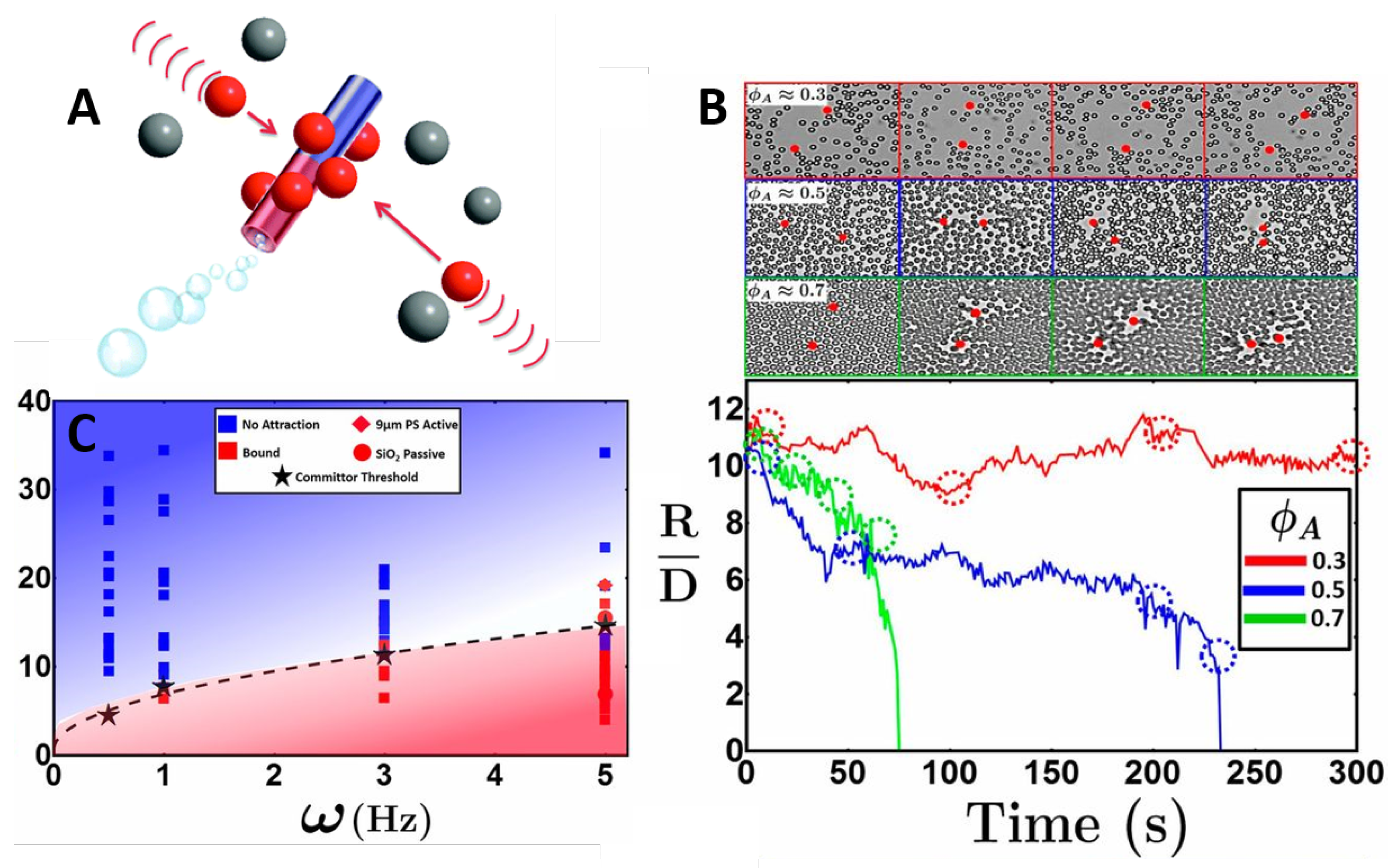
3.2.1. Diffusiophoresis
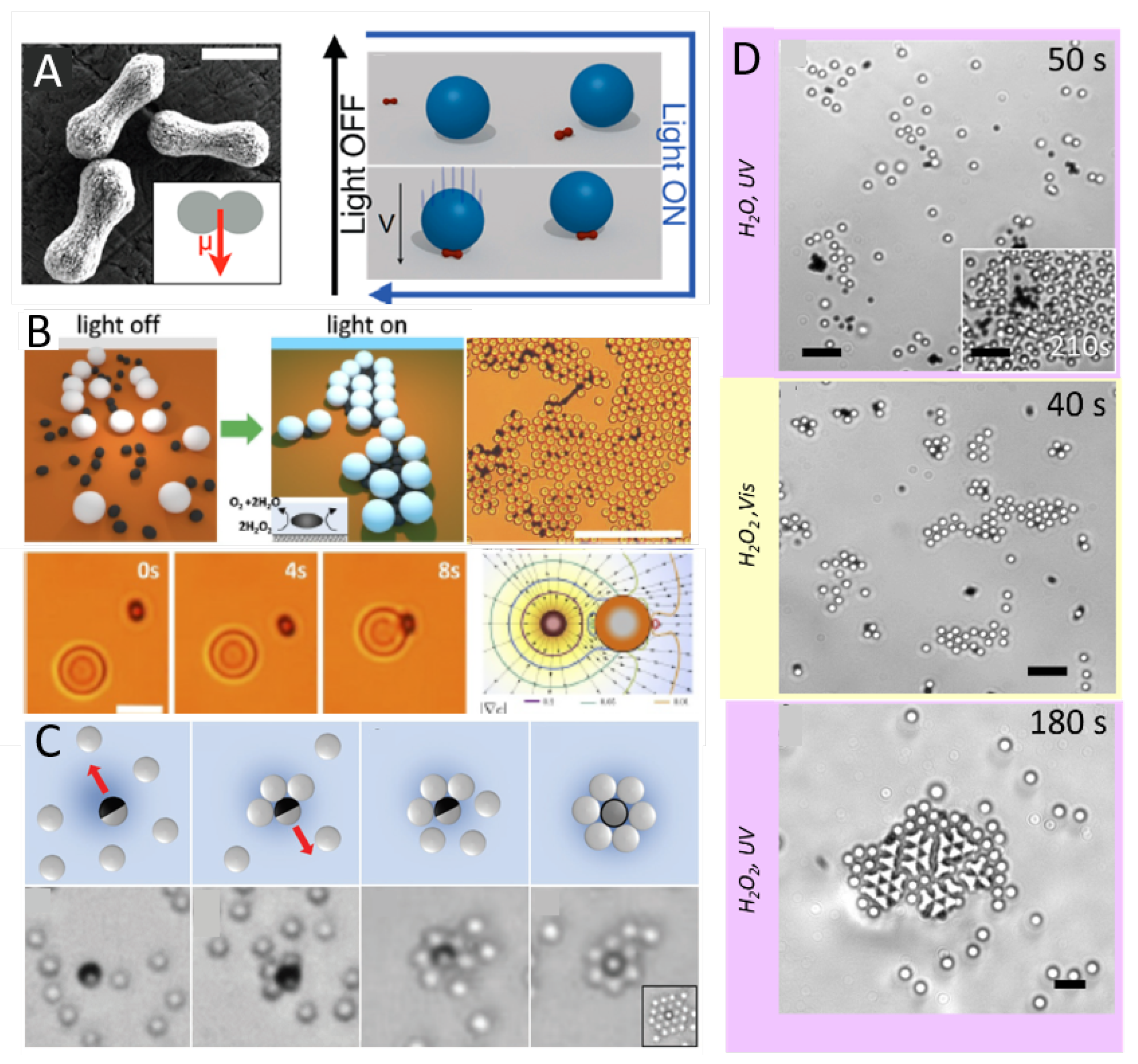
3.2.2. Light-Induced Phoresis
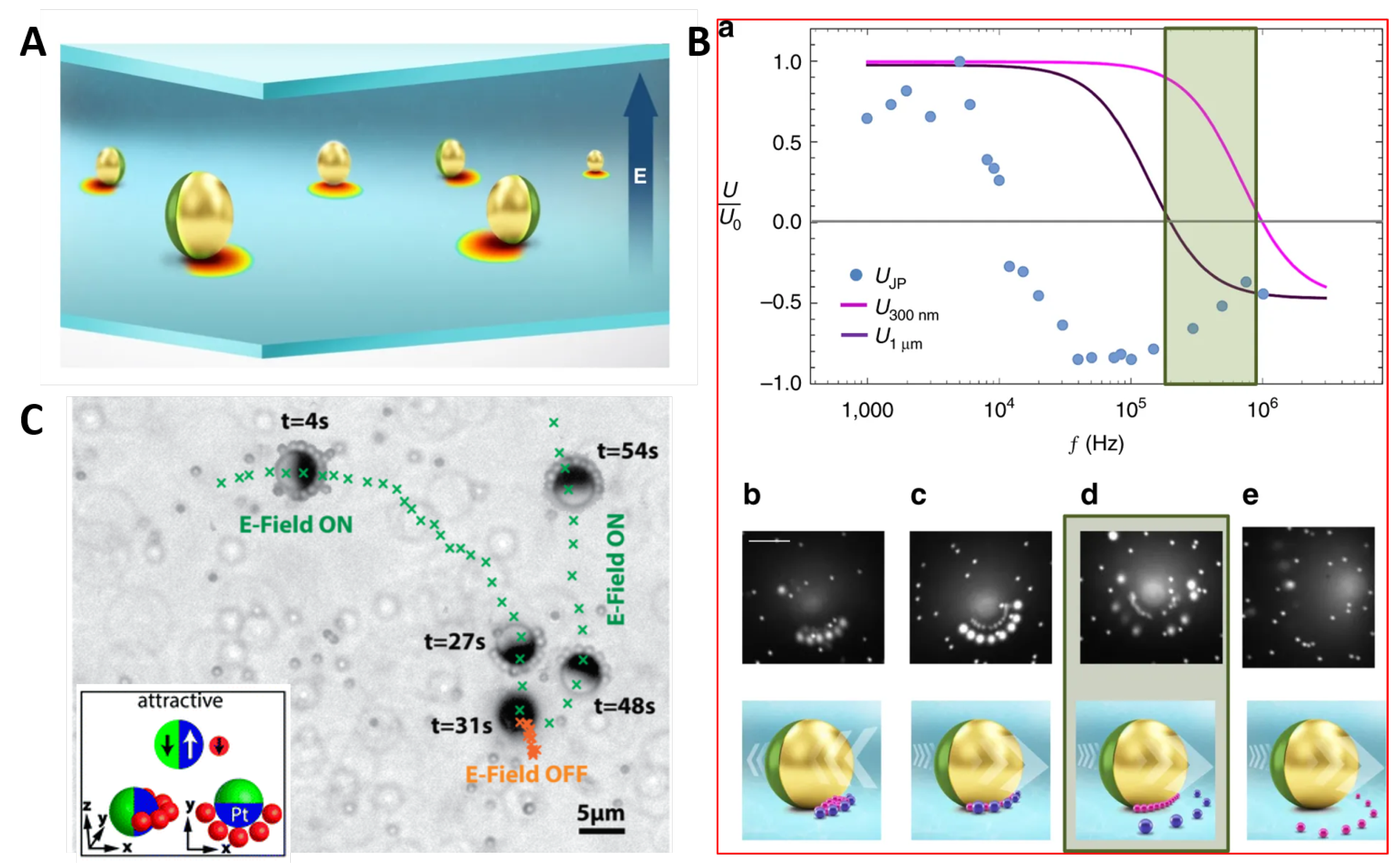
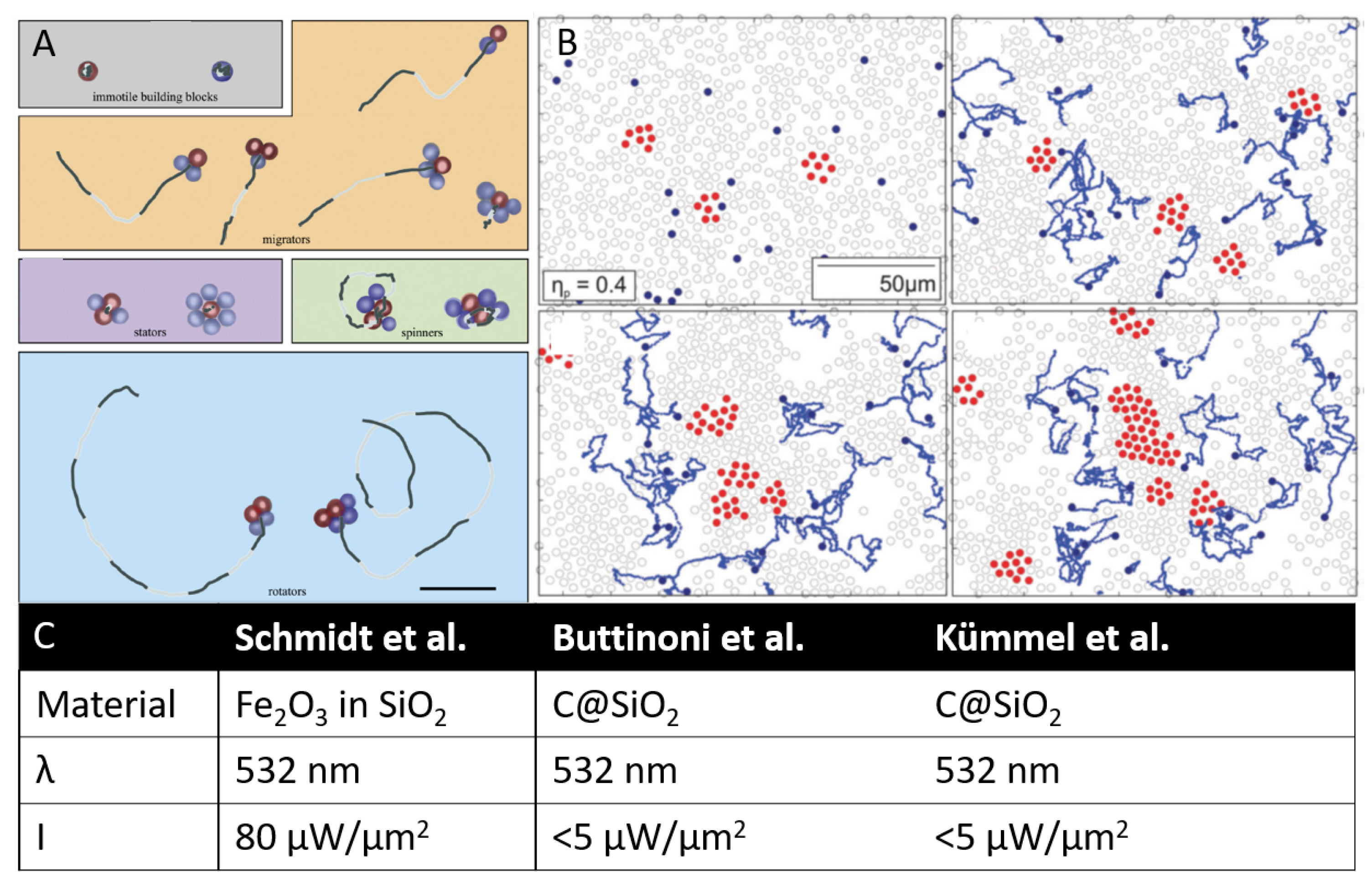
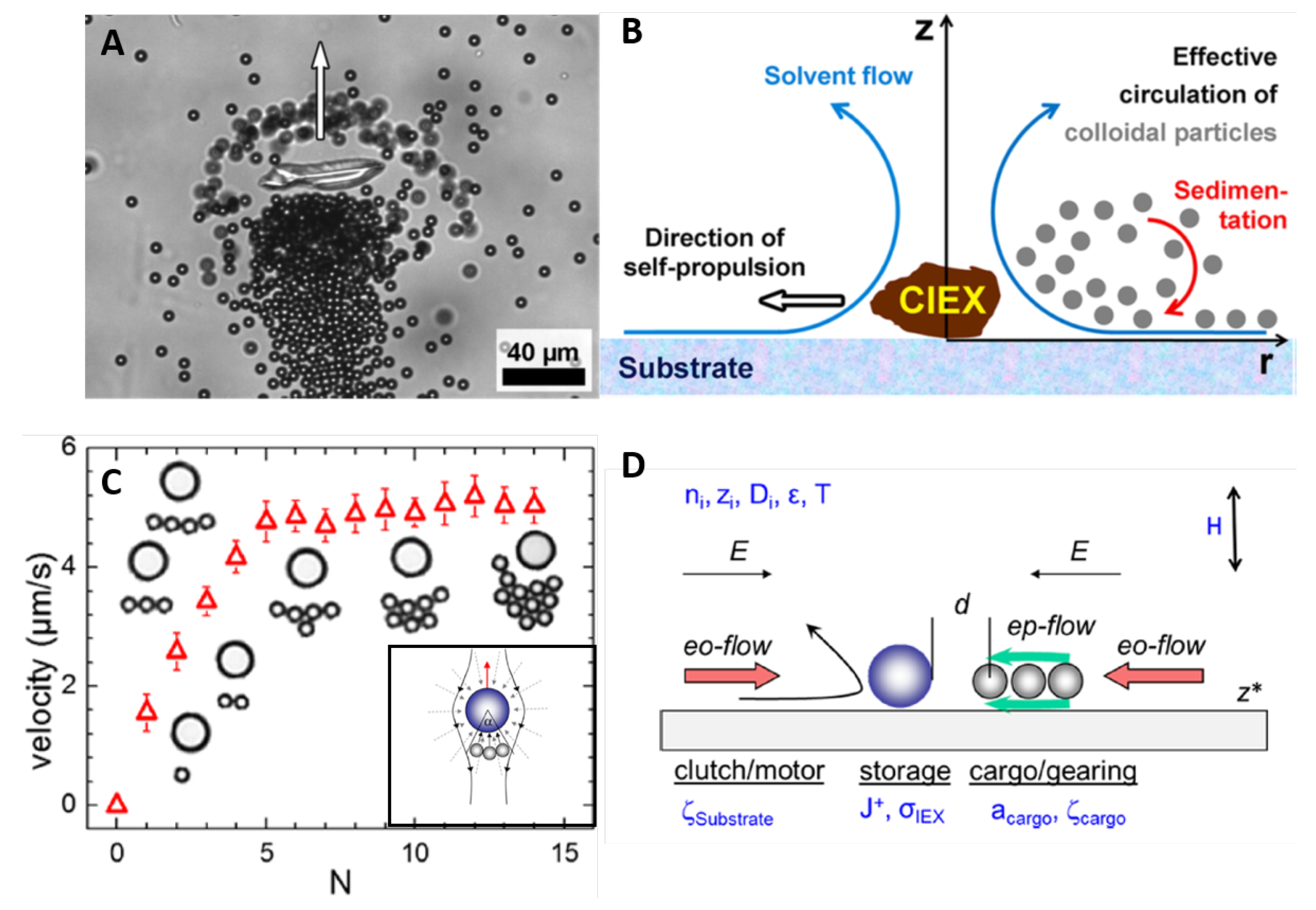
3.2.3. Electrophoresis
3.3. Induced Charge and Self-Dielectrophoresis
3.4. Thermophoresis
3.5. Demixing: Casimir Forces
3.6. Chemical Gradient
3.7. Magnetic Forces
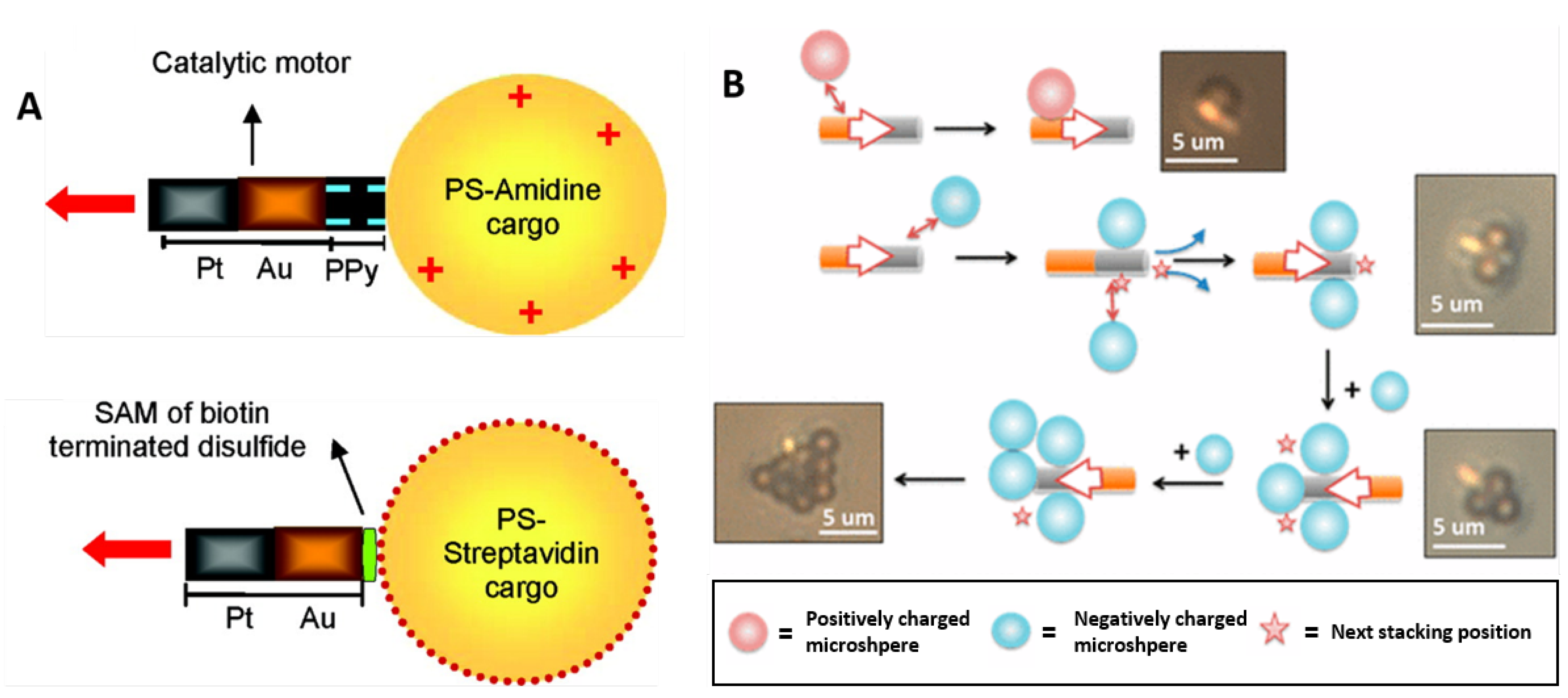
4. Applications
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Miller, J.H.; Butts, C.T.; Rode, D. Communication and cooperation. J. Econ. Behav. Organ. 2002, 47, 179–195. [Google Scholar] [CrossRef]
- Wang, W.; Duan, W.; Ahmed, S.; Sen, A.; Mallouk, T.E. From one to many: Dynamic assembly and collective behavior of self-propelled colloidal motors. Accounts Chem. Res. 2015, 48, 1938–1946. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Luijten, E.; Grzybowski, B.A.; Granick, S. Active colloids with collective mobility status and research opportunities. Chem. Soc. Rev. 2017, 46, 5551–5569. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, M.; Lai, Y.; Chi, L. Advanced colloidal lithography: From patterning to applications. Nano Today 2018, 22, 36–61. [Google Scholar] [CrossRef]
- Lin, Z.; Gao, C.; Chen, M.; Lin, X.; He, Q. Collective motion and dynamic self-assembly of colloid motors. Curr. Opin. Colloid Interface Sci. 2018, 35, 51–58. [Google Scholar] [CrossRef]
- Ning, H.; Zhang, Y.; Zhu, H.; Ingham, A.; Huang, G.; Mei, Y.; Solovev, A. Geometry Design, Principles and Assembly of Micromotors. Micromachines 2018, 9, 75. [Google Scholar] [CrossRef] [PubMed]
- Mallory, S.A.; Valeriani, C.; Cacciuto, A. An Active Approach to Colloidal Self-Assembly. Annu. Rev. Phys. Chem. 2017, 69. [Google Scholar] [CrossRef]
- Pan, Q.; He, Y. Recent advances in self-propelled particles. Sci. China Chem. 2017, 60, 1293–1304. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, J.; Mou, F.; Guan, J. Light-Controlled Swarming and Assembly of Colloidal Particles. Micromachines 2018, 9, 88. [Google Scholar] [CrossRef]
- Liu, C.; Xu, T.; Xu, L.P.; Zhang, X. Controllable swarming and assembly of micro/nanomachines. Micromachines 2017, 9, 10. [Google Scholar] [CrossRef]
- Niu, R.; Palberg, T. Modular approach to microswimming. Soft Matter 2018, 14, 7554–7568. [Google Scholar] [CrossRef] [PubMed]
- Tailleur, J.; Cates, M.E. Statistical Mechanics of Interacting Run-and-Tumble Bacteria. Phys. Rev. Lett. 2008, 100, 218103. [Google Scholar] [CrossRef] [PubMed]
- Wittkowski, R.; Stenhammar, J.; Cates, M.E. Nonequilibrium dynamics of mixtures of active and passive colloidal particles Related content Active cluster crystals. New J. Phys. 2017. [Google Scholar] [CrossRef]
- Liebchen, B.; Marenduzzo, D.; Cates, M.E. Phoretic Interactions Generically Induce Dynamic Clusters and Wave Patterns in Active Colloids. Phys. Rev. Lett. 2017, 118. [Google Scholar] [CrossRef] [PubMed]
- Liebchen, B.; Löwen, H. Which interactions dominate in active colloids? J. Chem. Phys. 2019, 150. [Google Scholar] [CrossRef]
- Popescu, M.N.; Domínguez, A.; Uspal, W.E.; Tasinkevych, M.; Dietrich, S. Comment on “Which interactions dominate in active colloids?”. J. Chem. Phys. 2019, 150. [Google Scholar] [CrossRef]
- Robertson, B.; Stark, H.; Kapral, R. Collective orientational dynamics of pinned chemically-propelled nanorotors. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 045109. [Google Scholar] [CrossRef]
- Stürmer, J.; Seyrich, M.; Stark, H. Chemotaxis in a binary mixture of active and passive particles. J. Chem. Phys. 2019, 150. [Google Scholar] [CrossRef]
- Lighthill, M.J. On the squirming motion of nearly spherical deformable bodies through liquids at very small reynolds numbers. Commun. Pure Appl. Math. 1952, 5, 109–118. [Google Scholar] [CrossRef]
- Blake, J.R. A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 1971, 46, 199–208. [Google Scholar] [CrossRef]
- Palagi, S.; Mark, A.G.; Reigh, S.Y.; Melde, K.; Qiu, T.; Zeng, H.; Parmeggiani, C.; Martella, D.; Sanchez-Castillo, A.; Kapernaum, N.; et al. Structured light enables biomimetic swimming and versatile locomotion of photoresponsive soft microrobots. Nat. Mater. 2016, 15. [Google Scholar] [CrossRef] [PubMed]
- Matas-Navarro, R.; Golestanian, R.; Liverpool, T.B.; Fielding, S.M. Hydrodynamic suppression of phase separation in active suspensions. Phys. Rev. E 2014, 90, 032304. [Google Scholar] [CrossRef] [PubMed]
- Zöttl, A.; Stark, H. Hydrodynamics Determines Collective Motion and Phase Behavior of Active Colloids in Quasi-Two-Dimensional Confinement. Phys. Rev. Lett. 2014, 112, 118101. [Google Scholar] [CrossRef] [PubMed]
- De Graaf, J.; Stenhammar, J. Lattice-Boltzmann simulations of microswimmer-tracer interactions. Phys. Rev. E 2017, 95, 023302. [Google Scholar] [CrossRef] [PubMed]
- Zöttl, A.; Yeomans, J.M. Enhanced bacterial swimming speeds in macromolecular polymer solutions. Nat. Phys. 2019. [Google Scholar] [CrossRef]
- Brown, A.T.; Vladescu, I.D.; Dawson, A.; Vissers, T.; Schwarz-Linek, J.; Lintuvuori, J.S.; Poon, W.C.K. Swimming in a crystal. Soft Matter 2016, 12, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Popescu, M.N.; Uspal, W.E.; Eskandari, Z.; Tasinkevych, M.; Dietrich, S. Effective squirmer models for self-phoretic chemically active spherical colloids. Eur. Phys. J. E 2018, 41. [Google Scholar] [CrossRef]
- Robertson, B.; Huang, M.J.; Chen, J.X.; Kapral, R. Synthetic Nanomotors: Working Together through Chemistry. Accounts Chem. Res. 2018, 51, 2355–2364. [Google Scholar] [CrossRef]
- Stark, H. Artificial Chemotaxis of Self-Phoretic Active Colloids: Collective Behavior. Accounts Chem. Res. 2018, 51, 2681–2688. [Google Scholar] [CrossRef]
- Kanso, E.; Michelin, S. Phoretic and hydrodynamic interactions of weakly confined autophoretic particles. J. Chem. Phys. 2019, 150. [Google Scholar] [CrossRef]
- Wu, X.L.; Libchaber, A. Particle Diffusion in a Quasi-Two-Dimensional Bacterial Bath. Phys. Rev. Lett. 2000, 84, 3017–3020. [Google Scholar] [CrossRef] [PubMed]
- Miño, G.; Mallouk, T.E.; Darnige, T.; Hoyos, M.; Dauchet, J.; Dunstan, J.; Soto, R.; Wang, Y.; Rousselet, A.; Clement, E. Enhanced diffusion due to active swimmers at a solid surface. Phys. Rev. Lett. 2011, 106, 048102. [Google Scholar] [CrossRef] [PubMed]
- Makarchuk, S.; Braz, V.C.; Ara, A.M.; Ciric, L.; Volpe, G. Enhanced propagation of motile bacteria on surfaces due to forward scattering. arXiv 2019, arXiv:1901.08682v1. [Google Scholar]
- Drescher, K.; Goldstein, R.E.; Michel, N.; Polin, M.; Tuval, I. Direct measurement of the flow field around swimming microorganisms. Phys. Rev. Lett. 2010, 105, 168101. [Google Scholar] [CrossRef] [PubMed]
- Jeanneret, R.; Pushkin, D.O.; Kantsler, V.; Polin, M. Entrainment dominates the interaction of microalgae with micron-sized objects. Nat. Commun. 2016, 7, 12518. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J. Colloid Transport By Interfacial Forces. Annu. Rev. Fluid Mech. 1989, 21, 61–99. [Google Scholar] [CrossRef]
- Ibele, M.E.; Lammert, P.E.; Crespi, V.H.; Sen, A. Emergent, Collective Oscillations of Self-Mobile Particles and Patterned Surfaces under Redox Conditions. ACS Nano 2010, 4, 4845–4851. [Google Scholar] [CrossRef]
- Simmchen, J.; Baeza, A.; Miguel-Lopez, A.; Stanton, M.M.; Vallet-Regi, M.; Ruiz-Molina, D.; Sánchez, S. Dynamics of novel photoactive AgCl microstars and their environmental applications. ChemNanoMat 2017, 3, 65–71. [Google Scholar] [CrossRef]
- Wang, X.; Baraban, L.; Misko, V.R.; Nori, F.; Huang, T.; Cuniberti, G.; Fassbender, J.; Makarov, D. Visible Light Actuated Efficient Exclusion Between Plasmonic Ag/AgCl Micromotors and Passive Beads. Small 2018, 14, 1802537. [Google Scholar] [CrossRef]
- Baraban, L.; Makarov, D.; Streubel, R.; Mönch, I.; Grimm, D.; Sanchez, S.; Schmidt, O.G. Catalytic Janus Motors on Microfluidic Chip: Deterministic Motion for Targeted Cargo Delivery. ACS Nano 2012, 6, 3383–3389. [Google Scholar] [CrossRef]
- Baraban, L.; Tasinkevych, M.; Popescu, M.N.; Sanchez, S.; Dietrich, S.; Schmidt, O.G. Transport of cargo by catalytic Janus micro-motors. Soft Matter 2012, 8, 48–52. [Google Scholar] [CrossRef]
- Uspal, W.; Katuri, J.; Popescu, M.N.; Sanchez, S. Distribution of tracer particles around a catalytic Janus particle. In Proceedings of the APS Meeting 2019, Boston, MA, USA, 4–8 March 2019. [Google Scholar]
- Chattopadhyay, P.; Simmchen, J. Interactions of Different Janus Particles with Passive Tracers. chemrXiv 2019. [Google Scholar] [CrossRef]
- Campbell, A.I.; Ebbens, S.J.; Illien, P.; Golestanian, R. Experimental Observation of Flow Fields Around Active Janus Spheres. arXiv 2018, arXiv:1802.04600. [Google Scholar]
- Gao, W.; Pei, A.; Feng, X.; Hennessy, C.; Wang, J. Organized self-assembly of janus micromotors with hydrophobic hemispheres. J. Am. Chem. Soc. 2013, 135, 998–1001. [Google Scholar] [CrossRef] [PubMed]
- Palacci, J.; Sacanna, S.; Vatchinsky, A.; Chaikin, P.M.; Pine, D.J. Photoactivated colloidal dockers for cargo transportation. J. Am. Chem. Soc. 2013, 135, 15978–15981. [Google Scholar] [CrossRef] [PubMed]
- Massana-Cid, H.; Codina, J.; Pagonabarraga, I.; Tierno, P. Active apolar doping determines routes to colloidal clusters and gels. Proc. Natl. Acad. Sci. USA 2018, 115, 10618–10623. [Google Scholar] [CrossRef]
- Singh, D.P.; Choudhury, U.; Fischer, P.; Mark, A.G. Non-Equilibrium Assembly of Light-Activated Colloidal Mixtures. Adv. Mater. 2017, 29, 1701328. [Google Scholar] [CrossRef]
- Wang, L.; Popescu, M.N.; Stavale, F.; Ali, A.; Gemming, T.; Simmchen, J. Cu@TiO2 Janus microswimmers with a versatile motion mechanism. Soft Matter 2018, 14, 6969–6973. [Google Scholar] [CrossRef]
- Wang, L.; Kaeppler, A.; Fischer, D.; Simmchen, J. Photocatalytic TiO2 Micromotors for Removal of Microplastics and Suspended Matter. ACS Appl. Mater. Interfaces 2019. [Google Scholar] [CrossRef]
- Esplandiu, M.J.; Zhang, K.; Fraxedas, J.; Sepulveda, B.; Reguera, D. Unraveling the Operational Mechanisms of Chemically Propelled Motors with Micropumps. Accounts Chem. Res. 2018, 51, 1921–1930. [Google Scholar] [CrossRef]
- Sundararajan, S.; Lammert, P.E.; Zudans, A.W.; Crespi, V.H.; Sen, A.; Park, U.V.; Pennsyl, V. Catalytic Motors for Transport of Colloidal Cargo. Nano Lett. 2008, 8, 1271–1276. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Duan, W.; Sen, A.; Mallouk, T.E. Catalytically powered dynamic assembly of rod-shaped nanomotors and passive tracer particles. Proc. Natl. Acad. Sci. USA 2013, 110, 17744–17749. [Google Scholar] [CrossRef] [PubMed]
- Gangwal, S.; Cayre, O.J.; Bazant, M.Z.; Velev, O.D. Induced-Charge Electrophoresis of Metallodielectric Particles. Phys. Rev. Lett. 2008, 058302. [Google Scholar] [CrossRef]
- Boymelgreen, A.; Yossifon, G.; Miloh, T. Propulsion of Active Colloids by Self-Induced Field Gradients. Langmuir 2016, 32, 9540–9547. [Google Scholar] [CrossRef] [PubMed]
- Boymelgreen, A.M.; Balli, T.; Miloh, T.; Yossifon, G. Active colloids as mobile microelectrodes for unified label-free selective cargo transport. Nat. Commun. 2018, 9, 760. [Google Scholar] [CrossRef] [PubMed]
- Demirörs, A.F.; Akan, M.T.; Poloni, E.; Studart, A.R. Active cargo transport with Janus colloidal shuttles using electric and magnetic fields. Soft Matter 2018, 14, 4741–4749. [Google Scholar] [CrossRef]
- Demirörs, A.F.; Eichenseher, F.; Loessner, M.J.; Studart, A.R. Colloidal shuttles for programmable cargo transport. Nat. Commun. 2017, 8, 1872. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Granick, S. Directed Self-Assembly Pathways of Active Colloidal Clusters. Angew. Chem. Int. Ed. 2016, 55, 5166–5169. [Google Scholar] [CrossRef]
- Würger, A. Thermophoresis in colloidal suspensions driven by Marangoni forces. Phys. Rev. Lett. 2007, 98, 138301. [Google Scholar] [CrossRef]
- Jiang, H.R.; Yoshinaga, N.; Sano, M. Active motion of a Janus particle by self-thermophoresis in a defocused laser beam. Phys. Rev. Lett. 2010, 105, 268302. [Google Scholar] [CrossRef]
- Bregulla, A.P.; Cichos, F. Size dependent efficiency of photophoretic swimmers. Faraday Discuss. 2015, 184, 381–391. [Google Scholar] [CrossRef] [PubMed]
- Wagner, M.; Ripoll, M. Hydrodynamic front-like swarming of phoretically active dimeric colloids. EPL (Europhys. Lett.) 2017, 119, 66007. [Google Scholar] [CrossRef]
- Io, C.W.; Chen, T.Y.; Yeh, J.W.; Cai, S.C. Experimental investigation of mesoscopic heterogeneous motion of laser-activated self-propelling Janus particles in suspension. Phys. Rev. E 2017, 96, 062601. [Google Scholar] [CrossRef] [PubMed]
- Cichos, F. Discussion during the SPP Meeting, Bonn, on Phoretic Interactions; Technical Report; U Leipzig: Leipzig, Germany, 2019. [Google Scholar]
- Volpe, G.; Buttinoni, I.; Vogt, D.; Kümmerer, H.J.; Bechinger, C. Microswimmers in patterned environments. Soft Matter 2011, 7, 8810–8815. [Google Scholar] [CrossRef]
- Buttinoni, I.; Bialké, J.; Kümmel, F.; Löwen, H.; Bechinger, C.; Speck, T. Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles. Phys. Rev. Lett. 2013, 110, 238301. [Google Scholar] [CrossRef] [PubMed]
- Kümmel, F.; Shabestari, P.; Lozano, C.; Volpe, G.; Bechinger, C. Formation, compression and surface melting of colloidal clusters by active particles. Soft Matter 2015, 11, 6187–6191. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, F.; Liebchen, B.; Löwen, H.; Volpe, G. Light-controlled assembly of active colloidal molecules. J. Chem. Phys. 2019, 150. [Google Scholar] [CrossRef] [PubMed]
- Reinmüller, A.; Schöpe, H.J.; Palberg, T. Self-organized cooperative swimming at low reynolds numbers. Langmuir 2013, 29, 1738–1742. [Google Scholar] [CrossRef][Green Version]
- Niu, R.; Botin, D.; Weber, J.; Reinmüller, A.; Palberg, T. Assembly and Speed in Ion-Exchange-Based Modular Phoretic Microswimmers. Langmuir 2017, 33, 3450–3457. [Google Scholar] [CrossRef]
- Palberg, T. Discussion during the SPP Meeting, Bonn, on Phoretic Interactions; Technical Report; U Mainz: Mainz, Germany, 2019. [Google Scholar]
- Zhao, G.; Wang, H.; Sanchez, S.; Schmidt, O.G.; Pumera, M. Artificial micro-cinderella based on self-propelled micromagnets for the active separation of paramagnetic particles. Chem. Commun. 2013, 49, 5147–5149. [Google Scholar] [CrossRef]
- Nourhani, A.; Brown, D.; Pletzer, N.; Gibbs, J.G. Engineering Contactless Particle-Particle Interactions in Active Microswimmers. Adv. Mater. 2017, 29. [Google Scholar] [CrossRef] [PubMed]
- Steimel, J.P.; Aragones, J.L.; Hu, H.; Qureshi, N.; Alexander-Katz, A. Emergent ultra-long-range interactions between active particles in hybrid active–inactive systems. Proc. Natl. Acad. Sci. USA 2016, 113, 4652–4657. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Ghosh, A. Mobile nanotweezers for active colloidal manipulation. Sci. Robot. 2018, 3. [Google Scholar] [CrossRef]
- Dunkel, J.; Heidenreich, S.; Drescher, K.; Wensink, H.H.; Bär, M.; Goldstein, R.E. Fluid Dynamics of Bacterial Turbulence. Phys. Rev. Lett. 2013, 110, 228102. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Simmchen, J. Review: Interactions of Active Colloids with Passive Tracers. Condens. Matter 2019, 4, 78. https://doi.org/10.3390/condmat4030078
Wang L, Simmchen J. Review: Interactions of Active Colloids with Passive Tracers. Condensed Matter. 2019; 4(3):78. https://doi.org/10.3390/condmat4030078
Chicago/Turabian StyleWang, Linlin, and Juliane Simmchen. 2019. "Review: Interactions of Active Colloids with Passive Tracers" Condensed Matter 4, no. 3: 78. https://doi.org/10.3390/condmat4030078
APA StyleWang, L., & Simmchen, J. (2019). Review: Interactions of Active Colloids with Passive Tracers. Condensed Matter, 4(3), 78. https://doi.org/10.3390/condmat4030078




