Direct Visualization of Spatial Inhomogeneity of Spin Stripes Order in La1.72Sr0.28NiO4
Abstract
1. Introduction
2. Materials and Methods
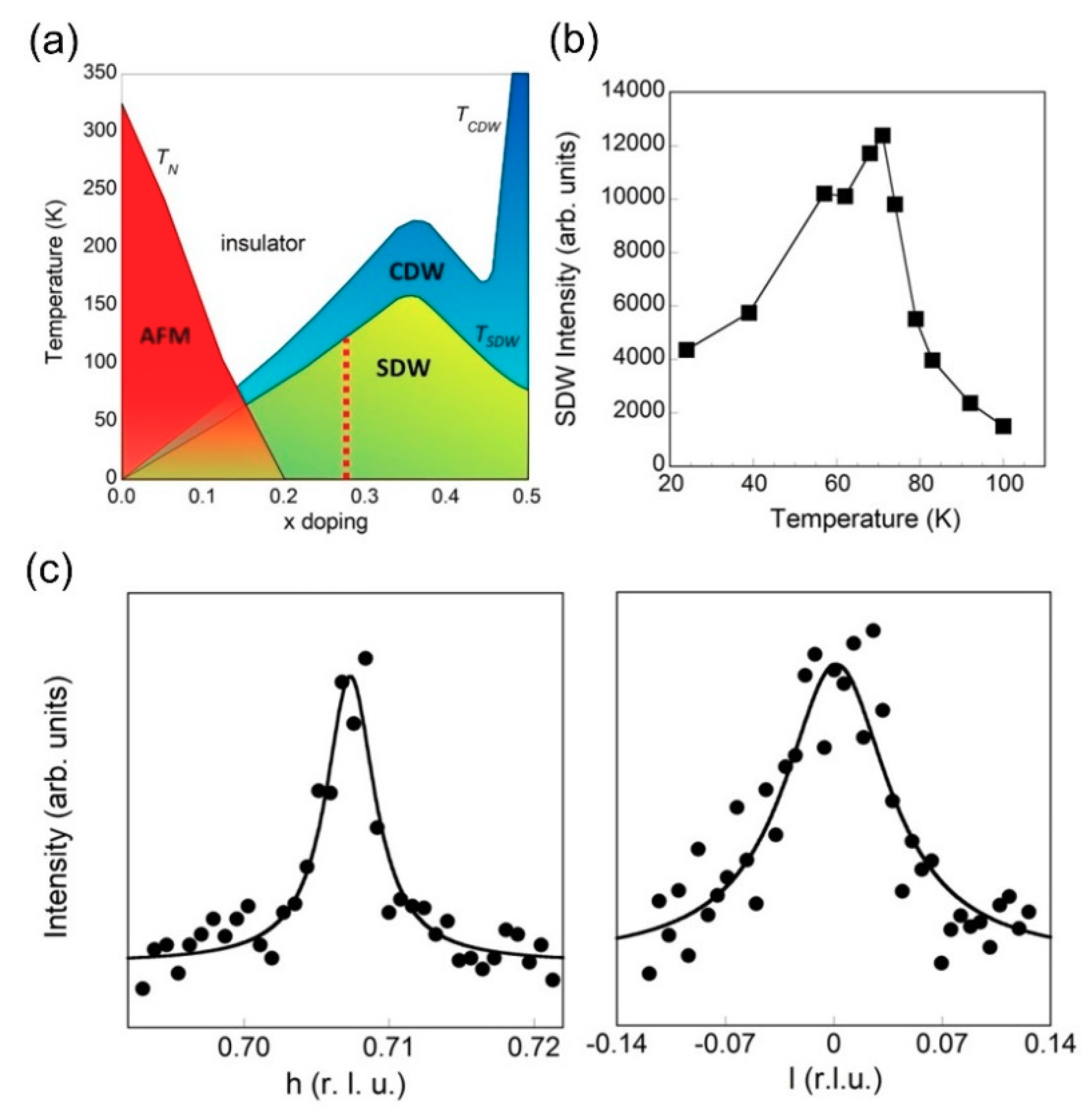
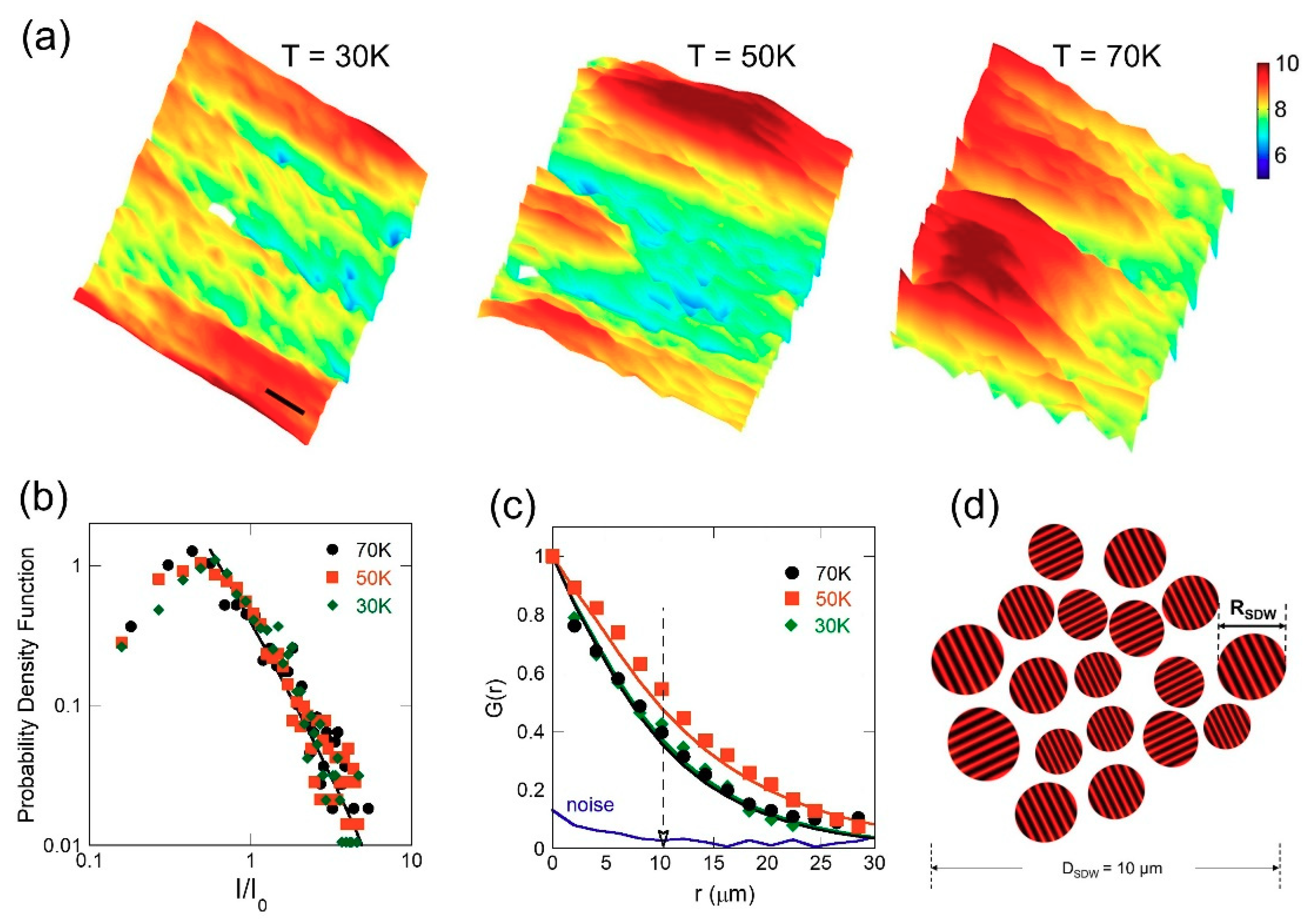
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dagotto, E. Complexity in strongly correlated electronic systems. Science 2005, 309, 257–262. [Google Scholar] [CrossRef] [PubMed]
- Vojta, M. Lattice symmetry breaking in cuprate superconductors: Stripes, nematics and superconductivity. Adv. Phys. 2009, 58, 699–820. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L. Stripes and Related Phenomena; Springer Science Business Media: Berlin, Germany, 2001. [Google Scholar]
- Campi, G.; Bianconi, A.; Poccia, N.; Barbo, G.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, D.N.; Kazakov, S.M.; Burghammer, M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef] [PubMed]
- Poccia, N.; Ricci, A.; Campi, G.; Fratini, M. Optimum inhomogeneity of local lattice distortions in La2CuO4+y. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 15685–15690. [Google Scholar] [CrossRef] [PubMed]
- Fratini, M.; Poccia, N.; Ricci, A.; Campi, G.; Burghammer, M.; Aeppli, G.; Bianconi, A. Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 2010, 466, 841–844. [Google Scholar] [CrossRef] [PubMed]
- Ulbrich, H.; Braden, M. Neutron scattering studies on stripe phases in non-cuprate materials. Phys. C Supercond. 2012, 481, 31–45. [Google Scholar] [CrossRef]
- Lee, S.H.; Cheong, S.W. Melting of quasi-two-dimensional charge stripes in La5/3Sr1/3 NiO4. Phys. Rev. Lett. 1997, 79, 2514. [Google Scholar] [CrossRef]
- Yoshizawa, H.; Kakeshita, T.; Kajimoto, R.; Tanabe, T.; Katsufuji, T.; Tokura, Y. Stripe order at low temperatures in La2−x SrxNiO4 with 0.289 ≲ x ≲ 0.5. Phys. Rev. B 2000, 61, R854. [Google Scholar] [CrossRef]
- Kajimoto, R.; Kakeshita, T.; Yoshizawa, H.; Tanabe, T.; Katsufuji, T.; Tokura, Y. Hole concentration dependence of the ordering process of the stripe order in La2−x SrxNiO4. Phys. Rev. B 2001, 64, 144432. [Google Scholar] [CrossRef]
- Lee, S.H.; Cheong, S.W.; Yamada, K.; Majkrzak, C.F. Charge canted spin order in La2-xSrxNiO4 (x = 0.275,1/3). Phys. Rev. B 2001, 63, 060405. [Google Scholar] [CrossRef]
- Boothroyd, A.T.; Freeman, P.G.; Prabhakaran, D.; Enderle, M.; Kulda, J. Magnetic order and dynamics in stripe-ordered La2-xSrxNiO4. Phys. B Condens. Matter 2004, 345, 1–5. [Google Scholar] [CrossRef]
- Freeman, P.G.; Christensen, N.B.; Prabhakaran, D.; Boothroyd, A.T. The temperature evolution of the out-of-plane correlation lengths of charge-stripe ordered La1.725Sr0.275NiO4. J. Phys. Conf. Ser. 2010, 200, 012037. [Google Scholar] [CrossRef]
- Chow, K.H.; Pattenden, P.; Blundell, S.J.; Hayes, W. Muon-spin-relaxation studies of magnetic order in heavily doped La2−xSrxNiO4+δ. Phys. Rev. B 1996, 53, R14725. [Google Scholar] [CrossRef] [PubMed]
- Schüßler-Langeheine, C.; Schlappa, J.; Tanaka, A.; Hu, Z.; Chang, C.F.; Schierle, E.; Benomar, M.; Ott, H.; Weschke, E.; Kaindl, G.; et al. Spectroscopy of stripe order in La1.8 Sr0.2NiO4 using resonant soft X-ray diffraction. Phys. Rev. Lett. 2005, 95, 156402. [Google Scholar] [CrossRef] [PubMed]
- Schlappa, J.; Chang, C.F.; Schierie, E.; Tanaka, A. Static and fluctuating stripe order observed by resonant soft X-ray diffraction in La1.8Sr0.2NiO4. arXiv 2009, arXiv:0903.0994v1. [Google Scholar]
- Coslovich, G.; Huber, B.; Lee, W.S.; Chuang, Y.D.; Zhu, Y.; Sasagawa, T.; Hussain, Z.; Bechtel, H.A.; Martin, M.C.; Shen, Z.X.; et al. Ultrafast charge localization in a stripe-phase nickelate. Nature Cmmun. 2013, 4, 2643. [Google Scholar] [CrossRef]
- Wilkins, S.B.; Hatton, P.D.; Liss, K.D.; Ohler, M.; Katsufuji, T.; Cheong, S.W. High-resolution high energy X-ray diffraction studies of charge ordering in CMR manganites and nickelates. Int. J. Mod. Phys. B 2000, 14, 3753–3758. [Google Scholar] [CrossRef]
- Chen, C.H.; Cheong, S.W.; Cooper, A.S. Charge modulations in La2-xSrxNiO4+y ordering of polarons. Phys. Rev. Lett. 1993, 71, 2461. [Google Scholar] [CrossRef]
- Ghazi, M.E.; Spencer, P.D.; Wilkins, S.B.; Hatton, P.D.; Mannix, D.; Prabhakaran, D. Incommensurate charge stripe ordering in in La2-xSrxNiO4 for x= (0.33, 0.30, 0.275). Phys. Rev. B 2004, 70, 144507. [Google Scholar] [CrossRef]
- Du, C.H.; Ghazi, M.E.; Su, Y.X.; Pape, I. Critical Fluctuations and quenched Disordered Two-Dimensional Charge Stripes in La5/3Sr1/3NiO4. Phys. Rev. Lett. 2000, 84, 3911. [Google Scholar] [CrossRef]
- Johnson, R.D.; Mazzoli, C.; Bland, S.R.; Du, C. Magnetically induced electric polarization reversal in multiferroic TbMn2O5: Terbium spin reorientation studied by resonant X-ray diffraction. Phys. Rev. B 2011, 83, 054438. [Google Scholar] [CrossRef]
- Vecchini, C.; Bombardi, A.; Chapon, L.C.; Lee, N.; Radaelli, P.G.; Cheong, S.W. Magnetic phase diagram and ordered ground state of GdMn2O5 multiferroic studied by X-ray magnetic scattering. J. Phys. Conf. Ser. 2014, 519, 012004. [Google Scholar] [CrossRef]
- Pincini, D.; Boseggia, S.; Perry, R.; Gutmann, M. Persistence of antiferromagnetic order upon La substitution in the Mott insulator Ca2RuO4. Phys. Rev. B 2018, 98, 014429. [Google Scholar] [CrossRef]
- Price, N.W.; Vibhakar, A.M.; Johnson, R.D.; Schad, J.; Saenrang, W.; Bombardi, A.; Chmiel, F.P.; Eom, C.B.; Radaelli, P.G. Strain engineering a multiferroic monodomain in thin-film BiFeO3. Phys. Rev. Appl. 2019, 11, 024035. [Google Scholar] [CrossRef]
- Caprara, S.; Sulpizi, M.; Bianconi, A.; Castro, C. Single-particle properties of a model for coexisting charge and spin quasicritical fluctuations coupled to electrons. Phys. Rev. B 1999, 59, 14980. [Google Scholar] [CrossRef]
- Carlson, E.W.; Yao, D.X.; Campbell, D.K. Spin waves in striped phases. Phys. Rev. B 2004, 70, 064505. [Google Scholar] [CrossRef]
- Raczkowski, M.; Fresard, R.; Oles, A.M. Microscopic origin of diagonal stripe phases in doped nickelates. Phys. Rev. B 2006, 73, 094429. [Google Scholar] [CrossRef]
- Bianconi, A.; Poccia, N.; Sboychakov, A.O.; Rakhmanov, A.L.; Kugel, K.I. Intrinsic arrested nanoscale phase separation near a topological Lifshitz transition in strongly correlated two-band metals. Supercond. Sci. Technol. 2015, 28, 024005. [Google Scholar] [CrossRef]
- Poccia, N.; Campi, G.; Fratini, M.; Ricci, A. Spatial inhomogeneity and planar symmetry breaking of the lattice incommensurate supermodulation in the high-temperature superconductor Bi2Sr2CaCu2O8+y. Phys. Rev. B 2011, 84, 100504. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Coneri, F.; Caporale, A.S.; Innocenti, D.; Burghammer, M.; Zimmermann, M.V.; Bianconi, A. Multiscale distribution of oxygen puddles in 1/8 doped YBa2Cu3O6.67. Sci. Rep. 2013, 3, 2383. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Coneri, F.; Barba, L.; Arrighetti, G.; Polentarutti, M.; Burghammer, M.; Sprung, M.; Zimmermann, M.V.; et al. Networks of superconducting nano-puddles in 1/8 doped YBa2Cu3O6.5+y controlled by thermal manipulation. New J. Phys. 2014, 16, 053030. [Google Scholar] [CrossRef]
- Campi, G.; Ricci, A.; Poccia, N.; Barba, L.; Arrighetti, G.; Burghammer, M.; Caporale, A.S.; Bianconi, A. Scanning micro-X-ray diffraction unveils the distribution of oxygen chain nanoscale puddles in YBa2Cu3O6.33. Phys. Rev. B 2013, 87, 014517. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Joseph, B.; Innocenti, D. Direct observation of nanoscale interface phase in the superconducting chalcogenide KxFe2−ySe2 with intrinsic phase separation. Phys. Rev. B 2015, 91, 020503. [Google Scholar] [CrossRef]
- Drees, Y.; Li, Z.W.; Ricci, A.; Rotter, M.; Schmidt, W.; Lamago, D.; Sobolev, O.; Rutt, U.; Gutowski, O.; Sprung, M.; et al. Hour-glass magnetic excitations induced by nanoscopic phase separation in cobalt oxides. Nature Commun. 2014, 5, 573. [Google Scholar] [CrossRef]
- Mu, Y.; Ma, Y. Self-organizing stripe patterns in two-dimensional frustrated systems with competing interactions. Phys. Rev. B 2003, 67, 014110. [Google Scholar] [CrossRef]
- Schmalian, J.; Wolynes, P.G. Stripe glasses: Self-generated randomness in a uniformly frustrated system. Phys. Rev. Lett. 2000, 85, 836. [Google Scholar] [CrossRef]
- Bogner, S.; Scheidl, S. Pinning of stripes in cuprate superconductors. Phys. Rev. B 2001, 64, 054517. [Google Scholar] [CrossRef]
- Poccia, N.; Chorro, M.; Ricci, A.; Xu, W.; Marcelli, A.; Campi, G.; Bianconi, A. Percolative superconductivity in La2CuO4.06 by lattice granularity patterns with scanning micro X-ray absorption near edge structure. Appl. Phys. Lett. 2014, 104, 221903. [Google Scholar] [CrossRef]
- Bianconi, A.; Di Castro, D.; Bianconi, G.; Pifferi, A.; Saini, N.L.; Chou, F.C.; Johnston, D.C.; Colapietro, M. Coexistence of stripes and superconductivity: Tc amplification in a superlattice of superconducting stripes. Phys. C: Supercond. 2000, 341, 1719–1722. [Google Scholar] [CrossRef]
- Chen, X.; Schmehr, J.L.; Islam, Z.; Porter, Z.; Zoghlin, E.; Finkelstein, K.; Ruff, J.P.C.; Wilson, S.D. Unidirectional spin density wave state in metallic (Sr1−x Lax)2IrO4. Nat. Commun. 2018, 9, 103. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. High-Temperature superconductivity in a hyperbolic geometry of complex matter from nanoscale to mesoscopic scale. J. Supercond. Nov. Magn. 2016, 29, 627–631. [Google Scholar] [CrossRef]
- Campi, G.; Di Gioacchino, M.; Poccia, N.; Ricci, A.; Burghammer, A.; Ciasca, G.; Bianconi, A. Nanoscale correlated disorder in out-of-equilibrium myelin ultrastructure. ACS Nano 2017, 12, 729–739. [Google Scholar] [CrossRef]
- Campi, G.; Cristofaro, F.; Pani, G.; Fratini, M.; Pascucci, B.; Corsetto, P.A.; Weinhausen, B.; Cedola, A.; Rizzo, A.M.; Visai, L.; et al. Heterogeneous and self-organizing mineralization of bone matrix promoted by hydroxyapatite nanoparticles. Nanoscale 2017, 9, 17274–17283. [Google Scholar] [CrossRef]
- Zaanen, J.; Littlewood, P.B. Freezing electronic correlations by polaronic instabilities in doped La2NiO4. Phys. Rev. B 1994, 50, 7222. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Di Castro, D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118–123. [Google Scholar] [CrossRef]
- Gavrichkov, V.A.; Shanko, Y.; Zamkova, N.G.; Bianconi, A. Is There Any Hidden Symmetry in Stripe Structure of Perovskite High-Temperature Superconductors? J. Phys. Chem. Lett. 2019, 10, 1840–1844. [Google Scholar] [CrossRef]
- Bianconi, G. Quantum statistics in complex networks. Phys. Rev. E 2002, 66, 056123. [Google Scholar] [CrossRef]
- Innocenti, D.; Ricci, A.; Poccia, N.; Campi, G.; Fratini, M.; Bianconi, A. A model for liquid-striped liquid phase separation in liquids of anisotropic polarons. J. Supercond. Nov. Magn. 2009, 22, 529–533. [Google Scholar] [CrossRef]
- Campi, G.; Innocenti, D.; Bianconi, A. CDW and similarity of the Mott insulator-to-metal transition in cuprates with the gas-to-liquid-liquid transition in supercooled water. J. Supercond. Nov. Magn. 2015, 28, 1355–1363. [Google Scholar] [CrossRef]
- Agrestini, S.; Saini, N.L.; Bianconi, G.; Bianconi, A. The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites. J. Phys. A Math. Gen. 2003, 36, 9133. [Google Scholar] [CrossRef]
- Bianconi, A.; Agrestini, S.; Bianconi, G.; Di Castro, D.; Saini, N.L. A quantum phase transition driven by the electron lattice interaction gives high Tc superconductivity. J. Alloy. Compd. 2001, 317, 537–541. [Google Scholar] [CrossRef]
- Lichtenstein, A.I.; Fleck, M.; Oles, A.M.; Hedin, L. Dynamical mean-field theory of stripe ordering. In Stripes and Related Phenomena; Bianconi, A., Saini, N.L., Eds.; Springer: Boston, MA, USA, 2002; pp. 101–109. [Google Scholar]
- Raczkowski, M.; Oleś, A.M. Competition between vertical and diagonal stripes in the Hartree-Fock approximation. AIP Conf. Proc. 2003, 678, 293–302. [Google Scholar]
- Oles, A.M. Charge and orbital order in transition metal oxides. Acta Phys. Polon. A. 2010, 118, 212. [Google Scholar] [CrossRef]
- Beale, T.A.W.; Wilkins, S.B.; Johnson, R.D.; Prabhakaran, D.; Boothroyd, A.T.; Steadman, P.; Dhesi, S.S.; Hatton, P.D. Advances in the understanding of multiferroics through soft X-ray diffraction. Eur. Phys. J. Spec. Top. 2012, 208, 99–106. [Google Scholar] [CrossRef][Green Version]
- Radaelli, P.G.; Dhesi, S.S. The contribution of Diamond light source to the study of strongly correlated electron systems and complex magnetic structures. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20130148. [Google Scholar] [CrossRef][Green Version]
- Mattoni, G.; Zubko, P.; Maccherozzi, F.; van der Torren, A.J.H.; Boltje, D.B.; Hadjimichael, M.; Manca, N.; Catalano, S.; Gibert, M.; Liu, Y.; et al. Striped nanoscale phase separation at the metal–insulator transition of heteroepitaxial nickelates. Nat. Commun. 2016, 7, 13141. [Google Scholar] [CrossRef]
- Varignon, J.; Grisolia, M.N.; Íñiguez, J.; Barthelemy, A.; Bibes, M. Complete phase diagram of rare-earth nickelates from first-principles. NPJ Quantum Mater. 2017, 2, 21. [Google Scholar] [CrossRef]
- Liu, M.; Sternbach, A.J.; Wagner, M.; Slusar, T.V.; Kong, T.; Budko, S.L.; Salinporn, K.; Qazibash, M.M.; McLeod, A.; Fei, Z.; et al. Phase transition in bulk single crystals and thin films of VO2 by nanoscale infrared spectroscopy and imaging. Phys. Rev. B 2015, 91, 245155. [Google Scholar] [CrossRef]
- Bianconi, A. Multiplet splitting of final-state configurations in X-ray-absorption spectrum of metal VO2: Effect of core-hole-screening, electron correlation and metal-insulator transition. Phys. Rev. B 1982, 26, 2741. [Google Scholar] [CrossRef]
- Marcelli, A.; Coreno, M.; Stredansky, M.; Xu, W. Nanoscale phase separation and lattice complexity in VO2: The metal–insulator transition investigated by XANES via Auger electron yield at the vanadium L23-edge and resonant photoemission. Condens. Matt. 2017, 2, 38. [Google Scholar] [CrossRef]
- Gioacchino, D.; Marcelli, A.; Puri, A.; Zou, C. Metastability phenomena in VO2 thin films. Condens. Matt. 2017, 2, 10. [Google Scholar] [CrossRef]
- Zhang, J.; McLeod, A.S.; Han, Q.; Chen, X.; Bechtel, H.A.; Yao, Z.; Gilbert, S.N.; Ciavatti, T.; Tao, T.H.; Aronson, M.; et al. Nano-resolved current-induced insulator-metal transition in the Mott insulator Ca2RuO4. Phys. Rev. X 2019, 9, 011032. [Google Scholar] [CrossRef]
- Luo, Y.; Pustogow, A.; Guzman, P.; Dioguardi, A.P.; Thomas, S.M.; Ronning, F.; Kikugawa, N.; Sokolov, D.A.; Jerzebeck, A.P.; Mackenzie, A.P.; et al. Normal state O17 NMR studies of Sr2RuO4 under uniaxial stress. Phys. Rev. X 2019, 9, 021044. [Google Scholar]
- Bauer, E.; Paul, C.; Berger, S.; Majumdar, S.; Michor, H.; Giovannini, M.; Saccone, A.; Binaconi, A. Thermal conductivity of superconducting MgB2. J. Phys. Condens. Matt. 2001, 13, L487. [Google Scholar] [CrossRef][Green Version]
- Agrestini, S.; Metallo, C.; Filippi, M.; Simonelli, L.; Gampi, G.; Sanipoli, C.; Liarokapis, E.; De Negri, S.; Giovannini, M.; Saccone, A.; et al. Substitution of Sc for Mg in MgB2: Effects on transition temperature and Kohn anomaly. Phys. Rev. B 2004, 70, 134514. [Google Scholar] [CrossRef]
- Kugel, K.I.; Rakhmanov, A.L.; Sboychakov, A.O.; Kusmartsev, F.V.; Poccia, N.; Bianconi, A. A two-band model for the phase separation induced by the chemical mismatch pressure in different cuprate superconductors. Supercond. Sci. Technol. 2008, 22, 014007. [Google Scholar] [CrossRef]
- Bianconi, G.; Rahmede, C. Emergent hyperbolic network geometry. Sci. Rep. 2017, 7, 41974. [Google Scholar] [CrossRef]
- Bianconi, G.; Ziff, R.M. Topological percolation on hyperbolic simplicial complexes. Phys. Rev. E 2018, 98, 052308. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Bianconi, A. Fermi-Bose mixtures and BCS-BEC crossover in high-Tc superconductors. Condens. Matt. 2019, 4, 51. [Google Scholar] [CrossRef]
- Yanagisawa, T. Mechanism of high-temperature superconductivity in correlated-electron systems. Condens. Matt. 2019, 4, 57. [Google Scholar] [CrossRef]
- Jurkutat, M.; Erb, A.; Haase, J. Tc and other cuprate properties in relation to planar charges as measured by NMR. Condens. Matt. 2019, 4, 67. [Google Scholar] [CrossRef]
- Caprara, S. The ancient romans’ route to charge density waves in cuprates. Condens. Matt. 2019, 4, 60. [Google Scholar] [CrossRef]
- Yamamoto, S.; Fujiwara, T.; Hatsugai, Y. Electronic structure of charge and spin stripe order in La2−xSrxNiO4 (x=1/3,1/2). Phys. Rev. B 2007, 76, 165114. [Google Scholar] [CrossRef]
- Campi, G.; Castro, D.D.; Bianconi, G.; Agrestini, A.; Saini, N.L.; Oyanagi, H.; Bianconi, A. Photo-Induced phase transition to a striped polaron crystal in cuprates. Phase Transit. 2002, 75, 927–933. [Google Scholar] [CrossRef]
- Campi, G.; Dell'Omo, C.; Di Castro, D.; Agretini, S.; Filippi, M.; Bianconi, G.; Barba, L.; Cassetta, A.; Colapirtro, M.; Saini, N.L.; et al. Effect of temperature and X-ray illumination on the oxygen ordering in La2CuO4.1 Superconductor. J. Supercond. 2004, 17, 137–142. [Google Scholar] [CrossRef]
- Poccia, N.; Bianconi, A.; Campi, G.; Fratini, M.; Ricci, A. Size evolution of the oxygen interstitial nanowires in La2CuO4+y by thermal treatments and X-ray continuous illumination. Superconductor Sci. Technol. 2012, 25, 124004. [Google Scholar] [CrossRef]
- Campi, G.; Ricci, A.; Poccia, N.; Fratini, M.; Bianconi, A. X-rays Writing/Reading of charge density waves in the CuO2 plane of a simple cuprate superconductor. Condens. Matt. 2017, 2, 26. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campi, G.; Poccia, N.; Joseph, B.; Bianconi, A.; Mishra, S.; Lee, J.; Roy, S.; Nugroho, A.A.; Buchholz, M.; Braden, M.; et al. Direct Visualization of Spatial Inhomogeneity of Spin Stripes Order in La1.72Sr0.28NiO4. Condens. Matter 2019, 4, 77. https://doi.org/10.3390/condmat4030077
Campi G, Poccia N, Joseph B, Bianconi A, Mishra S, Lee J, Roy S, Nugroho AA, Buchholz M, Braden M, et al. Direct Visualization of Spatial Inhomogeneity of Spin Stripes Order in La1.72Sr0.28NiO4. Condensed Matter. 2019; 4(3):77. https://doi.org/10.3390/condmat4030077
Chicago/Turabian StyleCampi, Gaetano, Nicola Poccia, Boby Joseph, Antonio Bianconi, Shrawan Mishra, James Lee, Sujoy Roy, Agustinus Agung Nugroho, Marcel Buchholz, Markus Braden, and et al. 2019. "Direct Visualization of Spatial Inhomogeneity of Spin Stripes Order in La1.72Sr0.28NiO4" Condensed Matter 4, no. 3: 77. https://doi.org/10.3390/condmat4030077
APA StyleCampi, G., Poccia, N., Joseph, B., Bianconi, A., Mishra, S., Lee, J., Roy, S., Nugroho, A. A., Buchholz, M., Braden, M., Trabant, C., Zozulya, A., Müller, L., Viefhaus, J., Schüßler-Langeheine, C., Sprung, M., & Ricci, A. (2019). Direct Visualization of Spatial Inhomogeneity of Spin Stripes Order in La1.72Sr0.28NiO4. Condensed Matter, 4(3), 77. https://doi.org/10.3390/condmat4030077








