1. Introduction
In a seminal paper [
1], Fishman (with D.R. Grempel and R.E. Prange) exposed a far-reaching link between a time-evolution problem, the motion of a quantum kicked rotor, and the static Anderson localization phenomenon of the theory of solids. The link quickly became paradigm, and it led to many interesting discoveries. Perhaps the most important of these, which required a further conceptual leap, was Chirikov and coworkers’ discovery of quantum localization of classical chaos [
2]. In extreme synthesis (it is certain that readers of this volume dedicated to Shmuel’s memory know it better), localization freezes quantum motion on a reduced set of states in the Hilbert space of a system, thus preventing the classical richness of dynamical complexity to unfold.
Coming from a different perspective, Ford and associates investigated the problem of quantum chaos from an informational theoretical perspective [
3,
4,
5,
6,
7,
8] and realized that such freezing might be interpreted as a bound to the complexity of quantum motion, which, in properly defined and rescaled units, was shown to be slowly increasing, as the logarithm of the action of the system, a fact that cast a severe limitation on the set of classical motions that can be obtained when quantum dynamics becomes more and more classical.
Confronted with these limitations and in search of a sort of Northwest passage to reconcile classical mechanics with quantum, called the correspondence principle by the founding fathers, researchers discovered that this goal could be somehow achieved by letting a random element enter the dynamics. In 1984, Guarneri [
9] showed that this could prevent quantum localization in the dynamics of a kicked rotor, precisely the system studied two years earlier by Shmuel and coworkers. Soon afterwards, Ott et al. [
10] studied the parameter dependence of the diffusion coefficient
D of the quantum diffusion generated in this way. In a more general setting, Dittrich and Graham [
11], Kolovsky [
12,
13,
14], and Sundaram et al. [
15] proved that coupling a quantum dynamical system to the environment leads to diffusion with coefficient
D that is comparable with the classical as long as
(
is the Lyapunov exponent of the chaotic classical system) is larger than
ℏ times a dimensional constant.
After these pioneering works, the so-called decoherence approach to quantum chaos flourished. It was a sort of phenomenological approach to decoherence, involving a Markov map for the evolution of the reduced density matrix of the system. This map represents, in a schematic way, the true dynamics of a system interacting with an environment. It often required strong assumptions, e.g., in the Caldeira–Legget model, to simulate an environment with infinitely many degrees of freedom, whose exact dynamics is too complicated to be dealt with exactly. This approach has been adopted to explain the behavior of quantum Schrödinger cats [
16] and the emergence of classical properties in quantum mechanics [
11,
12,
14,
17,
18,
19,
20,
21].
In this paper, we revisit a model that we introduced a few years ago [
22], to study decoherence phenomena in a completely dynamical way, that is, without any ad hoc or phenomenological assumptions. It is based on a combination of the principal example of classical chaos, the Arnol’d cat map [
4,
23,
24], with Joos and Zeh’s [
17] view of decoherence as due to collisions of particles. The model views Arnol’d cat dynamics as the motion of a particle on a ring, which is acted upon by a periodic, impulsive force. A number of lighter particles, also moving on the same ring and colliding elastically with the heavy one, are added to the system. The cat particle constitutes the system, and the lighter particles, the environment, but we treat all of them exactly, in a fully quantum mechanical way.
In [
22], we examined the Alicki–Fannes [
25,
26,
27] (AF) entropy of this system. This entropy is, in our view, the most proper generalization of the Kolmogorov–Sinai entropy to quantum dynamics. The results we obtained, although promising, are preliminary, due to the numerical difficulty [
28] of computing the decoherence matrix [
29,
30,
31] associated with the procedure. For earlier works discussing quantum entropies, see [
32,
33]. While we still believe that the Alicki–Fannes entropy is theoretically the best indicator of quantal complexity, it must be remarked that other indicators of some sort of irregularity have been proposed [
34,
35,
36,
37,
38,
39], each possessing its relevance and limitations.
In this paper, we consider one of these indicators, the von Neumann entropy of the reduced density matrix of the system. We refer in particular to the analysis in [
40], which, in line with other studies (e.g., [
41,
42,
43]), adopted a phenomenological model of decoherence. The main finding of [
40] was to show a relation between the chaotic dynamics of the classical model and the growth, in time, of the entropy. In this way, decoherence could serve as a means of reviving chaotic features in quantum mechanics that were inhibited—following any of the interpretations presented in the literature: by the logarithmic bound on complexity, by quantum localization, by the quantum Lyapunov time, et cetera. We employ the multiparticle Arnol’d cat to verify the dynamical robustness of this conclusion.
In the next section, we briefly review the properties of the classical Arnol’d cat and its quantization, following [
4]. In
Section 3, we introduce the multiparticle Arnol’d cat, both classically and quantum mechanically, following [
22]. In
Section 4, we introduce the reduced density matrix of the system, and we study its time evolution. We perform a first numerical experiment: by preparing the system in a Schrödinger cat state, we observe that out-diagonal matrix elements fade as time evolves. The main results of this paper are presented in
Section 5. They consists in the study of scaling relations for decoherence through three different kinds of numerical experiments. First, we compare the behavior of V-N entropy for the free rotation, the cat map, and cat maps where the “kick” is delayed (to be defined precisely below), which are characterized by smaller classical entropy. In the second experiment, we investigate the effect of varying the scattering intensity between the cat particle and the smaller ones. In the third, we increase the mass of the cat particle, which is a physically sound realization of the theoretical procedure of taking the so-called classical limit. The conclusion discusses the results of the numerical experiments and their theoretical implications in relation to previous studies.
2. Arnol’d Cat as a Single Particle Moving on a Ring
It is well known that an Arnol’d cat map can also describes the motion of a kicked particle of mass
M subject to move on a one dimensional torus of length
L, labeled by the variable
Q. This particle is also acted upon by an impulsive force, periodic of period
T, that instantaneously changes the particle’s momentum. This is formalized by the Hamiltonian
where
P is the conjugate momentum to
Q and
is a coupling constant. It is easily seen that the period evolution generated by this Hamiltonian is the Arnol’d cat mapping: if
are the dynamical variables measured at the instant of time
, immediately following the action of the impulsive force, the period evolution becomes
The dynamical momentum
P is conveniently rescaled by multiplication by
, so that the new quantity,
has the dimensions of a length. The rescaled period evolution becomes
Moreover, it is also assumed that the rescaled momentum variable
is periodic, of the same period
L as
Q, so that the phase-space of the system is a two-dimensional torus. This can be obtained by setting
and requiring that
be an integer. The particular choice
finally reveals the classical Arnol’d cat on the two-dimensional torus. We stick to this choice in this paper.
The Hamiltonian (
1) was originally quantized by semiclassical methods in [
24] and by canonical means in [
4]. The peculiarity might appear to be the requirement of periodicity of both coordinate and momentum, but this has been already discussed by Schwinger [
44] and, much later, formalized rigorously [
45]. Formal calculations are indeed elementary: in this section, we adopt the approach of [
4], which proceeds as follows. Periodicity in the
Q coordinate implies that that wave functions can be expanded on the momentum eigenfunctions
, with integer
k:
Obviously,
are the expansion coefficients. The quantum momentum operator is
, where, obviously,
h is Planck’s constant. Therefore,
with eigenvalue
.
Next, consider periodicity, with period
, in the variable
P, as done before in the classical case. This is possible if a wave-function, written in the momentum representation, is such that there exists an integer
N so that
and in Equation (
5), one has
for any
k. Without loss of generality, we put
here and in the following.
These considerations permit us to show that quantum kinematics can be effected in a finite dimensional Hilbert space of dimension
N: Equation (
8) imposes
=
in Equation (
5), so as to produce a periodic train of delta functions at the spatial locations
, with
, where
s is a fixed shift that can be taken to be null. Wave-functions can therefore be written as
in position representation, and letting
,
in the momentum representation. The dimension of the Hilbert space
N is directly proportional to the mass
M of the particle: the classical limit can be obtained by keeping
ℏ fixed to its real physical value and by considering particles of increasing mass
M.
The matrix representation of the evolution operator is computed in a straightforward fashion in [
4]. In the position representation, where the wave-function takes the values
,
, the evolution
induced by the free rotation
has matrix elements
We denote by
K the impulsive kick operator whose matrix elements are
where
is the Kronecker delta. Finally, the quantum Arnol’d cat evolution operator is the product
.
3. The MultiParticle Arnol’d Cat
The multiparticle Arnol’d Cat introduced in [
22] is a many-body system composed of a particle of mass
M and of
I lighter particles of mass
m, also bound to move on the circle of length
where the first particle evolves. We denote by
and
,
coordinates and momenta of these particles, respectively. Also imposing periodicity of period
in the momenta
yields the requirement
where
n must be an integer. The wave-functions of the new particles can also be written in the form of Equations (
9) and (
10), where
n substitutes
N: remark that these lighter particles are characterized by a smaller Hilbert space.
Neglecting any symmetry requirement, the many-particle wave-function can be written in the momentum basis as
To specify the coordinates
, which belong to a lattice of spacing
, containing
n points, we perform a similar analysis to that in the previous section. We choose
N as an integer multiple of
n (that is,
, which also implies that the mass
M is a multiple of
m, i.e.,
). We also require that the position–momentum lattice of a small particle is a subset of that of the large one: the position lattice of the
i-th particle is
where
an integer measuring the shift of the position lattice of the
i-th particle with respect to that of the large particle. The allowed values of the constants
range from zero to
. Similarly, the momenta
live on the lattice
, with
.
In the position representation, the state of the system is encoded in the values of at , which we label as using the index zero for the large particle. Mapping to and from the two representations is easily affected by the multidimensional discrete Fourier transformation.
The unitary evolution operator of the multiparticle Arnol’d cat is engendered by the Hamiltonian
where
V is a coupling constant and the function
depends only on the difference between the coordinates of the light particles with the large one. This form implies an elastic scattering between the heavy particle and each of the lighter ones, which, for simplicity, are assumed not to interact with each other—although a slight modification of theory and numerical codes would allow this. The form of the Hamiltonian (
16) is inspired by the decoherence program of Joos and Zeh [
17]: the large particle encounters frequent collisions with the small ones that should ultimately produce decoherence and classicality.
In fact, the interaction potential
appearing in the Hamiltonian (
16) should somehow reproduce a hard core potential equal to a Dirac delta function, representing a perfectly elastic scattering [
46,
47]. In our case, where kinematics take place in the tensor product of quantized two-dimensional tori, this requires a model that is easily treatable. At the same time, it yields significant new features in the scattering process, such as the possibility of missed interactions, which will be described in a different work.
The model that we choose is the following: we choose the interaction potential
in the form
in which
is the interaction matrix in the
subspace (for convenience of notation, we shall also let the index 0 label the position-momentum of the large particle:
,
) and
is the identity in the orthogonal complement of the
subspace. The interaction between the heavy (zero-th) particle and the
i-th is effective only when they occupy the same lattice point. It is therefore convenient to define the scattering potential directly in the position representation, where
is defined by its values at the lattice positions defined above:
. In this basis, we have
where
and where
and
range from 0 to
, while
and
range from 0 to
. As anticipated, the last Kronecker delta requires that the particle 0 and
i sit at the same lattice point. According to Equations (
17) and (
18), the full matrix elements of
are therefore
It is apparent that is diagonal in the coordinate representation.
Finally, the form of the Hamiltonian (
16) suggests a numerical technique for the quantum evolution. Write symbolically
where
is the free motion Hamiltonian,
is the scattering contribution, and
K is the impulsive force (acting only on the
Q coordinate). Then, the full period evolution operator
U can be written as the product of
and of the time-ordered exponential
that generates the rotation in the presence of scattering. This latter is conveniently computed in a Trotter product form
whose accuracy increases by increasing the number of subintervals
R of the interval
. It is apparent that each exponential must be computed in the basis where the corresponding operator is diagonal. This is easily obtained by the repeated usage of the multidimensional Fourier transform.
4. Evolution, Density Matrix, and Decoherence
It is well known that the most general formulation of a quantum system involves the concept of density matrix. This approach has been widely used in the investigation of decoherence. The initial point of the evolution is a density matrix composed of a pure state
defined as in Equation (
14):
. Its time evolution is fully unitary and follows from the evolution operator
defined by the Hamiltonian in Equation (
20).
Observe now that the Hilbert space
of the system is the tensor product of the single particle Hilbert spaces and that we focus our attention on the heavy particle: we may consider this latter as the system and the remaining ones as the environment, so that the Hilbert space is the product
The reduced density matrix of the system,
, is obtained by tracing over the degrees of freedom of the environment:
It contains the full information to determine the outcomes of measurements on the system
when the environment is not observed. The von Neumann entropy
S quantifies the amount of information in the eigenspectrum of
: this is easily seen, since
S is defined as
and since
is unit trace, Hermitean and positive semi-definite, letting
be its eigenvalues, one has
which is the Shannon entropy of the set of eigenvalues. At the same time, it is clear that when the density matrix is in the form of a pure state, it has a single non-zero eigenvalue whose value is one, and the entropy is null. Therefore, the von Neumann entropy can also be considered a measure of the decohering influence of the environment on the system.
A first consequence of decoherence is the fact that coupling to the environment suppresses the out-diagonal elements of the density matrix, or in other words, suppresses the coherence of entangled states. This can be verified in the model system under investigation by preparing the initial state of the system in a Schrödinger cat configuration and by turning off the kick Hamiltonian, i.e., setting
, so that only free motion and collisions play a role. We choose a heavy particle of mass
(recall that we choose
) interacting with three light particles of mass
, with coupling constant
. In
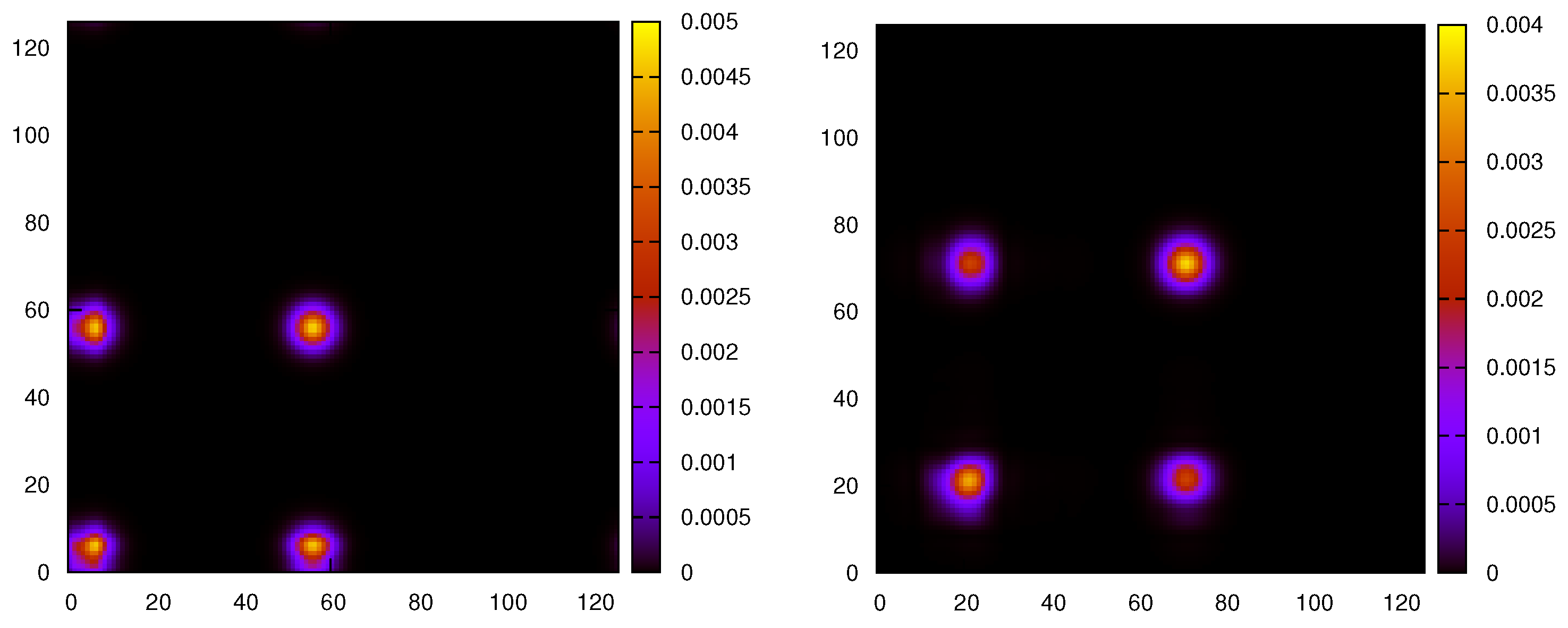
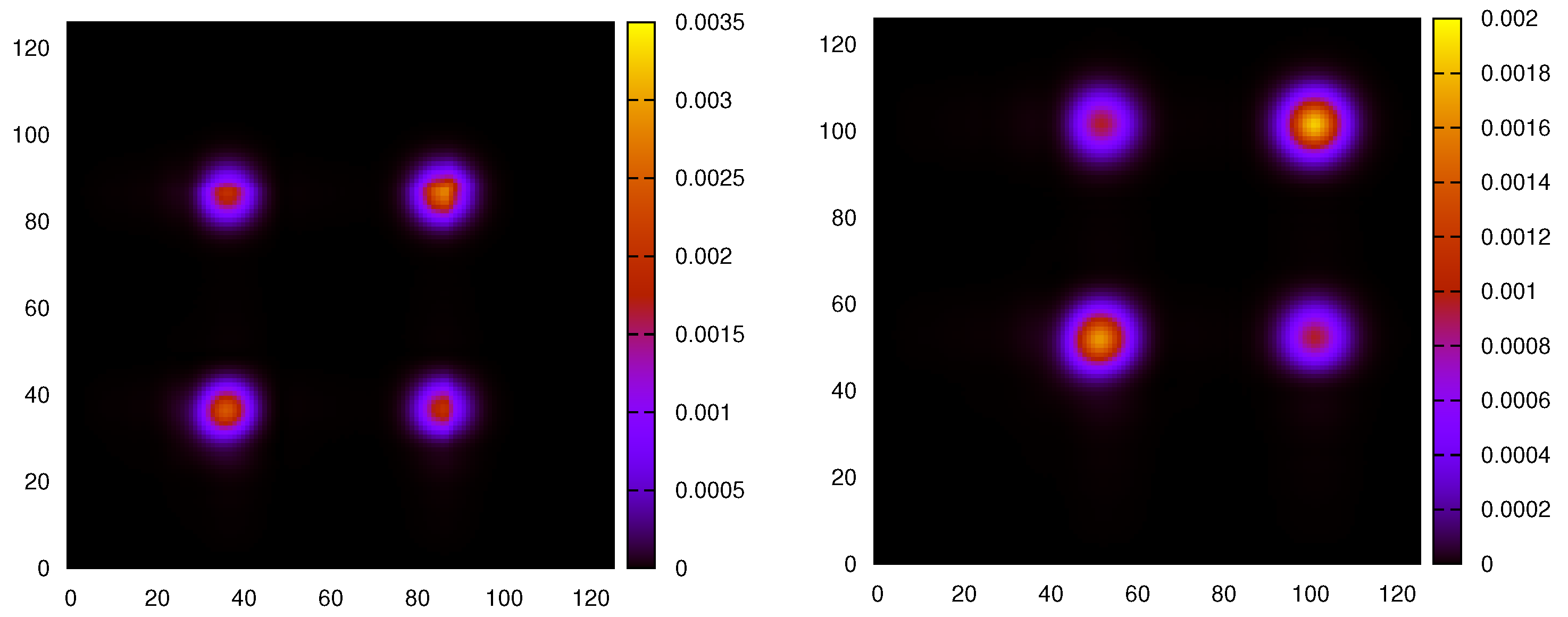
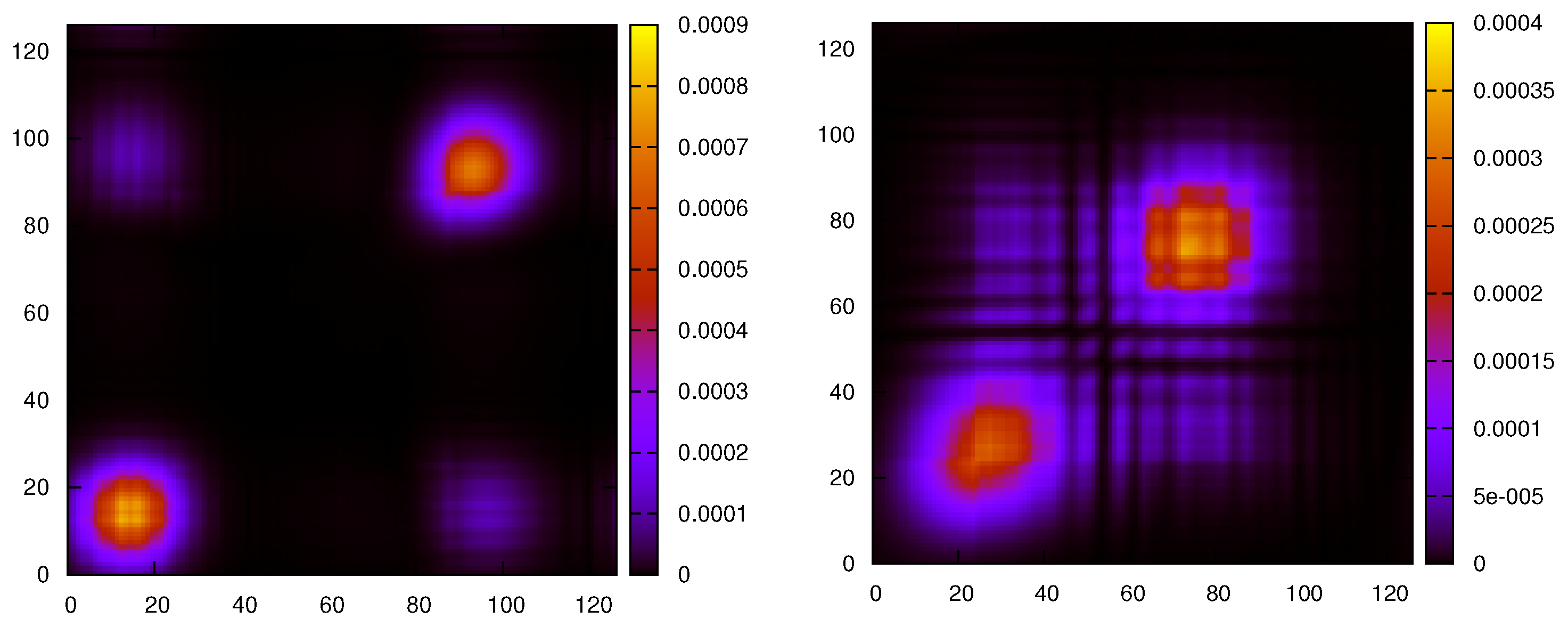
Figure 1, we plot the intensity profile of the density matrix, in the position representation, at time zero and at time
, while in
Figure 2, the same is represented at times
and
. Fading of the out-diagonal components is observed, which is almost complete at time
, pictured in the left frame of
Figure 3. In the right frame of the same figure, at time
, interference patterns due to the finite size of the Hilbert space start appearing.
5. Scaling Relations for Decoherence
The fully dynamical model introduced above permits us to study quantitatively the effect of collisions on the onset of decoherence in the motion of the heavy particle. This can be done in a sequence of experiments.
5.1. Behavior of V-N Entropy for Chaotic and Non-Chaotic Systems
Firstly, we want to investigate the characteristics of the entropy growth in time in chaotic and non-chaotic systems. This can be obtained by considering the evolution of the cat map system on the one side, and on the other side, of the free rotation. Among these extrema, one can also choose to act with the kick operator at times that are multiples of
T, of course while keeping the same intensity of the perturbation.
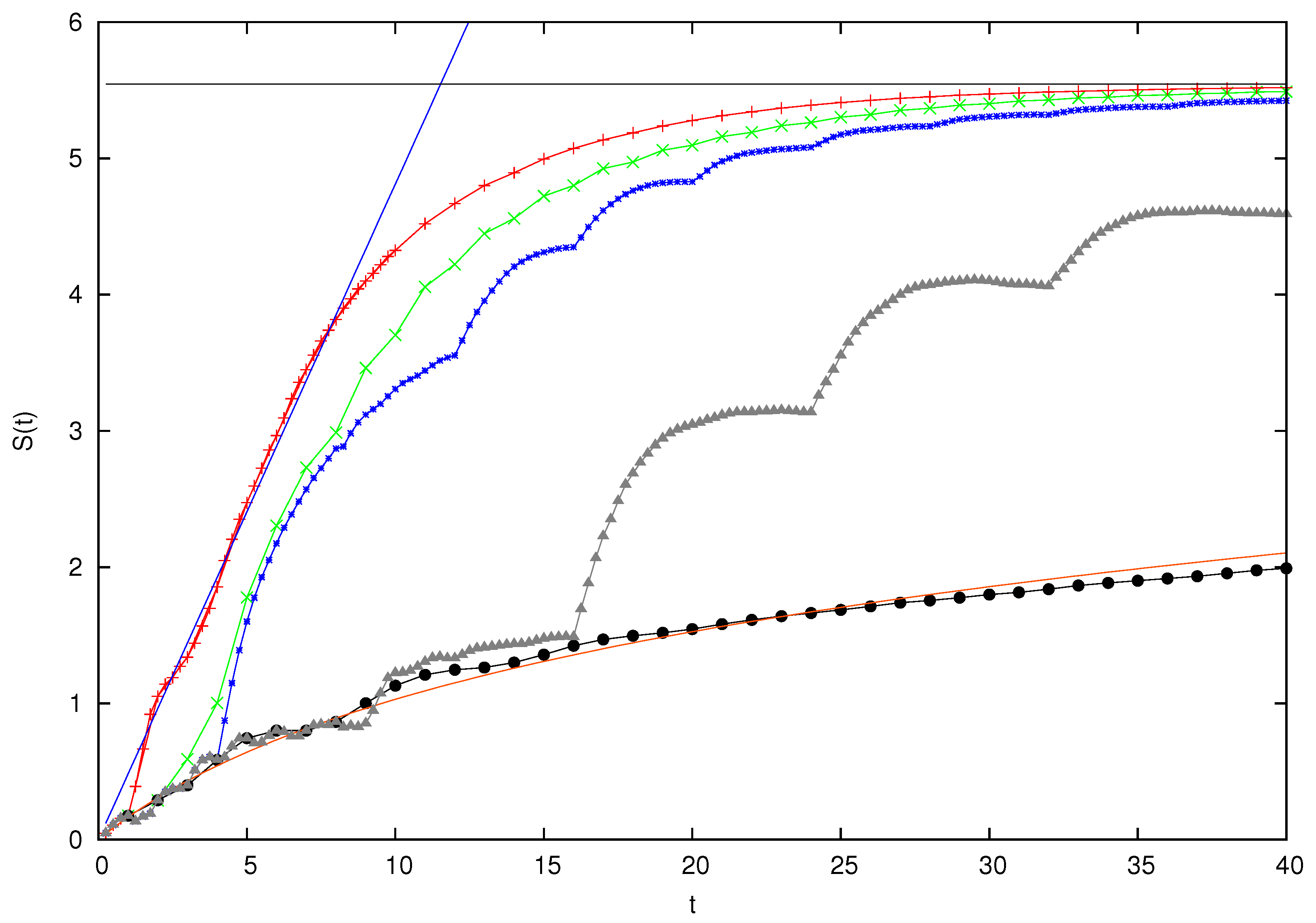
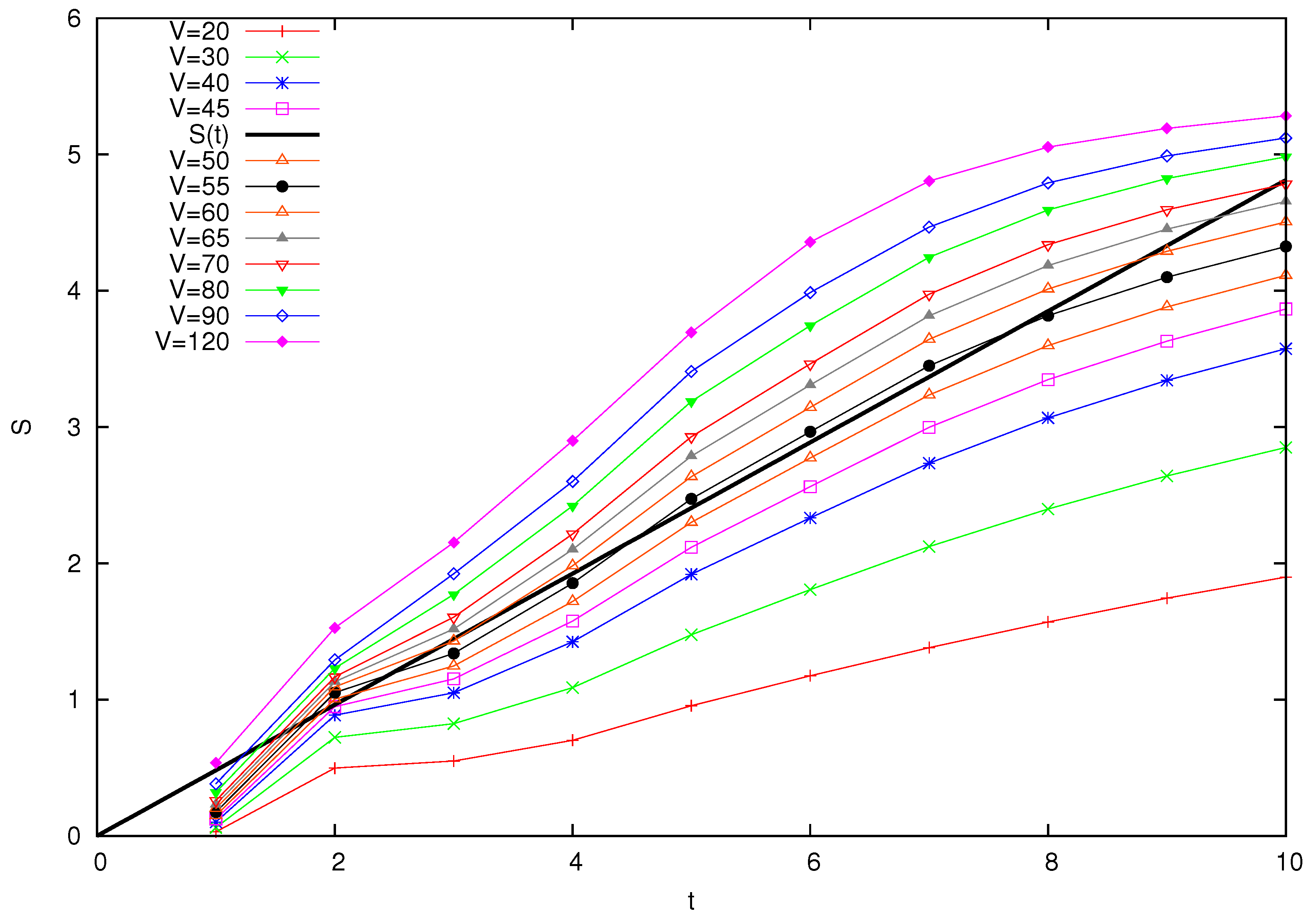
Figure 4 reports the results of this investigation. We choose
,
,
, and
. The adopted value of the intensity
V of the scattering coupling is derived from the analysis to be presented in the next section.
In the dynamics of the “conventional” cat, with kicks spaced at intervals, we observe an initial almost linear growth of the entropy, with slope approximately equal to the Lyapunov exponent of the classical map. For long times, the value of the entropy saturates at the theoretical limit , which in this case is .
When kicks are spaced every intervals of time, the entropy growth is still of the same kind. Next, consider data for spacings and . A moment reflection reveals that in the general case of spacing , with m being an integer, dynamics can be thought of as a periodic evolution, of period , composed of iterations of followed by one iteration of U. The picture shows that the amount of chaoticity infused by the action of U, which contains the combination free rotation and kick generating the Arnol’d cat, is immediately reflected by an increase of the von Neumann entropy. Successively, this increase slows down before the next action of U.
Finally, data are shown for when the dynamics are generated solely by , that is, free motion of all the particles and scattering. For what concerns the heavy particle, this is the motion of a system with, at most, linear separation of trajectories. We observe a logarithmic increase of entropy. We will comment in the conclusion on the relation of these findings with the more cogent test of A-F dynamical entropy.
5.2. Behavior of V-N Entropy When Increasing Scattering Intensity
One of the main conclusions of [
40] is that the rate of entropy production becomes independent of the intensity of decohering perturbation when this latter surpasses a certain threshold, and this rate, at short times, equals the classical dynamical entropy. While the model of decoherence in [
40] is admittedly phenomenological, the one examined here is fully dynamical and can be used to test this conclusion.
For this investigation, we have at our disposal the coefficient
V in Equation (
16), which can be varied to increase or decrease the scattering interaction between the heavy particle and the lighter ones. As in the previous section, we consider a system with
,
,
, and we let
V vary. Entropy versus time is plotted in
Figure 5. One must obviously focus on the initial part of the graph, before the saturation to the value
. In such a range, an almost linear increase is observed, in line with the theoretical prediction just discussed. Upon increasing the value of the coupling
V, the slope of the linear part increases, but apparently it does not reach a limiting value, which should be given by the logarithm of the Lyapunov exponent of the classical cat map,
. For large couplings, this value is surpassed.
This leads to two considerations. Firstly, as observed in the classical investigations of systems with added noise [
48], such interactions can add complexity to the motion. This is most likely the case here: coupling with light particles reveals the complexity of the motion of the heavy particle, but it also contributes a positive amount to the entropy. Secondly, it might be surmised that for this procedure to work, the amount of “disturbance” brought about by the small particles should be negligible yet effective. When considering the classical limit, i.e., the case of larger and larger
M, this might require a particular scaling relation between
M, the number of light particles, and their masses. This study has not been performed, and its physical significance is as yet unclear.
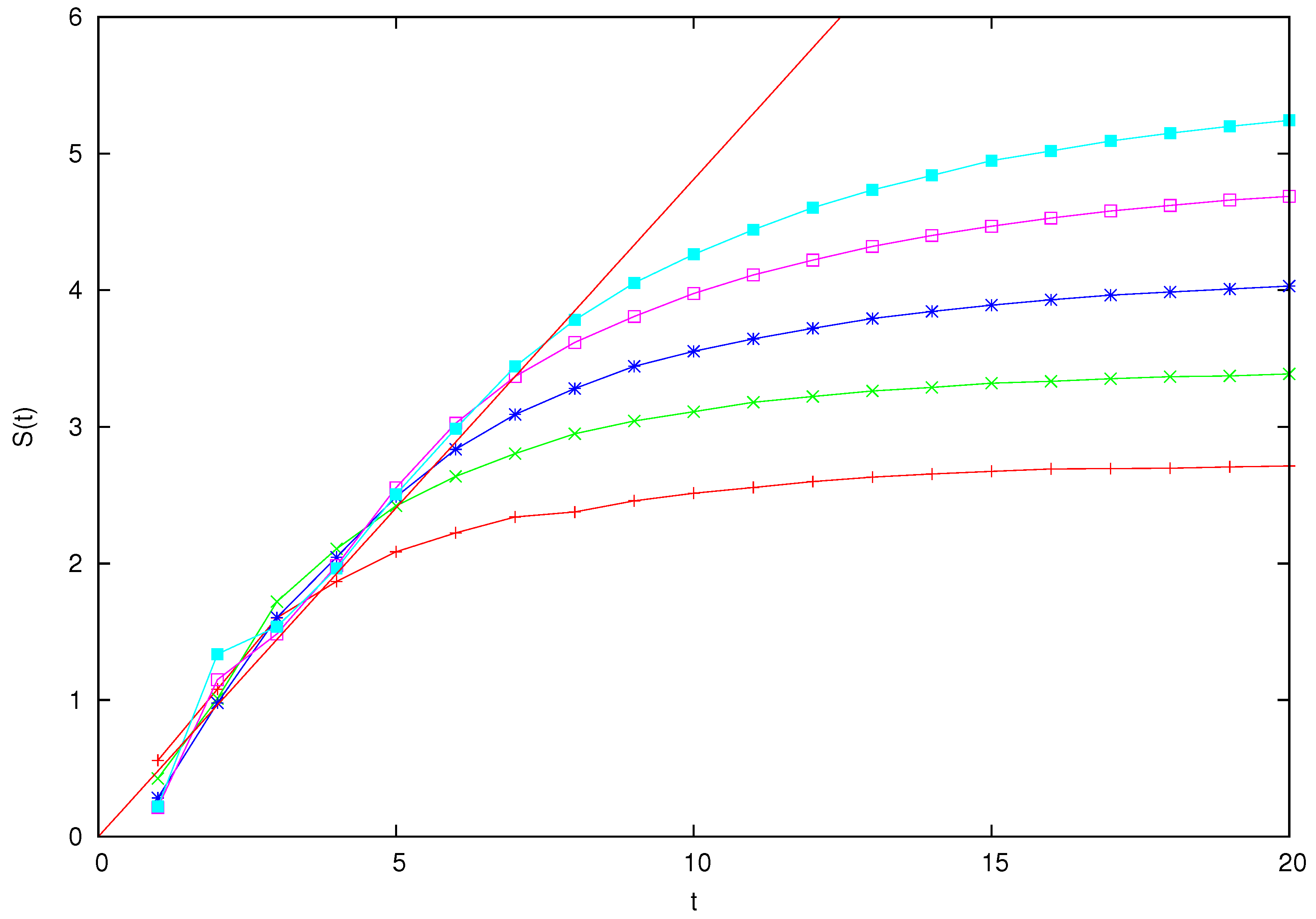
5.3. Behavior of V-N Entropy When Increasing the Mass of the Large Particle
Finally, let us examine the behavior of the V-N entropy when the mass of the heavy particle increases. As mentioned in the previous paragraph, this investigation is relevant to the deep question on the nature of the correspondence principle. In these numerical experiments, the large particle interacts with
particles of mass
. We let the mass
M increase by a factor two from
to
. In
Figure 6, we plot the corresponding graphs of the entropy as a function of time. As remarked in the previous sections, in order to have a region of linear increase with a slope comparable to the logarithm of the Lyapunov exponent, the intensity
V of the coupling must be chosen appropriately. Yet, since we elect in this section to keep the mass and the number of light particles constant while the large particle gets heavier and heavier, in order to have a comparable effect of the perturbation, the coupling constant must increase accordingly: when the mass
M doubles, so must
V. In the experiments,
for various values of
l, and therefore, we set
. We observe that the curves tend to adhere more and more to the linear part as the mass of the heavy particle increases. We can now comment on the relevance of these findings.
6. Conclusions: Quantum Dynamical Entropies and Decoherence
The behavior observed in
Figure 6 of the previous section is analogous to that found in the investigation of the A-F entropy of the Arnol’d cat mapping in [
28]: the finite size of the Hilbert space limits quantum pseudo-chaos (to use Chirikov’s terminology) to a time span that is only logarithmic in the semiclassical parameter. Yet, a fundamental difference is to be remarked: the calculation of A-F entropy does not require the introduction of a decohering mechanism but is defined on the quantal evolution plus the essential ingredient of defining a coarse-graining, which leads to symbolic dynamics. This considers the “quantum history” of a state vector
as the result of repeated projections on macro-states, followed by unitary evolution.
Secondly, but also importantly, the von Neumann entropy of the reduced density matrix is bounded by the logarithm of the cardinality of the Hilbert space, which we have seen here to be proportional to the mass of the particle under observation. The same bound also affects the A-F information (whose time increase defines the entropy), but only in the absence of decoherence. Indeed, the analysis of [
22] suggested that this bound could be overcome, precisely owing to decoherence. This fundamental capability is not shared by von Neumann entropy, which, in our view, puts it in a different level of theoretical relevance, as compared to that of Alicki and Fannes: it is more readily computable and applicable to derive physical consequences of real experiments, but it does not capture all the dynamical features of quantum motion.
Yet, it is to be recalled that in [
22], it was also found that too strong a decoherence results in an increase of A-F information larger than what is observed in the classical system. The same scenario is found in this paper when considering the von Neumann entropy: contrary to the case studied in [
40], we find that to achieve concordance with the classical entropy—albeit in a limited range—the parameter governing the momentum transfer from system to the environment must be accurately tuned.
It seems therefore, that to achieve the same results of classical mechanics, a balance between the mass of the semiclassical system and the intensity of decoherence should hold. Clearly, a theory of this sort can be physically satisfactory only if some sort of universality is found when taking this classical limit: as we suggested in [
22], this means that when letting the mass
M of the large particle grow, one should be able to find that for a large, physically reasonable set of sequences
m,
I,
V, the quantum von Neumann entropy
agrees with the classical information production.