1. Introduction
Equation of State (EOS) of materials is an inevitable ingredient in several fields of solid state science like geophysics, hydrodynamic applications for the analysis of inertial confinement fusion systems, stellar structures, nuclear weapons, etc. Other applications include fast reactor accident analysis and study of weapon effects in various media. Euler equations of hydrodynamics, which expresses conservation laws of mass, momentum, and energy, are routinely used to describe the dynamical behavior of materials [
1]. However, these equations describe the space-time evolution of four thermodynamic variables—viz., mass density (or specific volume), material velocity, specific internal energy, and pressure. The system of these equations is then closed with the addition of equation of state (EOS), which provides pressure when specific internal energy and density are given. The Mie–Grüneisen EOS [
1] with an empirical specification for Grüneisen parameter is the most commonly used EOS of this type. There is also Tillotson’s EOS [
2] which has a larger range of validity. However, a more complete EOS is specified by providing pressure and specific internal energy as functions of density and temperature. This temperature corresponds to thermodynamic equilibrium in the material, and can be eliminated from the expression for pressure in favor of specific internal energy to obtain the above mentioned relation between pressure, specific internal, energy, and density. An EOS of similar class, which treats pressure as independent variable, was proposed by Rice and Walsh [
3] to model water. Here, specific volume is expressed in terms of enthalpy using the enthalpy–parameter which depends on pressure. This class of EOS, generally called enthalpy-based EOS, has been developed to model shock compression of porous materials [
4], including explicit accounting of electronic effects [
5].
In the following sections, we describe a semi-analytical EOS model of the general type, where volume and temperature are independent variables. The different components of the EOS model, including correction terms, are discussed in detail. Experimental data for Cu on Shock-Hugoniot, critical point parameters, liquid–vapor phase diagram, and isobaric expansion are used to test the model. Good agreement obtained shows that the model can be employed to prepare extended EOS tables for use in hydrodynamics calculations.
2. Three Component EOS Model
In general, EOS models consist of three components [
6], which describe (i) the zero-temperature (or cold) isotherm, (ii) thermal ionic effects, and (iii) thermal electronic effects. Pressure and specific internal energy are then expressed as functions of volume
and temperature
:
where the terms denote, respectively, the three components mentioned above. The subscripts
c,
, and
stand for the terms ‘cold’, ‘thermal-ion’, and ‘thermal-electron’, respectively. There are interaction effects between ionic and electronic motion, however, these effects contribute only a few percent to pressure and energy and so may be neglected in high-pressure physics applications [
6]. Models for the different terms in Equations (
1) and (
2) of varying degrees of sophistication are currently available in the literature [
7].
First, principle methods using Density-functional theory (DFT) for
and quasi-harmonic approximation (QHA), based on density-functional perturbation theory, for lattice vibration contributions to
are now quite common [
8]. Such methods have proven to be extremely useful in thermodynamic studies of compounds of interest in Earth sciences [
9]. Further, electronic density of states determined from DFT calculations yield accurate estimates of
for lower ranges of temperature [
10]. Availability of efficient computer implementation [
11] of QHA, which uses DFT-generated data on
and volume-dependent vibration frequencies, make QHA the method of choice for detailed studies of thermodynamic properties of materials in the solid phase. However, for developing global EOS models, which deal with very high temperatures (∼keV) and pressures (∼ tens of megabar), it is necessary to take only the relevant information from DFT computations and supplement it with other models [
10] to incorporate effects of melting, extreme pressure and thermal ionization, expanded volume states, etc. The general approach is to use empirical fits to the cold isotherm [
12], Debye–Grüneisen model for lattice thermal motion [
13] and Thomas–Fermi model for thermal electron excitation [
14]. Such extended models are essential for some of the hydrodynamic applications mentioned in the beginning.
The global EOS model we describe below, which is applicable even at very high temperatures and pressures in the compressed as well as expanded volume states, indeed uses different parameters obtained from DFT analyses, particularly when accurate experimental data on these are unavailable.
3. Zero-Temperature Isotherm
The zero-temperature isotherm is a manifestation of the Fermi-pressure developed in degenerate electron systems, and is a quantum effect just like zero-point vibration energy. This contributes significantly to the total pressure in compressed solids, and becomes the dominant contribution at extreme compression. A variety of approximate expressions to describe it quantitatively are available in the literature [
15]. Computations using DFT, mentioned above, are now routinely used to determine energy versus specific volume (or volume per atom) tables, and thereafter the zero-temperature pressure–volume relation. Results of such analyses are then used in semi-empirical expressions. We propose to use a four-parameter model, developed by Li et al. [
16], which is expressed as:
The four parameters in the model are the specific volume
, the bulk modulus
, its pressure derivative
, and the cohesive energy
at zero temperature. These parameters occur in terms of dimensionless quantities
and
, and
a is related to the dimensionless length variable
x. Furthermore, if energy
is scaled with
and pressure
with
, then, these expressions are totally dimensionless—however, defined in terms of two parameters
and
. The specific volume
is slightly lower than the volume at ambient conditions (
K and
bar). In our approach, we adjust the value of
such that the zero-temperature pressure together with thermal pressure of ions and electrons is just one bar at 300 K. The four-parameter model is a refinement over Rose equation [
17] and Vinet equation [
18], and is found to provide quite accurate descriptions of the zero-temperature energy and pressure over compressed volume up to ∼
, which corresponds to about 100–150 GPa pressure, for about forty metals [
16]. It also provides accurate representation for energy and pressure in the expanded volume up to about ∼
. However, the formulation is inadequate in the region of extreme compression, as is evident from Equation (
3), which shows that
saturates as
. Theoretically, the zero-temperature energy and pressure should approach those of electron gas.
To rectify this problem, we use a procedure [
12] to smoothly go over from the four-parameter model to the the quantum statistical model (QSM) [
19], which is known to provide accurate descriptions of pressure and energy of electrons above few hundred GPa pressure. The QSM accounts for exchange and correlation effects in addition to corrections for electron density gradients [
20]. Electron pressure in a compressed atom within the QSM model is expressed as:
Here, e is electron charge, is atomic number, is the Bohr radius, and is the Wigner-Seitz cell radius in units of . Specific internal energy is obtained from pressure by integrating the thermodynamic relation from a suitable initial volume, say .
Now, choose a value of
V, say
, such that the four-parameter model
is accurate for
. That is, we assume that the zero-temperature isotherm
and
for
. Then, for lower values of
V, these are defined as
Here,
is a suitable interpolating function. Note that, by definition,
is continuous at
. Now, the parameters
in
are chosen such that
and its first two derivatives are also continuous at
[
12]. This procedure gives a smooth transition from the four-parameter model to the QSM. Plots of energy versus
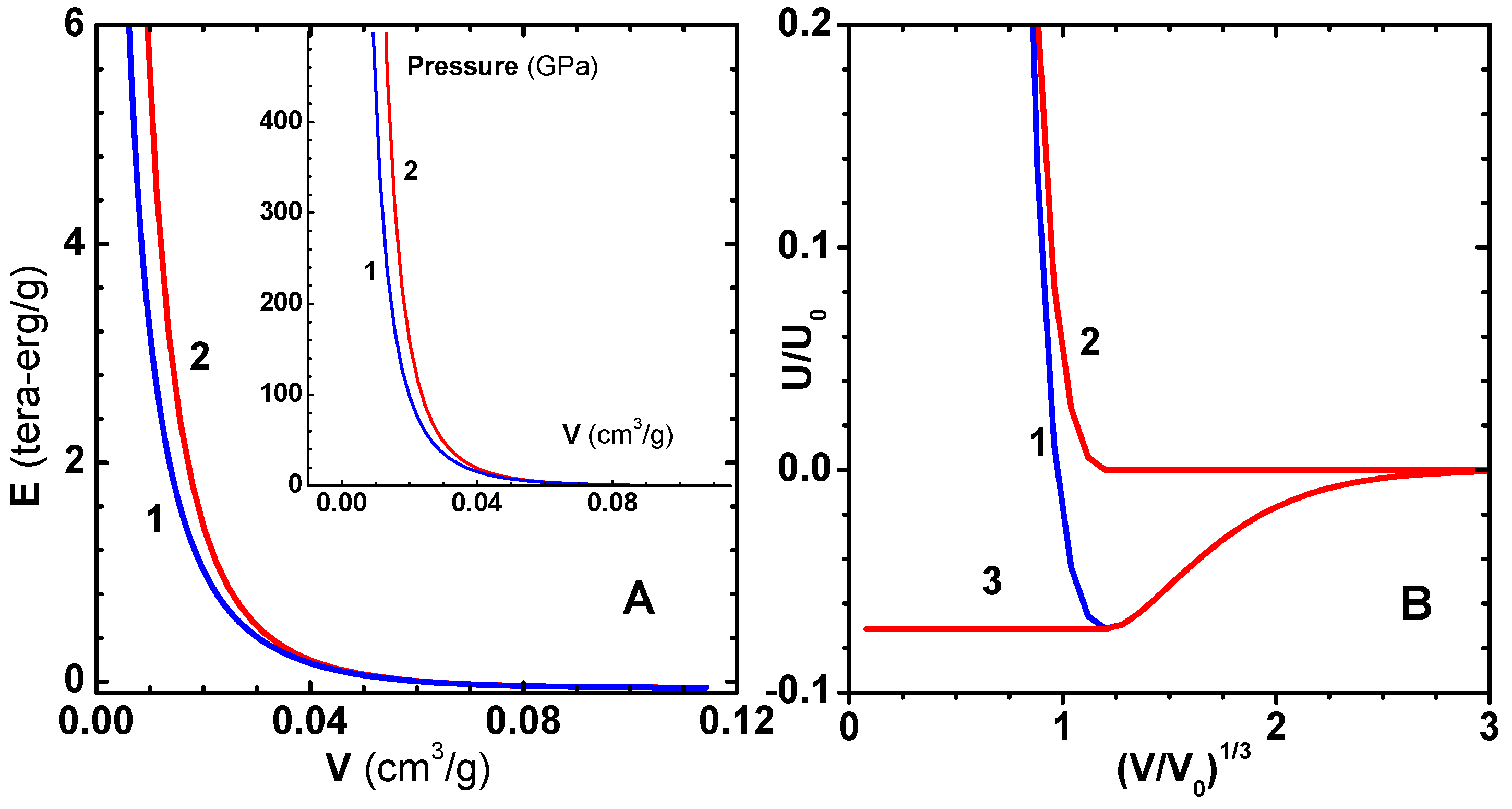
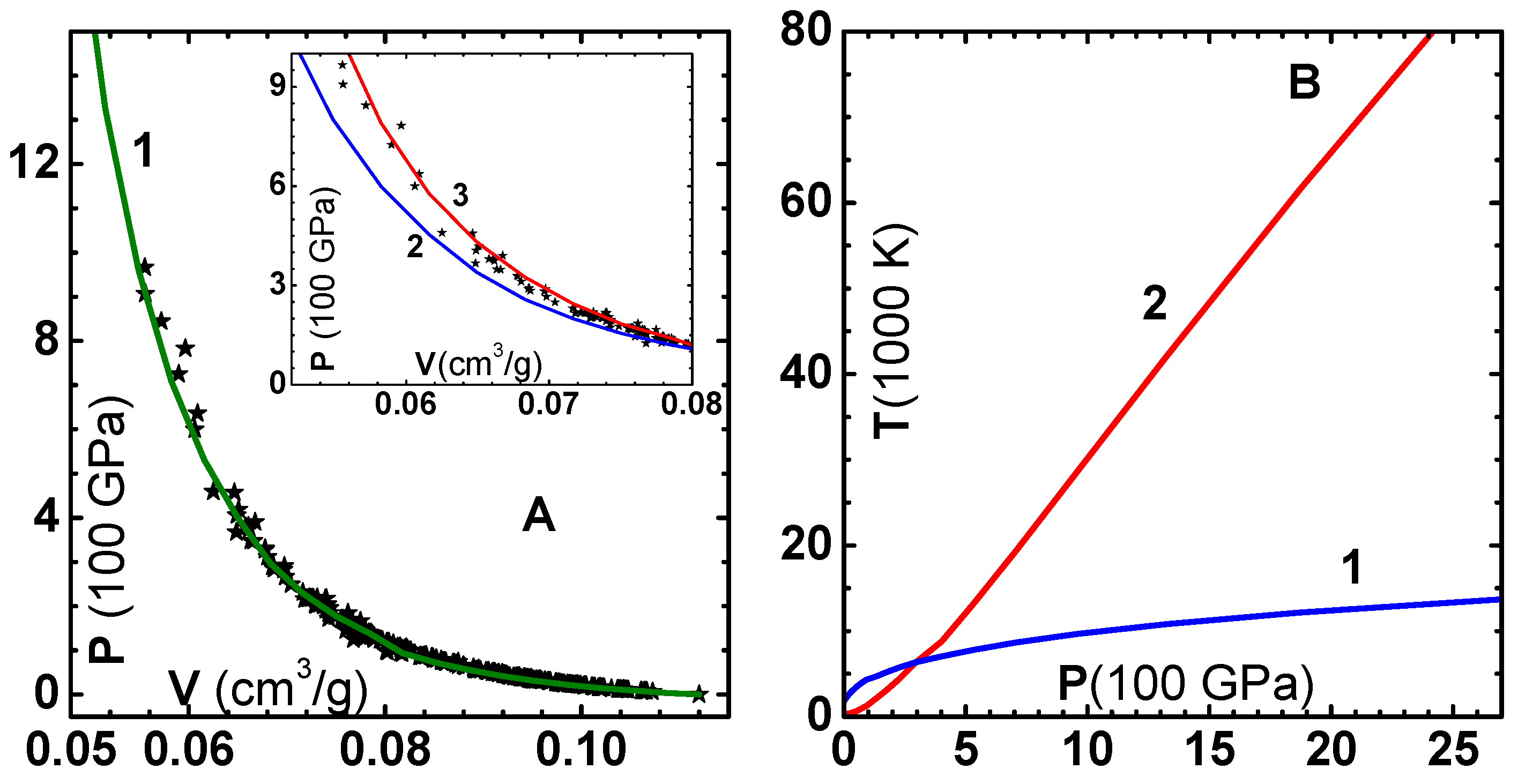
V for Cu using the two models are shown in
Figure 1A with the choice
cm
/g.
As an application of the zero-temperature energy
, we use the lattice inversion method [
21] and obtain an effective inter-particle potential between Cu atoms in the solid. We may imagine that the lattice is formed by assembling shells successively around a central atom. Then, the zero-temperature energy
per atom, where
is the scaled nearest-neighbor distance, can be readily written as a lattice sum involving the inter-particle potential
. The inversion method provides a similar formula [
22] for
in terms of
. For an FCC lattice, the direct formula for
and the inverse formula for potential
are given by
Here,
n is the shell index,
is the number of atoms in the shell,
is the normalized radius of the shell, and
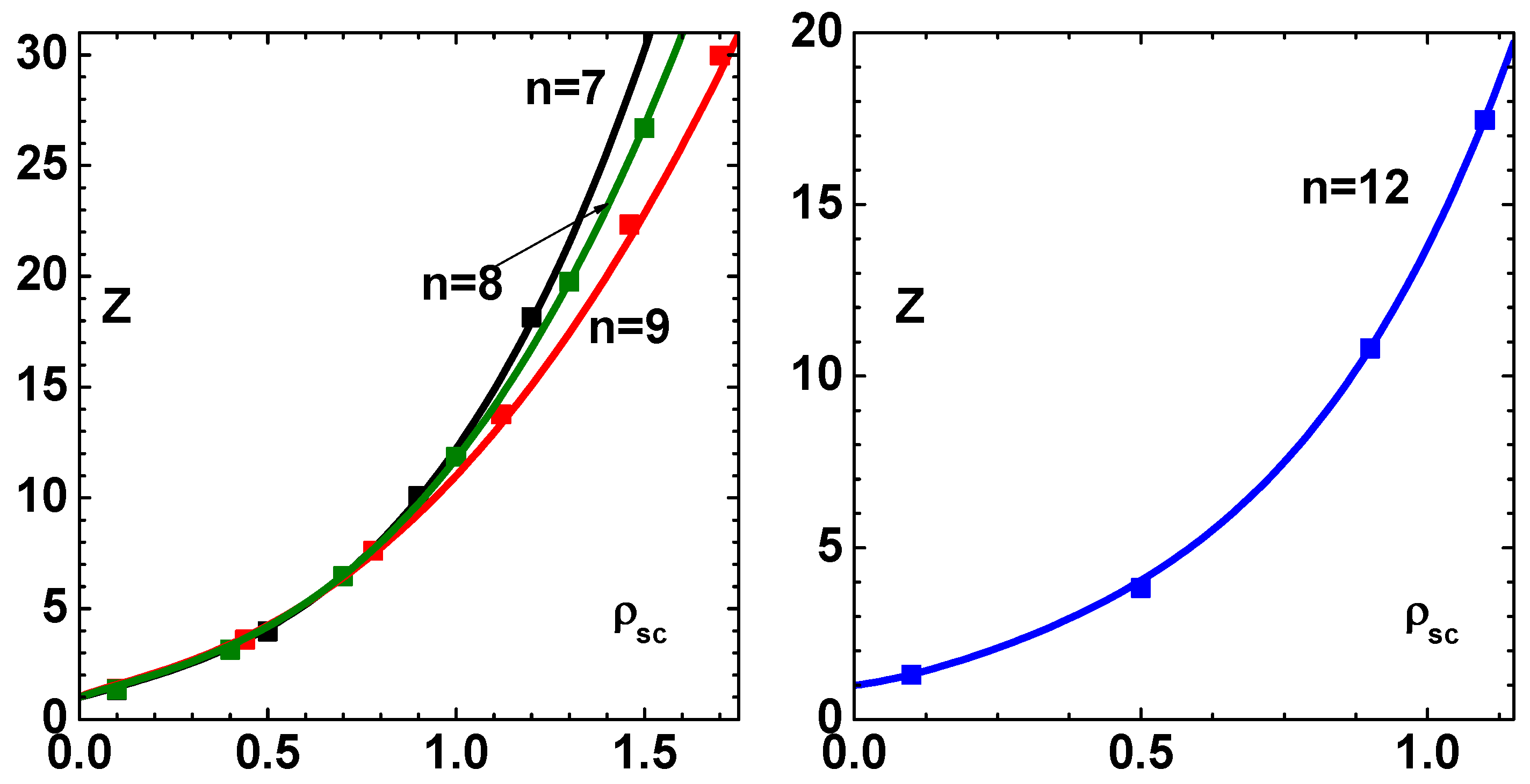
is the weight factor for the shell. This is a truncated formula, and the total number
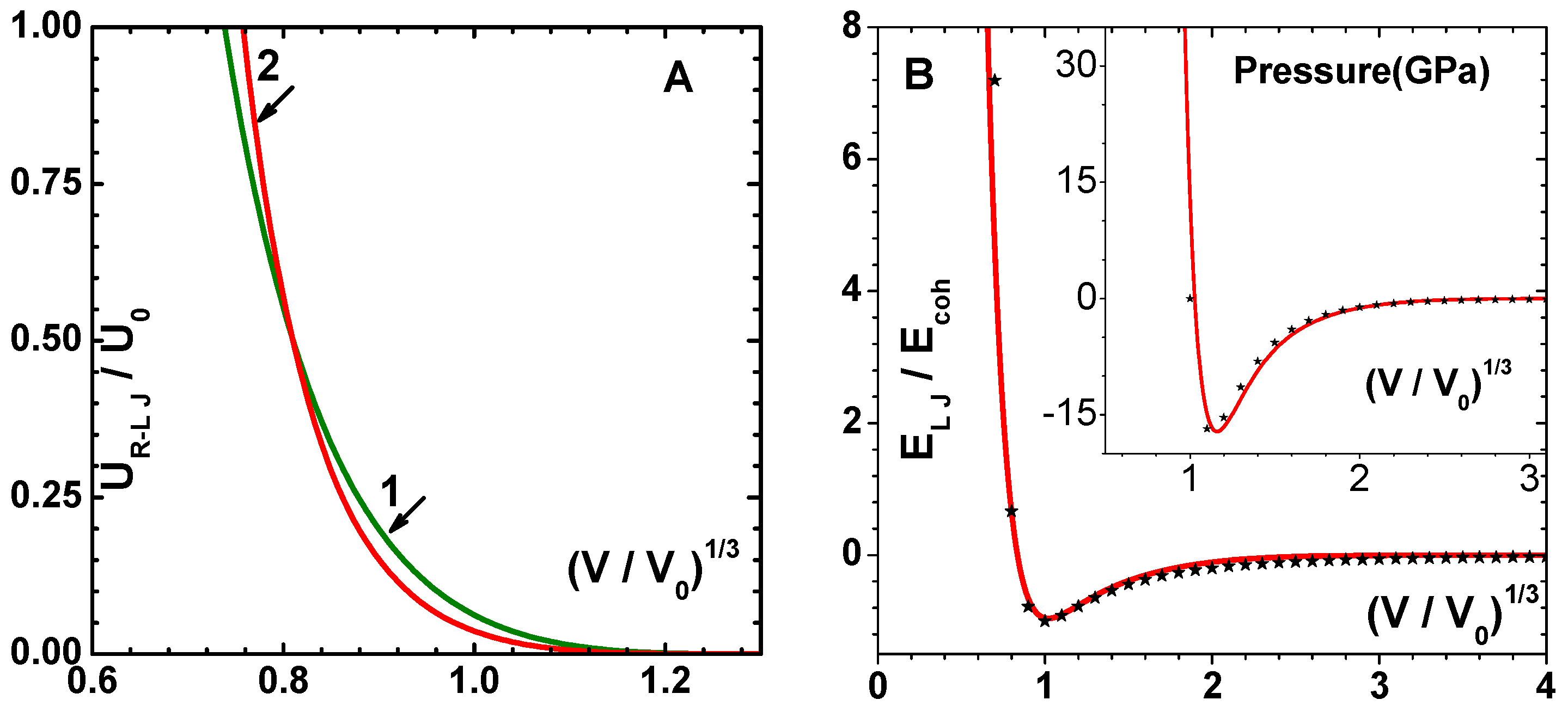
of shells considered should be sufficiently large for convergence. The total potential (curve-1) and its repulsive (curve-2) and attractive (curve-3) components, as per the Weeks–Chandler–Andersen prescription [
23], are shown in
Figure 1B. For the sake of completeness, we have listed the constants
and
for FCC lattice in
Table 1. The factors
and 2 in Equation (
7) arise because
is the energy for two atoms; while
is the energy per atom.
5. Electronic Thermal Component
Electronic thermal component of energy and pressure is significant at temperatures reached in shock compression of porous materials. The EOS codes mentioned earlier uses the well-known Thomas–Fermi (TF) model [
14] to describe electronic properties. However, the pressure and energy resulting from the approximations involved in this model need to be corrected in the low-temperature range. For example, the low-temperature specific heat constant predicted by the model differs from experimental values. Further, it is necessary to employ pressure and energy tables since in-line solutions of the TF equation are time consuming. Therefore, analytical fits [
34] to results of Latter’s calculations are sometimes employed [
25] in high-pressure studies. However, it is important to note that this fit is valid in the compressed volume region, even though TF model as such may be applied even to an isolated atom.
So, we propose a somewhat different approach. First of all, following Atzeni et al [
35], we assume that the Fermi gas model can be used to compute the thermal energy and pressure of electrons with a suitable average ionization degree
of atoms, which depends on density and temperature. We use an excellent analytical fit for
given by More [
36] using results of Thomas–Fermi model:
where
and
A are atomic number and mass number, respectively. We have introduced a multiplicative correction term, termed ‘
factor’ in the equation above, which needs to be adjusted so that
agrees with the experimental value of average ionization degree at
and
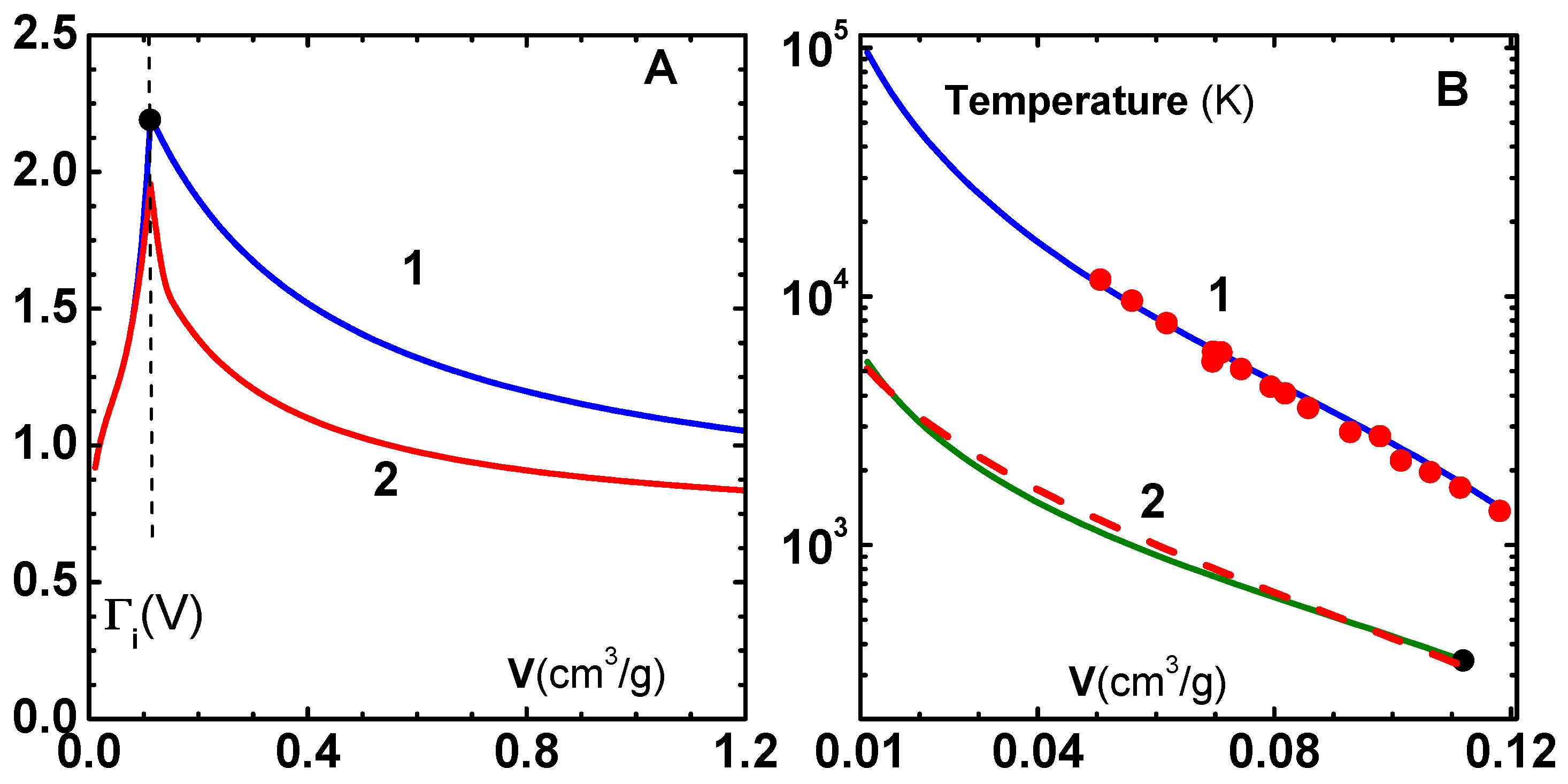
. It takes value 0.079 for Cu, and the corrected and uncorrected variation of
with temperature is shown in
Figure 7A. Note that
is corrected only in the lower ranges of temperature, and it correctly saturates to
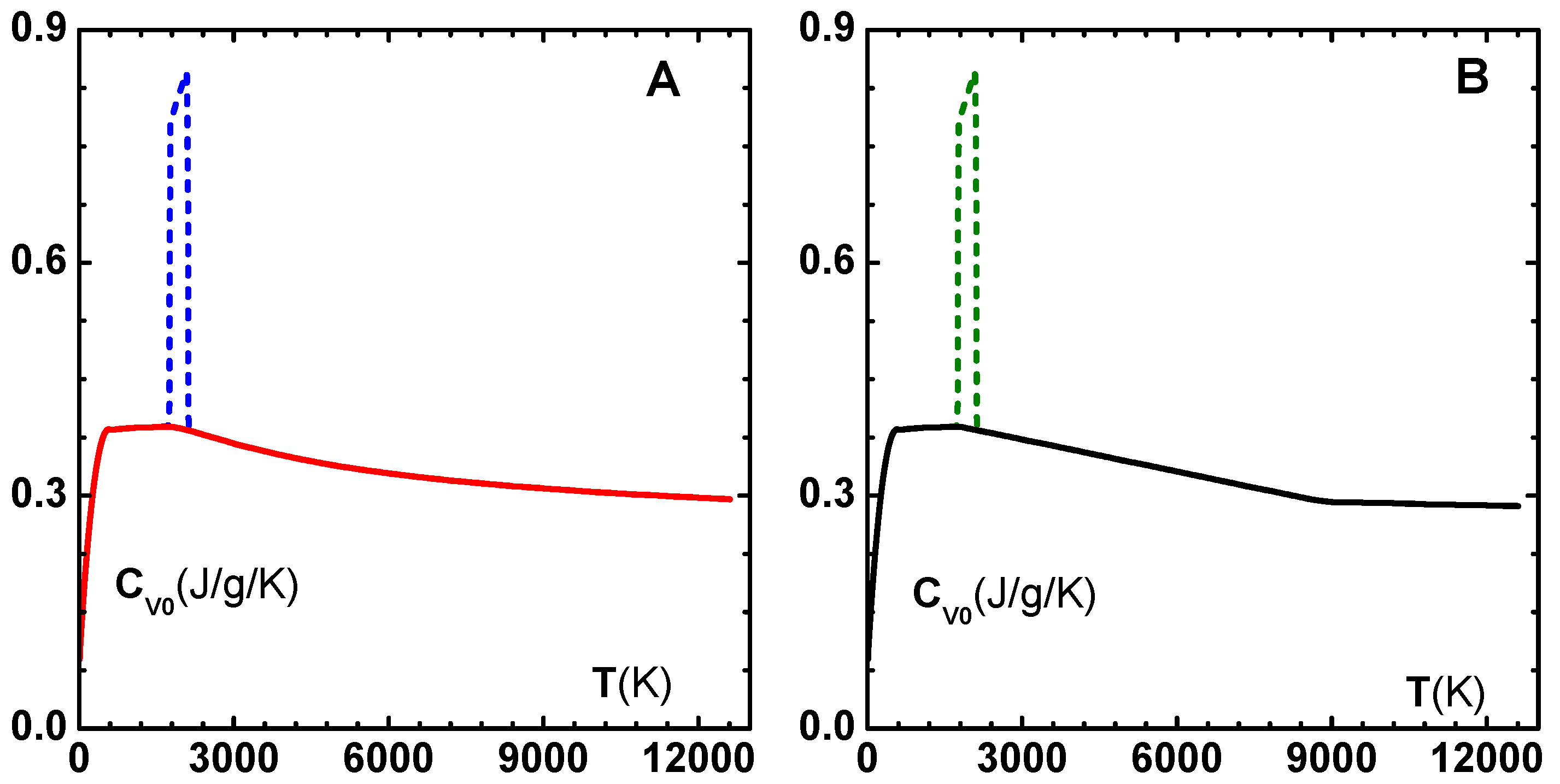
at high temperature. The insert in this figure shows specific heat variation for three densities: (1)
, (2)
, and (3)
. Similar correction factors for some other metals are given in
Table 2.
To test this approach, we have plotted in
Figure 7B the zero-temperature electron pressure
, where
versus density
using the uncorrected (curve-1) and corrected (curve-2) formula for
. Numerical results [
37] employing TF theory (filled circles) are also shown. It is interesting to note the TF results are accurately reproduced with the uncorrected
, while the correction gives lower pressures. Finally, the thermal component of electron energy and pressure, within the free electron gas model, are given by
Here,
is the Fermi energy, which is implicitly defined via Equation (
28); and
are Fermi–Dirac integrals. Very accurate rational approximations for these integrals are now available [
38]. The next level of improvement to the electron EOS is to add Coulomb interaction, exchange, and correlation energies, thereby accounting for all the terms in the uniform electron gas model [
39].
6. Applications
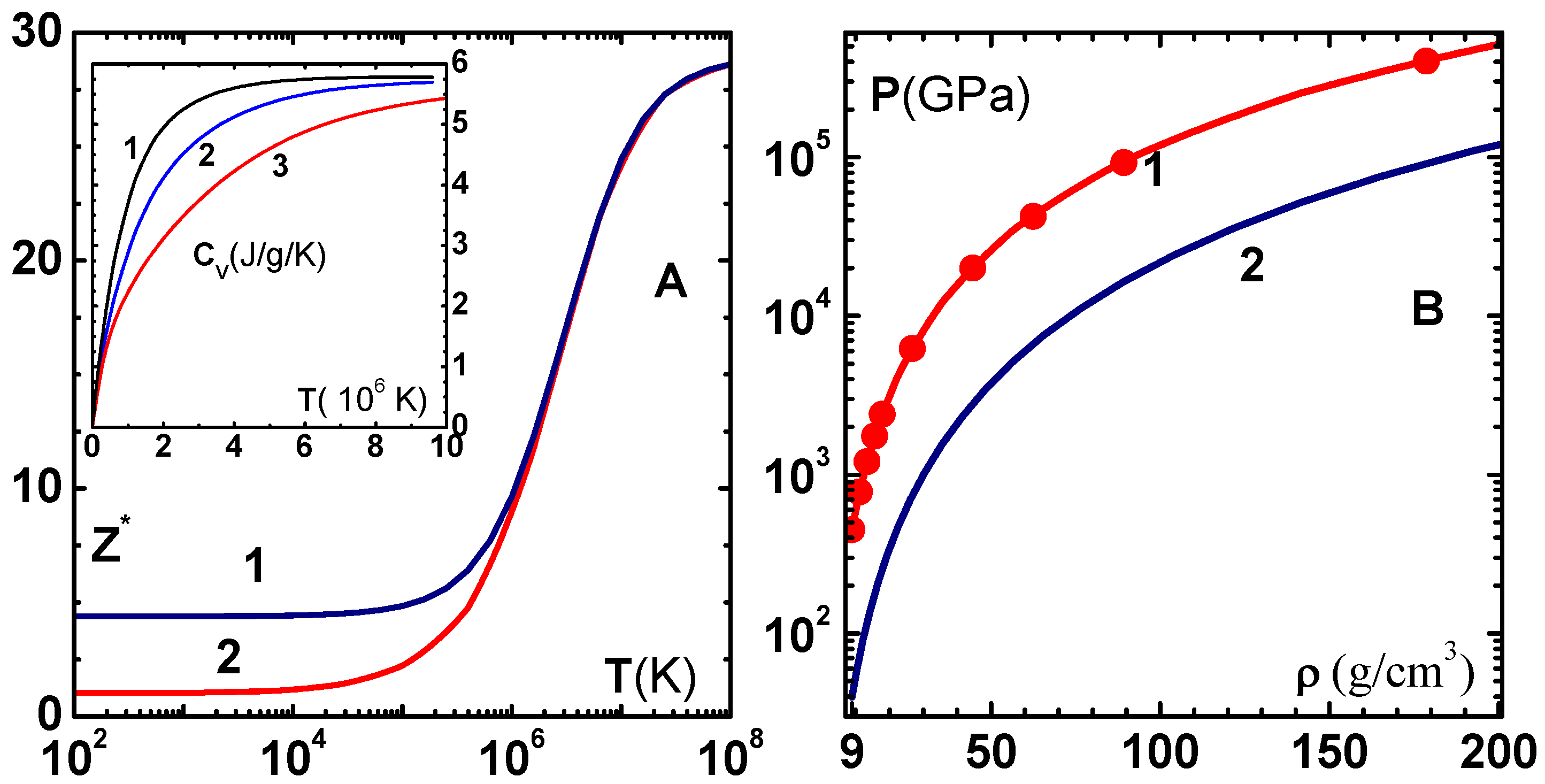
In this section, we discuss three more applications of the EOS model. The first is its application to the calculation of the shock Hugoniot. Extensive data available in the shock wave database [
40] is compared in
Figure 8A with predictions of the model (curve-1). We find excellent agreement throughout the range of pressures obtained in the experiments. In the insert figure, we have shown the results without correcting the zero-temperature isotherm (curve-2), and without adding electronic terms (curve-3). Correction to the zero-temperature isotherm is found to be quite important as the four-parameter isotherm is valid up to 100–150 GPa. Addition of the electron component is found to improve the prediction even for pressures in the range of 200 GPa. Contrary to the common feeling, pressure on the Hugoniot is decreased when electron contribution is added. This is because the electron degrees of freedom reduces temperature, and consequently the pressure, for a specified volume on the Hugoniot. Temperature along the Hugoniot (curve-1) and the melting temperature (curve-2) displayed in
Figure 8B show that melting occurs around 300 GPa pressure. Therefore, proper accounting of the melting transition is important even though the transition is not evident in the pressure–volume Hugoniot.
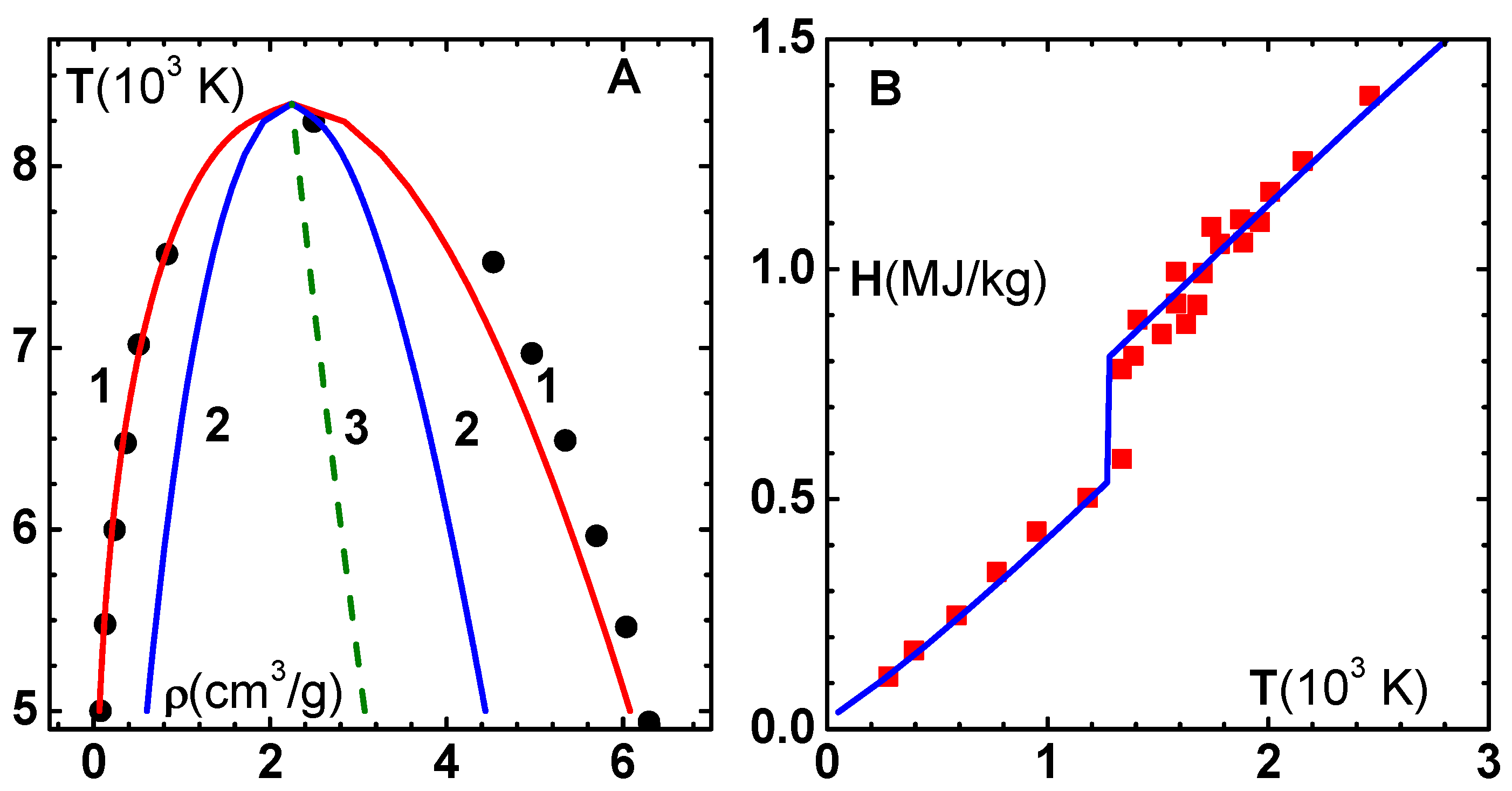
Next, we compare the liquid–vapor phase diagram of Cu employing the modified soft-sphere model, which was briefly considered in our earlier work [
29]. It is well known that the attractive and thermal components of energy finely balance to produce the van der Waals loops in the isotherms in the vapor–liquid co-existence region. The critical point parameters we have obtained, via Maxwell’s construction, (
g/cm
,
K, and
GPa) are very well within the range quoted in the literature [
41]. The phase diagram (curve-1) is shown in
Figure 9A, and compared with simulation data (filled circles) [
42]. These data were obtained via molecular dynamics simulations using an effective pair potential deduced from DFT calculations of energy–volume curve in the compressed and expanded volume regions. We find good comparison except in the liquid region of the phase diagram. The spinodal curve (curve-2), which is the locus of points where isothermal compressibility diverges; and the diameter (curve-3), which is the average of liquid and vapor phase densities on the phase diagram, are also shown in the figure.
In
Figure 9B, we have compared results of the EOS model for the enthalpy (H) of Cu versus temperature, along the 1-bar isobar, with experimental data taken from Trainor et al. [
43]. Starting from 50 K, the material expands from 0.1105 to 0.1268 (cm
/g), where it crosses the melting line around 1310 K. This results in a jump in enthalpy, and thereafter a smooth increase, as seen from the figure. The model for
employed in Johnson’s model is inappropriate in this volume region. Therefore, we have taken a constant value
, which is the experimental value at normal conditions, and corresponding expressions for
and
in lieu of Equations (
25) and (
26). Furthermore, we find that the heat of fusion to be added at the melting point is about 225 kJ/kg, in good agreement with the experimental value of 205 kJ/kg.
Finally, we mention that the EOS model described above (except the correction term for the zero-temperature isotherm and the free electron gas model) has been applied very successfully for the development and application of enthalpy-based approach to describe shock wave propagation in porous materials. There, we started with the computation of enthalpy-parameter, defined as
, and developed the method treating
P as independent variable. First, we showed [
5] (using analytical fits [
34] to results of TF theory) the correct approach to incorporate electronic effects explicitly. Then, we developed the modified soft-sphere model to properly evaluate the Hugoniot of highly porous materials, as their final shocked states are in the fluid region [
29]. In another development, we used the EOS to show that the enthalpy-based approach can be implemented [
44] in hydrodynamic simulations to describe shock wave propagation in solid as well as porous materials.
Applications of the EOS model to other materials can be easily carried out using the experimental/theoretical values of the parameters [
16,
33] employed in the different components of the model. A list of these parameters for Cu, Al, Fe, and W is given in our earlier publication [
44].
7. Summary
The main aim of this paper is to discuss the basic components of an EOS model for metals for high-pressure physics applications. Thus, we started with the division of the EOS in to three parts: Zero-temperature isotherm, thermal ionic component, and thermal electronic component. This division is convenient as there are theories of different levels of sophistication dealing with them. We mentioned that results of DFT-based electronic structure calculations can be suitably fitted into a functional form, as is done in the case of the four-parameter model. A method to correct this model—which is only valid in the lower pressure range, so as to approach the results of the quantum statistical model—was discussed. Similarly, in lieu of detailed lattice dynamic calculations for density of states of lattice vibration modes, we have used the simple Debye model with a suitable form for volume dependence of Debye temperature. However, we have stressed the need for incorporating the energy of fusion due to melting in the thermal ionic component. A model for this component, which incorporates continuous temperature dependence of constant volume-specific heat, was discussed. It is the valence electrons in the metal which contribute to the thermal electronic component, which we modeled using the results of the Fermi gas model. However, we have shown that the degree of ionization, and hence the free electron density, can be determined from the Thomas–Fermi model. A simple correction to get the experimental electron density at normal conditions was also discussed. Finally, for the purpose of demonstration, the model was applied to calculate the shock-Hugoniot, liquid-vapor phase diagram, and isobaric expansion of Cu. We hope that the model described here can be used to generate tables for hydrodynamic applications of impact experiments, shock wave studies, and above all, design and analysis of high-energy-density systems.