The Effect of Point Defects on the Electronic Density of States of ScMN2-Type (M = V, Nb, Ta) Phases
Abstract
1. Introduction
2. Computational Details
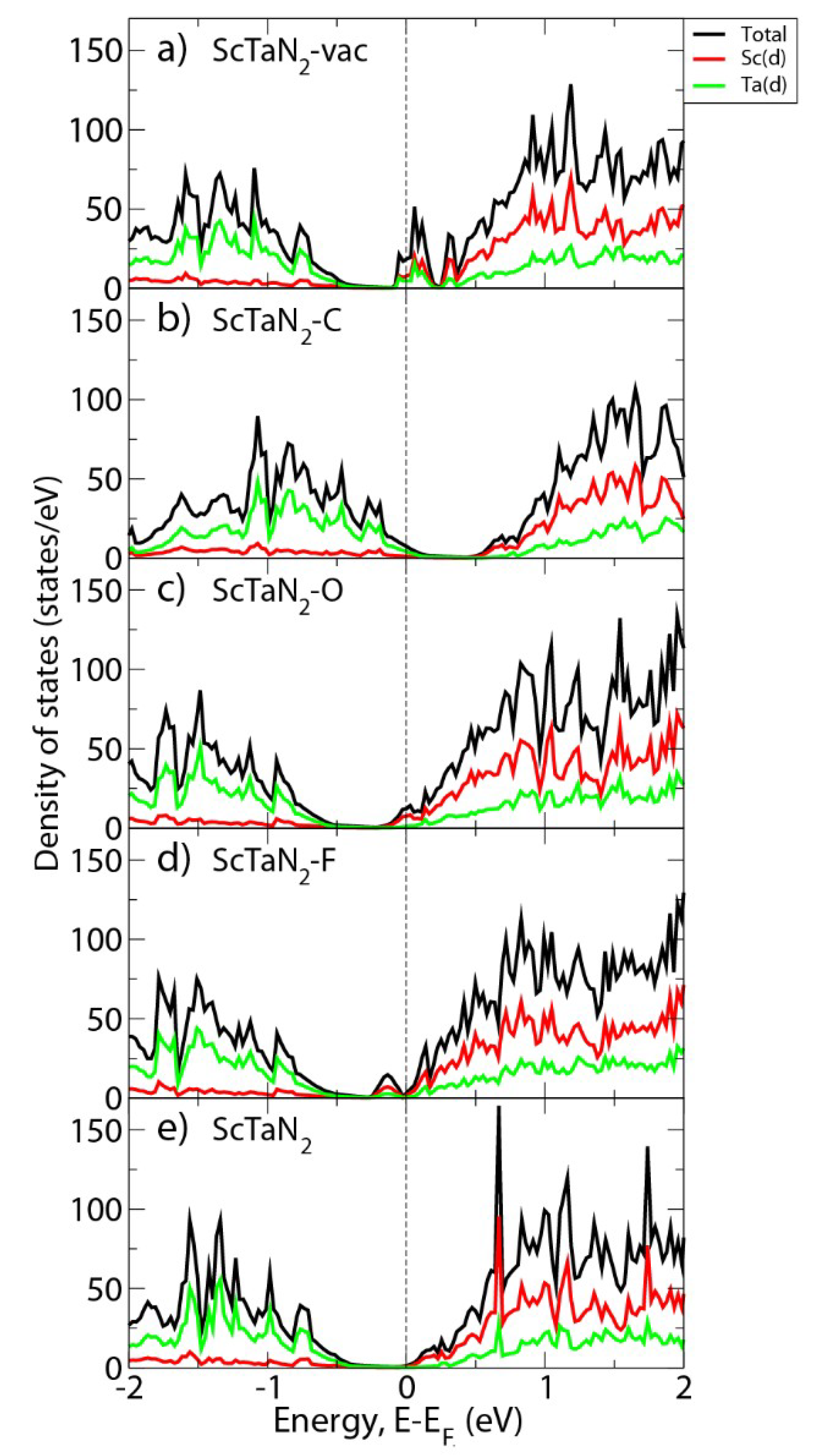
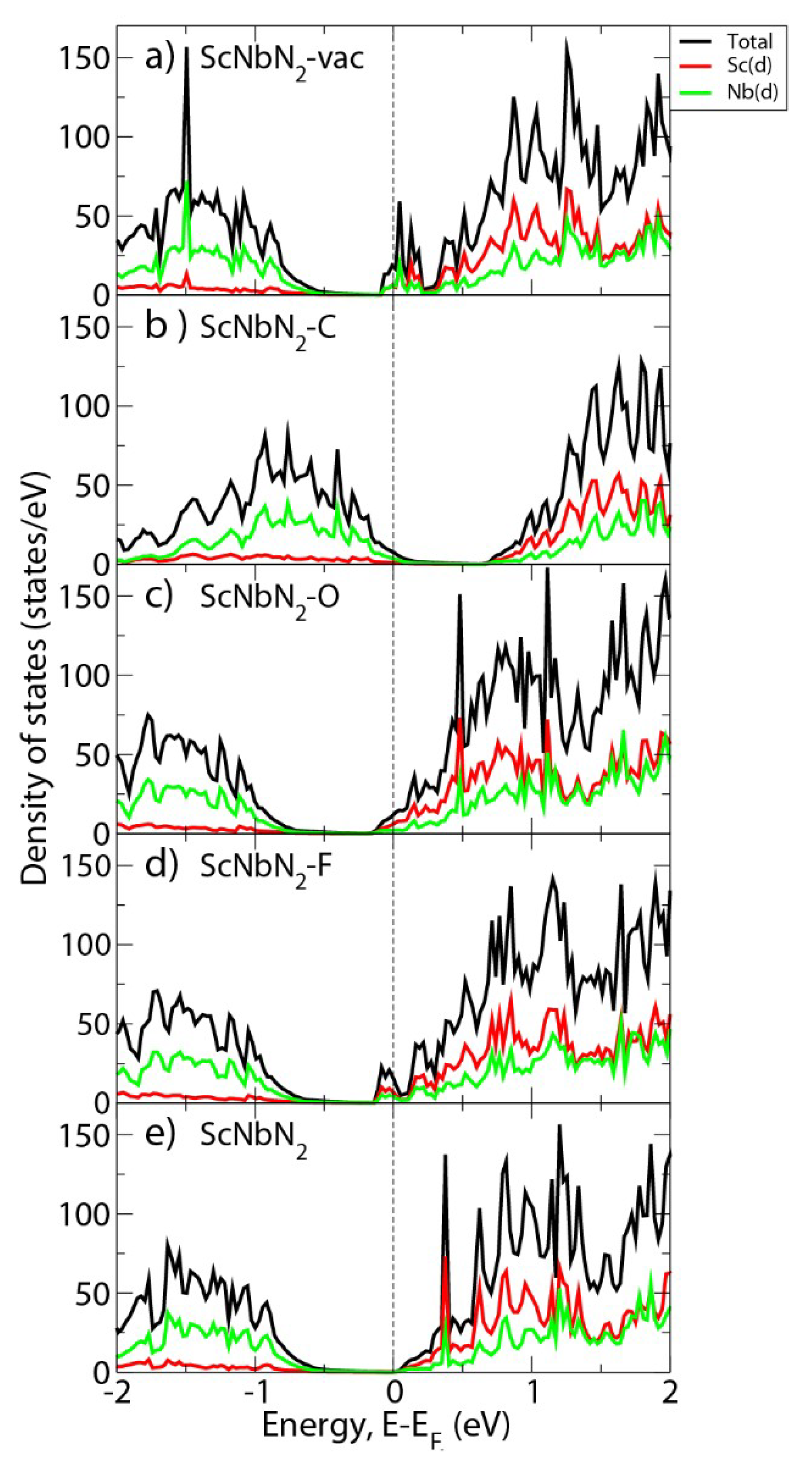
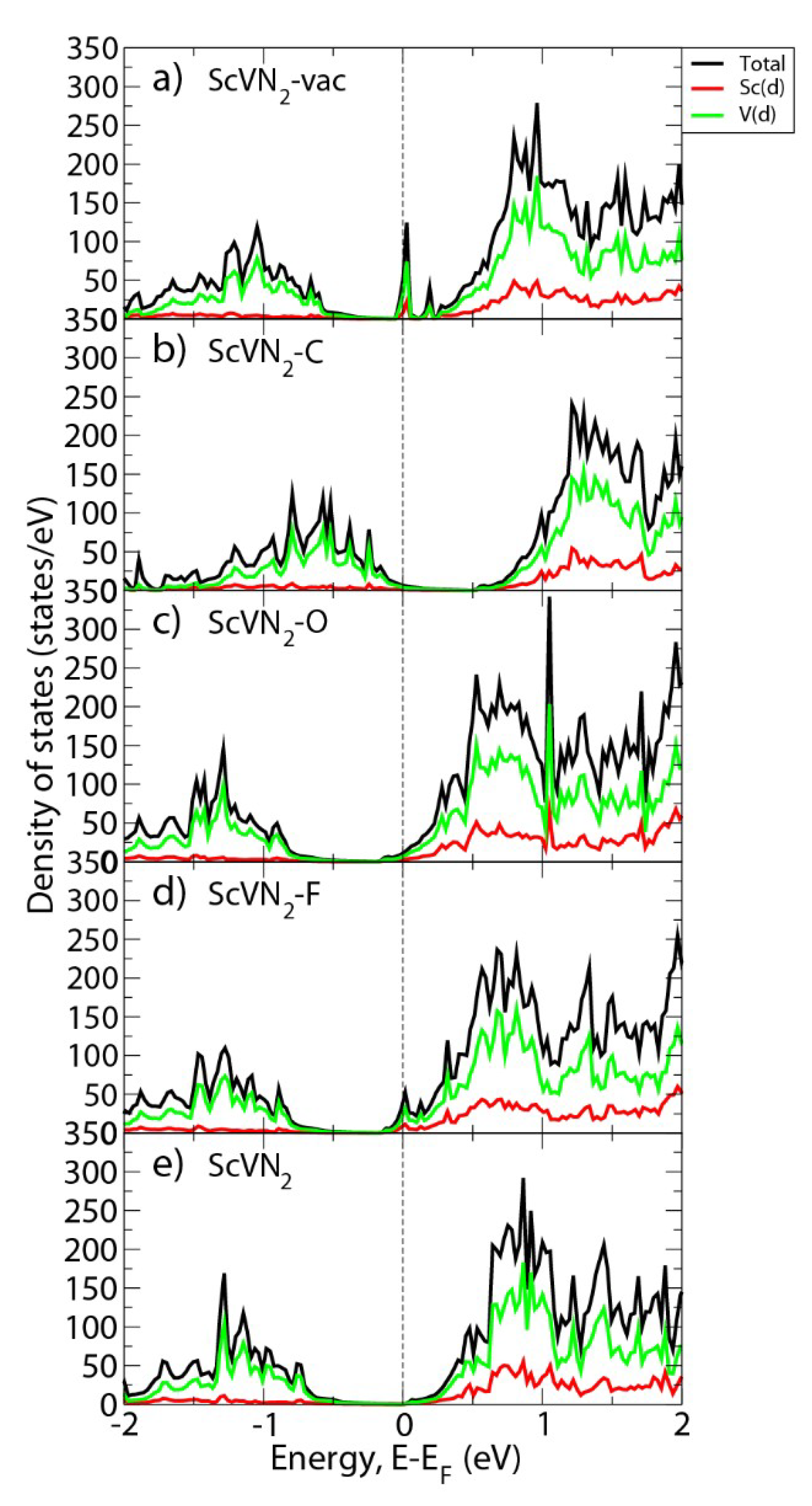
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, R.; Wang, Z.; Saito, M.; Shibata, N.; Ikuhara, Y. Atomistic mechanisms of nonstoichiometry-induced twin boundary structural transformation in titanium dioxide. Nat. Commun. 2015, 6, 7120. [Google Scholar] [CrossRef] [PubMed]
- Van de Walle, C.G.; Neugebauer, J. First-principles calculations for defects and impurities: Applications to III-nitrides. J. Appl. Phys. 2004, 95, 3851. [Google Scholar] [CrossRef]
- Wang, Z.; Saito, M.; McKenna, K.P.; Gu, L.; Tsukimoto, S.; Shluger, A.L.; Ikuhara, Y. Atom-resolved imaging of ordered defect superstructures at individual grain boundaries. Nature 2011, 479, 380–383. [Google Scholar] [CrossRef] [PubMed]
- Kerdsongpanya, S.; Alling, B.; Eklund, P. Effect of point defects on the electronic density of states of ScN studied by first-principles calculations and implications for thermoelectric properties. Phys. Rev. B 2012, 86, 195140. [Google Scholar] [CrossRef]
- Ma, D.; Ju, W.; Tang, Y.; Chen, Y. First-principles study of the small molecule adsorption on the InSe monolayer. Appl. Surf. Sci. 2017, 426, 244–252. [Google Scholar] [CrossRef]
- Wang, Z.; Tsukimoto, S.; Saito, M.; Ikuhara, Y. SiC/Ti3SiC2 interface: Atomic structure, energetics, and bonding. Phys. Rev. B 2009, 79, 045318. [Google Scholar] [CrossRef]
- Eklund, P.; Kerdsongpanya, S.; Alling, B. Transition-metal-nitride-based thin films as novel energy harvesting materials. J. Mater. Chem. C 2016, 4, 3905–3914. [Google Scholar] [CrossRef] [PubMed]
- Li, J.-F.; Liu, W.-S.; Zhao, L.-D.; Zhou, M. High-performance nanostructured thermoelectric materials. NPG Asia Mater. 2010, 2, 152–158. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Chen, G.; Tang, M.Y.; Yang, R.G.; Lee, H.; Wang, D.Z.; Ren, Z.F.; Fleurial, J.-P.; Gogna, P. New Directions for Low-Dimensional Thermoelectric Materials. Adv. Mater. 2007, 19, 1043–1053. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States. Science 2008, 321, 554–557. [Google Scholar] [CrossRef] [PubMed]
- Biswas, B.; Saha, B. Development of semiconducting ScN. Phys. Rev. Mater. 2019, 3, 020301. [Google Scholar] [CrossRef]
- Kerdsongpanya, S.; Alling, B.; Eklund, P. Phase stability of ScN-based solid solutions for thermoelectric applications from first-principles calculations. J. Appl. Phys. 2013, 114, 073512. [Google Scholar] [CrossRef]
- Kerdsongpanya, S.; Sun, B.; Eriksson, F.; Jensen, J.; Lu, J.; Koh, Y.K.; Nong, N.V.; Balke, B.; Alling, B.; Eklund, P. Experimental and theoretical investigation of Cr1−xScxN solid solutions for thermoelectrics. J. Appl. Phys. 2016, 120, 215103. [Google Scholar] [CrossRef]
- Saha, B.; Garbrecht, M.; Perez-Taborda, J.A.; Fawey, M.H.; Koh, Y.R.; Shakouri, A.; Martin-Gonzalez, M.; Hultman, L.; Sands, T.D. Compensation of native donor doping in ScN: Carrier concentration control and p-type ScN. Appl. Phys. Lett. 2017, 110, 252104. [Google Scholar] [CrossRef]
- Tureson, N.; Van Nong, N.; Fournier, D.; Singh, N.; Acharya, S.; Schmidt, S.; Belliard, L.; Soni, A.; Eklund, P. Reduction of the thermal conductivity of the thermoelectric material ScN by Nb alloying. J. Appl. Phys. 2017, 122, 025116. [Google Scholar] [CrossRef]
- Rawat, V.; Koh, Y.K.; Cahill, D.G.; Sands, T.D. Thermal conductivity of (Zr,W)N/ScN metal/semiconductor multilayers and superlattices. J. Appl. Phys. 2009, 105, 024909. [Google Scholar] [CrossRef]
- Saha, B.; Koh, Y.R.; Comparan, J.; Sadasivam, S.; Schroeder, J.L.; Garbrecht, M.; Mohammed, A.; Birch, J.; Fisher, T.; Shakouri, A.; et al. Cross-plane thermal conductivity of (Ti,W)N/(Al,Sc)N metal/semiconductor superlattices. Phys. Rev. B. 2016, 93, 45311. [Google Scholar] [CrossRef]
- Schroeder, J.L.; Saha, B.; Garbrecht, M.; Schell, N.; Sands, T.D.; Birch, J. Thermal stability of epitaxial cubic-TiN/(Al,Sc)N metal/semiconductor superlattices. J. Mater. Sci. 2015, 50, 3200–3206. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Bian, Z.; Singh, R.; Shakouri, A.; Wortman, R.; Rawat, V.; Sands, T. Thermoelectric Transport in a ZrN/ScN Superlattice. J. Electron. Mater. 2009, 38, 960–963. [Google Scholar] [CrossRef]
- Gharavi, M.A.; Kerdsongpanya, S.; Schmidt, S.; Eriksson, F.; Nong, N.V.; Lu, J.; Balke, B.; Fournier, D.; Belliard, L.; le Febvrier, A.; et al. Microstructure and thermoelectric properties of CrN and CrN/Cr2N thin films. J. Phys. D 2018, 51, 355302. [Google Scholar] [CrossRef]
- Saha, B.; Perez-Taborda, J.A.; Bahk, J.-H.; Koh, Y.R.; Shakouri, A.; Martin-Gonzalez, M.; Sands, T.D. Temperature-dependent thermal and thermoelectric properties of n-type and p-type Sc1−xMgxN. Phys. Rev. B 2018, 97, 085301. [Google Scholar] [CrossRef]
- Pilemalm, R.; Pourovskii, L.; Mosyagin, I.; Simak, S.; Eklund, P. Thermodynamic Stability, Thermoelectric, Elastic and Electronic Structure Properties of ScMN2-Type (M = V, Nb, Ta) Phases Studied by ab initio Calculations. Condens. Matter 2019, 4, 36. [Google Scholar] [CrossRef]
- Lengauer, W. The crystal structure of ScNbN1−x and comparisons with related nitride and carbide structures. J. Solid State Chem. 1989, 82, 186–191. [Google Scholar] [CrossRef]
- Lengauer, W.; Ettmayer, P. The Crystal Structure of ScTaN1−x. J. Less Common Met. 1988, 141, 157–162. [Google Scholar] [CrossRef]
- Burmistrova, P.V.; Maassen, J.; Favaloro, T.; Saha, B.; Salamat, S.; Rui Koh, Y.; Lundstrom, M.S.; Shakouri, A.; Sands, T.D. Thermoelectric properties of epitaxial ScN films deposited by reactive magnetron sputtering onto MgO(001) substrates. J. Appl. Phys. 2013, 113, 153704. [Google Scholar] [CrossRef]
- Burmistrova, P.V.; Zakharov, D.N.; Favaloro, T.; Mohammed, A.; Stach, E.A.; Shakouri, A.; Sands, T.D. Effect of deposition pressure on the microstructure and thermoelectric properties of epitaxial ScN(001) thin films sputtered onto MgO(001) substrates. J. Mater. Res. 2015, 30, 626–634. [Google Scholar] [CrossRef]
- Le Febvrier, A.; Tureson, N.; Stilkerich, N.; Greczynski, G.; Eklund, P. Effect of impurities on morphology, growth mode, and thermoelectricproperties of (1 1 1) and (0 0 1) epitaxial-like ScN films. J. Phys. D Appl. Phys. 2019, 52, 035302. [Google Scholar] [CrossRef]
- Niewa, R.; Zherebtsov, D.A.; Schnelle, W.; Wagner, F.R. Metal−Metal Bonding in ScTaN2. A New Compound in the System ScN−TaN. Inorg. Chem. 2004, 43, 6188–6194. [Google Scholar] [CrossRef]
- Barsoum, M.W. The MN+1AXN phases: A new class of solids; thermodynamically stable nanolaminates. Prog. Solid State Chem. 2000, 28, 201–281. [Google Scholar] [CrossRef]
- Barsoum, M.W. The MAX phases: Unique new carbide and nitride materials. Am. Sci. 2001, 89, 334. [Google Scholar] [CrossRef]
- Eklund, P.; Beckers, M.; Jansson, U.; Högberg, H.; Hultman, L. The Mn + 1AXn phases: Materials science and thin-film processing. Thin Solid Films 2010, 518, 1851–1878. [Google Scholar] [CrossRef]
- Kresse, G.; Furtmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furtmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B Condens. Matter Mater. Phys. 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 49, 14251–14269. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, F.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223. [Google Scholar] [CrossRef]
- Bagayoko, D. Understanding density functional theory (DFT) and completing it in practice. AIP Adv. 2014, 4, 127104. [Google Scholar] [CrossRef]
- Mahan, G.D.; Sofo, J.O. The best thermoelectric. Proc. Natl. Acad. Sci. USA 1996, 93, 7436–7439. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Wang, H.-Q.; Zheng, J.-C. Searching for the best thermoelectrics through the optimization of transport distribution function. J. Appl. Phys. 2011, 109, 073713. [Google Scholar] [CrossRef]
- Tureson, N.; Marteau, M.; Cabioch, T.; Van Nong, N.; Jensen, J.; Lu, J.; Greczynski, G.; Fournier, D.; Singh, N.; Soni, A.; et al. Effect of ion-implantation-induced defects and Mg dopants on the thermoelectric properties of ScN. Phys. Rev. B 2018, 98, 205307. [Google Scholar] [CrossRef]
| M in ScMN2 | Ef(vac) of ScMN2 (eV) | Ef(C) of ScMN2 (eV) | Ef(O) of ScMN2 (eV) | Ef(F) of ScMN2 (eV) |
|---|---|---|---|---|
| Ta | 1.91 | 1.67 | −1.04 | 1.13 |
| Nb | 2.96 | 1.82 | −1.21 | 0.79 |
| V | 2.14 | 1.86 | −1.48 | −0.06 |
| Parameter | |
|---|---|
| a (Å) | 3.1805 |
| b (Å) | 3.1805 |
| c (Å) | 11.1095 |
| α | 90.0° |
| β | 90.0° |
| γ | 119.4° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilemalm, R.; Simak, S.; Eklund, P. The Effect of Point Defects on the Electronic Density of States of ScMN2-Type (M = V, Nb, Ta) Phases. Condens. Matter 2019, 4, 70. https://doi.org/10.3390/condmat4030070
Pilemalm R, Simak S, Eklund P. The Effect of Point Defects on the Electronic Density of States of ScMN2-Type (M = V, Nb, Ta) Phases. Condensed Matter. 2019; 4(3):70. https://doi.org/10.3390/condmat4030070
Chicago/Turabian StylePilemalm, Robert, Sergei Simak, and Per Eklund. 2019. "The Effect of Point Defects on the Electronic Density of States of ScMN2-Type (M = V, Nb, Ta) Phases" Condensed Matter 4, no. 3: 70. https://doi.org/10.3390/condmat4030070
APA StylePilemalm, R., Simak, S., & Eklund, P. (2019). The Effect of Point Defects on the Electronic Density of States of ScMN2-Type (M = V, Nb, Ta) Phases. Condensed Matter, 4(3), 70. https://doi.org/10.3390/condmat4030070





