Q Dependence of Magnetic Resonance Mode on FeTe0.5Se0.5 Studied by Inelastic Neutron Scattering
Abstract
1. Introduction
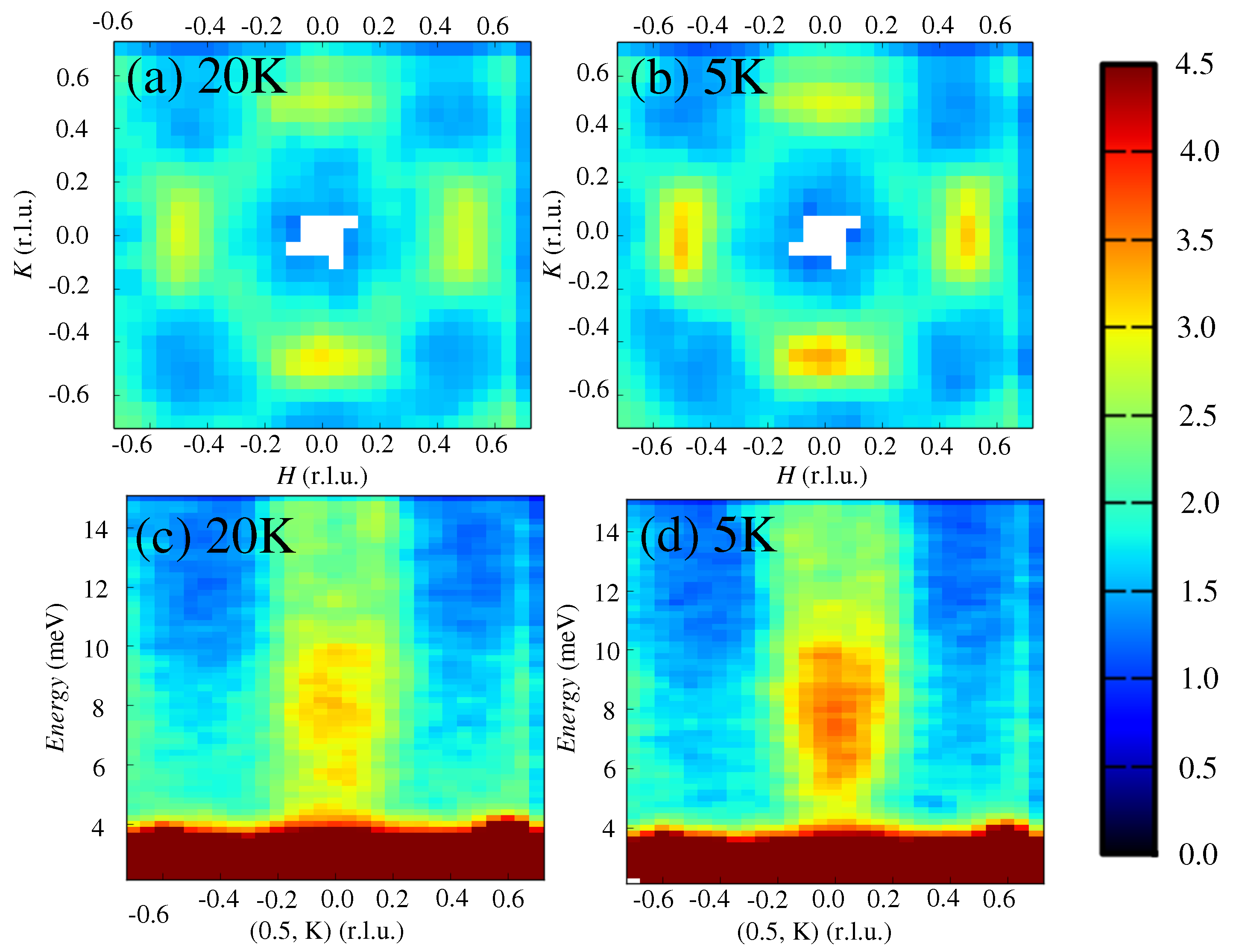
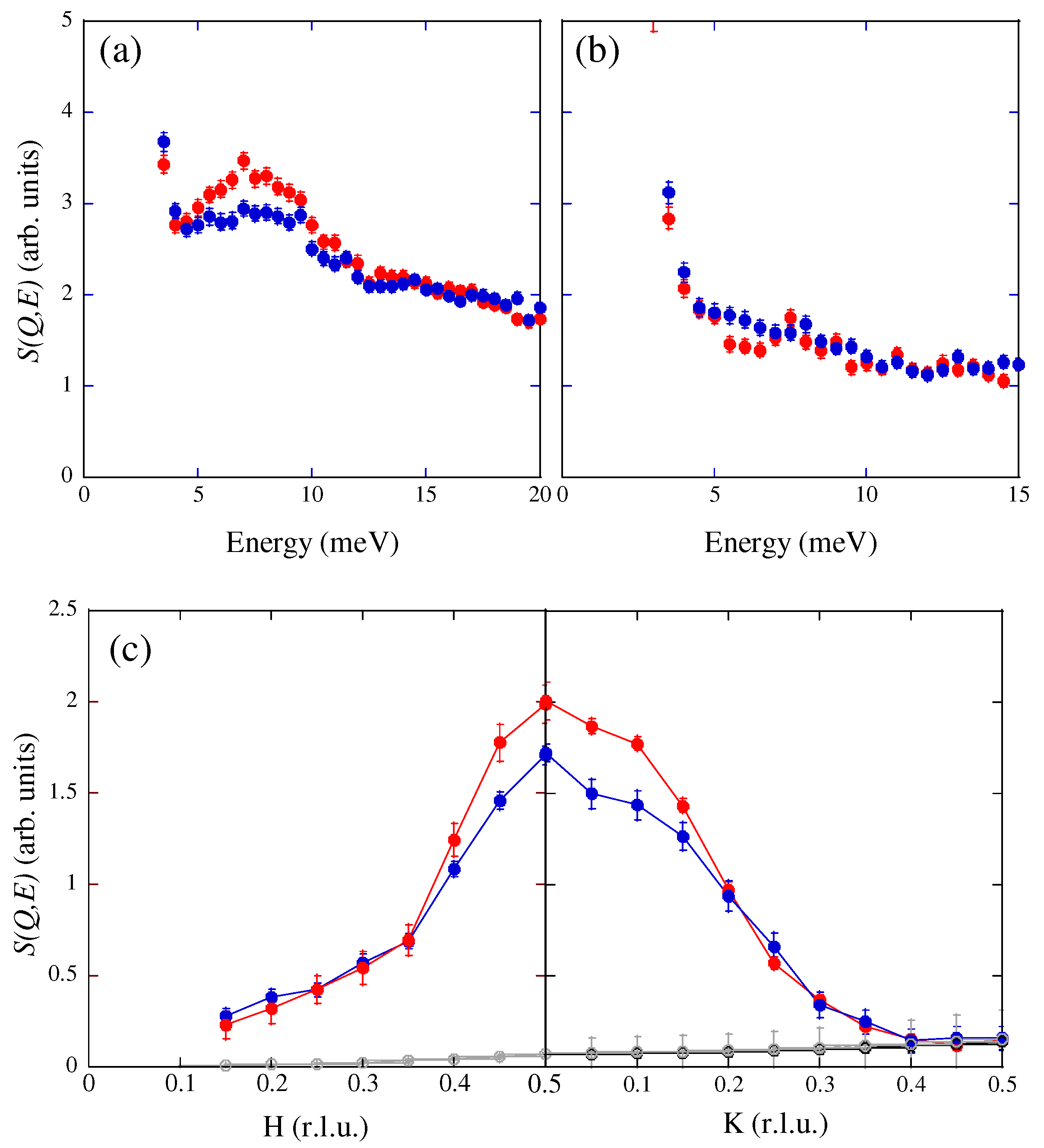
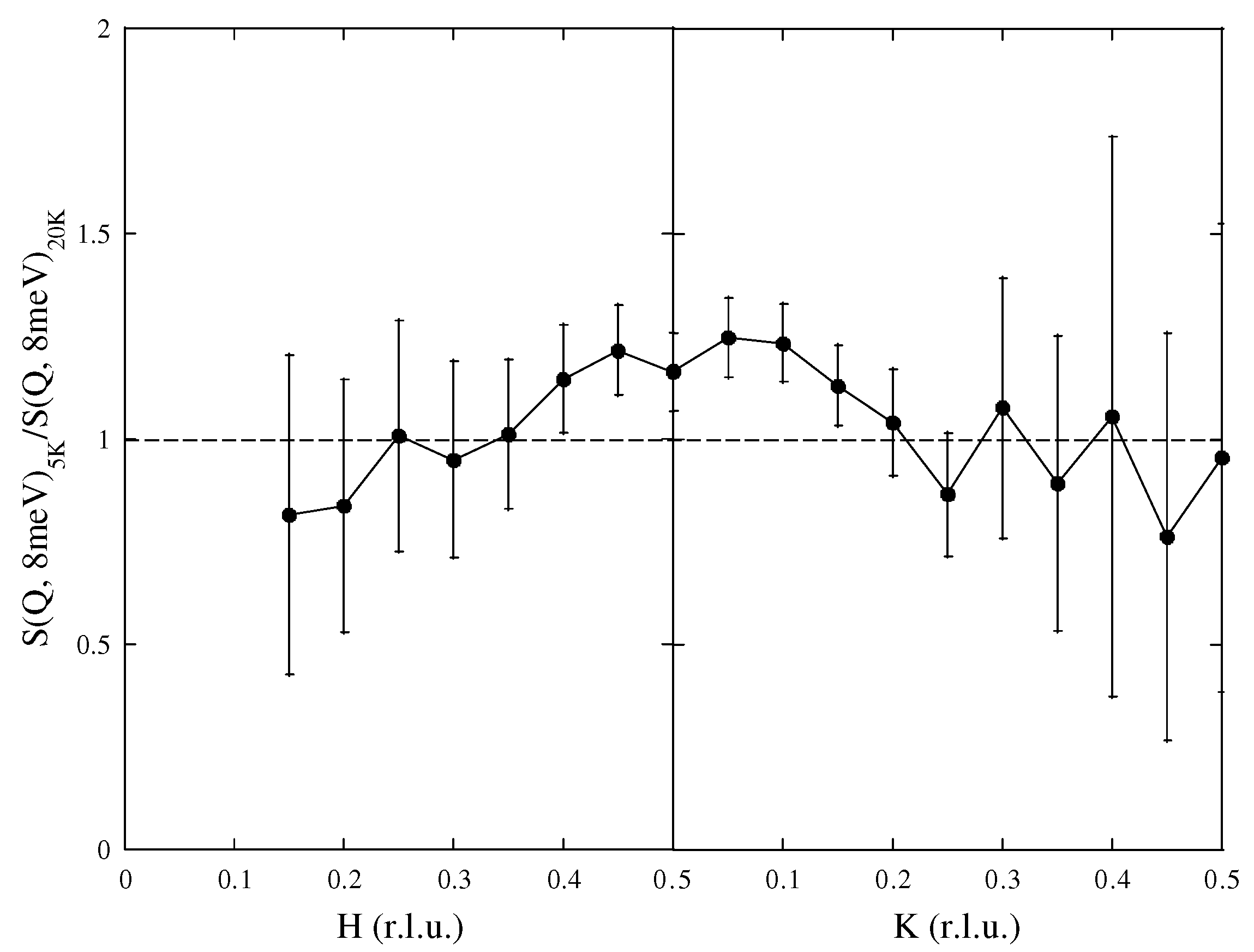
2. Experimental Results
3. Discussion
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-Based Layered Superconductor La[O1-xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef] [PubMed]
- Chubukov, A.V.; Efremov, D.V.; Eremin, I. Magnetism, superconductivity, and pairing symmetry in iron-based superconductors. Phys. Rev. B 2008, 78, 134512. [Google Scholar] [CrossRef]
- Boeri, L.; Dolgov, O.V.; Golubov, A.A. Is LaO1-xFxFeAs an electron-phonon superconductor? Phys. Rev. Lett. 2008, 101, 026403. [Google Scholar] [CrossRef] [PubMed]
- Mazin, I.I.; Singh, D.J.; Johannes, M.D.; Du, M.H. Unconventional Superconductivity with a Sign Reversal in the Order Parameter of LaFeAsO1-xFx. Phys. Rev. Lett. 2008, 101, 057003. [Google Scholar] [CrossRef] [PubMed]
- Kuroki, K.; Usui, H.; Onari, S.; Arita, R.; Aoki, H. Unconventional Pairing Originating from the Disconnected Fermi Surfaces of Superconducting LaFeAsO1-xFx. Phys. Rev. B 2008, 79, 224511. [Google Scholar] [CrossRef]
- Kontani, H.; Onari, S. Orbital-Fluctuation-Mediated Superconductivity in Iron Pnictides: Analysis of the Five-Orbital Hubbard-Holstein Model. Phys. Rev. Lett. 2010, 104, 157001. [Google Scholar] [CrossRef] [PubMed]
- Yanagi, Y.; Yamakawa, Y.; Ono, Y. Two types of s-wave pairing due to magnetic and orbital fluctuations in the two-dimensional 16-band d-p model for iron-based superconductors. Phys. Rev. B 2010, 81, 054518. [Google Scholar] [CrossRef]
- Onari, S.; Kontani, H.; Sato, M. Structure of neutron-scattering peaks in both s++-wave and s±-wave states of an iron pnictide superconductor. Phys. Rev. B 2010, 81, 060504(R). [Google Scholar] [CrossRef]
- Innocenti, D.; Valletta, A.; Bianconi, A. Shape resonance at a Lifshitz transition for high temperature superconductivity in multiband superconductors. J. Supercond. Novel Magn. 2011, 24, 1137–1143. [Google Scholar] [CrossRef]
- Bianconi, A. Shape resonances in multi-condensate granular superconductors formed by networks of nanoscale-striped puddles. J. Phys. Conf. Ser. 2013, 449, 012002. [Google Scholar] [CrossRef]
- Hanaguri, T.; Niitaka, S.; Kuroki, K.; Takagi, H. Unconventional s-wave superconductivity in Fe(Se,Te). Science 2010, 328, 474–476. [Google Scholar] [CrossRef] [PubMed]
- Sato, M.; Kobayashi, Y.; Lee, S.C.; Takahashi, H.; Satomi, E.; Miura, Y. Studies on Effects of Impurity Doping and NMR Measurements of La 1111 and/or Nd 1111 Fe-Pnictide Superconductors. J. Phys. Soc. Jpn. 2010, 79, 014710. [Google Scholar] [CrossRef]
- Wang, Q.; Park, J.T.; Feng, Y.; Shen, Y.; Hao, Y.; Pan, B.; Lynn, J.W.; Ivanov, A.; Chi, S.; Matsuda, M.; et al. Transition from Sign-Reversed to Sign-Preserved Cooper-Pairing Symmetry in Sulfur-Doped Iron Selenide Superconductors. Phys. Rev. Lett. 2016, 116, 197004. [Google Scholar] [CrossRef] [PubMed]
- Christianson, A.D.; Goremychkin, E.A.; Osborn, R.; Rosenkranz, S.; Lumsden, M.D.; Malliakas, C.D.; Todorov, I.S.; Claus, H.; Chung, D.Y.; Kanatzidis, M.G.; et al. Unconventional superconductivity in Ba0.6K0.4Fe2As2 from inelastic neutron scattering. Nature 2008, 456, 930–932. [Google Scholar] [CrossRef] [PubMed]
- Lumsden, M.D.; Christianson, A.D.; Parshall, D.; Stone, M.B.; Nagler, S.E.; MacDougall, G.J.; Mook, H.A.; Lokshin, K.; Egami, T.; Abernathy, D.L.; et al. Two-dimensional resonant magnetic excitation in BaFe1.84Co0.16As2. Phys. Rev. Lett. 2009, 102, 107005. [Google Scholar] [CrossRef] [PubMed]
- Chi, S.; Schneidewind, A.; Zhao, J.; Harriger, L.W.; Li, L.; Luo, Y.; Cao, G.; Xu, Z.; Loewenhaupt, M.; Hu, J.; et al. Inelastic Neutron-Scattering Measurements of a Three-Dimensional Spin Resonance in the FeAs-Based BaFe1.9Ni0.1As2 Superconductor. Phys. Rev. Lett. 2009, 102, 107006. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Chen, Y.; Chang, S.; Lynn, J.W.; Li, L.; Luo, Y.; Cao, G.; Xu, Z.; Dai, P. Spin gap and magnetic resonance in superconducting BaFe1.9Ni0.1As2. Phys. Rev. B 2009, 79, 174527. [Google Scholar] [CrossRef]
- Shamoto, S.; Ishikado, M.; Christianson, A.D.; Lumsden, M.D.; Wakimoto, S.; Kodama, K.; Iyo, A.; Arai, M. Inelastic neutron scattering study of the resonance mode in the optimally doped pnictide superconductor LaFeAsO0.92F0.08. Phys. Rev. B 2010, 82, 172508. [Google Scholar] [CrossRef]
- Onari, S.; Kontani, H. Neutron inelastic scattering peak by dissipationless mechanism in the s++-wave state in iron-based superconductors. Phys. Rev. B 2011, 84, 144518. [Google Scholar] [CrossRef]
- Korshunov, M.M.; Eremin, I. Theory of magnetic excitations in iron-based layered superconductors. Phys. Rev. B 2008, 78, 140509(R). [Google Scholar] [CrossRef]
- Okazaki, K.; Ito, Y.; Ota, Y.; Kotani, Y.; Shimojima, T.; Kiss, T.; Watanabe, S.; Chen, C.-T.; Niitaka, S.; Hanaguri, T.; et al. Evidence for a cos(4ϕ) Modulation of the Superconducting Energy Gap of Optimally Doped FeTe0:6Se0:4 Single Crystals Using Laser Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 2012, 109, 237011. [Google Scholar] [CrossRef] [PubMed]
- Hanaguri, T.; Iwaya, K.; Kohsaka, Y.; Machida, T.; Watashige, T.; Kasahara, S.; Shibauchi, T.; Matsuda, Y. Two distinct superconducting pairing states divided by the nematic end point in FeSe1−xSx. Sci. Adv. 2018, 4, eaar6419. [Google Scholar] [CrossRef] [PubMed]
- Nagai, Y.; Kuroki, K. Determination of the pairing state in iron-based superconductors through neutron scattering. Phys. Rev. B 2011, 83, 220516(R). [Google Scholar] [CrossRef]
- Nagai, Y.; Kuroki, K. Q-scan analysis of the neutron scattering in iron-based superconductors. Phys. Rev. B 2012, 85, 134521. [Google Scholar] [CrossRef]
- Lumsden, M.D.; Christianson, A.D.; Goremychkin, E.A.; Nagler, S.E.; Mook, H.A.; Stone, M.B.; Abernathy, D.L.; Guidi, T.; MacDougall, G.J.; de la Cruz, C.; et al. Evolution of spin excitations into the superconducting state in FeTe1−xSex. Nat. Phys. 2010, 6, 182–186. [Google Scholar] [CrossRef]
- Lumsden, M.D.; Christianson, A.D. Magnetism in Fe-based superconductors. J. Phys. Condens. Matter 2010, 22, 203203. [Google Scholar] [CrossRef]
- Friemel, G.; Park, J.T.; Maier, T.A.; Tsurkan, V.; Li, Y.; Deisenhofer, J.; Krug von Nidda, H.-A.; Loidl, A.; Ivanov, A.; Keimer, B.; et al. Reciprocal-space structure and dispersion of the magnetic resonant mode in the superconducting phase of RbxFe2−ySe2 single crystals. Phys. Rev. B 2012, 85, 140511(R). [Google Scholar] [CrossRef]
- Zhang, C.; Wang, M.; Luo, H.; Wang, M.; Liu, M.; Zhao, J.; Abernathy, D.L.; Maier, T.A.; Marty, K.; Lumsdenm, M.D.; et al. Neutron Scattering Studies of spin excitations in hole-doped Ba0.67K0.33Fe2As2 superconductor. Sci. Rep. 2011, 1, 115. [Google Scholar] [CrossRef]
- Inosov, D.S.; Park, J.T.; Bourges, P.; Sun, D.L.; Sidis, Y.; Schneidewind, A.; Hradil, K.D.; Lin, C.T.; Keimer, B.; Hinkov, V. Normal-state spin dynamics and temperature-dependent spin-resonance energy in optimally doped BaFe1.85Co0.15As2. Nat. Phys. 2010, 6, 178. [Google Scholar] [CrossRef]
- Qiu, Y.; Bao, W.; Zhao, Y.; Broholm, C.; Stanev, V.; Tesanovic, Z.; Gasparovic, Y.C.; Chang, S.; Hu, J.; Qian, B.; et al. Spin Gap and Resonance at the NestingWave Vector in Superconducting FeSe0.4Te0.6. Phys. Rev. Lett. 2009, 103, 067008. [Google Scholar] [CrossRef]
- Zhang, C.; Li, H.-F.; Song, Y.; Su, Y.; Tan, G.; Netherton, T.; Redding, C.; Carr, S.V.; Sobolev, O.; Schneidewind, A.; et al. Distinguishing s± and s++ electron pairing symmetries by neutron spin resonance in superconducting NaFe0.935Co0.045As. Phys. Rev. B 2013, 88, 064504. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Richard, P.; Nakayama, K.; Chen, G.-F.; Dong, S.; He, J.-B.; Wang, D.-M.; Xia, T.-L.; Umezawa, K.; Kawahara, T.; et al. Unconventional superconducting gap in NaFe0.95Co0.05As observed by angle-resolved photoemission spectroscopy. Phys. Rev. B 2011, 84, 064519. [Google Scholar] [CrossRef]
- Thirupathaiah, S.; Evtushinsky, D.V.; Maletz, J.; Zabolotnyy, V.B.; Kordyuk, A.A.; Kim, T.K.; Wurmehl, S.; Roslova, M.; Morozov, I.; Büchner, B.; et al. Weak-coupling superconductivity in electron-doped NaFe0.95Co0.05As revealed by ARPES. Phys. Rev. B 2012, 86, 214508. [Google Scholar] [CrossRef]
- Miao, H.; Richard, P.; Tanaka, Y.; Nakayama, K.; Qian, T.; Umezawa, K.; Sato, T.; Xu, Y.-M.; Shi, Y.B.; Xu, N.; et al. Isotropic superconducting gaps with enhanced pairing on electron Fermi surfaces in FeTe0.55Se0.45. Phys. Rev. B 2012, 85, 094506. [Google Scholar] [CrossRef]
- Hu, J.; Liu, T.J.; Qian, B.; Rotaru, A.; Spinu, L.; Mao, Z.Q. Calorimetric evidence of strong-coupling multiband superconductivity in Fe(Te0.57Se0.43) single crystal. Phys. Rev. B 2011, 83, 134521. [Google Scholar] [CrossRef]
- Bianconi, A. Quantum materials: Shape resonances in superstripes. Nat. Phys. 2013, 9, 536. [Google Scholar] [CrossRef]
- Caivano, R.; Fratini, M.; Poccia, N.; Ricci, A.; Puri, A.; Ren, Z.A.; Dong, X.-L.; Yang, J.; Lu, W.; Zhao, Z.-X.; et al. Feshbach resonance and mesoscopic phase separation neara quantum critical point in multiband FeAs-based superconductors. Supercond. Sci. Technol. 2008, 22, 014004. [Google Scholar] [CrossRef]
- Zhang, P.; Yaji, K.; Hashimoto, T.; Ota, Y.; Kondo, T.; Okazaki, K.; Wang, Z.; Wen, J.; Gu, G.D.; Ding, H.; et al. Observation of topological superconductivity on the surface of an iron-based superconductor. Science 2018, 360, 182–186. [Google Scholar] [CrossRef]
- Kajimoto, R.; Nakamura, M.; Inamura, Y.; Mizuno, F.; Nakajima, K.; Ohira-Kawamura, S.; Yokoo, T.; Nakatani, T.; Maruyama, R.; Soyama, K.; et al. The Fermi Chopper Spectrometer 4SEASONS at J-PARC. J. Phys. Soc. Jpn. 2011, 80, SB025. [Google Scholar] [CrossRef]
- Nakamura, M.; Kajimoto, R.; Inamura, Y.; Mizuno, F.; Fujita, M.; Yokoo, T.; Arai, M. First Demonstration of Novel Method for Inelastic Neutron Scattering Measurement Utilizing Multiple Incident Energies. J. Phys. Soc. Jpn. 2009, 78, 093002. [Google Scholar] [CrossRef]
- Inamura, Y.; Nakatani, T.; Suzuki, J.; Otomo, T. Development Status of Software “Utsusemi” for Chopper Spectrometers at MLF, J-PARC. J. Phys. Soc. Jpn. 2013, 82, SA031. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishikado, M.; Kodama, K.; Kajimoto, R.; Nakamura, M.; Inamura, Y.; Ikeuchi, K.; Ji, S.; Arai, M.; Shamoto, S.-i. Q Dependence of Magnetic Resonance Mode on FeTe0.5Se0.5 Studied by Inelastic Neutron Scattering. Condens. Matter 2019, 4, 69. https://doi.org/10.3390/condmat4030069
Ishikado M, Kodama K, Kajimoto R, Nakamura M, Inamura Y, Ikeuchi K, Ji S, Arai M, Shamoto S-i. Q Dependence of Magnetic Resonance Mode on FeTe0.5Se0.5 Studied by Inelastic Neutron Scattering. Condensed Matter. 2019; 4(3):69. https://doi.org/10.3390/condmat4030069
Chicago/Turabian StyleIshikado, Motoyuki, Katsuaki Kodama, Ryoichi Kajimoto, Mitsutaka Nakamura, Yasuhiro Inamura, Kazuhiko Ikeuchi, Sungdae Ji, Masatoshi Arai, and Shin-ichi Shamoto. 2019. "Q Dependence of Magnetic Resonance Mode on FeTe0.5Se0.5 Studied by Inelastic Neutron Scattering" Condensed Matter 4, no. 3: 69. https://doi.org/10.3390/condmat4030069
APA StyleIshikado, M., Kodama, K., Kajimoto, R., Nakamura, M., Inamura, Y., Ikeuchi, K., Ji, S., Arai, M., & Shamoto, S.-i. (2019). Q Dependence of Magnetic Resonance Mode on FeTe0.5Se0.5 Studied by Inelastic Neutron Scattering. Condensed Matter, 4(3), 69. https://doi.org/10.3390/condmat4030069




