Abstract
The stability of cubic HfV2 was investigated as a function of temperature as well as interstitially solved oxygen and hydrogen using density functional theory. Mechanical and energetic instability of pristine cubic HfV2 is obtained in the ground state at 0 K, which is unexpected as it can readily be synthesized. Combined Debye–Grüneisen and electronic entropy calculations indicate that HfV2 is stabilized with increasing temperature primarily as a result of lattice vibrations. In contrast, temperature-induced mechanical stabilization, considering the Born stability criteria, is achieved due to the electronic entropy. Interstitial incorporation of hydrogen and oxygen into the cubic structure contributes to the energetic and mechanical stabilization in the ground state for impurity concentrations as low as 1 at%, owing to strong ionic/covalent bond formation with the matrix atoms.
1. Introduction
HfV2 exhibits an exceptional combination of properties including superconductivity [1,2,3,4], low temperature structural transformations [4,5,6], high hydrogen storage capacity [7,8,9,10] and anomalous elasticity, namely increasing elastic moduli with temperature [1,11,12]. Thus, HfV2 has gained a lot of attention in the literature. The structural stability, thermoelastic anomaly and superconductive properties are closely related to the peculiar electronic structure of HfV2, exhibiting a high density of states at the Fermi level [6,13,14,15,16].
Experimentally, the cubic C15 Laves structure is found to be the stable phase from around 112 K up to the melting point of around 1820 K [1,17]. Upon cooling, a sequence of phase transitions from the cubic to tetragonal and to orthorhombic structure is observed within the narrow temperature range of 112 to 102 K [5]. Hereby, the low temperature structure of HfV2 is often described as a phase mixture consisting of an orthorhombic and an untransformed cubic part [4,5].
In addition to the pronounced effect of temperature on the stability of cubic C15 HfV2, real intermetallic compounds may exhibit H and O impurities due to their availability in atmosphere, and hence, presence in most production processes, in combination with the high hydrogen storage capacity of HfV2 [7,8,9,10] and the affinity for oxygen of the elemental constituents [18,19,20,21]. Indeed, intermetallic HfV2 was found to dissociate H2O at ambient temperatures and subsequently absorb the atomic constituents [22]. In general, point defects may lead to structural stabilization as found for cubic VN, which is stabilized by vacancies [23], as well as for cubic ZrO2, which can be stabilized by impurities [24].
Numerous first-principle calculations have been performed to study HfV2 [14,15,16,25,26], leading to controversial results regarding the stability of the cubic C15 structure. While some report that the cubic HfV2 structure exhibits negative energies of formation of −15.7 [14] and −18.0 meV/atom [15] in the ground state, others obtain positive energies of formation of 31.0 [27] and 34.8 meV/atom [28], respectively. Furthermore, theoretical studies conducted for cubic C15 ZrV2, as the stable phase above 116 K [29,30], yield solely positive energies of formation [26,31,32].
Hence, we systematically studied the effect of temperature as well as impurities of H and O on the stability of cubic C15 HfV2 using ab initio calculations. First, the ground state stability was investigated with respect to the energetic stability, evaluated based on the energy of formation, and the mechanical stability, studied by the calculated elastic constants compared to the Born stability criteria [33]. Second, the influence of temperature on both stability components was studied considering the contributions of the electronic entropy [33], as well as lattice vibrations, using the Debye–Grüneisen model [34,35]. Finally, we examined how the ground state stability is affected by interstitially dissolved H and O impurities in cubic C15 HfV2.
2. Methods
Calculations were performed within the framework of density functional theory (DFT) [36] as implemented in the Vienna ab initio simulation package (VASP) [37,38]. Projector augmented wave potentials were parameterized within the generalized-gradient approximation (GGA) by Perdew, Burke, and Ernzerhof (PBE) [39]. To support energetic stability data obtained utilizing GGA-PBE, additional ground state calculations were performed employing local density approximation (LDA) [40] (see Table 1). The ground state energy was obtained applying the Blöchl approach [41] and Brillouin zone integration was done on a converged 12 × 12 × 12 Monkhorst–Pack [42] k-point mesh for cubic HfV2, 23 × 23 × 15 for hexagonal Hf and 24 × 24 × 24 for bcc V. The total energy convergence criterion was <10−4 eV within a 500 eV cut-off. In cubic C15 HfV2, Hf atoms occupy 8a and V 16d Wyckoff sites [15] (origin choice 1). Configurations containing impurities were created by adding one H or O atom on the 96g Wyckoff site of the cell (see below), as the most favorable interstitial position for H in HfV2 [10]. For smaller impurity concentrations, a 2 × 2 × 1 supercell was employed and the k-point grid was adjusted accordingly. The resulting structures were relaxed by minimizing the interatomic forces prior to the determination of the equilibrium volumes and bulk moduli, which were all fitted according to the Birch–Murnaghan equation of state [43,44]. The energy of formation was calculated per atom by
where denotes the stoichiometric coefficients (negative for reactants; positive for products), the energy of the single constituents (bcc V, hexagonal Hf, gaseous H2 and O2) and the amount of atoms in the explored configuration.

Table 1.
Energy of formation Ef, lattice parameter a and elastic constants of cubic C15 HfV2.
Ground state elastic constants of hexagonal Hf were determined as proposed by Fast et al. [45]. For the cubic structures, volume conserving distortions were employed according to Music et al. [46], which were subsequently used to calculate the elastic moduli and Poisson´s ratio based on the Voigt–Reuss–Hill (VRH) approximation [47]. The electron density distributions were analyzed with VESTA software [48].
The influence of temperature on the energetic and mechanical stability of cubic HfV2 was studied based on the Helmholtz free energy exhibiting volume and temperature dependency, which can generally be expressed as
where denotes the electronic energy, the electronic entropy and the phonon vibrational free energy. The electronic entropy [33] is given by
with as the Fermi–Dirac distribution and as the density of states of the whole cell. By applying the frozen band approximation, , the electronic free energy is reduced to , with as the total ground state energy obtained from VASP calculations. The contribution of the phonon vibrational free energy was calculated within Debye theory according to Söderlind et al. [35] by
where is the Boltzmann constant and is the Debye temperature. The volume dependence was introduced into the calculation by extending the harmonic Debye theory with the Grüneisen theory, mimicking the anharmonic behavior of the lattice [34,35]. The input data for this model was obtained from VASP calculations except for Poisson´s ratio of cubic HfV2, which was taken to be 0.45 based on sound velocity measurements [1], as ground state elastic constants obtained within this work lead to an unphysical > 0.5 caused by mechanical instability at 0 K, which is further discussed in the Results section. For Hf and V, Poisson´s ratios of 0.25 and 0.4 were obtained herein. The Dugdale–McDonald approximation [49] was used to calculate the Grüneisen parameter. The electronic free energy and the vibrational free energy were evaluated between 100 and 1100 K in steps of 200 K to subsequently calculate the energy of formation as a function of temperature according to Equation (1).
Based on continuum elasticity theory, the isothermal elastic constants are given by the second order derivative of the Helmholtz free energy with respect to the deformation strain tensor [33]. Consequently, the temperature and volume dependency of the Helmholtz free energy is transferred to the elastic constants [50], enabling the calculation of elastic constants as a function of temperature. The approach conducted in this work, introduced by Huang et al. [50,51], was to treat these two contributions separately by keeping the other variable constant. Hence, the thermoelastic constants were calculated by
where describes the ground state elastic constant (, ), the volume dependent variations at constant temperature and the temperature dependent changes at constant volume. The contribution to the elastic constant caused by thermal expansion, , was determined at 0 K from a quadratic fit of the electronic energy vs. at volumes that correspond to the temperatures between 100 and 1100 K. In order to correlate the volume to the corresponding temperature, the linear thermal expansion coefficient of HfV2 was calculated by applying the Debye–Grüneisen model. An value of 8.4 × 10−6 1/K was obtained around 300 K, being in reasonable agreement with the experimental value of 9.9 × 10−6 1/K [52].
Due to the use of volume conserving distortions, the terms contribute equally to the overall free Helmholtz energy irrespective of the degree of distortion. Therefore, it is assumed that the contribution due to lattice vibrations does not affect the elastic constants within the Debye theory, which is widely accepted as a good approximation up to Debye temperature [35]. Thus, the vibrational energy contribution was neglected for the calculation of the thermoelastic constants and the overall temperature dependence of the elastic constant was reduced to the electronic free energy at equilibrium volume . Supplementary information about the approach can be found elsewhere [50,51,53,54].
3. Results and Discussion
3.1. Ground State Stability
First, the ground state stability of cubic HfV2 was investigated in terms of its energetic stability, evaluated based on the energy of formation , and its mechanical (also called structural, lattice or dynamic) stability, which can be analyzed based on the calculated elastic constants compared to the Born stability criteria [33]. For cubic lattice symmetry, an established formulation for these criteria is:
The results are summarized in Table 1.
Cubic C15 HfV2 exhibits a positive energy of formation of 32.7 meV/atom calculated using PBE exchange–correlation functionals. This result indicates an energetic instability at 0 K in agreement with other calculations based on plane waves [27,28]. In order to support the reliability of this result, additional calculations using local density approximation (LDA) were performed herein leading to a positive of 20.4 meV/atom. Thus, based on these results the decomposition of cubic HfV2 into bcc V and hexagonal Hf is energetically preferred at 0 K. However, this is contradictory to experimental findings where the decomposition has not been found for cubic HfV2 but a phase transformation of the cubic structure into a tetragonal and subsequently orthorhombic structure for decreasing temperatures from 112 to 102 K has been observed [5]. In order to test these structures for their ground state energetic stability, Ef was calculated resulting in values of 30.2 meV/atom for tetragonal and 30.1 meV/atom for orthorhombic HfV2. Hence, none of the experimentally observed structures of HfV2 exhibit a negative energy of formation. On the one hand, the expected decomposition into elemental V and Hf may be prevented by kinetic limitations at these low temperatures far below the melting points so that HfV2 remains as a metastable phase. On the other hand, it also needs to be considered that the obtained absolute energy differences of up to 50.7 meV/atom for the various calculations (see Table 1) may originate from inaccuracies of the employed codes. This notion is supported by the comparison to other calculations predicting energetic stability of the cubic phase using the all-electron linear muffin-tin orbital method (LMTO) with the LDA exchange–correlation functional with random phase approximation (RPA) parameters [14] and all-electron Wien2K calculations employing PBE [15]. However, similar calculations with Wien2K and PBE yield energetic instability of cubic HfV2 [28] in agreement with our results. Explicit treatment of strong correlation effects, as a potential explanation for the obtained discrepancies, is beyond the scope of this study as dynamic mean field theory is required and V exhibits on-site Coulomb repulsion dependent on the nearest neighbors [55,56,57]. Furthermore, addressing strong correlation effects may result in additional inconsistencies because the effective Hubbard potential may not be uniquely defined, as exemplified by Cr2AlC [58,59]. Nevertheless, the phase formation data obtained in this work are consistent with the experimentally reported sequence of phases as a function of temperature measured by high-resolution synchrotron X-ray diffraction [5]. In addition, comparable DFT results were reported for cubic C15 ZrV2, which is stable above 116 K [29,30], for which, to the best of our knowledge, exclusively positive energies of formations are reported [26,31,32].
Furthermore, the independent elastic constants , and were calculated to be 137, 146 and 0 GPa, respectively, leading to a of −4.5 GPa. Compared to the Born stability criteria for cubic symmetry [33], the two criteria and are violated, hence, revealing a mechanical instability of cubic HfV2 at 0 K in agreement with Krcmar et al. [25]. A direct comparison of the predicted ground state elastic constants to experimentally obtained values [1] is limited due to the pronounced temperature dependency of the elastic properties of cubic HfV2 [1,11,12]. At 200 K, Lüthi et al. [1] measured elastic constants of 13 and 17 GPa for and , respectively, (see Table 1) where the former further softens by almost 50% upon cooling until the transformation temperature (118 K) is reached. Hence, the results suggest that the experimentally observed transition from the cubic to tetragonal to orthorhombic structure [5] may be driven by a mechanical destabilization of the cubic structure with decreasing temperature. Furthermore, mechanical instability trough , denoted as the Born instability, is also reported for bcc Ti, Zr and Hf in the ground state, even though bcc is the equilibrium phase for all these metals above 1155, 1136 and 2030 K, respectively [60]. Thus, the calculations suggest that cubic C15 HfV2 exhibits both a mechanical and energetic instability in the ground state.
3.2. Temperature Effect on the Energetic Stability
In the following, the effect of temperature on the energetic stability is investigated. For this purpose, the energy of formation is calculated as a function of temperature considering the effect of the electronic entropy and lattice vibrations as illustrated in Figure 1.
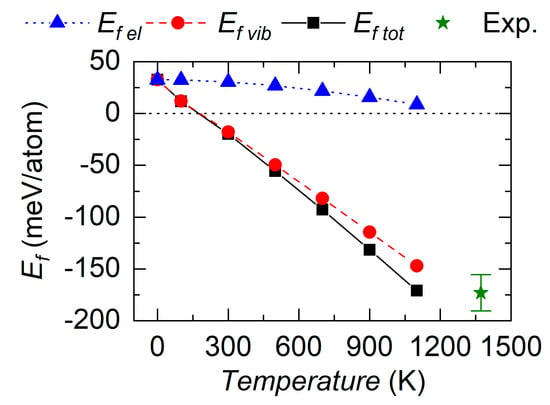
Figure 1.
Calculated energy of formation of cubic C15 HfV2 as a function of temperature by considering solely the electronic (triangles) and the vibrational energy (circles) contribution as well as the sum of both contributions (rectangles). High temperature calorimetry results (1373 K) are added for comparison [61].
The calculations show that both, lattice vibrations and electronic entropy, contribute to the stabilization of the cubic structure with lattice vibrations having a superior impact. Based on the electronic entropy only, remains positive in the investigated temperature range although it decreases continuously down to 9 meV/atom at 1100 K. Especially at temperatures up to 300 K, vibrational free energy exclusively yields the stabilization. A transition from energetically unstable to a stable system is obtained at around 150 K, which is in good agreement with experimental observations reporting cubic C15 HfV2 to be the stable phase above 112 K [1,17]. The results were further validated by extrapolation of the calculated energy of formation, yielding −225 meV/atom, to the measured result of −173 ± 18 meV/atom obtained at 1373 K by calorimetry [61].
3.3. Temperature Effect on the Mechanical Stability
In order to form a stable structure, not only energetic but also mechanical stability has to be achieved. Hence, the mechanical stability of cubic HfV2 was examined by predicting the temperature variation in the elastic constants and as depicted in Figure 2.
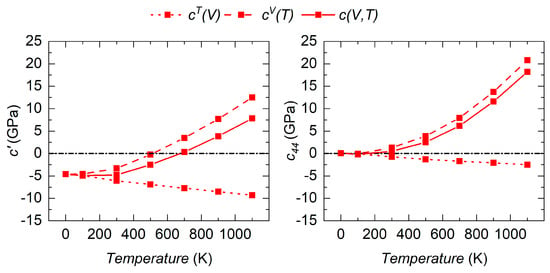
Figure 2.
Calculated thermoelastic constants of cubic C15 HfV2. The volume expansion contribution is shown by a dotted line, the intrinsic temperature dependency based on the electronic entropy is designated by a dashed line. The sum of both contributions is illustrated by the solid line.
The overall temperature behavior of and is composed of the volume dependent variation caused by volume expansion , as well as an intrinsic temperature dependency at constant volume (see Equation (5)). of cubic HfV2 shows a linear decline for both elastic constants, which may be rationalized by a reduction in bond strength induced by the increasing bond length upon expansion. This behavior corresponds to normal thermoelastic behavior [33]. The variation due to is superimposed by the intrinsic temperature dependency , for which an increase of and with temperature is predicted. The intrinsic temperature dependency originates from the electronic entropy, which is determined by electrons within a few around the Fermi level. The electronic structure calculations for HfV2 revealed a density of states of 2.5 states/atom eV at the Fermi level in good agreement with other calculations [6,10,13,14,15,16], that is, to the best of our knowledge, one of the highest values reported in the literature. In comparison, for Nb–Mo solid solutions, it has been shown that the intrinsic temperature dependency significantly affects the overall thermoelastic behavior mediated by ≥0.8 states/atom eV at the Fermi level [54]. As a result of both contributions, the calculated elastic constants and of cubic HfV2 exhibit a pronounced increase in both elastic constants with temperature, as found experimentally for these elastic constants [1] as well as for the elastic modulus [12]. At temperatures of ≥700 K, and fulfill the Born stability criteria for cubic symmetry demonstrating mechanical stabilization of the cubic structure induced by the electronic entropy. Deviations to the experimentally obtained formation range of cubic HfV2 (T ≥ 112 K) may originate from other factors influencing the low-temperature stability. A change in physical properties with time was reported for HfV2 when exposed to air, which is attributed to severe absorption of hydrogen into the cubic structure of HfV2 [12,22,30]. Furthermore, due to the high affinity for oxygen of the elemental constituents [18,19,20,21], the effect of O and H impurities on the stability of cubic C15 HfV2 was investigated.
3.4. Effect of Impurities on the Ground State Stability
Upon hydrogenation, cubic HfV2 shows no phase transformation but a pronounced storage capacity due to its 17 interstitial positions, which are classified as 8b, 32e and 96g Wyckhoff sites. For HfV2Hx (x = 1,2,3), it has been found that the g-site, in which hydrogen is surrounded by 2 Hf and 2 V atoms, is energetically preferred compared to the other sites [10]. Consequently, the 96g site was chosen for the incorporation of H as well as for O atoms into the structure (see below). The calculated ground state energy of formation of cubic HfV2 exhibiting O and H impurities is depicted in Figure 3 for impurity concentrations of 1 and 4 at%.
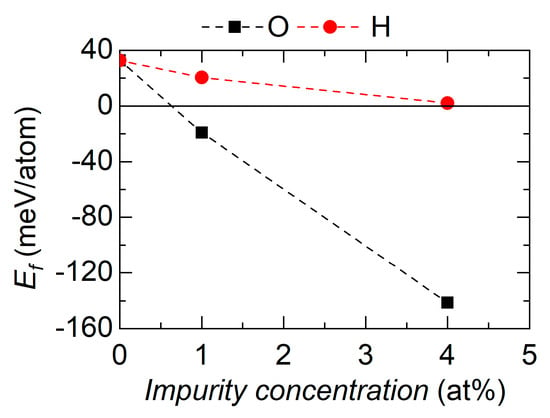
Figure 3.
Energy of formation Ef of cubic C15 HfV2 at 0 K as a function of interstitially incorporated oxygen and hydrogen.
The interstitial incorporation of 1 and 4 at% of O in the cubic HfV2 structure reduces the energy of formation to −19.0 and −141.4 meV/atom, respectively. Thus, the structure is thermodynamically stabilized at 0 K for oxygen concentrations as low as 1 at%. Upon addition of 1 and 4 at% of hydrogen, energies of formation of 20.4 and 2.0 meV/atom are obtained. Hence, hydrogen also contributes to the energetic stabilization of the cubic structure. In order to understand how these interstitials influence the ground state stability, the electronic structure is examined. Figure 4 contains the unit cell of cubic HfV2 with dissolved O and H as well as corresponding electron density distribution and calculated properties. Figure 4c shows the (110) electron density distribution, which cuts through the O and H impurity atom, respectively. The change in bulk modulus and lattice parameter of cubic HfV2 upon impurity incorporation is summarized in Figure 4b.
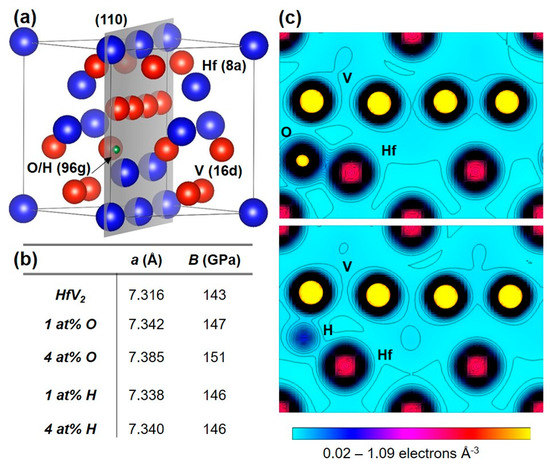
Figure 4.
(a) Unit cell of cubic C15 HfV2 with highlighted (110) plane. The Wyckoff position of the different species is given in brackets. (b) Calculated lattice parameter a and bulk modulus B of HfV2 with and without impurities. (c) Electron density distribution for HfV2 (110) containing an O (top panel) and H (bottom panel) impurity atom on the 96g site.
In the interatomic region far away from the impurity atom (see Figure 4c), the uniform distribution of electrons is observed showing a predominantly metallic character of the bonds. This coincides with the density of states at the Fermi level exhibiting 2.5 states/atom eV (see Section 3.3). Furthermore, neighboring V–V atoms indicate an overlap of electron densities representing covalent bonding in agreement with other theoretical studies [13,14,62]. In the region around the impurities, charge transfer and sharing between O–Hf and H–M (M = Hf, V), consistent with ionic and covalent interaction, respectively, is obtained. Investigations of HfO2 [63], HfH2 [64] or hydrogen containing V [65] support these findings. This implies that the formation of strong bonds eventually leads to the stabilization of the structure. This is consistent with the energy of formation data in Figure 3. The formation of strong bonds is also consistent with the change in the bulk modulus (Figure 4b), which increases gradually upon oxygen uptake from 143 to 151 GPa for 4 at% of O. Upon hydrogenation, an increase to 146 GPa for 1 and 4 at% of H is obtained. Furthermore, the lattice parameter also increases in both cases, with oxygen incorporation causing a larger lattice increase, as expected due to the larger atomic size of oxygen compared to hydrogen.
Finally, the influence of interstitially incorporated O and H on the mechanical stability of the cubic C15 structure was studied and compared to the impurity-free cell. The 0 K results are presented in Figure 5. By applying a c’-type lattice distortion to the impurity-free HfV2 structure, the ground state energy is decreased for distortions of up to ±2%, demonstrating the already discussed mechanical instability. The deformed cell corresponds to a tetragonal structure, as it was found experimentally as a low-temperature phase [5]. Upon -type distortion, the ground state energy is almost constant for distortions of up to ±2% leading to a of 0 GPa (see Table 1). Only for distortions >2%, a resistance of the cubic structure to the respective distortions is obtained. In contrast, for impurity concentrations of 1 at% O or H, the C15 structure is found to be mechanically stabilized, fulfilling both previously violated Born stability criteria for the cubic symmetry [33]. The calculated independent elastic constants , and are 175, 133 and 22 GPa, respectively, for cubic HfV2 containing 1 at% of O. For 1 at% of H in HfV2, elastic constant values of 171, 132 and 19 GPa, respectively, are obtained. The resulting elastic (Young´s) moduli EVRH are 61 and 55 GPa for concentrations of 1 at% of O and H, respectively.
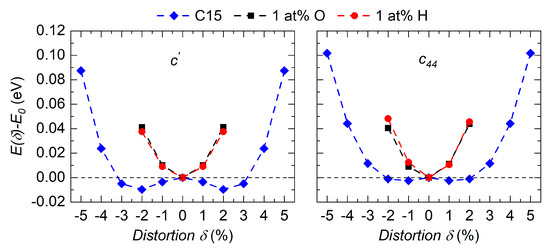
Figure 5.
Change in ground state energy of C15 HfV2 upon c’- (left panel) and c44-type (right panel) lattice distortions.
4. Conclusions
The energetic and mechanical stability of cubic C15 HfV2 was investigated considering the influence of temperature and interstitially solved O and H by applying DFT. In the ground state, cubic C15 HfV2 exhibits an energetic and mechanical instability facilitated by a positive energy of formation as well as a violation of the Born stability criteria. Combined Debye–Grüneisen and electronic entropy calculations indicate that the cubic structure is stabilized with increasing temperature primarily due to lattice vibrations. Furthermore, temperature dependent elastic constants were calculated, revealing an increase with temperature for and due to the electronic entropy induced by the high amount of states at the Fermi level of cubic HfV2, finally causing the mechanical stabilization of the defect-free structure with increasing temperature. Moreover, cubic C15 HfV2 can be energetically stabilized ( < 0) with 1 at% of O impurities incorporated interstitially. The incorporation of H also contributes to a decrease in energy of formation leading to an as low as 2 meV/atom for hydrogen concentrations of 4 at%. In addition, the interstitial incorporation of 1 at% of H or O results in the mechanical stabilization of HfV2 already at 0 K with all Born stability criteria for cubic symmetry being fulfilled. The impact of H and O on the stabilization of HfV2 may be rationalized by the formation of strong ionic–covalent bonds between impurities and metals. These results suggest that stabilization of cubic C15 HfV2 is achieved by a complex interplay of impurities potentially present in real compounds, lattice vibrations contributing to the energetic stabilization, and the electronic entropy supporting the mechanical stabilization.
Author Contributions
Conceptualization, P.K., D.M., M.S. and J.M.S.; methodology, P.K. and D.M.; investigation, P.K.; resources, J.M.S.; writing—original draft preparation, P.K.; writing—review and editing, P.K., D.M., M.S. and J.M.S.; visualization, P.K. and D.M.; project administration, J.M.S.
Funding
This research received no external funding.
Acknowledgments
Theoretical calculations were performed with computing resources granted by JARA HPC from RWTH Aachen University under Project No. JARA0131.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lüthi, B.; Herrmann, M.; Assmus, W.; Schmidt, H.; Rietschel, H.; Wühl, H.; Gottwick, U.; Sparn, G.; Steglich, F. Normal-state and superconducting properties of HfV2. Z. Phys. B Condens. Matter 1985, 60, 387–392. [Google Scholar] [CrossRef]
- Drymiotis, F.R.; Lashley, J.C.; Kimura, T.; Lawes, G.; Smith, J.L.; Thoma, D.J.; Fisher, R.A.; Phillips, N.E.; Mudryk, Y.; Pecharsky, V.K.; et al. Specific heat of single-crystal HfV2: Strong-coupling conventional superconductivity and the effect of the martensitic transition. Phys. Rev. B 2005, 72, 024543. [Google Scholar] [CrossRef]
- Dreßler, S.; Taylor, J.W.; Ouladdiaf, B.; Neumann, K.U.; Ziebeck, K.R.A. Suppression of the martensitic phase transition and the effect on superconductivity in HfV2. Solid State Commun. 2000, 113, 649–651. [Google Scholar] [CrossRef]
- Parsons, M.J.; Brown, P.J.; Crangle, J.; Neumann, K.U.; Ouladdiaf, B.; Smith, T.J.; Zayer, N.K.; Ziebeck, K.R.A. A study of the structural phase transformation and superconductivity in HfV2. J. Phys. Condens. Matter 1998, 10, 8523. [Google Scholar] [CrossRef]
- Zhao, Y.; Chu, F.; Von Dreele, R.B.; Zhu, Q. Structural phase transitions of HfV2 at low temperatures. Acta Crystallogr. Sect. B Struct. Sci. 2000, 56, 601–606. [Google Scholar] [CrossRef] [PubMed]
- Chu, F.; Thoma, D.J.; Mitchell, T.E.; Lin, C.L.; Šob, M. Phase stability of C15 MV2 (M=Zr, Hf or Ta): An electronic structure investigation. Philos. Mag. B 1998, 77, 121–136. [Google Scholar] [CrossRef]
- Forker, M.; Herz, W.; Simon, D.; Bedi, S.C. Perturbed-angular-correlation study of static and dynamic quadrupole interactions in the Laves-phase hydrides HfV2Hx. Phys. Rev. B 1995, 51, 15994–16007. [Google Scholar] [CrossRef]
- Däumer, W.; Khan, H.R.; Lüders, K. Electronic structure investigated by NMR and superconductivity of cubic Laves-phase hydrides: V2HfHx (0≤x≤4.5) and V2Hf0.5Zr0.5Hx(0≤x≤4.8). Phys. Rev. B 1988, 38, 4427–4436. [Google Scholar] [CrossRef]
- Heidinger, R.; Appel, H.; Then, G.; Thies, W.G. Observation of Radiation Damage in HfV2 and Its Hydrides by TDPAC. Phys. Status Solidi A 1990, 121, 445–454. [Google Scholar] [CrossRef]
- Radaković, J.; Belošević-Čavor, J.; Koteski, V. Hydrogen storage in Laves phases: First principles study of electronic structure and formation energies in HfV2 hydrides. Int. J. Hydrog. Energy 2013, 38, 9229–9235. [Google Scholar] [CrossRef]
- Finlayson, T.R.; Lanston, E.J.; Simpson, M.A.; Gibbs, E.E.; Smith, T.F. Elastic properties of (Hf,Zr)V2 superconducting compounds. J. Phys. F 1978, 8, 2269. [Google Scholar] [CrossRef]
- Balankin, A.S.; Skorov, D.M. Anomalies of elastic moduli in ZrV2 and HfV2 Laves phases at high temperatures. Sov. Phys. Solid State 1982, 24, 681–682. [Google Scholar]
- Zhang, C. Electronic structure and bonding properties for Laves-phase RV2 (R=Ti, Nb, Hf, and Ta) compounds. Phys. B 2008, 403, 2088–2092. [Google Scholar] [CrossRef]
- Ormeci, A.; Chu, F.; Wills, J.M.; Mitchell, T.E.; Albers, R.C.; Thoma, D.J.; Chen, S.P. Total-energy study of electronic structure and mechanical behavior of C15 Laves phase compounds: NbCr2 and HfV2. Phys. Rev. B 1996, 54, 12753–12762. [Google Scholar] [CrossRef]
- Charifi, Z.; Ali Hussain, R.; Baaziz, H. Electronic band structures of AV2 (A = Ta, Ti, Hf and Nb) Laves phase compounds. J. Phys. Condens. Matter 2009, 21, 025502. [Google Scholar] [CrossRef]
- Radaković, J.; Belošević-Čavor, J.; Koteski, V. First principles study of HfV2 and ZrV2 phases: Structural analysis and site preference of Cd and Ta dopants. Intermetallics 2013, 32, 90–95. [Google Scholar] [CrossRef]
- Rudy, E.; Windisch, S. The phase diagrams hafnium-vanadium and hafnium-chromium. J. Less-Common Met. 1968, 15, 13–27. [Google Scholar] [CrossRef]
- Morant, C.; Galán, L.; Sanz, J.M. An XPS study of the initial stages of oxidation of hafnium. Surf. Interface Anal. 1990, 16, 304–308. [Google Scholar] [CrossRef]
- Chourasia, A.R.; Hickman, J.L.; Miller, R.L.; Nixon, G.A.; Seabolt, M.A. X-Ray Photoemission Study of the Oxidation of Hafnium. Int. J. Spectrosc. 2009, 2009, 6. [Google Scholar] [CrossRef]
- Alov, N.; Kutsko, D.; Spirovová, I.; Bastl, Z. XPS study of vanadium surface oxidation by oxygen ion bombardment. Surf. Sci. 2006, 600, 1628–1631. [Google Scholar] [CrossRef]
- Romanyuk, A.; Oelhafen, P. Oxidation of vanadium with reactive oxygen plasma: A photoelectron spectroscopy study of the initial stages of the oxide growth process. Thin Solid Film. 2007, 515, 6544–6547. [Google Scholar] [CrossRef]
- Forker, M.; Herz, W.; Simon, D. Impurity trapping in the Laves phase HfV2 detected by perturbed angular correlations. J. Phys. Condens. Matter 1992, 4, 213. [Google Scholar] [CrossRef]
- Ivashchenko, V.I.; Turchi, P.E.A. Phonon softening and the phase transition in VN. Phys. Rev. B 2008, 78, 224113. [Google Scholar] [CrossRef]
- Stefanovich, E.V.; Shluger, A.L.; Catlow, C.R.A. Theoretical study of the stabilization of cubic-phase ZrO2 by impurities. Phys. Rev. B 1994, 49, 11560–11571. [Google Scholar] [CrossRef]
- Krčmar, M.; Fu, C.L. Effect of lattice anharmonicity in the structural phase transformation of Laves phase HfV2 alloy: A first-principles investigation. Acta Mater. 2013, 61, 7473–7480. [Google Scholar] [CrossRef]
- Chihi, T.; Fatmi, M.; Ghebouli, B. Ab Initio Calculations for Properties of Laves Phase V2M (M = Zr, Hf, Ta) Compounds. Am. J. Mod. Phys. 2013, 2, 88–92. [Google Scholar] [CrossRef]
- Levy, O.; Hart, G.L.W.; Curtarolo, S. Hafnium binary alloys from experiments and first principles. Acta Mater. 2010, 58, 2887–2897. [Google Scholar] [CrossRef]
- Vřešťál, J.; Pavlů, J.; Wdowik, U.D.; Šob, M. Modelling of phase equilibria in the Hf-V system below room temperature. J. Min. Metall. Sect. B Metall. 2017, 53, 239–247. [Google Scholar] [CrossRef][Green Version]
- Moncton, D.E. Lattice transformation in the superconductivity ZrV2 by neutron diffraction. Solid State Commun. 1973, 13, 1779–1782. [Google Scholar] [CrossRef]
- Smith, T.F.; Shelton, R.N.; Lawson, A.C. Superconductivity and structural instability of (Hf, Zr) V2 and (Hf, Ta) V2 alloys at high pressure. J. Phys. F 1973, 3, 2157. [Google Scholar] [CrossRef]
- Lumley, S.C.; Murphy, S.T.; Burr, P.A.; Grimes, R.W.; Chard-Tuckey, P.R.; Wenman, M.R. The stability of alloying additions in Zirconium. J. Nucl. Mater. 2013, 437, 122–129. [Google Scholar] [CrossRef]
- Widom, M. Prediction of Structure and Phase Transformations. In High-Entropy Alloys: Fundamentals and Applications; Gao, M.C., Yeh, J.-W., Liaw, P.K., Zhang, Y., Eds.; Springer: Cham, Germany, 2016; pp. 267–298. [Google Scholar] [CrossRef]
- Grimvall, G. Thermophysical Properties of Materials; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar] [CrossRef]
- Moruzzi, V.L.; Janak, J.F.; Schwarz, K. Calculated thermal properties of metals. Phys. Rev. B 1988, 37, 790–799. [Google Scholar] [CrossRef] [PubMed]
- Söderlind, P.; Nordström, L.; Yongming, L.; Johansson, B. Relativistic effects on the thermal expansion of the actinide elements. Phys. Rev. B 1990, 42, 4544–4552. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The Compressibility of Media under Extreme Pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Fast, L.; Wills, J.M.; Johansson, B.; Eriksson, O. Elastic constants of hexagonal transition metals: Theory. Phys. Rev. B 1995, 51, 17431–17438. [Google Scholar] [CrossRef] [PubMed]
- Music, D.; Takahashi, T.; Vitos, L.; Asker, C.; Abrikosov, I.A.; Schneider, J.M. Elastic properties of Fe–Mn random alloys studied by ab initio calculations. Appl. Phys. Lett. 2007, 91, 191904. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The Voigt-Reuss-Hill Approximation and Elastic Moduli of Polycrystalline MgO, CaF2, β-ZnS, ZnSe, and CdTe. J. Appl. Phys. 1967, 38, 2535–2540. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Dugdale, J.S.; MacDonald, D.K.C. The Thermal Expansion of Solids. Phys. Rev. 1953, 89, 832–834. [Google Scholar] [CrossRef]
- Huang, L.; Vitos, L.; Kwon, S.K.; Johansson, B.; Ahuja, R. Thermoelastic properties of random alloys from first-principles theory. Phys. Rev. B 2006, 73, 104203. [Google Scholar] [CrossRef]
- Huang, L.; Ramzan, M.; Vitos, L.; Johansson, B.; Ahuja, R. Anomalous temperature dependence of elastic constant c44 in V., Nb, Ta, Pd, and Pt. J. Phys. Chem. Solids 2010, 71, 1065–1068. [Google Scholar] [CrossRef][Green Version]
- Pushkarev, E.A.; Petrenko, N.S.; Finkel, V.A. Thermal expansion of the superconducting compound HfV2 at low temperatures. Phys. Status Solidi A 1978, 47, K145–K148. [Google Scholar] [CrossRef]
- Keuter, P.; Music, D.; Schnabel, V.; Stuer, M.; Schneider, J.M. From qualitative to quantitative description of the anomalous thermoelastic behavior of V, Nb, Ta, Pd and Pt. J. Phys. Condens. Matter 2019, 31, 225402. [Google Scholar] [CrossRef] [PubMed]
- Keuter, P.; Music, D.; Stuer, M.; Schneider, J.M. Electronic structure tuning of the anomalous thermoelastic behavior in Nb-X (X = Zr, V, Mo) solid solutions. J. Appl. Phys. 2019, 125, 215103. [Google Scholar] [CrossRef]
- Belozerov, A.S.; Poteryaev, A.I.; Anisimov, V.I. Evidence for strong Coulomb correlations in the metallic phase of vanadium dioxide. JETP Lett. 2011, 93, 70–74. [Google Scholar] [CrossRef]
- Isaacs, E.B.; Marianetti, C.A. Electronic correlations in monolayer VS2. Phys. Rev. B 2016, 94, 035120. [Google Scholar] [CrossRef]
- Tomczak, J.M.; Biermann, S. Multi-orbital effects in optical properties of vanadium sesquioxide. J. Phys. Condens. Matter 2009, 21, 064209. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.L.; Sun, Z.M.; Hashimoto, H.; Barsoum, M.W. Electron correlation effects in the MAX phase Cr2AlC from first-principles. J. Appl. Phys. 2011, 109, 063707. [Google Scholar] [CrossRef]
- Ramzan, M.; Lebègue, S.; Ahuja, R. Correlation effects in the electronic and structural properties of Cr2AlC. Phys. Status Solidi RRL 2011, 5, 122–124. [Google Scholar] [CrossRef]
- Grimvall, G.; Magyari-Köpe, B.; Ozoliņš, V.; Persson, K.A. Lattice instabilities in metallic elements. Rev. Mod. Phys. 2012, 84, 945–986. [Google Scholar] [CrossRef]
- Meschel, S.V.; Kleppa, O.J. The standard enthalpies of formation of some intermetallic compounds of transition metals by high temperature direct synthesis calorimetry. J. Alloy. Compd. 2006, 415, 143–149. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Z.; Wang, S.; Li, H.; Dong, J.; Xing, N.; Guo, Y.; Li, W. First-principles study of electronic structure for the Laves-phase compounds HfFe2 and HfV2. J. Alloy. Compd. 2008, 448, 53–58. [Google Scholar] [CrossRef]
- Jaffe, J.E.; Bachorz, R.A.; Gutowski, M. Low-temperature polymorphs of ZrO2 and HfO2: A density-functional theory study. Phys. Rev. B 2005, 72, 144107. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Duan, D.; Tian, F.; Liu, H.; Li, D.; Zhao, Z.; Sha, X.; Yu, H.; Zhang, H.; et al. First-principles study on the structural and electronic properties of metallic HfH2 under pressure. Sci. Rep. 2015, 5, 11381. [Google Scholar] [CrossRef] [PubMed]
- Aboud, S.; Wilcox, J. A Density Functional Theory Study of the Charge State of Hydrogen in Metal Hydrides. J. Phys. Chem. C 2010, 114, 10978–10985. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).