Abstract
ScMN2-type (M = V, Nb, Ta) phases are layered materials that have been experimentally reported for M = Ta and Nb, but they have up to now not been much studied. However, based on the properties of binary ScN and its alloys, it is reasonable to expect these phases to be of relevance in a range of applications, including thermoelectrics. Here, we have used first-principles calculations to study their thermodynamic stability, elastic, thermoelectric and electronic properties. We have used density functional theory to calculate lattice parameters, the mixing enthalpy of formation and electronic density of states as well as the thermoelectric properties and elastic constants (cij), bulk (B), shear (G) and Young’s (E) modulus, which were compared with available experimental data. Our results indicate that the considered systems are thermodynamically and elastically stable and that all are semiconductors with small band gaps. All three materials display anisotropic thermoelectric properties and indicate the possibility to tune these properties by doping. In particular, ScVN2, featuring the largest band gap exhibits a particularly large and strongly doping-sensitive Seebeck coefficient.
1. Introduction
MAX phases, where M is a transition metal, A is an A-group element and X is carbon and/or nitrogen, comprise a family of more than 70 compounds. Since the mid-1990s, there has been extensive research on MAX phases due to their unique combination of metallic and ceramic properties, manifested by their unusual combination of properties such as excellent thermal and electrical conductivities, ductility, resistance to thermal shock and oxidation. MAX phases can be used for a variety of applications, such as high temperature structural applications, protective coatings, sensors, low friction surfaces and electrical contacts [1,2,3,4,5,6]. The stoichiometry of a ternary MAX phase is Mn+1AXn, where n is 1,2 or 3 and the three different stoichiometries are referred to as 211 (n = 1), 312 (n = 2) and 413 (n = 3) [7,8].
A related structure to a 211 MAX phase is the ScTaN2- and ScNbN2-type structure. These phases have been observed experimentally [9,10,11], and a basic characterization of structure and some properties has been made. However, theoretical studies on these structures and how they relate to their physical properties are limited. Furthermore, ScVN2 is expected to exist based on thermodynamic stability calculations [12], but it has not been observed experimentally.
The structure of ScTaN2, ScNbN2 and ScVN2 can generally be described as the ScMN2-type structure [12], which has space group P63/mmc (#194) and comprises of alternating layers of ScN6/3 octrahedra and MN6/3 prisms. Sc occupies the 2a positions, M the 2d positions and N the 4f positions [11]. Table 1 shows experimentally characterized ScTaN2 and ScNbN2. Niewa et al. have also visualized the structure [11]. It can be noted that their positions are the inverse positions of a corresponding 211 MAX phase [1]. That is, the positions occupied by the M atoms in the 211 MAX structure correspond to the N positions in ScMN2. Because of this relationship to a MAX phase, we term this structure “inverse MAX phase” (in analogy with, e.g., inverse perovskites).

Table 1.
Atomic positions data and experimental lattice parameters (powder X-ray diffraction) of ScTaN2 [11] and ScNbN2 [9].
Furthermore, ScN is a semiconductor showing promise for thermoelectric applications due to its suitable thermal and electrical properties [12,13,14,15,16,17]. However, the thermal conductivity is relatively high (8–12 Wm−1K−1) [13,18], leading to a rather low thermoelectric figure of merit (ZT). Approaches to decrease the thermal conductivity include alloying [12,19,20,21], making artificial superlattices [22,23,24,25], or nanostructuring, as also exemplified for CrN [26]. In analogy with artificial superlattices, inherently nanolaminated materials like ScTaN2, ScNbN2 and ScVN2 could be of interest for this purpose. Assessing this, however, requires determining their structural and electronic properties, e.g., are they metallic or semiconductors? This motivates the present theoretical study of the material properties of the inverse MAX phases, in order to screen their possibility for thermoelectrics.
2. Computational Details
We consider the enthalpy of formation in order to estimate phase stability of ScMN2, where M is Ta, Nb or V, which is calculated as
Each enthalpy, H, is considered at zero pressure and the energy of each phase is taken at its equilibrium volume. For relaxation, the energy and force tolerance was 0.0001 eV and 0.001 eV/Å, respectively. To determine the thermodynamic stability, we consider as competing phases the experimentally known cubic (NaCl, B1) binary nitrides, as no other (ternary) phases are known in these systems. For the case of VN, it should be noted that, according to previous theoretical calculations [27], the energy at 0 K for WC-type VN is lower than that of the experimentally observed B1 VN phase. However, the cubic phase is expected to be stabilized by atomic vibration at higher temperatures, rendering it more stable than the WC-type phase. It is therefore more relevant to consider it as a competing phase here [28,29].
The calculations were performed using density functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP) [30,31,32,33]. Projector augmented wave basis sets [34] were used with a cutoff energy of 650 eV and the exchange–correlation potential was modeled with the generalized gradient approximation according to Perdew, Burke and Ernzerhof (PBE-GGA) [35]. For all systems, eight atom unit cells were used and 8 × 8 × 8 k-point mesh for energy calculations, while, for elastic calculations, 25 × 25 × 11 k-points mesh was used and an energy cutoff of 650 eV. The elastic tensor was determined in VASP from strain–stress relationships after the introduction of finite distortions in the lattice [36]. The magnitude of the strains was on the order of 0.015 Å.
Electronic density of states (DOS) was calculated with a plane wave cutoff of 650 eV, 17 × 17 × 5 k-point mesh and a plane. The tetrahedron method with Blöchl correction [37] for integration over the Brillouin zone was used in all DOS calculations. The value of the level broadening was 0.2 eV. The calculations of DOS were performed with both the PBE-GGA functional with a 24 × 24 × 24 k-points mesh and the Heyd–Scuseria–Ernzerhof hybrid functional (HSE06) [38] with a 17 × 17 × 5 k-point mesh, respectively.
Transport properties were evaluated using an ab initio approach combining the linearized augmented plane wave (LAPW) method as implemented in the Wien2k package [39] with the semiclassical BoltzTraP [40] code for evaluating the conductivity and Seebeck tensors. We first computed the electronic structures of ScMN2 by Wien2k using the lattice structures optimized previously by VASP. In these calculations, we employed the parameter RMTKmax = 7 as well as a dense mesh 105 k-points in the Brillouin zone. Our test calculations with RMTKmax = 9 showed little sensitivity of transport properties of this parameter. The transport integrals were subsequently evaluated from the converged Kohn–Sham band structure obtained by Wien2k using the BoltzTraP package [40].
3. Results and Discussion
Table 2 shows the calculated enthalpy of formation and calculated elastic constants of all three phases. For ScTaN2, the enthalpy of formation is –1.067 eV; for ScNbN2, it is −0.84 eV, and, for ScVN2, it is −0.22 eV. It can be noted that the enthalpy of formation, which is calculated with respect to binary rock salt B1 structures, is negative for all three systems. Generally, this is expected to be representative also for the Gibbs free energy i.e., when the effect of temperature is accounted for, as it is known to be valid for a wide range of layered phases [41]. The reservation should be stated that the energy of the competing B1 VN phase is likely underestimated, since it is stabilized by vibrational effects at higher temperature, as mentioned in the Computational details section. In addition, the elastic constants fulfill the elastic stability criteria C11 > |C12|, 2C213 < C33(C11 + C12), C44 > 0 and C11 − C12 > 0, which are necessary and sufficient conditions for a hexagonal structure [42]. Thus, it can be concluded that all three phases are thermodynamically stable relative to the considered competing phases. Because the conditions of elastic stability are also met, all three phases can exist.

Table 2.
Calculated enthalpy of formation, elastic constants, lattice parameters and fractional coordinate z of ScTaN2, ScNbN2 and ScVN2.
Table 2 furthermore reports the predicted hexagonal lattice parameters calculated with the energy relaxed with respect to volume of each phase. For ScNbN2, the lattice parameters are, a = 3.0824 Å and c = 10.6060 Å; for ScVN2, a = 2.9774 Å and c = 10.2591 Å; and, for ScTaN2, a = 3.0791 Å and c = 10.6254 Å. For the first and the third case, these results can be compared with earlier experimental determination based on X-ray powder diffraction in Table 1. The difference in lattice parameter of ScTaN2 and ScNbN2 is expected since the use of the PBE-GGA functional tends to overestimate lattice parameters [43,44].
Table 3 shows the bulk modulus (B) and the shear modulus (G) estimated by both the Voigt (subscript V) [45] and the Reuss (subscript R) [45,46] approximation. The difference between the two approximations is that Voigt’s assumes that the strain throughout the polycrystalline aggregate is uniform, while Reuss’ assumes uniform stress instead [45]. In the case of a hexagonal lattice, the Voigt shear modulus (GV) and the Voigt bulk modulus (BV) are:

Table 3.
Elastic (E), shear (G) and bulk (B) moduli estimated with Voigt (subscript V) and Reuss (subscript R) approximations.
The Reuss shear modulus (GR) and the Voigt bulk modulus (BR) are:
For the calculations of the Young’s modulus (E), we have, in both cases, used the following relation [45]:
To obtain a crude estimate of whether the materials can be expected to be ductile or brittle, the empirical Pugh’s criterion can be used, which suggests that, if G/B < 0.5, the material tends to be ductile [47]. In the case of the three studied material systems, none of them meets this criterion regardless if Reuss’ or Voigt’s approximation is used, which can be seen from Table 3. This implies that the materials are not expected to be ductile.
The elastic moduli of ScTaN2, ScNbN2 and ScVN2 can be compared to the elastic modulus of the MAX phase Ti2AlC that has a value of 277 GPa [48], which is a typical value for a MAX phase. As can be seen from Table 3, the three studied inverse MAX phases have elastic moduli in the interval from 432 to 479 GPa, which implies that the inverse MAX phases (at least in these three cases) are stiff materials and much stiffer than the regular MAX phases.
Figure 1, Figure 2 and Figure 3 show the electronic density of states (DOS) calculated for all three phases with the GGA-PBE functional as well as with the HSE06 hybrid functional [38]. The latter functional was used because the GGA functionals tend to underestimate bandgaps compared to experimental values [49], while hybrid functionals generally give more accurate bandgaps. For all three cases, when using the GGA-PBE functional, it was not obvious if the apparent bandgaps between occupied and empty states are real bandgaps or just pseudogaps. Using hybrid functionals, in contrast, it is clear that all three material systems exhibit small bandgaps. Other than the bandgaps, the structures of the density of states are very similar for PBE and HSE06. The bandgaps presented here are based on the calculations with hybrid functionals. In Appendix A, the energy band structures of the three phases are shown.
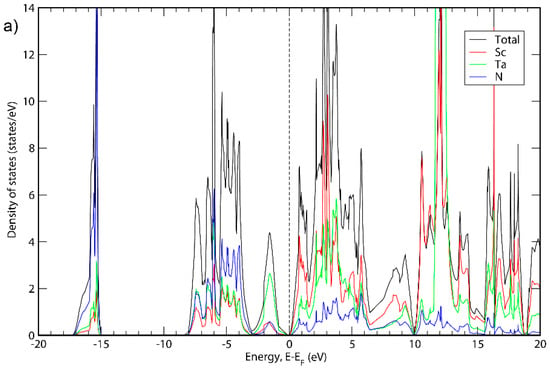

Figure 1.
Total DOS and DOS projections for ScTaN2 calculated with (a) GGA; (b) HSE06.
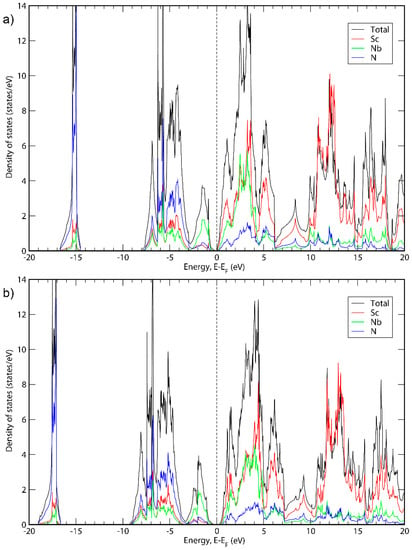
Figure 2.
Total DOS and DOS projections for ScNbN2 calculated with (a) GGA; (b) HSE06.

Figure 3.
Total DOS and DOS projections for ScVN2 calculated with (a) GGA; (b) HSE06.
It can be seen in Figure 1, Figure 2 and Figure 3 that the basic structure of the DOS is similar for all three material systems. The projected DOS indicated that the bands in the first peak of all three systems is mainly due to N. Furthermore, the main states around the top of the valence band are because of the presence of Ta, Nb or V for ScTaN2, ScNbN2 and ScVN2, respectively, while the main states around the bottom of the conduction band are in all three cases due to a mix of states originating from Sc and the M metal. For higher-level energies in the conduction band (above 5 eV), the contribution to the DOS for all three systems is mainly from the Sc states. These results are consistent with ScTaN2, where it has previously been shown that the first peak is mainly due to N (2p) states and the peak to the right of the chemical potential is due to Ta (5d) mixed with Sc (3d) states and the peak to the left of it is mainly due to Ta (5d) states [11].
Figure 1 shows the total DOS of ScTaN2 and the projected DOS of its elements calculated with the GGA-PBE functional (Figure 1a) and with the HSE06 functional (Figure 1b). The energy is adjusted so that the 0 eV corresponds to the highest occupied state. The bandgap calculated with HSE06 is 0.139 eV. Figure 2 shows the total DOS of ScNbN2 and the projected DOS of its elements calculated with the GGA-PBE functional (Figure 2a) and with the HSE06 functional (Figure 2b), showing a bandgap of 0.350 eV (HSE06). Figure 3 shows the total DOS of ScVN2 and the projected DOS of its elements calculated with the GGA-PBE functional (Figure 3a) and with the HSE06 functional (Figure 3b), showing a bandgap of 0.550 eV (HSE06). It can thus be concluded from here that ScTaN2, ScNbN2 and ScVN2 are all narrow-bandgap semiconductors, where ScTaN2 has the smallest bandgap and ScVN2 has the largest. The formation of a semiconductor bandgap in these compounds can be explained by a splitting of the d shell of M3+ ion in the trigonal prismatic crystal field. The lowest level of z2 symmetry is then completely filled in the case of d2 occupancy while the excited crystal-field levels are empty. The smallest bandwidth of 3d band in V3+ then leads to the largest band gap in ScVN2; the gap is progressively reduced with the d-band width increasing along the V → Nb → Ta sequence.
Experimentally, temperature-dependent transport measurements on ScTaN2 showed a metallic-like behavior by measurement of resistivity as a function of temperature, where it increased with temperature [11], but with high absolute values of resistivity. This is indicative of a highly doped degenerate semiconductor, typical also for ScN [13,14,17,19,50].
Previous calculations by Niewa et al. indicated a pseudogap in ScTaN2, but with the local density approximation (LDA), which underestimates bandgaps just like GGA. This is consistent with the here determined narrow bandgaps in ScMN2 (M = V, Nb, Ta), showing that all these materials are narrow-bandgap semiconductors. The bandgap is lower than the one in ScN (0.9 eV [51]). One can therefore expect quasimetallic behavior of the resistivity for ScMN2 with impurities and/or dopants (or antisite defects as observed in Ref. [11]) analogously with the case of ScN [16,50]. Thus, the electronic properties and electrical conductivity of the ScMN2 phases are at least qualitatively similar to those of ScN.
In order to obtain a qualitative estimate of the thermoelectric properties, we performed BoltzTraP calculations using the optimized lattice structures. The BoltzTraP code [40] implements the semiclassical Boltzmann theory of transport in the framework of the linearized augmented plane wave (LAPW) method Wien-2k [39]. Namely, by employing the approximation of a constant direction-independent relaxation time τ, the conductivity tensor can be written as
where is the group velocity alone the direction for the Kohn–Sham band and the vector of the Brillouin zone (BZ). The energy-projected conductivity tensor is then defined as
where is the Kohn–Sham band energy for the band and the BZ point , is the Dirac delta function. The transport tensors for given temperature and chemical potential are moments of the energy-projected conductivity tensors multiplied by the energy derivative of Fermi function :
where is the electric conductivity, and is the unit cell volume. The Seebeck coefficient tensor is given by
One immediately sees that, under the assumption of an energy and direction-independent relaxation time, the Seebeck coefficient is independent of τ and one may obtain its actual value by Equation (11). This approximation of energy and direction-independent relaxation time is employed by the BoltzTraP code [40]. The electrical conductivity is then proportional to τ. The estimation of relaxation time is not an objective of the present work; we thus calculated the ratio in order to determine the impact of band-structure evolution along the ScMN2 series on the electrical conductivity.
To capture the nonmetallic behavior of ScMN2 compounds in these calculations we employed the modified Becke–Johnson (mBJ) exchange-correlation potential [52], which is known to accurately reproduce semiconducting band gaps with a modest computational cost. Our DFT-mBJ calculations predict ScVN2 and ScNbN2 to be semiconducting with narrow band gaps of 0.135 eV and 0.046 eV, respectively. ScTaN2 is found to be metallic. The systematically smaller band gaps are thus predicted with the mBJ as compared to those obtained using the HSE06 hybrid functional. ScMN2 are apparently located at a metallic-semiconductor threshold with the value of the bandgap being very sensitive to the choice of exchange-correlation potential. However, the qualitative evolution towards a more metallic behavior upon the isoelectronic substitution V → Nb → Ta is reproduced by both approaches. Therefore, our calculations can be expected to capture a valid qualitative picture of the evolution of thermoelectric properties upon this substation, despite some uncertainty regarding the value of the bandgap.
Figure 4a shows the Seebeck tensor components Sxx and Szz at 290 K as a function of chemical potential for ScTaN2, ScNbN2 and ScVN2. The dependence vs. has been computed in the rigid band approximation using the band structure obtained for the undoped case by self-consistent calculations as described in the previous paragraph. The curves indicate that all three material systems are anisotropic. For instance, at the chemical potential 0, Sxx for all three materials is positive, while Szz is negative. This behavior—with an opposite sign of the Seebeck coefficient along the x-axis and z-axis—is analogous to that observed for the (metallic) Ti3SiC2 and Ti3GeC2 MAX phases, where the macroscopic Seebeck coefficient in randomly oriented bulk samples sum up to zero over a wide temperature range [3,53,54,55]. The opposite signs of Sxx and Szz in the undoped materials can be understood by noticing that the sign of Seebeck coefficient for a given direction α is determined by the shape of in the vicinity of μ—see Equations (10) and (11). Taking into account the fact that one sees that a positive (negative) Seebeck coefficient originates from a positive (negative) first moment of for being of the order of temperature. As is noted in our analysis of Figure 3, the z2 orbital forms the top of valence band, while other d orbitals mainly contribute to the empty d states just at the bottom of conduction one (see Figure 3 and the corresponding discussion of DOS). The z2 orbital should mostly contribute to the element of conductivity tensor (7), while the rest of d orbitals contributing more to the conductivity in the plane. Therefore, from Equations (7) and (8), one expects to be larger at the bottom of the conduction band than at the top of valence one; the opposite behavior is expected for . Such behaviors are indeed observed in our calculated and resulting in positive and negative , respectively, and thus in Sxx > 0 and Szz < 0.
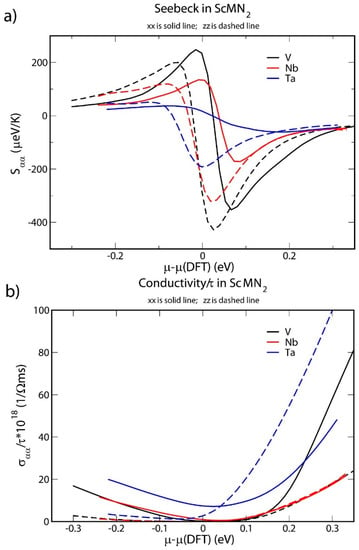
Figure 4.
(a) Seebeck tensor components Sxx and Szz as a function of chemical potential for ScMN2, where M is Ta, Nb or V; (b) σxx/τ and σzz/τ as a function of chemical potential for ScMN2, where M is Ta, Nb or V.
The maximum absolute values of the Seebeck components are high (in particular, more than 400 µV/K in ScVN2), suggesting that all three materials can be candidates for thermoelectric applications. The doping level (as indicated by the chemical potential) is predicted to change the sign of Seebeck coefficients, with a particular large sensitivity to the doping is again found in ScVN2. This indicates that both n- and p-type thermoelectric behavior could be obtained by an appropriate choice of dopants. Again, this is in analogy with ScN, which is n-type, but can be rendered p-type by sufficient doping with e.g., Mg [16,20,56].
Figure 4b shows the ratio of the conductivity-tensor components σxx and σzz to the relaxation time τ at 290 K as a function of chemical potential. The conductivity of undoped ScVN2 is low, as expected for a semiconductor. For ScNbN2, the predicted value of the gap is roughly of the same magnitude as the room-temperature energy, resulting in a noticeable thermally activated σxx but not σzz. Strong anisotropy can thus be noted also in this context. Furthermore, the electrical conductivity components, σxx and σzz, increase at chemical potential levels above 0 for all three material systems. That is, the electrical conductivity of the systems can also be increased by doping, and a tradeoff optimizing the power factor is possible.
4. Conclusions
We have used DFT calculations to investigate the mixing enthalpies, elastic properties, DOS, lattice parameters and thermoelectric properties of ScTaN2, ScNbN2 and ScVN2. The evaluated mixing enthalpy of formation and of elastic properties indicate that all three systems are thermodynamically as well as elastically stable.
The DOS calculations show that all three systems have small band gaps suggesting that they are narrow-bandgap semiconductors. The band gaps are smaller than, for instance, the band gap of ScN and a quasimetallic behavior can be expected. Finally, the three systems are found to have anisotropic thermoelectric properties and the results indicate that their thermoelectric properties can be tuned by doping.
Author Contributions
Conceptualization, P.E.; Supervision, P.E. and S.S., Software and computational design, R.P., I.M., and L.P.; Formal Analysis, R.P. and L.P.; Writing-Original Draft Preparation, R.P.; Writing-Review & Editing, P.E., L.P. and R.P.; Visualization, R.P. and L.P.; Project Administration, R.P.; Funding Acquisition, P.E., S.S. and L.P.
Funding
This research was funded by the Swedish Research Council (VR) through project Grant No. 2016-03365, the Knut and Alice Wallenberg Foundation through the Academy Fellows Program, the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-Liu No. 2009 00971) and the European Research Council through Grant No. ERC-319286-QMAC.
Acknowledgments
The calculations were performed using computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC). We would also like to thank Weine Olovsson at the NSC for giving practical guidance about the calculations.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A
Figure A1, Figure A2 and Figure A3 show the energy band structure of ScTaN2, ScNbN2 and ScVN2 calculated with PBE-GGA. It can be noted that one or two bands in each graph intersect the energy level 0 at the Γ-point, corresponding to a pseudogap as described in the main text. In Figure A1, the M-point also intersects the energy level at zero. However, the GGA-PBE functional underestimates the bandgap. The difference, if the bands were to be calculated with a hybrid functional, is that the bands would be displaced from the zero level, opening a bandgap (with values as stated in the main text) at the Γ-point.
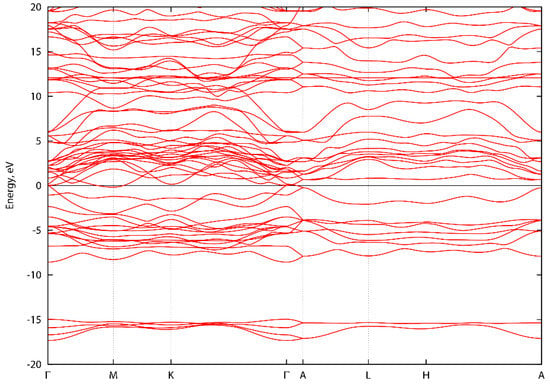
Figure A1.
Energy band structure of ScTaN2 along high symmetry directions.
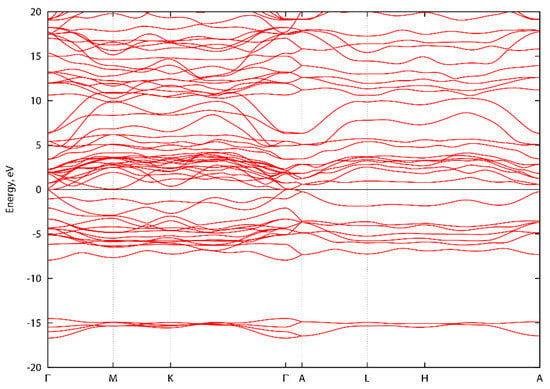
Figure A2.
Energy band structure of ScNbN2 along high symmetry directions.
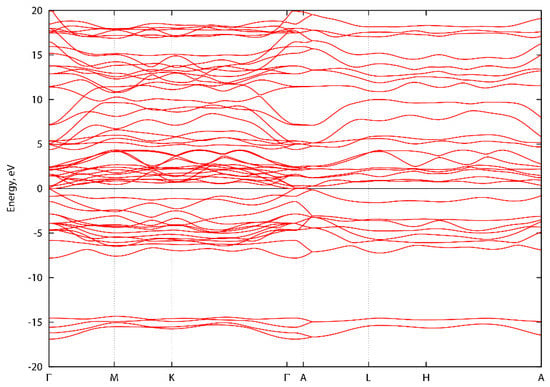
Figure A3.
Energy band structure of ScVN2 along high symmetry directions.
References
- Eklund, P.; Beckers, M.; Jansson, U.; Högberg, H.; Hultman, L. The Mn+1AXn phases: Materials science and thin-film processing. Thin Solid Films 2010, 518, 1851–1878. [Google Scholar] [CrossRef]
- Eklund, P.; Rosén, J.; Persson, P.O.A. Layered ternary Mn+1AXn phases and their 2D derivative MXene: An overview from a thin-film perspective. J. Phys. D 2017, 50, 113001. [Google Scholar] [CrossRef]
- Magnuson, M.; Mettesini, M. Chemical Bonding and Electronic-Structure in MAX phases as Viewed by X-ray Spectroscopy and Density Functional Theory. Thin Solid Films 2017, 621, 108–130. [Google Scholar] [CrossRef]
- Radovic, M.; Barsoum, M.W. MAX phases: Bridging the gap between metals and ceramics. Am. Ceram. Soc. Bull. 2013, 92, 20–27. [Google Scholar]
- Sun, Z.M. Progress in research and development on MAX phases: a family of layered ternary compounds. Int. Mater. Rev. 2013, 56, 143–166. [Google Scholar] [CrossRef]
- Wang, X.H.; Zhou, Y.C. Layered Materials and Electrically Conductive Ti2AlC and Ti3AlC2 Ceramics: A Review. J. Mater. Sci. Technol. 2010, 26, 385–416. [Google Scholar] [CrossRef]
- Barsoum, M.W. The MN+1AXN Phases: A New Class of Solids; Thermodynamically Stable Nanolaminates. Prog. Solid State 2000, 28, 201–281. [Google Scholar] [CrossRef]
- Barsoum, M.W. The MAX Phases: Unique New Carbide and Nitride Materials. Am. Sci. 2001, 89, 334–343. [Google Scholar] [CrossRef]
- Lengauer, W. The Crystal Structure of ScNbN1-x and Comparisons with Related Nitride and Carbide Structures. J. Solid State Chem. 1989, 82, 186–191. [Google Scholar] [CrossRef]
- Lengauer, W.; Ettmayer, P. THE CRYSTAL STRUCTURE OF ScTaN1-x. J. Less Common Met. 1988, 141, 157–162. [Google Scholar] [CrossRef]
- Niewa, R.; Zherebtsov, D.A.; Schnelle, W.; Wagner, F.R. Metal-Metal Bonding in ScTaN2. A New Compound in the System ScN-TaN. Inorg. Chem. 2004, 43, 6188–6194. [Google Scholar] [PubMed]
- Kerdsongpanya, S.; Alling, B.; Eklund, P. Phase stability of ScN-based solid solutions for thermoelectric applications from first-principles calculations. J. Appl. Phys. 2013, 114, 073512. [Google Scholar] [CrossRef]
- Burmistrova, P.V.; Maassen, J.; Favaloro, T.; Saha, B.; Salamat, S.; Rui Koh, Y.; Lundstrom, M.S.; Shakouri, A.; Sands, T.D. Thermoelectric properties of epitaxial ScN films deposited by reactive magnetron sputtering onto MgO(001) substrates. Appl. Phys. 2013, 113, 153704. [Google Scholar] [CrossRef]
- Burmistrova, P.V.; Zakharov, D.N.; Favaloro, T.; Mohammed, A.; Stach, E.A.; Shakouri, A.; Sands, T.D. Effect of deposition pressure on the microstructure and thermoelectric properties of epitaxial ScN(001) thin films sputtered onto Mgo(001) substrates. J. Mater. Res. 2015, 30, 626–634. [Google Scholar] [CrossRef]
- Gall, D.; Petrov, I.; Hellgren, N.; Hultman, L.; Sundgren, J.E.; Greene, J.E. Growth of poly- and single-crystal ScN on MgO(001): Role of low-energy N+2 irradiation in determining texture, microstructure evolution, and mechanical properties. J. Appl. Phys. 1998, 84, 6034–6041. [Google Scholar] [CrossRef]
- Kerdsongpanya, S.; Alling, B.; Eklund, P. Effect of point defects on the electronic density of states of ScN studied by first-principles calculations and implications for thermoelectric properties. Phys. Rev. B 2012, 86, 195140. [Google Scholar] [CrossRef]
- Le Febvrier, A.; Tureson, N.; Stilkerich, N.; Greczynski, G.; Eklund, P. Effect of impurities on morphology, growth mode, and thermoelectric properties of (111) and (001) epitaxial-like ScN films. J. Phys. D Appl. Phys. 2019, 52, 035302. [Google Scholar] [CrossRef]
- Kerdsongpanya, S.; Hellman, O.; Sun, B.; Koh, Y.K.; Lu, J.; Van Nong, N.; Simak, S.I.; Alling, B.; Eklund, P. Phonon thermal conductivity of scandium nitride for thermoelectrics from first-principles calculations and thin-film growth. Phys. Rev. B 2017, 96, 195417. [Google Scholar] [CrossRef]
- Kerdsongpanya, S.; Sun, B.; Eriksson, F.; Jensen, J.; Lu, J.; Koh, Y.K.; Nong, N.V.; Balke, B.; Alling, B.; Eklund, P. Experimental and theoretical investigation of Cr1-xScxN solid solutions for thermoelectrics. J. Appl. Phys. 2016, 120, 215103. [Google Scholar] [CrossRef]
- Saha, B.; Garbrecht, M.; Perez-Taborda, J.A.; Fawey, M.H.; Koh, Y.R.; Shakouri, A.; Martin-Gonzalez, M.; Hultman, L.; Sands, T.D. Compensation of native donor doping in ScN: Carrier concentration control and p-type ScN. Appl. Phys. Lett. 2017, 110, 252104. [Google Scholar] [CrossRef]
- Tureson, N.; Van Nong, N.; Fournier, D.; Singh, N.; Acharya, S.; Schmidt, S.; Belliard, L.; Soni, A.; Eklund, P. Reduction of the thermal conductivity of the thermoelectric material ScN by Nb alloying. J. Appl. Phys. 2017, 122, 025116. [Google Scholar] [CrossRef]
- Rawat, V.; Koh, Y.K.; Cahill, D.G.; Sands, T.D. Thermal conductivity of (Zr,W)N/ScN metal/semiconductor multilayers and superlattices. J. Appl. Phys. 2009, 105, 024909. [Google Scholar] [CrossRef]
- Saha, B.; Koh, Y.R.; Comparan, J.; Sadasivam, S.; Schroeder, J.L.; Garbrecht, M.; Mohammed, A.; Birch, J.; Fisher, T.; Shakouri, A.; et al. Cross-plane thermal conductivity of (Ti;W)N/(Al,Sc)N metal. Phys. Rev. B 2016, 93, 045311. [Google Scholar] [CrossRef]
- Schroeder, J.L.; Saha, B.; Garbrecht, M.; Schell, N.; Sands, T.D.; Birch, J. Thermal stability of epitaxial cubic-TiN/(Al,Sc)N metal/semiconductor superlattices. J. Mater. Sci. 2015, 50, 3200. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Bian, Z.; Singh, R.; Shakouri, A.; Wortman, R.; Rawat, V.; Sands, T. Thermoelectric Transport in a ZrN/ScN Superlattice. J. Elctron Mater. 2009, 38, 960–963. [Google Scholar] [CrossRef]
- Gharavi, M.A.; Kerdsongpanya, S.; Schmidt, S.; Eriksson, F.; Nong, N.V.; Lu, J.; Balke, B.; Fournier, D.; Belliard, L.; le Febvrier, A.; et al. Microstructure and thermoelectric properties of CrN and CrN/Cr2N thin films. J. Phys. D 2018, 51, 355302. [Google Scholar] [CrossRef]
- Ravi, C. First-principles study of ground-state properties and phase stability of vanadium nitrides. CALPHAD 2009, 33, 469–477. [Google Scholar] [CrossRef]
- Grumski, M.; Dholabhai, P.P.; Adams, J.B. Ab initio study of the stable phases of 1:1 tantalum nitride. Acta Mater. 2013, 61, 3799–3807. [Google Scholar] [CrossRef]
- Mei, A.B.; Hellman, O.; Wireklint, N.; Schlepuetz, C.M.; Sangiovanmi, D.; Alling, B.; Rockett, A.; Hultman, L.; Petrov, I.; Greene, J.E. Dynamic and structural stability of cubic vanadium nitride. Phys. Rev. B 2015, 91, 054101. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 54, 11169. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B Condens. Matter Mater. Phys. 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamis simulation of the liquid-metal-amorphous-semiconductor transition in germaniium. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, F.; Ernzerhof, M. Generalized Gradient Approxiamtion Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.; Kvasnicka, D.; Luitz, J. WIEN2k, An augmented Plane Wave + Local Orbitals for Calculating Crystal Properteis; Techn. Universität Wien: Vienna, Austria, 2001. [Google Scholar]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Thore, A.; Dahlqvist, M.; Alling, B.; Rosén, J. Temperature dependent phase stability of nanolaminated ternaries from first-principles calculations. Comput. Mater. Sci. 2014, 91, 251–257. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Haas, P.; Tran, F.; Blaha, P. Calculation of the lattice constant of solids with semilocal functionals. Phys. Rev. B 2009, 79, 085109. [Google Scholar] [CrossRef]
- Schimka, L.; Harl, J.; Kresse, G. Improved hybrid functional for solids: the HSEsol functional. J. Chem. Phys. 2011, 134, 024116. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristrallen auf der Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 55. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. Ser. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Barsoum, M.W. Mechanical properties of the MAX Phases. Annu. Rev. Mater. Res. 2011, 41, 195–227. [Google Scholar] [CrossRef]
- Bagayoko, D. Understanding density functional theory (DFT) and completing it in practice. AIP Adv. 2014, 4, 127104. [Google Scholar] [CrossRef]
- Kerdsongpanya, S.; Nong, N.V.; Pryds, N.; Žukauskaitė, A.; Jensen, J.; Birch, J.; Lu, J.; Hultman, L.; Wingqvist, G.; Eklund, P. Anomalously high thermoelectric power factor in epitaxial ScN thin films. Appl. Phys. Lett. 2011, 99, 132113. [Google Scholar] [CrossRef]
- Lambrecht, W.R.L. Electronic structure and optical spectra of the semimetal ScAs and of the indirect-band-gap semiconductors ScN and GdN. Phys. Rev. B 2000, 62, 13538. [Google Scholar] [CrossRef]
- Tran, F.; Blaha, P. Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef]
- Chaput, L.; Hug, G.; Pécher, P.; Scherrer, H. Thermopower of the 312 MAX phases Ti3 Si C2, Ti3 Ge C2 and Ti3 Al C2. Phys. Rev. B 2007, 75, 035107. [Google Scholar] [CrossRef]
- Chaput, L.; Hug, G.; Pécher, P.; Scherrer, H. Anisotropy and thermopower in Ti3SiC2. Phys. Rev. B 2005, 71, 121104. [Google Scholar] [CrossRef]
- Yoo, H.-I.; Barsoum, M.W.; El-Raghy, T. Ti3SiC2 has negligible thermopower. Nature 2000, 407, 581–582. [Google Scholar] [CrossRef]
- Saha, B.; Perez-Taborda, J.A.; Bahk, J.-H.; Koh, Y.R.; Shakouri, A.; Martin-Gonzalez, M.; Sands, T.D. Temperature-dependent thermal and thermoelectric properties of n-type and p-type Sc1-xMgxN. Phys. Rev. B 2018, 97, 085301. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).