The Magnetic Properties of 1111-type Diluted Magnetic Semiconductor (La1−xBax)(Zn1−xMnx)AsO in the Low Doping Regime
Abstract
1. Introduction
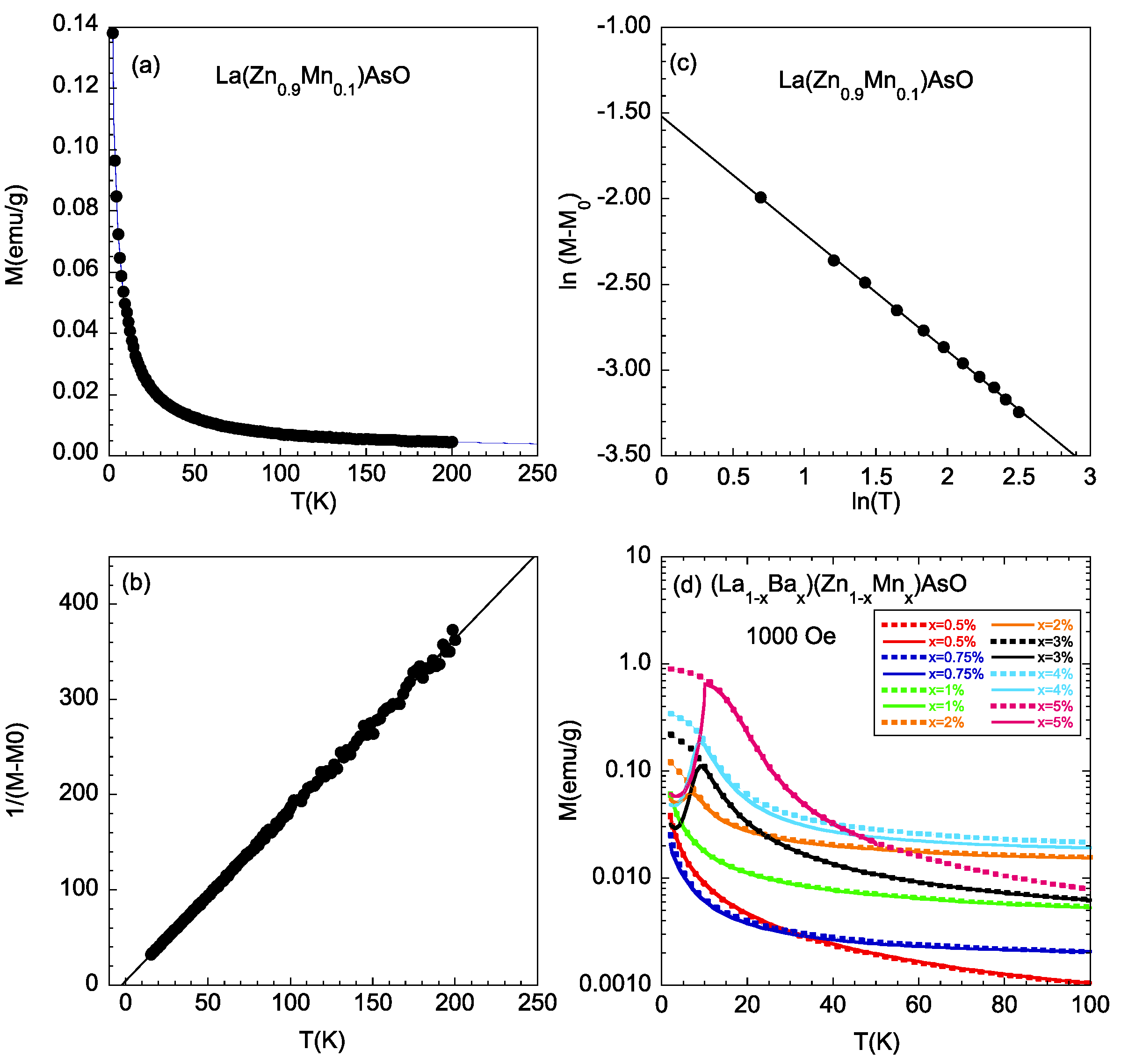
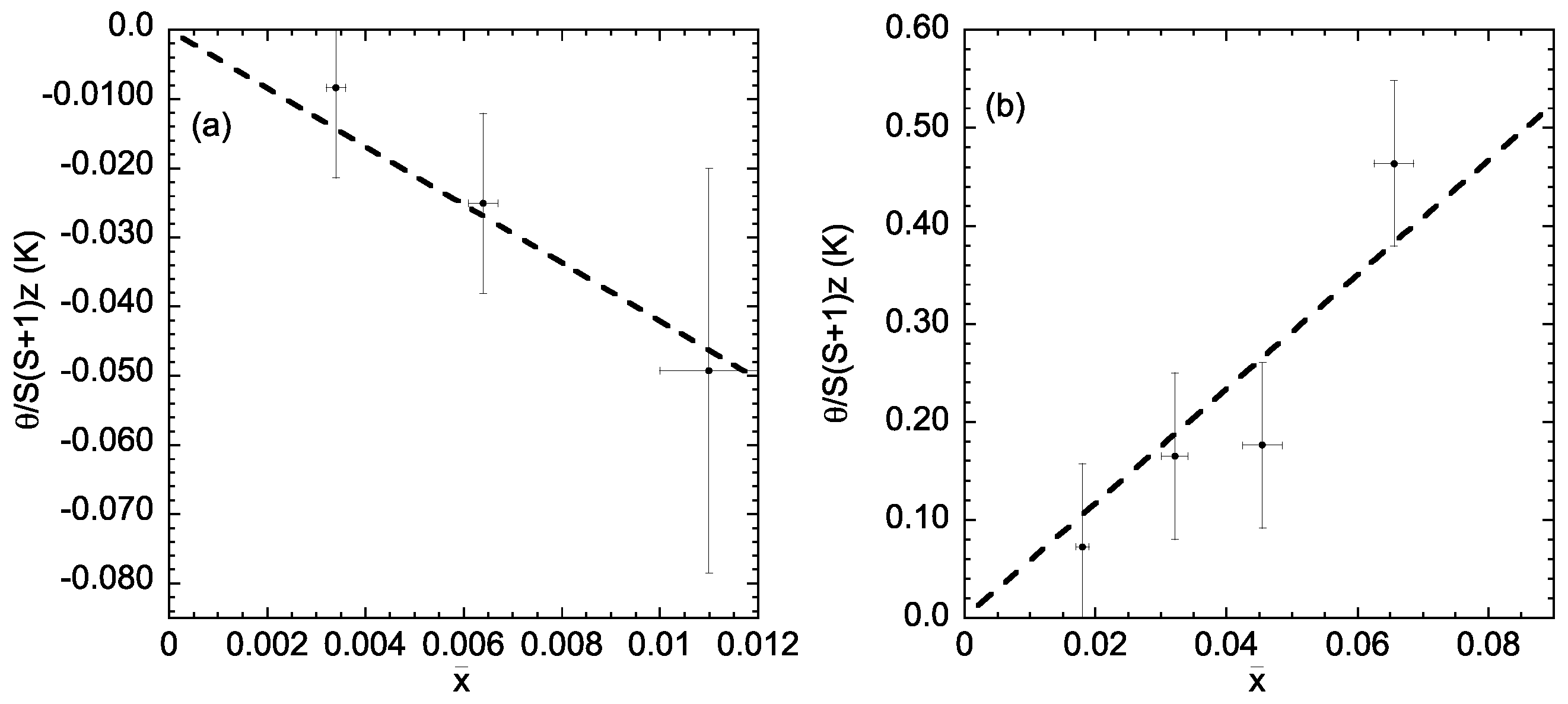
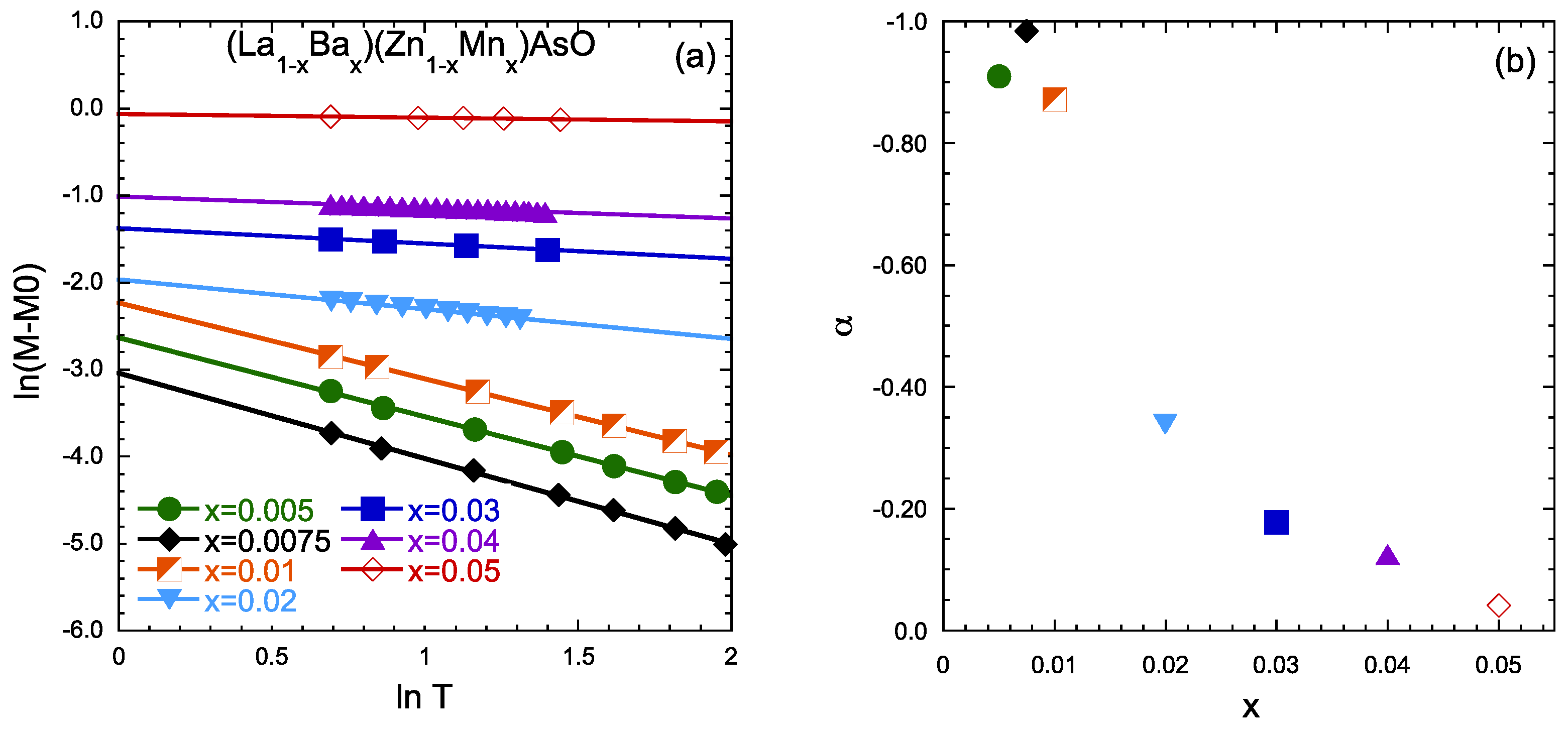
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DMSs | Diluted Magnetic Semiconductors |
| SR | Muon Spin Relaxation |
| NMR | Nuclear Magnetic Resonance |
| RKKY | Ruderman–Kittel–Kasuya–Yosida |
| BMP | Bound Magnetic Polaron |
| FC | Field Cooling |
| ZFC | Zero Field Cooling |
References
- Furdyna, J.K. Diluted magnetic semiconductor. J. Appl. Phys. 1988, 64, R29. [Google Scholar] [CrossRef]
- Zutic, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef]
- Jungwirth, T.; Sinova, J.; Masek, J.; Kucera, J.; MacDonald, A.H. Theory of ferromagnetic (III,Mn)V semiconductors. Rev. Mod. Phys. 2006, 78, 809–864. [Google Scholar] [CrossRef]
- Munekata, H.; Ohno, H.; von Molnar, S.; Segmüller, A.; Chang, L.L.; Esaki, L. Diluted magnetic III-V semiconductors. Phys. Rev. Lett. 1989, 63, 1849. [Google Scholar] [CrossRef] [PubMed]
- Ohno, H.; Shen, A.; Matsukura, F.; Oiwa, A.; Endo, A.; Katsumoto, S.; Iye, Y. (Ga,Mn)As: A new diluted magnetic semiconductor based on GaAs. Appl. Phys. Lett. 1996, 69, 363–365. [Google Scholar] [CrossRef]
- Samarth, N. A model ferromagnetic semiconductor. Nat. Mater. 2010, 9, 955–956. [Google Scholar] [PubMed]
- Chambers, S. Is it really intrinsic ferromagetism? Nat. Mater. 2010, 9, 956–957. [Google Scholar] [PubMed]
- Dietl, T. A ten-year perspective on dilute magnetic semiconductors and oxides. Nat. Mater. 2010, 9, 965–974. [Google Scholar] [CrossRef] [PubMed]
- Dietl, T.; Ohno, H. Diluted ferromagnetic semiconductors: Physics and spintronic structures. Rev. Mod. Phys. 2014, 86, 187–251. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, H.; Matsukura, F.; Cibert, J.; Ferrand, D. Zener Model Description of Ferromagnetism in Zinc-Blende Magnetic Semiconductors. Science 2000, 287, 1019–1022. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Campion, R.P.; Rushforth, A.W.; Edmonds, K.W.; Foxon, K.W.; Gallagher, B.L. Achieving high Curie temperature in (Ga,Mn)As. Appl. Phys. Lett. 2008, 93, 132103. [Google Scholar] [CrossRef]
- Chen, L.; Yan, S.; Xu, P.F.; Wang, W.Z.; Deng, J.J.; Qian, X.; Ji, Y.; Zhao, J.H. Low-temperature magnetotransport behaviors of heavily Mn-doped (Ga,Mn)As films with high ferromagnetic transition temperature. Appl. Phys. Lett. 2009, 95, 182505. [Google Scholar] [CrossRef]
- Chen, L.; Yang, X.; Yang, F.H.; Zhao, J.H.; Misuraca, J.; Xiong, P.; Molnar, S.V. Enhancing the Curie temperature of ferromagnetic semiconductor (Ga,Mn)As to 200 K via nanostructure engineering. Nano. Lett. 2011, 11, 2584–2589. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Jin, C.Q.; Liu, Q.Q.; Wang, X.C.; Zhu, J.L.; Feng, S.M.; Chen, L.C.; Yu, R.C.; Arguello, C.; Goko, T.; et al. Li(Zn,Mn)As as a new generation ferromagnet based on a I-II-V semiconductor. Nat. Commun. 2011, 2, 422–426. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Zhao, K.; Gu, B.; Han, W.; Zhu, J.L.; Wang, X.C.; Li, X.; Liu, Q.Q.; Yu, R.C.; Goko, T.; et al. Diluted ferromagnetic semiconductor Li(Zn,Mn)P with decoupled charge and spin doping. Phys. Rev. B 2013, 88, 081203(R). [Google Scholar] [CrossRef]
- Wang, Q.; Man, H.Y.; Ding, C.; Gong, X.; Guo, S.L.; Wang, H.D.; Chen, B.; Ning, F.L. Li1.1(Zn1−xCrx)As: Cr doped I-II-V diluted magnetic semiconductors in bulk form. J. Appl. Phys. 2014, 115, 083917. [Google Scholar] [CrossRef]
- Ning, F.L.; Man, H.Y.; Gong, X.; Guo, S.L.; Ding, C.; Wang, Q.; Goko, T.; Liu, L.; Frandsen, B.A.; Uemura, Y.J.; et al. Suppression of Tc by overdoped Li in the diluted ferromagnetic semiconductor Li1+y(Zn1−xMnx)P: A μSR investigation. Phys. Rev. B 2014, 90, 085123. [Google Scholar] [CrossRef]
- Zhao, K.; Deng, Z.; Wang, X.C.; Han, W.; Zhu, J.L.; Li, X.; Liu, Q.Q.; Yu, R.C.; Goko, T.; Frandsen, B.; et al. New diluted ferromagnetic semiconductor with Curie temperature up to 180 K and isostructural to the “122” iron-based superconductors. Nat. Commun. 2013, 4, 1442–1446. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Chen, B.J.; Zhao, G.Q.; Yuan, Z.; Liu, Q.Q.; Deng, Z.; Zhu, J.L.; Jin, C.Q. Ferromagnetism at 230 K in (Ba0.7K0.3)(Zn0.85Mn0.15)2As2 diluted magnetic semiconductor. Chin. Sci. Bull. 2014, 59, 2524–2527. [Google Scholar] [CrossRef]
- Yang, X.J.; Li, Y.K.; Zhang, P.; Luo, Y.K.; Chen, Q.; Feng, C.M.; Cao, C.; Dai, J.H.; Tao, Q.; Cao, G.H.; et al. K and Mn co-doped BaCd2As2: A hexagonal structured bulk diluted magnetic semiconductor with large magnetoresistance. J. Appl. Phys. 2013, 114, 223905. [Google Scholar] [CrossRef]
- Ding, C.; Man, H.Y.; Qin, C.; Lu, J.C.; Sun, Y.L.; Wang, Q.; Yu, B.Q.; Feng, C.M.; Goko, T.; Arguello, C.J.; et al. (La1−xBax)(Zn1−xMnx)AsO.: A two-dimensional 1111-type diluted magnetic semiconductor in bulk form. Phys. Rev. B 2013, 88, 041102(R). [Google Scholar] [CrossRef]
- Ding, C.; Gong, X.; Man, H.Y.; Zhi, G.X.; Guo, S.L.; Zhao, Y.; Wang, H.D.; Chen, B.; Ning, F.L. The suppression of Curie temperature by Sr doping in diluted ferromagnetic semiconductor (La1−xSrx)(Zn1−yMny)AsO. Eur. Phys. Lett. 2014, 107, 17004. [Google Scholar] [CrossRef]
- Han, W.; Zhao, K.; Wang, X.C.; Liu, Q.Q.; Ning, F.L.; Deng, Z.; Liu, Y.; Zhu, J.L.; Ding, C.; Man, H.Y.; et al. Diluted ferromagnetic semiconductor (LaCa)(Zn,Mn)SbO isostructural to “1111” type iron pnictide superconductors. Sci. China-Phys. Mech. Astron. 2013, 56, 2026–2030. [Google Scholar] [CrossRef]
- Ding, C.; Guo, S.L.; Zhao, Y.; Man, H.Y.; Fu, L.C.; Gu, Y.L.; Wang, Z.Y.; Liu, L.; Frandsen, B.A.; Cheung, S.; et al. The synthesis and characterization of 1111 type diluted ferromagnetic semiconductor (La1−xCax)(Zn1−xMnx)AsO. J. Phys. Condens. Matter 2016, 28, 026003. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.C.; Man, H.Y.; Ding, C.; Wang, Q.; Yu, B.Q.; Guo, S.L.; Wang, H.D.; Chen, B.; Han, W.; Jin, C.Q.; et al. The synthesis and characterization of 1111-type diluted magnetic semiconductors (La1−xSrx)(Zn1−xTMx)AsO (TM = Mn, Fe, Co). Eur. Phys. Lett. 2013, 103, 67011. [Google Scholar] [CrossRef]
- Yang, X.J.; Li, Y.K.; Shen, C.Y.; Si, B.Q.; Sun, Y.L.; Tao, Q.; Cao, G.H.; Xu, Z.A.; Zhang, F.C. Sr and Mn Co-doped LaCuSO: A wide band gap oxide diluted magnetic semiconductor with TC around 200 K. Appl. Phys. Lett. 2013, 103, 022410. [Google Scholar] [CrossRef]
- Man, H.Y.; Qin, C.; Ding, C.; Wang, Q.; Gong, X.; Guo, S.L.; Wang, H.D.; Chen, B.; Ning, F.L. (Sr3La2O5)(Zn1−xMnx)2As2: A bulk form diluted magnetic semiconductor isostructural to the “32522” Fe-based superconductors. Eur. Phys. Lett. 2014, 105, 67004. [Google Scholar] [CrossRef]
- Guo, S.L.; Ning, F.L. Progress of novel diluted ferromagnetic semiconductors with decoupled spin and charge doping: Counterparts of Fe-based superconductors. Chin. Phys. B 2018, 27, 097502. [Google Scholar] [CrossRef]
- Dunsiger, S.R.; Carlo, J.P.; Goko, T.; Nieuwenhuys, G.; Prokscha, T.; Suter, A.; Morenzoni, E.; Chiba, D.; Nishitani, Y.; Tanikawa, T.; et al. Spatially homogeneous ferromagnetism of (Ga,Mn)As. Nat. Mater. 2010, 9, 299–303. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Qin, C.; Man, H.Y.; Imai, T.; Ning, F.L. NMR investigation of the diluted magnetic semiconductor Li(Zn1−xMnx)P (x = 0.1). Phys. Rev. B 2013, 88, 041108(R). [Google Scholar] [CrossRef]
- Kusrayev, Y.G.; Kavokin, K.V.; Astakhov, G.V.; Ossau, W.; Molenkamp, L.W. Bound magnetic polarons in the very dilute regime. Phys. Rev. B 2008, 77, 085205. [Google Scholar] [CrossRef]
- Gorska, M.; Anderson, J.R. Magnetic susceptibility and exchange in IV-VI compound diluted magnetic semiconductors. Phys. Rev. B 1988, 38, 9120. [Google Scholar] [CrossRef]
- Anderson, J.R.; Gorska, M.; Azevedo, L.J.; Venturini, E.L. Magnetization of Hg1−xMnxTe. Phys. Rev. B 1986, 33, 4706. [Google Scholar] [CrossRef]
- Andres, K.; Bhatt, R.N.; Goalwin, P.; Rice, T.M.; Walstedt, R.E. Low-temperature magnetic susceptibility of Si: P in the nonmetallic region. Phys. Rev. B 1981, 24, 244. [Google Scholar] [CrossRef]
- Murayama, C.T.; Clark, W.G.; Sanny, J. Low-temperature magnetic properties of submetallic phosphorous-doped silicon. Phys. Rev. B 1984, 29, 6063. [Google Scholar] [CrossRef]
- Bhatt, R.N.; Lee, P.A. Scaling Studies of Highly Disordered Spin-½ Antiferromagnetic Systems. Phys. Rev. Lett. 1982, 48, 344. [Google Scholar] [CrossRef]
- Spal/ek, J.; Lewicki, A.; Tarnawski, Z.; Furdyna, J.K.; Galazka, R.R.; Obuszko, Z. Magnetic susceptibility of semimagnetic semiconductors: The high-temperature regime and the role of superexchange. Phys. Rev. B 1986, 33, 3407. [Google Scholar] [CrossRef]
- Karczewski, G.; von Ortenberg, M.; Wilamowski, Z.; Dobrowolski, W.; Niewodniczanska-Zawadzka, J. Magnetization of Pb1−xMnxS. Solid State Commun. 1985, 55, 249–252. [Google Scholar] [CrossRef]
- Braunstein, G.; Dresselhaus, G.; Heremans, J.; Partin, D. Magnetic properties of Pb1−xEuxTe grown by molecular-beam epitaxy. Phys. Rev. B 1987, 35, 1969. [Google Scholar] [CrossRef]
| x | (K) | 2J/k (K) | |
|---|---|---|---|
| 0.005 | 0.0064 ± 0.0003 | −0.9 ± 0.1 | −11.71 |
| 0.0075 | 0.0034 ± 0.0002 | −0.3 ± 0.1 | −7.47 |
| 0.01 | 0.011 ± 0.001 | −1.7 ± 0.2 | −13.45 |
| 0.02 | 0.018 ± 0.001 | 2.5 ± 0.2 | 12.12 |
| 0.03 | 0.032 ± 0.002 | 5.8 ± 0.1 | 15.44 |
| 0.04 | 0.046 ± 0.003 | 6.2 ± 0.1 | 11.64 |
| 0.05 | 0.066 ± 0.003 | 16.2 ± 0.2 | 21.22 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhi, G.; Wang, K.; Zhang, H.; Ding, C.; Guo, S.; Gu, Y.; Fu, L.; Ning, F.L. The Magnetic Properties of 1111-type Diluted Magnetic Semiconductor (La1−xBax)(Zn1−xMnx)AsO in the Low Doping Regime. Condens. Matter 2018, 3, 42. https://doi.org/10.3390/condmat3040042
Zhi G, Wang K, Zhang H, Ding C, Guo S, Gu Y, Fu L, Ning FL. The Magnetic Properties of 1111-type Diluted Magnetic Semiconductor (La1−xBax)(Zn1−xMnx)AsO in the Low Doping Regime. Condensed Matter. 2018; 3(4):42. https://doi.org/10.3390/condmat3040042
Chicago/Turabian StyleZhi, Guoxiang, Kai Wang, Haojie Zhang, Cui Ding, Shengli Guo, Yilun Gu, Licheng Fu, and F. L. Ning. 2018. "The Magnetic Properties of 1111-type Diluted Magnetic Semiconductor (La1−xBax)(Zn1−xMnx)AsO in the Low Doping Regime" Condensed Matter 3, no. 4: 42. https://doi.org/10.3390/condmat3040042
APA StyleZhi, G., Wang, K., Zhang, H., Ding, C., Guo, S., Gu, Y., Fu, L., & Ning, F. L. (2018). The Magnetic Properties of 1111-type Diluted Magnetic Semiconductor (La1−xBax)(Zn1−xMnx)AsO in the Low Doping Regime. Condensed Matter, 3(4), 42. https://doi.org/10.3390/condmat3040042





