The Study of Characteristic Environmental Sites Affected by Diverse Sources of Mineral Matter Using Compositional Data Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Compositional Data and Sample Space
2.2. Transformation of Compositional Data
2.3. Triangular Diagram Representation, Centering and Rescaling Technique
2.4. Perturbation Difference
2.5. Testing Hypothesis of Multivariare Normal Distribution
2.6. Testing Hypothesis about the Center and the Covariance Structure
3. Results and Discussion
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Anderson, J.O.; Thundiyil, J.G.; Stolbach, A. Clearing the air: A review of the effects of particulate matter air pollution on human health. J. Med. Toxicol. 2012, 8, 166–175. [Google Scholar] [CrossRef] [PubMed]
- Janssen, N.A.H.; World Health Organization. Health Effects of Black Carbon; World Health Organization, Regional Office for Europe: Copenhagen, Denmark, 2012; ISBN 978-92-890-0265-3. [Google Scholar]
- WHO (World Health Organization). Air Quality Guidelines: Global Update 2005: Particulate Matter, Ozone, Nitrogen Dioxide, and Sulfur Dioxide; World Health Organization, Regional Office for Europe: Geneva, Switzerland, 2006. [Google Scholar]
- Kelly, F.J.; Fussell, J.C. Size, source and chemical composition as determinants of toxicity attributable to ambient particulate matter. Atmos. Environ. 2012, 60, 504–526. [Google Scholar] [CrossRef]
- Heyder, J. Deposition of Inhaled Particles in the Human Respiratory Tract and Consequences for Regional Targeting in Respiratory Drug Delivery. Proc. Am. Thorac. Soc. 2004, 1, 315–320. [Google Scholar] [CrossRef] [PubMed]
- Pope, C.A., III; Dockery, D.W. Health effects of fine particulate air pollution: Lines that connect. J. Air Waste Manag. Assoc. 2006, 56, 709–742. [Google Scholar] [CrossRef] [PubMed]
- Caggiano, R.; D’Emilio, M.; Macchiato, M.; Ragosta, M. Experimental and statistical investigations on atmospheric heavy metals concentrations in an industrial area of Southern Italy. Nuovo Cimento C 2001, 24, 391–406. [Google Scholar]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of IPCC the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; ISBN 978-1-107-66182-0. [Google Scholar]
- Prospero, J.M.; Charlson, R.J.; Mohnen, V.; Jaenicke, R.; Delany, A.C.; Moyers, J.; Rahn, K. The atmospheric aerosol system: An overview. Rev. Geophys. 1983, 21, 1607–1629. [Google Scholar] [CrossRef]
- Haywood, J.; Boucher, O. Estimates of the direct and indirect radiative forcing due to tropospheric aerosols: A review. Rev. Geophys. 2000, 38, 513–543. [Google Scholar] [CrossRef]
- Prospero, J.M. African dust: Its large-scale transport over the Atlantic Ocean and its impact on the Mediterranean region. In Regional Climate Variability and Its Impacts in The Mediterranean Area; Springer: Dordrecht, The Netherlands, 2007; pp. 15–38. ISBN 978-1-4020-6429-6. [Google Scholar]
- Putaud, J.P.; Van Dingenen, R.; Alastuey, A.; Bauer, H.; Birmili, W.; Cyrys, J.; Flentje, H.; Fuzzi, S.; Gehrig, R.; Hansson, H.C.; et al. A European aerosol phenomenology–3: Physical and chemical characteristics of particulate matter from 60 rural, urban, and kerbside sites across Europe. Atmos. Environ. 2010, 44, 1308–1320. [Google Scholar] [CrossRef]
- Viana, M.; Kuhlbusch, T.A.J.; Querol, X.; Alastuey, A.; Harrison, R.M.; Hopke, P.K.; Winiwarter, W.; Vallius, M.; Szidat, S.; Prévôt, A.S.H.; et al. Source apportionment of particulate matter in Europe: A review of methods and results. J. Aerosol Sci. 2008, 39, 827–849. [Google Scholar] [CrossRef]
- Thorpe, A.; Harrison, R.M. Sources and properties of non-exhaust particulate matter from road traffic: A review. Sci. Total Environ. 2008, 400, 270–282. [Google Scholar] [CrossRef] [PubMed]
- Pant, P.; Harrison, R.M. Estimation of the contribution of road traffic emissions to particulate matter concentrations from field measurements: A review. Atmos. Environ. 2013, 77, 78–97. [Google Scholar] [CrossRef]
- Van Dingenen, R.; Raes, F.; Putaud, J.P.; Baltensperger, U.; Charron, A.; Facchini, M.C.; Decesari, S.; Fuzzi, S.; Gehrig, R.; Hansson, H.C.; et al. European aerosol phenomenology-1: Physical characteristics of particulate matter at kerbside, urban, rural and background sites in Europe. Atmos. Environ. 2004, 38, 2561–2577. [Google Scholar] [CrossRef]
- Colbeck, I. Environmental Chemistry of Aerosols; Blackwell Publishing Ltd.: Oxford, UK, 2008; ISBN 9781405139199. [Google Scholar]
- Liu, Y.; Zhang, S.; Fan, Q.; Wu, D.; Chan, P.; Wang, X.; Fan, S.; Feng, Y.; Hong, Y. Accessing the Impact of Sea-Salt Emissions on Aerosol Chemical Formation and Deposition over Pearl River Delta, China. Aerosol Air Qual. Res. 2015, 15, 2232–2245. [Google Scholar] [CrossRef]
- Caggiano, R.; Macchiato, M.; Trippetta, S. Levels, chemical composition and sources of fine aerosol particles (PM1) in an area of the Mediterranean basin. Sci. Total Environ. 2010, 408, 884–895. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, A.; Gupta, T. Chemical characterization and source apportionment of submicron (PM1) aerosol in Kanpur region, India. Aerosol Air Qual. Res. 2010, 10, 433–445. [Google Scholar] [CrossRef]
- Margiotta, S.; Lettino, A.; Speranza, A.; Summa, V. PM 1 geochemical and mineralogical characterization using SEM-EDX to identify particle origin–Agri Valley pilot area (Basilicata, southern Italy). Nat. Hazards Earth Syst. Sci. 2015, 15, 1551–1561. [Google Scholar] [CrossRef]
- Rogula-Kozłowska, W.; Rogula-Kupiec, P.; Mathews, B.; Klejnowski, K. Effects of road traffic on the ambient concentrations of three PM fractions and their main components in a large Upper Silesian city. Ann. Wars. Univ. Life Sci.-SGGW Land Reclam. 2013, 45, 243–253. [Google Scholar] [CrossRef]
- Matassoni, L.; Pratesi, G.; Centioli, D.; Cadoni, F.; Lucarelli, F.; Nava, S.; Malesani, P. Saharan dust contribution to PM10, PM2.5 and PM1 in urban and suburban areas of Rome: A comparison between single-particle SEM-EDS analysis and whole-sample PIXE analysis. J. Environ. Monit. 2011, 13, 732–742. [Google Scholar] [CrossRef] [PubMed]
- Makkonen, U.; Hellén, H.; Anttila, P.; Ferm, M. Size distribution and chemical composition of airborne particles in south-eastern Finland during different seasons and wildfire episodes in 2006. Sci. Total Environ. 2010, 408, 644–651. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Harrison, R.M. Pragmatic mass closure study for PM1.0, PM2.5 and PM10 at roadside, urban background and rural sites. Atmos. Environ. 2008, 42, 980–988. [Google Scholar] [CrossRef]
- Pérez, N.; Pey, J.; Querol, X.; Alastuey, A.; López, J.M.; Viana, M. Partitioning of major and trace components in PM10–PM2.5–PM1 at an urban site in Southern Europe. Atmos. Environ. 2008, 42, 1677–1691. [Google Scholar] [CrossRef]
- Chiari, M.; Del Carmine, P.; Lucarelli, F.; Marcazzan, G.; Nava, S.; Paperetti, L.; Prati, P.; Valli, G.; Vecchi, R.; Zucchiatti, A. Atmospheric aerosol characterisation by Ion Beam Analysis techniques: Recent improvements at the Van de Graaff laboratory in Florence. Nucl. Instrum. Methods Phys. Res. B 2004, 219, 166–170. [Google Scholar] [CrossRef]
- Chiari, M.; Lucarelli, F.; Mazzei, F.; Nava, S.; Paperetti, L.; Prati, P.; Valli, G.; Vecchi, R. Characterization of airborne particulate matter in an industrial district near Florence by PIXE and PESA. X-ray Spectrom. 2005, 34, 323–329. [Google Scholar] [CrossRef]
- Lim, S.; Lee, M.; Lee, G.; Kim, S.; Yoon, S.; Kang, K. Ionic and carbonaceous compositions of PM10, PM2.5 and PM1.0 at Gosan ABC Superstation and their ratios as source signature. Atmos. Chem. Phys. 2012, 12, 2007–2024. [Google Scholar] [CrossRef]
- Moreno, T.; Querol, X.; Alastuey, A.; Reche, C.; Cusack, M.; Amato, F.; Pandolfi, M.; Pey, J.; Richards, A.; Prévôt, A.S.H.; et al. Variations in time and space of trace metal aerosol concentrations in urban areas and their surroundings. Atmos. Chem. Phys. 2011, 11, 9415–9430. [Google Scholar] [CrossRef]
- Theodosi, C.; Grivas, G.; Zarmpas, P.; Chaloulakou, A.; Mihalopoulos, N. Mass and chemical composition of size-segregated aerosols (PM1, PM2.5, PM10) over Athens, Greece: Local versus regional sources. Atmos. Chem. Phys. 2011, 11, 11895–11911. [Google Scholar] [CrossRef]
- Speranza, A.; Caggiano, R.; Margiotta, S.; Trippetta, S. A novel approach to comparing simultaneous size-segregated particulate matter (PM) concentration ratios by means of a dedicated triangular diagram using the Agri Valley PM measurements as an example. Nat. Hazards Earth Syst. Sci. 2014, 14, 2727–2733. [Google Scholar] [CrossRef]
- Speranza, A.; Caggiano, R.; Margiotta, S.; Summa, V.; Trippetta, S. A clustering approach based on triangular diagram to study the seasonal variability of simultaneous measurements of PM10, PM2.5 and PM1 mass concentration ratios. Arab. J. Geosci. 2016, 9, 1–8. [Google Scholar] [CrossRef]
- Aitchison, J. The statistical analysis of compositional data (with discussion). J. R. Stat. Soc. Ser. B Stat. Methodol. 1982, 44, 139–177. [Google Scholar]
- Aitchison, J. The Statistical Analysis of Compositional Data; Chapman and Hall: London, UK, 1986; 416p, ISBN 0-412-28060-4. [Google Scholar]
- Pawlowsky-Glahn, V.; Buccianti, A. Visualization and modeling of sub-populations of compositional data: Statistical methods illustrated by means of geochemical data from fumarolic fluids. Int. J. Earth Sci. 2002, 91, 357–368. [Google Scholar] [CrossRef]
- Martín-Fernández, J.A.; Barceló-Vidal, C.; Pawlowsky-Glahn, V. Dealing with zeros and missing values in compositional datasets using nonparametric imputation. Math. Geol. 2003, 35, 253–278. [Google Scholar] [CrossRef]
- Buccianti, A.; Pawlowsky-Glahn, V. Statistical evaluation of compositional changes in volcanic gas chemistry: A case study. Stoch. Environ. Res. Risk Assess. 2006, 21, 25–33. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Buccianti, A. Compositional Data Analysis: Theory and Applications; John Wiley & Sons: Chichester, UK, 2011; ISBN 9780470711354. [Google Scholar]
- Buccianti, A.; Pawlowsky-Glahn, V. New perspectives on water chemistry and compositional data analysis. Math. Geol. 2005, 37, 703–727. [Google Scholar] [CrossRef]
- Visser, S.; Slowik, J.G.; Furger, M.; Zotter, P.; Bukowiecki, N.; Dressler, R.; Flechsig, U.; Appel, K.; Green, D.C.; Tremper, A.H.; et al. Kerb and urban increment of highly time-resolved trace elements in PM10, PM2.5 and PM1.0 winter aerosol in London during ClearfLo 2012. Atmos. Chem. Phys. 2015, 15, 2367–2386. [Google Scholar] [CrossRef]
- Putaud, J.P.; Van Dingenen, R.; Raes, F. Submicron aerosol mass balance at urban and semirural sites in the Milan area (Italy). JGR-Atmospheres 2002, 107, 8198. [Google Scholar] [CrossRef]
- Putaud, J.P.; Raes, F.; Van Dingenen, R.; Brüggemann, E.; Facchini, M.C.; Decesari, S.; Fuzzi, S.; Gehrig, R.; Hüglin, C.; Laj, P.; et al. A European aerosol phenomenology—2: Chemical characteristics of particulate matter at kerbside, urban, rural and background sites in Europe. Atmos. Environ. 2004, 38, 2579–2595. [Google Scholar] [CrossRef]
- Colbeck, I.; Nasir, Z.A.; Ahmad, S.; Ali, Z. Exposure to PM10, PM2.5, PM1 and carbon monoxide on roads in Lahore, Pakistan. Aerosol Air Qual. Res. 2011, 11, 689–695. [Google Scholar] [CrossRef]
- Vallius, M.J.; Ruuskanen, J.; Mirme, A.; Pekkanen, J. Concentrations and estimated soot content of PM1, PM2.5, and PM10 in a subarctic urban atmosphere. Environ. Sci. Technol. 2000, 34, 1919–1925. [Google Scholar] [CrossRef]
- Lundgren, D.A.; Hlaing, D.N.; Rich, T.A.; Marple, V.A. PM10/PM2.5/PM1 data from a trichotomous sampler. Aerosol Sci. Technol. 1996, 25, 353–357. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J. Compositional data and their analysis: An introduction. In Compositional Data Analysis in the Geosciences: From Theory to Practice; Special Publications; Buccianti, A., Mateu-Figueras, G., Pawlowsky-Glahn, V., Eds.; Geological Society: London, UK, 2006; Volume 264, pp. 1–10. [Google Scholar]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barceló-Vidal, C. Isometric logratio transformations for compositional data analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J.; Tolosana Delgado, R. Lecture Notes on Compositional Data Analysis. 2007. Available online: http://dugi-doc.udg.edu//handle/10256/297 (accessed on 8 February 2008).
- Graham, D.J.; Midgley, N.G. TECHNICAL COMMUNICATION-Graphical Representation of Particle Shape using Triangular Diagrams: An Excel Spreadsheet Method. Earth Surf. Processes Landf. 2000, 25, 1473–1478. [Google Scholar] [CrossRef]
- Comas-Cufí, M.; Thió-Henestrosa, S. CoDaPack 2.0: A stand-alone, multi-platform compositional software. In Proceedings of the CoDaWork’11: 4th International Workshop on Compositional Data Analysis, Sant Feliu de Guíxols, Girona, Spain, 10–13 May 2011. [Google Scholar]
- R Development Core Team R. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008; ISBN 3-900051-07-0. [Google Scholar]
- Buccianti, A.; Pawlowsky-Glahn, V.; Barceló-Vidal, C.; Jarauta-Bragulat, E. Visualization and modeling of natural trends in ternary diagrams: A geochemical case study. In Proceedings of the IAMG, Trondheim, Norway, 6–11 August 1999; Volume 99, pp. 139–144. [Google Scholar]
- Martín-Fernández, J.A.; Bren, M.; Barceló-Vidal, C.; Pawlowsky-Glahn, V. A measure of difference for compositional data based on measures of divergence. In Proceedings of the IAMG, Trondheim, Norway, 6–11 August 1999; Volume 99, pp. 211–216. [Google Scholar]
- Von Eynatten, H.; Pawlowsky-Glahn, V.; Egozcue, J.J. Understanding perturbation on the simplex: A simple method to better visualize and interpret compositional data in ternary diagrams. Math. Geol. 2002, 34, 249–257. [Google Scholar] [CrossRef]
- Aitchison, J.; Egozcue, J.J. Compositional data analysis: Where are we and where should we be heading? Math. Geol. 2005, 37, 829–850. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J.; Tolosana-Delgado, R. Modeling and Analysis of Compositional Data; John Wiley & Sons: Chichester, UK, 2015; ISBN 9781118443064. [Google Scholar]
- Stephens, M.A. EDF statistics for goodness of fit and some comparisons. J. Am. Stat. Assoc. 1974, 69, 730–737. [Google Scholar] [CrossRef]
- Aitchison, J. A Concise Guide to Compositional Data Analysis. In 2nd Compositional Data Analysis Workshop—CoDaWork’05; Universitat de Girona: Girona, Spain, 2005; Available online: http://ima.udg.edu/Activitats/CoDaWork05/A_concise_guide_to_compositional_data_analysis.pdf (accessed on 19 October 2015).
- Harrison, R.M.; Yin, J.; Mark, D.; Stedman, J.; Appleby, R.S.; Booker, J.; Moorcroft, S. Studies of the coarse particle (2.5–10 μm) component in UK urban atmospheres. Atmos. Environ. 2001, 35, 3667–3679. [Google Scholar] [CrossRef]
- Jones, A.M.; Harrison, R.M. Assessment of natural components of PM10 at UK urban and rural sites. Atmos. Environ. 2006, 40, 7733–7741. [Google Scholar] [CrossRef]
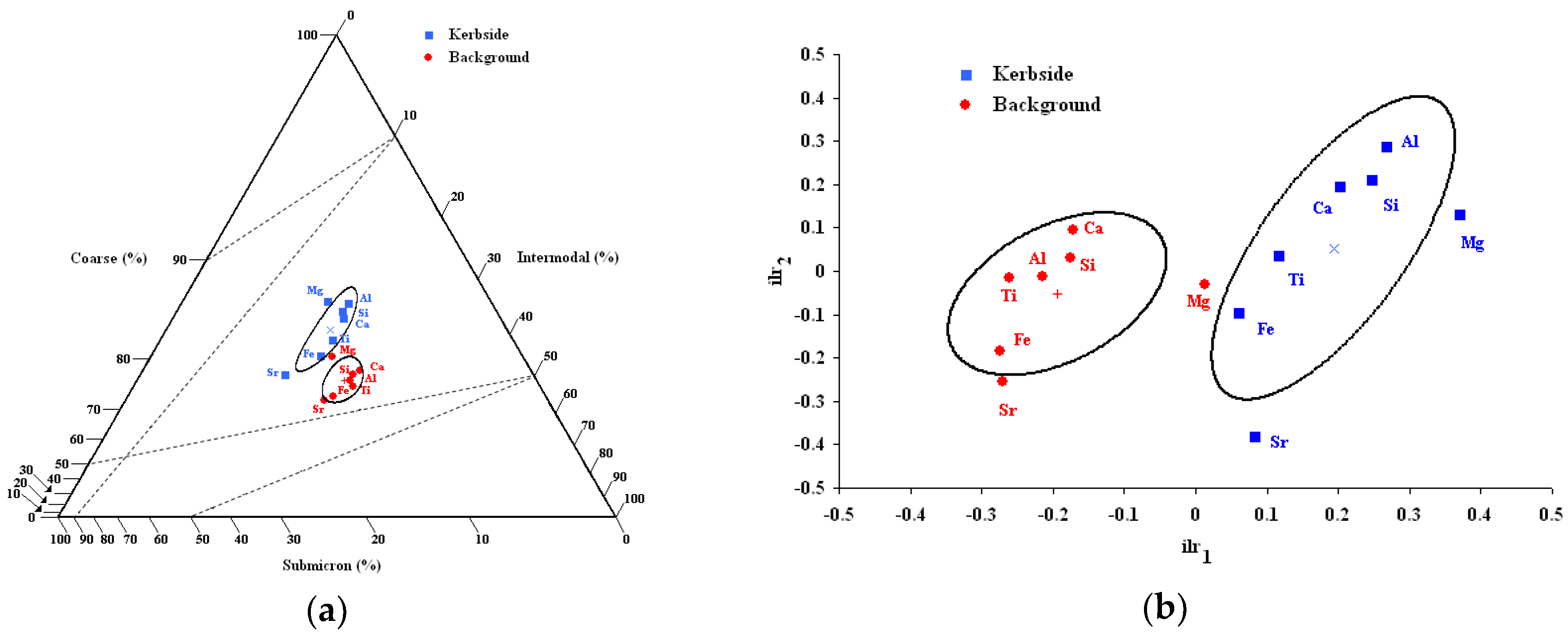
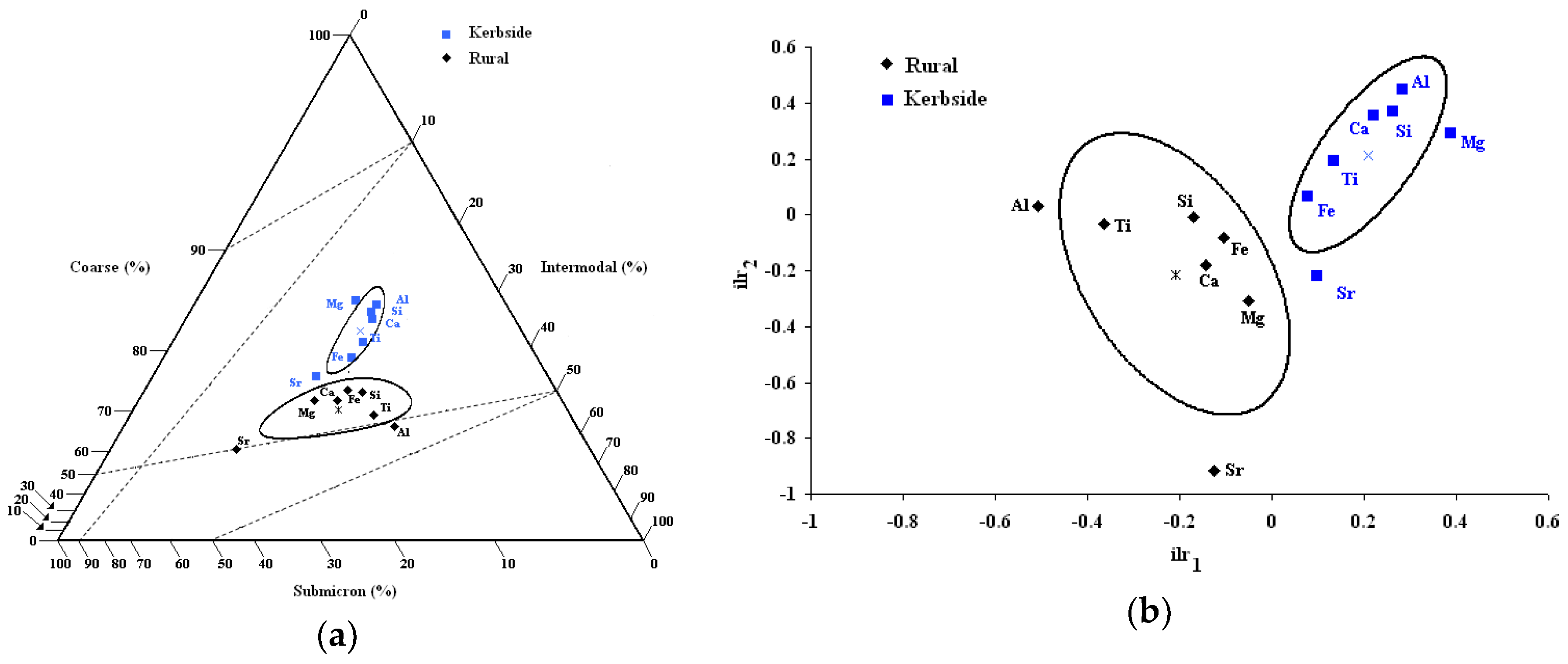
| Sites | Anderson–Darling | Cramer–von Mises | Watson |
|---|---|---|---|
| Rural | |||
| ilr1 marginal distribution | 0.6727 | 0.1260 | 0.1244 |
| ilr2 marginal distribution | 0.8657 | 0.1405 | 0.1377 |
| Bivariate angle test statistics | 1.7077 | 0.2927 | 0.0608 |
| Kerbside | |||
| ilr1 marginal distribution | 0.2821 | 0.0420 | 0.0419 |
| ilr2 marginal distribution | 0.4277 | 0.0646 | 0.0633 |
| Bivariate angle test statistics | 1.6273 | 0.3314 | 0.1293 |
| Background | |||
| ilr1 marginal distribution | 0.6848 | 0.1024 | 0.1004 |
| ilr2 marginal distribution | 0.4985 | 0.0951 | 0.0944 |
| Bivariate angle test statistics | 0.7345 | 0.0804 | 0.0510 |
| Hypothesis | Test Value | χ2 Critical Value (α = 0.05) | Degrees of Freedom | Significance |
|---|---|---|---|---|
| µ1 = µ2, ∑1 = ∑2 | 25.57 | 11.07 | 5 | 0.0001 |
| µ1 ≠ µ2, ∑1 = ∑2 | 2.70 | 7.81 | 3 | 0.4403 |
| µ1 = µ2, ∑1 ≠ ∑2 | - | 5.99 | 2 | - |
| Hypothesis | Test Value | χ2 Critical Value (α = 0.05) | Degrees of Freedom | Significance |
|---|---|---|---|---|
| µ1 = µ2, ∑1 = ∑2 | 27.26 | 11.07 | 5 | 0 |
| µ1 ≠ µ2, ∑1 = ∑2 | 8.42 | 7.81 | 3 | 0.0381 |
| µ1 = µ2, ∑1 ≠ ∑2 | 17.72 | 5.99 | 2 | 0.0001 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Speranza, A.; Caggiano, R.; Pavese, G.; Summa, V. The Study of Characteristic Environmental Sites Affected by Diverse Sources of Mineral Matter Using Compositional Data Analysis. Condens. Matter 2018, 3, 16. https://doi.org/10.3390/condmat3020016
Speranza A, Caggiano R, Pavese G, Summa V. The Study of Characteristic Environmental Sites Affected by Diverse Sources of Mineral Matter Using Compositional Data Analysis. Condensed Matter. 2018; 3(2):16. https://doi.org/10.3390/condmat3020016
Chicago/Turabian StyleSperanza, Antonio, Rosa Caggiano, Giulia Pavese, and Vito Summa. 2018. "The Study of Characteristic Environmental Sites Affected by Diverse Sources of Mineral Matter Using Compositional Data Analysis" Condensed Matter 3, no. 2: 16. https://doi.org/10.3390/condmat3020016
APA StyleSperanza, A., Caggiano, R., Pavese, G., & Summa, V. (2018). The Study of Characteristic Environmental Sites Affected by Diverse Sources of Mineral Matter Using Compositional Data Analysis. Condensed Matter, 3(2), 16. https://doi.org/10.3390/condmat3020016




